《23.4 相似多边形的性质》PPT课件
合集下载
《相似多边形》相似图形PPT 图文

示,镶在其外围的木质边框宽7.5cm。边框的
内外边缘所成的矩形相似吗?为什么?
E
3m
F
A
B
1.5m
(1.5+0.075 2)m
D
H
(3+0.075 2)m
1.5︰3≠1.65︰3.15
C G
直观有时是不可靠的
1、五边形ABCDE∽五边形 A´B´C´D´E´,则
∠ E=_80_°,∠ 中:①所有的正方形都相似;② 所有的矩形都相似;③所有的三角形都相似; ④所有的等腰三角形都相似;⑤所有的直角三 角形都相似;⑥所有的等腰直角三角形都相似; ⑦所有的等边三角形都相似;⑧所有的正五边 形都相似;其中正确的命题有_________ (填序号)
一块长3m、宽1.5m的矩形黑板如下图所
无论什么,我仍心怀感激,或许 你我只 是在人 生的烟 雨小巷 里,水 榭楼亭 旁一场 花的邂 逅,一 场流水 的情缘 。谢谢 你,曾 经来过 我的世 界,不 惊,不 扰!
如若有缘,总会有那么一个人, 即便跋 山涉水 ,历经 千辛万 苦,也 会向你 奔赴而 来;如若 有缘, 总会有 那么一 个人, 即便拨 开万千 人群, 拨开姹 紫嫣红 ,也会 站在光 阴的廊 桥上, 没有早 一步, 没有晚 一步, 只为在 最美的 季节里 ,与你 相遇相 知,与 你在时 光的铜 镜里勾 勒成一 个完 美的圆 。
10 正方形
8 矩形
10
(2)
12
答:不相似。因为虽然它们对应角相等, 但它们对应边不成比例。
2. 如果两个多边形不相似,那么它们的对应 角可能都相等吗? 对应边可能都成比例 吗?
答:如果两个多边形不相似,它们的对应角 可能都相等;如果两个多边形不相似,对应边 也可能成比例。
相似多边形 ppt课件

2
A´
6
E´
80°
五边形A´B´C´D´E´与五边形. ABCDE的相似比为_2:_1
C´
D´
E
2、如图:下面的两个菱形相似吗?为什么?
60°
满足什么条件的两个菱形一定相似?AFra bibliotek120°
H
F
D
B
ppt课件
C
13
G
纸张的大小
见课本《读一读》
请同学们用一张纸实际验证一下﹗
ppt课件
14
各角对应相等,各边对应成比例的两个 多边形叫做相似多边形.
F
A
BC
ppt课件
2
观看动画 A
F E
B C
D
A1 F1
E1
B1 C1
D1
(1)在上图两个多边形中,是否有相等的内角?
∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,∠E=∠E1,∠F=∠F1
(2)在上图两个多边形中,相等内角的两边是否成比例? AB BC CD DE EF FA A1B1 B1C1 C1D1 D1E1 E1F1 F1 A1
答:如果两个多边形不相似,它们的对应角 可能都相等;如果两个多边形不相似,对应边 也可能成比例。
但如果两个多边形不相似,那么它们不可 能各角对应相等且各边对应成比例.
ppt课件
11
一块长3m、宽1.5m的矩形黑板如下图所
示,镶在其外围的木质边框宽7.5cm。边框的
内外边缘所成的矩形相似吗?为什么?
相似多边形对应边的比叫做相似比。
相似多边形的对应角相等,对应边成比例.
ppt课件
15
习题4.5 第1、2、3题
《相似多边形》图形的相似PPT精品课件

∵正三角形的三边都相等,
∴
.
B
C
D
E
F
4.3 相似多边形
例1 下列每组图形形状相同,它们的对应角有怎样的关系?对应边呢?
(2) 正方形 ABCD 与正方形 EFGH.
A
B
解:(1)∵正方形的每个角都是直角,
∴
D
C
∵正方形的四边相等,
E
F
∴
H
G
4.3 相似多边形
归纳
相似多边形:各角分别相等、各边对应成比例的两个多边形叫做相似 多边形. 相似比:相似多边形对应边的比叫做相似比 .
教案下载: . /jiaoan/
ppt论坛: . .cn
ppt课件: . /kejian/
语文课件: . /kejian/yuwen/ 数学课件: . /kejian/shuxue/
英语课件: . /kejian/yingyu/ 美术课件: . /kejian/meishu/
科学课件: . /kejian/kexue/ 物理课件: . /kejian/wuli/
4.3 相似多边形
思考 1:任意两个正 n 边形相似吗? 答:任意两个正 n 边形都相似.
思考 2:任意两个菱形相似吗? 答:任意两个菱形不一定相似.
4.3 相似多边形
1. 观察下面两组图形,图中的两个图形相似吗?为什么?
10 正方形
12
菱形
10
12
答:不相似. 因为虽然它们对应边是成比例的,但它们的对应角不相等.
与 F1A1 的比都相等,称为对应边.
A1
B1
A
B
F
C
F1
C1
ED
E1
《相似多边形》图形的相似PPT课件教学课件

4 J
5I
解:(1)相似比=CD : HI=3 : 5 (2)∵五边形ABCDE相似于五边形FGHIJ ∴ ∠F =∠A=120o, ∠C= ∠H=90o, ∴AB : FG = BC : GH = CD : HI = DE : IJ = EA : JF 即2 : FG = BC : 6 = 3/5 = 2.2 : IJ = AE :4 解得FG =10/3 cm, BC =18/5cm, IJ=11/3cm,AE=12/5cm
C´D´=__4
3A B 1°18 E
C 2 D B´
A´
6
E´
80°
五边形A´B´C´D´E´与五边形 . ABCDE的相似比为_2:_1
C´
D´
E
2、如图:下面的两个菱形相似吗?为什么? 满足什么条件的两个菱形一定相似?
6°0
A H
F
D
1°20 B
C
G
随堂练习
判断:
(1)任意两个矩形都是相似图形( ) (2)任意两个圆形是相似图形( )
对应角相等
AB = BC = AC ,A1B1 = B1C1 = A1C1
AB : A1B1 = BC : B1C1 = CD : C1D1 对应边成比例
对应角有什么关系?
A 150° B
F 正正八八边边形形 放放大大 B1
E
A1 150°
F1 E1
C
D
C1
∠A =∠A1, ∠B =∠B1, ∠C =∠C1 ∠D =∠D1, ∠E =∠E1, ∠F =∠F1
2、在记两个多边形相似时,要把表示对应角顶点的字母写 在对应的位置上。
A F
E
B C
D
《23.4 相似多边形的性质》ppt
开启
E
D
智慧
C E1 A1
D1
C1 B1
A
B
因为五边形ABCDE∽五边形A1B1C1D1E1,相似比为K 所以∠E= ∠E1, ∠B= ∠B1,
即
AB BC DE EA K A1B1 B1C1 D1E1 E1 A1
△ABC∽ △A1B1C1, △ADE ∽ △A1D1E1 △ACD∽ △A1C1D1 (为什么?)
还记得相似三角形的性质吗?
定理1 相似三角形对应高的比、对应中 线的比、对应角平分线的比 等于相似比. 定理2 相似三角形周长的比等于相似比.
定理3 相似三角形面积的比等于相似比 的平方.
从三角形到四边形
知识源于悟
四边形ABCD ∽四边形A1B1C1D1,相似比为k C C1 讨论: D D1 A B
因为
所以
SABC SACD SADE 2 K (等比性质) SA1B1C1 SA1C1D1 SA1D1E1
SABC SACD SADE K2 SA1B1C1 SA1C1D1 SA1D1E1
多边形A1A2A3…An∽多边形B1B2B3……Bn,相似比为K
A1 B 1 C 1 A1 C 1 D 1 A 2 B 2 C 2 A 2 C 2 D 2
• 如果把四边形换成五边形,那么结论又如何? ……? 换成n边形呢? 通过上面的活动,你得 出了什么结论?
C1
C2 D2 B2
D1
A1 B1 A2 相似多边形周长的比等于 相似比 , 对应对角线的比等于 相似比 , 对应三角形相似,且相似比等于 相似多边形的相似比 对应三角形面积的比等于 相似比的平方 ; 相似多边形面积的比等于 相似比的平方 .
相似多边形 ppt课件

重
难
题
型
突
破
思路点拨
4.3 相似多边形
重
难
题
型
突
破
解题通法
解决此类问题,一般是根据对应边成比例,列出比例
式求解,注意结果要符合实际.
4.3 相似多边形
易 ■ 判定相似多边形时忽略条件
错
例 下列各组图形中一定是相似多边形的是 (
易
混
A. 两个直角三角形
分
析
B. 两个等边三角形
C. 两个菱形
D. 两个矩形
A. 甲和乙
B. 甲和丙
C. 乙和丙
D. 甲、乙和丙
4.3 相似多边形
[解题思路]
考
点
矩形已经满足各角分别相等,判断各边是否成比例即可
清
单
≠
,∴ 甲与乙不相似;∵ =
,∴ 甲与丙
解 .∵
.
.
.
读
.
≠
[答案]
B
相似;∵
.
.
,∴ 乙与丙不相似.
4.3 相似多边形
考 ■考点二 相似多边形的性质
读
∴BC=12.
[答案]
48 12
4.3 相似多边形
重 ■题型 相似多边形性质与判定的应用
难
例 如图,一个矩形广场的长为 90 m,宽为 60 m,广
题
型 场内有两横、两纵四条小路,如果两条横向小路的宽均为
突
破 1.2 m,那么每条纵向小路的宽为多少时小路内外边缘所围
成的两个矩形相似?
4.3 相似多边形
)
4.3 相似多边形
[解题思路]
难
题
型
突
破
思路点拨
4.3 相似多边形
重
难
题
型
突
破
解题通法
解决此类问题,一般是根据对应边成比例,列出比例
式求解,注意结果要符合实际.
4.3 相似多边形
易 ■ 判定相似多边形时忽略条件
错
例 下列各组图形中一定是相似多边形的是 (
易
混
A. 两个直角三角形
分
析
B. 两个等边三角形
C. 两个菱形
D. 两个矩形
A. 甲和乙
B. 甲和丙
C. 乙和丙
D. 甲、乙和丙
4.3 相似多边形
[解题思路]
考
点
矩形已经满足各角分别相等,判断各边是否成比例即可
清
单
≠
,∴ 甲与乙不相似;∵ =
,∴ 甲与丙
解 .∵
.
.
.
读
.
≠
[答案]
B
相似;∵
.
.
,∴ 乙与丙不相似.
4.3 相似多边形
考 ■考点二 相似多边形的性质
读
∴BC=12.
[答案]
48 12
4.3 相似多边形
重 ■题型 相似多边形性质与判定的应用
难
例 如图,一个矩形广场的长为 90 m,宽为 60 m,广
题
型 场内有两横、两纵四条小路,如果两条横向小路的宽均为
突
破 1.2 m,那么每条纵向小路的宽为多少时小路内外边缘所围
成的两个矩形相似?
4.3 相似多边形
)
4.3 相似多边形
[解题思路]
《相似多边形》PPT课件

记作如:
六边形ABCDEF∽六边形A1B1C1D1E1F1
注意:记两个多边形相似时,要把对应 顶点的字母写在对应的位置.
•相似多边形对应边的比叫做相似比
相似比与表达的顺序有关.
1、观察下面两组图形,图4-12〔1〕中的 两个图形相似吗?为什么?图4-12 〔2〕中的两个图形呢?与同桌交流.
10 正方形 12 菱形
A’= 1—5—0 B’=1—2—0 C’=1—0—5 D’=1—3—5
E’=1—2—0
F’= —90—
A’B’= B’C’=
——1131——
mm mm
C’D’=—12— mm
D’E’= —10— mm
E’F’= —15— mm
F’A’= —9— mm
从以上数据你能得到什么结论?
A= A’ B= B’ C= C’ D= D’
愿知识与您相伴 让我们共同成长 感谢您的阅读与支持
可爱的同学,找资料眼 睛累了吧!长时间屏幕,眼 睛会干涩、酸痛、疲劳的。
不过现在教同学们一个 小办法,左边我为大家准备 了一张视力保健“远眺图” ,看看图就能缓解眼疲劳, 起到远眺解乏的作用。
远眺图是利用心理学 空间知觉原理,在一张二维 空间平面上,强烈显示出三 维空间的向远延伸的立体图 形,远视和视力良好的人在 长时间近距离用眼情况下引 起的视力疲劳,可以通过此 种方法获得一定的缓解。
A1
B1
AB
F
C F1
C1
六边形ABCDEF与六边形 E D
A1B1C1D1E1F1的相似比
E1
D1
为K1= 1 2
(1)
(1)
图4-11
六边形A1B1C1D1E1F1与六边形ABCDEF的相似比为K2=2
六边形ABCDEF∽六边形A1B1C1D1E1F1
注意:记两个多边形相似时,要把对应 顶点的字母写在对应的位置.
•相似多边形对应边的比叫做相似比
相似比与表达的顺序有关.
1、观察下面两组图形,图4-12〔1〕中的 两个图形相似吗?为什么?图4-12 〔2〕中的两个图形呢?与同桌交流.
10 正方形 12 菱形
A’= 1—5—0 B’=1—2—0 C’=1—0—5 D’=1—3—5
E’=1—2—0
F’= —90—
A’B’= B’C’=
——1131——
mm mm
C’D’=—12— mm
D’E’= —10— mm
E’F’= —15— mm
F’A’= —9— mm
从以上数据你能得到什么结论?
A= A’ B= B’ C= C’ D= D’
愿知识与您相伴 让我们共同成长 感谢您的阅读与支持
可爱的同学,找资料眼 睛累了吧!长时间屏幕,眼 睛会干涩、酸痛、疲劳的。
不过现在教同学们一个 小办法,左边我为大家准备 了一张视力保健“远眺图” ,看看图就能缓解眼疲劳, 起到远眺解乏的作用。
远眺图是利用心理学 空间知觉原理,在一张二维 空间平面上,强烈显示出三 维空间的向远延伸的立体图 形,远视和视力良好的人在 长时间近距离用眼情况下引 起的视力疲劳,可以通过此 种方法获得一定的缓解。
A1
B1
AB
F
C F1
C1
六边形ABCDEF与六边形 E D
A1B1C1D1E1F1的相似比
E1
D1
为K1= 1 2
(1)
(1)
图4-11
六边形A1B1C1D1E1F1与六边形ABCDEF的相似比为K2=2
相似多边形的性质课件

使用哪个定理来判断多边形是否相似。
三边对应成比例判定定理
总结词
通过两个多边形的三边对应成比例,可以判定两个多 边形相似。
详细描述
三边对应成比例判定定理是相似多边形判定定理的一 种,它基于两个多边形的三边对应成比例,从而判定 两个多边形相似。这个定理在实际应用中非常有用, 因为它只需要比较三个边的长度就可以判断两个多边 形是否相似,相对于其他判定定理更为简便。然而, 需要注意的是,这个定理只适用于三边对应成比例的 情况,对于更多边的多边形,需要使用其他判定定理 进行判断。
总结词
通过比较相似多边形的面积和相似比, 证明面积比等于相似比的平方。
详细描述
首先,计算两个相似多边形的面积。 然后,计算它们的相似比。最后,比 较面积和相似比的关系,如果面积比 等于相似比的平方,则证明了面积比 等于相似比的平方。
THANKS
感谢观看
多边形相似。
02
相似多边形的性质
相似多边形的对应角相等
总结词
相似多边形的对应角是相等的,这是相似多边形的基本性质之一。
详细描述
根据相似多边形的定义,如果两个多边形相似,则它们的对应角必定相等。这 意味着无论多边形的大小如何变化,只要它们是相似的,它们的对应角就会保 持不变。
相似多边形的对应边成比例
角-角-边判定定理
总结词
通过两个多边形的对应角相等,且对应边成比例,可以判定两个多边形相似。
详细描述
角-角-边且对应边成比例,从而判定 两个多边形相似。在几何学中,这个定理是非常重要的,因为它提供了一种简单而有效的方法来判断两个多边形 是否相似。
相似多边形的性质
相似多边形的面积之 比等于对应边长的平 方之比。
相似多边形的对应角 相等,对应边成比例。
三边对应成比例判定定理
总结词
通过两个多边形的三边对应成比例,可以判定两个多 边形相似。
详细描述
三边对应成比例判定定理是相似多边形判定定理的一 种,它基于两个多边形的三边对应成比例,从而判定 两个多边形相似。这个定理在实际应用中非常有用, 因为它只需要比较三个边的长度就可以判断两个多边 形是否相似,相对于其他判定定理更为简便。然而, 需要注意的是,这个定理只适用于三边对应成比例的 情况,对于更多边的多边形,需要使用其他判定定理 进行判断。
总结词
通过比较相似多边形的面积和相似比, 证明面积比等于相似比的平方。
详细描述
首先,计算两个相似多边形的面积。 然后,计算它们的相似比。最后,比 较面积和相似比的关系,如果面积比 等于相似比的平方,则证明了面积比 等于相似比的平方。
THANKS
感谢观看
多边形相似。
02
相似多边形的性质
相似多边形的对应角相等
总结词
相似多边形的对应角是相等的,这是相似多边形的基本性质之一。
详细描述
根据相似多边形的定义,如果两个多边形相似,则它们的对应角必定相等。这 意味着无论多边形的大小如何变化,只要它们是相似的,它们的对应角就会保 持不变。
相似多边形的对应边成比例
角-角-边判定定理
总结词
通过两个多边形的对应角相等,且对应边成比例,可以判定两个多边形相似。
详细描述
角-角-边且对应边成比例,从而判定 两个多边形相似。在几何学中,这个定理是非常重要的,因为它提供了一种简单而有效的方法来判断两个多边形 是否相似。
相似多边形的性质
相似多边形的面积之 比等于对应边长的平 方之比。
相似多边形的对应角 相等,对应边成比例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A1B1 B1C1 C1D1 D1E1 E1F1 F1 A1
六边形ABCDEF的周长 六边形A1 B1C1 D1 E1 F1的周长
k.
四边形ABCD ∽四边形A1B1C1D1,相似比为k
D
C
C1
D1
讨论: 它们的面积比会是多少?
A
B A1
B1
1.连接相应的对角线AC, A1C1所得的 因为四边形ABCD∽四边形A1B1C1D1,相似比为K
3.四边形ABCD与A1B1C1D1面积比各是多少? △ABC∽ △A1B1C1, △ADC ∽ △ A1D1C1
因为
S ABC S ACD K 2
S A1B1C1
S A1C1D1
所以
S ABC S ACD K 2
S S A1B1C1
A1C1D1
S ABCD K 2 S A1B1C1D1
A1B1 B1C1 D1E1 E1A1
即
△ABC∽ △A1B1C1, △ADE ∽ △A1D1E1
△ACD∽ △A1C1D1 (为什么?)
因为 所以
SABC SACD SADE K 2
S S S A1B1C1
A1C1D1
A1D1E1
SABC SACD SADE K 2 (等比性质)
S S S A1B1C1
A
B
A1
B1
解 ∵五边形ABCD∽五边形A1B1C1D1, 且相似比是k.
解 : AB BC CD DE EF FA k. A1B1 B1C1 C1D1 D1E1 E1F1 F1 A1
相似多边形对应边成比例, 对应边的比叫做相似比
AB BC CD DE EF FA k等比.
1.过A1连接多边形A1A2A3…An的 所有对角线,这样对角线有多少条?
△ABC与△ A1B1C1有什么关系?相似
吗?△ACD与△ A1C1D1呢?
所以∠D= ∠D1, ∠B= ∠B1,
AB BC CD DA K A1B1 B1C1 C1D1 D1 A1
2.如果相似,它们的相似比各是多少? 面积比各是多少?
在△ABC与△ A1B1C1中
∠B= ∠B1
AB BC K A1B1 B1C1
……?
换成n边形呢?
通过上面的活动,你得
C1
出了什么结论?
D1
C2 D2
A1
B1 A2
B2
相似多边形周长的比等于 相似比 ,
对应对角线的比等于 相似比 , 对应三角形相似,且相似比等于 相似多边形的相似比 , 对应三角形面积的比等于 相似比的平方 ;
相似多边形面积的比等于 相似比的平方.
相似四边形的周长比等于_相__似___比__, 面积比等于_相__似___比__的__平___方_。
(等比性质)
四边形ABCD ∽四边形A1B1C1D1,相似比为k
(1).四边形ABCD 与四边 D
形A1B1C1D1周长的比是 多少?
(2).连接相应的对角线 A
C
D1
B A1
C1 B1
A1C1, A2C2所得的 △A1B1C1与△ A2B2C2相 似吗?
(3).设△A1B1C1, △A1C1D1, △ A2B2C2, △ A2C2D2.的面 积分别是S△A1B1C1, S△A1C1D1
A1B1 B1C1 C1D1 D1E1 E1F1 F1 A1
六边形ABCDEF的周长 六边形A1 B1C1 D1 E1 F1的周长
k.
开启D
E
智慧
D1
C
E1
C1
A
B
A1
B1
因为五边形ABCDE∽五边形A1B1C1D1E1,相似比为K
所以∠E= ∠E1, ∠B= ∠B1, AB BC DE EA K
如果把四边形换成五边形, 你们刚才的结论是否仍然 成立呢
• 如果把四边形换成五边形,那么结论又如何?
五边形ABCDE∽五边形A1B1C1D1E1,
相似比为K
D
E A
D1
C E1
C1
B
A1
B1
周长的比 面积的比
结论还成立吗?
五边形ABCDE∽五边形A1B1C1D1E1,相似比为K D
D1
E
C
E1Байду номын сангаас
C1
A1C1D1
A1D1E1
多边形A1A2A3…An∽多边形B1B2B3……Bn,相似比为K
……?
A5
A4
An-1
B5
B4
换成n边形呢?
Bn-1 A3
An
通过上面的活动,你得
B3 Bn
出了什么结论?
A1
A2
B1
B2
解 ∵多边形A1A2A3…An∽多边形B1B2B3……Bn,
相似比为K
A1 A2 A2 A3 A3 A4 L An1 An An A1 k.
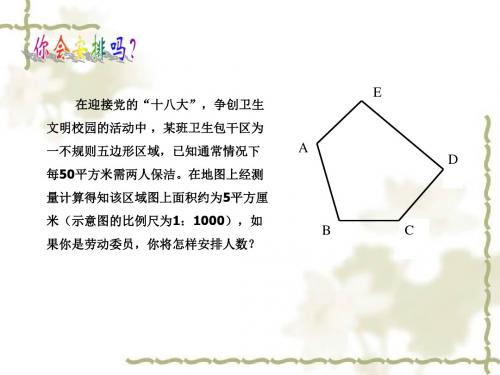
在迎接党的“十八大”,争创卫生 文明校园的活动中 ,某班卫生包干区为 一不规则五边形区域,已知通常情况下 每50平方米需两人保洁。在地图上经测 量计算得知该区域图上面积约为5平方厘 米(示意图的比例尺为1:1000),如 果你是劳动委员,你将怎样安排人数?
A B
E D
C
23.4 相似多边形的性质
怀宁县高河初级中学 江海河
B1B2 B2 B3 B3 B4
Bn1Bn Bn B1
,
AB BC CD DE EF FA k .
A1B1 B1C1 C1D1 D1E1 E1F1 F1 A1
ABCDEF k.
A1 B1C1 D1 E1 F1
多边形A1A2A3…An∽多边形B1B2B3……Bn,相似比为 k
还记得相似三角形的性质吗?
定理1 相似三角形对应高的比、对应中 线的比、对应角平分线的比 等于相似比.
定理2 相似三角形周长的比等于相似比. 定理3 相似三角形面积的比等于相似比 的平方.
从三角形到四边形 知识源于悟
四边形ABCD ∽四边形A1B1C1D1,相似比为k
D
C
C1 D1
讨论: 它们周长的比是多少?
△A1C1D1与△ A2C2D2呢? 如果相似,它们的相似比各
SSA△1BA1C21B,2CS2,A1SC1△D1A各 2C2是 D2,多 那么少,?
是多少?
S
S
A 2 B 2 C 2
A 2 C 2 D 2
(4).四边形A1B1C1D1与四边形A2B2C2D2.面积的比是多少?
• 如果把四边形换成五边形,那么结论又如何?
A
B A1
B1
解 ∵四边形ABCD∽四边形A1B1C1D1, 且相似比是k.
解 : AB BC CD DE EF FA k. A1B1 B1C1 C1D1 D1E1 E1F1 F1 A1
相似多边形对应边成比例, 对应边的比叫做相似比
AB BC CD DE EF FA k等比.
六边形ABCDEF的周长 六边形A1 B1C1 D1 E1 F1的周长
k.
四边形ABCD ∽四边形A1B1C1D1,相似比为k
D
C
C1
D1
讨论: 它们的面积比会是多少?
A
B A1
B1
1.连接相应的对角线AC, A1C1所得的 因为四边形ABCD∽四边形A1B1C1D1,相似比为K
3.四边形ABCD与A1B1C1D1面积比各是多少? △ABC∽ △A1B1C1, △ADC ∽ △ A1D1C1
因为
S ABC S ACD K 2
S A1B1C1
S A1C1D1
所以
S ABC S ACD K 2
S S A1B1C1
A1C1D1
S ABCD K 2 S A1B1C1D1
A1B1 B1C1 D1E1 E1A1
即
△ABC∽ △A1B1C1, △ADE ∽ △A1D1E1
△ACD∽ △A1C1D1 (为什么?)
因为 所以
SABC SACD SADE K 2
S S S A1B1C1
A1C1D1
A1D1E1
SABC SACD SADE K 2 (等比性质)
S S S A1B1C1
A
B
A1
B1
解 ∵五边形ABCD∽五边形A1B1C1D1, 且相似比是k.
解 : AB BC CD DE EF FA k. A1B1 B1C1 C1D1 D1E1 E1F1 F1 A1
相似多边形对应边成比例, 对应边的比叫做相似比
AB BC CD DE EF FA k等比.
1.过A1连接多边形A1A2A3…An的 所有对角线,这样对角线有多少条?
△ABC与△ A1B1C1有什么关系?相似
吗?△ACD与△ A1C1D1呢?
所以∠D= ∠D1, ∠B= ∠B1,
AB BC CD DA K A1B1 B1C1 C1D1 D1 A1
2.如果相似,它们的相似比各是多少? 面积比各是多少?
在△ABC与△ A1B1C1中
∠B= ∠B1
AB BC K A1B1 B1C1
……?
换成n边形呢?
通过上面的活动,你得
C1
出了什么结论?
D1
C2 D2
A1
B1 A2
B2
相似多边形周长的比等于 相似比 ,
对应对角线的比等于 相似比 , 对应三角形相似,且相似比等于 相似多边形的相似比 , 对应三角形面积的比等于 相似比的平方 ;
相似多边形面积的比等于 相似比的平方.
相似四边形的周长比等于_相__似___比__, 面积比等于_相__似___比__的__平___方_。
(等比性质)
四边形ABCD ∽四边形A1B1C1D1,相似比为k
(1).四边形ABCD 与四边 D
形A1B1C1D1周长的比是 多少?
(2).连接相应的对角线 A
C
D1
B A1
C1 B1
A1C1, A2C2所得的 △A1B1C1与△ A2B2C2相 似吗?
(3).设△A1B1C1, △A1C1D1, △ A2B2C2, △ A2C2D2.的面 积分别是S△A1B1C1, S△A1C1D1
A1B1 B1C1 C1D1 D1E1 E1F1 F1 A1
六边形ABCDEF的周长 六边形A1 B1C1 D1 E1 F1的周长
k.
开启D
E
智慧
D1
C
E1
C1
A
B
A1
B1
因为五边形ABCDE∽五边形A1B1C1D1E1,相似比为K
所以∠E= ∠E1, ∠B= ∠B1, AB BC DE EA K
如果把四边形换成五边形, 你们刚才的结论是否仍然 成立呢
• 如果把四边形换成五边形,那么结论又如何?
五边形ABCDE∽五边形A1B1C1D1E1,
相似比为K
D
E A
D1
C E1
C1
B
A1
B1
周长的比 面积的比
结论还成立吗?
五边形ABCDE∽五边形A1B1C1D1E1,相似比为K D
D1
E
C
E1Байду номын сангаас
C1
A1C1D1
A1D1E1
多边形A1A2A3…An∽多边形B1B2B3……Bn,相似比为K
……?
A5
A4
An-1
B5
B4
换成n边形呢?
Bn-1 A3
An
通过上面的活动,你得
B3 Bn
出了什么结论?
A1
A2
B1
B2
解 ∵多边形A1A2A3…An∽多边形B1B2B3……Bn,
相似比为K
A1 A2 A2 A3 A3 A4 L An1 An An A1 k.
在迎接党的“十八大”,争创卫生 文明校园的活动中 ,某班卫生包干区为 一不规则五边形区域,已知通常情况下 每50平方米需两人保洁。在地图上经测 量计算得知该区域图上面积约为5平方厘 米(示意图的比例尺为1:1000),如 果你是劳动委员,你将怎样安排人数?
A B
E D
C
23.4 相似多边形的性质
怀宁县高河初级中学 江海河
B1B2 B2 B3 B3 B4
Bn1Bn Bn B1
,
AB BC CD DE EF FA k .
A1B1 B1C1 C1D1 D1E1 E1F1 F1 A1
ABCDEF k.
A1 B1C1 D1 E1 F1
多边形A1A2A3…An∽多边形B1B2B3……Bn,相似比为 k
还记得相似三角形的性质吗?
定理1 相似三角形对应高的比、对应中 线的比、对应角平分线的比 等于相似比.
定理2 相似三角形周长的比等于相似比. 定理3 相似三角形面积的比等于相似比 的平方.
从三角形到四边形 知识源于悟
四边形ABCD ∽四边形A1B1C1D1,相似比为k
D
C
C1 D1
讨论: 它们周长的比是多少?
△A1C1D1与△ A2C2D2呢? 如果相似,它们的相似比各
SSA△1BA1C21B,2CS2,A1SC1△D1A各 2C2是 D2,多 那么少,?
是多少?
S
S
A 2 B 2 C 2
A 2 C 2 D 2
(4).四边形A1B1C1D1与四边形A2B2C2D2.面积的比是多少?
• 如果把四边形换成五边形,那么结论又如何?
A
B A1
B1
解 ∵四边形ABCD∽四边形A1B1C1D1, 且相似比是k.
解 : AB BC CD DE EF FA k. A1B1 B1C1 C1D1 D1E1 E1F1 F1 A1
相似多边形对应边成比例, 对应边的比叫做相似比
AB BC CD DE EF FA k等比.
