电路理论基础(陈希有)习题答案第二章
《电路分析基础》习题参考答案

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出,P2=6W吸收,P3=16W吸收,P4=-lOW发出,PS=-7W发出,PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开:UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合:12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。
《电路理论基础》(第三版陈希有)习题答案第十章

i答案10.1解:t ::: 0时,电容处于开路,故u C (0 _) = 10mA 2k 「- 20V 由换路定律得:u C (0 .) +(0”20V换路后一瞬间,两电阻为串联,总电压为 u C (0 )。
所以再由节点①的KCL 方程得:i C (0 ) =10mA -i 1(0 .)二(10-5)mA =5mA答案10.2解:t :::0时电容处于开路,电感处于短路,3门电阻与61电阻相并联,所以45V6i(0J3A ,L(0Ji(0」= 2A(5+8 + 6 3)0 6+36+3u C (0J =8 i(0J = 24V 由换路定律得:U C (0 ) 7C (0J =24V ,匚(0.) “L (0_)=2A由KVL 得开关电压:u(0 ) --U c (0 ) 8 匚(0 .)=(-24 8 2)V 8V答案10.3解:t ::: 0时电容处于开路,i =0 ,受控源源电压4i =0 ,所以U C (0 J =U C (0」=U 1(0」61.5V = 0.6V(9 6尸等效电阻i i (0 )=%(0 .) (2 2)k 」=5mA(b)所示。
R 段「4i (6 3)i容i时间常数二 R C 二 0 ・1st 0后电路为零输入响应,故电容电压为:u C (t)二 u C (0 ,)e~ =0.6e A0°V6“电阻电压为:“⑴工―6门 i 6门 ^C-dUc ^0.72e 10t V (t 0)dt答案10.43解:t :::0时电感处于短路,故L(0J= 39A=3A ,由换路定律得:6 + 3i L (0^i L (0J=3A求等效电阻的电路如图(b)所示。
等效电阻R 「6 •色卫=8」,时间常数.二L/R =0.5s6+3t 0后电路为零输入响应,故电感电流为i L (t) =i L (0 .)e^^ =3e 2t A (t _o ) 电感电压._2tu ,(t)二 L 匕二-24e V (t .0)dt31电阻电流为U 36C 汽L +U 1小2八i 3 2e A33「3「31电阻消耗的能量为:W3°= f 30i ;dt = f12/dt =12[-0.25ed=3W答案10.5解:由换路定律得i L (0.) “L (0」=0,达到稳态时电感处于短路,故LG) =20/4=5A求等效电阻的电路如图(b)所示。
电路理论基础(哈尔滨工业大学陈希有第3版) 第1章-第5章

a 电位: 任选一点p作为电位参考点,电路中某点与参考点之间的电压称为该点的电 位,用 表示。有了电位的概念,两点之间的电压便等于这两点的电位之差。
uab Ec dl
a A
(a)
a A
(b)
u ab
u ba
A
(c)
a uA
b
b
b
电压参考方向的表示法
一个元件上的电压和电流的参考方向取成相同的,并称为关联参考方向。
2 基尔霍夫电流定律
基尔霍夫电流定律(Kirchhoff's Current Law,简称KCL)表述为:在集中 参数电路中,任一时刻流出(或流入)任一节点的支路电流代数和等于零, 即
i
k
0
( ik 表示第 k 条支路电流)
规定: ik 参考方向为流出节点时, ik 前面 取“+”号; 流入节点时, ik 前面取“-”号。
i1
A
i2
1、在集中参数电路中,任一时刻流出(或流入) 任一闭合边界 S 的支路电流代数和等于零。
KCL的其它表述
2、任一时刻,流出任一节点(或闭合边界)电 流的代数和等于流入该节点电流的代数和。
根据右图,列写KCL方程 1)基本表述方 式——对节点
3 i3
④
S
4 i4 i6 7 i7 ③
节点① :
① u1 1
u
电压降
= u电压升
6 ③ u6 l1 5 u5 l2 7 u7 ⑤ 基尔霍夫电压定律示例
u2
l3 ②
2
说明:平面电路网孔上的KVL方程是一组独立方程。设电路有b个支路n个节 点,可以证明:平面电路的网孔数即独立KVL方程的个数等于b-(n-1)。当然 取网孔列方程只是获得独立KVL方程的充分条件,而不是必要条件。
电路分析基础第二章答案.docx
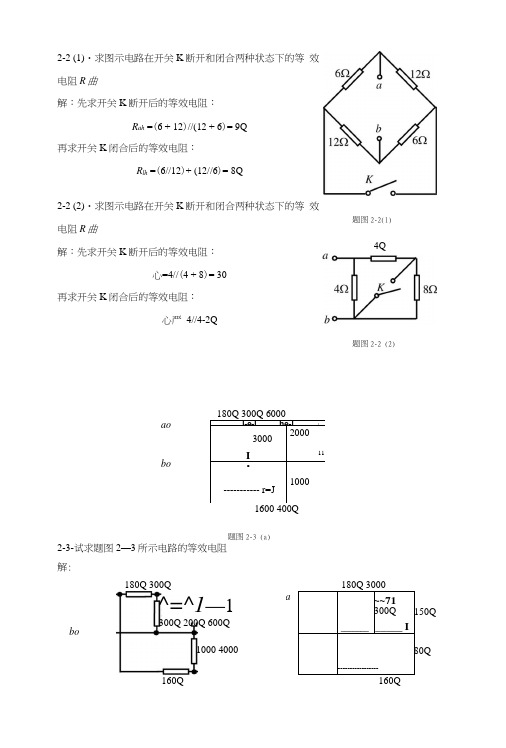
2-2 (1)・求图示电路在开关K 断开和闭合两种状态下的等 效电阻R 曲解:先求开关K 断开后的等效电阻:R ah =(6 + 12)//(12 + 6)= 9Q再求开关K 闭合后的等效电阻:R lh =(6//12)+ (12//6)= 8Q2-2 (2)・求图示电路在开关K 断开和闭合两种状态下的等 效电阻R 曲解:先求开关K 断开后的等效电阻:心=4//(4 + 8)= 30再求开关K 闭合后的等效电阻:心严 4//4-2Q2-3-试求题图2—3所示电路的等效电阻解:bo180Q 300Q 1000 4000^=^1—1300Q 200Q 600Q160Q_______ ~~71300Q_____ I-----------------80Qa150Q160Qaobo_____ l -e-l ____ he-l ____ 卜3000I200011• ----------- r=J1000题图2-2(1)4Q题图2-2 (2)题图2-3 (a)(b)》a300Q_____—450Q9240QI80Qtit -------------360Q240Q心二2400〃3600 = 1440ahbo67 0bo题图2-3 (b)解:60Q20060Qbo180Q180Q240Qt ------- X24()0 360020040Q20040QE—<_Z]_I60Q200200 20Q60Q10Q600bo6003()0心=40Q2-25 (1)・求图示电路a、b两点间的等效电阻R ahO解:在图中画一条垂线,使左右两边对称,参见图中虚线所示。
显然虚线为等位线,没有电流流过,故图中电阻可去掉,其等效电阻为:R ah =[(8 + 8)//(8 + 8)]//8 = 4Q2-25 (2)・求图示电路a、b两点间的等效电阻R ah o题图2-25 (1) 解:此题与上题相同,只是其中电阻的阻值不同,但仍保持其对称性。
电路理论课后答案,带步骤
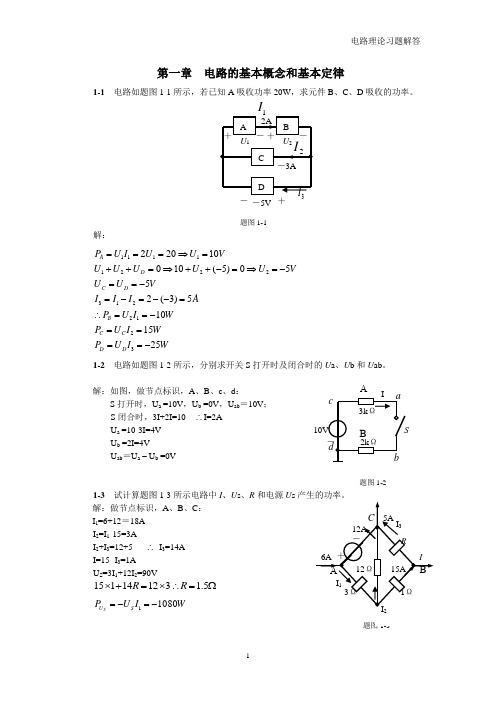
解:(1)该电路有三个网孔。设网孔电流分别为 、 ,
参考方向如图3-4所示。并设受控源两端电压为U。
(2)列写网孔方程:
辅助方程为:
联立求解得:
U= V
所以: mW
3-5电路如题图3-5所示,试用网孔分析法求电流 和电压 。
题图3-5题图3-5(b)
解:(1)将原图中20A电流源与2 电阻并联部分等效为40V电压源与2 电阻串联,如图3-5(b)所示。
(2)列写节点方程:
整理得:
求解得: V
V
所以: V
3-7电路如题图3-7所示,①试用节点分析法列写电路的节点方程;②该电路能否用网孔分析法分析?为什么?
题图3-7题图3-7(b)
①解:
(1)将原图中的 电压源与 串联部分等效为 电流源与 并联。
且 。如图3-7(b)所示。
(2)该电路有5个节点,以节点5为参考点,节点电压分别设为: 、 、 ,
Ua=10-3I=4V
Ub=2I=4V
Uab=Ua–Ub=0V
题图1-2
1-3试计算题图1-3所示电路中I、Us、R和电源Us产生的功率。
解:做节点标识,A、B、C:
I1=6+12=18A
I2=I1-15=3A
I2+I3=12+5 I3=14A
I=15- I3=1A
US=3I1+12I2=90V
题图1-3
2-15题图2-15所示电路,试问当电阻R等于何值时,可获得最大功率,最大功率等于多少?
题图2-15图2-15(b)
解:先将a,b与R断开,则
得:
所以:共戴维南等效电路为图(a)所示
所以:当 时,获得最大功率
电路理论基础课后习题答案 陈希有主编 第十到十四章

答案10.1解:0<t时,电容处于开路,故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得:V 20)0()0(==-+C C u u换路后一瞬间,两电阻为串联,总电压为)0(+C u 。
所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得:m A5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解:0<t时电容处于开路,电感处于短路,Ω3电阻与Ω6电阻相并联,所以A3)363685(V45)0(=Ω+⨯++=-i,A 2)0(366)0(=⨯+=--i i LV 24)0(8)0(=⨯=--i u C由换路定律得:V24)0()0(==-+C C u u ,A 2)0()0(==-+L L i i由KVL 得开关电压:V8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u答案10.3解:0<t 时电容处于开路,0=i ,受控源源电压04=i ,所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C>t 时,求等效电阻的电路如图(b)所示。
等效电阻Ω=++-==5)36(4i ii i i u R 时间常数s 1.0i ==C R τ0>t 后电路为零输入响应,故电容电压为:V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为:V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4 解:<t 时电感处于短路,故A 3A 9363)0(=⨯+=-L i ,由换路定律得: A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。
(b)等效电阻Ω=+⨯+=836366i R ,时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应,故电感电流为 A e 3e )0()(2/t t L L i t i --+==τ)0(≥t电感电压V e 24d d )(21t Lti Lt u --==)0(>t Ω3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为:W3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解:由换路定律得0)0()0(==-+L L i i ,达到稳态时电感处于短路,故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。
电路理论基础(哈尔滨工业大学陈希有第3版)13共44页文档

5 3
6 ② 1
两个子图
③
①
4
3
2
6
②
(a)
③①
4
③
6
②
(b)
有向图:图中的所有支路都指定了方向,则称为有向图;反之为无向图
回 路: 从图中某一节点出发,经过若干支路和节点(均只许经过一次)又 回到出发节点所形成的闭合路径称为回路。 割 集: 连通图的割集是一组支路集合,并且满足:
(1)如果移去包含在此集合中的全部支路(保留支路的两个端点),则 此图变成两个分离的部分。
单树支割集
4
5
3
4
5
3
c1
1
2
6
c2 1
2
6
1
(a)
(b)
(c)
基本割集:每取一个树支作一个单树支图割基本集割,集称为基本割集。
基本割集的方向规定为所含树支的方向。
基本割集的性质 图中3个基本割集 KCL方程是(独立):
c1
i1i5i6 0
c 2 i2i4i5i60
1 3 . 1 网 络 的 图 树
基本要求:掌握网络的图、子图、连通图、割集和树等概念。
1 网络的图
图( graph) :由“点” 和“线”组成。 • “点”也称为节点或顶点(vertex),“线”也称为支路或
边(edge)。 • 图通常用符号G来表示。
图 (a) 电路只含二端元件,对应的图如图 (b)所示。
用点表示王宫,用线表示王宫间的 道路,便抽象成图。问题变成该图 是否为平面图?
4 四色定理
四色问题:只须4种不同颜色,就能使平面地图上任何两个相 邻的国家的颜色不同。
图论问题:用点表示国家,用边表示国家直接相邻。证明只 须4种颜色就可使所有相邻顶点具有不同颜色。
电路理论基础(陈希有)习题答案第二章
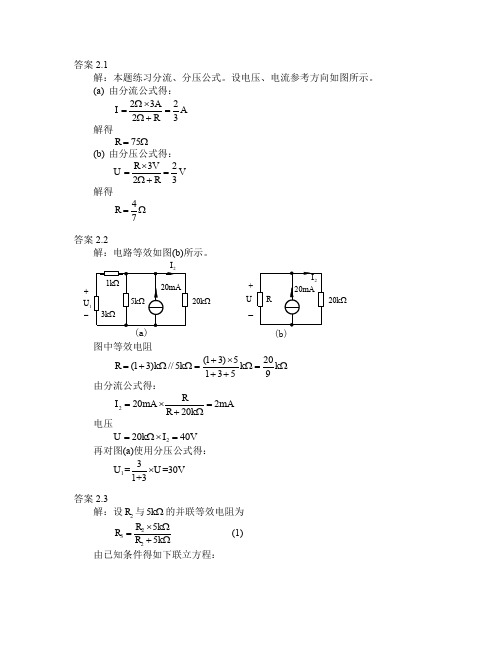
答案 2.13 解:选网孔为独立回路,如图所示
4
Im2 2 1 5 5V I m3 3 10V
I
I m1
所列方程如下: (1 2 3) I m1 2 I m 2 3 I m3 10V 2 I m1 (2 4) I m 2 5V 3I m1 (3 5) I m3 5V 联立解得 I m1 2.326A , I m2 1.61A , I m3 1.71A 。 利用回路电流求得支路电流 I I m1 I m2 0.717A 答案 2.14 解:选如图所示独立回路,其中受控电流源只包含在 l 3 回路中,其回路电流
(0.5 1) I x (0.5 1) I 1 2 I 5V (1 0.5) I x (0.5 1 2 1) I 3 2 I 0
I
76V 4Ω
0.5 I
0.6I
5Ω
I
76V 4Ω (b-2)
(b-1)
I
76V 5Ω 0.5I
0.1I 5Ω 4Ω
(d)
(b-3)
对等效化简后的电路,由 KVL 得 76V 0.5I (4 5) I I 76V / 9.5 8A 答案 2.9 解: (a) 此电路为平衡电桥,桥 30Ω电阻上的电流均为零,将其断开或短接不影响 等效电阻,分别如图(a-1)和(a-2)所示。
R3 I3 R4 I 4 U S R2 I 2 R3 I3 R5 I5 rI 4
(b)对独立节点列 KCL 方程 节点①: I1 I 2 I3 I S 节点②: I 2 I3 I 4 0 对网孔列 KVL 方程,电流源所在支路的电流是已知的,可少列一个网孔的 KVL 方程。 网孔 m1: R1I1 R2 I 2 R4 I 4 U S
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(b)对独立节点列 KCL 方程 节点①: I1 I 2 I3 I S 节点②: I 2 I3 I 4 0 对网孔列 KVL 方程,电流源所在支路的电流是已知的,可少列一个网孔的 KVL 方程。 网孔 m1: R1I1 R2 I 2 R4 I 4 U S
网孔 m2 : R2 I 2 R3 I3 U S 答案 2.12 解:图(a)、(b)为同一电路模型,选取了不同的回路列支路电流方程。图(a)选取 网孔作为回路,网孔 2 和网孔 3 包含电流源,电流源的电压 U 是未知的,对包含电 流源的回路列 KVL 方程时必须将此未知电压列入方程。图(b)所取回路只让回路 3 包含电流源,如果不特别求取电流源电压,可以减少一个方程。 (a) 对节点①列 KCL 方程: I1 I 2 I3 0.1A 对图示网孔列 KVL 方程 网孔 m1: 10I1 20I 2 4V 网孔 m2 : 网孔 m3:
(0.5 1) I x (0.5 1) I 1 2 I 5V (1 0.5) I x (0.5 1 2 1) I 3 2 I 0
答案 2.1 解:本题练习分流、分压公式。设电压、电流参考方向如图所示。 (a) 由分流公式得: 2 3A 2 I A 2 R 3 解得 R 75 (b) 由分压公式得: R 3V 2 U V 2 R 3 解得 4 R 7 答案 2.2 解:电路等效如图(b)所示。
由图(a-1)得: (30 40) R 35 2 或由图(a-2)得 30 40 R 35 2 2 (b) 对图(b)电路,将 6Ω和 3Ω并联等效为 2Ω,2Ω和 2Ω并联等效为 1Ω,4Ω 和 4Ω并联等效为 2Ω,得图(b-1)所示等效电路:
0.2 0.2 1
答案 2.11 解:如图所示
I 5 rI 4 R5 m3 R3 m2 R2 I 2 R1 I1 m1 I4 I3
①
②
I2 m1 U S I6 R3 I 3 m2 I4
① ③
R4
②
US R4
I1 R2
IS
R1
④ (a)
③ (b)
(a)对独立节点列 KCL 方程 节点①: I1 I 2 I5 0 节点②: I 2 I3 I 6 0 节点③: I3 I 4 I5 0 对网孔列 KVL 方程 R1I1 R2 I 2 U S 网孔 m1 : 网孔 m2 : 网孔 m3:
将两个并联的电流源电流相加得图最简等效电路(a-3)。
1A 10V 5 1A 2A 5 3A 5
(a-1)
(a-2)
(a-3)
(b) 图(b)中与电压源并联的 5 电阻不影响端口电压、电流。电路的化简过程 如图(b-1)至图(b-3)所示。
10A 50V 50V 100V (b-2) (b-3) 5 5
20I 2 5 0.1 U 5 0.1A 10I3 U 2V
(b) 对节点①列 KCL 方程: I1 I 2 I3 0.1A 对图示回路列 KVL 方程 回路 l1: 10I1 20I 2 4V 回路 l 2 : 回路 l 3 :
20I 2 10I3 2V 5 0.1A 10I3 U 2V
再对图(a)使用分压公式得: 3 U1 = U =30V 1+3 答案 2.3 解:设 R2 与 5k 的并联等效电阻为 R 5k R3 2 (1) R2 5k 由已知条件得如下联立方程:
R3 U 2 U R R 0.05 1 3 1 R R R 40k 1 3 eq
10 I1
30V
10
10 10 I2 10 I1
30V
10 10 (a)
10 10
I2 10
I1
30V
10 10
10 10 (c)
10
I 图中 1 R 10 (10 10) 20 2 30V I1 1.5A R 由分流公式得 1 I 2 I1 0.75A 2 解法二: 将图中下方的三角形联接等效成星形联接,如图(d)。进一步化简成 图(e)
10
I1 10 10 10 3 3 (d) 10 3 I2 I1 30V
10
5 10 3 (e) 5 3
30V
10
由图(e)求得:
30V 1.5A (10 10 / 3 5 5 / 3) 再由图(d)求得: 1 I 2 0.75A A 0.75A 2 I1
Rx ( R R 2 4Rr ) / 2 因为电阻为正值,所以应保留正的等效电阻, 即 Rx ( R R 2 4Rr ) / 2
(1)
(b) 图(b)为无限长链形电路, 所以从 11' 和 22' 向右看进去的等效电阻均为 Rx , 故计算 Rx 的等效电路如图(b-1)所示。参照图(a-1)及式(1)得:
50V
5 5
(b-1)
注释:在最简等效电源中最多含两个元件:电压源与串联电阻或电流源与并联 电阻。 答案 2.8 解:(a) (1)将电压源串电阻等效为电流源并电阻,如图(a-1)
+
3A 2 6A 4V
_ 2
I
2
7
(a-1)
(2)将两并联电流源电流相加,两 2 电阻并联等效为 1 电阻,2A 电流源与 2 电阻并联等效为 4V 电压源与 2 电阻串联,如图(a-2)
由方程(2)、(3)解得 R1 38k R3 2k 再将 R3 代入(1)式得 10 R2 k 3
(2) (3)
答案 2.4 解:由并联电路分流公式,得 8 I1 20mA 8mA (12 8) 6 I 2 20mA 12mA (4 6) 由节点①的 KCL 得 I I1 I 2 8mA 12mA 4mA 答案 2.5 解:首先将电路化简成图(b)。
I2
270
160
I2 I3 120 I1
140
10A I1 100
U
U3
10A
R2
U1 200
R1
(a)
图 题2.5
(b)
图中
R1 (140 100) 240
(200 160) 120 R2 270 360 (200 160) 120 由并联电路分流公式得 R2 I1 10A 6A R1 R2 及 I 2 10 I1 4A
+
9A 1 4V _ 2 1
+
4V _ 2 I
I
7 9V
7
(a-2)
(a-3)
(3)再等效成图(a-3),由(a-3)求得 (9 4)V I 0.5A (1 2 3)
(b) (1) 将电压源串电阻等效为电流源并电阻,电流源并电阻等效成电压源串电阻, 如图(b-1); (2)将两并联受控电流源电流相加,如图(b-2); (3)再将电流源并电阻等效成电压源串电阻,如图(b-3);
1 3
2 2 2 R
2
4
2
R 1
(b-1)
(b-2)
在图(b-1)中有一平衡电桥,去掉桥(1/3)Ω的电阻,再等效成图(b-2),易求得 1 R 0.2 1 1 1 1 2 4 2 答案 2.10 解:此题有两种解法。 解法一: 由图(a)可以看出, 此图存在平衡电桥。 可将图(a)化为图(b)或(c)的形式。
1
10
Rx
1'
7.5
Rx
(b-1)
Rx ( R R 2 4Rr ) / 2
代入数据得:
Rx
所以
10 102 4 10 7.5 15 2
Rx 15
答案 2.7 解 (a)
电流源 I S 与电阻 R 串联的一端口,其对外作用,可用电流源 I S 等效代
替,如图(a-1);再将电压源与电阻的串联等效成电流源与电阻的串联,如图(a-2);
答案 2.13 解:选网孔为独立回路,如图所示
4
Im2 2 1 5 5V I m3 3 10V
I
I m1
所列方程如下: (1 2 3) I m1 2 I m 2 3 I m3 10V 2 I m1 (2 4) I m 2 5V 3I m1 (3 5) I m3 5V 联立解得 I m1 2.326A , I m2 1.61A , I m3 1.71A 。 利用回路电流求得支路电流 I I m1 I m2 0.717A 答案 2.14 解:选如图所示独立回路,其中受控电流源只包含在 l 3 回路中,其回路电流
Il1 10 I1 ,并且可以不用列写该回路的 KVL 方程。回路电流方程如下:
4 12V
Il 2
3 2 Il1 I1 5
10 I1
Il 3
I
6
(2 3 5) Il1 (3 5) Il 2 5 Il 3 0 (3 5) Il1 (3 4 6 5) Il 2 (5 6) Il 3 12V Il 3 10 Il1 联立解得 Il1 1A Il 2 5A Il 3 10A 所求支路电流 I Il 2 Il 3 5A 答案 2.15 解:适当选取独立回路使受控电流源只流过一个回路电流,如图所示。
I
76V 4Ω
0.5 I
0.6I
5Ω
I
76V 4Ω (b-2)
(b-1)
I
76V 5Ω 0.5I
0.1I 5Ω 4Ω
(d)
