连续时间系统的时域分析卷积法
第二章 连续系统的时域分析

du (t ) 整理方程组得:d 2u2 (t ) + 7 2 + 6u2 (t ) = 6e(t ) dt 2 dt 特征方程:a2+7a+6=0 特征根:a=-1, a=-6 齐次解:rh(t) = A1e-t +A2e-6t
5
第二章 连续系统的时域分析
② 选定特解后,将它代入到原微分方程,即得到一个由 yh(t)及其各阶导数以及激励共同组成的一个非齐次微 分方程,依据此方程求出待定系数,然后可确定方程 的特解。
3. 求系统的全响应y(t)
y(t)=方程的全解y(t)=齐次解yh(t) + 特解 yP(t)
=自由响应+强迫响应 将上面方程的全解代入系统的初始条件即可得齐次解中 的待定系数,从而进一步得到系统的全响应。此时, 方程的齐次解yh(t)为系统的自由响应,特解yP(t)为系 统的强迫响应(固有响应)。
解: 由原方程可得
dh 2 (t ) dh(t ) +3 + 2h(t ) = 2δ ′(t ) + 3δ (t ) 2 dt dt
(t ≥ 0)
特征方程: λ2+3λ+2 = 0 特征根: λ1= -1,λ2= -2,且n > m
h (t ) = Ae − t u (t ) + e −2 t (t ) u(t)
20
第二章 连续系统的时域分析
式中A、B为待定系数,将h(t)代入原方程 式,解得A=1,B=1。因此,系统的冲激 响应为 h(t ) = e − t u(t ) + e −2 t (t )
21
第二章 连续系统的时域分析
信号与系统第二章第一讲

则相应于1的k阶重根,有k项:
( A1t k 1 A2t k 2 Ak 1t Ak )e1t ( Ai t k i )e1t
i 1
k
例2-3
信 号 与 系 统
求如下所示的微分方程的齐次解。
Hale Waihona Puke d3 d2 d r (t ) 7 2 r (t ) 16 r (t ) 12r (t ) e(t ) 3 dt dt dt
等式两端各对应幂次的系数应相等,于是有:
信 号 与 系 统
特解为: 联立解得:
3B1 1 4 B1 3B2 2 2 B 2 B 3 B 0 2 3 1
统
线性时不变系统
线性的常系数微分方程
按照元件的约束特性及 系统结构的约束特性
也即:
具体系统物理模型
常系数微分方程建立
(1)元件端口的电压与电流约束关系
iR (t ) R
信 号 与 系 统
vR (t )
C
vR (t ) iR (t ) R
dvC (t ) iC (t ) C dt
vR (t ) Ri R (t )
与
时域经典法就是直接求解系统微分方程的方法。这种方 系 法的优点是直观,物理概念清楚,缺点是求解过程冗繁,应 用上也有局限性。所以在20世纪50年代以前,人们普遍喜欢 统 采用变换域分析方法(例如拉普拉斯变换法),而较少采用时 域经典法。20世纪50年代以后,由于δ(t)函数及计算机的普 遍应用,时域卷积法得到了迅速发展,且不断成熟和完善, 已成为系统分析的重要方法之一。时域分析法是各种变换域 分析法的基础。
信 号 与 系 统
is (t )
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解-第2章 连续时间系统的时域分析【圣才

Ri(t) v1(t) e(t)
Ri(t)
1 C
t
i(
)d
v1 (t )
e(t)
vo (t) v1(t)
消元可得微分方程:
6 / 59
圣才电子书
十万种考研考证电子书、题库视频学习平
1
台
C
d
dt
vo (t)
1 R
vo (t)
R
e(t)
2-2 图 2-2-2 所示为理想火箭推动器模型。火箭质量为 m1,荷载舱质量为 m2,两 者中间用刚度系数为 k 的弹簧相连接。火箭和荷载舱各自受到摩擦力的作用,摩擦系数分 别为 f1 和 f2。求火箭推进力 e(t)与荷载舱运动速度 v2(t)之间的微分方程表示。
M
di1 (t ) dt
Ri2 (t)
0
化简方程组可得微分方程:
(L2
M
2
)
d4 dt 4
vo
(t)
2RL
d3 dt 3
vo
(t)
2L C
R2
d2 dt 2
vo
(t)
2R C
d dt
vo
(t)
1 C2
vo
(t)
MR
d2 dt 2
e(t)
(3)由图 2-2-1(c)所示列写电路方程,得:
C
dv1 (t ) dt
b.自由响应由两部分组成,其中,一部分由起始状态决定,另一部分由激励信号决 定,二者都与系统的自身参数有关;当系统 0-状态为零,则零输入响应为零,但自由响应 可以不为零。
c.零输入响应在 0-时刻到 0+时刻不跳变,此时刻若发生跳变,可能为零状态响应分 量。
连续时间信号的时域分析和频域分析

时域与频域分析的概述
时域分析
研究信号随时间变化的规律,主 要关注信号的幅度、相位、频率 等参数。
频域分析
将信号从时间域转换到频率域, 研究信号的频率成分和频率变化 规律。
02
连续时间信号的时
域分析
时域信号的定义与表示
定义
时域信号是在时间轴上取值的信号, 通常用 $x(t)$ 表示。
表示
时域信号可以用图形表示,即波形图 ,也可以用数学表达式表示。
05
实际应用案例
音频信号处理
音频信号的时域分析
波形分析:通过观察音频信号的时域波形,可 以初步了解信号的幅度、频率和相位信息。
特征提取:从音频信号中提取出各种特征,如 短时能量、短时过零率等,用于后续的分类或 识别。
音频信号的频域分析
傅里叶变换:将音频信号从时域转换 到频域,便于分析信号的频率成分。
通信系统
在通信系统中,傅里叶变 换用于信号调制和解调, 以及频谱分析和信号恢复。
时频分析方法
01
短时傅里叶变换
通过在时间上滑动窗口来分析信 号的局部特性,能够反映信号的 时频分布。
小波变换
02
03
希尔伯特-黄变换
通过小波基函数的伸缩和平移来 分析信号在不同尺度上的特性, 适用于非平稳信号的分析。
将信号分解成固有模态函数,能 够反映信号的局部特性和包络线 变化。
频域信号的运算
乘法运算
01
在频域中,两个信号的乘积对应于将它们的频域表示
相乘。
卷积运算
02 在频域中,两个信号的卷积对应于将它们的频域表示
相乘后再进行逆傅里叶变换。
滤波器设计
03
在频域中,通过对频域信号进行加权处理,可以设计
信号与系统杨晓非课后答案

信号与系统杨晓非课后答案【篇一:《信号与系统》考试大纲】>(一)信号与系统的基本概念信号的基本概念及其分类,信号的表示方法,典型连续信号及其性质,典型离散信号及性质,信号的基本运算和变换,系统的基本概念及其分类,线性非时变系统及其性质,系统性质的判定,连续系统与离散系统的数学模型,离散系统数学模型的建立,连续系统的时域模拟。
(二)连续系统的时域卷积分析法 lti连续系统的时域经典分析法。
冲激响应、阶跃响应及其与冲激响应的关系;任意波形信号的时域分解与卷积积分的定义,卷积积分的图解法和阶跃函数法、求解卷积的运算性质,lti连续系统零状态响应的卷积分析法,运用杜阿密尔积分求解系统的零状态响应。
lti离散系统的时域经典分析法。
单位序列响应、阶跃响应及其与单位序列响应的关系;任意波形离散信号的时域分解与积卷和的定义,卷积和的图解法、时限序列卷积和的不进位乘法和算式法求解、卷积和的运算性质,lti离散系统零状态响应的卷积和分析法。
(三)信号的频谱分析与傅里叶变换分析法周期信号表为傅里叶级数,周期信号的频谱及其特点,周期信号的功率谱。
非周期信号的傅里叶变换,频谱密度及其特点,典型信号的傅里叶变换,傅里叶变换的性质,周期信号的傅里叶变换,能量谱密度和功率谱密度。
频域系统函数h(j?),lti连续系统零状态响应的傅里叶变换分析法,系统无失真传输的条件;无失真传输系统和理想低通滤波器的冲激响应与阶跃响应,抽样定理。
(四)拉普拉斯变换分析法拉普拉斯变换及其收敛域,单边拉普拉斯变换,典型信号的单边拉普拉斯变换,单边拉普拉斯变换的性质,求拉普拉斯反变换的部分分式展开法和留数法,单边拉普拉斯变换与傅里叶变换的关系。
微分方程的拉普拉斯变换解,lti连续系统的s域分析法,电路的s 域分析法,系统函数h(s)在系统分析中的意义及求取,系统信号流图及其化简与模拟。
系统函数的零、极点概念,零极点图,连续系统函数h(s)的零极点分布与系统的时间特性、频率特性、因果性以及稳定性的定性关系,系统稳定性的判别。
考研专业课郑君里版《信号与系统》第二章补充习题——附带答案详解
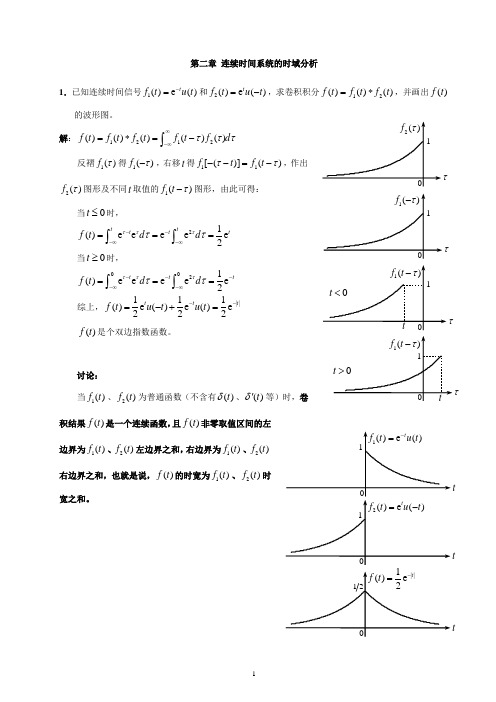
第二章 连续时间系统的时域分析1.已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-,求卷积积分12()()()f t f t f t =*,并画出()f t 的波形图。
解:1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-,右移t 得11[()]()f t f t ττ--=-,作出2()f τ图形及不同t 取值的1()f t τ-图形,由此可得:当0t ≤时,21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时,0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上,||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。
讨论:当1()f t 、2()f t 为普通函数(不含有()t δ、()t δ'等)时,卷积结果()f t 是一个连续函数,且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和,右边界为1()f t 、2()f t 右边界之和,也就是说,()f t 的时宽为1()f t 、2()f t 时宽之和。
τttt2.计算题图2(a )所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=,并画出)(t f 的图形。
解法一:图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b),由此可得: 当10t +≤,即1t ≤-时,()0f t = 当011t ≤+≤,即10t -≤≤时,120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤,即01t ≤≤时,1()21f t d ττ==⎰当011t ≤-≤,即12t ≤≤时,121()21(1)t f t d t ττ-==--⎰当11t -≥,即2t ≥时,()0f t =综上,220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。
第二章 连续时间系统的时域分析 重要公式

零状态响应 rzs ( t ) 的求解有两种方法 方法一:直接求解微分方程 步骤: (1)求出通解;
(k ) (0 + ) = r (k ) (0 + ) − r (k ) (0 − ) 确定 n 个待定常数。 (2)由跳变量 rzs
方法二:卷积积分法 步骤: (1)先求冲激响应 h(t ) ; (2)再利用 rzs (t ) = h(t ) ∗ e(t ) 求零状态响应。 五、冲激响应 h ( t ) 和阶跃响应 g ( t ) 1、冲激响应 h ( t ) 的定义 定义: 系统在单位冲激信号 δ ( t ) 的激励下产生的零状态响应, 称为冲激响应。 冲激响应 h ( t ) 满足的微分方程为:
4
方法一:比较系数(等式两端奇异函数项相平衡)法求 h ( t ) 步骤:a. 先求特征根,直接写出冲激响应的函数形式; b. 再用冲激函数平衡法确定系数 Ak 。 方法二:利用系统的线性时不变特性求 h ( t ) 对于 h ( t ) 满足的微分方程
dn d n −1 d h(t ) + a n −1 n −1 h(t ) + + a1 h(t ) + a 0 h(t ) n dt dt dt
dn d n −1 d ( ) r t a + r (t ) + + a1 r (t ) + a 0 r (t ) n −1 n n −1 dt dt dt
= bm dm d m −1 d ( ) e t b e(t ) + + b1 e(t ) + b0 e(t ) + m −1 m m −1 dt dt dt
dn d n −1 d ( ) h t a h(t ) + + a1 h(t ) + a 0 h(t ) + n −1 n n −1 dt dt dt
信号与系统-第2章

f (t)
K
两式相加:
cosωt =
1 2
(e
jωt
+
e
jωt )
(2-4)
0 K
t
两式相减:
sinωt =
1 2j
(e
jωt
-e
jωt )
(2-5)
(3) 复指数信号: f(t) = Ke st = Ke (σ+ jω)t
= Keσt (cosωt + j sinωt)
当 σ > 0 时为增幅振荡 ω = 0 时为实指数信号 σ < 0 时为衰减振荡
2
01
t
f(
1 2
t)
=
1 2
t
0
0<t <4 其它
f(12 t)
2 0
4t
注意: 平移、反折和展缩都是用新的时间变量去代换原来的
时间变量, 而信号幅度不变.
t +2 -2<t<0 例2-5:已知 f(t) = -2t + 2 0<t<1
f (t)
2
0
其它
-2 0 1
t
求 f(2t-1),
f(
1 2
(1) 相加和相乘
信号相加: f t f1t f2 t fn t 信号相乘: f t f1t f2 t fn t
0 t<0 例2-1:已知 f1(t) = sint t ≥ 0 , f2(t) =-sint, 求和积.
解: f1(t) + f2(t) =
-sint 0
t<0 t≥0
0
t<0
f1(t) f2(t) = -sin2t t ≥ 0 也可通过波形相加和相乘.
∞ t=0 作用: 方便信号运算.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1 计算
例2 计算
R(t)
f (t) 1
0
t 1
h(t) 1
0
2t
二、卷积的性质
已知 f (t) f1(t) f2 (t) 则 f1(t t1) f2 (t t2 ) f (t t1 t2 )
f1(at) f2(at)
1 a
f (at)
位移特性证明:
f1(t t1) f2 (t t2 ) f1( t1) f2 (t t2 )d
0
3
例1
卷积积分的计算和性质
一、卷积积分的计算
f (t)
f1(t)
f2(t)
f1
(
)
f2
(t
)d
1)将 f1(t)和f2(t)中的自变量由 t 和 ,成为函数的
自变量; 2)把其中一个信号翻转、平移;
f2 ( ) 翻转 f2 ( ) 平移 t f2 (( t)) f2 (t
3)将 f1(t)与 f2(t 相乘;对乘积后的图形积分。
已知 f (t) f1(t) f2 (t)
则 f1(t t1) f2 (t t2 ) f1(t t2 ) f2 (t t1) f (t t1 t2 )
证明:
f1(t t1) f2(t t2) f1(t) (t t1) f2(t) (t t2) f1(t) (t t2) f2(t) (t t1)
代入方程
a (t) b (t) c (t) du(t) 7a (t) b (t) cu(t)
10[a (t) bu(t)] (t) 6 (t) 4 (t)
得a 1 b 7a 6 c 7b 10a 4
a 1 b 1 c 1
代入h(t)
A12A1A2
1 5A2
d
2r dt
(t
2
)
4
dr(t dt
)
4r
(t
)
2
de(t dt
)
3e(t
),
t0
系统的初始状态为 r(0) 2,r(0) 1 ,求系统的零
输入响应 rzi (t) 。 解:系统的特征方程为 4 4
( 2
系统的特征根为
2 (两相等实根)
rzi (t) ( A1 A2t)e2t
5 6 ( 3
系统的特征根为
2, 3
rzi (t) A1e2t A2e3t
r(0) rzi (0) A1 A2 1
解得 A1 6, A2 5
r(0) rzi (0) 2A1 3A2 3
rzi (t) 6e2t 5e3t , t 0
例2 已知某线性时不变连续系统的动态方程式为:
试求系统的单位冲激响应。
解:当 e(t) (t)时,r(t) h(t), 即 dh(t) 3h(t) 2 (t)
dt
动态方程式的根 ,且n m,故h(t)的形式为
h(t) Ae3tu(t)
d [ Ae3tu(t)] 3Ae3tu(t) 2 (t)
dt
Ae3t (t) 3Ae3tu(t) 3Ae3tu(t) 2 (t) Ae 3t (t) 2 (t)
由于t 0 后,方程右端为零,故n m时
h(t
)
(
n
Ak
e
k
t
)u
(t
)
k 1
n m时,为使方程两边平衡,h(t)应含有冲激函数及其 各阶导数
h(t)
(
n
Ak
ekt
)u(t)
mn
Bl
l
(t)
k 1
l 0
将h(t )代入微分方程,使方程两边平衡,确定系数Ak,Bl
例1 已知某线性时不变连续系统的动态方程式为: dr(t) 3r(t) 2e(t), t 0 dt
Ae6t (t) B (t) 6B (t) 2 (t) 3 (t)
A 6B 2 B 3
解得 A 16, B 3
h(t) 3 (t) 16e6tu(t)
例2-9 对例2-5所示电路,求电流i(t)对激励e(t) (t)
的冲激响应。
解:
d2 dt 2
i(t)
7
d dt
i(t)
1
a
f1(x) f2 (at x))dx
1 a
f (at)
二、卷积的性质
6)微分特性
d dt
[
f1(t
)
f2 (t)]
f1(t
)
df2 (t dt
)
f1(t)
f (1) 2
(t
)
7)积分特性
df1(t) dt
f2 (t)
f2(t)
f (1)
1
(t
)
t[ f1(
f2 ( )]d
f1(t) t
e(t) e( ) t )d
rzs (t) e( )h(t d
rzs (t) e( )h(t d e(t) h(t)
例4已知某LTI系统的动态方程式为 r(t) 3r(t) 2e(t), 系统的冲激响应h(t) 2e3tu(t),e(t) 3u(t), 试求系统的
零状态响应rzs (t) 。
10i(t)
d2 dt 2
e(t)
6
d dt
e(t
)
4e(t)
系统冲激响应h(t),满足方程
d2 dt 2
h(t)
7
d dt
h(t)
10h(t)
(t)
6
(t)
4
(t)
它的奇次解形式为 h(t) A1e2t A2e5t (t 0 )
用冲激函数匹配法求h(0 )和h(0 )
h(t) a (t) b (t) c (t) du(t) h(t) a (t) b (t) cu(t) h(t) a (t) bu(t)
1
因为a 1,即h(t)中有一项a (t)
hh((00))
b h(0) c h(0)
1 1
A1 A2
4 13
3
h(t)
(t)
4 3
e2t
1 3
e5t
u(t)
冲激平衡法小结
n
mn
h(t) ( Akekt )u(t) Bl l (t)
k 1
l 0
n
1)由系统的特征根来确定 Akekt的形式。 k 1
t[ f1(
f2 ( )]d
f2
(t
)
t
f1()d
例:利用位移特性及u(t) u(t) R(t),计算y(t) f (t) h(t)。
f (t)
h(t)
1
1
0
t
1
0
t 2
y(t) f (t) h(t) [u(t) u(t 1)][u(t) u(t 2)] u(t) u(t) u(t) u(t 1) u(t) u(t 2) u(t 1) u(t 2) R(t) R(t 1) R(t 2) R(t 3)
f2 ( )d
f1(t)
f
( 1) 2
(t
)
f2
(t
)
t
f1()d
f2(t)
f (1)
1
(t
)
推广导高阶导数或多重积分
设 s(t) [ f1(t) f2 (t)]
则有
s(i) (t)
f1( j) (t)
f
(i 2
j
)
(t
)
微分特性证明:
同理
d
dt
[
f1 (t )
f2 (t)]
d dt
f1( ) f2 (t )d
t0
系统的初始状态为 r(0) 1,r(0) 3 ,求系统的零
输入响应 rzi (t) 。 解:系统的特征方程为 2 5
系统的特征根为 1 2 j, 1 2 j
rzi (t) et ( A1 cos 2t A2 sin 2t)
r(0) rzi (0) A1 1 r(0) rzi (0) A1 2 A2 3
dt 动态方程式的特征根 6, 且 n m, 故 h(t) 的形式为
h(t) Ae6tu(t) B t)
d [ Ae6tu(t) B (t)] 6[ Ae6tu(t) B (t)] 2 (t) 3 (t)
dt
Ae6t (t) 6Ae6tu(t) B (t) 6Ae6tu(t) 6B (t) 2 (t) 3 (t)
f (t) (k) (t) f (k) (t) f (t) (k) (t t0 ) f (k) (t t0 )
例3
f1(t t2 ) f2 (t t1)
f1(t t1) f2(t t2) f1(t) (t t1) f2(t) (t t2)
f1(t) f2 (t) (t t2 ) (t t1) f (t) (t t1 t2)
f (t t1 t2 )
三、奇异信号的卷积
t1x
f1(x) f2 (t t2 t1 x)dx
f (t t1 t2 )
展缩特性证明:
f1(at) f2 (at) f1(a ) f2(a(t ))d
a x
1 a
f1(x) f2 (at x))dx
1 a
f1(x) f2 (at x))dx
a0 a0
f1
(
)
d dt
f2 (t )d
f1
(t
)
df2 (t dt
)
d[ dt
f1(t)
f2 (t)]
df1 (t ) dt
f2 (t)
积分特性证明:
t[ f1( f2()]d
t
t
f1( ) f2 (
)d d
t
f1
