完全四点形的调和性
完全四点形和完全四线形调和性质应用例析

完全四点形和完全四线形调和性质应用例析作者:何璇摘要本文对高等几何中的完全四点(线)形的调和性质进行了归纳整理,主要研究内容是通过运用完全四点形和完全四线形调和性质解决一些几何证明、几何作图、研究二次曲线的一些性质等几何问题,来体现高等几何的一些思想观点和方法。
从而能够用现代几何学的观点处理初等几何问题,使解题更简洁,拓宽解题思路 ,提高解题能力。
关键词:完全四点(线)形;调和性质;高等几何;初等几何AbstractThe paper gives a simple summary to harmonicity of complete quadrangle (complete quadrilateral) in Higher Geometry. Its main research content is to figure out some problems including geometrical proving, geometrical drawing and researching the characters of the conics via the harmonicity of the complete quadrangle (complete quadrilateral), which incarnates some viewpoints and methods in higher geometry. Accordingly, we can deal with the problems on elementary geometry by using views of modernistic geometry, which can simply solve problems, broaden train of thought and improve the capacity to solve problems.Key words: complete quadrangle (complete quadrilateral); harmonicity; Higher Geometry; Elementary Geometry1.前言射影几何对初等几何教学的指导,不仅表现在提高数学思想与观点上,还直接表现于对初等几何图形的射影性质的研究中(参见文[9][11])。
完全四边形与完全四点形

4.3 完全四点形和完全四线形内容解析定义4.5 平面内无三点共线的四点及其两两连线所构成的图形,叫做完全四点形. 见图4-3,这个图形含有四个点D C B A ,,,,及六条直线AB ,BC ,CD ,DA ,BD ,AC ,每一个点称为顶点,每一条直线称为边.如图4-5所示,不过同一顶点的两边称为对边(如AD 与BC ),共有三对对边.每一对对边的交点称为对边点或对角点(如AD 与BC 的交点S ),三个对边点(SQR )构成的三角形(三点形)称为对边三角形.定义4.6 平面内无三线共点的四直线及其两两的交点#所构成的图形,叫做完全四线形.见图4-6,这个图形含有四条直线(d c b a ,,,)和六个点(A ,B ,C ,D ,E ,F ),每一条直线称为边,每一个点称为顶点.不在同一边上的两个顶点称为对顶点(如A 与D ).六个顶点分为三对,每一对对顶点的连线,称为对顶线(AD ,EC ,BF ),三条对顶线构成的三角形称为对角三角形(PQR ).完全四点形和完全四线形具有如下性质.定理4.9 完全四点形通过每一个对角点有一组调和线束,即通过这个对角点的两边和34-图B C DA 54-图B CD A S Q R 64-图P Q R a b c dAB CD E F对角三角形的两边.如图4-5,比如对角点S 的两边SA 、SB 和对角三角形SQR 的两边SR 、SQ .是一组调和线束. 定理4.10 完全四线形的每一条对角线上有一组调和点列,即这条直线上的两个顶点及对角三角形的两个点.如图4-6,比如对角线CE 上的两个顶点C 、E 和对角三角形PQR 的两个顶点P 、Q , 是一组调和点列.典型例题例1 设XYZ 是完全四点形ABCD 的对边三点形,XZ 分别交BD AC ,于M L ,,不用笛沙格定理,证明CM BL YZ ,,共点.证明如图4-7,54-图BC D AS QR64-图PQ R a b c dAB CD E F 74-图对四线形ABCD ,根据定理4.10可知,在对角线AC 边上的四点L Y C A ,,,调和共轭,即1),(-=YL AC .在四点形YBZL 中,LB 与YZ 交于N ,设MN 与YL 交于C ',由定理4.9可知,过对角点M 有一组调和线束,即MA 、C M '和MY 、ML ,于是1),(-='YL C A ,所以,点C 应与点C '重合,即CM BL YZ ,,共点.(二)完全四点形与完全四线形的调和性习题答案1.设XYZ 是完全四点形ABCD 的对边三点形,XZ 分别交AC 、BD 于L 、M ,不用狄沙格定理证明:YZ 、BL 、CM 共点。
复习要点

二、仿射变换的性质、代数式、图形的仿射性质 仿射变换的性质、代数式、 1. 单比的概念: ( ABC ) =
AC BC
2. (ABC)= -1的充要条件是C是AB的中点,
x3 − x1 y3 − y1 = 3. 单比的代数表达式: ( ABC ) = x3 − x2 y3 − y2
4. 仿射变换的不变性质:同素性、结合性、平行性、共线 三点的单比不变、二平行线段之比不变、二封闭图形面积之 比不变 注:仿射变换的基本不变量是单比
第三章
射影变换与射影坐标
一、交比的定义、性质、代数表达式 交比的定义、性质、 1 交比的定义: ( AB, CD) = 2. 交比的性质: 1) (AB,CD)=(CD,AB)
1 2) (BA,CD)=(AB,DC)= ( AB, CD) ( ABC ) AC BD = ( ABD) BC AD
3) (AB,CD)=(BA,DC) 4) (AC,BD)=(DB,CA)=1 -(AB,CD)
第二章
射影平面
一、扩大欧氏平面的必要性 引进无穷远元素的方法: 二、 引进无穷远元素的方法: 1 无穷远点是二维空间中二平行线的交点;无穷远直线是
三维空间中二平行平面的交线; 2. 每一条有穷远直线上有一个唯一的无穷远点,这个无穷 远点是与该直线平行的所有直线的公共交点; 3. 无穷远直线上所有点都是无穷远点,即平面上两个无穷 远点的连线必是无穷远直线;
三、直径和共轭直径 1. 直径和共轭直径的仿射定义 2. 直径的方程 3. 两条直径成为共轭的条件 四、二次曲线的渐近线 1. 渐近线的仿射定义 2. 渐近线的性质 3. 渐近线的方程
3 x 2 + 2 xy − 2 y 2 + 4 x + 2 y + 1 = 0 1. 判定二次曲线
关于点共线、线共点问题的多种证法

关于点共线、线共点问题的多种证法学生姓名:贾娟 指导教师:杨慧摘要: 在初等几何中,我们常常会遇到点共线、线共点这方面的问题。
而射影几何的基本不变性是点线的结合性,因此点共线、线共点问题是射影几何的主要研究对象之一。
对于点共线、线共点问题的解决方法也有很多,本文则主要探讨的是利用射影几何方法与初等几何方法解决这类问题,通过比较发现具体问题用哪种方法更合适,以及解题时需要注意的问题。
关键词: 射影变换 德萨格定理 完全四点形 赛瓦定理 一维基本形的透视对应作为师范类院校的学生,将来若想成为一名合格的中学数学教师,就必须在学习解析几何的基础上再进一步学习高等几何。
而高等几何对中学数学教师几何基础的培养、解题观点的提高、思维方法的多样性等都起着重要的指导作用。
对于高等几何到来说,尤其是其中的射影几何,既包含了解析几何中主要研究图形性质的内容,也融合了欧氏几何中主要研究空间几何结构的内容。
因此,学习高等几何知识,不仅使我们开阔了几何学的视野,也让我们更好地理解、把握了初等几何的本质。
比如初等几何中点共线、线共点的问题,在中学数学教学中既是一个重点也是一个难点。
如果只是用初等几何方法去解决,有时会很复杂,相反若要用射影几何中的知识如完全四点形的调和性质、德萨格定理及其逆定理、一维基本形的透视对应性质等知识点来解决,会更简便。
这样也为我们提供了多种解决初等几何问题的研究方法。
用高等几何的观点指导初等几何的教学内容,进而不断地改进初等几何的教学方式,这样也有助于提高中学几何的教学质量。
1.主要定义及定理 一维基本形的透视对应:定义1如果一个点列与一个线束的元素之间建立了一一对应且对应元素是结合的,则这个对应叫做点列与线束之间的透视对应。
同理,如果两个点列与同一线束成透视对应,则这两个点列叫做透视点列;如果两个线束与同一点列成透视对应,则这两个线束叫透视线束。
由此可知,两个成透视对应的点列,其对应点之连线共点。
高等几何2.2
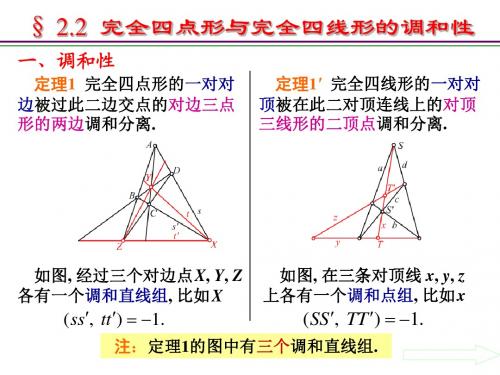
一、调和性
定理1 完全四点形的一对对 边被过此二边交点的对边三点 形的两边调和分离. 定理1' 完全四线形的一对对 顶被在此二对顶连线上的对顶 三线形的二顶点调和分离.
如图, 经过三个对边点 X, Y, Z 各有一个调和直线组, 比如 X
如图, 在三条对顶线 x, y, z 上各有一个调和点组, 比如 x
比如在边t上, 有
( XY , PQ) 1.
比如经过顶点T, 有
( xy, pq) 1.
注:推论1的图中有三个调和点组.
§ 2.2 完全四点形与完全四线形的调和性
推论2 在完全四点形的每条 边上有一个调和点组, 其中一 对为顶点, 另一对中一个为对 边点, 一个为该边与对边三点 形的边的交点. 推论2' 通过完全四线形的每 个顶点有一个调和直线组, 其 中一对为边, 另一对中, 一条为 对顶线, 一条为该顶点与对顶 三线形顶点的连线.
比如在边AB上, 有
比如经过顶点a×b, 有
( AB, PZ ) 1.
(ab, pz) 1.
注:推论2的图中有六个调和点组.
§ 2.2 完全四点形与完全四线形的调和性
二、应用
1. 第四调和元素的作图 例1 已知直线l上相异三点P1, P2, P3. 求作第四调和点P4. 分析: 利用推论1, 构造一个完全四点形, 以l为其对边三点形的一边, P1, P2是对边点, 使第三对对边中, 一条过P3, 则另一条与l的 交点即为P4. 作法: (1). 在l外任取一点 A, 连AP1, AP2. (2). 过P3作直线分别交AP1, AP2于B, D.
§ 2.2 完全四点形与完全四线形的调和性
高等几何第二章2013

§ 2.1 交比
一、点列中四点的交比 1. 定义
2. 性质 3. 特殊情况 定理2.3 共线四点的交比值出现0, 1, 三者之一这四点中有 某二点相同. 证明 根据定理2.1,令P1=P2或P2=P3或P3=P4或P4=P1直接验证. 此时, 上述6个不同的交比值又只有3组:0, 1, .
§ 2.1 交比
一、点列中四点的交比 1. 定义
4. 调和比 5. 交比的计算 (1) 由坐标求交比 例2 已知P1(3,1,1), P2(7,5,1), Q1(6,4,1), Q2(9,7,1). 求(P1 P2, Q1 Q2). 解 第一步. 验证四点共线. 第二步. 以P1, P2为基点, 参数表示Q1, Q2. 令 iQi P i P2 . i=1,2. 1 对于i=1, 利用P.34例1.3, 有1 3. 对于i=2, 同理求得 2 3. 于是, 2. 性质 3. 特殊情况
而 于是
1 ( p1 p2 , p3 p4 ) ( P P2 , P3 P4 ). 1 2
§ 2.1 交比
二、线束中四直线的交比
1. 线束的参数表示 则 2. 定义 3. 交比为射影不变量
定理2.6 设线束S(p)中四直线pi被直线s截于四点Pi(i=1,2,3,4).
( p1 p2 , p3 p4 ) ( P P2 , P3 P4 ). 1
( PP2 , P P4 ) k , 1 3
(k 0,1, )
和其中三点的坐标. 则第四点的坐标可唯一确定.
§ 2.1 交比
一、点列中四点的交比 1. 定义
4. 调和比 5. 交比的计算 (2) 由交比求坐标 例3 已知P1, P2分别是x轴、y轴上的无穷远点, P3是斜率为1的 方向上的无穷远点, 且(P1P2,P3P4)=r. 求P4的坐标. 解:由题设知P1, P2, P3的坐标分别为(1,0,0), (0,1,0), (1,1,0). 设
高等几何中的调和共轭
高等几何中的调和共轭调和共轭是高等几何中最重要的概念之一, 有关平面图形与二次曲线的许多重要概念和性质都与此密切相关。
它是联系高等几何中各主要概念的一条主线。
本文系统讨论调和共轭概念在高等几何中的重要应用。
1 调和共轭的概念及其重要应用调和共轭: 已知共线四点A、B、C、D, 如果按此顺序的交比(AB, CD) = - 1, 那么就称C、D 关于A、B 成调和共轭, 或称A、B、C、D 成调和点列。
对偶地, 对于共点的四直线a、b、c、d, 如果按此顺序的交比(ab, cd) = - 1则称c、d 关于a、b 成调和共轭, 或称a、b、c、d 成调和线束。
下面列举出可由调和共轭导引出的一些重要概念, 这里略去了全部结论的证明。
(1) 射影变换: 射影变换是将成调和共轭的任意四元素仍变为调和共轭四元素的点变换或线变换。
(2) 线段的中点: 线段的中点是这直线上无穷远点关于线段两端点的调和共轭点。
角的平分线: 角的内、外角平分线关于角的两边成调和共轭。
( 3) 线段的调和中项: 若A、B、C、D 成调和点列, 则线段CD 是线段CA 和CB 的调和中项。
(4) 关于圆的反演: 平面上(不在圆周上的) 一点P 关于已知圆的反演点P′是点P 关于连线PP′与圆的两交点的调和共轭点。
(5) 对合对应: 对合对应中的任一对对应点关于这对合的两个二重元素成调和共轭。
(6) 完全四点形的调和性质: 完全四点形过每一对角点有一组调和线束, 即过这对角点的对角三角形的两条边关于过这对角点的完全四点形的两条边成调和共轭。
完全四线形的调和性质: 完全四线形的每一条对角线上有一组调和点列, 即这对角线上的对角三角形的两顶点关于这对角线上的完全四线形的两顶点成调和共轭。
(7) 关于二次曲线的共轭点: 给定点P, 若另一点P′使得点P、P′关于它们的连线PP′与二次曲线# 的两交点成调和共轭, 则点P′称为点P 关于二次曲线# 的一个共轭点。
完全四边形调和点列证明
完全四边形调和点列证明完全四边形调和点列是指在平面上给定4个不共线的点A、B、C、D及它们的共轭点A'、B'、C'、D',并且这8个点满足调和性质,即(ABCD)=-1。
其中,ABCD表示A与B连线、C与D连线的交点。
调和性质可以表示为以下等式:(AA')/(AC') * (BD')/(BA') = -1(BB')/(BD') * (CA')/(CB') = -1(CC')/(CA') * (DB')/(DC') = -1(DD')/(DB') * (AC')/(AD') = -1对于完全四边形调和点列的证明,我们可以从多个角度进行阐述。
一、几何证明方法:1.利用平行线性质证明:在平面上,如果一组平行线通过一个调和四边形的对角线,则它们必定也通过该调和四边形的共轭对角线。
根据这个性质,我们可以得出扩展的拉美定理(扩展的拉美定理表示:如果A、B、C是一条直线上的三个点,D、E、F是另一条直线上的三个点,那么如果AD、BE、CF交于一点,则AE、DF和BC也必定交于一点)。
利用扩展的拉美定理,可以证明完全四边形调和点列中的任意四个点满足调和性质。
2.利用交比性质证明:在平面几何中,交比是指若干条线段的比值,可以用于表示调和性质。
对于完全四边形调和点列,我们可以使用逆向交比等式进行证明,具体通过运用调和性质的定义和多个交比定义来推导。
二、代数证明方法:可以使用代数运算进行证明,通过直线与坐标系的关系来推导出调和点列的性质。
具体可以通过线的方程来证明四个点的交点满足调和性质,并通过坐标的代数运算来证明三、向量证明方法:利用向量的加法与减法、数量积和矢积等定义和性质进行证明。
具体可以通过定义向量的坐标映射,利用向量的线性叠加性质进行证明。
四、复数证明方法:可以利用复数与几何的关系进行证明。
第二节调和比
X
M E
Y
又因为DX⊥DY,所以AD、BC平分∠EDF。
菠萝岩
边上有一个调和点组, 其中一
对为顶点, 另一对中一个为对 边点, 一个为该边与对边三点 形的边的交点.
例1 已知直线l上相异三点P1, P2, P3. 求作第四调和点P4. 分析:利用推论1, 构造一个完全四点形, 以l为其对边三点形的一边, P1, P2是对边点, 使第三对对边中, 一条过P3, 则另一条与l的 交点即为P4. 解. 作法: (1). 在l外任取一点A, 连AP1, AP2. (2). 过P3作直线分别交AP1, AP2于B, D. (3). 连P1D, P2B交于C. (4). 连AC交l于P4为所求. 注1 上述实际上也是利用推论2作图. 注2 本例引申
§2 完全四点形的调和性
1. 调和比 例1 (1)设C为线段AB的中点,P为直线AB上的无穷 远点, 试求: (AB, CP) 。
(2) 设直线c, d分别是由直线a, b所成角的平分线,
试求: (ab,cd)。
点偶P ,P ,与P ,P (互为)调和分离 1 2 3 4 定义 若(P1P2,P3P4 )= –1, 则称 点偶P1,P2,与P3,P4(互为)调和共轭 交比值“–1” 为 调和比。 点P4为P1,P2,P3的第四调和点
推论1 在完全四点形的对
边三点形的每条边上, 有一个 调和点组, 其中一对为对边点, 另一对为该边与第三组对边的 交点. 推论2 在完全四点形的每条
推论1’ 通过完全四线形的
对顶三线形的每个顶点有一个 调和直线组, 其中一对为对顶 线,另一对为该顶点与第三对 对顶的连线. 推论2’ 通过完全四线形的每 个顶点有一个调和直线组, 其 中一对为边,另一对中, 一条 为对顶线, 一条为该顶点与对 顶三线形顶点的连线.
几何中的调和分割及应用
几何中的调和分割及应用郑皎月(安康学院数学系 陕西 安康 725000)摘要: “调和分割”又称“调和共轭”,它是交比研究中的一个重要特例,也是 贯穿大学《高等几何》课程的一个重要概念,应用它解决初等几何中有关平分角、平分线段以及高等几何中有关对合的性质、完全四点型的调和分割、完全四线型调和分割以及拉盖尔定理的推广等性质有着积极的意义。
关键字:调和分割 高等几何 应用 性质若C 点分割线段AB 的比值和D 点分割AB 的比值只差一个符号(因而一个是内分点,另一个是外分点),这时我们说C 、D 两点调和分割AB,或C 与D 对于线段AB 成调和共轭点偶,用符号1),(-=CD AB 表示。
在调和分割中,两对点的关系是完全对等的,这意思是说,当C 与D 调和分AB 时, A 与B 也调和分割CD,因而我们已知道,若1),(-=CD AB ,便也有1),(-=AB CD .一、几何中的调和分割 1.关于平分角中的调和分割三角形中一个角的内角和外角的平分线,将对边分成两线段的比值,都和两邻边成证明:由三角形中一个角的内角和外角的平分线,将对边分成两线段的比值,都和两临边成比例有EB AEDB DA CB AC EB AE ==, 即 DB DACB AC = 1=**CBDA DBAC则1-=**BCAD BDAC因此 1),(-=CD AB2、关于线段的调和分割一线段被它的中点和这直线上的无穷远点所调和分割,即证明:1),(-=∞CP AB证: ∞∞∞∞∞*=**=AP BP BC AC BC AP BP AC CP AB ),(因为 CB AC = 所以 1-=BCAC即1-=**∞∞BC AP BP AC则 1),(-=∞CP AB 3、关于对合的调和分割对合有两个二重元素,这两个元素是不重合的,可能是共轭复元素,并且这两个二重元素调和分割任意一对对应元素。
证明:由于对合的表达式是),0(,0)(2''≠-=+++b ad d u u b auu 所以决定二重元素的方程022=++d bs as不能有等根,所以两根1s 和2s 或者是不等式实根(双曲型对合),或者是共轭复根(椭圆型对合).由于对合是射影变换,因此保留交比,即),(),('21'21u u s s uu s s =,利用交比性质,此式可写作),(1),('21'21uu s s uu s s =从而1),('21=uu s s 或1),('21-=uu s s ,但1),('21=uu s s 将导致u 与'u 重合,这与对合不是恒同变换的假设抵触,从而1),('21-=uu s s . 4、关于完全四点形和完全四线形的调和分割完全四点形 完全四点形通过每一个对角点有一组调和线束,即通过这对角点的两边和对角三角形的两边。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
完全四点(线)形的调和性在初等几何中的应用黄毅1 胡志杰1 李锦杰2摘要:本文对高等几何中完全四点(线)形的性质做了具体而系统的整理,并通过初等几何与高等几何的内在联系,通过初等几何中平分角、平分线、共点、共线、平行、作图等几个具体问题的探究及其在中学竞赛中的运用,化难为易,丰富和拓展初等几何的内容。
关键词: 完全四点(线)形 应用 调和性 初等几何高等几何是一门聚集多方面知识体系的优秀学科。
高等几何可以说是在初等几何领域上的一个延伸与拓展。
它可以给出初等几何中某些问题的简单证明,为初等几何提供理论依据和注入新的数学思维。
完全四点(线)形的调和性是高等几何的一项重要内容,在几何学中占有重要地位。
它对初等几何的研究亦具有重要的指导意义。
比如说,它在初等几何的平分角度问题、共点共线问题、中点问题、线段比值问题及平行性等问题的研究中都有广泛的应用。
对高等几何当中某些特殊性质(四点形的调和性)的研究,可以让很多的数学爱好者,更加清楚的了解高等几何的重要性。
同时,也可以促进数学爱好者对初等几何学习的积极性。
本文着重分析完全四点(线)的调和性在初等几何中的一些应用。
一.完全四点(线)形的定义1.1 平面上四个点(无三点共线)以及联结其中任意两点的六条直线所组成的图形称为完全四点形。
(其中,每一个点称为顶点,每一条直线称为边,不共顶点的两边称为对边,对边的交点为对边点,以对边点为顶点的三角形为对角三角形。
)1.2 平面内无三线共点的四直线及其两两交点所构成的图形称为完全四线形。
(其中,每一条直线称为边,每一个点成为顶点,不共边的两个顶点为对顶点,对顶点连成对顶线,一对顶线为边的三角形成为对角三角形。
) 二 .完全四点(线)的调和性质2.1完全四点形(图一中的四点形ABCD )的两个对边点X 、Y 的连线交第三对对边于S 、T ,则(XY ,ST) = –1.(图一) (图二)2.2完全四线形(图二中的四线形abcd )的两条对顶线x, y 的交点O 与第三对对X t顶点相连得直线s,t,则(xy,st) = –1.2.3在完全四点形的对边三点形的每条边上, 有一个调和点组, 其中一对为对边点, 另一对为该边与第三组对边的交点.2.4在完全四点形的每条边上有一个调和点组,其中一对为顶点, 另一对中一个为对边点, 一个为该边与对边三点形的边的交点.三.完全四点(线)形的调和性在初等几何中的应用 3.1 解决平分角问题例1 如图,AD 垂直于BC ,M 是AD 上的任意一点,BM 交AC 于E ,CM 交AB 于F ,证明:AD 、BC 平分DE 与DF 所成的角。
证明:连直线EF 分别交直线AD 、BC 于X ,Y 。
考察完全四点形AFME ,由完全四点形的调和性,得 (EF, XY) = – 1, 即 D(EF, XY) = – 1 , 又因为DX ⊥DY ,所以AD 、BC 平分∠EDF 。
3.2解决平分线段问题例2:求证梯形两腰延长线的交点与对角线的交点连线平分上下底.证明:如图, 四边形ABCD 为梯形, AD//BC, E, F 分别为两腰和对角线的交点. EF 交AD, BC 于P, Q. 考察完全四点形EAFD. 设AD ×BC=G ∞. 由完全四点形的调和性知(BC, QG ∞) = –1, 因为AD//BC, 故 G ∞ 是无穷远点, 从而Q 为BC 的中点.3.3解决点共线问题 例3:求证三角形的三条外角平分线和对边相交所得三点共线. 证明:如图所示,ABC ∆的三条外角平分线与对边交与G,H,I。
设ABC ∆的三条内角平分线交与点M。
AD ,BE,CF 交与点M ,则有迪沙格定理知,两个三角形对应边连线的交点共线。
设AB 与DE 交与G ’,AC 与DF 交与H ’,BC 与EF 交与I ’,则G ’,H ’,I ’,三点共线。
又ACB ∠的外角平分线交AB 与G ,ABC ∠的外角平分线交AC 与H ,CAB ∠的外角平分线交BC 与I ,所以有 (BA,FG )=-1,(BC,DI)=-1,(CA,EH)=-1.在完全四点形CDME 中由调和性知BI(BA ,FG ’)=-1.所以有(BA,FG )=(BA ,FG ’)=-1.,即G 与G ’重合。
同理可知,H 与H ’,I 与I ’重合,所以G ,H ,I 三点共线。
3.4解决作图问题例4.1 用无刻度直尺完成以下作图:已知一线段BC 中点Q 及其线外一点A ,求过A 作该线段的平行线。
方法:1.连接BA ,并在其延长线上取一点E 。
2.连接CA ,QE 交与点F. 3.连接BF,CE 交与点D 。
4.连接AD ,则直线AD 为所求直线。
例4.2 已知一线段BC 和一直线L,并且BC 平行L ,求BC 的中点方法:1.在直线L 上取两点A ,D 2.连接BA,CD 交与点E 3.连接BD ,CA 交与点F4.连接EF 交BC 与Q ,那么点Q 即BC 中点3.5 解决平行问题例5:如图,在ABC ∆中,AD 是A ∠的内角平分线,在AD 上任取点H ,连BH 交AC 与E ,连CH 交AB 与F ,EF 交BC 与G ,求证:垂直于AG 的直线平行于AD 。
证明:如图,设,G BAD DAC DA αβ∠=∠=∠=。
视四边形AEHF为完全四线形,则由调和性知(.,.G)1AB AC AD A =-,又由线束交比的定义知,s i n (,)s i n (,G )s i n s i n (.,.G )1s i n (,G )s i n (,)s i n ()s i n ()A B A D A C A A B A C A D A A B A A C A D αβαβα===-+- 故sin sin()βαθ=+,sin sin()βθα=-所以sin()sin()θαθα-=+,即cos sin 0θα=,故cos 0θ=或sin 0α=,于是 2πθ=或απ=,但是α是ABC ∆的一个内角,不可能等于π,所以2πθ=,从而AG AD ⊥,即垂直于AG 的直线平行于AD ,并且AG 为A ∠的外角平分线。
A G3.6解决线共点问题例6.设X 、Y 、Z 是完全四点形ABCD 的三个对顶点,XZ 分别交AC 、BD 于L 、M ,证明:YZ 、BL 、CM 共点。
证明:如图,在完全四点形ABCD 中,边AC 上的四个点A 、C 、Y 、L 是一组调和点,即()1,-=YL AC 。
又在完全四点形YBZL 中,设LB 与YZ 交于N ,MN 交YL 于'C ,边YL 上的四点Y 、L 、'C 、A 是一组调和点,即()1,'-=AC YL 。
由于()()1,,-==YL AC AC YL ,故'C C ≡,所以 YZ 、BL 、CM 共点。
3.7中学竞赛问题例7 (全国高中数学联赛,1999)如图,在四边形ABCD 中,对角线AC 平分∠BAD 。
在CD 上取一点E ,BE 与AC 相交于F ,延长DF 交BC 于G 。
求证:∠GAC=∠证明 如图, 过A 作AC 的垂线AH ,连BD 分别交 根据角平分线的性质知(BD,IH )=–1。
连GE 交AH 于H ’,交AC 于J 。
根据完全四点形CEFG 的调和性知 (BD ,IH ’)=–1,由 (BD ,IH )=(BD ,IH ’)知H 与H ’重合。
由AC 与AH 垂直,且 (GE ,JH )=(BD ,IH )=–1知AC 与AH 是∠GAE 的内外平分线。
所以 ∠GAC=∠EAC例8(加拿大奥林匹克数学试题5,1994)ΔABC 为锐角三角形,AD 为BC 边上的高,H 为D 内一点。
直线BH 、CH 分别交AC 、AB 于E 、F ,证明∠EDH=∠FDH 。
证明:如图,连EF 交BC 的延长线于G AEHF 的调性知A BHAC'MXDY L C NZB(BC ,DG )= —1,因为 AD ⊥BC ,所以AD 是∠EDF 的平分线,所以 ∠EDH=∠FDH 。
例9(第36届IMO 预选题)∠EDH=∠FDH 。
ΔABC 的内切圆分别切三边BC 、CA 、AB 于点D 、E 、F ,点X 是ΔABC 的一个内点,ΔBC 相切,并与CX 、XB 分别相切于点Y 、Z 。
证明:证明: 因为D 、Y 、Z 是切点,所以XD 、BY 、CZ 点)。
设YZ 交BC 于P ',则由完全四点形XYJZ 1),(-='P D BC 。
同理由AD 、BE 、CF 共点(ΔABC 的葛尔刚点) 和完全四点形的调和性得1),(-=DP BC所以P 与P '重合,即YZ 、EF 、BC 共点。
于是由切割线定理知 PZ PY PD PF PE ⋅==⋅2,所以E 、F 、Y 、Z 共圆。
参考文献:【1】梅向明,刘增贤,王汇淳,等.高等几何【M 】.第三版.北京:高等教育出版社,2008【2】闻仲良.高等几何【M 】.成都:四川大学出版社,2005 【3】朱德祥.高等几何【M 】.北京:高等教育出版社,1999【4】梁林,袁丽晴,马嘉芸.高等几何中完全四点(线)形的调和性应用于初等几何中某些问题的初探【J 】.楚雄师范学院学报第十七卷第三期,2002D。
