《数字信号处理》课后习题答案111

1 2π 1 2π 1 2π 1 2π 1 2π 1 2π
∫
∫ (∫
+∞ −∞
F1 ( Ω ) ∗ e − jΩt ⋅ f 2 ( t ) dt
+∞ −∞
F1 ( y ) ⋅ e
− j ( Ω− y )t
dy ⋅ f
)
2
( t ) dt
∫ ∫
−∞ +∞ −∞
+∞
+∞
∫ (∫ ∫
+∞ −∞
−∞
F1 ( y ) e
− j ( Ω− y ) t
⋅ f 2 ( t ) dydt
+∞
−∞
f 2 ( t ) e− j (Ω− y )t dt F1 ( y ) dy
)
F2 ( Ω − y ) ⋅ F1 ( y ) dy
F1 ( Ω ) ∗ F2 ( Ω )
3
数字信号处理
习题解答 2005
所以
f1 ( t ) f 2 ( t ) ↔
n =−∞
∑ δ ( Ω + nΩ )
0
n =−∞
∑ δ ( Ω + nΩ ) ∑ δ ( Ω + nΩ )
0 ∞
n =−∞
∑ e − jnT Ω =
∞
n =−∞
(2) 右边：
n =−∞
∑ F (Ω + nΩ ) ，傅氏变换：
0
∞
∞ ∞ ∞ ∞ F ∑ F (Ω + nΩ 0 ) = ∑ f (t )e − jnΩ0t = f (t ) ∑ δ (t + nT ) = ∑ Tf (nT ) δ (t − nT ) n = −∞ n = −∞ n =−∞ n = −∞
− j Ωt
(2) 用 （a） 的结果，证明频域卷积定理
f1 (t ) f 2 (t ) ↔
证明： （1）
1 F1 (Ω) ∗ F2 (Ω) 2π
F ( Ω ) ∗ e− jΩt = ∫ F ( y ) e− j (Ω− y )t dy = ∫ F ( y ) e− jΩt e jyt dy
−∞ −∞
1
数字信号处理
习题解答 2005
故为非线性。 设输入为：
x '(n ) = x(n − n0 )
则输出为：
y ' ( n) = 2 x ( n − n 0 ) + 3 = y ( n − n 0 )
故是非移变系统。 (2)设输入为 x1(n) 和 x2(n)，对应输出为 y1(n) 和 y2(n) 则输出为：
数字信号处理
习题解答 2005
第一章 习题
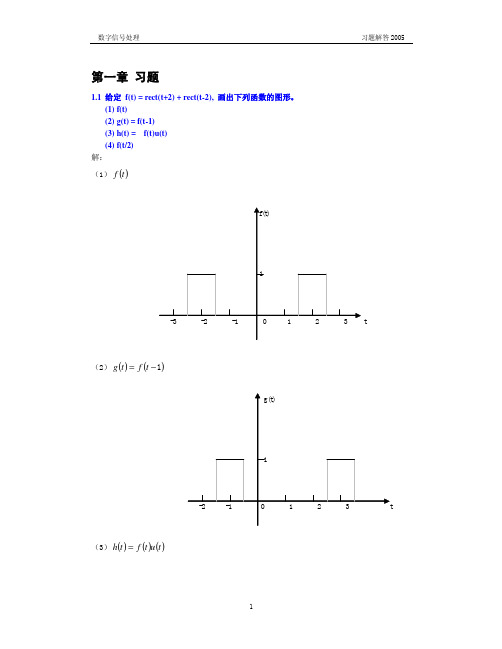
1.1 给定 f(t) = rect(t+2) + rect(t-2), 画出下列函数的图形。 (1) f(t) (2) g(t) = f(t-1) (3) h(t) = f(t)u(t) (4) f(t/2) 解： （1） f (t )
f(t)
1
-3
-2
-1
所以
1 Fn = T F0 ( Ω ) Ω=Ω0
1 Ω0
⋅1 =
1 Ω0
=
1 T Ω0
∞ ∞
则
F f ( t ) = F ( Ω ) = 2π = =
所以
1 Ω0 2π T Ω0 ∞ ∞
n =−∞
∑ F δ ( Ω − nΩ ) = 2π ∑
n 0 0
n =−∞
1 T Ω0
δ ( Ω + nΩ0 )
左边：傅氏反变换：
∞ ∞ ∞ F −1 T ∑ f ( nT ) e− jnT Ω = T ∑ f ( nT ) ⋅ δ ( t − nT ) = ∑ Tf ( nT ) ⋅ δ ( t − nT ) n =−∞ n =−∞ n =−∞
所以两者相等，原式成立。
6
数字信号处理
习题解答 2005
试确定抽样后的离散信号表达式。 解：
Ts = 1/ f s = 1/ 200 xa (n ) = xa (t ) |t =nTs = 6cos(0.3π n ) + 3sin(1.5π n ) + 2 cos(1.7π n ) + 4 cos(2.5π n ) + 10sin(3.3π n )
2.3 下列系统中，y(n) 表示输出， x(n) 表示输入，试确定输入输出关系是否线性？是否 非移变？ (1) y(n) = 2x(n) +3 2 (2) y(n) = x (n)
1 2π
F 1 ( Ω ) ∗ F2 ( Ω )
1.4 求下图中 f(t) 脉冲的傅氏变换。
T/4 解： 令τ =
T
T ，脉冲幅度为 1，截取 f(t) 的一个周期 f0(t)。 2
则 f0(t) 的傅立叶变换为：
(ωτ ) T (ωT ) F0 (ω ) = F [ f 0 (t )] = T 2 ⋅ Sa 2 = 2 ⋅ Sa 4
0
1
2
3
t
（2） g (t ) = f (t − 1)
g(t)
1
-2
-1
0
1
2
3
t
（3） h(t ) = f (t )u (t )
1
数字信号处理
习题解答 2005
h(t)
1
0
1
2
3
t
t （4） f ( 2 )
t f (2 )
1
-5
-4
-3
-2
-1
0
1
2
3
4
5
t
1.2 设 f(t) 是某一函数，a, t0, T 为实常数，证明： (1) f ( t )δ (
∞
∞
= e − jΩt ∫ F ( y ) e jyt dy = 2π f ( t ) e − jΩt
−∞
∞
（2）
F f1 ( t ) f 2 ( t ) =∫ = = = = = =
+∞
−∞
f1 ( t ) f 2 ( t ) e− jΩt dt =
+∞ −∞
1 2π
∫
+∞
−∞
2π f1 ( t ) e − jΩt ⋅ f 2 ( t ) dt
证明： 设 g (t ) = 则：
∞ ∞ − jnT Ω F g t F f nT δ t nT = − = ( ) ( ) ( ) ∑ ∑ f ( nT ) e n =−∞ n =−∞
n = −∞
∑ f (nT )δ (t − nT )
∞
=
n =−∞ +∞
∑e
∞
所以
1/ 3 = fTs
因此
解出 f = 2000 / 3
x(t ) = 2cos(4000π t / 3)
2.2 以抽样频率 fs=200Hz 对模拟正弦信号 xa ( t ) 进行抽样
xa ( t ) = 6cos(60π t ) + 3sin(300π t ) + 2cos(340π t ) + 4 cos(500π t ) + 10sin(660π t )
则输出为：
y ' (n) = x 2 (n − n0 )
而
y(n − n0 ) = x 2 (n − n0 ) = y ' (n)
故是非移变系统。 (3) 设输入为 x1(n) 和 x2(n)，对应输出为 y1(n) 和 y2(n) 则输出为：
− a nT
e− jnT Ω =
+∞
n =−∞
∑ e anT e − jnTΩ + ∑ e − anT e − jnT Ω
n =1
0
+∞
= ∑ e − anT e jnT Ω + ∑ e − anT e − jnT Ω
n =0 +∞ n =1
= ∑ e − nT (a − jΩ ) + ∑ e − nT (a + jΩ)
f (t )δ
( ) = f (t ) a δ (t − t ) = a f (t )δ (t − t ) = a f (t )δ (t − t )
t − t0 a 0 0 0 0
2
数字信号处理
习题解答 2005
(2)
δ t − ta0 f ( t ) δ ( at − t0 ) = f ( t ) 1 a = =
= T f (t ) =T
∞
n =−∞
∑ δ (t − t
− nT )
n =−∞
∑ f ( t ) δ (t − t
0 − nT ) = T
n =−∞
∑ f (t
0
1.3 (1) 如 f(t) F(Ω)，证明：
− jΩt
F (Ω ) ∗ e
= ∫ F ( y) e
−∞
∞
− j ( Ω− y )t
dy = 2πf (t ) e
得
1 Fn = T F0 (ω ) ω = nω1
=1 2 Sa
( ),ω
nω1T 4 n
1
=
2π T
所以
F f ( t ) = F ( ω ) = 2π =π
∞
n =−∞
∑ F δ (ω − nω )
1 1
∞
n =−∞
∑ Sa ( ) δ (ω − nω )
nω1T 4
注：如果用 sinc 函数表示，结果：
t − t0 a
) = a f ( t 0 )δ ( t − t 0)
)= 1 f ( t 0 )δ ( t − t 0 ) a a a )= T