选修4-5-证明不等式的基本方法(课堂PPT)
合集下载
课件 选修4-5不等式的基本性质-经典公开课(优秀公开课件).ppt

用数学式子表示为:
a b a-b0 a b a-b0 a b a-b0
基本理论
a b a - b 0; a b a - b 0; a b a-b 0.
上式中的左边部分反映的是实数的大小顺序,而 右边部分则是实数的运算性质,合起来就成为实 数的大小顺序与运算性质之间的关系. 这一性质 不仅可以用来比较两个实数的大小,而且是推导 不等式的性质、不等式的证明、解不等式的主要 依据.
4.(1)可乘性:a>b,c>0⇒ac>bc; a>b,c<0⇒ac<bc. (2)同向同正可乘性:a>b>0,c>d>0⇒ac>bd.
5.乘、开方法则:a>b>0⇒an>bn,n a n b (n∈N,n≥2). 6.倒数性质:a>b,且ab>0⇒
1 1 . a b
n 特别地,当 n为奇数时, 条件可放宽为: a > b, 也有a n > bn, a n b (n∈N, n ≥2).
x 3 x - 3 0, x 1 0, x -1 0
A- B 0
故A B
作差比较法常见的变形手段是: 通分、因式分 解或配方等;变形的结果是常数、若干个因式 的积或完全平方式等.
b, 试比较a abb与abba的大小。
注意: 2.以上不等式的基本性质可以得到严格证明;
3.要会用自然语言描述上述基本性质;
1.注意公式成立的条件,要特别注意“符号问题”;
4.上述基本事实和基本性质是我们处理不等式问题 的理论基础.
不等式的基本性质
【例2】 判断下列命题是否正确,并说明理由。
(1)若a > b, 则ac > bc ; a b ( 2)若 2 2 ,则 a b; c c 1 1 (3)若a b,ab 0, 则 ; a b (4)若a b,c d , 则ac bd; 1 1 (5)若a b 0, ,则 ; a b (6)若 | a | b, , 则a 2 b2 ;
人教版高中数学选修4-5课件:模块复习课 第二课 证明不等式的基本方法 (共39张PPT)

2.放缩法 将需要证明的不等式的值适当地放大(或缩小),使不等 式由繁化简,达到证明的目的.
【变式训练】1.对于任何大于1的自然数n,证明:
【(1证 31明() 1】 51设)(a1>71b)>…0(,1m 2>n10,1则)>a
2n 1 . 2 m<a,
所以
bm b
1
1 2k 1
2k 2k 1
n
n 2
1<Sn<
n
12
2
【学习力-学习方法】
优秀同龄人的陪伴 让你的青春少走弯路
小案例—哪个是你
忙忙叨叨,起早贪黑, 上课认真,笔记认真, 小A 就是成绩不咋地……
好像天天在玩, 上课没事儿还调皮气老师, 笔记有时让人看不懂, 但一考试就挺好…… 小B
目 录/contents
1. 什么是学习力 2. 高效学习模型 3. 超级记忆法 4. 费曼学习法
(2)用分析法证明不等式时,一定要注意用好反推符号, 或“要证明”“只需证明”“即证明”等词语. (3)用放缩法时,放缩要得当,不能“过大”也不能“过 小”.
类型一 比较法证明不等式 【典例1】设a≥b>0,求证:3a3+2b3≥3a2b+2ab2. 【证明】3a3+2b3-(3a2b+2ab2) =3a2(a-b)+2b2(b-a)=(a-b)(3a2-2b2). 因为a≥b>0,所以a-b≥0,3a2-2b2>2a2-2b2≥0. 从而(3a2-2b2)(a-b)≥0,故3a3+2b3≥3a2b+2ab2成立.
如何利用规律实现更好记忆呢?
超级记忆法-记忆 规律
记忆中
选择恰当的记忆数量
人教B版数学选修4-5课件:1.1.1 不等式的基本性质

向可加性等;
②作差法或作商法; ③函数的单调性.
(2)在直接利用不等式的性质证明不等式时,特别注意以下几点:
①是不是同向不等式; ②此性质是不是可以逆用.
题型一 题型二 题型三 题型四
易错辨析
易错点:由于多次应用同向不等式相加(乘)法则导致变量的取值
范围扩大.
【例4】 已知f(x)=mx2-n,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值
对于④,当 a=1,b=0,c=-1,d=-2 时,ac>bd 不成立;
对于⑤,当 cd 不一定大于 0,故不正确.
答案:②
1.使用不等式的性质时要注意哪些问题?
剖析:(1)在应用传递性时,如果两个不等式中有一个带等号,而另
一个不带等号,那么等号是不能传递的.如a≤b,b<c⇒a<c.
(2)在乘(除)中,要特别注意乘(除)数的符号.
.
解析:(x2-x)-(x-2)=x2-2x+2=(x-1)2+1.
因为(x-1)2≥0,所以(x-1)2+1>0,
即(x2-x)-(x-2)>0.
所以x2-x>x-2.
答案:x2-x>x-2
【做一做1-2】 设x=a2b2+5,y=2ab-a2-4a,若x>y,则实数a,b应满足
的条件为
.
解析:∵x>y,
范围.
错解:依题意,有
-4 ≤ ������-������ ≤ -1, -1 ≤ 4������-������ ≤ 5,
加减消元,得0≤m≤3,1≤n≤7,
从而,得-7≤f(3)=9m-n≤26,即f(3)的取值范围是[-7,26].
题型一 题型二 题型三 题型四
②作差法或作商法; ③函数的单调性.
(2)在直接利用不等式的性质证明不等式时,特别注意以下几点:
①是不是同向不等式; ②此性质是不是可以逆用.
题型一 题型二 题型三 题型四
易错辨析
易错点:由于多次应用同向不等式相加(乘)法则导致变量的取值
范围扩大.
【例4】 已知f(x)=mx2-n,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值
对于④,当 a=1,b=0,c=-1,d=-2 时,ac>bd 不成立;
对于⑤,当 cd 不一定大于 0,故不正确.
答案:②
1.使用不等式的性质时要注意哪些问题?
剖析:(1)在应用传递性时,如果两个不等式中有一个带等号,而另
一个不带等号,那么等号是不能传递的.如a≤b,b<c⇒a<c.
(2)在乘(除)中,要特别注意乘(除)数的符号.
.
解析:(x2-x)-(x-2)=x2-2x+2=(x-1)2+1.
因为(x-1)2≥0,所以(x-1)2+1>0,
即(x2-x)-(x-2)>0.
所以x2-x>x-2.
答案:x2-x>x-2
【做一做1-2】 设x=a2b2+5,y=2ab-a2-4a,若x>y,则实数a,b应满足
的条件为
.
解析:∵x>y,
范围.
错解:依题意,有
-4 ≤ ������-������ ≤ -1, -1 ≤ 4������-������ ≤ 5,
加减消元,得0≤m≤3,1≤n≤7,
从而,得-7≤f(3)=9m-n≤26,即f(3)的取值范围是[-7,26].
题型一 题型二 题型三 题型四
第一讲 不等式和绝对值不等式 知识归纳 课件(人教A选修4-5)

对于不等式恒成立求参数范围问题,常见类型及其解法
如下:
(1)分离参数法:
运用“f(x)≤a⇔f(x)max≤a,f(x)≥a⇔f(x)min≥a”可解决恒成立
中的参数范围问题.
(2)更换主元法:
不少含参不等式恒成立问题,若直接从主元入手非常 困难或不可能时,可转换思维角度,将主元与参数互换,
常可得到简捷的解法.
5 ②当- ≤x≤2 时, 2 3 原不等式变形为 2-x-2x-5>2x,解得 x<- . 5 5 3 ∴解集为{x|- ≤x<- }. 2 5 ③当 x>2 时,原不等式变形为 x-2-2x-5>2x, 7 解得 x<- ,∴原不等式无解. 3 3 综上可得,原不等式的解集为{x|x<- }. 5
2|≤1+2|y-2|+2≤5,即|x-2y+1|的最大值为5.
答案:5
3.(2011· 陕西高考)若不等式|x+1|+|x-2|≥a对任意x∈R 恒成立,则a的取值范围是________.
解析:令 f(x)=|x+1|+|x-2|= -2x+1x≤-1, 3-1<x<2, 2x-1x≥2, ∴f(x)≥3. ∵|x+1|+|x-2|≥a 对任意 x∈R 恒成立,∴a≤3.
[解析]
x+3z 由 x-2y+3z=0 得 y= , 2
2 2 y2 x +9z +6xz 6xz+6xz 则xz= ≥ =3, 4xz 4xz
当且仅当 x=3z 时取“=”.
[答案]
3ቤተ መጻሕፍቲ ባይዱ
1 1 1 [例 3] 设 a, c 为正实数, b, 求证:3+ 3+ 3+abc≥2 3. a b c 1 [证明]因为 a,b,c 为正实数,由平均不等式可得 3+ a
2020版高考数学大一轮复习不等式选讲第2讲不等式的证明课件理新人教A版选修4_5

“放”和“缩”的常用技巧
在不等式的证明中,“放”和“缩”是常用的推证技巧.
常见的放缩变换有:
(1)变换分式的分子和分母,如k12<k(k1-1),k12>k(k1+1),1k
<
2 k+
k-1,
1k>
2 k+
k+1.上面不等式中
k∈N*,k>1;
(2)利用函数的单调性; (3)真分数性质“若 0<a<b,m>0,则ab<ab+ +mm”. [提醒] 在用放缩法证明不等式时,“放”和“缩”均需把握一 个度.
2.不等式的证明方法 证明不等式常用的方法有比较法、综合法、分析法、反证法、 放缩法、数学归纳法等. 3.数学归纳法证明不等式的关键 使用数学归纳法证明与自然数有关的不等式,关键是由 n=k 时不等式成立推证 n=k+1 时不等式成立,此步的证明要具有 目标意识,要注意与最终达到的解题目标进行分析、比较,以 便确定解题方向.
(2)证明:要证1a-b-abcc>1,只需证|1-abc|>|ab-c|, 只需证 1+a2b2c2>a2b2+c2,只需证 1-a2b2>c2(1-a2b2), 只需证(1-a2b2)(1-c2)>0, 由 a,b,c∈A,得-1<ab<1,c2<1,所以(1-a2b2)(1-c2)>0 恒 成立. 综上,1a-b-abcc>1.
所以 a2+2ab+b2=1.
因为 a>0,b>0,
所以a12+b12=(a+a2b)2+(a+b2b)2=1+2ab+ba22+1+2ba+ab22=
2 + 2ab+2ba + ba22+ab22 ≥ 2 + 2
2ab·2ba + 2
高中数学新人教A版选修4-5课件:第一讲不等式和绝对值不等式1.1.1不等式的基本性质

探究四
探究一不等式的基本性质
对于考查不等式的基本性质的选择题,解答时,一是利用不等式的相关
性质,其中,特别要注意不等号变号的影响因素,如数乘、取倒数、开方、平
方等;二是对所含字母取特殊值,结合排除法去选正确的选项,这种方法一般
要注意选取的值应具有某个方面的代表性,如选取 0、正数、负数等.
J 基础知识 Z 重点难点
几乎都有类似的前提条件,但结论会根据不同的要求有所不同,因而这需要
根据本题的四个选项来进行判断.选项 A,还需有 ab>0 这个前提条件;选项
B,当 a,b 都为负数时不成立,或一正一负时可能也不成立,如 2>-3,但 22>(-3)2
1
a
b
不正确;选项 C,c2+1>0,由 a>b 就可知c2+1 > c2 +1,故正确;选项 D,当 c=0 时不
A.P≥Q
B.P>Q
C.P≤Q
1
−
a+1+ a
解析:P-Q=( a + 1 − a)-( a − a-1)=
a-1- a+1
=
D.P<Q
.
( a+1+ a)( a+ a-1)
∵a≥1,∴ a-1 < a + 1,即 a-1 − a + 1<0.
又∵ a + 1 + a>0, a + a-1>0,
a-1- a+1
格依据不等式的性质和运算法则进行运算,是解答此类问题的基础.在使用
不等式的性质中,如果是由两个变量的范围求其差的范围,一定不能直接作
5.3 证明不等式的基本方法 课件(人教A版选修4-5)
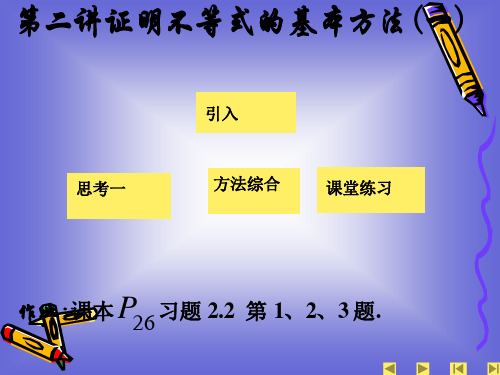
附课本例 3.已知 a , b 是正数,且 a b , 求证: a b a b 证明:∵ a , b 是正数,且 a b ,
a b b a
∴要证 aabb abba ,只要证 lg (aabb ) lg(abba ) , 只要证 a lg a b lg b b lg a a lg b . (a lg a b lg b) (b lg a a lg b)
4 求证: 1 a b . 3
4. 比较 loga (1 x) 与 loga (1 x)
的大小( a 0且a 1,0 x 1).
作业:课本 P 习题 2.2 第 1、2、3 题. 26
1.若实数 x 1 ,求证: 3(1 x 2 x4 ) (1 x x 2 )2 . 证明:采用差值比较法: 2 4 2 2 3(1 x x ) (1 x x ) = 3 3 x2 3 x4 1 x2 x4 2 x 2 x2 2 x3 = 2( x 4 x 3 x 1) = 2( x 1)2 ( x 2 x 1) 1 2 3 2 = 2( x 1) [( x ) ]. 2 4 1 2 3 2 x 1, ( x 1) 0, 且( x ) 0, 2 4 12 3 2 ∴ 2( x 1) [( x ) ] 0, ∴ 3(1 x 2 x4 ) (1 x x 2 )2 . 2 4
证明不等式的常用的方法有: 比较法、综合法、分析法,它们各有其 优点.解题有法,但无定法,具体运用时,应 该对具体问题的特点作具体分析,选择合适 的方法.当问题比较复杂时,通常用分析法寻 找证明的思路,而用综合法来叙述、表达整个 证明过程.
思考二.(课本第 25 页例 4) a 2b2 b2c 2 c 2a 2 ≥ abc . 已知 a , b, c 0, 求证: abc
人教A版高中数学选修4-5第一讲二绝对值不等式上课课件

证明
3x 2 y 3a 3b 3 x a 2 y b
2 xa 3 yb
3 2 5
所以:3x 2 y 3a 2b 5 .
例2
两个施工队分别被安排在公路沿线的两 个地点施工,这两个地点分别位于公路路碑 的第10km和第20km处。现要在公路沿线建两 个施工队的共同临时生活区,每个施工队每 天在生活区和施工区地点之间往返一次。要 使两个施工队每天往返的路程之和最小,生 活区应该建在何处?
分析
本题是绝对值不等式的应用,第一把 实际问题划归为数学问题,即归结为求解 形如y x a x b 的函数的极值问题, 这类问题借助于绝对值三角不等式解答。
解:设生活区建于公路路碑的第xkm处,两个施 工队每天往返的路程之和为S(x)km,
则S x 2 x 10 x 20 .
因 :x 10 x 20 x 10 20 x 10, 且 x 1020 x 0 取等 。
因此:a b a b .
其几何意义是三角形的两边之和大于 第三边(如下图)。
x
a+b b
由此可称 定理1为绝 对值三角
不等式
a
y
0
(2)当向量a,b共线时,分以下两种情况: 如果向量a,b方向相同时,a b a b ; 如果向量a,b方向相反时,a b a b .
一般地,我们有 a b a b .
.. . . x . . .. x
0 a b a+b
a+b b a 0
图1
(2)当ab<0时,又可以分a>0,b<0和a<0,b>0两 中情况.
如果a>0,b>0时,如图2-1,a b a b .
.. b a+b
3x 2 y 3a 3b 3 x a 2 y b
2 xa 3 yb
3 2 5
所以:3x 2 y 3a 2b 5 .
例2
两个施工队分别被安排在公路沿线的两 个地点施工,这两个地点分别位于公路路碑 的第10km和第20km处。现要在公路沿线建两 个施工队的共同临时生活区,每个施工队每 天在生活区和施工区地点之间往返一次。要 使两个施工队每天往返的路程之和最小,生 活区应该建在何处?
分析
本题是绝对值不等式的应用,第一把 实际问题划归为数学问题,即归结为求解 形如y x a x b 的函数的极值问题, 这类问题借助于绝对值三角不等式解答。
解:设生活区建于公路路碑的第xkm处,两个施 工队每天往返的路程之和为S(x)km,
则S x 2 x 10 x 20 .
因 :x 10 x 20 x 10 20 x 10, 且 x 1020 x 0 取等 。
因此:a b a b .
其几何意义是三角形的两边之和大于 第三边(如下图)。
x
a+b b
由此可称 定理1为绝 对值三角
不等式
a
y
0
(2)当向量a,b共线时,分以下两种情况: 如果向量a,b方向相同时,a b a b ; 如果向量a,b方向相反时,a b a b .
一般地,我们有 a b a b .
.. . . x . . .. x
0 a b a+b
a+b b a 0
图1
(2)当ab<0时,又可以分a>0,b<0和a<0,b>0两 中情况.
如果a>0,b>0时,如图2-1,a b a b .
.. b a+b
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
式.成立
2假设 nkk当 1时 ,不等,即 式 |s有 成 ik n| 立 k|sin |.
当nk1时,
|s k i 1 n | |sk i c n o c k s o s|i s n 22
|sk in c o | |s ck o ss i|n
|sk i|n |co | |c sk o ||s si|n
(ab)(ab)2
a ,b 0 , a b 0 又 a b (a b )2 0
故 ( a b ) a ( b ) 2 0 即 ( a 3 b 3 ) ( a 2 b a 2 ) b 0
a3b3a2ba2b
例2 如果a用 k白 g 糖制 bk出 糖 g 溶,则 液其浓度 a, 为 b
abc 故 a 2b 2 b 2c 2 c 2a 2 abc
abc
三、反证法与放缩法
(1)反证法
先假设要证的命题不成立,以此为出发点,结合已知条 件,应用公理,定义,定理,性质等,进行正确的推理,得到 和命题的条件(或已证明的定理,性质,明显成立的事实 等)矛盾的结论,以说明假设不正确,从而证明原命题成 立,这种方法称为反证法.对于那些直接证明比较困难 的命题常常用反证法证明.
1 x 与 1 y 中至少有一个小于
2
y
x
例 2已 a ,b ,c 知 为,a 实 b c 数 0 a, b b c c a 0, a b 0 求 c , :a 证 0 b ,0 c ,0.
证 明: 假 设a,b,c不 全 是 正,数 即 其 中 至 少 有 一 个正不数是, 不妨先设 a 0,下面分a 0和a 0两种情况讨. 论 (1)如果a 0,则abc 0,与abc 0矛盾,a 0不可能. (2)如果a 0,那么由abc 0可得bc 0,又abc 0, bc a 0,于是abbcca a(bc)bc 0, 这和已知 abbcca 0相矛盾.a 0也不可能 . 综上所述 a 0,同理可证 b 0,c 0,所以原命题成. 立
24
当nk1时,
1xk1 1x1xk 1x1kx1xk xk2x 1k1x.
所 式成立
你能说出证明中每的 一理 步由中?吗
25
a
b
ab
.
1ab 1ab 1a 1b
21
四、数学归纳法
例 2 证明不 |sinn 等 |n|式 sin|nN.
分析这是一个涉及n正 的整 三数 角函数, 问题 又与绝对值,在 有证 关明递推关 ,应系注时意利 用三角函数的性对质值及不绝等 . 式
证1 明 当 n 1 时 ,上式 |s i左 |n 右 ,边 不 边 等
由 于 a,b,c不 全 相 ,所等 以 上 述 三 个少式有子一中个 取 等,把 号它 们 相 加 得
a(b2c2)b(c2a2)c(a2b2)6abc
例 2已 a 1 ,a 知 2 , ,a n R ,且 a 1 a 2 a n 1 求 (1 证 a 1 )1 ( a 2 ) (1 a n ) 2 n
例 3已a,b 知 ,c,d R ,求 证
1 a b c d 2 abd bca cdb dac
证明 : a , b , c , d 0 ,
a
a a
abcd abd ab
b
b b
abcd bca ab
c
c c
abcd cd b cd
d
d d
abcd d ac cd
把以上四个不等式得相加
证明: a1 R ,1 a1 2 a1 , 同理1 a2 2 a2 , ,1 an 2 an a1,a2, ,an R ,由不等式的性,质得 (1 a1)(1 a2) (1 an) 2n a1a2 an 2n. ai 1时,1 ai 2 ai 取等号, 所以原式在a1 a2 an 1时取等号.
(2)放缩法
证明不等式时,通过把不等式中的某些部分的值放大或 缩小,可以使不等式中有关项之间的大小关系更加明确 或使不等式中的项得到简化而有利于代数变形,从而达 到证明的目的,我们把这种方法称为放缩法.
通常放大或缩小的方法是不唯一的,因而放缩法具有 较在原灵活性;另外,用放缩法证明不等式,关键是放、 缩适当,否则就不能达到目的,因此放缩法是技巧性较 强的一种证法.
例1 已知x, y0,且x y2,
试证1x,1 y中至少有一个2.小于 yx
证明
: 假设
1
x
1 ,
y
都不小于
2,
yx
即 1 x 2,且 1 y 2,
y
x
x , y 0 , 1 x 2 y , 1 y 2 x ,
2 x y 2(x y) x y 2,
这与已知条件 x y 2 矛盾 .
abcd a b c d abcd abd bca cbd dac
abcd. 即 ab cd
1 a b c d 2 abd bca cba dac
例 4已 a ,b 是 知,求 实a 证 数 bab. 1 a b1 a1 b
证 明 :0 ab a b
ab
1
1
1
1
ab
1ab 1ab 1ab 1ab
下面给出证明
bm b
amam(ba) bm b b(bm)
baba0,又 a,b,m都 是,正 数
m(ba)0,b(bm)0
m (b a ) 0即 a m a 0 a m a b (b m ) b mb b mb
(2)作商比较法
例 3已a知 ,b是 正 ,求数 a证 abbabba, 当且a仅 b时 当 ,等号. 成立
(2)分析法
从要证的结论出发,逐步寻求使它成立的充分条件,直至 所需条件为已知条件或一个明显成立的事实(定义、公 理或已证的定理、性质等),从而得出要证的命题成立, 这种证明方法叫做分析法.这是一种执果索因的思考和 证明方法.
用分析法证明不等式的逻辑关系
BB1 B2 Bn A 结 (步步寻求不等已 式 论 成立的充分) 条知 件
用分析法证“若A则B”这个命题的模式是: 为了证明命题B为真, 只需证明命题B1为真,从而有…… 只需证明命题B2为真,从而有……
…… 只需证明命题A为真. 而已知A为真,故B必真.
例 3求2 证 736
证明 : 2 7和 3 6都是正数 , 所以要证 2 7 3 6 , 只需证 ( 2 7 )2 ( 3 6 )2 , 展开得 9 2 14 9 2 18 , 只需证 14 18 , 只需证 14 18 , 14 18 成立 , 所以 2 7 3 6成立 .
证:明 a ab ab ba baabbbaa bab
根 据 要 证 的 不点 等 (交式 换 a,的 b的特 位,不 置等 式)不
不 妨a设 b0,则a1,ab0,aab 1
b
b
当且仅 a当 b时,等号成 . 立
aabbabba,当且a 仅 b时 ,等 当号. 成立
二、综合法与分析法
(1)综合法
在不等式的证明中,我们经常从已知条件和不等式的性 质、基本不等式等出发,通过逻辑推理,推导出所要证明 的结论.这种从已知条件出发,利用定义、公理、定理、 性质等,经过一系列的推理、论证而得出命题成立,这种 证明方法叫做综合法.又叫顺推证法或由因导果法.
用综合法证明不等式的逻辑关系
AB1B2BnB (已 知 )(逐 步 推 演 不 等 必式 要成 条 )(结 立 件 论 ) 的
若在上述溶液m 中k白 再 g 糖 添 ,此加 时溶液的浓
增加a到 m,将这个事实抽问 象题 为 ,并数 给学 出.证 bm
解:可以把上述事如 实下 抽不 象等 成式 : 问
已知 a,b,m都是正 ,并数 ab且,则ama bm b
解:可以把上述事如 实下 抽不 象等 成式 : 问
已知 a,b,m都是正 ,并数 ab且,则ama
那 么 1有 xn1n.x
分析贝努利不等式个 中字 涉,x母 及 表两 示大 于1且不等 0的于任意,实 n是数大1的 于自然 , 数 我们用数学归对 纳n进 法行 只归 能 . 纳
证明 1当 n2时 ,由x于 0得 1x212xx212x,不等式 . 成立
2假设 n当 kk2时不等,式 即成 有立 1xk 1kx.
例 1已a,知 b,c0,且 不,全 相 等
求a(证 b2c2)b(c2a2)c(a2b2)6abc
证 : b 2 明 c 2 2 b ,a c 0 , a ( b 2 c 2 ) 2 ab c 2 a 2 2 a ,b c 0 , b ( c 2 a 2 ) 2 abc a 2 b 2 2 a ,c b 0 , c ( a 2 b 2 ) 2 abc
例 4已 a ,b ,知 c 0 ,求 a 2 b 证 2 b 2 c 2 c 2 a 2 ab a b c
分析:要证的不等式可化为 a2b2 b2c2 c2a2 abc(a bc) 观察上式 ,左边各项是两个字平母方的之积 , 右边各项涉及三个,字 可母 以考虑用 x2(y2 z2) 2x2yz
|sikn ||sin|
k|sin ||sin |
k1|sin |.
所以n当k1时不等式.成立
由 12可,知 不等式对一 n均 切成 正 . 立 整
你能说出证明中每的 一理 步由中?吗
23
例 3 证明贝 B努 ern利 不 ou等 ll:i 式
如x果 是 实 ,且 数 x1,x0,n为 大 1的 于自,然 数
一、比较法 (1)作差比较法
例 1已 a , b 都 知 ,是 且 a b ,求 实 a 3 b 证 3 数 a 2 b a 2
证 : ( a 3 b 3 明 ) ( a 2 b a 2 ) b ( a 3 a 2 b ) ( a 2 b b 3 )
a 2 ( a b ) b 2 ( a b ) ( a 2 b 2 )a (b )
2假设 nkk当 1时 ,不等,即 式 |s有 成 ik n| 立 k|sin |.
当nk1时,
|s k i 1 n | |sk i c n o c k s o s|i s n 22
|sk in c o | |s ck o ss i|n
|sk i|n |co | |c sk o ||s si|n
(ab)(ab)2
a ,b 0 , a b 0 又 a b (a b )2 0
故 ( a b ) a ( b ) 2 0 即 ( a 3 b 3 ) ( a 2 b a 2 ) b 0
a3b3a2ba2b
例2 如果a用 k白 g 糖制 bk出 糖 g 溶,则 液其浓度 a, 为 b
abc 故 a 2b 2 b 2c 2 c 2a 2 abc
abc
三、反证法与放缩法
(1)反证法
先假设要证的命题不成立,以此为出发点,结合已知条 件,应用公理,定义,定理,性质等,进行正确的推理,得到 和命题的条件(或已证明的定理,性质,明显成立的事实 等)矛盾的结论,以说明假设不正确,从而证明原命题成 立,这种方法称为反证法.对于那些直接证明比较困难 的命题常常用反证法证明.
1 x 与 1 y 中至少有一个小于
2
y
x
例 2已 a ,b ,c 知 为,a 实 b c 数 0 a, b b c c a 0, a b 0 求 c , :a 证 0 b ,0 c ,0.
证 明: 假 设a,b,c不 全 是 正,数 即 其 中 至 少 有 一 个正不数是, 不妨先设 a 0,下面分a 0和a 0两种情况讨. 论 (1)如果a 0,则abc 0,与abc 0矛盾,a 0不可能. (2)如果a 0,那么由abc 0可得bc 0,又abc 0, bc a 0,于是abbcca a(bc)bc 0, 这和已知 abbcca 0相矛盾.a 0也不可能 . 综上所述 a 0,同理可证 b 0,c 0,所以原命题成. 立
24
当nk1时,
1xk1 1x1xk 1x1kx1xk xk2x 1k1x.
所 式成立
你能说出证明中每的 一理 步由中?吗
25
a
b
ab
.
1ab 1ab 1a 1b
21
四、数学归纳法
例 2 证明不 |sinn 等 |n|式 sin|nN.
分析这是一个涉及n正 的整 三数 角函数, 问题 又与绝对值,在 有证 关明递推关 ,应系注时意利 用三角函数的性对质值及不绝等 . 式
证1 明 当 n 1 时 ,上式 |s i左 |n 右 ,边 不 边 等
由 于 a,b,c不 全 相 ,所等 以 上 述 三 个少式有子一中个 取 等,把 号它 们 相 加 得
a(b2c2)b(c2a2)c(a2b2)6abc
例 2已 a 1 ,a 知 2 , ,a n R ,且 a 1 a 2 a n 1 求 (1 证 a 1 )1 ( a 2 ) (1 a n ) 2 n
例 3已a,b 知 ,c,d R ,求 证
1 a b c d 2 abd bca cdb dac
证明 : a , b , c , d 0 ,
a
a a
abcd abd ab
b
b b
abcd bca ab
c
c c
abcd cd b cd
d
d d
abcd d ac cd
把以上四个不等式得相加
证明: a1 R ,1 a1 2 a1 , 同理1 a2 2 a2 , ,1 an 2 an a1,a2, ,an R ,由不等式的性,质得 (1 a1)(1 a2) (1 an) 2n a1a2 an 2n. ai 1时,1 ai 2 ai 取等号, 所以原式在a1 a2 an 1时取等号.
(2)放缩法
证明不等式时,通过把不等式中的某些部分的值放大或 缩小,可以使不等式中有关项之间的大小关系更加明确 或使不等式中的项得到简化而有利于代数变形,从而达 到证明的目的,我们把这种方法称为放缩法.
通常放大或缩小的方法是不唯一的,因而放缩法具有 较在原灵活性;另外,用放缩法证明不等式,关键是放、 缩适当,否则就不能达到目的,因此放缩法是技巧性较 强的一种证法.
例1 已知x, y0,且x y2,
试证1x,1 y中至少有一个2.小于 yx
证明
: 假设
1
x
1 ,
y
都不小于
2,
yx
即 1 x 2,且 1 y 2,
y
x
x , y 0 , 1 x 2 y , 1 y 2 x ,
2 x y 2(x y) x y 2,
这与已知条件 x y 2 矛盾 .
abcd a b c d abcd abd bca cbd dac
abcd. 即 ab cd
1 a b c d 2 abd bca cba dac
例 4已 a ,b 是 知,求 实a 证 数 bab. 1 a b1 a1 b
证 明 :0 ab a b
ab
1
1
1
1
ab
1ab 1ab 1ab 1ab
下面给出证明
bm b
amam(ba) bm b b(bm)
baba0,又 a,b,m都 是,正 数
m(ba)0,b(bm)0
m (b a ) 0即 a m a 0 a m a b (b m ) b mb b mb
(2)作商比较法
例 3已a知 ,b是 正 ,求数 a证 abbabba, 当且a仅 b时 当 ,等号. 成立
(2)分析法
从要证的结论出发,逐步寻求使它成立的充分条件,直至 所需条件为已知条件或一个明显成立的事实(定义、公 理或已证的定理、性质等),从而得出要证的命题成立, 这种证明方法叫做分析法.这是一种执果索因的思考和 证明方法.
用分析法证明不等式的逻辑关系
BB1 B2 Bn A 结 (步步寻求不等已 式 论 成立的充分) 条知 件
用分析法证“若A则B”这个命题的模式是: 为了证明命题B为真, 只需证明命题B1为真,从而有…… 只需证明命题B2为真,从而有……
…… 只需证明命题A为真. 而已知A为真,故B必真.
例 3求2 证 736
证明 : 2 7和 3 6都是正数 , 所以要证 2 7 3 6 , 只需证 ( 2 7 )2 ( 3 6 )2 , 展开得 9 2 14 9 2 18 , 只需证 14 18 , 只需证 14 18 , 14 18 成立 , 所以 2 7 3 6成立 .
证:明 a ab ab ba baabbbaa bab
根 据 要 证 的 不点 等 (交式 换 a,的 b的特 位,不 置等 式)不
不 妨a设 b0,则a1,ab0,aab 1
b
b
当且仅 a当 b时,等号成 . 立
aabbabba,当且a 仅 b时 ,等 当号. 成立
二、综合法与分析法
(1)综合法
在不等式的证明中,我们经常从已知条件和不等式的性 质、基本不等式等出发,通过逻辑推理,推导出所要证明 的结论.这种从已知条件出发,利用定义、公理、定理、 性质等,经过一系列的推理、论证而得出命题成立,这种 证明方法叫做综合法.又叫顺推证法或由因导果法.
用综合法证明不等式的逻辑关系
AB1B2BnB (已 知 )(逐 步 推 演 不 等 必式 要成 条 )(结 立 件 论 ) 的
若在上述溶液m 中k白 再 g 糖 添 ,此加 时溶液的浓
增加a到 m,将这个事实抽问 象题 为 ,并数 给学 出.证 bm
解:可以把上述事如 实下 抽不 象等 成式 : 问
已知 a,b,m都是正 ,并数 ab且,则ama bm b
解:可以把上述事如 实下 抽不 象等 成式 : 问
已知 a,b,m都是正 ,并数 ab且,则ama
那 么 1有 xn1n.x
分析贝努利不等式个 中字 涉,x母 及 表两 示大 于1且不等 0的于任意,实 n是数大1的 于自然 , 数 我们用数学归对 纳n进 法行 只归 能 . 纳
证明 1当 n2时 ,由x于 0得 1x212xx212x,不等式 . 成立
2假设 n当 kk2时不等,式 即成 有立 1xk 1kx.
例 1已a,知 b,c0,且 不,全 相 等
求a(证 b2c2)b(c2a2)c(a2b2)6abc
证 : b 2 明 c 2 2 b ,a c 0 , a ( b 2 c 2 ) 2 ab c 2 a 2 2 a ,b c 0 , b ( c 2 a 2 ) 2 abc a 2 b 2 2 a ,c b 0 , c ( a 2 b 2 ) 2 abc
例 4已 a ,b ,知 c 0 ,求 a 2 b 证 2 b 2 c 2 c 2 a 2 ab a b c
分析:要证的不等式可化为 a2b2 b2c2 c2a2 abc(a bc) 观察上式 ,左边各项是两个字平母方的之积 , 右边各项涉及三个,字 可母 以考虑用 x2(y2 z2) 2x2yz
|sikn ||sin|
k|sin ||sin |
k1|sin |.
所以n当k1时不等式.成立
由 12可,知 不等式对一 n均 切成 正 . 立 整
你能说出证明中每的 一理 步由中?吗
23
例 3 证明贝 B努 ern利 不 ou等 ll:i 式
如x果 是 实 ,且 数 x1,x0,n为 大 1的 于自,然 数
一、比较法 (1)作差比较法
例 1已 a , b 都 知 ,是 且 a b ,求 实 a 3 b 证 3 数 a 2 b a 2
证 : ( a 3 b 3 明 ) ( a 2 b a 2 ) b ( a 3 a 2 b ) ( a 2 b b 3 )
a 2 ( a b ) b 2 ( a b ) ( a 2 b 2 )a (b )
