实数的概念及分类
《实数》知识点归纳

引言概述:本文将对《实数》这一知识点进行详细的归纳和总结。
实数是数学中重要而广泛使用的概念,它包括有理数和无理数。
有理数是指可以用整数的比值表示的数,而无理数是指不能表示成有理数形式的数。
实数可以用于解决不同领域的问题,如代数、几何等,因此掌握实数的性质和运算规则是学习数学的基础。
接下来,本文将从五个大点出发,详细阐述实数的相关内容。
正文内容:一、实数的分类1.有理数的定义和性质i. 有理数是可以表示为两个整数的比值。
ii. 有理数可以是正数、负数或零。
iii. 有理数的大小可以通过大小关系进行比较。
2.无理数的定义和性质i. 无理数是不能表示为有理数的比值。
ii. 无理数可以用无限不循环小数或无限循环小数表示。
iii. 无理数的大小一般通过大小关系无法直接比较。
二、实数的运算规则1.实数的加法i. 实数相加时,可以先对有理数和无理数分别进行加法,再将结果合并。
ii. 加法满足交换律、结合律和分配律。
2.实数的减法i. 实数相减时,可以通过加上相反数来实现。
ii. 减法满足减去一个数的相反数等于加上这个数的规则。
3.实数的乘法i. 实数相乘时,可以先对有理数和无理数分别进行乘法,再将结果合并。
ii. 乘法满足交换律、结合律和分配律。
4.实数的除法i. 实数相除时,可以通过乘以倒数来实现。
ii. 除法满足除以一个数的倒数等于乘以这个数的规则。
5.实数的幂运算i. 实数的幂指的是一个数自乘若干次的运算。
ii. 幂运算的特点是指数为正时,数的大小增加;指数为负时,数的大小减小;指数为零时,结果为1。
三、实数的大小比较1.实数的大小关系i. 在实数范围内,任意两个实数可以通过大小关系进行比较。
ii. 实数的大小关系可以通过数轴和数线图进行表示。
2.实数的绝对值i. 绝对值是指一个数与0的距离,用|a|表示,其中a是一个实数。
ii. 绝对值有非负性和非零性。
四、实数的性质1.实数的闭包性i. 实数集合在加法和乘法下封闭。
实数教学总结知识点

实数教学总结知识点一、实数的定义和分类1. 实数的定义实数是指能用数线上的一点表示的数。
包括有理数和无理数两个部分。
有理数是指可以表示为两整数之比的数,无理数是指不能表示为有理数的数。
2. 实数的分类实数分为有理数和无理数两大类。
有理数包括整数、有限小数和无限循环小数,而无理数是指不能表示为有理数的数,比如π和e等。
二、实数的性质和运算1. 实数的大小比较实数之间可以通过大小关系进行比较,可以使用大小关系进行排序。
在实数范围内,大于0的数为正数,小于0的数为负数。
2. 实数的加法和减法实数的加法和减法遵循交换律和结合律,满足加法逆元和减法逆元的性质。
3. 实数的乘法和除法实数的乘法和除法也遵循交换律和结合律,分母不为0时可进行除法运算。
4. 实数的运算性质实数的运算满足分配律、结合律、交换律和消去律等性质。
三、实数的代数运算1. 实数的乘方和开方对于实数的乘方运算,有着指数运算的法则,例如乘方和开方的逆运算。
2. 实数的多项式运算实数的多项式运算包括加法、减法、乘法和除法等运算。
3. 实数的根式运算根式运算是对实数的开方运算,需要注意分母不为0,并且运算结果可能是有理数或无理数。
四、实数的应用1. 实数在代数方程中的应用实数在代数方程中起到了重要作用,可以通过实数的代数运算解决方程,例如一元一次方程、二元一次方程等。
2. 实数在几何中的应用实数在几何中有着广泛的应用,比如用实数表示坐标、长度、面积和体积等概念。
3. 实数在金融和经济中的应用实数在金融和经济中也有着广泛的应用,比如利息计算、货币兑换和股票投资等。
五、实数教学方法和策略1. 实数教学方法在实数教学中,老师可以采用讲解、示范、演练、实验、讨论等多种教学方法,提高学生对实数的理解和应用能力。
2. 实数教学策略在实数教学中,老师可以引导学生进行探究性学习,激发学生的学习兴趣,培养学生的实际动手能力和解决问题的能力。
六、实数教学中的注意事项1. 注重基础知识的建立实数是数学的基础,老师要注重实数的基本概念和分类,使学生能够对实数有一个清晰的认识。
初中实数概念及分类

初中实数概念及分类实数是数学中的基本概念之一,在数轴上表示,包括有理数和无理数两个部分。
有理数可以表示为一个整数除以另一个非零整数的商,而无理数则表示为一个无限不循环小数或一个无穷不循环循环小数。
下面将详细介绍实数的概念及分类。
一、实数的概念实数是指可以在数轴上表示的所有数的集合。
数轴上的每一个点都对应一个实数,实数包括有理数和无理数两部分。
有理数:可以表示为两个整数的比值。
有理数集合通常用Q 表示,Q = {a/b | a, b是整数,且b≠0}。
无理数:无理数无法表示为两个整数的比值,通常可以通过无穷不循环小数来表示。
无理数集合通常用R-Q表示。
二、实数的分类1. 有理数的分类有理数可以分为整数、正整数、负整数、分数、正分数和负分数等几个分类。
(1)整数:整数包括正整数、负整数和0。
整数集合通常用Z表示。
(2)正整数:正整数是大于0的整数。
(3)负整数:负整数是小于0的整数。
(4)分数:分数是可以表示为一个整数除以另一个整数的商的数,其中分母不为0。
(5)正分数:正分数是大于0的分数。
(6)负分数:负分数是小于0的分数。
2. 无理数的分类无理数可以分为无限不循环小数和无穷不循环循环小数两类。
(1)无限不循环小数:无限不循环小数是指小数部分无限延伸,且没有循环节的小数。
例如,π、e、根号2等都是无限不循环小数。
(2)无穷不循环循环小数:无穷不循环循环小数是指小数部分有无线循环的小数。
例如,1/3 = 0.333...、1/7 = 0.142857142857...等都是无穷不循环循环小数。
三、实数的性质1. 实数的加法性质(1)交换律:对于任意实数a和b,a + b = b + a。
(2)结合律:对于任意实数a、b和c,(a + b) + c = a + (b + c)。
(3)存在零元:存在一个实数0,使得任意实数a + 0 = a。
(4)存在负元:对于任意实数a,存在一个实数-b,使得a + (-b) = 0。
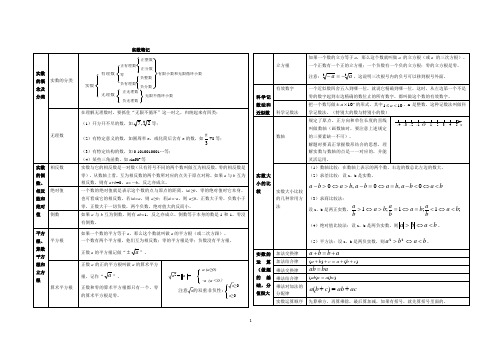
实数知识点总结

第六章实数知识网络:考点一、实数的概念及分类1、实数的分类2、无理数在理解无理数时,要抓住“无限不循环”这一点,归纳起来有四类(1)开方开不尽的数,如32,7等;(2)有特定意义的数,如圆周率π,或化简后含有π的数,如3π+8等;(3)有特定结构的数,如0.1010010001…等;(4)某些三角函数,如sin60o 等(这类在初三会出现)判断一个数是否是无理数,不能只看形式,要看运算结果,如0,16是有理数,而不是无理数。
3、有理数与无理数的区别(1)有理数指的是有限小数和无限循环小数,而无理数则是无限不循环小数;(2)所有的有理数都能写成分数的形式(整数可以看成是分母为1的分数),而无理数则不能写成分数形式。
考点二、平方根、算术平方根、立方根1、概念、定义(1)如果一个正数x的平方等于a,即,那么这个正数x叫做a的算术平方根。
(2)如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方跟)。
如果,那么x叫做a的平方根。
(3)如果一个数的立方等于a,那么这个数就叫做a 的立方根(或a 的三次方根)。
如果,那么x叫做a的立方根。
2、运算名称(1)求一个正数a的平方根的运算,叫做开平方。
平方与开平方互为逆运算。
(2)求一个数的立方根的运算,叫做开立方。
开立方和立方互为逆运算。
3、运算符号(1)正数a的算术平方根,记作“a”。
(2)a(a≥0)的平方根的符号表达为。
(3)一个数a的立方根,用表示,其中a是被开方数,3是根指数。
4、运算公式4、开方规律小结(1)若a ≥0,则a 的平方根是a ±,a 的算术平方根a ;正数的平方根有两个,它们互为相反数,其中正的那个叫它的算术平方根;0的平方根和算术平方根都是0;负数没有平方根。
实数都有立方根,一个数的立方根有且只有一个,并且它的符号与被开方数的符号相同。
正数的立方根是正数,负数的立方根是负数,0的立方根是0。
(2)若a<0,则a 没有平方根和算术平方根;若a 为任意实数,则a 的立方根是。
第一章实数笔记
(2)求差比较:设a、b是实数,
(3)求商比较法:
设a、b是两正实数,
(4)绝对值比较法:设a、b是两负实数,则 。
(5)平方法:设a、b是两负实数,则 。
实数的运算(做题的基础,分值很大
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法对加法的分配律
科学记数法
把一个数写做 的形式,其中 ,n是整数,这种记数法叫做科学记数法。(特别大的数与特别小的数)
实数大小的比较
数轴
规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注意上述规定的三要素缺一不可)。
解题时要真正掌握数形结合的思想,理解实数与数轴的点是一一对应的,并能灵活运用。
实数大小比较的几种常用方法
倒数
如果a与b互为倒数,则有ab=1,反之亦成立。倒数等于本身的数是1和-1。零没有倒数。
平方根、算数平方根和立方根
平方根
如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方跟)。
一个数有两个平方根,他们互为相反数;零的平方根是零;负数没有平方根。
正数a的平方根记做“ ”。
算术平方根
正数a的正的平方根叫做a的算术平方根,记作“ ”。
实数运算顺序
先算乘方,再算乘除,最后算加减,如果有括号,就先算括号里面的。
正数和零的算术平方根都只有一个,零的算术平方根是零。
立方根
如果一个数的立方等于a,那么这个数就叫做a的立方根(或a的三次方根)。
一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。
注意: ,这说明三次根号内的负号可以移到根号外面。
科学记数法和近似数
实数的有关概念ppt完美版

考点聚焦
归类探究
回归教材
中考预测
第1讲┃实数的有关概念
4.绝对值:数轴上表示数 a 的点与原点的__距__离____,记作|a|,
第6行 16 23 …
第第11讲 讲┃┃实实数数的的有有间关关概概依念念 次多一个0),共有2个。
理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称,即有限小数和无限循环小数都是有理数,而无限不
循环小数是无理数.无理数有:-π,0.
解 析 第1行的第1列与第2列差个2,第2列与第3列差个3,第3列与第4列差个4,…,第6列与第7列差个7;
解 析 1亿=108,11.2亿=1.12×109。
考点聚焦
归类探究
回归教材
中考预测
第1讲┃实数的有关概念
带有计数单位的数,一般要把计数单位化去,再 用科学记数法表示。
考点聚焦
归类探究
回归教材
中考预测
第1讲┃实数的有关概念
探究四 创新应用题
命题角度:
1.探究数字规律;
2.探究图形与数字的变化关系.
考点聚焦
第1讲┃实数的有关概念
探究三 科学记数法
命题角度: 用科学记数法表示数.
例3 [2013·邵阳] 据邵阳市住房公积金管理会 议透露,今年我市新增住房公积金11.2亿元,其中 11.2亿元可用科学记数法表示为( B )
A.11.2×108元 B.1.12×109元 C.0.112×1010元 D.112×107元
初中实数概念及分类

初中实数概念及分类实数是数学中的一个重要的数系,包括有理数和无理数。
实数可以用于描述物理、化学等自然科学问题,也可以用于解决经济、统计等社会科学问题。
实数的概念及其分类是初中数学的基础知识,下面就此展开讨论。
一、实数概念:实数是可以直观地表示在数轴上的数,它包括有所有的有理数和无理数。
实数在数轴上按大小是有序的,两个实数之间有无穷多个实数。
二、实数的分类:1. 有理数:有理数是可以表示为两个整数的比的数。
有理数包括整数、正整数、负整数、零以及分数。
有理数之间的运算有加法、减法、乘法和除法等。
2. 无理数:无理数是不能表示为两个整数的比的数,即不能写成分数形式的数。
无理数包括无限不循环小数和无限循环小数两类。
(1)无限不循环小数:无限不循环小数是指小数部分有无穷无尽的数字,并且没有循环节。
如开不尽的根号2、根号3等。
(2)无限循环小数:无限循环小数是指小数部分有一段数字不断循环出现。
如1/3=0.3333...、22/7=3.142857142857...等。
3. 整数:整数包括正整数、负整数和零。
整数是有理数的一种特殊类型。
4. 正数和负数:正数是大于零的数,负数是小于零的数。
正数和负数都是有理数的一种特殊类型。
5. 零:零是整数中既不是正数也不是负数的数。
零是有理数及整数的一种特殊类型。
6. 小数:小数是没有到达个位的十进制数,它包括有理数中的所有小数和无理数中的无限不循环小数。
三、实数的性质:1. 有理数和无理数共同构成了实数集合,任意两个实数之间存在着无穷多个实数。
2. 实数在数轴上是有序的,可以比较大小。
对于任意的两个实数a和b,必定有且仅有下面三种关系之一:a=b、a>b或a<b。
3. 实数之间满足加法、减法、乘法和除法的运算规则。
实数运算遵循整数和有理数的运算规律。
4. 实数也具有传递性、互补性、逆元性、等式性、分配率等基本性质。
综上所述,实数是数学中的一个重要概念,包括了有理数和无理数,可以用来描述各种自然科学和社会科学问题。
《实数概念理解》 讲义

《实数概念理解》讲义一、实数的定义实数,这个在数学中经常出现的名词,到底是什么呢?简单来说,实数是有理数和无理数的总称。
有理数,大家应该都比较熟悉,像整数(正整数、0、负整数)和分数(正分数、负分数),它们都可以表示为两个整数的比值。
而无理数,则是那些无限不循环小数,比如圆周率π、根号 2 等等。
二、实数的分类为了更好地理解实数,我们可以对其进行分类。
实数可以分为正实数、零和负实数。
正实数包括正有理数和正无理数。
正有理数像 1、2、3 这样的正整数,以及像 1/2、2/3 这样的正分数。
正无理数比如π、根号 3 等等。
零,是一个特殊的实数,它既不是正数也不是负数。
负实数则包括负有理数和负无理数。
负有理数像-1、-2、-3 这样的负整数,以及像-1/2、-2/3 这样的负分数。
负无理数比如π、根号 2 等等。
三、有理数有理数是实数中比较有规律的一部分。
整数很好理解,像 0、1、-1 等等。
而分数,其实就是把一个整数分成若干等份的表示形式。
比如3/4 ,表示把一个整体平均分成 4 份,取其中的 3 份。
有理数有很多特性。
它们可以写成有限小数或者无限循环小数。
比如 1/2 可以写成 05 , 1/3 可以写成 0333(无限循环)。
四、无理数无理数相对来说比较神秘和难以捉摸。
它们不能表示为两个整数的比值,并且其小数部分是无限不循环的。
例如,圆周率π约等于 31415926,它的小数位是无穷无尽且没有循环规律的。
还有像根号 2 约等于 141421356,也是无限不循环小数。
无理数的发现对于数学的发展有着重要的意义,它们让我们对数字的世界有了更深入和全面的认识。
五、实数的性质实数具有很多重要的性质。
首先是有序性,任意两个实数都可以比较大小。
比如 2 大于 1 ,-3 小于 0 。
其次是稠密性,也就是说在任意两个不同的实数之间,都存在着无穷多个实数。
比如在 1 和 2 之间,有 15 、 125 、 11 等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练一练
判断:
1、所有的有理数都可以用数轴上的点表示( ) 2、数轴上的所有点都表示有理数( ) 3、所有的无理数都可以用数轴上的点表示( )
4、数轴上的所有点都表示无理数( )
5、所有的实数都可以用数轴上的点表示( ) 6、数轴上的所有点都表示实数( )
13.3实数
徽县四中
李祚菊
议一议
2
都不 是!
是怎样的一个数,你对它有哪些了解? 我们知道,有理数包括整数和分 数,那么
2 是整数吗?是分数吗?
感知概念
事实上,人们已经 证明 2是一个无限 不循环小数,它的 值为: 1.414 213 562 373 095 048 802 688 724 209 7……
圆周率π
小数点后20000位
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 3809525720 1065485863 2788659361 5338182796 8230301952 0353018529 6899577362 2599413891 2497217752 8347913151 5574857242 4541506959 5082953311 6861727855 8890750983 8175463746 4939319255 。。。。。。
归纳
无限不循环小数又叫无 理数 有理数和无理数统称为实 数
举例探究
谁能举出几个无理数的例子
∏,3∏-5,
2
与 ∏ 有关的数 开不尽方的数
2
,3
2, 3 5 2
1.1010010001……
(两个1之间依次多1个0)
有规律变化的 无限不循环小数
没有变化规律的 无限不循环小数
实 数
1.257905438……
7
3
2
0. 6 0
36
3
无理数集合
有理数集合
2、把下列各数填入相应的集合内:
9
3
5
64
3
(1)有理数集合: 9
(2)无理数集合: (3)整数集合: (4)负数集合: (5)分数集合: (6)实数集合: 9
3 9 3 64 0 . 6 4 3 0.13
0. 6
3
3 4
课堂小结
通过本节课的学习,谁能从 知识点、数学方法、数学能力 等方面谈一下自己的收获
课外作业
教科书86页练习第1题; 87页第7题
这就是实数的四种类型
自主探索
1Hale Waihona Puke 按照定义分有理数实数分类
整数 分数 正整数 0 负整数 正分数 负分数 有限小数和 无限循环小数 无限不循环小数
实 数
无理数
2、按照大小分
正实数
正有理数 负有理数
正无理数 负无理数
分类
实 数
0
负实数
不重 不漏
练一练
1、把下列各数分别填在相应的集合里
22 , 3.14159265, ,-8, 7 7 3 0 . 6 , 0, 36 , 3 , 2 22 -8 7 3.14159265
0.13
5
3
3
9
9
3 4
64
9
3 4
3
0. 6
3
0.13
5
64
0. 6
3 4
3
9 3 0.13
数形结合:直径为1个单位长度的圆从原点沿数 ,, 轴向右滚动一周,圆上的一点由原点到达点O , 点O 的坐标是多少?
2
2
归纳1:实数与数轴上的点一一对应。 即每一个实数都可以用数轴上的一个 点来表示;反之数轴上的每一点都表 示一个实数。
