平面弯曲2-梁的应力
合集下载
梁的弯曲应力
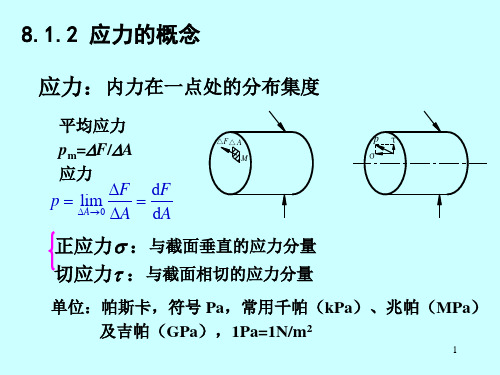
校核强度: 截面设计:
max
M max WZ
[ ]
Wz
M max [ ]
确定许用荷载: Mmax Wz [ ]
23
3、梁的切应力强度校核
(1)切应力计算公式
max
F S* Qmax Z max Izb
FQmax— 梁内最大剪力
Sz*— 面积A对中性轴静矩
Iz — 截面惯性矩
6
dθ ρ
1
2
1
2
o1
o2
y
ab
1 dx 2
o'1
z
(中性轴)
a'
dx
o'2 b'
y
1
2
y
(对称轴)
纵向纤a)维线应变变化b)规律:
c)
变形前: ab o1o2 dx
变形后: ab ( y)d o1o2 dx d
ab的伸长量: S ab dx ( y)d d yd
Pa=14.4MPa
B
FQ S zB Izb
(
200103 120000109 2.29107 1012 100103
)
Pa=10.4MPa
21
(3) 求圆形截面最大的切应力
max
4 3
FQ A
(4 3
2001003 ) Pa=19.1MPa
1 π 133.52 106
1
8.4 平面弯曲杆件的应力和变形
8.4.1 基本概念 8.4.2 梁横截面上的正应力公式 8.4.3 梁的切应力 8.4.4 梁的挠度和转角
2
梁的弯曲(应力、变形)

2
回顾与比较
内力
应力
F
A
FAy
编辑ppt
T
IP
M
?
?
FS
3
§9-6 梁的弯曲时的应力及强度计算
一、弯曲正应力 Normal stress in bending beam
梁段CD上,只有弯矩,没有剪力--纯弯曲Pure bending
梁段AC和BD上,既有弯矩,又有剪力--剪力弯曲Bending by
transverse force
编辑ppt
4
研究对象:等截面直梁 研究方法:实验——观察——假定
编辑ppt5Leabharlann 实验观察——梁表面变形特征
横线仍是直线,但发生 相对转动,仍与纵线正交
纵线弯成曲线,且梁的 下侧伸长,上侧缩短
以上是外部的情况,内部如何? 想象 —— 梁变形后,其横截面仍为平面,且垂直
x
61.7106Pa61.7MPa
编辑ppt
13
q=60kN/m
A
1m
FAY
C
l = 3m
FS 90kN
M ql /867.5kNm 2
x
2. C 截面最大正应力
120
B
x
180
K
30 C 截面弯矩
z
MC60kN m
FBY
y
C 截面惯性矩
IZ5.83120 5m 4
x 90kN
C max
M C y max IZ
于变形后梁的轴线,只是绕梁上某一轴转过一个角度 透明的梁就好了,我们用计算机模拟 透明的梁
编辑ppt
6
编辑ppt
7
总之 ,由外部去 想象内部 —— 得到
梁的弯曲应力

Iz=πD4/64 Iz=π(D4-d4)/64 若设圆环的直径比d/D=α,则相
应的截面抗弯系数为
Wz
=
π D3 32
Wz
=
π D3 32
(1−α 4 )
y 第10章 梁的弯曲应力 C Dz
y
O
z
d D
工程力学
q=60kN/m
A
1m
C
l = 3m
FS 90kN
(+ ) (− )
M ql2 / 8 = 67.5kN⋅ m
T形截面外伸梁尺寸及受载如图,截面对形心轴z的惯性矩
Iz=86.8cm4,yl=3.8cm。求梁横截面上的最大拉应力和最大压应力。
解 1)由静力平衡
2kN
0.8kN
y1 y2 6cm
方程求出梁的支反力
FA=0.6kN,FB=2.2kN A
C
BD
zC
作弯矩图。 得最大正弯矩在截面
1m 1m 1m
FA
FB
=
−
E ρ
I
z
1 ρ
=
Mz EIz
重要公式 σ = − Mz y Iz
工程力学
σ = − My Iz
第10章 梁的弯曲应力
M AZ y
x
y 横截面上正应力分布规律: (1)中性轴是过横截面形心的一条直线。中性轴上,正应力为零。 (2)以中性轴为界,横截面上的一侧受拉,一侧受压。 (3)离中性轴越远,正应力的绝对值越大。在横截面上离中性轴 最远的边或点上有最大的拉应力和最大的压应力。
几何关系 ( 平截面假定 )
正应变与中性层曲率间的关系
物理关系 ( Hooke 定律 )
正应力与中性层曲率间的关系
大学工程力学第7章平面弯曲2

主轴平面:如果梁的横截面没有对称轴,但是都有通过 横截面形心的形心主轴,所有相同的形心主轴组成的平面,
称 为 梁 的 主 轴 平 面 (plane including principal axes)。 由于对称轴一定是主轴, 所以对称面也一定是主轴 平面。
3
水利土木工程学院工程力学课程组
第7章 平面弯曲 §7.3 梁横截面上的应力
纯弯曲时梁横截面上的正应力
- y
1 d dx
其中为中性面弯曲后的曲率半
径,也就是梁的轴线弯曲后的曲率
半径。因为与y坐标无关,所以在 上述二式中,为常数。
16
水利土木工程学院工程力学课程组
第7章 平面弯曲 §7.3 梁横截面上的应力
纯弯曲时梁横截面上的正应力
应用弹性范围内的应力-应变关 系的虎克定律:
7
水利土木工程学院工程力学课程组
第7章 平面弯曲 §7.3 梁横截面上的应力
梁弯曲的若干定义与概念
中 性 层 与 中 性 轴
8
水利土木工程学院工程力学课程组
第7章 平面弯曲 §7.3 梁横截面上的应力
纯弯曲时梁横截面上的正应力
分析梁横截面上的正应力,就是要确定梁横截面上各 点的正应力与弯矩、横截面的形状和尺寸之间的关系。可 以根据梁的变形情形推知梁横截面上的正应力分布。
E
得到正应力沿横截面高度分布的数学 表达式
- E y Cy
式中 C E / 为待定的比例常数,E为 材料的弹性模量。
17
水利土木工程学院工程力学课程组
第7章 平面弯曲
§7.3 梁横截面上的应力
纯弯曲时梁横截面上的正应力
- E y Cy
这表明,横截面上的弯曲正应 力,沿横截面的高度方向从中性 轴为零开始呈线性分布。
称 为 梁 的 主 轴 平 面 (plane including principal axes)。 由于对称轴一定是主轴, 所以对称面也一定是主轴 平面。
3
水利土木工程学院工程力学课程组
第7章 平面弯曲 §7.3 梁横截面上的应力
纯弯曲时梁横截面上的正应力
- y
1 d dx
其中为中性面弯曲后的曲率半
径,也就是梁的轴线弯曲后的曲率
半径。因为与y坐标无关,所以在 上述二式中,为常数。
16
水利土木工程学院工程力学课程组
第7章 平面弯曲 §7.3 梁横截面上的应力
纯弯曲时梁横截面上的正应力
应用弹性范围内的应力-应变关 系的虎克定律:
7
水利土木工程学院工程力学课程组
第7章 平面弯曲 §7.3 梁横截面上的应力
梁弯曲的若干定义与概念
中 性 层 与 中 性 轴
8
水利土木工程学院工程力学课程组
第7章 平面弯曲 §7.3 梁横截面上的应力
纯弯曲时梁横截面上的正应力
分析梁横截面上的正应力,就是要确定梁横截面上各 点的正应力与弯矩、横截面的形状和尺寸之间的关系。可 以根据梁的变形情形推知梁横截面上的正应力分布。
E
得到正应力沿横截面高度分布的数学 表达式
- E y Cy
式中 C E / 为待定的比例常数,E为 材料的弹性模量。
17
水利土木工程学院工程力学课程组
第7章 平面弯曲
§7.3 梁横截面上的应力
纯弯曲时梁横截面上的正应力
- E y Cy
这表明,横截面上的弯曲正应 力,沿横截面的高度方向从中性 轴为零开始呈线性分布。
第九章第六节梁弯曲时的应力及强度计算(上课用)

m
V
( Stresses in Beams)
m
m
M
V
m m
只有与剪应力有关的切向内力元素 d V = dA 才能合成剪力
只有与正应力有关的法向内力元素 d FN = dA 才能合成弯矩
剪力V 内力 弯矩M 正应力 剪应力
所以,在梁的横截面上一般
既有 正应力, 又有 剪应力
先观察下列各组图
所以,可作出如下 假设和推断:
1、平面假设:
2.单向受力假设: 各纵向纤维之间互不挤压,纵向纤维均处于单向受拉或受压的状态。 因此梁横截面上只有正应力σ而无剪应力τ
各横向线代表横截面,实验表 明梁的横截面变形后仍为平面。
梁在弯曲变形时,上面部分纵向纤维缩短,下面部分纵向纤维伸长,必 有一层纵向纤维既不伸长也不缩短,保持原来的长度,这一纵向纤维层称为 中性层. 中性层与横截面的交线称为中性轴,中性轴通过截面形心,是一条形心轴。 且与截面纵向对称轴y垂直,将截面分为受拉区及受压区。梁弯曲变形时, 各横截面绕中性轴转动。
(3)横截面上任一点处的剪应力计算公式(推导略)为
V S I zb
Z
V——横截面上的剪力
Iz——整个横截面对中性轴的惯性矩
b——需求剪应力处的横截面宽度 S*Z——横截面上需求剪应力处的水平线 以外(以下或以上)部分面积A*(如图 )对 中性轴的静矩
V
3V 4 y2 (1 2 ) 2bh h
应力状态按主应力分类:
(1)单向应力状态。在三个相对面上三个 主应力中只有一个主应力不等于零。 (2)双向应力状态。在三个相对面上三个 主应力中有两个主应力不等于零。
(3)三向应力状态。其三个主应力都不等于零。例 如列车车轮与钢轨接触处附近的材料就是处在三向应 力状态下.
梁的应力

Q
s
t
t
第9章梁的应力
8.5梁的正应力和剪应力强度条件 带翼缘的薄壁截面,最大正应力与最大剪应力的情况与上 述相同;还有一个可能危险的点,在Q和M均很大的截面 腹、翼相交处。
M
s
Q
t
s t
1.2 正应力和剪应力强度条件:
s max
M max Wz
s
t max
Qmax
S
z max
b Iz
t
Q A
4t
3
③ 薄壁圆环:
t
max
2
Q A
2t
第9章梁的应力
8.5梁的正应力和剪应力强度条件
8.5 梁的正应力和剪应力强度条件
1 梁的正应力和剪应力强度条件 1.1 危险面与危险点分析
一般截面,最大正应力发生在弯矩绝对值最大截面的上下 边缘上;最大剪应力发生在剪力绝对值最大截面的中性轴 处。
M
ss
8.2 梁横截面上的正应力
8.2 梁横截面上的正应力
1 弯曲构件横截面上的(内力)应力
内力
剪力Q 弯矩M
剪应力t 正应力s
第9章梁的应力
8.2 梁横截面上的正应力
2 两个概念
中性层:梁内一层纤维既不伸长也不缩短,因而纤维不 受拉应力和压应力,此层纤维称中性层。
中性轴:中性层与横截面的交线。
第9章梁的应力
M图
(KN.m)
281
375
281
解:1、求支座反力;
FAy=FBy=112.5KN(↑);
作弯矩图,确定最大弯矩;
Mmax=375KN.m
第9章梁的应力
8.5梁的正应力和剪应力强度条件
2、求满足强度要求时梁的抗弯截面系数Wz.
梁的应力

ac
M
⑵、纵向线:由直线变为曲
线,且靠近上部的纤维缩短,
靠近下部的纤维伸长。
b
d
3、假设:
(1)弯曲平面假设:梁变形前原为平面的横截面变形后仍为平 面,且仍垂直于变形后的轴线。
第九章 梁的应力
梁是由许多纵向纤维组成的
凹入一侧纤维缩短
突出一侧纤维伸长
根据变形的连续性可知, 梁弯曲时从其凹入一侧的 纵向线缩短区到其凸出一 侧的纵向线伸长区,中间 必有一层纵向无长度改变
z
A2 20120mm2 y2 80mm
yc
80 2010 120 2080 80 20 120 20
52mm
(2)求截面对中性轴z的惯性矩
Iz
Hale Waihona Puke 80 203 1280 20 422
y
201203 20120 282
12
7.64106 m4
第九章 梁的应力
横截面上应力分布
b
d2
c,m ax
h yt,max yc,max d1
oz y
Oz
y b
t,m ax
中性轴 z 不是横截面的对称轴时,其横截面上最大拉
应力值和最大压应力值为
t,m ax
My t ,m a x Iz
c,m ax
Myc ,m a x Iz
第九章 梁的应力
例 对于图示 T形截面梁,求横截面上的最大拉应力和最大压 应力.已知: I z 290 .6 10 8 m4
d
在弹性范围内, E E Ey ...... (2)
O
O1
A1
B1 x
y
第九章 梁的应力
应力的分布图:
梁的弯曲应力和强度计算
88
7.5 106 7.6 106
88 86.8MPa
弯曲正应力计算
三、计算题
27.一矩形截面简支梁,梁上荷载如图所示.已知P=6kN、 l=4m、b=0.1m、h=0.2m,试画出梁的剪力图和弯矩图并求 梁中的最大正应力. 解:(1) 作剪力图、弯矩图
(2)求最大正应力
Mmax 6kN m
横向线:仍为直线,仍与纵向线正交,相对转动了一个角度 纵向线:曲线,下部伸长,上部缩短
(2)假设 平面假设:横截面在变形前为平面,变形后仍为平面,且仍
垂直于变形后梁的轴线,只是绕横截面上某个轴 旋转了一个角度。 单向受力假设:梁由无数根纵向纤维组成,之间无横向挤压,
只受轴向拉伸与压缩。
中性层
3、正应力计算公式 〖1〗几何变形关系
内容回顾
弯曲正应力 1. 基本假设:
(1)平面假设:变形前为平面的横截面,变形后仍为平面,但转动了一角度。 (2)单向受力假设:杆件的纵截面(与杆轴平行的截面)上无正应力。
2.中性轴Z:
中性层与横截面的交线,平面弯曲时中性轴过形心且与对称轴垂直。
3.正应力计算公式:
中性层
4.正应力分布规律:沿截面高度呈线性分布。
4、正负号确定 1)M、y 符号代入公式
2)直接观察变形
5、适用范围及推广
〖1〗适用范围: 平面弯曲(平面假设、单向受力假设基础上)、 线弹性材料
〖2〗推广: ① 至少有一个对称轴的截面; ② 细长梁 (l/h>5);
6、最大正应力
工程上关心的是极值应力:
只与截面形状、尺寸有关
抗弯截面模量
对剪切(横力)弯曲: 矩形:
解:(1)作弯矩图,
求最大弯矩
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Wz A3n 2
梁的合理设计
二 合理设计梁的外形——变截面梁
圆形、方形、矩形、工字形截面的比较 截面优化 一般做法:
Wz M max
→等截面梁
q
B
存在问题:
A l
M图
轴向优化
Mmax=ql2/8
梁的合理设计
改进方法: 思路:“按需分配”
W Wz xz
q
A
l
M图
B
M max x
30 300 2 180 120 30 300 12 90 303 2 240 15 90 30 12
3
360
30 z C
O1
Ⅰ
y2 z y1 360
z0
z
Ⅱ
30 30
Ⅲ
315.46106 mm4
(4) 求抗弯截面系数
I 315.46106 W1 1.315103 m3 y1 240
中性层
dA
z z
横截面
确定中性轴的位置
y
E
y
A
A
E
y
dA 0
ydA 0
即: S z 0
结论:z轴(中性轴)通过截面的形心
●推导正应力的计算公式
E
y
M z y d A M
A
M
y
dA z z y
A
yE
y
dA M
M
E
1
A
y dA M
2
dA
x
EIz
M EI z
这表明:梁在外力作用下,横截面上的弯矩愈 大,梁的弯曲程度就愈大;EIz愈大,梁的弯曲程 度就愈小。 EIz:梁的抗弯刚度(Flexural rigidity),其意 义是梁抵抗弯曲变形的能力
M y Iz
M : 所求截面上的弯矩
I z : 截面惯性矩
y:
?
梁的合理设计
3 根据材料特性选择截面形状 如果[t] <[c] 思路:“劫富济贫”
y1 c ? y2 t
cmax
z
cmax
y1
z y2
tmax M max c y1 cmax Iz M max t y2 Iz
F A B l/ 3 l
360
q
30
,
O1
Ⅰ
C
z
C
Ⅱ
y2 z y1 360
z0 z
30 30
Ⅲ
90 y
分析: max (1) 如果横截面上、下对称
M y Iz
h
b
z
+max
max M max min Wz
y
-max
最大拉应力和最大压应力在同一个截面上,且 有max= -min
●实验分析
(1)平面假设(Hypothesis of plane section) 横截面在变形后仍为平面,并和弯曲后的纵向层正交 (2)单向受力假设 假设梁由纵向线组成,各纵向 线之间互不挤压,即每一纵向线受单向拉伸或压缩
a
b
a'
b'
M
c
M
d'
d
c'
(3)梁变形后,同一层纵向纤维的长度相同,即同 层各条纤维的伸长(或缩短)相同 (4)中性层(Neutral layer): 既不伸长也不缩短的纵向层 中性轴(Neutral axis): 中性层与横截面的交线
梁的应力
1 梁的正应力
2 梁的合理截面形状及变截面梁
3 矩形截面梁的切应力
4 *工字形及其它形状截面梁的切应力
5 梁的强度条件
平面弯曲
1 概述及弯曲内力 2 弯曲正应力 3 弯曲切应力
4 梁的强度条件
5 弯曲中心
1 梁的正应力 (Normal Stress of The Beam)
●内力在横截面上的分布形式
2 物理方面
E
E
y
此式表明:横截面 上离中性轴愈远的地 方,其正应力愈大; 梁弯曲后曲率愈大时, 同一位置的正应力也 愈大
O
z yA
A
y
y?
?
3 静力学方面
dA 0 FN A
M y Az d A 0
Mz
中性轴
M y dA x
A
y d A M
Young’s Modulus
托马斯.杨(Thomas. Young,1773~ 1829)英国物理学家。1807年,提出弹 性模量的定义,为此后人称弹性模量为 杨氏模量。
梁的合理设计
cmax
z O
y
M y Iz
tmax
t max cmax
如果[t][c],如何设计截面
i 1
n
A
i 1
n
30
Ⅲ
90
i
y
360 30 15 300 30 180 30 90 345 120mm 360 30 300 30 30 90
(3)求截面对中性轴的惯性矩
360 303 2 120 15 360 30 Iz 12
所求点的y坐标
●正应力在横截面上的分布规律
M
中性轴
max
M ymax Iz
I z ymax Wz
max
z
Maximum normal stress
M Wz
y
弯曲截面系数(section Wz : modulus of bending)
●在使用正应力计算公式时,要注意以下几点:
(1)公式中的M与y是代数量,应将其数值与正负号 一并代入公式,如果得到的为正,则表明是拉应力; 反之为压应力。实际应用时,也可以绝对值代入,得 的数值,再根据变形(Me正负)来判断其正负。
式中:Mmax为绝对值最大 如果[t][c]
?
如果[t][c] →不对称截面
-max max max
-
+max
+max +max
宽翼边缘受拉,窄翼边缘受压
(2) 如果横截面上、下不对称
ⅰ)梁上只有正弯矩或负弯矩; 最大拉应力和最大压应力在同一个截面上 ⅱ)全梁最大正弯矩为M1,最大负弯矩为M2(绝对值) 最大拉应力和最大压应力不一定在同一个截面上 z C z y1 y2
5 x 4
3m 50kN FS图
+
1m 30kN
y
x
-
70kN
30kN.m
5 5 5 125 50 40 M max 4 4 8 4
M图
+
-
M max 31.25kN.m
(2)求横截面的形心C的位置
360
30 z C
O1
Ⅰ
y2 z y1 360
z0
z
Ⅱ
30
y2 Ai yi
l l0 l1
y d d yd
l l
y
y
Ky
y
Ky
上式表明:梁在纯弯曲时,其纵向纤维的线应变 与纤维所在的位置有关,离中性层愈远,纤维的线应 变愈大;线应变与梁变形后的弯曲层度有关,曲率K 愈大时,同一位置的线应变也愈大。
Mmax=ql2/8
→变截面梁(beam with non-constant section)
梁的合理设计
F
A
x
具体做法:
B 写出弯矩方程M(x)
b h (x) y z
l
hmin
a b a' b'
M
c d
中性轴
M
d'
中性层
c'
O
dx y
z
z
y
Oy:竖向对称轴 Oz: 中性轴
?
y, z
E y, z
y
O'
曲率中心O'
中性层曲率半径
d K dx
曲率K
a y O1 K1 c
d
1
b dx O2 x K2 d
剪力FQ 弯矩 M 正应力 切应力
?
M
纵向平面
横截面
FQ
●纯弯曲(Pure bending) : 梁受力弯曲后,横截面上只产生弯矩而无剪力 的弯曲( AB段) 剪切弯曲(Transverse bending ):AC、BD段
F
C l F a a
F
D
A
B
FQ图
F Fa M图
★纯弯曲梁的正应力公式 思路: 实验观察得应变 的变化规律
b d z O y A=42cm2 z O h O
截面 形状
a
y
A=42cm2
O y A=42cm2
z
z
y A=42cm2
弯曲截面 系数Wz (cm3)
38.4
45.4
55.6
309.0
z——中性轴
梁的合理设计
结论:(截面面积相同情况下)工字形最好、矩形 次之、方形再次、圆形最差 物理解释(应力分布)
例:已知1-1 截面上的弯矩 M<0,试判断其上A点正应力 的正负号。
M y Iz
1-1 O
z A
y
M
M
(2)公式中不含弹性模量E,说明正应力的大小
与材料无关。但在推导公式的过程中应用了胡克
梁的合理设计
二 合理设计梁的外形——变截面梁
圆形、方形、矩形、工字形截面的比较 截面优化 一般做法:
Wz M max
→等截面梁
q
B
存在问题:
A l
M图
轴向优化
Mmax=ql2/8
梁的合理设计
改进方法: 思路:“按需分配”
W Wz xz
q
A
l
M图
B
M max x
30 300 2 180 120 30 300 12 90 303 2 240 15 90 30 12
3
360
30 z C
O1
Ⅰ
y2 z y1 360
z0
z
Ⅱ
30 30
Ⅲ
315.46106 mm4
(4) 求抗弯截面系数
I 315.46106 W1 1.315103 m3 y1 240
中性层
dA
z z
横截面
确定中性轴的位置
y
E
y
A
A
E
y
dA 0
ydA 0
即: S z 0
结论:z轴(中性轴)通过截面的形心
●推导正应力的计算公式
E
y
M z y d A M
A
M
y
dA z z y
A
yE
y
dA M
M
E
1
A
y dA M
2
dA
x
EIz
M EI z
这表明:梁在外力作用下,横截面上的弯矩愈 大,梁的弯曲程度就愈大;EIz愈大,梁的弯曲程 度就愈小。 EIz:梁的抗弯刚度(Flexural rigidity),其意 义是梁抵抗弯曲变形的能力
M y Iz
M : 所求截面上的弯矩
I z : 截面惯性矩
y:
?
梁的合理设计
3 根据材料特性选择截面形状 如果[t] <[c] 思路:“劫富济贫”
y1 c ? y2 t
cmax
z
cmax
y1
z y2
tmax M max c y1 cmax Iz M max t y2 Iz
F A B l/ 3 l
360
q
30
,
O1
Ⅰ
C
z
C
Ⅱ
y2 z y1 360
z0 z
30 30
Ⅲ
90 y
分析: max (1) 如果横截面上、下对称
M y Iz
h
b
z
+max
max M max min Wz
y
-max
最大拉应力和最大压应力在同一个截面上,且 有max= -min
●实验分析
(1)平面假设(Hypothesis of plane section) 横截面在变形后仍为平面,并和弯曲后的纵向层正交 (2)单向受力假设 假设梁由纵向线组成,各纵向 线之间互不挤压,即每一纵向线受单向拉伸或压缩
a
b
a'
b'
M
c
M
d'
d
c'
(3)梁变形后,同一层纵向纤维的长度相同,即同 层各条纤维的伸长(或缩短)相同 (4)中性层(Neutral layer): 既不伸长也不缩短的纵向层 中性轴(Neutral axis): 中性层与横截面的交线
梁的应力
1 梁的正应力
2 梁的合理截面形状及变截面梁
3 矩形截面梁的切应力
4 *工字形及其它形状截面梁的切应力
5 梁的强度条件
平面弯曲
1 概述及弯曲内力 2 弯曲正应力 3 弯曲切应力
4 梁的强度条件
5 弯曲中心
1 梁的正应力 (Normal Stress of The Beam)
●内力在横截面上的分布形式
2 物理方面
E
E
y
此式表明:横截面 上离中性轴愈远的地 方,其正应力愈大; 梁弯曲后曲率愈大时, 同一位置的正应力也 愈大
O
z yA
A
y
y?
?
3 静力学方面
dA 0 FN A
M y Az d A 0
Mz
中性轴
M y dA x
A
y d A M
Young’s Modulus
托马斯.杨(Thomas. Young,1773~ 1829)英国物理学家。1807年,提出弹 性模量的定义,为此后人称弹性模量为 杨氏模量。
梁的合理设计
cmax
z O
y
M y Iz
tmax
t max cmax
如果[t][c],如何设计截面
i 1
n
A
i 1
n
30
Ⅲ
90
i
y
360 30 15 300 30 180 30 90 345 120mm 360 30 300 30 30 90
(3)求截面对中性轴的惯性矩
360 303 2 120 15 360 30 Iz 12
所求点的y坐标
●正应力在横截面上的分布规律
M
中性轴
max
M ymax Iz
I z ymax Wz
max
z
Maximum normal stress
M Wz
y
弯曲截面系数(section Wz : modulus of bending)
●在使用正应力计算公式时,要注意以下几点:
(1)公式中的M与y是代数量,应将其数值与正负号 一并代入公式,如果得到的为正,则表明是拉应力; 反之为压应力。实际应用时,也可以绝对值代入,得 的数值,再根据变形(Me正负)来判断其正负。
式中:Mmax为绝对值最大 如果[t][c]
?
如果[t][c] →不对称截面
-max max max
-
+max
+max +max
宽翼边缘受拉,窄翼边缘受压
(2) 如果横截面上、下不对称
ⅰ)梁上只有正弯矩或负弯矩; 最大拉应力和最大压应力在同一个截面上 ⅱ)全梁最大正弯矩为M1,最大负弯矩为M2(绝对值) 最大拉应力和最大压应力不一定在同一个截面上 z C z y1 y2
5 x 4
3m 50kN FS图
+
1m 30kN
y
x
-
70kN
30kN.m
5 5 5 125 50 40 M max 4 4 8 4
M图
+
-
M max 31.25kN.m
(2)求横截面的形心C的位置
360
30 z C
O1
Ⅰ
y2 z y1 360
z0
z
Ⅱ
30
y2 Ai yi
l l0 l1
y d d yd
l l
y
y
Ky
y
Ky
上式表明:梁在纯弯曲时,其纵向纤维的线应变 与纤维所在的位置有关,离中性层愈远,纤维的线应 变愈大;线应变与梁变形后的弯曲层度有关,曲率K 愈大时,同一位置的线应变也愈大。
Mmax=ql2/8
→变截面梁(beam with non-constant section)
梁的合理设计
F
A
x
具体做法:
B 写出弯矩方程M(x)
b h (x) y z
l
hmin
a b a' b'
M
c d
中性轴
M
d'
中性层
c'
O
dx y
z
z
y
Oy:竖向对称轴 Oz: 中性轴
?
y, z
E y, z
y
O'
曲率中心O'
中性层曲率半径
d K dx
曲率K
a y O1 K1 c
d
1
b dx O2 x K2 d
剪力FQ 弯矩 M 正应力 切应力
?
M
纵向平面
横截面
FQ
●纯弯曲(Pure bending) : 梁受力弯曲后,横截面上只产生弯矩而无剪力 的弯曲( AB段) 剪切弯曲(Transverse bending ):AC、BD段
F
C l F a a
F
D
A
B
FQ图
F Fa M图
★纯弯曲梁的正应力公式 思路: 实验观察得应变 的变化规律
b d z O y A=42cm2 z O h O
截面 形状
a
y
A=42cm2
O y A=42cm2
z
z
y A=42cm2
弯曲截面 系数Wz (cm3)
38.4
45.4
55.6
309.0
z——中性轴
梁的合理设计
结论:(截面面积相同情况下)工字形最好、矩形 次之、方形再次、圆形最差 物理解释(应力分布)
例:已知1-1 截面上的弯矩 M<0,试判断其上A点正应力 的正负号。
M y Iz
1-1 O
z A
y
M
M
(2)公式中不含弹性模量E,说明正应力的大小
与材料无关。但在推导公式的过程中应用了胡克
