2-1 力传感器_应变式-2013
A-2013工程测试与信号处理技术02-常用传感器原理

于是,电桥输出为:
DR1 = DR3 = DR2 = DR4
v»0
12-10-23
第二章 工程常用传感技术
10
2-2-4 电桥的预调平衡以及温度补偿方法
W:电位器,可选100~500KΩ; 1、预调平衡阻值选择 Rt:20~50KΩ; 2、温度对测量过程和测量结果的影响
➢ 信号调理电路的热稳定性:温度引起供桥电压变化或放大 电路增益改变而造成的测量结果偏离实际值;
➢ 被测物体表面处理:首先清理待测区域表面的油漆、锈斑、氧化层、油污、 灰尘等,清理干净后用沙纸打磨平整,再用丙酮或无水酒精擦拭干净。
➢ 标记定位线:用钢针在测点处画十字定位线,交叉点为应变片栅区中心。
➢ 粘合剂选用:短期测试(数月范围内)可用502胶水及其改性产品,长期测 试则应采用厂家提供的专用胶水,并采用指定的粘贴固化工艺流程。所用粘 合剂固化后应该有足够硬度,不能用凝固后呈显弹性状态的粘合剂。
➢ 热应变:温度变化引起被测对象热涨冷缩而形成的应变; ➢ 应变片的温度效应 与 热应变的区别:二者均是温度引起的桥
臂电阻值改变,但前者直接取决于温度变化量,而后者取决 于温度引起的应变量。 例如:温度升高后铸铁套受铜材圆柱膨胀作用的径向增加量(铜 线膨胀系数17ppm/K,铸铁11.2ppm/K)。测量方法:用一个材 质和结构完全相同的铸铁套作为补偿件。将待测件和补偿件置于 同温环境下,改变温度,进行测量应变。
12-10-23
第二章 工程常用传感技术
12
例如:梁式称重传感器。
截面1、2处的应变值1 和2 正比于待测重力F 及
其作用距离:
e1 = C × F ×( L + L0 )
e2 = C × F × L0
应变式力传感器原理

应变式力传感器原理
应变式力传感器利用材料的弹性变形特性来测量力的大小。
其工作原理如下:
1. 工作原理简述:
应变式力传感器由弹性材料制成,通常是金属或合金材料。
当外部施加力作用于传感器时,传感器内部的弹性材料会发生变形,而该变形会导致材料内部的应变产生变化。
2. 弹性材料的工作原理:
弹性材料具有弹性恢复能力,即当外力去除后能够恢复到初始状态。
在施加力之前,弹性材料的晶体结构处于初始状态,其晶体格子之间的距离是稳定的。
而当外力作用于材料时,晶格结构会发生略微的变化,晶体格子之间的距离会发生微小的变化。
3. 应变的产生:
当外力作用于弹性材料时,晶格结构的微小变化会导致材料内部产生应变。
应变是指单位长度的变形量,通常用应变率(单位长度的变形比例)来表示。
弹性材料的应变率与外力的大小成正比。
4. 电桥测量原理:
为了测量应变的变化,应变式力传感器通常采用了电桥测量原理。
电桥由四个电阻组成,其中一个电阻位于弹性材料上。
当材料受到外力作用时,其内部的应变发生变化,导致电阻值发生微小变化。
这会导致电桥的输出电压发生变化,从而可以通
过测量输出电压的变化来确定外界施加的力的大小。
总结:
应变式力传感器通过利用弹性材料的应变特性,测量外界施加的力的大小。
其工作原理主要包括弹性材料的应变产生和电桥测量原理。
通过测量电桥输出电压的变化,可以确定外界施加的力的大小。
第二章 电阻应变式(1)2013

d dV C V
dV dL d (r 2 ) 1 2 x 2 V L r
R [1 2 C 1 2 ] x K s x R
Ks 越大越好!
金属材料应 变灵敏系数
Ks:导线每单位应变引起的电阻值的相对变化量。
S L 2 S L
为材料的泊松比, 金属:0.2~0.4 ;半导体:0.35。
R L 1 2 R L
2.1.1 电阻应变片的工作原理
定义轴向应变为
x ,径向应变为 L/ L
y r / r
公式(2-6)
R L 1 2 x 1 2 R L
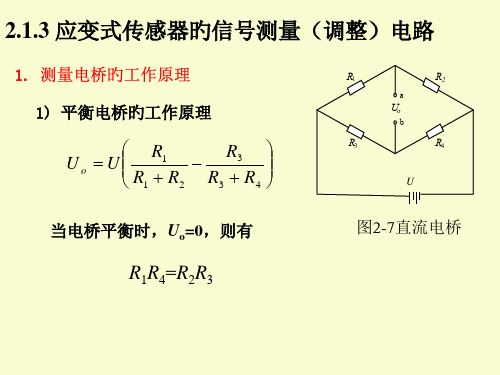
U o I1 R2 I 2 R4 UR2 UR4 R1 R2 R3 R4
R2 R3 R1 R4 Uo U ( R1 R2 )(R4 R3 )
当电桥平衡时,U0=0, 则有:
U I1 R1 R2
U I2 R3 R4
R1R4 R2 R3
或
R1 R3 R2 R4
直流电桥电路
(1)直流电桥平衡条件
R1R4 R2 R3 Uo E ( R1 R2 )(R4 R3 )
R1R4 R2 R3
R1 R3 R2 R4
2.1.3 测量电路
(2)电压灵敏度
单臂电桥:只有一个臂的应变片电阻变化, 其他的桥臂无变化,这时的输出电压 U 0 0 , 电桥处于非平衡状态。
优点:灵敏系数大,比金属电阻应变片打50~70倍;把弹性元 件与应变电阻集成一体,易于大批量生产,能够方便实现微型 化、集成化、智能化。 缺点:电阻和灵敏系数的温度系数大、非线性大和分散性大。
应变传感器pp2-1z

Kx
R R x
同样,当ε=0时,可得横向灵敏度系数
Ky
R R y
r
横向灵敏系数与轴向灵敏系数之比值,称为横向效应系数H。即
H K y (n 1) r K x 2nl (n 1) r
(2-10)
由(2-10)式可见,r愈小,l愈大,则H愈小。即敏感栅愈窄、基长愈Βιβλιοθήκη §2-1 金属应变片式传感器
4.零点漂移和蠕变 对于粘贴好的应变片,当温度恒定时,即使被测试件未承受应力,
应变片的指示应变也会随时间增加而逐渐变化,这一变化就是应变片的零 点漂移。产生零点漂移的主要原因是敏感栅通以工作电流后的温度效应; 应变片的内应力逐渐变化;粘结剂固化不充分等。
当应变片承受恒定的机械应变量,应变片的指示应变却随时间而变 化,这种特性称为蠕变。蠕变产生的原因是由于胶层之间发生“滑动”, 使力传到敏感栅的应变量逐渐减少。 5.应变极限
应变为εr。
若敏感栅有n根纵栅,每根长为l,半径为r,在轴向应变 ε作用下,
全部纵栅的变形视为△L1,则
△L1=nlε
半圆弧横栅同时受到ε和εr的作用,在任一微分小段长度dl=rdθ上的应变εθ 可由《材料力学》公式求得
1
2
r
1
2
r cos2
每个圆弧形横栅的变形量△l为
力(包括机械应力和热应力)所引起的表面应变。当应变量不大时,应变
片的指示应变值随试件表面真实应变的增加而线性增加。如曲线1所示。
当起初应变不断增加时,曲线1由直线1逐渐变弯,产生非线性误差,用相
对误差δ表示为
z i 100% z
属本身的特性有关,如康铜C≈1,Ks≈2.0,其它金属或合金,Ks一般在 1.8~3.6范围内。 (二)应变片的结构与材料
传感器:第2章应变式传感器

如果电桥各臂都改变,则有
Ug
E
(R1 R1)(R4 R4 ) (R2 R2 )(R3 R3) (R1 R1 R2 R2 )(R3 R3 R4 R4 )
(一)等臂电桥
当 R1 R2 R3 R4 时,称为等臂电桥。此时
Ug
E
R(R1 R2 R3 R4 ) R1R4 R2R3 (2R R1 R2 )(2R R3 R4 )
应变式传感器包括两部份,一是弹性敏感元件,将被 测量转换为应变;二是应变片,将应变转化为电阻 的变化。
被测量
应变量
弹性元件
电阻
应变片
变化
(一)柱式压力传感器 圆柱式压力传感器分为实心和空心两种。
柱式力传感器应变片的粘贴方式
对于柱式压力传感器其轴向应变和圆周方向应变与轴 向受力成正比例关系。
轴向应变
下面分析横向效应产生的原因。设轴向应变为 , 横向应变为 r。
2006.9.11 JC204->
若敏感栅有 n 个纵栅,每根长为 l ,圆弧横栅的半
径为 r ,在轴向应变 作用下,全部纵栅的形
变 L1 nl 。
在半圆弧上取一小微元 dl rd ,上面的应变为
1 2
(
r )
1 2
(
r ) cos 2
一、压阻效应 单晶硅材料在受到应力后,其电阻率发生明显的变化,
这种现象被称为压阻效应。 对于一条形的半导体材料,其电阻变化与应变的关系
d ( r 2 ) r2
2 dr r
2 r
根据泊松效应,有
r 上式中 为泊松系数。
由实验结果有
通常 C 1
d C dV V
由于 V S l
dV V
dS S
应变式传感器
(1)差动电桥
B R1+R1
+
R2-R2
A
C
Uo
R3
R4
-
D
B
R1+R1
+
R2-R2
A
C
Uo
R3-R3 D
R4+R4
-
E
E
(a)
(b)
图2-9 差动电桥
半桥差动:在试件上安装两个工作应变片,一种受拉应变,一种受 压应变, 接入电桥相邻桥臂。
Uo
U R1
R1 R1 R1 R2 R2
R3 R3 R4
Uo
U R1
R1 R1 R1 R2 R2
R3
R3 R3 R3 R4 R4
若ΔR1=ΔR2=ΔR3=ΔR4 , R1=R2=R3=R4,则得
Uo
U
R1 R1
R R
B R R
A
C
Uo
R R R R D
U
可知:Uo 与ΔR1/R1成线性关系,无非线性误差,而且电 桥电压敏捷度Su=U,是单臂工作时旳4倍。
U R 1
Uo
4
R1
1
R1 2R1
U
' 0
U 4
R1 R1
U Su 4
应用:根据上式,假如已知应变,就能够求出输出电压;反之依然。
2.非线性误差及其补偿措施
实际情况(保存分母中旳ΔR1/R1项):
n R1
U0
U
1 n
R1 R1 R1
(1
n)
若n=1:
理想情况(略去分母中旳ΔR1/R1项):
/
2)
2
内贴取“+”
式中: h——圆环厚度; b——圆环宽度; E——材料弹性模量。
传感器原理及应用(第三版)第2章

金属丝的应变灵敏系数
K0由两部 分组成
①受力后材料几何尺寸变化(1+2μ)
②受力后材料电阻率的变化(Δρ/ρ)/ε(与几何尺寸及 金属丝本身特性有关)
对于金属电阻丝(1+2μ )>>(Δ ρ /ρ )/ε ,金属丝应变片灵敏 系数k0主要由材料的几何尺寸变化决定,即对于用金属制成的应变片 来说,起主要作用的是应变效应(电阻的相对变化与伸长或缩短间 存在比例关系叫应变)。金属丝的μ =0.25~0.5(钢的μ =0.285)故 k0≈1+2μ ,k0≈1.5~2。 对于半导体则不同:当半导体材料受到应力作用后,其电阻率发生 明显的变化,称为压阻效应。因此(Δρ/ρ)/ε=πE >> (1+2μ ) 故可忽略(1+2μ )的影响,即对于用半导体制成的压阻传感器来说, 起主要作用的是压阻效应。半导体的k0≈ πE ≈ 50~100,灵敏度是 金属材料的几十到上百倍。 弹性模 压阻系
AR RK
上一页
下一页
返
回
不引入补偿块(如下图所示) – 起到温度补偿作用 – 可提高灵敏度
A:如图,R1、RB正交粘结 则: U AR' RK (1 )
0
R正反面(R1受拉,应变为正;RB受压,应变为负) 则: '
U0 2 AR RK
应变计
应变片的粘贴
1. 检查通断 13.固定 5 .用透明胶带将应变片与构件在引脚处 临时固定,移动胶带位置使应变片达到 3 .再用细砂纸精磨( 45度交叉纹)。 粘贴、焊接后,用胶布将引线和 正确定位。 2 .在选定贴应 被测对象固定在一起,防止拉动 4 .用棉纱或 引线和应变片。 变片的位置划
应变式压力传感器

应变式压力传感器作者:袁夫康来源:《中学物理·高中》2015年第07期1 应变式压力传感器发展简介应变式称重传感器,1938年美国加利福尼亚理工学院教授E·Simmons(西蒙斯)和麻省理工学院教授A·Ruge(鲁奇)分别同时研制出纸基丝绕式电阻应变计,以他们名字的字头和各有二位助手命名为SR-4型,由美国BLH公司专利生产.1940年美国BLH公司和Revere公司总工程师A·Thurston利用SR一4型电阻应变计研制出圆柱结构的应变式负荷传感器,用于工程测力和称重计量,成为应变式负荷传感器的创始者.1973年美国学者霍格斯特姆为克服正应力负荷传感器的固有缺点,提出不利用正应力,而利用与弯矩无关的切应力设计负荷传感器的理论,并设计出圆截工字形截面悬臂剪切梁型负荷传感器.打破了正应力负荷传感器的一统天下,形成了新的发展潮流.这是负荷传感器结构设计的重大突破.1974年前后美国学者斯坦因和德国学者埃多姆分别提出建立弹性体较为复杂的力学模型,利用有限单元计算方法,分析弹性体的强度、刚度,应力场和位移场,求得最佳化设计.为利用现代分析手段和计算方法设计与计算负荷传感器开辟了新途径.经历了70年代的切应力负荷传感器和铝合金小量程负荷传感器两大技术突破;80年代称重传感器与测力传感器彻底分离,制定R60国际建议和研发出数字式智能称重传感器两项重大变革;90年代在结构设计和制造工艺中不断纳入高新技术迎接新挑战,加速了称重传感器技术的发展;2000年OIML R60首次引入族和组、分配系数PL范围等新概念.2 应变式压力传感器原理将电阻应变片粘贴在弹性元件特定表面上,当力、扭矩、速度、加速度及流量等物理量作用于弹性元件时,会导致元件应力和应变的变化,进而引起电阻应变片电阻的变化.电阻的变化经电路处理后的以电信号的方式输出,这就是电阻应变式传感器的工作原理.电阻丝应变片一般是粘贴在传感器的弹性体上,当传感器承受压力后,弹性体产生形变,引起粘贴在弹性体上的应变片电阻值变化.在一般情况下,传感器内都是由4个应变片组成一个测量电桥,在大多数的使用情况下,传感器内部4个应变片同时受力,并且在受压形变的作用下,2个应变片阻值增大,2个变小.检测电路的功能是把电阻应变片的电阻变化转变为电压输出.因为电桥具有很多优点,如可以抑制温度变化的影响,可以抑制侧向力干扰,可以比较方便的解决称重传感器的补偿问题等,所以电桥在称重传感器中得到了广泛的应用.因为全桥式等臂电桥的灵敏度最高,各臂参数一致,各种干扰的影响容易相互抵消,所以称重传感器均采用全桥式等臂电桥.3 应变式力学传感器应用实例-电子秤3.1 电子秤构造浙江天煌科技实业有限公司,生产的TH-DZC型电子秤,是以一种比较简单的机构来演示用改变电阻来测量质量的方法.构造如图3所示.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平均应变εm与中点应变εt相对误差δ为:
t
m
1 m
s 1
t
t
in l
l
可见,δ只取决于 l。
误差δ的计算结果
l
δ(%)
1/10
1.62
1/20
0.52
由表可知,应变片栅长与正弦应变波波长之比愈小,δ愈小。
当应变片栅长为应变波长的1/10~1/20时,δ小于2%。
取l/=1/10,则由=v/f 得:f=0.1v/l。
x 0 sin
2
x
应变片中点的应变为
t
0 sin
2
xt
xt为t时刻应变片的中点坐标。 测试得到的应变片在栅长范围内的平均应变为εm,则
其数值等于l范围内应变波曲线下的面积除以 l,即
l
m
1 l
2 xt
l 2
sin xt
l 2
0
xdx
0
sin
2
sin
xt
l
2.1 电阻应变式传感器
缺点:有非线性,输出信号微弱,抗干扰能力较差,只能测量一点 或应变栅范围内的平均应变。
2.1 电阻应变式传感器
2.1.1 应变效应和工作原理
应变效应:导体或半导体材料受外力(拉或压力)作用时, 会产生机械变形,机械变形导致其电阻值变化。
设一长l、截面积为S、电阻率为ρ的园柱体,其电阻为
R l
S
设外力F作用下圆导体被拉伸(或压 缩),则:
件材料必须一样,两者线膨胀系数相同。 ③ 两应变片应处于同一温度场。
2.1 电阻应变式传感器
在某些测试条件下,可通过改变应变片的粘贴位置, 实现温度补偿,并可提高应变片的灵敏系数。
差动电桥补偿法
例如上图中,若将RB贴在被测试件的合适位置,并正确接 入差动电桥电路可得到很好的补偿效果。外力F作用下, RB 与R1的变化值符号相反, 借助差动电路可使得电桥的输出 电压增加。RB既起到温度补偿作用, 又提高灵敏度, 同 时补偿非线性误差。
应变极限
2.1 电阻应变式传感器
(5) 绝缘电阻和最大工作电流* 应变片的绝缘电阻指已粘贴的应变片的引线与被测件 之间的电阻值 Rm 。通常要求 Rm 在50MΩ~100MΩ以上。绝 缘电阻下降将使测量系统的灵敏度降低,使应变片的指示 应变产生误差。
对于已安装的应变片,最大工作电流是指允许通过敏 感栅而不影响其工作特性的最大电流 Imax 。工作电流的选 取要根据试件的导热性能及敏感栅形状和尺寸来决定。
2.1 电阻应变式传感器
2.1.3 电阻应变片的主要特性 (1)应变片的灵敏系数 K R R
t
K 表示安装在被测试件上的应变片在其轴向受单向应 力时,引起的电阻相对变化R/R与其单向应力引起的试件
表面轴向应变t之比。应变片的K值的准确性直接关系应变
测量精度,其误差大小是衡量质量优劣的重要标志。
实验表明,金属应变片的电阻相对变化与应变ε在很宽
化的影响可忽略;
对于半导体材料,其电阻的相对变化以材料的电阻率
变化(压阻效应)为主,即灵敏系数k0主要 结构尺寸变化的影响可忽略。
/
由决定,
一般金属导体的k0在1.6~4.8之间,而半导体的k0远比导 体的大,可达150~200。
对确定的材料,k0保持不变,即恒定。因此:
R R
k0
2.1 电阻应变式传感器
应变片的时间很短(估计约0.2μs),只需考虑应变沿应变片轴
向传播时的动态响应。
设一频率为 f 的正弦应变波在构件中以速度 v 沿应变片
栅长方向传播,在某瞬时
ε
t,应变量沿构件分布如图所示。
ε1
应变片
ε0
x
l
x1 λ
应变片对应变波的动态响应
2.1 电阻应变式传感器
设应变波波长为λ,则λ=v/f;应变片栅长为l,t时刻应 变波沿构件轴向(栅长方向)的分布为
种现象称为应变片的横向效应。
2.1 电阻应变式传感器
(3)机械滞后、零漂和蠕变*
机械滞后
应变片安装在试件上以后,在 加载和卸载过程中,对同一机械应 变量,两过程的特性曲线并不重合, 卸载时的指示应变高于加载时的指 示应变,这种现象称为应变片的机 械滞后。
产生机械滞后的主要原因是敏感 栅、基底和粘合剂在承受机械应变 之后留下的残余变形所致。
箔式应变片的基本结构
2.1 电阻应变式传感器
对金属电阻应变片敏感栅材料的基本要求*
① 灵敏系数k0 值大,且在较大应变范围内保持常数。 ② 电阻温度系数小。 ③ 电阻率大。 ④ 机械强度高,且易于拉丝或辗薄。 ⑤ 与铜丝的焊接性好,与其他金属的接触热电势小。
2.1 电阻应变式传感器
薄膜应变片* 采用真空蒸发或真空沉积的方法,将金属敏感材料直 接镀制于弹性基片上。相对于金属粘贴式应变片,薄膜应 变片的应变传递性能得到了极大的改善,几乎无蠕变,并 且具有应变灵敏系数高,稳定性好、可靠性高、工作温度 范围宽(-100℃~180℃)、使用寿命长、成本低等优点,是 一种很有发展前途的新型应变片。
2.1 电阻应变式传感器
(2)自补偿方法 即利用自身具有温度补偿作用的应变片进行补偿。
1) 选择式自补偿法(又称单丝自补偿法)
ΔR R
(Δ R R
)1
(Δ R R
)2
αt
Δ t
k (β g
β s ) Δ t
只需: α t k β g β s
该方法优点:应变片容易加工、成本低; 缺点:只适用特定材料、温度补偿范围也较窄
dR R dl R dS R d l S
S
dl
S2
dS
l S
d
圆柱体伸长后几何尺寸变化
2.1 电阻应变式传感器
用相对变化表示
dR dl dS d RlS
对于半径为r的导体,截面面积 S πr2
则:
dS 2πrdr
记圆柱体的轴向(纵向)相对变化dl/l为,即 = dl/l, 称为圆柱
2.1 电阻应变式传感器
2.1.5 测量电路
1. 直流电桥
1) 直流电桥平衡条件
ε Δ R 测量电路电压电流
R
当RL→∞时,电桥输出电压为
Uo
R1 R1 R2
R3 R3 R4
U
R1R4
R1 R2
R2
R3
R3 R4
U
当 R1R4
R2 R3
或
R1 R2
R3 时,电桥平衡。
R4
注意不同教材手册对电桥 电阻的编号顺序差异!
3) 材料* 金属电阻应变片常用的敏感栅材料有康铜、镍铬合
金、镍铬铝合金、铁铬铝合金、铂、铂钨合金等。
2.1 电阻应变式传感器
4) 电阻应变片的粘贴* 一般,应变片应用时用粘合剂粘贴到试件表面,粘合剂 的性能及粘结工艺的质量直接影响应变片的工作特性,因此 必须合理选择粘合剂,遵循正确的粘结工艺,保证粘贴质量, 这与电阻应变片的测量精度有着极其重要的关系。 此外粘贴时还要考虑到应变片的工作条件,如温度、相 对湿度、稳定性要求、粘贴时间长短的要求以及贴片固化时 加热加压的可能性等。
2.1 电阻应变式传感器
(4)应变极限 应变片的应变极限指在一定
温度下,应变片的指示应变 i 与
试件真实应变 j 的相对误差达到
规定值(一般为10%)时的真实应 变值 g 。
疲劳寿命*:对于已安装的应变 片,在恒定幅值的交变力作用下, 可连续工作而不产生疲劳损坏的 循环次数N称为应变片的疲劳寿 命。
2.1 电阻应变式传感器
2) 组合式自补偿(又称双丝自补偿法)*
敏感栅由两种不同温度系数
的电阻丝组成。
(a)二者有不同符号的电阻温
度系数,即 Δ R1t Δ R2t
R2t
也即: R1 R2
R2
R1t
组合式自补偿法 之一
R1
通过调节两种电阻丝的长度来控制应变片的温度补偿效果。
2.1 电阻应变式传感器
2. 力敏传感器
被测机械量↕→电参数↕ 测量电路 输出
力学量/机械量传感器种类繁多,应用广泛,主要应用 于对力、压力、称重、位移、加速度、扭矩、温度等 的测量、检测。它们是生产过程检测、生产自动化以 及人们生活不可缺少的手段之一。主要种类:
应变式传感器 电感式传感器 电容式传感器 压电式传感器
2.1 电阻应变式传感器
的范围内均为线性关系。 注意,应变片的K并不等于其敏感栅整体长度的材料的
灵敏系数k0,一般,K<k0。K值是通过实验测定的。
2.1 电阻应变式传感器
(2) 横向效应 将直的电阻丝绕成敏感栅后,虽然长度不变,应
变状态相同,但在圆弧处,除受纵向拉应变外,根据
泊松关系,还存在横向的负应变(y x),使电阻减 小,因而其灵敏系数K较整长电阻丝的灵敏系数小,这
1
t
t
b.敏感材料和试件材料的膨胀系数不同
R R
2
K(g
s ) t
2.1 电阻应变式传感器
因此,由环境温度变化形成总的电阻相对变化为:
R R
R R
1
R R
2
ttBiblioteka K(gs)
t
相应地由温度引起的热输出为:
i
R R
K
t
k
t
g s
t
要消除此项误差,需要采取温度补偿措施。
R R
1
2
/
设 则:
k0 1 2
/
R R
k0
k0为圆柱材料的电阻应变灵敏系数,它受两因素影响:该导体 的几何变形(尺寸变化)和电阻率变化,也即导体的电阻相对变
化由其几何变形和电阻率变化引起。
