系统聚类分析PPT课件
合集下载
(2021年)系统聚类分析法在大气污染中的应用优秀ppt

(1) 试用系统聚类分析法对这现象进行研究, 并绘制谱系图来进行分类。
(2) 根据(1)中的分类结果,谈谈你自己 的建议?
表1 2009年某城市记录的14个监测点的大气污染数据
样品号
污染元素 二氧化硫( X 1 ) 氮氧化物( X 2 ) 飘尘( X 3 )
再从新的距离矩阵中选出最小者 1,把 和 归并成新类0.;045
G2
0.304
G3
0.440
G4
0.000
G5
0.217
G6
1.000
G7
0.401
GG 98
0.932
G 10 G 11
0.G81089 0.242
G 12
G 13
0.082
0.155
G 14
0.976
X2 0.506 0.454 0.734 0.000 0.152 0.797 0.873 0.873 1.000 0.722 0.063 0.152 0.823
(2)由此,我们用互不相关的前5个主要成分 来代替原来的18个指标变量损失的信息不大, 所以结论分析(建议)如下: {1,2}这三个观测点,污染极轻,应加以保持。 {4,5,11,12,9,10}这五个观测点,污染较轻, 应注意减少污染物的排放。 {6,8,13}这三个观测点,大气污染较严重,应 加强城市绿化工作,建立城市立体绿化体系。 {7}观测点污染较重,应该进行整治。 {14}观测点污染很重应该按照环保工作总体方 案进行大气环境污染综合整治工作部署,以大 气污染企业污染治理和全面达标为重点。 {3}观测点,污染极重应大力的、系统的整治。
0.215
二、聚类要素的数据处理
在聚类分析中,聚类要素的选择是十分重 要的,它直接影响分类结果的准确性和可靠性。
(2) 根据(1)中的分类结果,谈谈你自己 的建议?
表1 2009年某城市记录的14个监测点的大气污染数据
样品号
污染元素 二氧化硫( X 1 ) 氮氧化物( X 2 ) 飘尘( X 3 )
再从新的距离矩阵中选出最小者 1,把 和 归并成新类0.;045
G2
0.304
G3
0.440
G4
0.000
G5
0.217
G6
1.000
G7
0.401
GG 98
0.932
G 10 G 11
0.G81089 0.242
G 12
G 13
0.082
0.155
G 14
0.976
X2 0.506 0.454 0.734 0.000 0.152 0.797 0.873 0.873 1.000 0.722 0.063 0.152 0.823
(2)由此,我们用互不相关的前5个主要成分 来代替原来的18个指标变量损失的信息不大, 所以结论分析(建议)如下: {1,2}这三个观测点,污染极轻,应加以保持。 {4,5,11,12,9,10}这五个观测点,污染较轻, 应注意减少污染物的排放。 {6,8,13}这三个观测点,大气污染较严重,应 加强城市绿化工作,建立城市立体绿化体系。 {7}观测点污染较重,应该进行整治。 {14}观测点污染很重应该按照环保工作总体方 案进行大气环境污染综合整治工作部署,以大 气污染企业污染治理和全面达标为重点。 {3}观测点,污染极重应大力的、系统的整治。
0.215
二、聚类要素的数据处理
在聚类分析中,聚类要素的选择是十分重 要的,它直接影响分类结果的准确性和可靠性。
聚类分析 ppt课件
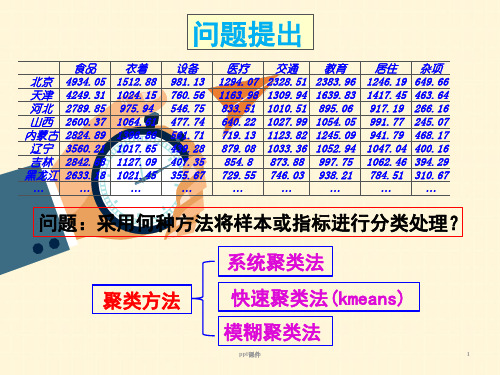
(2)相关系数
(3)距离和相关系数转换
di2j 1Ci2j
ppt课件
9
7.3 系统聚类法
1.基本思想 n个样本分成n类 计算任何两类距离 最小距离归为1类
整个过程画成聚类图
最短距离
最长距离 取
距 类平均法
离
方
重心法
法
中心距离法
离差平方和法 (Ward法)
ppt课件
10
2.系统聚类法计算公式
(1)最短距离法
…
教育 2383.96 1639.83 895.06 1054.05 1245.09 1052.94 997.75 938.21
…
居住 杂项
1246.19 649.66
1417.45 463.64
917.19 266.16
991.77 245.07
941.79 468.17
1047.04 400.16
0 0 0
0
结论:六种系统聚类法的并类原则和过程完全相同, 不同之处在于类与类之间的距离定义不同。
ppt课件
15
(7)程序实现
hc<-hclust(dist(X),method="single") #最短距离法 cbind(hc$merge,hc$height) #分类过程 plot(hc) #聚类图
[,1] [,2] [,3] [1,] -4 -5 1 [2,] -1 1 1.414 [3,] -2 2 4.123 [4,] -3 3 4.123
…
设备 981.13 760.56 546.75 477.74 561.71 439.28 407.35 355.67
…
医疗 1294.07 1163.98 833.51 640.22 719.13 879.08 854.8 729.55
(3)距离和相关系数转换
di2j 1Ci2j
ppt课件
9
7.3 系统聚类法
1.基本思想 n个样本分成n类 计算任何两类距离 最小距离归为1类
整个过程画成聚类图
最短距离
最长距离 取
距 类平均法
离
方
重心法
法
中心距离法
离差平方和法 (Ward法)
ppt课件
10
2.系统聚类法计算公式
(1)最短距离法
…
教育 2383.96 1639.83 895.06 1054.05 1245.09 1052.94 997.75 938.21
…
居住 杂项
1246.19 649.66
1417.45 463.64
917.19 266.16
991.77 245.07
941.79 468.17
1047.04 400.16
0 0 0
0
结论:六种系统聚类法的并类原则和过程完全相同, 不同之处在于类与类之间的距离定义不同。
ppt课件
15
(7)程序实现
hc<-hclust(dist(X),method="single") #最短距离法 cbind(hc$merge,hc$height) #分类过程 plot(hc) #聚类图
[,1] [,2] [,3] [1,] -4 -5 1 [2,] -1 1 1.414 [3,] -2 2 4.123 [4,] -3 3 4.123
…
设备 981.13 760.56 546.75 477.74 561.71 439.28 407.35 355.67
…
医疗 1294.07 1163.98 833.51 640.22 719.13 879.08 854.8 729.55
《应用多元统计分析》第五版PPT(第六章)-简化版(JMP13.1)

23
一、最短距离法
❖ 定义类与类之间的距离为两类最近样品间的距离, 即
DKL
min
iGK , jGL
dij
图6.3.1 最短距离法:DKL=d23
24
最短距离法的聚类步骤
❖ (1)规定样品之间的距离,计算n个样品的距离矩阵 D(0),它是一个对称矩阵。
❖ (2)选择D(0)中的最小元素,设为DKL,则将GK和GL合 并成一个新类,记为GM,即GM= GK∪GL。
❖ 聚集系统法的基本思想是:开始时将n个样品各自作 为一类,并规定样品之间的距离和类与类之间的距 离,然后将距离最近的两类合并成一个新类,计算 新类与其他类的距离;重复进行两个最近类的合并 ,每次减少一类,直至所有的样品合并为一类。
20
一开始每个样品各自作为一类
21
❖ 分割系统法的聚类步骤与聚集系统法正相反。由n个 样品组成一类开始,按某种最优准则将它分割成两 个尽可能远离的子类,再用同样准则将每一子类进 一步地分割成两类,从中选一个分割最优的子类, 这样类数将由两类增加到三类。如此下去,直至所 有n个样品各自为一类或采用某种停止规则。
12
➢ 一般地,若记 m1:配合的变量数 m2:不配合的变量数
则它们之间的距离可定义为
d x, y m2
m1 m2 ➢ 故按此定义,本例中x 与y 之间的距离为2/3。
13
二、相似系数
❖ 变量之间的相似性度量,在一些应用中要看相似系 数的大小,而在另一些应用中要看相似系数绝对值 的大小。
❖ 相似系数(或其绝对值)越大,认为变量之间的相 似性程度就越高;反之,则越低。
❖ 类与类之间的距离定义为两类最远样品间的距离, 即
DKL
max
一、最短距离法
❖ 定义类与类之间的距离为两类最近样品间的距离, 即
DKL
min
iGK , jGL
dij
图6.3.1 最短距离法:DKL=d23
24
最短距离法的聚类步骤
❖ (1)规定样品之间的距离,计算n个样品的距离矩阵 D(0),它是一个对称矩阵。
❖ (2)选择D(0)中的最小元素,设为DKL,则将GK和GL合 并成一个新类,记为GM,即GM= GK∪GL。
❖ 聚集系统法的基本思想是:开始时将n个样品各自作 为一类,并规定样品之间的距离和类与类之间的距 离,然后将距离最近的两类合并成一个新类,计算 新类与其他类的距离;重复进行两个最近类的合并 ,每次减少一类,直至所有的样品合并为一类。
20
一开始每个样品各自作为一类
21
❖ 分割系统法的聚类步骤与聚集系统法正相反。由n个 样品组成一类开始,按某种最优准则将它分割成两 个尽可能远离的子类,再用同样准则将每一子类进 一步地分割成两类,从中选一个分割最优的子类, 这样类数将由两类增加到三类。如此下去,直至所 有n个样品各自为一类或采用某种停止规则。
12
➢ 一般地,若记 m1:配合的变量数 m2:不配合的变量数
则它们之间的距离可定义为
d x, y m2
m1 m2 ➢ 故按此定义,本例中x 与y 之间的距离为2/3。
13
二、相似系数
❖ 变量之间的相似性度量,在一些应用中要看相似系 数的大小,而在另一些应用中要看相似系数绝对值 的大小。
❖ 相似系数(或其绝对值)越大,认为变量之间的相 似性程度就越高;反之,则越低。
❖ 类与类之间的距离定义为两类最远样品间的距离, 即
DKL
max
聚类分析 PPT课件
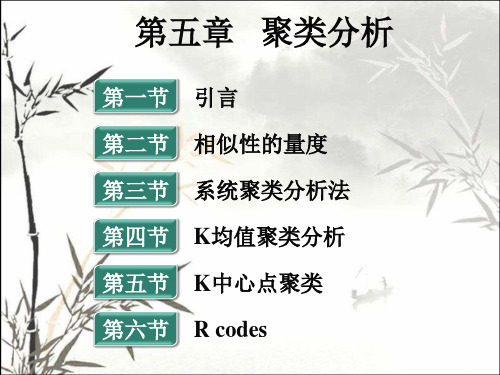
(f) (f) p dij f 1 ij d (i, j) (f) p f 1 ij
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
08-4.3 系统聚类法

3
1.最短距离法
❖ 定义类与类之间的距离为两类最近样品间的距离,即 DKL min d iGK ,jGL ij
4
最短距离法的递推公式
❖ 将类GK和GL合并成一个新类GM,则GM与任一类GJ之间距离的递推公 式为
DMJ minDKJ , DLJ
5
❖ 例1 (书中例6.3.1) 设有五个样品,每个只测量了一个指标,分别是 1,2,6,8,11,试用最短距离法将它们分类。
x7 478.42 570.84 364.91 281.84 287.87 330.24 360.48 317.61 720.33 429.77 575.76
《多元统计分析》MO O C
4.3 系统聚类法
王学民
一、系统聚类法的概念
❖ 系统聚类法(或层次聚类法)是通过一系列相继的合并或相继的分割 来进行的,分为聚集的和分割的两种。系统聚类法适用于样品数目n不 是非常大的情形。
❖ 聚集系统法的基本思想是:开始时将n个样品各自作为一类,并规定样 品之间的距离和类与类之间的距离,然后将距离最近的两类合并成一 个新类,计算新类与其他类的距离;重复进行两个最近类的合并,每 次减少一类,直至所有的样品合并为一类。
例1的最长距离法树形图
例1的类平均法树形图
例1的离差平方和法树形图
17
三、案例分析
❖ 例2 (书中例6.3.3) 下表列出了1999年全国31个省、直辖市和自治 区的城镇居民家庭平均每人全年消费性支出的八个主要变量数据。这
八个变量是
x1:食品 x2:衣着 x3:家庭设备用品及服务 x4:医疗保健
x5:交通和通讯 x6: 娱乐教育文化服务 x7 :居住 x8:杂项商品 和服务
➢ 记G1={1},G2={2},G3={6},G4={8},G5={11},样品间采用绝对值 距离。
聚类分析法ppt课件全

8/21/2024
25
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(3)分类函数
按照修改原则不同,动态聚类方法有按批修改法、逐个修改法、混合法等。 这里主要介绍逐步聚类法中按批修改法。按批修改法分类的原则是,每一步修 改都将使对应的分类函数缩小,趋于合理,并且分类函数最终趋于定值,即计 算过程是收敛的。
8/21/2024
23
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(2)初始分类 有了凝聚点以后接下来就要进行初始分类,同样获得初始分类也有不同的
方法。需要说明的是,初始分类不一定非通过凝聚点确定不可,也可以依据其 他原则分类。
以下是其他几种初始分类方法: ①人为分类,凭经验进行初始分类。 ②选择一批凝聚点后,每个样品按与其距离最近的凝聚点归类。 ③选择一批凝聚点后,每个凝聚点自成一类,将样品依次归入与其距离
8/21/2024
14
1.2 聚类分析的种类
(2)系统聚类分析的一般步骤 ①对数据进行变换处理; ②计算各样品之间的距离,并将距离最近的两个样品合并成一类; ③选择并计算类与类之间的距离,并将距离最ቤተ መጻሕፍቲ ባይዱ的两类合并,如果累的个
数大于1,则继续并类,直至所有样品归为一类为止; ④最后绘制系统聚类谱系图,按不同的分类标准,得出不同的分类结果。
8/21/2024
18
1.2 聚类分析的种类
(7)可变法
1 2 D kr
2 (8)离差平方和法
(D k 2 pD k 2 q)D p 2q
D k 2 rn n ir n n p i D i2 pn n ir n n q iD i2 qn rn in iD p 2 q
8/21/2024
spss聚类分析PPT课件

G7
G3
G4
G8
G7
0
G3
3
0
G4
5
2
0
G8
7
4
2
0
30
10/16/2024
(3)在D(1)中最小值是D34=D48=2,由于G4与G3合并, 又与G8合并,因此G3、G4、G8合并成一个新类G9,其与其 它类的距离D(2)
G7
G9
G7
0
G9
3
0
31
10/16/2024
(4)最后将G7和G9合并成G10,这时所有的六个样品聚为一 类,其过程终止。 上述聚类的可视化过程如下:
1
2
3
4
5
1
0
8.062 17.804 26.907 30.414
2
8.062 0
25.456 34.655 38.21
3
17.804 25.456 0
9.22 12.806
4
26.907 34.655 9.22 0
3.606
5
30.414 38.21 12.806 3.606 0
26
10/16/2024
系统聚类过程是:假设总共有n个样品(或变量)
第一步:将每个样品(或变量)独自聚成一类,共有 n类;
第二步:根据所确定的样品(或变量)“距离”公式, 把距离较近的两个样品(或变量)聚合为一类,其 它的样品(或变量)仍各自聚为一类,共聚成n 1 类;
第三步:将“距离”最近的两个类进一步聚成一类, 共聚成n 2类;……,以上步骤一直进行下去,最后17 将所有的样品(或变量)全聚成一类。
(1)选择样品距离公式,绝对距离最简单,形成D(0)
多元统计分析——基于R 语言 PPT课件-聚类分析

步骤:
(1)把样品粗略分成K个初始类。
(2)进行修改,逐个分派样品到其最近均值类中(通常用标准化数据或非标准化数据计算欧氏距
离)。重新计算接受新样品的类和失去样品的类的形心(均值)。
(3)重复第2步,直到各类无元素进出。
注意:
样品的最终聚类在某种程度上依赖于最初的划分或种子点的选择。
为了检验聚类的稳定性,可用一个新的初始分类重新检验整个聚类算法。如果最终分类与原来
✓有序样品的聚类:n个样品按某种原因(时间、地层深度等)排成次序,必须是
次序相邻的样品才能聚成一类。
✓分解法:首先所有的样品均在一类,然后用某种最优准则将它分为两类,再试
图用同种准则将这两类各自分裂为两类,从中选一个使目标函数较好者,这样
由两类变成三类,如此下去,一直分裂到每类只有一个样品为止(或采用其他停
1. 可能的分类数目
′
对于有序样品,n个样品分成k类的一切可能的分法有: , =
−
−
2. 最优分割法(又称Fisher算法)
(1)定义类的直径
设某一类 是{ , +1 , … , }( > ),均值为ഥ
,ഥ
=
σ= 。
−+
(2)定义目标函数
= ≤≤ { − , − + , }
当我们要分k类时,首先找 使上式达到最小,即
(2)最长距离法: , = max{ | ∈ , ∈ },表示类 与类 最邻近的两个样本距
离。
定义
(3)类平均法: , =
σ∈ σ∈
,表示类 与类 任两个样品距离的平均。
(4)重心法: , = ഥpഥ ,表示两个重心ഥ
(1)把样品粗略分成K个初始类。
(2)进行修改,逐个分派样品到其最近均值类中(通常用标准化数据或非标准化数据计算欧氏距
离)。重新计算接受新样品的类和失去样品的类的形心(均值)。
(3)重复第2步,直到各类无元素进出。
注意:
样品的最终聚类在某种程度上依赖于最初的划分或种子点的选择。
为了检验聚类的稳定性,可用一个新的初始分类重新检验整个聚类算法。如果最终分类与原来
✓有序样品的聚类:n个样品按某种原因(时间、地层深度等)排成次序,必须是
次序相邻的样品才能聚成一类。
✓分解法:首先所有的样品均在一类,然后用某种最优准则将它分为两类,再试
图用同种准则将这两类各自分裂为两类,从中选一个使目标函数较好者,这样
由两类变成三类,如此下去,一直分裂到每类只有一个样品为止(或采用其他停
1. 可能的分类数目
′
对于有序样品,n个样品分成k类的一切可能的分法有: , =
−
−
2. 最优分割法(又称Fisher算法)
(1)定义类的直径
设某一类 是{ , +1 , … , }( > ),均值为ഥ
,ഥ
=
σ= 。
−+
(2)定义目标函数
= ≤≤ { − , − + , }
当我们要分k类时,首先找 使上式达到最小,即
(2)最长距离法: , = max{ | ∈ , ∈ },表示类 与类 最邻近的两个样本距
离。
定义
(3)类平均法: , =
σ∈ σ∈
,表示类 与类 任两个样品距离的平均。
(4)重心法: , = ഥpഥ ,表示两个重心ഥ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经过这种标准化所得的新数据,各要素的 极大值为1,极小值为0,其余的数值均在0与1 之间。
例题:表3.4.2给出了某地区9个农业区的7项 指标,它们经过极差标准化处理后,如表 3.4.3所示。
表3.4.2 某地区9个农业区的7项经济指标数据
区
人均
劳均
代
耕地X1
耕地X2
· · 号 /(hm2 人-1) /(hm2 个-1 )
水田 比重
X3 /%
G1 0.294
G2 0.315 G3 0.123 G4 0.179 G5 0.081 G6 0.082 G7 0.075 G8 0.293 G9 0.167
1.093
0.971 0.316 0.527 0.212 0.211 0.181 0.666 0.414
5.63
0.39 5.28 0.39 72.04 43.78 65.15 5.35 2.9
③ 明科夫斯基距离
1
dijkn1xikxjkpp
(i,j1,2, ,m )(3.4.5)
(i,j1,2, ,m)(3.4.6)
(i,j1,2, ,m) (3.4.7)
④ 切比雪夫距离。当明科夫斯基距 p
时,有
d ij m k x ia k x x jk
(i,j 1 ,2 , ,m ) (3.4.8)
据表3.4.3中的数据,用公式(3.4.5)式计
算可得9个农业区之间的绝对值距离矩阵如下
0
1.52 0
3.10 2.70 0
2.19 1.47 1.23 0
D
(di
j
)995.86 来自6.023.644.77
0
4.72 4.46 1.86 2.99 1.78 0
5.79 5.53 2.93 4.06 0.83 1.07 0
复种 指数
x4 /%
粮食 单产x5
· /(kg hm -2
)
113.6 4 510.5
95.1 148.5 111 217.8 179.6 194.7 94.9 94.8
2 773.5 6 934.5 4 458 12 249 8 973 10 689 3 679.5 4 231.5
人均粮食x6
· /(kg 人-1 )
③ 极大值标准化,即
x i j m ix { ix jia } j x (i 1 ,2 , ,m ;j 1 ,2 , (3,n .4) .3)
经过这种标准化所得的新数据,各要素的 极大值为1,其余各数值小于1。
④ 极差的标准化,即
x ij m ix ix j im ja im i x x ij x iiji nn ( i 1 ,2 , ,m ;j( 31 .,42 .,4 ),n )
0.26 0.04 0.00 0.15
X6
X7
1.00 0.14
0.24 0.00
0.08 0.07
0.13 0.00
0.45 1.00
0.13 0.59
0.13 1.00
0.43 0.09
0.00 0.00
二、距离的计算
常见的距离有
① 绝对值距离
n
dij xikxjk
② 欧氏距i 离1
n
dij (xikxjk)2 k1
假设有m 个聚类的对象,每一个聚类对象
都有n个要素构成。它们所对应的要素数据可
用表3.4.1给出。
表3.4.1 聚类对象与要素数据
聚类对象
1 2 i m
要
素
x1 x2 xj xn
x11 x12 x1 j x1n
x21 x22 x2 j x2n
x i1 x i 2 x ij x in
x m1 x m 2 x mj x mn
在聚类分析中,常用的聚类要素的数据处 理方法有如下几种:
① 总和标准化。分别求出各聚类要素所
对应的数据的总和,以各要素的数据除以该要
素的数据的总和,即
xijm xij
xij
(i1,2, ,m ;j1,2, ,n) (3.4.1)
i1
这种标准化方法所得到的新数据满足
1 036.4
稻谷 占粮 食比 重 x7/%
12.2
683.7 611.1 632.6 791.1 636.5 634.3 771.7 574.6
0.85 6.49 0.92 80.38 48.17 80.17 7.8 1.17
表3.4.3 极差标准化处理后的数据
x1
G1 0.91 G2 1.00 G3 0.20 G4 0.44 G5 0.03 G6 0.03 G7 0.00 G8 0.91 G9 0.38
第4节 系统聚类分析
➢聚类要素的数据处理
➢ 距离的计算 ➢ 直接聚类法 ➢ 最短距离聚类法 ➢ 最远距离聚类法 ➢ 系统聚类法计算类之间距离的统一公式
➢系统聚类分析实例
一、聚类要素的数据处理
在聚类分析中,聚类要素的选择是十分重 要的,它直接影响分类结果的准确性和可靠性。
在地理分类和分区研究中,被聚类的对象 常常是多个要素构成的。不同要素的数据往往 具有不同的单位和量纲,其数值的变异可能是 很大的,这就会对分类结果产生影响。因此当 分类要素的对象确定之后,在进行聚类分析之 前,首先要对聚类要素进行数据处理。
1.32 0.88 2.24 1.29 5.14 3.96 5.03 0
2.62 1.66 1.20 0.51 4.84 3.06 3.32 1.40
(3.4.9)
0
三、直接聚类法
▪ 原理
先把各个分类对象单独视为一类,然后根 据距离最小的原则,依次选出一对分类对象, 并成新类。如果其中一个分类对象已归于一类, 则把另一个也归入该类;如果一对分类对象正 好属于已归的两类,则把这两类并为一类。每 一次归并,都划去该对象所在的列与列序相同 的行。经过m-1次就可以把全部分类对象归为 一类,这样就可以根据归并的先后顺序作出聚 类谱系图。
m
xij 1 (j 1,2,,n)
i1
② 标准差标准化,即
x ijx is j jxj (i 1 ,2 , ,m ;j 1 ,2 , ,n ) (3.4.2)
由这种标准化方法所得到的新数据,各要 素的平均值为0,标准差为1,即有
xj m 1im 1xij0
sj m 1im 1(xijxj)2 1
x2
x3
x4
X5
1.00 0.07 0.15 0.18
0.87 0.00 0.00 0.00
0.15 0.07 0.44 0.44
0.38 0.00 0.13 0.18
0.03 1.00 1.00 1.00
0.03 0.61 0.69 0.65
0.00 0.90 0.81 0.84
0.53 0.07 0.00 0.10
例题:表3.4.2给出了某地区9个农业区的7项 指标,它们经过极差标准化处理后,如表 3.4.3所示。
表3.4.2 某地区9个农业区的7项经济指标数据
区
人均
劳均
代
耕地X1
耕地X2
· · 号 /(hm2 人-1) /(hm2 个-1 )
水田 比重
X3 /%
G1 0.294
G2 0.315 G3 0.123 G4 0.179 G5 0.081 G6 0.082 G7 0.075 G8 0.293 G9 0.167
1.093
0.971 0.316 0.527 0.212 0.211 0.181 0.666 0.414
5.63
0.39 5.28 0.39 72.04 43.78 65.15 5.35 2.9
③ 明科夫斯基距离
1
dijkn1xikxjkpp
(i,j1,2, ,m )(3.4.5)
(i,j1,2, ,m)(3.4.6)
(i,j1,2, ,m) (3.4.7)
④ 切比雪夫距离。当明科夫斯基距 p
时,有
d ij m k x ia k x x jk
(i,j 1 ,2 , ,m ) (3.4.8)
据表3.4.3中的数据,用公式(3.4.5)式计
算可得9个农业区之间的绝对值距离矩阵如下
0
1.52 0
3.10 2.70 0
2.19 1.47 1.23 0
D
(di
j
)995.86 来自6.023.644.77
0
4.72 4.46 1.86 2.99 1.78 0
5.79 5.53 2.93 4.06 0.83 1.07 0
复种 指数
x4 /%
粮食 单产x5
· /(kg hm -2
)
113.6 4 510.5
95.1 148.5 111 217.8 179.6 194.7 94.9 94.8
2 773.5 6 934.5 4 458 12 249 8 973 10 689 3 679.5 4 231.5
人均粮食x6
· /(kg 人-1 )
③ 极大值标准化,即
x i j m ix { ix jia } j x (i 1 ,2 , ,m ;j 1 ,2 , (3,n .4) .3)
经过这种标准化所得的新数据,各要素的 极大值为1,其余各数值小于1。
④ 极差的标准化,即
x ij m ix ix j im ja im i x x ij x iiji nn ( i 1 ,2 , ,m ;j( 31 .,42 .,4 ),n )
0.26 0.04 0.00 0.15
X6
X7
1.00 0.14
0.24 0.00
0.08 0.07
0.13 0.00
0.45 1.00
0.13 0.59
0.13 1.00
0.43 0.09
0.00 0.00
二、距离的计算
常见的距离有
① 绝对值距离
n
dij xikxjk
② 欧氏距i 离1
n
dij (xikxjk)2 k1
假设有m 个聚类的对象,每一个聚类对象
都有n个要素构成。它们所对应的要素数据可
用表3.4.1给出。
表3.4.1 聚类对象与要素数据
聚类对象
1 2 i m
要
素
x1 x2 xj xn
x11 x12 x1 j x1n
x21 x22 x2 j x2n
x i1 x i 2 x ij x in
x m1 x m 2 x mj x mn
在聚类分析中,常用的聚类要素的数据处 理方法有如下几种:
① 总和标准化。分别求出各聚类要素所
对应的数据的总和,以各要素的数据除以该要
素的数据的总和,即
xijm xij
xij
(i1,2, ,m ;j1,2, ,n) (3.4.1)
i1
这种标准化方法所得到的新数据满足
1 036.4
稻谷 占粮 食比 重 x7/%
12.2
683.7 611.1 632.6 791.1 636.5 634.3 771.7 574.6
0.85 6.49 0.92 80.38 48.17 80.17 7.8 1.17
表3.4.3 极差标准化处理后的数据
x1
G1 0.91 G2 1.00 G3 0.20 G4 0.44 G5 0.03 G6 0.03 G7 0.00 G8 0.91 G9 0.38
第4节 系统聚类分析
➢聚类要素的数据处理
➢ 距离的计算 ➢ 直接聚类法 ➢ 最短距离聚类法 ➢ 最远距离聚类法 ➢ 系统聚类法计算类之间距离的统一公式
➢系统聚类分析实例
一、聚类要素的数据处理
在聚类分析中,聚类要素的选择是十分重 要的,它直接影响分类结果的准确性和可靠性。
在地理分类和分区研究中,被聚类的对象 常常是多个要素构成的。不同要素的数据往往 具有不同的单位和量纲,其数值的变异可能是 很大的,这就会对分类结果产生影响。因此当 分类要素的对象确定之后,在进行聚类分析之 前,首先要对聚类要素进行数据处理。
1.32 0.88 2.24 1.29 5.14 3.96 5.03 0
2.62 1.66 1.20 0.51 4.84 3.06 3.32 1.40
(3.4.9)
0
三、直接聚类法
▪ 原理
先把各个分类对象单独视为一类,然后根 据距离最小的原则,依次选出一对分类对象, 并成新类。如果其中一个分类对象已归于一类, 则把另一个也归入该类;如果一对分类对象正 好属于已归的两类,则把这两类并为一类。每 一次归并,都划去该对象所在的列与列序相同 的行。经过m-1次就可以把全部分类对象归为 一类,这样就可以根据归并的先后顺序作出聚 类谱系图。
m
xij 1 (j 1,2,,n)
i1
② 标准差标准化,即
x ijx is j jxj (i 1 ,2 , ,m ;j 1 ,2 , ,n ) (3.4.2)
由这种标准化方法所得到的新数据,各要 素的平均值为0,标准差为1,即有
xj m 1im 1xij0
sj m 1im 1(xijxj)2 1
x2
x3
x4
X5
1.00 0.07 0.15 0.18
0.87 0.00 0.00 0.00
0.15 0.07 0.44 0.44
0.38 0.00 0.13 0.18
0.03 1.00 1.00 1.00
0.03 0.61 0.69 0.65
0.00 0.90 0.81 0.84
0.53 0.07 0.00 0.10
