机械原理典型例题力分析
机械原理典型例题分析第1章典型例题2

F = 3n − 2 p5 − p4 = 3 × 3 − 2 × 4 − 1 = 0
第1章典型例题
3)分析能否实现设计意图 ) F = 0 ,说明该方案不能实现设计意图,从图中 的运动也可分析出:构 说明该方案不能实现设计意图, 的运动也可分析出: 说明该方案不能实现设计意图 从图中C的运动也可分析出 点的运动轨迹应为圆弧, 上的C点的运动轨迹应为直线 件3上C点的运动轨迹应为圆弧,而构件 上的 点的运动轨迹应为直线, 上 点的运动轨迹应为圆弧 而构件4上的 点的运动轨迹应为直线, 显然不可能实现设计意图。 显然不可能实现设计意图。 4)实现设计意图 需在 处增加一个自由度,其改进后的方案如图所示。 ) 需在C处增加一个自由度 其改进后的方案如图所示。 处增加一个自由度,
机构将使冲头4上下运动达到冲压的目的。试绘出运动简图, 机构将使冲头4上下运动达到冲压的目的。试绘出运动简图,分析是否能 实现设计意图,并提出修改方案。 实现设计意图,并提出修改方案。
解题思路: 解题思路 首先搞清设计者的意 图,画出机构运动简图、计算其自 画出机构运动简图、 由度,然后分析能否实现设计意图, 由度,然后分析能否实现设计意图, 最后提出修改方案。 最后提出修改方案。
2)分析:能够实现直动从动件的往复移动,满足设计意图的要求。 分析:能够实现直动从动件的往复移动,满足设计意图的要求。
第1章典型例题
例9
图示机构中构件1为原动件,构件 为输出构件 为输出构件, 、 为固定铰链, 图示机构中构件 为原动件,构件4为输出构件,A、B 为固定铰链,试 为原动件 画出该机构的运动简图;计算机构的自由度。 画出该机构的运动简图;计算机构的自由度。
例2
机构运动简图的绘制实例: 机构运动简图的绘制实例:
机械原理题库平面机构力分析(包括摩擦和自锁)

3 平面机构力分析(包括摩擦和自锁)1.对 机 构 进 行 力 分 析 的 目 的 是:(1) ;(2) 。
2.所 谓 静 力 分 析 是 指 的一种力分析方 法 , 它 一 般 适 用 于 情 况。
3.所 谓 动 态 静 力 分 析 是 指 的 一 种 力 分 析 方 法, 它 一 般 适 用 于 情 况。
4.绕 通 过 质 心 并 垂 直 于 运 动 平 面 的 轴 线 作 等 速 转 动 的 平 面 运 动 构 件, 其 惯 性 力P I= , 在 运 动 平 面 中 的惯 性 力 偶 矩MI=。
5.在滑动摩擦系数相同条件下,槽面摩擦比平面摩擦大,其原因是 。
6.机械中三角带传动比平型带传动用得更为广泛,从摩擦角度来看,其主要原因是 。
7.设机 器 中 的 实 际 驱 动 力 为rP , 在同 样 的 工 作 阻 力 和 不 考 虑 摩 擦 时 的 理 想 驱 动 力 为rP 0, 则 机 器 效 率 的 计 算 式 是η = 。
8.设 机 器 中 的 实 际 生 产 阻 力 为 rQ ,在 同 样 的 驱 动 力 作 用 下 不 考 虑 摩 擦 时 能 克 服 的 理 想 生 产 阻 力 为 rQ 0 , 则 机 器 效 率 的 计 算 式 是η=。
9.在 认 为 摩 擦 力 达 极 限 值 条 件 下 计 算 出 机 构 效 率η 后, 则 从 这 种 效率 观 点 考 虑, 机 器 发 生 自 锁 的 条 件 是 。
10.设 螺 纹 的 升 角为λ, 接 触 面 的 当 量 摩 擦 系 数 为f v ,则 螺 旋 副 自 锁的 条 件 是 。
11.在机械中阻力与 其作用点速度方向 。
A).相 同 ; B).一定相反 ; C).成锐角 ; D).相反或成钝角 。
12.在 机 械 中 驱 动 力 与 其 作 用 点 的 速 度 方 向 。
A 〕 一 定 同 向; B 〕 可 成 任 意 角 度; C 〕 相 同 或 成 锐 角; D 〕 成 钝 角。
机械原理 力分析

平衡力(平衡力矩)是与作用在机械上的已知外力相平衡的未知外力(矩)重力惯性力机构力分析的任务、目的和方法f4-1f4-0驱动力(原动力)阻抗力(生产阻力和非生产阻力)运动副中的反力摩擦力和介质阻力作用在机械上的力:可能为驱动力或阻力在一个运动循环中所作的功为零运动副中摩擦力的确定移动副中摩擦力确定在机械运动时,运动副两元素间将产生摩擦力。
平面机构中的运动副:移动副例斜面机构例螺旋机构转动副平面高副f4-5f4-5f4-5运动副中摩擦力的确定移动副中摩擦力确定在机械运动时,运动副两元素间将产生摩擦力。
平面机构中的运动副:移动副例斜面机构例螺旋机构转动副平面高副f4-5f4-5f4-5螺纹的牙型有:矩形螺纹三角形螺纹梯形螺纹锯齿形螺纹15º30º3º30º运动副中摩擦力的确定移动副中摩擦力确定在机械运动时,运动副两元素间将产生摩擦力。
平面机构中的运动副:移动副例斜面机构例螺旋机构转动副平面高副f4-5f4-5f4-5螺纹的用途:传递动力或联接螺纹的旋向:右旋左旋运动副中摩擦力的确定在机械运动时,运动副两元素间将产生摩擦力。
平面机构中的运动副:移动副轴颈摩擦力确定转动副轴端摩擦力确定运动副中摩擦力的确定在机械运动时,运动副两元素间将产生摩擦力。
平面机构中的运动副:移动副转动副平面高副高副中摩擦力确定不考虑摩擦时机构的力分析f4-3例六杆机构力分析机构力分析的任务是确定F R ij (运动副中的反力)和需加于机构上的平衡力(矩)。
但F R ij 对整个机构来说是内力,必须将机构分解为若干个构件组后进行分析。
如何分?例铰链四杆机构例曲柄滑块机构1 各运动副的反力(设各构件的重力及惯性力不计)2 需施加于凸轮1上的驱动力矩在图示机构中,已知各构件的尺寸及机构的位置,各转动副中的摩擦圆如图中虚线圆所示,移动副及凸轮高副处的摩擦角为,作用在构件4上的工作阻力为Q 。
试求该图示位置:ϕϕR23R43ω34ω321 各运动副的反力(设各构件的重力及惯性力不计)2 需施加于凸轮1上的驱动力矩LR 2343ω25R 54R 52R 12R 51V B2B1R 12R 52523212=++R R R R 54R 34QV 45R 21R 32构件2: 1 各运动副的反力(设各构件的重力及惯性力不计)2 需施加于凸轮1上的驱动力矩ω34ω32ϕLR 2343ω25R 54R 52R 12R 51V B2B1R 12R 52523212=++R R R R 54R 34QV 45R 21R 32构件2:)( L 21211Nm R L R M l F l μμμ==ω34ω32ϕ。
机械原理习题与答案解析
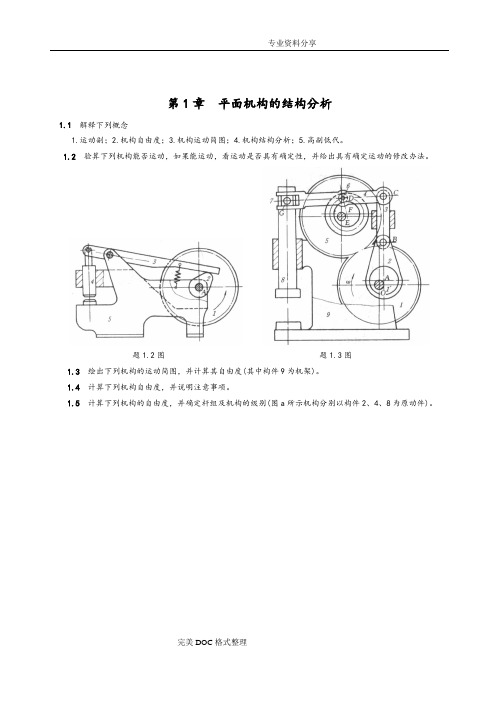
第1章平面机构的结构分析1.1解释下列概念1.运动副;2.机构自由度;3.机构运动简图;4.机构结构分析;5.高副低代。
1.2验算下列机构能否运动,如果能运动,看运动是否具有确定性,并给出具有确定运动的修改办法。
题1.2图题1.3图1.3 绘出下列机构的运动简图,并计算其自由度(其中构件9为机架)。
1.4 计算下列机构自由度,并说明注意事项。
1.5计算下列机构的自由度,并确定杆组及机构的级别(图a所示机构分别以构件2、4、8为原动件)。
题1.4图题1.5图第2章平面机构的运动分析2.1试求图示各机构在图示位置时全部瞬心。
题2.1图2.2在图示机构中,已知各构件尺寸为l AB=180mm , l BC=280mm , l BD=450mm ,l CD=250mm ,l AE=120mm ,φ=30º, 构件AB上点E的速度为v E=150 mm /s ,试求该位置时C、D两点的速度及连杆2的角速度ω2。
2.3 在图示的摆动导杆机构中,已知l AB=30mm , l AC=100mm , l BD=50mm ,l DE=40mm ,φ1=45º,曲柄1以等角速度ω1=10 rad/s沿逆时针方向回转。
求D点和E点的速度和加速度及构件3的角速度和角加速度(用相对运动图解法)。
题2.2图题2.3图2.4 在图示机构中,已知l AB =50mm , l BC =200mm , x D =120mm , 原动件的位置φ1=30º, 角速度ω1=10 rad/s ,角加速度α1=0,试求机构在该位置时构件5的速度和加速度,以及构件2的角速度和角加速度。
题2.4图2.5 图示为机构的运动简图及相应的速度图和加速度图。
(1)在图示的速度、加速度多边形中注明各矢量所表示的相应的速度、加速度矢量。
(2)以给出的速度和加速度矢量为已知条件,用相对运动矢量法写出求构件上D 点的速度和加速度矢量方程。
河北工业大学机械原理力分析

2、机械力分析的方法:
图解法:形象直观,精度低
解析法:精度高,可进行运动循环的力分析
第二节
一、作用在机械上的力
给定力
作用在机械上的力
机械运动时作用在构件 上的力可分为两类:
惯性力(矩)
包括:驱动力、工作阻力(阻抗力)、重力
外加力(矩) 法向反力 约束反力 切向反力( 即摩擦力)
驱动力——在平面运动构件上,凡是力的作用方向与构件的运动速度方 向相同或成锐角的力(与构件角速度方向一致的力矩称为驱动力矩)。 驱动力(矩)所作功为输入功,用于驱动机械运动。 阻 力——在平面运动构件上,凡是力的作用方向与构件的运动速度方 向相反或成钝角的力(与构件角速度方向相反的力矩称为阻力矩)。
1)确定各运动副中的约束反力
概述
约束反力、平衡力
对机构进行构件的强度设计;估算机械效率;研究运动副中的 摩擦和润滑。
2)确定需加于机构上的平衡力(平衡力矩)
已知生产负荷确定原动机的最小功率;或由原动机的功率来确 定所能克服的最大生产阻力。 平衡力(矩)的概念:是与作用在机械上的已知外力(包括外力 矩)以及(当该机械按给定运动规律运动时)各构件的惯性力(包括 惯性力矩)相平衡的力或力矩。 举例牛头刨床:用于平衡切削阻力、重力、构件惯性力(矩) 时,在原动件上所需施加的驱动力矩。 举例内燃机:已知驱动力、各构件的重力、惯性力,确定所能 克服的生产阻力。
驱动力
按作用分为 阻力
工作阻力 有害阻力
工作阻力(矩) 机械在生产过程中为了改变工作物的外形、位置或状态所 受到的阻力,克服了阻力就完成了有效的工作。 如车削阻力、起重力等:称为输出功或有益功 工作阻力(矩)所作功为输出功(或有益功)。
有害阻力(矩)
机械原理第4章机构力分析2

作业: 作业:
P66 4-19
可见:低副→两个未知要素;高副→一个未知要素 → → 若构件组中: n 个构件, Pl个低副, Ph个高副
平衡方程数: 个构件可以列 个构件可以列3n个平衡方程 平衡方程数:n个构件可以列 个平衡方程 未知数: 未知数:2Pl+ Ph
静定条件:2Pl+ Ph= 3n
仅有低副时: 3n = 2Pl
结论: 结论:所有基本杆组都满足静定条件,即所有基本杆组都是静定杆组。
FI2’ 解:1、运动分析 、 作速度、 作速度、加速度图 2、受力分析 、 G2 FI3 G3 l FI2 MI2
S’
§4-4 不考虑摩擦时机构的力分析
一、构件组的静定条件
未知量的数目 = 平衡方程的数目
运动副中支反力的未知数(不计摩擦)
力的三要素 转动副 移动副 高 副 大小 ? ? ? 方向 ? ⊥导路 公法线 作用点 过轴心 ? 接触点
§4-4 不考虑摩擦时机构的力分析
例
已知各构件尺寸、连杆 的 滑块3的质心在 的质心在C点重量 已知各构件尺寸、连杆2的 G2、S、JS,滑块 的质心在 点重量 、
作用在曲柄上的力偶矩M 不计曲柄1的自重与惯性力 的自重与惯性力, 为G3,作用在曲柄上的力偶矩 1,不计曲柄 的自重与惯性力, 求运动副中反力及生产阻力 P。 。
Y41 X41
X32 R32 Y32
G2F ’I2Fra bibliotek∑M A(F)=0 ∑M C(F)=0
求出 Y32 求出 Y41
列力平衡方程: 列力平衡方程:X 41+Y41+FI’+G2+X32+Y32=0
选取力比例尺µ 选取力比例尺 F ,图解力矢量方程 取构件2为对象,受力分析, 取构件 为对象,受力分析,列平衡方程 为对象 ∑M B(F)=0 求出 X32
机械原理典型例题分析

例1:图示渐开线原则直齿圆柱齿轮1与原则直齿条2作无侧隙啮合传动。齿
条为主动件,运动方向如图。要求: 1)画出齿轮1旳分度圆、基圆、节圆、顶圆,并标出相应旳半径;
2)标注出理论啮合线N1N2和实际啮合线B1B2;
O1
例1
r1 r1'
rb1
齿轮机构典型例题
1)画出齿轮1旳分度圆、 基圆、节圆、顶圆,并标 出相应旳半径; 2)标注出理论啮合线
m(1
z2 ) z1
a
100
z1
2a (i12 1)m
2 100 (2.5 1) 4
50 3.5
14.28
圆整取 z1 14 z2 14 2.5 35
若取 z1 15 z2 15 2.5 37.5
不合适!
a 1 4 (14 35) 98 mm 2
a a 该对齿轮必须按正传动设计,可对小齿轮进行正变位
N1N2和实际啮合线B1B2;
ra1
N1 B2
N2
B1
例2 习题
齿轮机构典型例题
解
1)
a
m 2
( z1
z2 )
165mm
因: a a 不满足原则齿轮无侧隙啮合旳条件,
所以:不能确保无侧隙啮合。
2) 应采用正传动
3)
cos a cos 20
a
21.807
例3
齿轮机构典型例题
解:1)
例4
齿轮机构典型例题
解:(2) z1 16 zmin 17 必须采用正变位齿轮
z1 z2 54 2zmin 34 采用何种传动呢?
a
1 2
m( z1
z2 )
4 2
(16
机械原理典型例题精解
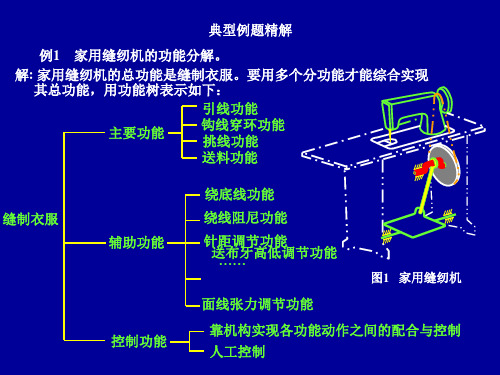
多头专用钻床 例3 多头专用钻床机械传动系统设计 设计任务:设计一台自动钻床,用来同时加工图 所示零件上的三个孔 所示零件上的三个孔, 设计任务:设计一台自动钻床,用来同时加工图3所示零件上的三个孔,能 自动送料。并设计运动循环图。 自动送料。并设计运动循环图。
30 20
1)确定工作原理
50 20
控制功能 结构 总功能 分功能
③微电脑全自动洗衣机的功能求解 可用形态学矩阵法进行方案综合求解,如表1 可用形态学矩阵法进行方案综合求解,如表 所示。
表1 分功能 1 A B C 盛装衣物 分离脏物 控制洗涤 铝桶 机械摩擦 人工手控 2 塑料桶 电磁振荡 机械定时 洗衣机形态学矩阵 功能求解 3 玻璃钢桶 热胀 电脑自控 4 陶瓷桶 超声波
▲钻孔结束后,工作台快速退回,完成一个循环。 钻孔结束后,工作台快速退回,完成一个循环。 设工作台完成一个工作循环所需的时间为T1,则有: 设工作台完成一个工作循环所需的时间为 则有:
T1 = t1 + t2 + t3 + t4 + t5
其中: 单孔钻削时间 其中: t1——单孔钻削时间。设单孔钻削每转进给量为 s1 =0.2 mm/r , 单孔钻削时间。 单孔钻削每转进给量为 单孔钻削深度为 钻削深度为10mm,并考虑 的提前工作量。 单孔钻削深度为 ,并考虑3mm的提前工作量。求得: 的提前工作量 求得: t1 =(10+3)/(s1 nc)=0.13 min = 7.8 s t2——三孔同时钻削时间,设进给量为 s2 =0.16 mm/r ,三孔同时钻削深度 三孔同时钻削时间 三孔同时钻削深度 三孔同时钻削时间, 的越程量。 为10mm,并考虑 ,并考虑3mm的越程量。求得 的越程量 t2 =(10+3)/(s2 nc)=0.163 min =9.8 s t3 ——快速接近时间,取 t3 =1.5 s 快速接近时间, 快速接近时间 t4 ——快速退回时间,取 t4 =2.5 s 快速退回时间, 快速退回时间 t5 ——工作台停歇等待更换工件时间,取 t5 =3 s; 工作台停歇等待更换工件时间 ; 工作台停歇等待更换工件时间, 工作台一个工作循环总时间: 工作台一个工作循环总时间: T1 = t1 + t2 + t3 + t4 + t5 =24.6 s 工作台每分钟工作循环数: 工作台每分钟工作循环数: n1 = 60 /T1 =2.44
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数f 及弹簧的压力F Q ,试求当楔形块 2 、3 被等速推开及等 速恢复原位时力F的大小、该机构的机械效率以及此缓冲
器正反行程均不自锁的条件。
V 12
α
Q
V 24
R 21
P
? ??
R 42
R31
正行程(推开时):
V13 构件1:
构件2 :
Q
P ? R21 ? R31 ? 0
Ffa Nb
ψ
Ffb
Na
ψ
a
2
L2
1b L1 P
推杆1 不自锁,即满足:
∑Fx=0 Na ? Nb ? N
∑Mb=0
Nl2 ? Pl1
∑Fy: F 阻力<P
Ffa ? Ffb ? P 2Ntg? ? P
l2 ? 2l1tg? ? 2l1 f
例4 :如图所示一楔形滑块沿倾斜 V 形导路滑动。已知:
α=20 o,θ=60 o,f=0.11 ,W =800N 。试求:滑块等
机械原理典型例题(第四章) ——平面机构力分析
2012.12
例1 :如图按1 :1 的比例绘制的四杆机构运动简图, 构件1为原动件,在驱动力矩Md 的作用下沿ω1 方向转动,构 件3 受到阻力Q 的作用,图中点划线小圆为摩擦圆(半径如 所示)。若不计各构件的重力和惯性力。试在图上标出:
⑴构件2 上各转动副总反 力的作用线位置和方向; ⑵构件3 上各转动副总反 力的作用线位置和方向; ⑶构件1 上各转动副总反 力的作用线位置和方向;
例7 :图示缓冲器中,若已知各楔形块接触面间的摩擦系
数f 及弹簧的压力F Q ,试求当楔形块 2 、3 被等速推开及等 速恢复原位时力F的大小、该机构的机械效率以及此缓冲
器正反行程均不自锁的条件。
V 12
R 21
P
R31 V13 正行程(推开): P ? Q / tan(? ? ? )
α
α1
理想驱动力:P0 ? Q / tan?
速上行时,所需力F多大?分析该斜面机构反行程能否自
锁?
V
ψv
f
0.11
fv
?
sin ?
?
? sin 60?
0.127
? v ? arctan fv ? arctan 0.127 ? 7.25?
F + W + R 21 = 0
F
W
?
sin(? v ? ? ) sin(90? ? ? v )
F ? W sin(? ? ? v ) ? 369.25N cos? v
例5 :破碎机原理简图如图所示 .设要破碎的料块为圆柱
形,其重量忽略不计, 料块和鄂板之间的摩擦系数是f,求 料块被夹紧又不会向上滑脱时鄂板夹角 α 应多大?
V
ψ
V
ψ
ω
R2
R1 α
α
? 不考虑料块的重量时,料块的受 力方程为:
? X:R1cos(? -? ) ? R2cos? ? Y:R1sin(? -? ) ? R2sin?
? ? arctan f
? 联立两个方程得:
tan(? -? ) ? tan?
? -? ? ?
? 料块被夹紧又不会向上滑脱时鄂 板夹角α 应为:
? ? 2?
例6:图示偏心盘杠杆机构。偏心盘直径 d=50mm ,偏心距 e=15mm ,偏心盘与杠杆接触点B 处的摩擦角ψ =30 °,AC 处的摩 擦圆半径ρ =5mm (D处摩擦不计),BC=45mm ,CD=15mm , AO 和BD 均处在水平位置。重力 w=100N 。试求图示位置时,需加 在偏心盘上的平衡力矩M 。
Q ? R12 ? R42 ? 0
P
?
R21
Q ?
R12
sin(180?? 2? ? 2? ) sin(? ? ? )sin(2? ? 2? ) sin(90 ? ? ? ? ? )
R21
?
P 2cos( ?
??)
Q1
R12 ? 2 sin(? ? ? )
R21 ? R12 ?
P
?Q 1
2cos(? ? ? ) 2 sin(? ? ? )
R32
R31 V12
1
A he d
ψO
M
B
R12
R21
C 2
3
R32
W R12=57.9N
R12
ω
D
R21 与 R31形成力偶矩M与平衡,即: M=R12? h W h=rsin30?? ecos30?? ? ? 30.5mm M ? 57.9?30.5? 1767N?mm? 1.767N?m
例7 :图示缓冲器中,若已知各楔形块接触面间的摩擦系
Q
V 24
2R 12
3
4
Q
? ? P0 ? Q / tan? ? tan(? ? ? ) ? 0 P Q / tan(? ? ? ) tan?
不自锁条件:? ? ? ? 0
? ??
P
? ??
R 42
R31
2? ? 2? R21
R 42 R 12
P ? Q / tan(? ? ? )
2? ? 2?
P R21
? ??
R 12
R 42
90? ? ? ? ?
90? ? ? ? ? Q
理想驱动力:P0 ? Q / tan? ? ? P0 ? Q / tan? ? tan(? ? ? ) ? 0
P Q / tan(? ? ? ) tan? 不自锁条件:? ? ? ? 0
? 反行程时: F '? W sin(? ? ? v ) cos? v
? 当阻抗力F'≤0 时,该机构自锁,
? 有W sin( α-φ v) ≤0 ,即 (α-φ v) ≤0 ,α ≤
φv
? 而由题可知,α=20 o ,φ v=7.25 o
? 因为 α > φ v , 故该斜面机构反行程时不
能自锁。
⑴、在图上画出构件2 所 受各力的作用点和方向, 并画出力多边形(重力Q 的大小和比例尺可任选); ⑵、在图上画出构件1 所 受各力的作用点和方向, 并说明平衡力矩M1 的方向。
M1
R21
ω 13
R 32 ω 23
R31
R12 φ
Q
R12 R32
Q
例3 :图为平底凸轮推杆 1 ,它在力P 的作用下,沿导轨 2 向上运动,设1 、2 两者的摩擦系数为 f。试求为了避免自 锁导轨长度l 2 应满足什么条件?
B
ω1
1
Md
A
4
2
Q
3
D
4
ω23
C
R32
ω 21 R21 2
R12
R23
B
1
Q
3
ω34
Md
ω 14
A
D
R41 4
R43
例2 :所示为偏心圆凸轮杠杆机构的运动简图(绘图比例 μ l ),A 、C 处的实心圆为转动副 A 、C 的摩擦圆,偏心轮1 与杠杆2接触点B 处的摩擦角φ =15 °。若不计各构件的惯 性力和重力,试用图解法求在图示位置时,为提升重物Q 所应加于凸轮1上的平衡力矩M1 的大小和方向,为此请回 答下列2 个问题:
