异方差的解决方法
异方差的补救措施

异方差的补救措施1. 考虑使用对数变换或其他非线性变换来减少异方差性。
2. 采用加权最小二乘法,权重与残差的方差成反比。
3. 使用Robust标准误差来处理异方差性。
4. 利用广义最小二乘法(GLS)来估计异方差。
5. 进行异方差稳健的回归分析。
6. 考虑使用白色噪音模型对异方差进行建模。
7. 通过Heteroscedasticity-Consistent标准误差来纠正异方差带来的偏误。
8. 检验残差的自相关结构,尝试消除异方差。
9. 利用广义估计方程(GEE)来处理异方差问题。
10. 进行对残差进行加权以减轻异方差效应。
11. 尝试使用聚类标准误差校正异方差。
12. 使用稳健标准误差修正异方差带来的影响。
13. 采用异方差稳健的假设检验。
14. 借助异方差自回归模型(ARCH/GARCH)来处理异方差问题。
15. 考虑使用面板数据模型来处理异方差。
16. 将数据进行分组来减轻异方差效应。
17. 利用分位数回归来对抗异方差性。
18. 采用bootstrapping方法估计参数,降低异方差的影响。
19. 通过变量变换来消除异方差性,如差分或比率变换。
20. 使用异方差稳健的方差分解技术。
21. 考虑使用时间序列分析方法来处理异方差。
22. 尝试使用交叉验证来验证模型对异方差的适应性。
23. 利用Lagrange乘数检验来识别异方差模型。
24. 考虑使用非参数回归方法来对抗异方差效应。
25. 结合机器学习技术来降低异方差对分析的影响。
26. 利用异方差稳健的置信区间来进行参数估计。
27. 通过重抽样方法来估计模型参数,减轻异方差影响。
28. 考虑采用深度学习技术来预测异方差。
29. 利用奇异谱分析来识别时间序列数据中的异方差性。
30. 使用异方差稳健的模型比较方法。
31. 采用广义自回归条件异方差(GARCH)模型来拟合异方差性。
32. 结合非参数统计方法来应对异方差问题。
33. 通过交叉验证法来比较不同模型对异方差的适应性。
第五章-4异方差的解决方法

11.58966
Log likelihood
-220.1929 F-statistic
29.21043
Durbin-Watson stat 1.149682 Prob(F-statistic) 0.000008
UnWeighted Statistics
WLS处理后的残差图
2000
Hale Waihona Puke 0-2000-4000
补救异方差的基本思路:
变异方差为同方差; 尽量缓解方差变异的程度 为了补救异方差造成的(不再具有最小方差; 参数的显著性检验失效;预 测精度降低)的严重后果
方法:
一、加权最小二乘法
二、对原模型变换的方法
三、“一般解决法”(模型的对数变换)
1、加权最小二乘法的思路
根据离差平方和最小建立起来的OLS法 同方差时:认为各 ei 提供信息的重要程度是一致的,即将各样本点提供的残差一视同仁。 异方差时:离散程度大的ei 对应的回归直线的位置很不精确,拟合直线时理应不太重视 们提供的信息。即 Xi 对应的 ei 偏离大的所提供的信息贡献应打折扣,而偏离小的所提供的 信息贡献则应于重视。因此采用权数对残差提供的信息的重要程度作一番校正,以提高估计 精度。这就是 WLS(加权最小二乘法)的思路。
1
Xi
2
ui Xi
Var
ui Xi
1
X
2 i
Var
ui
2
例2 Yi 1 2 X i ui
Var(ui)
2 i
2
X
i
Yi Xi
1
Xi
2
Xi
ui Xi
Var
ui Xi
1
X
i
stata异方差检验和解决命令

stata异方差检验和解决命令在数据分析中,异方差是一个常见的问题。
异方差指不同样本的方差不相等,这会导致统计结果的不准确性。
Stata提供了许多方法来检验和解决异方差问题。
一、异方差检验检验异方差通常使用Breusch-Pagan-Godfrey(BPG)检验或White检验。
这里以BPG检验为例,该检验的原假设是方差相等,备择假设是方差不相等。
命令格式:estat hettest示例代码:reg y x1 x2 x3estat hettest如果p值小于0.05,则拒绝原假设,说明存在异方差问题。
二、异方差稳健标准误当检测到异方差问题时,可以使用异方差稳健标准误来解决。
异方差稳健标准误在计算系数的标准误时考虑了异方差问题,从而提高了结果的准确性。
命令格式:robust示例代码:reg y x1 x2 x3, robust使用robust命令后,结果中的Standard Error一栏即为异方差稳健标准误。
三、异方差稳健回归如果异方差问题比较严重,只使用异方差稳健标准误可能无法解决问题。
此时可以使用异方差稳健回归。
命令格式:robust示例代码:reg y x1 x2 x3, vce(robust)使用vce(robust)参数后,回归结果中的系数和标准误都是异方差稳健的,并且t值和p值也已经经过了调整。
总结:通过Breusch-Pagan-Godfrey检验或White检验可以检验异方差问题,如果存在异方差问题,可以使用异方差稳健标准误或异方差稳健回归来解决。
在使用robust命令时,不需要进行任何假设检验,因为参数已经考虑了异方差问题。
异方差性的检验及处理方法

异方差性的检验及处理方法异方差性是指随着自变量变化,因变量的方差不保持恒定,即方差存在不均匀的变化趋势。
在统计分析中,如果忽视了异方差性,可能会导致误差的不准确估计,从而影响对因变量的显著性检验和参数估计结果的准确性。
为了避免异方差性给统计分析带来的影响,需要进行异方差性的检验和处理。
下面将介绍几种常用的异方差性检验及处理方法。
一、异方差性的检验方法:1.绘制残差图:绘制因变量的残差(观测值与拟合值之差)与自变量的散点图,观察残差是否随着自变量的变化而存在明显的模式。
如果残差图呈现出锥形或漏斗形状,则表明存在异方差性。
2.帕金森检验:帕金森检验是一种常用的检验异方差性的方法。
该方法的原理是通过对残差进行变换,判断变换后的残差是否与自变量相关。
3. 布罗斯-佩根检验(Breusch-Pagan test):布罗斯-佩根检验是一种常用的检验异方差性的方法。
该方法的原理是通过计算残差与自变量的相关系数,进而判断是否存在异方差性。
4. 品尼曼检验(Leve ne’s test):品尼曼检验是一种非参数的检验方法,可以用于检验不同组别的方差是否存在显著差异。
二、异方差性的处理方法:1.变量转换:通过对因变量和自变量进行变换,可以使数据满足异方差性的假设。
比如可以对因变量进行对数转换或平方根转换,对自变量进行标准化处理等。
2.使用加权最小二乘法(WLS):加权最小二乘法是一种可以处理异方差性的回归分析方法。
该方法的原理是通过对残差进行加权,使得残差的方差与自变量无关。
3.使用广义最小二乘法(GLS):广义最小二乘法是一种可以处理异方差性的回归分析方法。
该方法的原理是通过对残差进行加权,使得残差的方差可以通过自变量的一个线性组合来估计。
4.进行异方差性的鲁棒估计:鲁棒估计是一种对异常值和异方差性具有较好鲁棒性的估计方法。
通过使用鲁棒估计,可以减少异方差性对参数估计的影响。
综上所述,异方差性是统计分析中需要重视的问题。
logit异方差

Logit模型中的异方差问题通常指的是误差项的方差不是常数,而是随着自变量的变化而变化。
在Logit模型中,异方差性是一个需要注意的问题,因为它可能违反了模型的基本假设,从而影响参数估计的准确性和统计推断的有效性。
首先,需要明确的是,Logit模型假设因变量的条件分布是Logistic分布,并且误差项独立于自变量。
如果存在异方差,那么这个假设可能不成立。
在这种情况下,可以考虑以下几种方法来处理异方差问题:
1. 模型诊断:使用统计检验来检测是否存在异方差。
虽然Logit模型没有类似OLS模型中的`hetprob`命令来进行异方差检验,但可以使用其他统计软件或编写自定义程序来进行类似的检验。
2. 变换数据:有时候对数据进行适当的变换可以减轻异方差的影响。
例如,可以尝试对自变量进行变换,或者对因变量的概率进行Logit变换。
3. 加权最小二乘法(WLS):如果检测到异方差,可以使用加权最小二乘法(WLS)来估计模型参数。
这种方法通过给不同的观测赋予不同的权重来调整异方差的影响。
4. 稳健标准误:在存在异方差的情况下,可以使用稳健标准误来进行参数估计。
稳健标准误不依赖于误差分布的具体形式,因此可以在异方差存在的情况下提供更准确的标准误估计。
5. 模拟方法:使用蒙特卡洛模拟等方法来估计模型参数和标准误,这些方法不依赖于误差分布的具体形式,因此可以在一定程度上解决异方差问题。
6. 选择其他模型:如果Logit模型不适用,可以考虑使用其他更适合数据的模型,如Probit模型或者其他非线性模型。
异方差性的解决方法.

由于在极小化过程中对通常意义得残差平 方加上了权数ω i,所以称为加权最小二乘法 (Weighted Least Square—WLS )。 ω i有两个作用:一是权重,二是为了消除 异方差。 注意权数的变化趋势应与异方差的变化趋 势相反,通常将ω i直接取成1/σ i2 。
模型变换法的实质就是WLS 例如,对于模型 yi=a+bxi+ε i 如果σ i2 =D(ε i)=λ xi2,则模型变换成
③选定Weighted LS方法,在权数变量栏中输入权 数变量,点击OK返回; ④点击OK,采用WLS方法估计模型。 (4)对估计后 q1模型,再使用White检验判断是否 消除了异方差性。
4.4.3
模型的对数变换
如果在模型yt=b0+b1xt+ut中,分别用lnyt、lnxt 取代,对对数模型 lnyt=b0+b1lnxt+ut 进行回归通常可以降低异方差性的影响。 其原因在于(1)通过对数变换将两个数值之 间原来10倍的差异缩小到只有2.3倍左右的差 异。(2)经过对数变换后的线性模型,其残 差et表示为相对误差,而相对误差往往具有较 小的差异。
* i
y ax bx
* 2i
* i
i 1 此时 D ( ) D ( ) 2 D ( i ) 1 i i 使用OLS估计模型,应使得: yi 1 ˆ xi *2 * * 2 ˆ b ) ˆi ) ( a ei ( yi y i i i 1 ˆx ) 2 min ˆ b 2 ( yi a i i 1 ˆ ˆ i yi (a ˆ bxi ) 若记: ei yi y 并设:i 2 i 2 则以上估计过程是使得: i ei min
异方差性的检验及处理方法
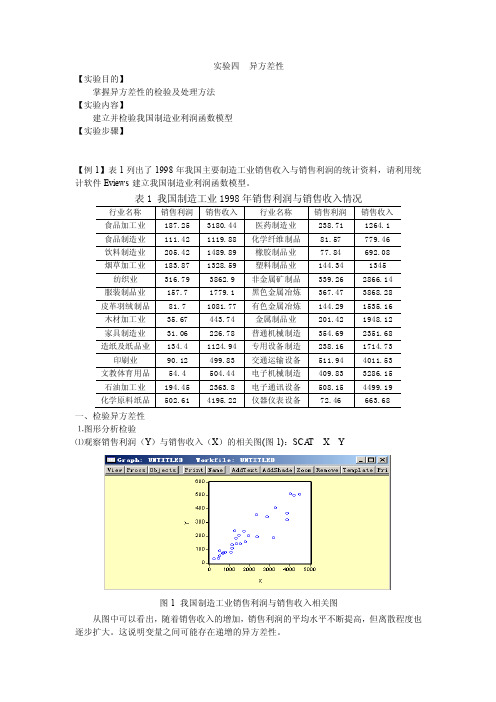
实验四异方差性【实验目的】掌握异方差性的检验及处理方法【实验内容】建立并检验我国制造业利润函数模型【实验步骤】【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型。
一、检验异方差性⒈图形分析检验⑴观察销售利润(Y)与销售收入(X)的相关图(图1):SCA T X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出,随着销售收入的增加,销售利润的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序(命令格式为:SORT 解释变量),然后建立回归方程。
在方程窗口中点击Resids按钮就可以得到模型的残差分布图(或建立方程后在Eviews工作文件窗口中点击resid对象来观察)。
图2 我国制造业销售利润回归模型残差分布图2显示回归方程的残差分布有明显的扩大趋势,即表明存在异方差性。
⒉Goldfeld-Quant检验⑴将样本按解释变量排序(SORT X)并分成两部分(分别有1到10共11个样本合19到28共10个样本)⑵利用样本1建立回归模型1(回归结果如图3),其残差平方和为2579.587。
SMPL 1 10LS Y C X图3 样本1回归结果⑶利用样本2建立回归模型2(回归结果如图4),其残差平方和为63769.67。
SMPL 19 28LS Y C X图4 样本2回归结果⑷计算F 统计量:12/RSS RSS F ==63769.67/2579.59=24.72,21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时,查F 分布表得44.3)1110,1110(05.0=----F ,而44.372.2405.0=>=F F ,所以存在异方差性⒊White 检验⑴建立回归模型:LS Y C X ,回归结果如图5。
图5 我国制造业销售利润回归模型⑵在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图6。
第四节异方差性的补救措施

F 5.0762 F0.05 (6, 6) 4.28 拒绝原假设,表明模型存在异方差。
38
(三)White检验
存在异方差
39
四、异方差的修正
加权最小二乘法(WLS)
分别选用权重:
w1
1 Xi
, w2
1 Xi
, w3
1 X 1.5
i
, w4
1 Xi2
经估计检验发现用权数w2可以消除异方差性。
◆对数变换能使变量取值的尺度缩小。 ◆经过对数变换后的模型,其残差表示相对误差,往往比
绝对误差有较小的差异。
注意:取对数后变量的经济意义。
34
第五节 案例分析
一、问题的提出和模型设定
为了给制定医疗机构的规划提供依据,分析比 较医疗机构与人口数量的关系,建立卫生医疗机 构数与人口数的回归模型。
假定医疗机构数与人口数之间满足线性约束, 则理论模型设定为:
经检验ui存在异方差,且已知方差表达式为
var(ui )
2 i
2
f
(Xi)
用 f (Xi ) 除以模型的两端得:
Yi =
f Xi
f
β1
X
i
+
β2
Xi +
f Xi
ui
f Xi
记 Yi* 则有:
Yi f (Xi)
;
X
* i
Xi f (Xi)
; 1*
Yi*
1*
2
X
* i
vi
1
f (Xi)
; vi
ui f (Xi)
1
2 i
Yi 1* 2* X i
2
1
2 f Xi
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广义最小二乘估计量为
~ ( X *' X * )1 X *'Y *
(5.4.20)
将(5.4.17)代入(5.4.20)
~ [(PX )(PX )]1(PX )(PY)
( X PPX )1 X PPY ( X 1 X )1 X 1Y
(5.4.20)′
(5.4.20)(或(5.4.20)′)称为广义最小二乘估计式。这种
ui ) V (ui ) k 2 f (xi ) k 2 f (xi ) f (xi ) f (xi )
因此,对模型(5.4.5)应用OLS法,即可得出参数 α、β的最佳线性无偏估计量,问题得以解决。
例5.4.1
设模型(5.4.1)中ui的异方差结构为
2uiຫໍສະໝຸດ k2xi2(这是一种最常见的异方差结构),求α、β的最佳
将原模型(5.4.11)进行适当变换,变为模型(5.4.18),
然后对新模型(5.4.18)应用普通最小二乘法,求得参数
估计量,称作对原模型的广义最小二乘法,记作GLS。
当Ω = In时, ( X ' X )1 X 'Y ˆ
(5.4.21)
此时广义最小二乘法就是普通最小二乘法。
参数的协方差矩阵
, x*2i
ui f (xi)
xi f (xi)
(5.4.3)
,u*i
ui (5.4.4)
f (xi)
则模型(5.4.3)变为
y*i x1*i x*2i u*i
(5.4.5)
(5.4.5)中的参数α和β即原模型中的参数,但是随
机项 ui* 已经没有异方差性了。因为:
V (ui*) V (
2
i
f (xi)
(
yi f (xi)
f
1 (xi
)
(
y
i
ˆ
ˆ
xi )2
ˆ
f (xi)
ˆ )2
f (xi)
(5.4.10)
最小。显然,能使(5.4.10)达到最小的 ˆ 、ˆ 也一定 能使(5.4.9)式达到最小,因为二者只差一个常数因子。 即两种方法得到的结果相同。两种方法实质上是一回 事。对原模型进行变换的方法实际上是加权最小二乘 法当 1 1 时的特例,也可以看作是加权最小二乘法
1 '1
n k 1
(5.4.23)
其中ε为广义最小二乘估计量所对应的模型(5.4.11) 的样本残差。
四、广义最小二乘法的应用之一 —— 异方差问题的处理
设模型
Y X U
(5.4.24)
§5.4 异方差性问题的解决方法 一、对原模型进行变换
设原模型为
yi xi ui
(5.4.1)
其中ui具有异方差性(其余假定都满足)。假定现在已知
V
(ui
)
2
ui
k 2 f (xi )
(5.4.2)
其中k2为常数。现在的问题是经典假定遭到了破坏的
情况下,如何求出参数α、β的最佳线性无偏估计量?
解决这个问题的基本想法是对原模型(5.4.1)作适当
的变换,使变换后的随机项不再具有异方差,从而
可用OLS法求出参数的最佳线性无偏估计量。
用 f (xi ) 去除(5.4.1)式两端,则得到新的模型:
yi f (xi)
f (xi)
f(
x
i
)
x
i
记
y*i
yi f (xi)
, x1*i
1 f (xi)
线性无偏估计量。
在本例中 f (xi) xi2 , f (xi) xi ,用 xi 去除(5.4.1) 式各项,得
改写成
yi ui
xi xi
xi
其中
yi* xi* ui*
y*i
yi xi
,
x*i
1 xi
, u*i ui xi
由于变换后的模型中的随机项
u
* i
已没有异方差,
(5.4.8)
将(5.4.8)代入(5.4.7)得加权最小二乘法,要求
2 i
2 ui
k2
1 f(
xi)
(
y
i
ˆ
ˆ
xi )2
达到最小。
现在对原模型(5.4.1)作变换:
(5.4.9)
yi f (xi)
f (xi)
f (xi) xi
ui f (xi)
(5.4.3)
对(5.4.3)应用普通最小二乘法,要求残差平方和:
PY PX PU
令
Y * PY X * PX U * PU
(5.4.16) (5.4.17)
则(5.4.16)变为
Y* X * U*
(5.4.18)
此时
E(U
*U
*
'
)
E(PUU
P)
PE(UU
)P
2 u
I
n
(5.4.19)
可见,变换后的模型(5.4.18),已满足全部基本假定,
可以对模型(5.4.18)应用普通最小二乘法,求得β的
nn
n1 n2
1n
2n
nn
(5.4.13)
其它基本假定不变,称之为广义线性模型。
若将Ω换成In,则模型(5.4.11)就变成一般古典线性模型。 由于Ω为正定对称矩阵,必存在一个(n×n)阶非奇异矩
阵P,使得
PP ' In
(5.4.14)
且有
1 P ' P
(5.4.15)
利用矩阵P对原模型进行变换,用P左乘(5.4.11)得,
V
COV
(~)
2 u
(X
*
X
* ) 1
u2[(PX )(PX ) ]1
2 u
(
X
1
X
) 1
(5.4.22)
ˆ u 2
*' *
n k 1
n
1 k
(Y * 1
X
*
)' (Y *
X
*
)
1 (PY PX )'(PY PX )
n k 1
1 (Y X )' 1(Y X )
n k 1
k2 的直接应用。
三、广义最小二乘法 ( GLS ) 广义最小二乘法是处理广义线性模型的一种估计方法。
广义线性模型是指线性模型
Y X U
(5.4.11)
并且有
E(U ) 0
E
(UU
')
u
2
(5.4.12)
其中 u2为未知常数,Ω是一个已知的n×n阶正定
对称矩阵:
11 12 21 22
V (ui )
2 ui
作为εi2的权数是合理的。
现在我们可以用权数将普通最小二乘法修正为: 使加权残差平方和
2 i
2 ui
1
2 ui
(
y
i
ˆ
ˆ
xi )2
(5.4.7)
达到最小。这就是加权最小二乘法。
下面我们说明,这种加权最小二乘法同样可以消除
异方差性的影响。
设异方差是xi的函数
2 ui
k2 f (xi )
应用OLS法得α和β的最佳线性无偏估计量:
ˆ
xi* yi* xi*2
ˆ y* ˆ x *
二、加权最小二乘法(WLS)
在OLS法中,其基本原则是使残差平方和
2 i
(
y
i
ˆ
ˆ
x
2
i)
(5.4.6)
达到最小,这是对满足经典回归假定而言,也就
是在等方差的情况下进行的。当随机项具有异方差
时,用
1 1
