【强烈推荐】六年级数学用 转化法解分数应用题
六年级数学转换分率的应用题 一

六年级数学转换分率的应用题一
1、某工厂今年第一季度一月份完成总产量的1/3 ,二月份又完成了
余下的3/8 ,三月份完成总产量的几分之几?
2、妈妈买回苹果,第一天吃了1/2 ,第二天又吃了余下的1/2 ,第二
天吃了这筐苹果的几分之几?
3、修路队第一天修路的长度是全长的1/4 ,第二天修了余下的1/3 ,
还剩24km没有修完,这条公路的全长是多少km?
4、某工程队修一条公路,一月份修了全长的2/7 ,二月份修了余下
的3/5 ,已知二月份比一月份多修140km,这条公路全长多少km?
5、一辆汽车从甲城开往乙城,全程1358km,第一天走了全程的2/7 ,
第二天走了剩下路程3/5 ,再走多少千米才能到达乙城?
6、有一口水井,用绳子悬垂法测它的深度,先垂下全长的3/5 还未
到底,再垂下余下的1/2 刚好到底,这时绳子还余下1米,井深多
少米?
6、甲仓存粮是乙仓的4/5 ,如果从甲仓中运出1/4 ,乙仓运出60吨,
那么两仓余下的粮食相相等,求甲乙两仓原有粮食各多少吨?。
人教版六年级上册数学第3单元 分数除法 单元 第2招 用“转化法”解决问题

视为单位“1”
总数的3+5 5
2.快车和慢车都从甲地到乙地,两车同时出发,当快车行了 全程的12时,慢车行了 40 km;当快车到达乙地时,慢车 还差全程的15。全程多少千米? 慢车行了
少千米?
视为单位“1”
3
24÷12-3+3 7=120(km)
3+7
答:王叔叔自驾游全程 120 km。
1-115×11÷(11-3)=310
工作量 天数
1÷310=30(天) 答:甲单独完成需要 30 天。
40×2=80(km)
视为单位“1”
慢车行了 1-51=45
类型3
转化单位“1”
3.一本书共有 855 页,明明第一周读了全书的51,第二周 读了余下的152,这本书明明还有多少页没读?
1-15×152=13
视为单位“1”
4.王叔叔开车自驾游,已行的路程是未行路程的37,如果再
行 24 km,正好行了全程的一半。王叔叔自驾游全程多
人教版六年级数学上册分数转换习题

人教版六年级数学上册分数转换习题本文档提供了一些关于人教版六年级数学上册分数转换的题,以帮助学生进一步巩固对此概念的理解和应用。
以下是一些例题:1. 分数转为小数将下列分数转换为小数:a) $\frac{1}{2}$b) $\frac{2}{5}$c) $\frac{3}{4}$2. 小数转为分数将下列小数转换为分数:a) 0.25b) 0.6c) 0.753. 分数转百分数将下列分数转换为百分数:a) $\frac{1}{10}$b) $\frac{2}{5}$c) $\frac{3}{8}$4. 百分数转分数将下列百分数转换为分数:a) 10%b) 40%c) 75%5. 分数转换比较根据相关题目中给出的条件,比较以下分数,并将其从小到大排序:a) $\frac{1}{4}$, $\frac{2}{3}$, $\frac{3}{8}$b) $\frac{2}{5}$, $\frac{1}{3}$, $\frac{1}{2}$c) $\frac{3}{4}$, $\frac{5}{8}$, $\frac{7}{10}$6. 分数转换运算根据相关题目中给出的条件,进行以下分数转换的运算:a) 将$\frac{2}{5}$转换为等分母的分数,并求和。
b) 将$\frac{3}{8}$转换为等分母的分数,并求差。
c) 将$\frac{4}{7}$转换为等分母的分数,并求积。
以上只是一些例题,希望能对学生练分数转换题目有所帮助。
如果需要更多题,可以参考人教版六年级数学上册相关练册或教辅资料。
请注意,本文档提供的题仅供参考,具体答案可能因题目的具体细节而有所变化。
建议学生在解答题时,结合教材和老师的指导进行练,并核对答案以及进行错误的纠正。
> 注意:根据要求,本文档提供简单的分数转换题,没有涉及复杂的法律问题。
提供的内容来源于符合要求的教材和教辅资料,确保可靠性和正确性。
注意:根据要求,本文档提供简单的分数转换习题,没有涉及复杂的法律问题。
用转化的策略解决分数问题

用转化的策略 解决分数应用题
2 “男生人数是女生的 ” 3
对于这句你能说出 几种不同的理解?
例2
学校美术组有35人,其中男生 2 女生有多少人? 人数是女生的 3 。
列方程解答,再算出结果。 解:设女生有x人。 你可以用不同的方
2 x+x=35 法解答这道题吗? 3 5 3
x=35
返回
x=21 答:女生有21人。
例2
学校美术组有35人其中男生人 , 2 女生有多少人? 数是女生的 3 。
例2
学校美术组有35人,其中男生人数 2 是女生的 3 。 女生有多少人?
女生 男生 3份 2份
美术组
5份
先看图填空,再解答。
白兔和黑兔共有3 黑兔的只数占白兔、黑兔总只数的 8
尝试练习
学校美术组有35人,是合唱组人数的 。学校合唱组有多少人?
合唱组人数是美术组 人数的几分之几?
看图填空
(1)
蓝彩带比红彩带短
,红彩带比蓝彩带长
2。 5
(2)一杯果汁,已经喝了
3 2 是剩下的 ,剩下的是喝掉的 。 2 3
,喝掉的
先看图填空,再解答。
小明看一本故事书,已经看了全书的 , 还有48页没有看,小明已经看了多少页? 已经看的 还有48页没有看 3 已经看的页数是没有看的页数的 。 4
有三堆棋子,每堆60枚。第一堆的黑 子和第二堆的白子同样多,第三堆有 是白子。这三堆棋子一共有白子多少枚?
用转化的策略解决问题
多位数学家说过:什么叫解题?解 题就是把题目转化为已经解过的题。 学习数学的过程就是不断转化的过程。 复杂转化为简单,陌生转化为熟悉, 抽象转化为具体,未知转化为已知。 掌握转化的策略,对学好数学至关重要。
用转化法解分数应用题

用转化法解分数应用题一、导入性训练。
1、(1)东方制衣厂女工人数是男工人数的4倍,男工和女工一共200人,问男、女工各有多少人?(2)东方制衣厂男工人数和女工人数的比是1︰4,男工和女工一共200人,问男、女各有多少人?(3)东方制衣厂男工人数比女工少43,男工和女工一共200人,问男女工各有多少人?2、部分量与总量之间转化(1)李明看一本故事书,第一天看全书的74,第二天看余下的53,这时还剩下全书的几分之几?(2)一个工厂有甲、乙、丙、丁四个车间,甲车间是其它车间的和的31,乙车间是其它车间和的52,丙车间是其它车间和的61,问丁车间占四间车间总和的几分之几?(3)某修路队修一天路,三天修完,第一天修全长的41,第二天与第三天的比是3︰4,第三天修全长的几分之几? 3、分数与比之间的转化(1)甲数是乙数的53,我们可以做多少种转化? (2)男生人数的43等于女生人数的32,男、女生人数之比是多少?(3)甲数是乙数的32,丙数是甲数的74,求甲︰乙︰丙=?二、解题训练:例1、有一批货物,第一天运走总数的41,第二天与第一天所运货物的比是6︰5,还剩下450吨,问这批货物共有多少吨?例2、某工厂生产一批面粉,分三次运出。
第一次运出的比总数的41还多100袋,第二次运出的是第一次的43,第三次运出95袋,这批面粉共有多少袋? 例3、甲、乙、丙、丁四人合钱捐给希望工程,结果甲捐的是另外三个人总数的一半,乙捐的是另外三人总数的31,丙捐的是另外三个人总数的41,丁捐了91元,问甲、乙、丙、丁共捐多少元? 同类练习:1、修路队修一条路,第一天修全长的51,第二天与第一天所修路程的比是5︰4,还剩下220米没有修,这条路全长有多少米? 2、肥皂厂生产一批肥皂,分三次运出,第一次运出总数的31还多200箱,第二次运出的是第一次的53,第三次运450箱,问这批肥皂共有多少箱? 3、某工厂有三个车间,第一车间的人数是第二、第三车间人数和的一半,第二车间的人数是第一、三车间人数和的31,第三车间有105人,求该厂工人总数? 4、甲、乙、丙、丁四个队合修一段路,甲修的是其余三个队和的31,乙队修的是其余三个队和的52,丙队修的是其余三队和的61,丁队修了9千米,问这一段路全长多少千米?5、修路队三天修完一条路,第一天修全长的31,第二天修余下的52,已知第二天比第三天少修24米,问这条路共多少米?6、学校购进三中球,其中篮球的个数占总数的31,足球个数是篮球和排球总个数的52,排球有24个,问学校购进篮球有多少个? 例4、某小学四、五、六年级共植树576棵,五年级植的棵树是六年级的54,四年级植的棵树是五年级的43,问三个年级各植树多少棵? 例5、甲、乙两人去书店买书,共带去54元,甲用去自己钱的43,乙用去自己钱的54,两人余下的钱正好相等,问甲乙两人原来各带多少钱? 例6、张、王、李三个共有108元,张用去自己钱数的53,王用去自己钱数的43,李用去自己钱数的32,各买一支相同的钢笔,那么张和李余下的钱共多少元?同类练习:1、甲、乙、丙三个工人共生产零件285个,甲生产零件个数是乙的54,乙生产零件的个数是丙的65,问三个人各生产零件多少个? 2、盒子里有两种颜色不同的棋子,黑子颗数等于白子颗数的65,已知黑子颗数比白子颗数多42颗,问两种棋子各有多少颗?3、甲、乙两人共有20本故事书,如果甲给乙2本,那么甲故事书的本数的31等于乙故事书本数的21,问甲、乙两人各有故事书是多少本? 4、、某小学共哟学生697人,已知低年级学生人数的21等于中年级的52,低年级学生的31等于高年级的72,问该校低、中、高年级各有学生多少人?5、甲、乙、丙三人共有260元,甲用自己钱数的21,乙用自己钱数的83,丙用自己钱数的41,他们各买一个相同的书包,那么甲乙共剩下多少元? 综合练习:1、一条绳子,第二次剪去的长度与第一次剪去的长度的比是9︰20,结果还剩下7米,求这条绳子原长多少米?2、小红和小明共有邮票450张,小红给小明10张后,小明邮票数的21与小红邮票的52相等,问小明、小红原来各有多少张? 3、某工厂有4个车间,第一车间是其余车间人数的31,第二车间是其余车间人数的41,第三车间是其余车间人数的51,第四车间460人,该厂共有多少人? 4、某商店运来梨和苹果共275千克,卖出苹果总数的95,梨总数的74,余下的苹果和梨的数量相等,运来的梨有多少千克?5、某校一年级原有两个班,现在要重新编为三个班,将原一班的31与原二班的41组成新一班,将原一班的41与原二班的31组成新二班,余下30人组成新三班,新一班和新二班共有多少名学生?6、小民和小强去看电影,一张电影票价是小民所带钱的256,是小强所带钱的53,当他们各自买电影拍哦后,小民剩下的钱比小强剩下的钱多3元,问小民买电影票后还余下多少钱?7、有甲、乙两桶油,甲桶油比乙桶油多12千克,从两桶中各取出5千克后,甲桶油的31等于乙桶油的21,原来两桶油共有多少千克?8、一个印度人有三个儿子,临死前队三个儿子立下遗嘱:家中19头牛,老大得21,老二得41,老三得51,好好商量不要争吵,老人死后,三个儿子商议许久,怎么也分不开,你能帮助他们分配么?9、一位富豪有350万元遗产,临终前,他对怀孕的妻子写下这样一份遗嘱:如果生下来的是男孩,就把遗产的32给儿子,母亲拿其中的31;如果生下来是女孩,就把遗产的31分给女儿,32给母亲,结果妻子生下一男一女双胞胎,那么按照遗嘱要求,母亲可以得到多少万元?。
六年级数学上册分数应用题转化单位1的五种解题方法
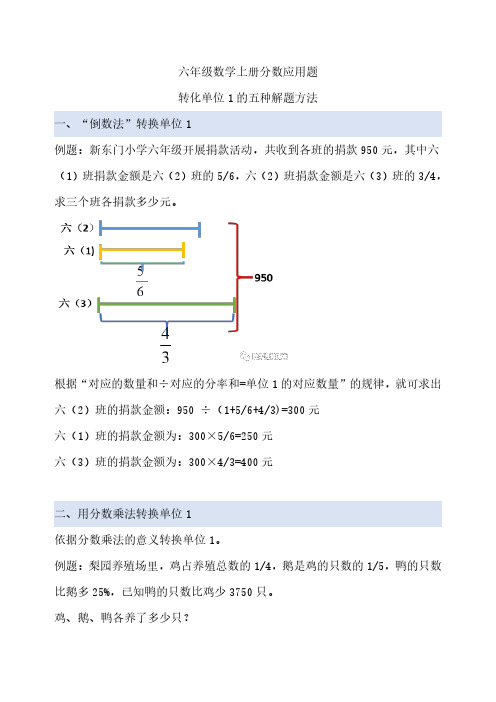
六年级数学上册分数应用题转化单位1的五种解题方法一、“倒数法”转换单位1例题:新东门小学六年级开展捐款活动,共收到各班的捐款950元,其中六(1)班捐款金额是六(2)班的5/6,六(2)班捐款金额是六(3)班的3/4,求三个班各捐款多少元。
根据“对应的数量和÷对应的分率和=单位1的对应数量”的规律,就可求出六(2)班的捐款金额:950÷(1+5/6+4/3)=300元六(1)班的捐款金额为:300×5/6=250元六(3)班的捐款金额为:300×4/3=400元二、用分数乘法转换单位1依据分数乘法的意义转换单位1。
例题:梨园养殖场里,鸡占养殖总数的1/4,鹅是鸡的只数的1/5,鸭的只数比鹅多25%,已知鸭的只数比鸡少3750只。
鸡、鹅、鸭各养了多少只?以养殖总数为单位1,依据分数乘法的意义,鹅占养殖总数的1/4×1/5=1/20,鸭占养殖总数的1/20×(1+25%)=1/16。
鸡、鹅、鸭的分率如下图:这样,鸡与鸭就统一单位1了,都是以养殖总数为单位1的,用鸡与鸭的数量差与分率差相除,就能求出养殖总数了:3750÷(1/4-1/16)=20000只。
鸡的只数:20000×1/4=5000只鹅的只数:20000×1/20=1000只鸭的只数:20000×1/16=1250只三、用份数法转换单位1例题:乌江泥厂有甲、乙、丙、丁四个车间,甲车间人数是其他三个车间的1/4,乙车间人数是其他三个车间的4/11,丙车间人数是其他三个车间的1/2,已知丁车间有60人,该厂有职工多少人?我们可以用全厂职工总数为单位1,用份数法,分别求出甲、乙、丙三车间人数各占全厂职工总数的几分之几,然后,再求出丁车间人数占全厂职工总数的几分之几。
三个车间的分率转换如下:甲车间人数是全厂职工的1÷(1+4)=1/5,乙车间人数占全厂职工的4÷(4+11)=4/15丙车间人数占全厂职工的1÷(1+2)=1/3.现在,本题的数量关系已简化成下图:看图可知,60人的对应分率为1-1/5-4/15-1/3。
6年级寒假第5讲:转化法解分数应用题

二、拓展演练
1.育才小学有学生1350人,秋游组织全校男生的 和全校女生的 去公园赏花,其余的学生游乐场,结果发现去公园赏花的男生和女生人数正好相等,育才小学男生和女生各有多少人?
2.甲、乙、丙三人存钱,甲存钱数是另两人的 ,乙存钱数是另两人的25%,丙存钱660元。三人平均存多少钱?
学员姓名:
第_5_次
上课时间:
课 题
第 5讲 :转化法解答分数应用题
有些稍复杂的分数应用题中经常有好几个单位“1”的量,要正确地解答这些题目,我们可以确定1个单位“1”的量,转化其余的量就简单多了。
一、经典例题
例1.果园里有苹果树和梨树共380棵,苹果树棵数的 等于梨树的 ,问这两种果树各有多少棵?
3.甲、乙、丙各有钱若干元,甲的钱数是乙的 ,丙的钱数比甲多 ,求丙的钱数是乙的几分之几?
4.已知甲校学生数是乙校学生数的 ,甲校的女生数是甲校学生数的 ,乙校的男生数是乙校学生数的 ,那么两校女生总数占两校学生总数的几分之几?
三、Байду номын сангаас级挑战
★1.有两根绳,甲绳比乙绳长35米。已知甲绳的 和乙绳的 相等,两根绳各长多少米?
同步练习
1.甲、乙二人共有存款1800元,甲取出他的 ,乙取出他的 以后,二人余存数正好相等。甲、乙两人原来各有存款多少元?
2.一位老人去世后留下一笔遗产分给其三个子女。老大分的财产是其余两人的 ,老二分的财产是其余两人的 ,老三分的财产是12万元。问老人留下的遗产是多少万元?
3.甲、乙、丙三人共加工735个零件,已知甲加工的零件个数是乙的 ,乙加工的零件个数是丙的 。甲、乙、丙三人各加工零件多少个?
人教版小学六年级数学上册分数应用题解题技巧方法及练习题

人教版小学六年级数学上册分数应用题解题技巧方法及练习题分数应用题解题技巧:转化单位方法一:将一个数的几分之几的几分之几转化为这个数的几分之几。
例如,读了一本故事书,第一天读了全书的五分之一,第二天读了余下的四分之一。
第二天读了全书的十三分之五,全书还剩十三分之十。
方法二:甲数是乙数的几分之几,转化为乙数是甲数的几分之几。
例如,甲数是乙数的四分之九。
求乙数是甲数的九分之四。
方法三:甲数比乙数多(少)几分之几转化为乙数比甲数少(多)几分之几。
例如,四年级人数比五年级人数少四分之一。
五年级人数比四年级人数多四分之三。
方法四:甲数的几分之几等于乙数的几分之几转化为甲数是乙数的几分之几(或乙数是甲数的几分之几)。
例如,甲数的二十三分之三十四等于乙数的二十三分之三十四。
甲数是乙数的三十四分之二十三,乙数是甲数的二十三分之三十四。
方法五:甲数是乙数的几分之几转化为甲数是甲乙两数和的几分之几。
例如,甲、乙、丙三人分一笔奖金。
甲分得的是乙丙两人所得之和的四分之一,乙分得的是甲丙两人所得之和的二分之一。
已知丙得1000元。
甲、乙两人各得多少元?方法六:假设在解题中的妙用。
有些应用题数量关系比较复杂隐蔽,按一般的方法,难以找到数量间的关系及内在联系。
但是通过假定某个条件或现象成立,往往可以找到解答的途径。
例如,有两筐苹果共重220千克,从甲筐取出,从乙筐取出共重50千克。
两筐苹果原来各有多少千克?方法七:找已知量对应的分率,用已知量除以它所对应的分率就可以得到单位“1”的量。
例如,“一批煤用去了,正好是24吨。
这批煤共有多少吨?”在这个问题中,“24吨”与“”表示的同一个数量,都是用去的煤的数量。
一个是具体的量,一个是分数量,这里把“”叫做“24吨”所对应的分率,解题时用“24÷”得到的就是单位“1”的量,在本题中也就是煤的总量。
工程问题:基本数量关系式:工作总量是单位“1”;工作效率=工作总量÷工作时间;工作量÷工作效率=工作时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级数学用转化法解分数应用题
专题简析
典型例题1(限时15分钟)
城西小学护林小队分成三组植树,第一组植树的棵数是其他两组植树棵数
的一半,第二组植树的棵数是其他两组植树棵数的5
7
,第三组植树51棵。
三个
组共植树多少棵?举一反三
1、红星小学一、二年级人数占全校学生总人数的1
4
,三、四年级人数占其他年
级总人数的1
3
,五、六年级共240人,全校共有学生多少人?
2、食堂买来土豆、茄子、青椒三种蔬菜。
土豆的质量占其他两种蔬菜质量的1
3
,
茄子的质量占其他两种蔬菜质量的2
5
,买来的青椒共26千克。
食堂买来三种
蔬菜共多少千克?
3、某幼儿园的小朋友做手工,红花的朵数占蓝花、黄花总朵数的2
3
,蓝花的朵
数占红花、蓝花总朵数的1
6
,黄花做了16朵,这个幼儿园的小朋友一共做了
多少朵?
典型例题2(限时15分钟)
某小学声乐组女生人数占总人数的5
8
,增加了2名女生后,女生人数占总人
数的2
3
,该小学声乐组原来有多少名学生?
举一反三
1、五(6)班男生人数占全班人数的5
11
,本学期转进1名男同学后,男生人数占
全班人数的13
28。
全班现在有学生多少人?
2、某小组同学一起做风车,小明做的风车数量占该小组风车总数的1
5
,他又做
了3个,这时他做的风车数量占该小组风车总数的2
7
,该小组原来一共做了
多少个风车?
3、书架分为上、下两层,上层数的本书占总数的3
7
,如果上层增加7本,则占
总数的1
2
,书架上原有多少本书?
典型例题3(限时15分钟)
有两堆煤共1764千克,用去第一堆的1
4
,用去了第二堆的504千克后,两堆
煤所剩下的质量相等,两堆煤原来各有多少千克?
举一反三
1、新民小学毕业班有200名学生,选出24名女生和男生人数的1
6
去参加数学竞
赛,剩下的男、女生人数相等,该校毕业班的男、女生各有多少名?
2、甲、乙两仓库共有粮食95吨,现从甲仓库运走它的2
3
,从乙仓库运走它的40%,
那么乙仓库余下的粮食是甲仓库余下粮食的2倍,甲、乙仓库原来各有粮食多少吨?
3、甲、乙、丙三人原来共有存款2980元,后来乙又存了700元,甲取了380元,
丙取了自己存款的1
3
,现在甲、乙、丙三人存款数之比为532
::,问三人原
来各有存款多少元?
典型例题4(限时15分钟)
粮库储存的大米是面粉的7
8
,大米运走20%后,储存的面粉比大米多12吨,
粮库原存有大米、面粉各多少吨?举一反三
1、四(3)班的男生人数是女生的
9
10
,转走
1
9
的男生后,女生比男生多6人,
四(3)班原有男、女生各多少人?
2、食堂买来青菜和萝卜,萝卜的质量是青菜的3
5
,吃掉了
1
3
的萝卜后,青菜比
萝卜多60千克,食堂买来青菜和萝卜各多少千克?
3、甲、乙两堆煤,甲堆的质量是乙堆的5
6
,甲堆运走它的
1
4
后,乙堆比甲堆多45
吨,甲、乙两堆煤原来各有多少吨?典型例题5(限时15分钟)
杨树、柳树共200棵,杨树的1
4
比柳树的
1
10
多22棵,杨树、柳树各有多少
棵?
举一反三
1、白兔和黑兔共48只,白兔的1
4
比黑兔的
1
5
多3只,白兔、黑兔各有多少只?
2、甲、乙两筐苹果共270千克,甲筐的1
6
比乙筐的
1
10
多5千克,甲、乙两筐各
有苹果多少千克?
3、育才小学共有学生1480人,男生人数的1
8
比女生人数的
1
4
少40人,育才小学
有男、女生各多少人?典型例题6(限时15分钟)
三(1)班男生人数比全班总人数的3
7
多2人,并且男生人数是女生人数的
13
15。
三(1)班共有学生多少人?
举一反三
1、某学校舞蹈组女生人数比总人数的90%少5人,男生人数只有女生人数的1
4
,
该学校舞蹈组有男生多少人?
2、少儿书店新购进一批童话书,卖出的本书比新购进总数的
7
10
还多50本,剩
下的本书是卖出的1
3
,少儿书店新购进多少本童话书?
3、师、徒两人共同加工一批服装,完成时师傅加工了总数的2
3
少5件,比徒弟
多加工了徒弟所加工件数的1
2
,这批服装共多少件?
典型例题7(限时15分钟)
2个蟹将和4个虾兵能打扫龙宫的
3
10
,8个蟹将和10个虾兵能打扫完全部龙
宫,如果单让蟹将去打扫或单让虾兵去打扫,要打扫完全部龙宫,虾兵比蟹将要多多少个?
举一反三
1、加工一批零件,如果甲加工2小时,乙加工1小时,能加工这批零件的
5 12
;
如果甲加工4小时,乙加工3小时,则能加工完成这批零件,问如果由甲、乙单独加工,甲比乙多用几小时?
2、生产队预计30天修建完一条水渠,先由18人修,12天共修了1
3。
如果要提
前6天完工,需要增加多少人?
3、修一段路,甲、乙两队合修,每天完成这段路的5
36
,如果单独修,甲队修完
1 2与乙队修完
1
3
所用的天数相等,甲、乙两队单独修各需要多少天?。
