弯矩二次分配法EXCEL计算
二次弯矩分配表格

0.000 0.000 0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000 0.000
0.000
0.000 0.000 0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000
0.000
0.000 0.000 0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000 0.000
0.000
0.000 0.000 0.000 0.000 0.000 0.000
分配系数分配系数分配系数分配系数分配系数分配系数分配系数分配系数分配系数分配系数分配系数分配系数分配系数分配系数偏心矩偏心矩偏心矩偏心矩0000输入弯矩输入弯矩0000输入弯矩输入弯矩0000输入弯矩输入弯矩00001212000value
上柱 下柱 右梁 分配系数 分配系数 分配系数 偏心矩 0.000 输入弯矩 0.000 #VALUE! #VALUE! 0.000 #VALUE! #VALUE!
0.000 0.000 0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000 0.000
0.000
0.000 0.000 0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000 0.000
右梁 分配系数 输入弯矩 #VALUE! #VALUE! #VALUE! #VALUE!
弯矩二次分配法excel

弯矩二次分配法excel弯矩二次分配法(Moment Distribution Method)是结构分析中常用的一种计算方法,适用于解决梁、桁架等结构的弯矩分配问题。
通过多次迭代计算,可以准确地求解结构的内力分布。
在Excel中,可以使用各种函数和公式来实现弯矩二次分配法的计算。
首先,需要建立一个适当的数据表格,包括输入数据和计算结果。
输入数据通常包括结构的几何尺寸、材料性质、荷载大小和位置等。
计算结果包括节点的位移、弯矩和剪力等。
为了进行弯矩二次分配法的计算,首先需要确定结构的支座刚度矩阵。
支座刚度矩阵包括结构的刚度和弯矩分配系数。
可以使用Excel中的数组函数来计算支座刚度矩阵。
然后,根据结构的约束条件,可以得到初始的节点位移。
接下来,需要进行迭代计算,直至收敛。
在每一次迭代中,需要计算每个节点的弯矩分配系数和弯矩修正系数。
可以使用Excel中的循环函数和条件函数来实现这一步骤。
然后,根据弯矩分配系数和弯矩修正系数,可以计算每个节点的弯矩和剪力。
在完成迭代计算后,可以得到结构的最终结果,包括节点的位移、弯矩和剪力。
可以使用Excel中的图表功能来可视化结果,并进行必要的分析和评估。
需要注意的是,弯矩二次分配法是一种近似方法,结果的精度受到迭代次数和初始条件的影响。
因此,在使用Excel进行计算时,需要进行适当的设置和调整,以保证结果的准确性和可靠性。
总之,通过在Excel中使用弯矩二次分配法,可以方便地进行结构的弯矩分析。
这种方法的优点是简单易用,适用于各种结构类型。
然而,对于复杂的结构和边界条件,可能需要借助更为专业的结构分析软件来进行分析和计算。
弯矩二次分配法及后续弯矩剪力轴力计算表

3
32.684 31.363 21.35
3
32.684 31.363 -21.35
3
32.329 32.022 21.45
3
32.329 32.022 -21.45
3
30.022 31.755 20.59
3
30.022 31.755 -20.59
3
32.594 37.707 23.43
3
32.594 37.707 -23.43
24.263 12.132
-4.640
31.755
-76.30 24.263 27.773 12.971 -10.511
-4.640 -5.311
32.594 -64.349
0.34 0.272 0.388
25.942 12.132 -0.367 37.707
20.754
-0.293 20.460
-76.30 29.604 -11.053 -0.419 -58.167
剪力
V1
q
b
V0
剪力
MC
q
b
V5AB 47.26 17.66
0.3
44.61 M5AB 25.058 44.61
0.3
V5BA 53.40 17.66
0.3
50.75 M5BA 42.545 50.75
0.3
V5BC 11.81 9.84
0.3
10.33 M5BC 16.562 10.33 0.3
V4AB 72.77 28.18
-76.30 27.773 -10.511 -4.654 -63.692
0.318 0.318 0.364
24.263 12.132 -4.373 32.022
二次弯矩分配系数计算表EXCEL
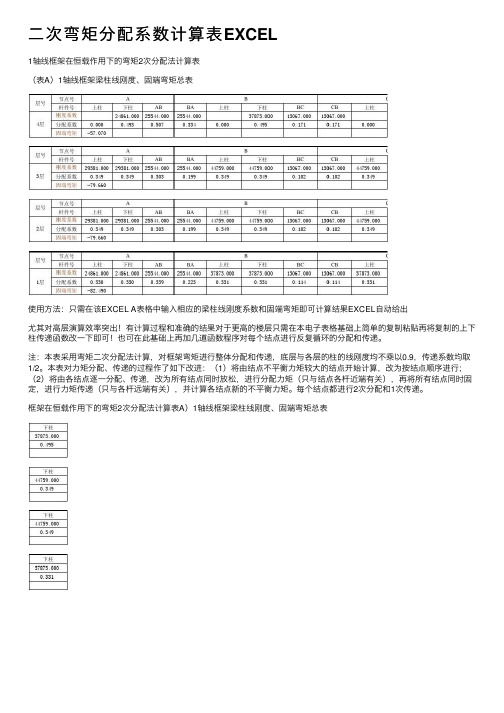
⼆次弯矩分配系数计算表EXCEL
1轴线框架在恒载作⽤下的弯矩2次分配法计算表
(表A)1轴线框架梁柱线刚度、固端弯矩总表
使⽤⽅法:只需在该EXCEL A表格中输⼊相应的梁柱线刚度系数和固端弯矩即可计算结果EXCEL⾃动给出
尤其对⾼层演算效率突出!有计算过程和准确的结果对于更⾼的楼层只需在本电⼦表格基础上简单的复制粘贴再将复制的上下柱传递函数改⼀下即可!也可在此基础上再加⼏道函数程序对每个结点进⾏反复循环的分配和传递。
注:本表采⽤弯矩⼆次分配法计算,对框架弯矩进⾏整体分配和传递,底层与各层的柱的线刚度均不乘以0.9,传递系数均取1/2。
本表对⼒矩分配、传递的过程作了如下改进:(1)将由结点不平衡⼒矩较⼤的结点开始计算,改为按结点顺序进⾏;(2)将由各结点逐⼀分配、传递,改为所有结点同时放松,进⾏分配⼒矩(只与结点各杆近端有关),再将所有结点同时固定,进⾏⼒矩传递(只与各杆远端有关),并计算各结点新的不平衡⼒矩。
每个结点都进⾏2次分配和1次传递。
框架在恒载作⽤下的弯矩2次分配法计算表A)1轴线框架梁柱线刚度、固端弯矩总表
C
C
C
C
(表B )弯矩2次分配与传递表4层。
弯矩二次分配

只需讲颜色框内数据更改,自动生成数据
计 算 表
分配系数
固端弯矩
分配弯矩
传递弯矩
2次分配
最终弯矩
分配弯矩
传递弯矩
2次分配
最终弯矩
分配弯矩
传递弯矩
2次分配
最终弯矩
分配弯矩
7传递弯矩
2次分配
最终弯矩
分配弯矩
6传递弯矩
2次分配
分配弯矩
5传递弯矩
2次分配
最终弯矩
分配弯矩
传递弯矩
42次分配
最终弯矩
分配弯矩
传递弯矩
32次分配
最终弯矩
分配弯矩
传递弯矩
22次分配
最终弯矩
分配弯矩
传递弯矩
12次分配
最终弯矩
弯矩二次分配法计算
法计算均布荷载作用下的框架梁柱弯矩。
四层两跨框架弯矩二次分配计算表

跨度、层高不同仅供参考
AB跨梁端弯矩 AB跨梁端剪力
左
右
左
右
-87.19 107.66 99.577 -105.3
####### 125.72 108.55 -110.2
####### 124.60 108.35 -110.4
####### 118.82 107.9 -110.8
BC跨梁端弯矩
左
右
24.38 0.00 108.55 111.21 408.08 432.45 24.38 -110.2 20.18 119.34
24.38 0.00 108.35 111.21 652.01 676.38 24.38 -110.4 20.46 119.34
30.94 0.00 107.90 111.21 895.49 926.43 30.94 -110.8 22.12 119.34
0.341 0.319 13.90 -131.24 40.01 37.43 20.01 -14.96 -11.86 -11.09 62.06 -119.86
0.341 0.341 0.319
分配弯矩 传递弯矩 2次分配 最终弯矩
40.01 20.01 -9.06 50.96
13.90 40.01 21.53 -9.06 66.38
###### ###### 30.94 -4.83
0 100.67 449.43 480.36
BC跨中弯矩
Mb
Mc
M中
###### 3.91 -6.66
###### 3.89 -3.40
###### 3.59 -3.47
###### 2.20 -4.33
1 23.92 11.92 203.18 -108.23 118.82 89.65 11.96
六层三跨荷载作用下弯矩二次分配法有附加弯矩.xls

-72.52 9.78 -4.29 -0.15 -67.17
0.35 0.253
0.00 23.76 -11.88 -0.54 11.34
17.18 8.59 -0.39 25.37
0.253 0.144
4.62 17.18 9.13 -0.39 25.92
-72.52 9.78 -4.29 -0.22 -67.25
0.99 0.76 -23.01 -11.94
-4.62 -17.18 -8.59 0.26 -25.51
0.00 -23.76 11.88 0.35 -11.53
0.144 0.253 0.253 0.35
72.52 -9.78 4.29 0.22 67.25
-17.18 -8.59 0.39 -25.37
-4.62 -17.18 -9.13 0.39 -25.92
0.00 -23.76 11.88 0.54 -11.34
左梁 0.468
0 6.58 -3.29 -1.89 1.40
上柱
下柱 0.339 偏心矩 1.16 4.77 8.59 -1.37 11.99
右梁 0.193
-15.23 2.72 -1.26 -0.78 -14.55
0.35 0.253
0.00 23.77 -11.89 1.82 13.71
0.222
-43.05 8.57 -4.89 -2.41 -41.78
左梁 0.193
15.23 -2.72 1.26 0.78 14.55
上柱
下柱 0.339 偏心矩 -1.16 -4.77 -8.59 1.37 -11.99
右梁 0.468
0.00 -6.58 3.29 1.89 -1.40
弯矩二次分配法excel

弯矩二次分配法excel弯矩二次分配法是一种结构力学中常用的计算方法,用于计算超静定梁或桁架的内力和位移。
本文将介绍如何在Excel中使用弯矩二次分配法进行计算。
首先,我们需要确定梁或桁架的几何参数和荷载条件。
假设我们要计算一个简支梁的内力和位移,其长度为L,截面形状为矩形,弹性模量为E,惯性矩为I,荷载为集中力P施加在距离左支点a处。
在Excel中,我们可以设置以下的参数:L,a,P,E,I。
可以将这些参数放在Excel的不同单元格中,并赋予相应的数值。
接下来,我们需要进行弯矩二次分配法的计算步骤。
1. 计算反力:根据力的平衡条件,可以得到右支点的反力为RA = P * (L - a)/L,左支点的反力为RB = P * a/L。
2. 计算弯矩系数:对于简支梁,弯矩系数为1。
可以将这个系数设定为Excel中的一个单元格。
3. 计算初始剪力分布:根据几何约束和力的平衡条件,当x =0到a时,剪力为V1 = RB,当x = a到L时,剪力为V2 = -RA。
4. 计算初始弯矩分布:根据剪力的分布和弯矩的定义,可以求得初始弯矩分布为M0 = 0,M1 = V1 * x,M2 = RB * x - V2 *(x - a)。
5. 计算修正剪力分布:根据弯矩的修正条件,可以得到修正剪力分布为V'1 = V1 + (M0 - M1) / L,V'2 = V2 + (M0 - M2) / L。
6. 计算修正弯矩分布:根据修正剪力分布和弯矩的定义,可以求得修正弯矩分布为M'1 = M1 + V'1 * (x - a),M'2 = M2 + V'2 * (x - a)。
7. 计算位移:根据弯曲方程和边界条件,可以得到位移方程为y = (P * a * x * (L - x) * (L - 2a)) / (6 * E * I * L)。
通过将以上的计算公式应用到Excel中,我们可以得到弯矩分布、剪力分布和位移的数值结果。
