一次函数中的最值问题
专题:一次函数最值问题

专题:一次函数最值问题类型一:线段和例1.已知,如图,在平面直角坐标系xOy中,直线l1:y=x+3分别交x轴、y轴于点A、B两点,直线l2:y=﹣3x过原点且与直线l1相交于C,点P为y轴上一动点.(1)求点C的坐标;(2)求出△BCO的面积;(3)当P A+PC的值最小时,求此时点P的坐标.练习.已知,如图,直线y=8﹣2x与y轴交于点A,与x轴交于点B,直线y=x+b与y轴交于点C,与x轴交于点D,如果两直线交于点P,且AC:CO=3:5(AO>CO)(1)求点A、B的坐标;(2)求四边形COBP的面积S;(3)在y轴上找一点M,使得BM+PM的值最小,求出点M的坐标和BM+PM的最小值;类型二:多条线段和例2.已知直线l1:y=﹣x﹣1分别与x、y轴交于点A、B.将直线l1平移后过点C(4,0)得到直线l2,l2交直线AD于点E,交y轴于点F,且EA=EC.(1)求直线l2的解析式;(2)若点P为x轴上任一点,是否存在点P,使△DEP的周长最小,若存在,求周长的最小值及点P的坐标;练习.如图1,直线MN分别与x轴正半轴、y轴正半轴交于点M、N,且OM=6,∠OMN =45°,点P从点O出发,以每秒钟1个单位的速度沿折线ONM运动,设点P运动时间为t(s),△POM的面积S.(1)当S=△OMN时,请直接写出点P的坐标;(2)当t=6+5时,直线x=上有一个动点C和y轴上有一动点D,当PD+DC+OC 值最小时,求C、D两点的坐标及此时PD+DC+OC最小值;练习2.已知直线l1:y=x+b与x轴交于点A,直线l2:y=x﹣与x轴交于点B,直线l1、l2交于点C,且C点的横坐标为1.(1)求直线l1的解析式;(2)过点A作x轴的垂线,若点P为垂线上的一个动点,点Q为y轴上的一个动点,当CP+PQ+QA的值最小时,求此时点P的坐标;练习3.如图1,已知直线AC的解析式为y=﹣x+b,直线BC的解析式为y=kx﹣2(k≠0),且△BOC的面积为6.(1)求k和b的值;(2)如图1,将直线AC绕A点逆时针旋转90°得到直线AD,点D在y轴上,若点M 为x轴上的一个动点,点N为直线AD上的一个动点,当DM+MN+NB的值最小时,求此时点M的坐标及DM+MN+NB的最小值;(3)如图2,将△AOD沿着直线AC平移得到△A′O′D′,A′D′与x轴交于点P,连接A′D、DP,当△DA′P是等腰三角形时,求此时P点坐标.例3.已知:在平面直角坐标系中,四边形OABC满足OA∥BC,OC∥AB,OA=AB=4,且∠OAB=60°.(1)如图1.求直线AB的解析式;(2)如图2.将线段AB沿线段AC方向从点A向点C平移,记平移中的线段AB为A′B′,当△CA′B′为直角三角形时,在x轴上找一点P,使|PB′﹣PC|最大,请求出|PB′﹣PC|的最大值;练习.如图,在直角坐标系中,直线l:y=x+8与x轴、y轴分别交于点B,点A,直线x =﹣2交AB于点C,D是直线x=﹣2上一动点,且在点C的上方,设D(﹣2,m)(1)求点O到直线AB的距离;(2)当四边形AOBD的面积为38时,求点D的坐标,此时在x轴上有一点E(8,0),在y轴上找一点M,使|ME﹣MD|最大,请求出|ME﹣MD|的最大值以及M点的坐标;例4.如图1,△ABC的三个顶点均在坐标轴上,且A、C的坐标分别为(﹣1,0)和(0,﹣3),点B在x轴正半轴上,△ABC的面积为,过点A的直线AD与y轴正半轴交于点D,∠DAB=45°.(1)求直线AD和BC的解析式;(2)如图2,点E在直线x=2上且在直线BC下方,当△BCE的面积为6时,一线段FG=4(点F在G的左侧)在直线AD上移动,求当四边形BEFG的周长最小时点F 的坐标;练习.如图,一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),与正比例函数y=x的图象交于点C(4,c)(1)求k和b的值;(2)如图1,点P是y轴上一个动点,当|P A﹣PC|最大时,求点P的坐标;(3)如图2,设动点D,E都在x轴上运动,且DE=2,分别连接BD,CE,当四边形BDEC的周长取最小值时直接写出点D和E的坐标并求出四边形周长的最小值.练习2.如图,平面直角坐标系中一平行四边形ABCO,点A的坐标(﹣2,4),点B的坐标(4,4),AC与BO交于点E,AB与y轴交于点G,直线EF交y轴于点F且G为线段FO的中点.(1)求出直线EF的解析式.(2)若点Q是点F关于点E的对称点,P点为线段AB上的一动点,过点P作PH⊥x 轴,垂足为H,连接FP,QH.问FP+PH+HQ是否有最小值,如果有,求出相应的点P 的坐标;如果没有,请说明理由.练习3.如图1,在平面直角坐标系中,直线y=﹣x﹣与x轴交于点A,与y轴交于点B,点C在x轴正半轴上,且OC=3AO,过点A作BC的平行线l.(1)求直线BC的解析式;(2)作点A关于BC的对称点D,一动点P从C点出发按某一路径运动到直线l上的点M,再沿垂直BC的方向运动到直线BC上的点N,再沿某一路径运动到D点,求点P运动的最短路径的长以及此时点N的坐标;类型五:胡不归例5.已知直线l1:y=﹣x+b与直线l2:y=kx+3相交于y轴的B点,且分别交x轴于点A、C,已知OC=OA.(1)如图1,求点C的坐标及k的值;(2)如图,若E为直线l1上一点,且E点的横坐标为.点P为y轴上一个动点,Q 为x轴上一个动点;求当|PC﹣PE|最大时,点P的坐标,并求出此时PQ+QA的最小值;练习.如图,已知直线l AC:y=﹣x﹣2交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.将△OBC关于BC边翻折,得到△O′BC,过点O′作直线O′E垂直x轴于点E.(1)求点B的坐标及直线BC的解析式;(2)P是直线O′E上任意一点,①当|P A﹣PC|最大时,请求出P点的坐标;②在①的条件下,P、Q两点关于x轴对称,F是y轴上一点,求QF+FC的最小值.类型七:一定两动,线段和例6.在平面直角坐标系中,已知点A在函数y=x的图象上,点B(4,0),且BA⊥OA,P(0,10).(1)如图1,把△ABO沿直线y=x方向平移,得到△CDE,连接PC、PE.当PC+PE 的值最小时,在x轴上存在Q点,在直线y=x上存在点R使QR+DR的值最小,求出DQ+BQ的最小值,并求出此时点Q的坐标.练习.如图①,在平面直角坐标系xOy中,平行四边形OCDE的边OC在x轴的正半轴,D、E在第一象限,直线AB经过点D与x轴、y轴分别交于点A、B,已知点E的坐标为(,),OC=且OA=2OC.(1)求直线AB的解析式;(2)如图②在直线AB上有一点P,在x轴上有一点F,当EF+PF最小时,求点P的坐标及EF+PF的最小值。
初中数学一次函数的最值问题

初中数学一次函数的最值问题一次函数在自变量x允许取值范围(即全体实数)内,它是没有最大或最小值的。
但是,如果给定了自变量的某一个取值范围(全体实数的一部分),那么y=kx+b 的最大值或最小值就有可能存在。
一般地,有下面的结论:1、如果,那么有最大值或最小值(如图1):当时,,;当时,,。
图12、如果,那么有最小值或最大值(如图2):当时,;当时,。
图23、如果,那么有最大值或最小值(如图3)当时,;当,。
图34、如果,那么既没有最大值也没有最小值。
凡是用一次函数式来表达实际问题,求其最值时,都需要用到边界特性,像物质的运输与供应、生产任务的分配和订货、邮件的投递及空袋的调运等。
下面是一道利用一次函数的最小值的决策问题,供参考:某送奶公司计划在三栋楼之间建一个奶站,三栋楼在同一条直线上,顺次为A楼,B楼,C楼,其中A楼与B楼之间的距离为40m,B楼与C楼之间的距离为60m,已知A楼每天有20人取奶,B楼每天有70人取奶,C楼每天有60人取奶,送奶公司提出两种建站方案:方案一:让每天所有取奶的人到奶站的距离总和最小;方案二:让每天A楼与C楼所有取奶的人到奶站的距离之和等于B楼所有取奶的人到奶站距离之和。
(1)若按照方案一建站,取奶站应建在什么位置?(2)若按照方案二建站,取奶站应建在什么位置?(3)在方案二的情况下,若A楼每天取奶的人数增加(增加的人数不超过22人),那么取奶站将离B楼越来越远,还是越来越近?请说明理由。
解:(1)设取奶站建在距A楼xm处,所有取奶的人到奶站的距离总和为ym.。
①当时,∴当x=40时,y的最小值为4400。
②当时,,此时y的值大于4400。
因此按方案一建奶站,取奶站应建在B楼处。
(2)设取奶站建在距A楼xm处。
①当时,,解得(舍去)。
②当时,解得x=80,因此按方案二建奶站,取奶站应建在距A楼80m处。
(3)设A楼取奶人数增加a()人,①当时,,解得(舍去)。
②当时,,解得,当a增大时,x增大。
例析一次函数最值问题

—
彩 电
1
— —
冰 箱
1
— —
1
—
—
2
3
4
产值 ( 元1
4 0 0 0
30 0 0
20 0 0
问 : 周 生 产 空 调 器 、 电 、 箱 各 多 少 台 , 能 使 总 产 值 最 高 ? 高 每 彩 冰 才 最
总产值 是 多少 ? 解 析 : 据 表 中 提 供 的 关 系 , 没 出 未 知 数 , 出 相 应 的 式 子 , 寻 根 先 列 再
备 每 周 ( 1 0个 T 时 计 算 ) 产 空 调 器 、 电 、 箱 共 3 0 台 , 冰 箱 至 按 2 生 彩 冰 6 且
少 生 产 6 台 .已 知 生 产 这 些 家 电产 品 每 台 所 需 的 T 时 和 每 台 家 电 的 产 0
值 如下 表所示 .
表 2
空 调 器
的 运 费 分 别 为 40 0元 和 5 0元 . 0
没从 A 市 、 市 各 调 运 台 机 器 到 D 市 . 2 B 当 8台 机 器 全 部 调 运 完 毕 后 , 求 总 运 费 ( J 于 ( J 函数 关 系式 , 求 元 关 台 的 并 朗化. 也是解 这类 问题 的常用方法 之一. 这
,
一
引
口河
南
张 瑞 红
在 一 次 函 数 的 应 用 题 中 , 一 类 是 和 一 次 函 数 的 最 大 值 最 小 值 有 关 有 的 . 际 上 , 次 函 数 的 最 大 值 与 最 小 值 在 做 决 策 时 用 处 很 大 . 关 键 是 实 一 其
对 问 题 的 原 始 形 态 进 行 分 析 、 想 、 象 、 括 , 而 构 建 相 应 的 函数 关 联 抽 概 进 系. 面举几个 较典 型的例 子. 下 例 1 市 、 市 和 C 市 分 别 有 某 种 机 器 1 台 、 0 台 和 8台 . 决 定 曰 0 1 现
中考数学重难点专题13 一次函数的实际应用中最值问题(学生版)

中考数学复习重难点与压轴题型专项突围训练(全国通用版)专题13一次函数的实际应用中最值问题【典型例题】1.(2022·河南汝阳·九年级期末)为满足市场需求,某超市在新年来临前夕,购进一款商品,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,如果每盒售价每提高1元,则每天要少卖出20盒.(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;(2)要使每天销售的利润为6000元,且让顾客得到最大的实惠.售价应定为多少元?(3)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?【专题训练】一、解答题1.(2022·山东青岛·模拟预测)“菊润初经雨,橙香独占秋”,如图,橙子是一种甘甜爽口的水果,富含丰维生素C.某水果商城为了了解两种橙子市场销售情况,购进了一批数量相等的“血橙”和“脐橙”供客户对比品尝,其中购买“脐橙”用了420元,购买“血橙”用了756元,已知每千克“血橙”进价比每千克“脐橙”贵8元.(1)求每千克“血橙”和“脐橙”进价各是多少元?(2)若该水果商城决定再次购买同种“血橙”和“脐橙”共40千克,且再次购买的费用不超过600元,且每种橙子进价保持不变.若“血橙”的销售单价为24元,“脐橙”的销售单价为14元,则该水果商城应如何进货,使得第二批的“血橙”和“脐橙”售完后获得利润最大?最大利润是多少?2.(2022·山东莱芜·九年级期末)2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价每件40元,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示,设每月获得的利润为W(元).(1)求出每月的销售量y(件)与销售单价x(元)之间的函数关系式;(2)这种文化衫销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?(3)为了扩大冬奥会的影响,物价部门规定这种文化衫的销售单价不高于60元,该商店销售这种文化衫每月要获得最大利润,销售单价应定为多少元?每月的最大利润为多少元?3.(2022·河南·郑州中学九年级期末)冰墩墩(Bing Dwen Dwen),是2022年北京冬季奥运会的吉祥物.将熊猫形象与富有超能量的冰晶外壳相结合,头部外壳造型取自冰雪运动头盔,装饰彩色光环,整体形象酷似航天员.冬奥会来临之际,冰墩墩玩偶非常畅销.小冬在某网店选中A,B两款冰墩墩玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如表:(1)第一次小冬550元购进了A,B两款玩偶共30个,求两款玩偶各购进多少个.(2)第二次小冬进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小冬计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?(3)小冬第二次进货时采取了(2)中设计的方案,并且两次购进的玩偶全部售出,请从利润率的角度分析,对于小冬来说哪一次更合算?(注:利润率=(利润÷成本)×100%).4.(2021·山东青岛·一模)某学校为进一步做好疫情防控工作,计划购进A,B两种口罩.已知每箱A种口罩比每箱B种口罩多10包,每箱A种口罩和每箱B种口罩的价格分别是630元和600元,而每包A种口罩和每包B种口罩的价格分别是这一批口罩平均每包价格的0.9倍和1.2倍.(1)求这一批口罩平均每包的价格是多少元.(2)如果购进A,B两种口罩共5500包,最多购进3500包A种口罩,为了使总费用最低,应购进A种口罩和B种口罩各多少包?总费用最低是多少元?5.(2022·江苏滨湖·八年级期末)小李在某网店选中A、B两款玩偶,确定从该网店进货并销售.两款玩偶的进货价和销售价如表:(1)第一次小李用1100元购进了A、B两款玩偶共30个,求两款玩偶各购进多少个?(2)第二次小李进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半,小李计划购进两款玩偶60个.设小李购进A款玩偶m个,售完两款玩偶共获得利润W元,问应如何设计进货方案才能获得最大利润?并求W的最大值.6.(2021·山东北区·一模)六一前夕,某商场采购A、B两种品牌的卡通笔袋,已知每个A品牌笔袋的进价,比每个B品牌笔袋的进价多2元;若用3000元购进A品牌笔袋的数量,与用2400元购进B品牌笔袋的数量相同.(1)求每个A品牌笔袋和每个B品牌笔袋的进价分别是多少元;(2)该商场计划用不超过7220元采购A、B两种品牌的笔袋共800个,且其中B品牌笔袋的数量不超过400个,求该商场共有几种进货方式;(3)若每个A品牌笔袋售价16元,每个B品牌笔袋售价12元,在第(1)(2)问的前提下,不计其他因素,将所采购的A、B两种笔袋全部售出,求该商场可以获得的最大利润为多少元.7.(2022·四川简阳·八年级期末)某校准备组织八年级280名学生和5名老师参加研学活动,已知用1辆小客车和2辆大客车每次可运送120人;用3辆小客车和1辆大客车每次可运送135人.(1)每辆小客车和每辆大客车各能坐多少人?(2)若学校计划租用小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满.①请你设计出所有的租车方案;②若小客车每辆需租金6000元,大客车每辆需租金7500元,总租金为W元,写出W与m的关系式,根据关系式选出最省钱的租车方案,并求出最少租金.8.(2022·山东城阳·八年级期末)七月份河南暴雨,鸿星尔克因捐款5000万爆红网络,为表达对品牌的支持,国人掀起购物潮.我区一家鸿星尔克门店有库存上衣和裤子共1450件,若上衣按每件获利50元卖,裤子按每件获利80元卖,则售完这些库存共可获利92000元.(1)该门店库存有上衣、裤子各多少件?。
一次函数绝对值和最值问题

含绝对值函数综合问题一、含绝对值函数的最值1、含一个绝对值的一次绝对值函数的最值、单调性、对称性(1)()||f x x =的图像是以原点为顶点的“V ”字形图像;函数在顶点处取得最小值“(0)0f =”,无最大值;在函数(,0],[0,)x ∈-∞↓+∞↑;对称轴为:0x =(2)()||(0)f x kx b k =+≠图像是以(,0)b k-为顶点的“V ”字形图像;在顶点取得最小值:“()0b f k -=”,无最大值;函数在(,],[,)b b x k k ∈-∞-↓-+∞↑;对称轴为:b x k=- (3)函数()||(0)f x k x b k =+≠: 0k >时,函数是以(,0)b -为顶点的“V ”字形图像;函数在顶点取得最小值:“()0f b -=”,无最大值;函数在(,],[,)x b b ∈-∞-↓-+∞↑;对称轴为:x b =-0k <时,是以(,0)b -为顶点的倒“V ”字形图像,函数在顶点取得最大值:“()0f b -=”,无最小值;函数在(,],[,)x b b ∈-∞-↑-+∞↓;对称轴为:x b =-2、含两个绝对值的一次绝对值函数的最值、单调性、对称性(1)函数()||||()f x x m x n m n =-+-<的图像是以点(,),(,)A m n m B n n m --为折点的“平底形”图像;在[,]x m n ∈上的每点,函数都取得最小值n m -,无最大值;函数在(,],[,)x m x n ∈-∞↓∈+∞↑ ,在[,]x m n ∈无单调性;对称轴为2m n x +=。
(2)函数()||||f x x m x n =---: 当m n >时,()f x 是以点(,),(,)A m n m B n m n --为折点的“Z 字形”函数图像;在(,]x n ∈-∞上的每点,函数都取得最大值m n -,在[,)x m ∈+∞上的每点,函数都取得最小值n m -;函数在[,]x n m ∈↓,在(,]x n ∈-∞及[,)x m ∈+∞上无单调性;对称中心为(,0)2m n +; 当n m >时,()f x 是以点(,),(,)A m m n B n n m --为折点的“反Z 字形”函数图像; 在(,]x m ∈-∞上的每点,函数都取得最小值m n -,在[,)x n ∈+∞上的每点,函数都 取得最大值n m -;函数在[,]x m n ∈↑,在(,]x n ∈-∞及[,)x m ∈+∞上无单调性;对称中心为(,0)2m n +; (3)()||||()f x a x m b x n m n =-+-<图像是以(,()),(,())A m f m B n f n 为折点的折线。
一次函数最值问题

一次函数最值问题
一次函数一般形式为 y = kx + b,其中 k 和 b 是常数,且k ≠ 0。
对于一次函数,其斜率为 k。
1. 当 k > 0 时,函数 y = kx + b 是增函数,即随着 x 的增加,y 也增加。
因此,函数的最大值出现在 x 的正无穷大处,此时 y 的值为正无穷大。
函数的最小值出现在 x = -b/k 处,此时 y 的值为 -b。
2. 当 k < 0 时,函数 y = kx + b 是减函数,即随着 x 的增加,y 减小。
因此,函数的最大值出现在 x 的负无穷大处,此时 y 的值为正无穷大。
函数的最小值出现在 x = -b/k 处,此时 y 的值为 -b。
需要注意的是,由于一次函数的定义域是全体实数,因此其最值是相对于定义域而言的。
在实际情况中,我们可能需要考虑函数的定义域和值域,以及函数的实际应用背景来求解最值问题。
一次函数知识点 最值
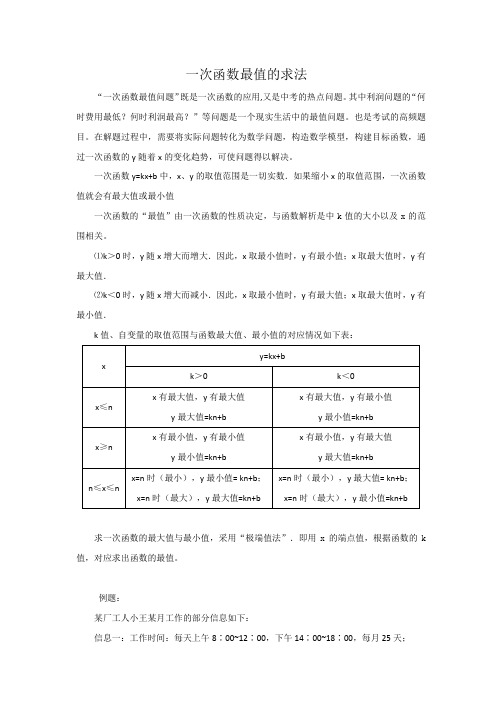
一次函数最值的求法“一次函数最值问题”既是一次函数的应用,又是中考的热点问题。
其中利润问题的“何时费用最低?何时利润最高?”等问题是一个现实生活中的最值问题。
也是考试的高频题目。
在解题过程中,需要将实际问题转化为数学问题,构造数学模型,构建目标函数,通过一次函数的y随着x的变化趋势,可使问题得以解决。
一次函数y=kx+b中,x、y的取值范围是一切实数.如果缩小x的取值范围,一次函数值就会有最大值或最小值一次函数的“最值”由一次函数的性质决定,与函数解析是中k值的大小以及x的范围相关。
⑴k>0时,y随x增大而增大.因此,x取最小值时,y有最小值;x取最大值时,y有最大值.⑵k<0时,y随x增大而减小.因此,x取最小值时,y有最大值;x取最大值时,y有最小值.k值、自变量的取值范围与函数最大值、最小值的对应情况如下表:求一次函数的最大值与最小值,采用“极端值法”.即用x的端点值,根据函数的k 值,对应求出函数的最值。
例题:某厂工人小王某月工作的部分信息如下:信息一:工作时间:每天上午8∶00~12∶00,下午14∶00~18∶00,每月25天;信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.生产产品件数与所用时间之间的关系见下表:生产甲产品件数(件) 生产乙产品件数(件) 所用总时间(分)1010 350 30 20 850信息三:按件计酬,每生产一件甲产品可得1.50元,每生产一件乙产品可得2.80元. 根据以上信息,回答下列问题:(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?解:(1)设生产一件甲种产品需x 分钟,生产一件乙种产品需y 分钟,由题意得:10103503020850x y x y +=⎧⎨+=⎩ 解得:1520x y =⎧⎨=⎩所以生产一件甲产品需要15分钟,生产一件乙产品需要20分钟.(2)设生产甲种产品共用了x 分钟,生产乙种产品需用(25860)x ⨯⨯-分钟,则生产甲种产品15x 件,生产乙种产品2586020x ⨯⨯-件. 258601.5 2.81520x x w ⨯⨯-∴=⨯+⨯总额120000.1 2.820x x -=+⨯ 0.116800.14x x =+-0.041680x =-+∵6015x ≥, ∴900x ≥∵-0.04<0∴当x 取最小值900时w 取得最大值为0.0490016801644w =-⨯+=(元)甲生产了9006015=(件), 乙生产了25860900120009005552020⨯⨯--==(件) 所以小王该月最多能得到1644元,此时生产甲、乙两种产品分别为60件和555件.。
人教版八年级下册数学一次函数与动点最值问题

一次函数与动点最值问题知识导航1.关于x 的一次函数y =k (x -m )+n 或y =kx -km +n 一定过定点(m ,n ).2.直线外一点与直线上各点的连线中,垂线段最短.3.利用三角形两边之和大于第三边,两边之差小于第三边求最值.4.利用平方数,绝对值,算术平方根的非负性求最值.【板块一】过定点的直线题型一 定点动直线【例1】(1)一次函数y =kx 一定经过点_________;若一次函数的图象经过原点,那么该一次函数的解析式可设为_________.(2)一次函数y =kx +2一定经过点_________;若一次函数的图象经过点(0,-4),那么该一次函数的解析式可设为_________;(3)一次函数y =kx -2k +1一定经过点_________;若一次函数的图象经过点(-2,4),该一次函数的解析式可设为_________. 题型二 动点定直线【例2】利用坐标判断点在定直线上. (1)点P (m ,m +2)一定在直线_________上; (2)点P (m +1,2m -3)一定在直线_________上.针对练习11.过定点的动直线的应用: 已知一次函数y =2kx -k +2. (1)其图象过定点_________;(2)直线y =2kx -k +2和直线y =4x 的交点是_________; (3)若0<k <2,不等式2kx -k +2≤4x 的解集是_________; (4)当x =1时,y <0,则k 的取值范围是_________;(5)若A (32,3),B (4,-3),该一次函数的图象与线段AB 有交点,则k 的取值范围是_________.2.动点在定直线上的应用:直线AB:y=2x+4交x轴于点A,交y轴于点B,C(1,0),点P为直线AB上一点,将线段PC绕点C 顺时针旋转90°,得CQ.(1)若点P横坐标为-1时,求点Q坐标;(2)若点P横坐标为m,试用含m的式子表示点Q的坐标;(3)当点P在直线AB上运动时,则点Q总在直线l上运动,求直线l的解析式.【板块二】直线型动点最值问题题型三点到直线的距离最短方法技巧利用垂线段最短,可求定点到直线型动点的最小值问题.【例1】点P是x轴上一点,A(0,4),将线段P A绕点A逆时针旋转90°得到线段AQ,求OQ的最小值.【例2】如图,A(4,0),△OAB为等边三角形,点C为x轴上一动点,以BC为边在直线BC的右侧作等边△BCD,连接OD.(1)点D在某一确定的函数图象上运动,其解析式为_________;(2)OD的最小值为_________.题型四两线段或多线段的和差最值问题方法技巧利用两边之和大于第三边,两边之差小于第三边,求两线段或多线段的和差最大值或最小值;在平面直角坐标系中,常作一个定点的对称点,然后连接这一对称点与另一定点,求最值.这一方法也叫化折为直.【例3】如图,A(-4,2),B(-1,1),在x轴上找一点P,使△P AB的周长最小,求这个最小值及点P的坐标.【例4】如图,A(-4,2),B(-1,1),在x轴上找一点P,使|P A-PB|的值最大,并求此时点P的坐标.针对练习21.一次函数y=k(x-1)+3k-4的图象与x轴交于点A,与y轴交于点B,则点O到该直线的距离的最大值是_________;2.如图,B(0,3),点A为x轴上一动点,将线段AB绕点A顺时针旋转90°得线段AC,连接OC.(1)设A(a,0),用含a的式子表示点C坐标_________;(2)点C在某一确定的函数图象上运动,其解析式为_________;(3)OC长度的最小值为_________.3.如图,A(0,23),点B为x轴上一动点,将线段AB绕点A逆时针旋转60°,得线段AC,线段OC的最小值是_________.第2题第3题第4题第5题4.如图,在△ABC中,∠ACB=90°,AC=BC=4,点M为AB的中点,点D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ME,点D在运动的过程中,ME的最小值为()A.2B.2 2C.4D.4 25.如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE的最小值为_________.6.如图,直线y=x+4与坐标轴交于点A,B,点C(-3,m)在直线AB上,在y轴上找一点P,使P A+PC的值最小,求这个最小值及点P的坐标.【板块三】动点的运动路径(轨迹)问题方法技巧动点的运动路径问题解题方法:1.选取三个或多个特殊点探索三个或多个特殊位置,一般选取起点,终点,和另外的特殊点探索;2.根据这些特殊点的位置猜想运动路径,然后验证.现阶段多用全等转换求值.【例1】如图,直线AB:y=2x+4交x轴于点A,交y轴于点B,C(1,0),点P为直线AB上一点,将线段PC绕点C顺时针旋转90°得CQ.(1)当点P从点A运动到点B时,点Q的运动路径长为_________;(2)线段OQ的最小值为_________.【例2】如图,A(4,0),B(0,4),点P在线段AB上运动,PQ⊥PO且PQ=PO.(1)试说明点Q在某一确定的直线上;(2)点M是OQ的中点,当点P从点A运动到点B时,求点M运动的路径长.针对练习31.在平面直角坐标系中,A(0,4),点B沿着某条路径运动,以点B为旋转中心,将点A逆时针旋转60°到点C(m,2).若-5≤m≤5,则点B运动的路径长为_________.2.在平面直角坐标系中,已知点A(a,0),C(0,b),且a,b满足(a+1)2+b+3=0.(1)直接写出:a=_________,b=_________;(2)如图1,点B为x轴正半轴上的一点,BE⊥AC于点E,交y轴于点D,连接OE.若OE平分∠AEB,求直线BE的解析式;(3)如图2,在(2)的条件下,点M为直线BE上的一动点,连接OM,将线段OM绕点M逆时针旋转90°,点O的对应点为N,当点M运动时,判断点N的运动路线是什么图形,并说明理由.图1图23.如图1,直线y=-3x+33分别与y轴、x轴交于点A,B,点C的坐标为(-3,0),点D为直线AB 上的一动点,连接CD交y轴于点E.(1)点B的坐标为_________,不等式-3x+33>0的解集为_________;(2)若S△COE=S△ADE,求点D的坐标;(3)如图2,以CD为边作菱形CDFG,且∠CDF=60°,当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.图1图2一次函数大综合——数形结合1.已知点A(a,3),点B(b,6),点C(5,c),AC⊥x轴,CB⊥y轴,点B在第二象限且到两坐标轴的距离相等.(1)写出A,B,C三点的坐标;(2)求△ABC的面积;(3)若点P为线段OB上的动点,当△BCP面积大于12小于16时,求点P的横坐标的取值范围.2. 在平面直角坐标系中,A(a,b),B(c,d),且a-c+4+|b-d-6|=0.(1)直接写出a与c,b与d的关系式;(2)如果b=c=0,点P(m,32m+6),且m>0,S△P AB=4S△AOB,求点P的坐标;(3)如果b=3,连接AB交x轴于点Q.①直接写出点Q的坐标(用含a的式子表示);②若S△AOB≤24,求a的取值范围.3. (2019黄陂区期末)如图,在平面直角坐标系中,点A在第一象限,AB⊥x轴于点B.AC⊥y轴于点C,点A(4a,3a),且四边形ABOC的面积为48.(1)如图1,直接写出点A的坐标为_________;(2)如图2,点D从点O出发以每秒1个单位长度的速度沿y轴正半轴运动,同时,点E从点A出发,以每秒2个单位长度的速度沿射线BA运动,DE交线段AC于点F,设运动的时间为t秒,当S△AEF<S△CDF 时,求t的取值范围;(3)如图3,将线段BC平移,使点B的对应点M恰好落在y轴负半轴上,点C的对应点为N,连接BN交y轴轴于点P,当OM=3OP时,求点M的坐标.4. 在平面直角坐标系中,已知点A(a,0),B(a,6),C(a-2,2).(1)若a=2,则△ABC的面积为_________;(2)将线段BC向右平移m个单位,若△ABC的面积小于4,求m的取值范围;(3)若点D(a+8,8),连结AD,将线段BC向右平移n个单位,若线段BC与线段AD有公共点,请直接写出n的取值范围_________.5.在平面直角坐标系中,点A(a,b),B(c,d),且a-c+3+|b-d-4|=0.(1)如果a=-1,b=-3,求A,B两点的坐标;(2)如果a=-1,b=-3,求直线AB与x轴的交点M以及与y轴的交点N的坐标;(3)如果点A在x轴上方平行于x轴,且在到x轴距离等于2的直线上运动,若△ABO的面积不超过21,求a的取值范围.6.如图,在平面直角坐标系中,直线l交x轴于点A,交y轴于点B,下表列举的是直线l上的点P(x,y)的取值情况:(1)直线l上的点P(x,y)的横、纵坐标之间的数量关系是_________(直接写出结果);(2)若点P(-2,2),点Q(q,0),若以P,Q,O,B为顶点的四边形的面积大于5,求q的取值范围;(3)已知坐标平面内第一象限的点M(m,n),N(m+4,n+4),若△PMN的面积是12,求m,n的数量关系.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师大三附中
教师
习富云
一次函数中的最值问题
时间
由实际问题中的最值问题建立数学模型引入,然后利用图形变换和一
知识与技能 次函数在直角坐标系中确定最值点,巩固一次函数的知识并进一步体
教
会数形结合思想.
学
目
体会图形变换在解决问题中的转化作用,利用一次函数的解析式求直 过程与方法
标
线的交点,增强数学的应用意识.
问题数学 化.
学生思考,讨论交 流. 利用轴对称变换和 一次函数解决问题.
回忆轴对 称变换的
知识.
让学生复 习一次函 数的有关 知识
由辅助问
提出问题:轴对称变换在解决问题中起了什么作 用?
题的铺垫, 学生独立思考并回
利用轴对
二、拓展
问题 2 如图,已知点 A
答
(4,3)。若点 C 是直线
y=-x+4 上一点,B 是直线
让学生明 确轴对称 变换在该 题中的转 化作用.
如何求解,引导学 生理解运用轴对称 变换求解最短路线 的实质,即“折化 直”关键抓住点 A 通过两次轴对称变 换后得到的 A1、A2 为定点, 同时由轴 对称性质可将三角 形周长转化为非封 闭的折线段的长 度,从而利用问题 1 的结论又可求解该 题.
情感价值观
在解决问题的过程中,帮助学生认识数学,体验探索的快乐与成功的 喜悦.
教学 重点 教学 难点
教 学 过 程
图形变换和一次函数的应用.
如何通过图形变换进行转化, 确定对称点坐标然后求解析式进而求得最值点
活动内容 一、问题探究 1. 提出问题 问题 1 如图,要在燃气管道 l 上修建一个泵站,分 别向 A,B 两城镇供气.泵站修在什么地方,可使所 用的输气管线最短?
求得,k=1
∴ AB' 所在直线的解析式为 y=x-1
教 ∴点 C 坐标为(1,0) 学 5.思考 过 提出问题: 如图,已知点 程 A(4,3),点 B(0,-1)。
若点 C 是 x 轴上一动点,
当 AC BC 的值最大
B
时,求 C 点坐标.
得将实际
学生想到通过求直 线的解析式再求其 与 x 轴的交点.
8 8
5
称变换和 一次函数 求解该题.
使学生从 另一个角 度对利用 轴对称变 换求解该 题作说明, 进一步理 解轴对称 变换.
C A1
A2 B
y=-x+4
学生读完题后尝试 独立求解,教师巡 视指导. 学生在解该题时可 能模仿问题 1 容易 想到利用轴对称变 换求解,但对为什 么这样做缺少理性 思考,此时提问学生
分析:可将点向右平移 1 个单位到 B1 (2,2),再
教 学
做 B1 关于 x 轴的对称点 B2 (2,-2),连接 A B2 交 x
过 轴于点 D,将点 D 向左平移得到点 C。
程
B1 CD B2
三、总结反思
教 ① 怎样将实际问题转化为数学问题?
教师引导,学生思
学 将实际问题中的条件作数学化的简化或抽象是解决 考、回答
2. 实际问题数学化
如图,已知点 A、B 在直线 l 的同侧.在 l 上找点 P,
使 PA+PB 最小.
A
师生活动
学生独立思考,教师 巡视.观察学生是否 作数学化,同时对转 化正确的同学给予 肯定,并指出实际问 题转化为数学问题 是解决实际问题的 第一步.
.
设计意图 选用“西气 东输”作为 背景,引导 学生了解 数学来源 于生活.
一动点,当 AC BC
B
的值最小时,求 C 点
坐标.
提问: 如何在直角坐标系中确定两条直线的交点 4.画图找点
解:做 B 点关于 x 轴的对
称点 B' (0,-1)
连接 B B' 交 x 轴与点 C
C
设 AB' 所在直线的解析
B'
式为
y=kx+b,将 A, B' 两点坐
标代入
b 1 4k b 3
B
提问: 1).线段和的最小值的理论依据是什么 2).如何将两条线段的和转化到一条线段上 3. 几何问题代数化
. 学生会回答:利用 让 学 生 明
l 两点之间线段最短; 利用图形变换实现 确 用 数 学
问题的转化
方法解决
实际问题,
提问:“如图,已知点
A(4,3),点 B(0,
1)。若点 C 是 x 轴上
对实际问题数
过 实际问题时的常用方法.例如将管道、河流近似看成 程 直线,但这种简化或抽象不是普遍适用的.
学化,及转化的
② 图形变换所起的作用是什么? 利用图形变换将多条路径转化到一条直线上,从而
解题思想进行
解决最短路线问题. (将未知问题转化为已知问题,复杂问题转化简单
提炼总结.
问题.)
四、再探究 如图,已知点 A(4,3),B(-1,-2)。 积极鼓励学生进 若点 C 是直线 y=2 上一点,D பைடு நூலகம் x 轴上一点,CD 行思考,鼓励他们 在问题 4 的基
B
.
学生独立思考、交 流讨论解决问题.
与前面问题相 似,都是涉及路 径的最短问题.
让学生在收获
成功喜悦的同
问题 4 如图,已知点 A(4,3),B(1,2)。若点 C、D 是 x 轴上两点,且 CD=1 当使四边形 ABCD 的周长最小时,求 C、D 两点的坐标. 解:
B
时,对转化的思
引导学生考虑我 想上升到理性 们学过的图形变 换除了轴对称之 层面. 外还有平移变换, 探讨是否可以通 过平移变换实现 问题的转化
A2 (6,3)两点坐标代入
k b 0 6k b 3
求得,k= 3 ,b=- 3 55
∴ AB' 所在直线的解析式为 y= 3 x- 3 55
∴
y y
x 4 3x3 55
∴点 C 坐标为 23 , 9 ,B 的坐标为 5,12 。
问题 2 在这 里起承上 启下的作 用.该题变 得更复杂, 但究其实 质,与问题
1 一样都是 利用轴对 称变换将 多条路径 转化到一 条直线上, 从而解决 路线最短 问题.
问题 3 如图,已知点 A(4,3),B(1,2)。若点 C 是 y 轴上点,D 是 x 轴上一点,当四边形 ABCD 的周长最小时,求 C、 D 两点的坐标.
⊥x 轴,当四边形 AC+CD+BD 最小
畅所欲言。
础上,积极发挥
时,求 C、D 两点 的坐标.
图形变换的转
化作用,激发学
B
四、作业
生的灵感和学
习兴趣
x=5 上一点,当△ABC 的
周长最小时,求 C、B 两点
的坐标.
分析:先找点 A 关于两条直线的对称点 A1(1,0)、
A2 (6,3),连接 A1 A2 分别较两条直线于 B、C
从而将△ABC 的周长转化为线段 A1 A2 的长
设 A1 A2 所在直线的解析式为 y=kx+b,将 A1(1,0)、
