专题训练十四 一次函数背景下的线段和差最值问题(共14张PPT)
一次函数综合—线段和差、存在性问题解析
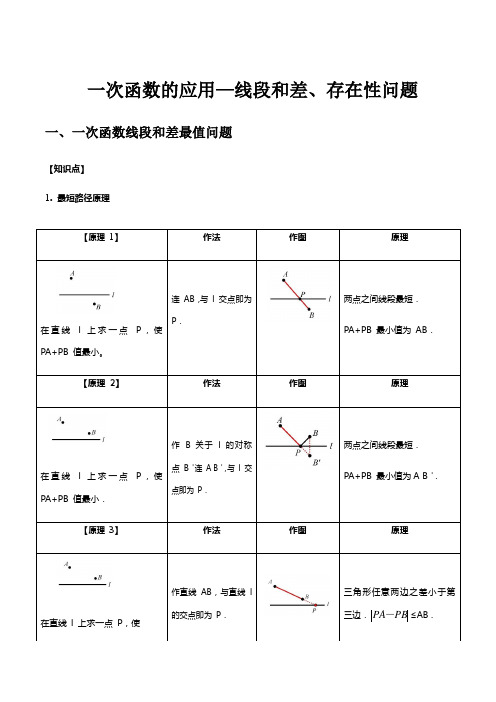
一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P，使PA+PB 值最小。
连AB，与l 交点即为P．两点之间线段最短．PA+PB 最小值为AB．【原理2】作法作图原理在直线l 上求一点P，使PA+PB 值最小．作 B 关于l 的对称点B＇连A B＇，与l 交点即为P．两点之间线段最短．PA+PB 最小值为A B＇．【原理3】作法作图原理在直线l 上求一点P，使作直线AB，与直线l的交点即为P．三角形任意两边之差小于第三边．≤AB .PBPA－（1）求线段和最小时动点坐标或直线解析式； （2）求三角形周长最小值；（3）求线段差最大时点的坐标或直线解析式。
3. 口诀：“和小异，差大同”（一）一次函数线段和最小值问题【例题讲解】★★☆例题1．在平面直角坐标系xOy 中，y 轴上有一点P ，它到点(4,3)A ，(3,1)B 的距离之和最小，则点P 的坐标是( ) A ．(0,0)B ．4(0,)7C ．5(0,)7D ．4(0,)5【答案】C的值最大 .【原理 4】作法作图原理在直线 l 上求一点 P ，使的值最大 .作 B 关于 l 的对称点 B ＇作直线 A B ＇，与 l 交点即为 P ．三角形任意两边之差小于第三边．≤A B ＇ .PB PA －PB PA －PB PA －【解析】解：作A 关于y 轴的对称点C ，连接BC 交y 轴于P ，则此时AP PB +最小，即此时点P 到点A 和点B 的距离之和最小，(4,3)A ，(4,3)C ∴-，设直线CB 的解析式是y kx b =+，把C 、B 的坐标代入得：3413k bk b =-+⎧⎨-=+⎩，解得：47k =-，57b =，4577y x ∴=-+，把0x =代入得：57y =， 即P 的坐标是5(0,)7，故选：C ．【备注】本题考查了轴对称-最短路线问题，一次函数的解析式，坐标与图形性质等知识点，关键是能画出P 的位置，题目比较典型，是一道比较好的题目．★★☆练习1．如图，在平面直角坐标系中，已知点(2,3)A ，点(2,1)B -，在x 轴上存在点P 到A ，B 两点的距离之和最小，则P 点的坐标是 ．【答案】(1,0)-【解析】解：作A 关于x 轴的对称点C ，连接BC 交x 轴于P ，则此时AP BP +最小，A 点的坐标为(2,3)，B 点的坐标为(2,1)-，(2,3)C ∴-，设直线BC 的解析式是：y kx b =+，把B 、C 的坐标代入得：2123k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩．即直线BC 的解析式是1y x =--，当0y =时，10x --=，解得：1x =-，P ∴点的坐标是(1,0)-．故答案为：(1,0)-．【备注】本题考查了一次函数图象上点的坐标特征，用待定系数法求一次函数的解析式，轴对称-最短路线问题的应用，关键是能找出P 点，题目具有一定的代表性，难度适中．★★☆练习2．如图，直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，以线段AB 为边在第一象限内作正方形ABCD ．若点P 为x 轴上的一个动点，求当PC PD +的长最小时点P 的坐标．【答案】详见解析【解析】解：直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，则点A 、B 的坐标分别为：(0,3)，(4,0)，如图所示，过点C 作CH x ⊥轴交于点H ，90ABO BAO ∠+∠=︒，90ABO CBH ∠+∠=︒，CBH BAO ∴∠=∠，又90AOB CHB ∠=∠=︒，AB BC =，()AOB BHC AAS ∴∆≅∆，4CH OB ∴==，3HB OA ==，故点(7,4)C ，同理可得点(3,7)D ，确定点C 关于x 轴的对称点(7,4)C '-，连接C D '交x 轴于点P ，则此时PC PD +的长最小，将点C '、D 的坐标代入一次函数表达式并解得： 直线CD 的表达式为：116144y x =-+， 当0y =时，6111x =，故点61P，0)．(11【备注】本题考查的是一次函数上坐标点的特征，涉及到点的对称性、正方形性质等，本题的难点在于：通过证明三角形全等，确定点C、D的坐标．★★☆例题2．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，3OB=，D为边OB的中点，若E为x轴上的一个动点，当CDE∆的周长最小时，求点E OA=，4的坐标()A．(3,0)-B．(1,0)C．(0,0)D．(3,0)【答案】B【解析】解：如图，作点D关于x轴的对称点D'，连接CD'与x轴交于点E，连接DE．若在边OA上任取点E'与点E不重合，连接CE'、DE'、D E''由DE CE D E CE CD D E CE DE CE'+'=''+'>'='+=+，可知CDE∆的周长最小．OB=，D为边OB的中点，42∴=，OD∴，(0,2)D在矩形OACB 中，3OA =，4OB =，D 为OB 的中点，3BC ∴=，2D O DO '==，6D B '=，//OE BC ，Rt ∴△D OE Rt '∽△D BC '，∴OE D OBC D B '=' 即236OE = 1OE =，∴点E 的坐标为(1,0)故选：B ．【备注】此题主要考查轴对称--最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是三角形两边之和大于第三边．★★☆练习1．如图，在平面直角坐标系中，点A 、B 的坐标分别为(1,4)和(3,0)，点C 是y 轴上的一个动点，连接AC 、BC ，当ABC ∆的周长最小值时，ABC ∆的面积为 ．【答案】3【解析】解：如图，作点A 关于y 轴的对称点A '，连接A B '交y 轴于点C '，此时ABC ∆'的周长最小，设直线A B ' 的解析式为y kx b =+，(1,4)A '-，(3,0)B ，∴430k b k b -+=⎧⎨+=⎩，1k ∴=-，3b =，∴直线A B ' 的解析式为3y x =-+，当0x =时，3y =，(0,3)C ∴'，ABC AA BAA C S SS∆'''∴=-11242122=⨯⨯-⨯⨯ 413=-=．所以ABC ∆'的面积为3．故答案为：3．【备注】本题考查了轴对称、最短路线问题、坐标与图形性质、三角形的面积，解决本题的关键是掌握轴对称的性质．★★☆练习2．如图，在平面直角坐标系中，直线122y x =+与x 轴、y 轴分别交于A 、B 两点，以AB 为边 在第二象限内作正方形ABCD ．（1）求点A 、B 的坐标，并求边AB 的长；（2）求点C 和点D 的坐标；（3）在x 轴上找一点M ，使MDB ∆的周长最小，请求出M 点的坐标，并直接写出MDB ∆的周长最小值．【答案】详见解析【解析】解： （1）对于直线122y x =+， 令0x =，得到2y =；令0y =，得到4x =-，(4,0)A ∴-，(0,2)B ，即4OA =，2OB =， 则224225AB =+=；（2）过D 作DE x ⊥轴，过C 作CF y ⊥轴，四边形ABCD 为正方形，AB BC AD ∴==，90ABC BAD BFC DEA AOB ∠=∠=∠=∠=∠=︒，90FBC ABO ∠+∠=︒，90ABO BAO ∠+∠=︒，90DAE BAO ∠+∠=︒，FBC OAB EDA ∴∠=∠=∠，()DEA AOB BFC AAS ∴∆≅∆≅∆，2AE OB CF ∴===，4DE OA FB ===，即426OE OA AE =+=+=，246OF OB BF =+=+=，则(6,4)D -，(2,6)C -；（3）如图所示，连接BD ，找出B 关于y 轴的对称点B '，连接DB '，交x 轴于点M ，此时BM MD DM MB DB +=+'='最小，即BDM ∆周长最小，(0,2)B ，(0,2)B ∴'-，设直线DB '解析式为y kx b =+，把(6,4)D -，(0,2)B '-代入得：642k b b -+=⎧⎨=-⎩，解得：1k =-，2b =-，∴直线DB '解析式为2y x =--，令0y =，得到2x =-，则M 坐标为(2,0)-， 此时MDB ∆的周长为21062+．【备注】本题属于一次函数综合题，涉及的知识有：待定系数法求一次函数解析式，坐标与图形性质，勾 股定理，全等三角形的判定与性质，正方形的性质，对称性质，以及一次函数与坐标轴的交点，熟练掌握 性质及定理是解本题的关键（二）一次函数线段差最大值问题【例题讲解】★★☆例题1．已知，如图点(1,1)A ，(2,3)B -，点P 为x 轴上一点，当||PA PB -最大时，点P的坐标为( )A ．1(,0)2B ．5(,0)4C ．1(,0)2-D ．(1,0)【答案】A【解析】解：作A 关于x 轴对称点C ，连接BC 并延长交x 轴于点P ， (1,1)A ，C ∴的坐标为(1,1)-，连接BC ，设直线BC 的解析式为：y kx b =+，∴123k b k b +=-⎧⎨+=-⎩， 解得：21k b =-⎧⎨=⎩， ∴直线BC 的解析式为：21y x =-+， 当0y =时，12x =， ∴点P 的坐标为：1(2，0)，当B ，C ，P 不共线时，根据三角形三边的关系可得：||||PA PB PC PB BC -=-<，∴此时||||PA PB PC PB BC -=-=取得最大值．故选：A ．【备注】此题考查了轴对称、待定系数法求一次函数的解析式以及点与一次函数的关系．此题难度较大，解题的关键是找到P 点，注意数形结合思想与方程思想的应用．★★☆练习1．平面直角坐标系中，已知(4,3)A 、(2,1)B ，x 轴上有一点P ，要使PA PB -最大，则P 点坐 标为【答案】(1,0)【解析】解：(4,3)A 、(2,1)B ，x 轴上有一点P ，||PA PB AB ∴-，∴当A ，B ，P 三点共线时，PA PB -最大值等于AB 长，此时，设直线AB 的解析式为y kx b =+，把(4,3)A 、(2,1)B 代入，可得3412k b k b =+⎧⎨=+⎩， 解得11k b =⎧⎨=-⎩， ∴直线AB 的解析式为1y x =-，令0y =，则1x =，P ∴点坐标为(1,0)，故答案为：(1,0)． 【备注】本题主要考查了坐标与图形性质，利用待定系数法求得直线AB 的解析式是解决问题的关键． ★★☆练习2．如图，在平面直角坐标系中，点A 的坐标为(0,4)，点B 的坐标为(6,0)，点P 在一次函数1322y x =+的图象上运动，则PB PA -的最大值为( )A ．2B ．233C ．4D ．143【答案】C【解析】解：如图，作点A 关于直线1322y x =+的对称点K ，连接AK 交直线于H ，连接PK ．AK PH ⊥，(0,4)A ，∴直线AK 的解析式为24y x =-+，由132224y x y x ⎧=+⎪⎨⎪=-+⎩，解得12x y =⎧⎨=⎩， (1H ∴，20，AH KH =，(2,0)K ∴．PB PA PB PK KB ∴-=-，∴当点P 在BK 的延长线上时，P B P K BK '-'=的值最大，最大值为624-=，故选：C ．【备注】本题考查一次函数图象上的点的特征、轴对称等知识，解题的关键是学会利用对称解决最值问题 属于中考常考题型．【题型知识点总结】一次函数最短路径问题注意事项：1. 根据“和小异，差大同”判断是否需要作对称；2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。
最新初中几何中线段和差的最大值与最小值练习题(最全)打印版
初中几何中线段和（差）的最值问题一、两条线段和的最小值。
基本图形解析： 一）、已知两个定点：1、在一条直线m 上，求一点P ，使PA+PB 最小； （1）点A 、B 在直线m 两侧：（2）点A 、B 在直线同侧：A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ，使PA+PQ+QB 最小。
（1）两个点都在直线外侧：（2）一个点在内侧，一个点在外侧：（3）两个点都在内侧：mmB mA Bmn mnn mnnnm（4）、台球两次碰壁模型变式一：已知点A 、B 位于直线m,n 的内侧，在直线n 、m 分别上求点D 、E 点，使得围成的四边形ADEB 周长最短.填空：最短周长=________________变式二：已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二）、一个动点，一个定点： （一）动点在直线上运动：点B 在直线n 上运动，在直线m 上找一点P ，使PA+PB 最小（在图中画出点P 和点B ）1、两点在直线两侧：2、两点在直线同侧：mnm nm nm（二）动点在圆上运动点B 在⊙O 上运动，在直线m 上找一点P ，使PA+PB 最小（在图中画出点P 和点B ） 1、点与圆在直线两侧：2、点与圆在直线同侧：三）、已知A 、B 是两个定点，P 、Q 是直线m 上的两个动点，P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点，使得PA+PQ+QB 的值最小。
(原理用平移知识解) （1）点A 、B 在直线m 两侧：过A 点作AC ∥m,且AC 长等于PQ 长，连接BC,交直线m 于Q,Q 向左平移PQ 长，即为P 点，此时P 、Q 即为所求的点。
（2）点A 、B 在直线m 同侧：mmmmQ Q练习题1．如图，∠AOB =45°，P 是∠AOB 内一点，PO =10，Q 、R 分别是OA 、OB 上的动点，求△PQR 周长的最小值为 ．2、 如图1，在锐角三角形ABC 中，AB=4,∠BAC=45°，∠BAC 的平分线交BC 于点D ，M,N 分别是AD 和AB 上的动点，则BM+MN 的最小值为 ． 3、如图，在锐角三角形ABC 中 ，AB=BAC=45，BAC 的平分线交BC 于D ，M 、N 分别是AD 和AB 上的动点，则BM+MN 的最小值是多少？4、如图4所示，等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点.若AE=2,EM+CM 的最小值为 .5、如图3，在直角梯形ABCD 中，∠ABC ＝90°，AD ∥BC ，AD ＝4，AB ＝5，BC ＝6，点P 是AB 上一个动点，当PC ＋PD 的和最小时，PB 的长为__________．6、 如图4，等腰梯形ABCD 中，AB=AD=CD=1，∠ABC=60°，P 是上底，下底中点EF 直线上的一点，则PA+PB 的最小值为 ．Q二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析：1、在一条直线m 上，求一点P ，使PA 与PB 的差最大； （1）点A 、B 在直线m 同侧：解析：延长AB 交直线m 于点P ，根据三角形两边之差小于第三边，P ’A —P ’B ＜AB ，而PA —PB=AB 此时最大，因此点P 为所求的点。
2020年中考复习专题：线段和差最值问题课件(共18张PPT)
∴抛物线的表达式为y＝－1x2＋5x－2 ，
∵抛物线y＝－1x2＋5x－22可化为2 y＝－1(x2－5x)－2＝－1(x－5)2＋9
22 ∴顶点D的坐标为( 5，9
28
2 )，对称轴l为直线x＝
5
2
；
2 28
(2)设点G是y轴上一点，是否存在点G，使得GD＋GB的值最小，若存在，求出 点G的坐标；若不存在，请说明理由； 温馨提示：要使GD＋GB的值最小，一般是通过轴对称作出 对称点来解决．
解：存在．如解图②，要使GD＋GB的值最小，取点B关于y 轴的对称点B′，点B′的坐标为(－1，0)． 连接B′D，直线B′D与y轴的交点G即为所求的点，
解：如解图①，由点E在x轴上，可设点E的坐标为(e，0)，连接CE，
则AE＝AO－OE＝4－e，
在Rt△COE中，根据勾股定理得
CE2＝OC2＋OE2＝4＋e2，
存在．要使△BCF的周长最小，即BC＋BF＋CF最小，如解 图③所示，连接BC. 在Rt△OBC中，OB＝1，OC＝2，由勾股定理得BC＝ 12＋22 ＝ 5 ，为定值， ∴当BF＋CF最小时，△BCF的周长最小，
∵点B与点A关于直线l对称，
∴AF＝BF，
则BF＋CF＝AF＋CF，
∴直线AC与对称轴l的交点即为所求的点F，连接BF，
在△BFE和△EGB″中，
∠BFE＝∠EGB″＝90° ∠FBE＝∠GEB″
∴△BFE≌△EGB″，
BE＝EB″
∴EG＝BF＝ 3 ，B″G＝EF＝ 6 ，
∴B″(
8＋3，5－(6＋6) 55 55
5 )，即B″(
11，－12 55
)，
设直线B′B″的表达式为y＝k′x＋b′，
初中几何中线段和差的最大值与最小值练习题(最全)
初中几何中线段和差的最大值与最小值练习题(最全)初中几何中线段和（差）的最值问题一、两条线段和的最小值基本图形解析：一）已知两个定点：1、在一条直线m上，求一点P，使PA+PB最小。
1）点A、B在直线m两侧：在直线m上找到点P使得PA=PB，则PA+PB最小。
2）点A、B在直线同侧：在直线m上找到点A'，使得A'是关于直线m的对称点，再找到点P使得PA'+PB最小，则PA+PB最小。
2、在直线m、n上分别找两点P、Q，使PA+PQ+QB最小。
1）两个点都在直线外侧：在直线m上找到点A'，使得A'是关于直线m的对称点，在直线n上找到点B'，使得B'是关于直线n的对称点，再找到点P和Q，使得PA'+PQ+QB'最小，则PA+PQ+QB最小。
2）一个点在内侧，一个点在外侧：在直线m上找到点P，使其与A点连线垂直直线m，再在直线n上找到点Q，使其与B点连线垂直直线n，使PA+PQ+QB最小。
3）两个点都在内侧：在直线m上找到点A'，使得A'是关于直线m的对称点，在直线n上找到点B'，使得B'是关于直线n的对称点，再找到点P和Q，使得PA'+PQ+QB'最小，则PA+PQ+QB最小。
4）、台球两次碰壁模型变式一：已知点A、B位于直线m,n的内侧，在直线n、m分别上求点D、E点，使得围成的四边形ADEB周长最短。
在直线m上找到点A'，使得A'是关于直线m的对称点，在直线n上找到点B'，使得B'是关于直线n的对称点，连接A'和B'，交直线m和n于D和E，使ADEB为矩形，则ADEB周长最短。
变式二：已知点A位于直线m,n的内侧,在直线m、n分别上求点P、Q点PA+PQ+QA周长最短。
在直线m上找到点A'，使得A'是关于直线m的对称点，连接AA'，在直线n上找到点Q，使得A'Q垂直直线n，连接AQ，使得PA+PQ+QA最小。
线段和最小及差最大问题
精心整理①当两点A和B在直线l同侧时，若求直线l上点P.使PA+PB最小值作点B关于直线l的对称点B’,连结AB’交直线l于点P,此时PA+PB=PA+PB’=AB’取除此之外的任意一点P’,根据三角形两边之和大于第三边，P’A+P’B=P’A+P’B’＞AB’,所以点P满足PA+PB最小值l（⋅＝OQ【分析】连接AB并延长交x轴于点P，作A点关于y轴的对称点A′连接A′B交y轴于点Q，求出点Q与y轴的交点坐标即可得出结论：连接AB并延长交x轴于点P，由三角形的三边关系可知，点P即为x轴上使得|PA－PB|的值最大的点。
∵点B是正方形ADPC的中点，∴P（3，0）即OP=3。
作A点关于y轴的对称点A′连接A′B交y轴于点Q，则A′B即为QA+QB的最小值。
∵A′（-1，2），B（2，1），设过A′B的直线为：y=kx+b，则2k b12k b=-+⎧⎨=+⎩，解得1k35b3⎧=-⎪⎪⎨⎪=⎪⎩。
∴Q（0，53），即OQ=53。
∴OP?OQ=3×53=5。
（2012四川攀枝花4分）如图，正方形ABCD中，AB=4，E是BC的中点，点P是对角线AC上一动点，则PE+PB同理，在Rt△AOC中，OA＝10，AC＝8，∴OC＝＝＝6。
∴CD＝8＋6＝14。
作点B关于MN的对称点B′，连接AB′，则AB′即为PA＋PB的最小值，B′D＝BD＝6，过点B′作AC的垂线，交AC的延长线于点E。
在Rt△AB′E中，∵AE＝AC＋CE＝8＋6＝14，B′E＝CD＝14，∴AB′＝＝＝14。
例6.（2012湖北十堰6分）阅读材料：P（x，0）是x可以看成点P与点A（0，1P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA＋PB的最小值．设点A关于x轴的对称点为A′，则PA=PA′，因此，求PA＋PB的最小值，只需求PA′＋PB的最小值，而点A′、B A′C=3，CB=3（1B的距（2（2）（1，如图所示：设点A关于x轴的对称点为A′，则PA=PA′，∴求PA＋PB的最小值，只需求PA′＋PB的最小值，而点A′、B间的直线段距离最短。
初中几何中线段及差的最大值和最小值练习试题(最全)
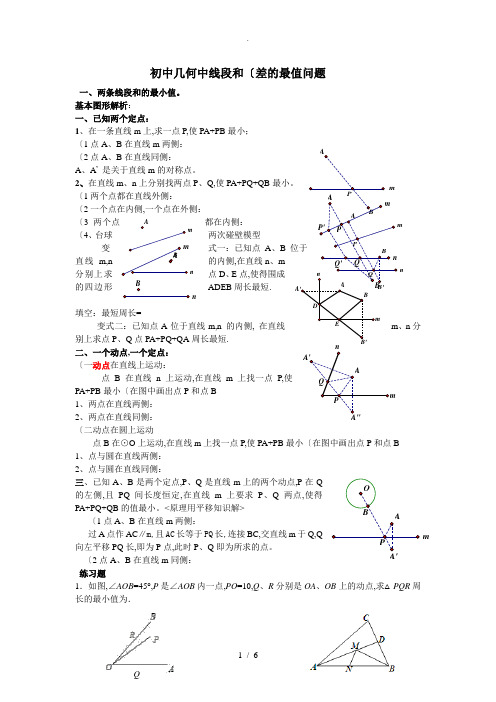
初中几何中线段和〔差的最值问题一、两条线段和的最小值。
基本图形解析：一、已知两个定点：1、在一条直线m 上,求一点P,使PA+PB 最小；〔1点A 、B 在直线m 两侧： 〔2点A 、B 在直线同侧：A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q,使PA+PQ+QB 最小。
〔1两个点都在直线外侧： 〔2一个点在内侧,一个点在外侧： 〔3两个点都在内侧： 〔4、台球两次碰壁模型变式一：已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短. 填空：最短周长=________________ 变式二：已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. 二、一个动点,一个定点： 〔一动点在直线上运动： 点B 在直线n 上运动,在直线m 上找一点P,使PA+PB 最小〔在图中画出点P 和点B 1、两点在直线两侧：2、两点在直线同侧：〔二动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P,使PA+PB 最小〔在图中画出点P 和点B1、点与圆在直线两侧：2、点与圆在直线同侧：三、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
<原理用平移知识解> 〔1点A 、B 在直线m 两侧：过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
〔2点A 、B 在直线m 同侧：练习题1．如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为．P m A B Q P n m A B P'Q' n m A B Q P n m A B B' n m A B P m O A B A'E D m n A B A'B'P Qm n A A"A'2、如图1,在锐角三角形ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值为．3、如图,在锐角三角形ABC中,AB=52,∠BAC=45,BAC的平分线交BC于D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少？4、如图4所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为.5、如图3,在直角梯形ABCD中,∠ABC＝90°,AD∥BC,AD＝4,AB＝5,BC＝6,点P是AB上一个动点,当PC＋PD的和最小时,PB的长为__________．6、如图4,等腰梯形ABCD中,AB=AD=CD=1,∠ABC=60°,P是上底,下底中点EF直线上的一点,则PA+PB的最小值为．7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为．8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm．10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点．则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为．13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为．14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为cm．〔结果不取近似值．15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则P A+PC的最小值是．16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN＝30°,B为AN弧的中点,P是直径MN上一动点,则PA＋PB的最小值为< ><A>2 <B><C>1 <D>2解答题1、如图9,正比例函数y=x的图象与反比例函数y=〔k≠0在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.〔1求反比例函数的解析式；〔2如果B为反比例函数在第一象限图象上的点〔点B与点A不重合,且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2〔x1＜x2是抛物线y=ax2+bx+c与x轴的两个交点B,C的横坐标,且此抛物线过点A〔3,6．〔1求此二次函数的解析式；〔2设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标；〔3在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标．3、如图10,在平面直角坐标系中,点A的坐标为〔1, ,△AOB的面积是.〔1求点B的坐标；〔2求过点A、O、B的抛物线的解析式；〔3在〔2中抛物线的对称轴上是否存在点C,使△AOC的周长最小？若存在,求出点C的坐标；若不存在,请说明理由；4．如图,抛物线y＝错误!x2－错误!x＋3和y轴的交点为A,M为OA的中点,若有一动点P,自M点处出发,沿直线运动到x轴上的某点〔设为点E,再沿直线运动到该抛物线对称轴上的某点〔设为点F,最后又沿直线运动到点A,求使点P运动的总路程最短的点E,点F的坐标,并求出这个最短路程的长．5．如图,已知在平面直角坐标系xOy中,直角梯形OABC的边OA在y轴的正半轴上,OC在x 轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D．将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于点E和F．〔1求经过A、B、C三点的抛物线的解析式；〔2当BE经过〔1中抛物线的顶点时,求CF的长；〔3在抛物线的对称轴上取两点P、Q〔点Q在点P的上方,且PQ＝1,要使四边形BCPQ的周长最小,求出P、Q两点的坐标．6．如图,已知平面直角坐标系,A,B两点的坐标分别为A<2,－3,B<4,－1若C<a,0>,D<a+3,0>是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短．7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.〔1若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标；〔2若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题<运用三角形两边之差小于第三边>基本图形解析：1、在一条直线m上,求一点P,使PA与PB的差最大；yCl x B A〔1点A 、B 在直线m 同侧：解析：延长AB 交直线m 于点P,根据三角形两边之差小于第三边,P ’A —P ’B ＜AB,而PA —PB=AB此时最大,因此点P 为所求的点。
线段和差的最值问题教案课件PPT
2、对于动点Q（1，n），
求PQ+QB的最小值 .
第一步 寻找、构造几何模型
要求PQ+QB的最小值？
经典模型：牛喝水！
第二步 计算——勾股定理
把PQ+QB转化为PQ+QA ！ 当Q运动到E时，PQ+QA最小
AP
3 3 3 2
2 2
第二步 计算——勾股定理
把PQ+QB转化为PQ+QA ！ 当Q运动到E时，PQ+QA最小
B C A E F
D/ D
O
例5、例6中的最小值问题所涉及到的路 径，虽然都是由三条动线段连接而成， 且路径都是“定点→动点→动点→定 点”，但是例5中的量动点间的线段长度 不确定，而例6的两动点间的线段长度为 定值，正是由于这点的不同，使得它们 的解题方法有很大差异，例5是根据两点 之间线段最短找到动点的位置，例6是通 过构造平行四边形先找到所求的其中一 个动点的位置，另一个位置也随之确定。
A D
P O C
B
A D
O
P
B
C
例3，例4中最小值问题，所涉及到的 路径虽然都是有两条动线段连接而成， 且路径都是“定点→动点→定点”， 但是动点运动的路线不同，例3是直线， 例4是曲线，因此它们的解法有很大不 同，例3是根据两点之间线段最短找到 动点的位置，例4是根据垂线段最短找 到所求的两个动点的位置。
CB 3 3 3 2
2 2
小结
E? F!
3.如图，∠AOB=45，角内有一动点 P ，PO=10，在AO，BO上有两动点Q， R，求△PQR周长的最小值。 B D
R
P
O
Q
E
A
线段和差的最值问题解题策略课件
高阶练习题
总结词
挑战综合应用
详细描述
高阶练习题难度较高，需要综合运用线段和 差最值问题的多种解题策略，挑战解题者的 思维深度和广度，培养综合应用能力。
06 问题拓展与思考
相关问题链接
线段和差与面积关系
探讨线段和差与面积的最值问题，如何通过线段和差来求解面积 的最值。
线段和差与其他几何量关系
研究线段和差与周长、体积等其他几何量的最值问题之间的联系。
生产制造中的应用
探讨线段和差最值问题在生产制造、工艺设计和 优化中的实际应用，如何提高生产效率和降低成 本。
THANKS
02 解题策略
代数法
通过代数运算，将问题转化为函数最值问题，利用求导或不 等式性质求解。
代数法是解决线段和差最值问题的基本方法之一。首先，将 问题中的线段长度表示为变量，然后通过代数运算，将问题 转化为一个函数最值问题。接下来，利用求导或不等式性质 ，找到函数的最值点，从而得到线段和差的最值。
几何法
详细描述
解决这类问题需要理解线段的性质和 几何定理，如勾股定理、三角形的三 边关系等。通过这些定理可以推导出 线段和差的最值条件，从而找到解决 问题的关键点。
三角形中的线段和差问题
总结词
三角形中的线段和差问题涉及到三角 形的边长和角度，需要结合三角形的 性质进行求解。
详细描述
解决这类问题需要掌握三角形的边角 关系，如正弦定理、余弦定理等。通 过这些定理可以推导出线段和差与角 度之间的关系，从而找到最值条件。
将参数方程转换为普通方程，便 于计算和比较线段长度。
05 练习题与解析
基础练习题
总结词
掌握基础概念
详细描述
基础练习题主要涉及线段和差最值问题的基本概念和简单应用，适合初学者通过练习理解和掌握基本 解题方法。
一次函数之最短路径问题ppt课件【可编辑全文】
课下任务
3、如图，直线y=-x+7与两坐标轴分别交于AB两点，O为坐标原点，点Q 为直线AB上一个动点
y A
Q ● P●
-1 o●
B x
30
课下任务
3、如图，直线y=-x+7与两坐标轴分别交于AB两点，O为坐标原点，点Q 为直线AB上一个动点
y A
垂线段最短
-1 o● P●
Q ●
B x
31
20
任务拓展 变式五：如图，已知平面直角坐标系中，A、B 两点的坐标分别为A(2,—3）B(4, 1）， 若点P(m,0)和点Q(m+1,0) 是x轴上的两个动点， 则当m= 时， AP+PQ+QB最小．
21
任务拓展
将点B(4,1)向左平移1个单位到B'(3,1),连接AB'交x轴于点P,再将点P向右平移一 个单位即为点Q
在平面直角坐标系中，矩形 半轴上， ， ，
的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正
OACB
D为边OB的中点. (1)若E为边OA上的一个动点，
OA 3 OB 4
y
当△CDE的周长最小时， 求点E的坐标；
B
C
D
O
Ax
E
11
任务演练
如图，作点D关于x轴的对称点 ，
连 由接题意得C与CDx(3轴,4交) D于(0点,2E),即为所求。
2、直线y=kx+b过点A（2，-3）和点B(4,1),则这条直线解析式为：
. 它与
x轴交点(4,坐1)标为
，与y轴交点坐标为
(-4,-1)
( 7 ,0) (0,-7) 自任主务独要立求完：2成
线段的和差(53张PPT)数学
答案
解析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
CD
CB
解析 由题图可知：BD＝BC＋CD，AD＝AC＋BD－CB.
(2)如果CD＝4 cm，BD＝7 cm，B是AC的中点，那么AB的长为_____cm.
答案
解析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
3
解析 如果CD＝4 cm，BD＝7 cm，B是AC的中点，则BC＝BD－CD＝7－4＝3 cm，∴AB＝BC＝3 cm.
∴点O是线段AB的中点；∵AB＝2OB，∴点O是线段AB的中点.故选C.
答案
解析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
4.如图，C是线段AB上的一点，点D是线段BC的中点，若AB＝10，AC＝6，则AD等于( )A.4 B.6 C.7.5 D.8
D
解析 ∵BC＝AB－AC＝4，点D是线段BC的中点，∴CD＝DB＝ BC＝2，∴AD＝AC＋CD＝6＋2＝8.故选D.
中点
知识点2 与中点有关的计算
答案
自我检测2.点C是线段AB的中点，则下列结论不成立的是( )A.AC＝BC B.AC＝ ABC.AB＝2AC D.BC＝ AB
B
答案
返回
【八年级压轴精选】一次函数背景下的存在性问题与最值问题，一题通关！
【八年级压轴精选】一次函数背景下的存在性问题与最值问题，一题通关！自编一题，融合多种存在性问题和最值问题，若有兴趣补充编题的请留言，八下内容，解法要避开相似。
1、求解析式①用尺规作出直线BC和点D，②求直线BC的解析式，③求点D坐标；2、存在性问题(1)全等三角形存在性：①P为平面内一动点，且满足△ABC与△ABP全等，求点P坐标；②P为直线BC上一动点，Q为x轴上一动点，且满足△ABC与△CQP全等，求点P坐标(2)等腰三角形存在性：P为直线BC上一动点，△ABP为等腰三角形，求点P坐标；(3)直角三角形存在性：直线l过原点，且与BC平行，P为直线l上一动点，△ABP为直角三角形，求点P坐标；(4)等腰直角三角形存在性：P为第二象限内上一动点，△ABP为等腰直角三角形，求点P坐标；(5)等边三角形存在性（九年级用）P为第二象限内上一动点，△ABP为等边三角形，求点P坐标；(7)平行四边形存在性：①三定一动：P为平面内一动点，且以A、B、C、P为顶点的四边形为平行四边形，求点P坐标；②两定两动：P为直线AB上一动点，Q为y轴上一动点，且以B、C、P、Q为顶点的四边形为平行四边形，求点P、Q的坐标；(8)菱形存在性：P为直线BC上一动点，Q为平面内一动点，且以A、B、P、Q为顶点的四边形为菱形，求点P、Q的坐标；(9)矩形存在性：直线l过原点，且与BC平行，P为直线l上一动点，Q为平面内一动点，且以A、B、P、Q为顶点的四边形为矩形，求点P、Q的坐标；本讲先来解析部分小题：1、求解析式①用尺规作出直线BC和点D，②求直线BC的解析式，③求点D坐标；（考查内容：尺规作图、图形折叠、待定系数法求解析式，勾股定理或等积法求线段长）①折叠想到重合，全等，可得BC为∠ABO平分线，完成基本作图作已知角的角平分线即可，由D、O重合，可知BD=BO，CD=CO，CD⊥AB，所以在AB上截取BD=BO或CD=CO，或过C作CD⊥AB 于D(此法较繁)②待定系数法求直线解析式，需知两点，已知B（0，6）只要知道点C坐标，算OC长，八年级求线段长两种方法：勾股和等积，如下：再来解析2（7），考查平行四边形存在性，解法参考我之前文章：“平四”存在性问题探究2(7)平行四边形存在性：①三定一动：P为平面内一动点，且以A、B、C、P为顶点的四边形为平行四边形，求点P坐标；②两定两动：P为直线AB上一动点，Q为y轴上一动点，且以B、C、P、Q为顶点的四边形为平行四边形，求点P、Q的坐标；②码字太累，手写版本：上面方法优点：1、不会漏解，2、无需画图(5)等边三角形存在性（九年级用）P为第二象限内上一动点，△ABP为等边三角形，求点P坐标；解法参考我之前文章：一题5解。
一次函数求最值问题PPT讲稿
所以当购买8本A种笔记本、22本B种笔记 本时花费最少，最少为272元。
成功达标：
“5.12”汶川大地震震惊全世界，面对这人类特大灾 害，在党中央国务院的领导下，全国人民万众一心，众 志成城，抗震救灾.现在A、B两市各有赈灾物资500吨 和300吨，急需运往汶川400吨，运往北川400吨，从A、 B两市运往汶川、北川的耗油量如下表：
他们准备购买者两种笔记本共30本． (1) 如果他们计划用300元购买奖品，那么能买这两
种笔记本各多少本? (2) 两位老师根据演讲比赛的设奖情况，决定所购买
的A种笔记本的数量要少于B种笔记本数量的三分之二， 但又不少于B种笔记本数量的三分之一，如果设他们买 A种笔记本n本，买这两种笔记本共花费w元．
（1）写出这天停车场的收费总额P（元）与大车停 放辆次x（辆）之间的函数关系式。 解：（（2）1）这P天=停10车x+场5(1的00收0-费x)总=5额x+最50多00为多少元？ 解：（（3）2）如∵果P这随天x的停增放大的而大增汽大车，不0低≤x于≤1停00车0总辆次的 60%，那么，这天停车场的收费总额最少为多少元？
归纳总结
一、一次函数最值在数学问题中的 确定方法：
1.有ቤተ መጻሕፍቲ ባይዱ定的一次函数关系式； 2.有自变量的取值范围； 3.根据一次函数的增减性确定它的最值。
学习目标：
1.会用一次函数解决数学中的最值问题 2.掌握用一次函数最值在实际问题中的解答思 路和方法
快乐导学：
二、一次函数最值在实际问题中的确定方法
1.某汽车停车场预计五一这天将停放大小汽车1000 辆次，该停车场的收费标准为：大车每辆次10元，小车 每辆次5元。
一次函数求最值问题课件
智慧导入：
人教版初中数学八年级下册第19章《一次函数综合能力题专项训练》课件(共13张PPT)
E
问题展示 思考探究
解:（5）③若点M为等腰△BMP的顶角的顶点 此时MP=MB, ∴点M在线段BP的垂直平分线上
P(1,4) N
M4
B(3,0)
EF
∵点N为PB中点，作NF⊥BE于点F,可求点N坐标为(2,2)
等腰三角形腰和底边不确定要分类讨论，用两圆一线找点并灵活应用所学知识求点坐标
解决数学问题的方法有很多（数形结合、分类讨论、 待定系数法、转化法、等积法、构造法等等）如何从 中找到正确合理的解题方法是关键
问题展示 思考探究
解:(1）
问题展示 思考探究
解:(2） ∴可求点A坐标（0，6），点B的坐标（3，0）
一次函数与几何图形相结合，会利用较简便的等面积法求垂线段的长度
问题展示 思考探究
解:(3）
分两种情况讨论
即-2t<3，
A(0,6)
(-2t,0)
C1
B(3,0)
问题展示 思考探究
解:(3）
数学题千变万化，我们在做题时要注意数学思想和数 学方法的归纳与总结以及做题经验的积累才能达到举 一反三，触类旁通的目的
基础过关：如图，一次函数的图象过点A(3,0),B(0,3)l两点 （1）求直线AB的函数解析式 （2）直线y=-3x-3交x轴于点C，点E为直线AB上的一个动点
①求线段CE的最小值 ②求直线CE的解析式
∵OB=3,
P(1,4)
ቤተ መጻሕፍቲ ባይዱ
M1
B(3,0)
M2
E
问题展示 思考探究
解:（5）②若点P为等腰△BMP的顶角的顶点 此时PM=PB
此时PM3=PB ∵因为等腰三角形底边上三线合一 ∴M3E=BE=2, ∵OE=1, ∴OM3= M3E -OE=2-1=1, ∴点M3坐标为（-1,0)
《线段的和与差》PPT精品教学课件
A
C PD
B
2、如图，点C在线段上，线段AC=6㎝,BC=4 ㎝，M、N分别是线段AC，BC的中点，线段 MN的长度是 5㎝
C
A
B
M
N
3、已知线段AB=AC，请判断点A是否为线段BC的中 点？
B
C
B
A
C
所以点A不一定是线段BC的中点 A
4、如图，B、C为线段AD上的两点，C为 线段AD的中点，AC=5厘米，BD=6厘米， 求线段AB的长.
昨天跟同学一起吃饭，同学说：“他说，感谢你成就了他”。当时也只是报以微笑回应，分手四年了，这四年里始终单身，不敢在谈爱，我怕会时不时冷战，也怕周末约逛街、景点走一走的时候还没到目的地就已经闹的不开心却还要顾及其他人而强颜欢笑……习惯了单身，是真的会上瘾，这句话一点都没错。这几年我去了很多的地方，走了很多城市，看了很多曾经不曾看过的风景。 想回到过去，刚在一起的时候，想告诉曾经的自己，这段感情，不会有结果。也想狠狠的骂自己一顿，清醒点，一个不适合自己的人，不要在坚持，所有的一切都是徒劳，不开心的日子会比快乐多，你该现在放手。 我用青春成就了你，换来了我在也不想触碰爱。
愿每一个菇凉都不在委曲求全，不适合请潇洒的转身。 习惯了周末的时候，坐在电脑前，手机里播放着常听的歌曲，双手在键盘上敲打着心情，当然我不知道这心情是好，还是坏，只是说不上来的感觉，就像飘浮于蓝天中的白云，浮浮沉沉。什么时候，有了这种空洞的心际，什么时候缺少了一份关爱，努力的在过往的岁月里寻觅可以清晰可见的记忆，努力的去寻回原本属于内心欢快的声音，却总是无处可寻。 习惯了一个人单枪匹马的日子，却也习惯了和友人朝夕相伴的情怀，在这喧嚣红尘中，我曾努力的让自己有一天可以远离这人情深海，却又因为情到深处而跌落，我渴望可以惊天动地，轰轰烈烈，却又同时期待，在平淡如水的日子里，和你从青丝走到白丝，我不求有一天，我们双宿双飞，生死与共，只求这一生自身可为真爱而追寻。
专题14 一次函数中的最值问题(解析版)
2 m 2 专题十四 一次函数中的最值问题考点一 坐标系中两点之间的距离最值问题【方法点拨】①点到直线的垂线段最短；②两点之间线段最短。
1.如图，点 P 的坐标为（2，0），点 B 在直线 y ＝x +m 上运动，当线段 PB 最短时，PB 的长度是 2 + 2． 【思路点拨】当线段 PB 最短时，PB 与直线 y ＝x +m 垂直，根据解析式即可求得 C 、D 的坐标，然后根据勾股定理求得 CD ，然后根据三角形相似即可求得 PB 的最短长度．【解析】解：当线段 PB 最短时，PB ⊥CD ，如图所示：由直线 y ＝﹣x +m 可知，直线与坐标轴的交点为 C （﹣m ，0），D （0，m ），∴OC ＝m ，OD ＝m ，∴CD = 2m ，∵点 P 的坐标为（2，0），∴PC ＝2+m ，∵∠PCB ＝∠DCO ，∠PBC ＝∠DOC ＝90°，∴△PBC ∽△DOC ，PB ∴OD = PC PB ，即 = 2+n ， CD n ∴PB = 2 + 2 ． 2 m故答案为： 2 + 2m ． 【点睛】本题考查了垂线段最短的性质，一次函数图象上点的坐标特征，勾股定理的应用，三角形相似2n3 5 2 的判定和性质，熟知垂线段最短是解题的关键．2.如图，点 P 在第一象限，△ABP 是边长为 2 的等边三角形，当点 A 在 x 轴的正半轴上运动时，点 B 随之在 y 轴的正半轴上运动，运动过程中，点 P 到原点的最大距离是 1+ ；若将△ABP 的 PA 边长改为 2 2，另两边长度不变，则点 P 到原点的最大距离变为 1+ ．1【思路点拨】根据当 O 到 AB 的距离最大时，OP 的值最大，得到 O 到 AB 的最大值是2AB ＝1，此时在 斜边的中点 M 上，由勾股定理求出 PM ，即可求出答案；将△ABP 的 PA 边长改为 2 2，另两边长度不变，根据 22+22= (2 2)2，得到∠PBA ＝90°，由勾股定理求出 PM 即可【解析】解：取 AB 的中点 M ，连 OM ，PM ，在 Rt △ABO 中，OM = AB=1，在等边三角形 ABP 中，PM = 3，无论△ABP 如何运动，OM 和 PM 的大小不变，当 OM ，PM 在一直线上时，P 距 O 最远，1 ∵O 到 AB 的最大值是2 AB ＝1， 此时在斜边的中点 M 上，由勾股定理得：PM = 22 — 12 = 3，∴OP ＝1+ 3，将△AOP 的 PA 边长改为 2 2，另两边长度不变，∵22+22= (2 2)2，∴∠PBA ＝90°，由勾股定理得：PM = 12 + 22 = 5，∴此时 OP ＝OM +PM ＝1+5． 故答案为：1+ 3，1+ 5．【点睛】本题主要考查对直角三角形斜边上的中线性质，坐标与图形性质，三角形的三边关系，勾股定理的逆定理等边三角形的性质等知识点的理解和掌握，能根据理解题意求出 PO 的值是解此题的关键．2 ， 考点二 坐标内的线段和（差）最值问题【方法点拨】运用“将军饮马”模型和最小，差最大31. 如图，已知点 A 的坐标为（0，1），点 B 的坐标为（2，﹣2），点 P 在直线 y ＝﹣x 上运动，当|PA ﹣PB | 最大时点 P 的坐标为（）A ．（2，﹣2）B ．（4，﹣4）C ．（ 5 — 5）D ．（5，﹣5）2 【思路点拨】根据轴对称的性质及待定系数法可求得答案．【解析】解：作 A 关于直线 y ＝﹣x 对称点 C ，易得 C 的坐标为（﹣1，0）；连接 BC ，可得直线 BC 的方程为 y =— 4x — 4；5 5求 BC 与直线 y ＝﹣x 的交点，可得交点坐标为（4，﹣4）；此时|PA ﹣PB |＝|PC ﹣PB |＝BC 取得最大值，其他 BCP 不共线的情况，根据三角形三边的关系可得|PC ﹣PB |＜BC ；故选：B ．【点睛】本题考查轴对称的运用，有很强的综合性，难度较大．2. 如图，在平面直角坐标系中，Rt △OAB 的顶点 A 在 x 轴正半轴上，顶点 B 的坐标为（3， 3），点 C 的13 31 3+ 19 22 1坐标为（2，0）点 P 的斜边 OB 上一个动点，则 PC +PA 的最小值为（）A. 2 B ． 2 C ． 2 D ．2 7【思路点拨】作 A 关于 OB 的对称点 D ，连接 CD 交 OB 于 P ，连接 AP ，过 D 作 DN ⊥OA 于 N ，则此时PA +PC 的值最小，求出 AM ，求出 AD ，求出 DN 、CN ，根据勾股定理求出 CD ，即可得出答案．【解析】解：作 A 关于 OB 的对称点 D ，连接 CD 交 OB 于 P ，连接 AP ，过 D 作 DN ⊥OA 于 N ， 则此时 PA +PC 的值最小，∵DP ＝PA ，∴PA +PC ＝PD +PC ＝CD ，∵B （3， 3），∴AB = 3，OA ＝3，∵tan ∠AOB = AB = 3，OA 3∴∠AOB ＝30°，∴OB ＝2AB ＝2 3，由三角形面积公式得：1 ×OA ×AB = 1×OB ×AM ， 2 2∴AM = 3， ∴AD ＝2× 3 =3，∵∠AMB ＝90°，∠B ＝60°，∴∠BAM ＝30°，∵∠BAO ＝90°，∴∠OAM ＝60°，∵DN ⊥OA ，∴∠NDA ＝30°，31 2 3 ∴AN = 1AD = 3，由勾股定理得：DN =3 3， 22 21 ∵C （2，0）， ∴CN ＝3— 1 — 3=1， 2 2在 Rt △DNC 中，由勾股定理得：DC = 31 2 ，即 PA +PC 的最小值是．故选：B ．【点睛】本题考查了三角形的内角和定理，轴对称﹣最短路线问题，勾股定理，含 30 度角的直角三角形性质的应用，关键是求出 P 点的位置，题目比较好，难度适中．3. 如图所示的平面直角坐标系中，点 A 的坐标是（﹣4，4）、点 B 的坐标是（2，5），在 x 轴上有一动点 P ，要使 PA +PB 的距离最短，则点 P 的坐标是 ( — 4 ，O) ．【思路点拨】先作出点 A 关于 x 轴的对称点 A 1，再连接 A 1B ，求出直线 A 1B 的函数解析式，再把 y ＝0 代入即可得．【解析】解：作点 A 关于 x 轴的对称点 A 1（﹣4，﹣4），连接 A 1B 交 x 轴于 P ，12 + ( 323 )2 =∵B的坐标是（2，5），3．3∴直线A1B 的函数解析式为y＝1.5x+2，把P 点的坐标（n，0）代入解析式可得n=—4∴点P 的坐标是( —4 ，O)．【点睛】此题主要考查轴对称﹣﹣最短路线问题，综合运用了一次函数的知识．4.如图所示，四边形OABC 为正方形，边长为6，点A、C 分别在x 轴，y 轴的正半轴上，点D 在OA 上，且D点的坐标为（2，0），P是OB上的一个动点，试求PD+PA和的最小值是21O．【思路点拨】作出D关于OB的对称点D′，则D′的坐标是（0，2）．则PD+PA的最小值就是AD′的长，利用勾股定理即可求解．【解析】解：作出D关于OB的对称点D′，则D′的坐标是（0，2）．则PD+PA的最小值就是AD′的长．则OD′＝2，因而AD′=O Dะ2+O A2=4+36=21O．则PD+PA 和的最小值是21O．故答案是：2 1O．22【点睛】本题考查了正方形的性质，以及最短路线问题，正确作出 P 的位置是关键．5. 如图，一次函数 y = 1x +2 的图象分别与 x 轴、y 轴交于点 A 、B ，以线段 AB 为边在第二象限内作等腰 Rt △ABC ，∠BAC ＝90°．（ 可能 用到 的 公式 ： 若 A （ x 1 ， y 1 ）， Bx 2 ， y 2 ）， ①AB 中 点坐 标为 （x 1+x 2 ， y 1+y 2 ）； 2 2②AB = (x 1 — x 2)2 + (y 1 — y 2)2）（1） 求线段 AB 的长；（2） 过 B 、C 两点的直线对应的函数表达式．（3） 点 D 是 BC 中点，在直线 AB 上是否存在一点 P ，使得 PC +PD 有最小值？若存在，则求出此最小值；若不存在，则说明理由．【思路点拨】（1）求出一次函数图象与 x 轴交点坐标，再利用勾股定理求出 AB 的长即可；（2） 过 C 作 CE 垂直于 x 轴，可得出三角形 ACE 与三角形 AOB 全等，进而确定出 C 坐标，利用待定系数法求出直线 BC 解析式即可；（3） 根据中点坐标公式，可得 D 点坐标，根据轴对称的性质，可得 D ′点，两点之间线段最短，可得 P点，根据解方程组，可得 E 点坐标，根据中点坐标公式，可得 D ′，根据两点间的距离，可得答案．【解析】解：（1）对于一次函数 y = 1x +2，令 x ＝0，得到 y ＝2，令 y ＝0，得到 x ＝﹣4，即 A （﹣4，0），B （0，2），∴OA ＝4，OB ＝2，则 AB = OA 2 + OB 2 =2 5；（2）过 C 作 CE ⊥x 轴，可得∠ECA +∠CAE ＝90°，3 3 ∵△BAC 为等腰直角三角形，∴AC ＝AB ，且∠BAC ＝90°，∴∠CAE +∠OAB ＝90°，∴∠ECA ＝∠OAB ，在△ECA 和△OAB 中，²ECA = ²OAB ²CEA = ²AOB = 9O° CA = AB∴△ACE ≌△BAO （AAS ），∴CE ＝OA ＝4，AE ＝OB ＝2，即 OE ＝OA +AE ＝6，∴点 C 的坐标为（﹣6，4）．设直线 BC 解析式为 y ＝kx +b ，把 B （0，2）与 C （﹣6，4）代入得： b = 2 ， — 6k + b = 4解得： k =— 1，b = 2 则直线 BC 解析式为 y =— 1x +2；（3） ，作出 D 关于直线 AB 的对称点 D ′，连接 CD ′，交直线 AB 于点 P ，此时 CP +DP 最小，∵点 D 为 BC 的中点，O —6 2+4∴点 D 的坐标为（ 2 ，2 ），即 D （﹣3，3）， ∵直线 AB 解析式为 y = 1x +2，k = 1，2 2∴直线 DD ′的 k ＝﹣2，设直线 DD ′的解析式为 y ＝kx +b ，将 k ＝﹣2，D （﹣3，3）代入，解得 b ＝﹣3，∴直线 DD ′解析式为 y ＝﹣2x ﹣3，( — 6 + 1)2 + (4 + 1)2 2与直线 AB 解析式联立得： 解得： x =— 2， y = 1y =— 2x — 3 y = 1 x + 2 ，即两直线交点 E 坐标为（﹣2，1）．设D ′（x ，y ），由中点坐标公式，得x —3y+3 2=—2， 2 =1， 解得 x ＝﹣1，y ＝﹣1，∴D ′（﹣1，﹣1），则最小值为 CD ′==5 2．【点睛】本题考查了一次函数综合题，解（1）的关键是利用两点间的距离公式；解（2）的关键是利用全等三角形的判定与性质得出 C 点坐标，又利用了待定系数法求函数解析式；解（3）的关键是利用轴对称的性质得出 P 点坐标，又利用了对称点的中点在对称轴上得出 D ′点坐标．6. 在平面直角坐标系上，已知点 A （8，4），AB ⊥y 轴于 B ，AC ⊥x 轴于 C ，直线 y ＝x 交 AB 于 D ．（1） 直接写出 B 、C 、D 三点坐标；（2） 若 E 为 OD 延长线上一动点，记点 E 横坐标为 a ，△BCE 的面积为 S ，求 S 与 a 的关系式；（3） 当 S ＝20 时，过点 E 作 EF ⊥AB 于 F ，G 、H 分别为 AC 、CB 上动点，求 FG +GH 的最小值．【思路点拨】（1）首先证明四边形 ABOC 是矩形，再根据直线 y ＝x 是第一象限的角平分线，可得 OB ＝BD ，延长即可解决问题；（2） 根据 S ＝S △OBE +S △OEC ﹣S △OBC 计算即可解决问题；（3） 首先确定点 E 坐标，如图二中，作点 F 关于直线 AC 的对称点 F ′，作 F ′H ⊥BC 于 H ，交 AC 于G ．此时 FG +GH 的值最小；【解析】解：（1）∵AB ⊥y 轴于 B ，AC ⊥x 轴于 C ，∴∠ABO＝∠ACO＝∠COB＝90°，∴四边形ABOC 是矩形，∵A（8，4），∴AB＝OC＝8，AC＝OB＝4，∴B（0，4），C（8，0），∵直线y＝x 交AB 于D，∴∠BOD＝45°，∴OB＝DB＝4，∴D（4，4）．（2）由题意E（a，a），1 ×4×a+ 1 ×8×a—1 ×4×8＝6a﹣16．∴S＝S OBE+S OEC﹣S OBC=△△△ 2 2 2（3）当S＝20 时，20＝6a﹣16，解得a＝6，∴E（6，6），∵EF⊥AB 于F，∴F（6，4），如图二中，作点F 关于直线AC 的对称点F′，作F′H⊥BC 于H，交AC 于G．此时FG+GH 的值最小．∵∠ABC＝∠F′BH，∠BAC＝∠F′HB，∴△ABC∽△HBF′，AC BC∴=，4 51O ∵AC ＝4，BC = 42 + 82 =4 5，BF ′＝AB +AF ′＝8+2＝10，4∴F ะะ = ，∴F ′H ＝2 5，∴FG +GH 的最小值＝F ′H ＝2 5．【点睛】本题考查一次函数综合题、矩形的判定和性质、三角形的面积、相似三角形的判定和性质、轴对称最短问题等知识，解题的关键是学会利用分割法求三角形的面积，学会利用轴对称解决最短问题， 属于中考压轴题．考点三 坐标系中三角形周长最小问题【方法点拨】通常已知一线段是定值，运用“将军饮马”模型求另外两线段和最小1. 如图，在直角坐标系中，点 A 、B 的坐标分别为（1，4）和（3，0），点 C 是 y 轴上的一个动点，且 A 、B 、C 三点不在同一条直线上，当△ABC 的周长最小时，点 C 的坐标是 （0，3） ．【思路点拨】根据轴对称做最短路线得出 AE ＝B ′E ，进而得出 B ′O ＝C ′O ，即可得出△ABC 的周长最小时 C 点坐标．【解析】解：作 B 点关于 y 轴对称点 B ′点，连接 AB ′，交 y 轴于点 C ′，此时△ABC 的周长最小，∵点 A 、B 的坐标分别为（1，4）和（3，0），∴B ′点坐标为：（﹣3，0），AE ＝4，则 B ′E ＝4，即 B ′E ＝AE ，∵C ′O ∥AE ，∴B ′O ＝C ′O ＝3，∴点 C ′的坐标是（0，3），此时△ABC 的周长最小．故答案为（0，3）．【点睛】此题主要考查了利用轴对称求最短路线以及平行线的性质，根据已知得出C 点位置是解题关键．2.在平面直角坐标系中，矩形OACB 的顶点O 在坐标原点，顶点A、B 分别在x 轴y 轴的正半轴上，OA＝3，OB＝4，D 为OB 的中点，点E 为边OA 上的一个动点．（1）求线段CD 所在直线的解析式；（2）当△CDE 的周长最小时，求此时点E 的坐标；（3）当点E 为OA 中点时，坐标平面内，是否存在点F，使以D、E、C、F 为顶点的四边形是平行四边形？若存在，请直接写出F 点的坐标；若不存在，请说明理由．【思路点拨】（1）先求出C、D 的坐标，再用待定系数法即可求出线段CD 所在直线的解析式；（2）当△CDE 的周长最小时，DE+CE 最小；作点D 关于OA 的对称点D′，连接CD′交OA 于E，DE+CE 最小，证明△OED′∽△AEC，得出比例式求出OE 即可；（3）分三种情况：①CE 为对角线时，作FM⊥x 轴于M；证明△EMF≌△CBD，得出OM＝BC＝3，FM ＝DB＝2，OM＝1.5+3＝4.5，即可得出F 的坐标；②DE 为对角线时，作FN⊥x 轴于N，则F1N∥FM，根据平行线分线段成比例定理得出NE＝ME＝3，NF1＝FM＝2，ON＝1.5，即可得出结果；③DC 为对角线时，作F1Q⊥y 轴于Q，作F2P⊥y 轴于P；同②，即可得出结果．【解析】解：（1）∵四边形OACB是矩形，∴AC＝OB＝4，∠OBC＝90°，332∵D 为 OB 的中点，∴OD ＝BD ＝2，∴C （3，4），D （0，2），设线段 CD 所在直线的解析式为 y ＝kx +b ，代入 C （3，0），D （0，2）得： 3k + b = 4， b = 2解得：k = 2，b ＝2， ∴线段 CD 所在直线的解析式为：y = 2x +2； （2） 当△CDE 的周长最小时，DE +CE 最小；作点 D 关于 OA 的对称点 D ′，连接 CD ′交 OA 于 E ，如图 1 所示：则 D ′（0，﹣2），DE ＝DE ′，∴DE +CE ＝D ′E +CE ═CD ′，∵∠OBC ＝90°，BD ′＝6，∵AC ∥OB ，∴△OED ′∽△AEC ，O EO D ะ2 1 ∴AE = AC = 4 = ， ∴AE ＝2AE ，∵OA ＝3，∴OE ＝1，∴E （1，0）；（3） 存在；分三种情况：①CE 为对角线时，作 FM ⊥x 轴于 M ；如图 2 所示：∵BC ∥OA ，∴∠MEC ＝∠BCE ，∵四边形 DEFC 是平行四边形，∴CD ∥EF ，∴∠FEC ＝∠DCE ，∴∠MEF ＝∠BCD ，在△EMF 和△CBD 中，²FะE = ²DBC = 9O°²ะEF = ²BCD ，EF = CD∴△EMF≌△CBD（AAS），∴OM＝BC＝3，FM＝DB＝2，∴OM＝1.5+3＝4.5，∴F（4.5，2）；②DE 为对角线时，作F1N⊥x 轴于N，则F1N∥FM，如图2 所示：∵EF1＝CD＝EF1，∴NE＝ME＝3，NF1＝FM＝2，∴ON＝1.5，∴F1（﹣1.5，﹣2）；③DC 为对角线时，作F1Q⊥y 轴于Q，作F2P⊥y 轴于P，如图所示：同②得：PF2＝F1Q＝ON＝，1.5，PD＝DQ＝4，∴OP＝6，∴F2（1.5，6）；综上所述：F点的坐标为（4.5，2），或（1.5，6），或（﹣1.5，2）．【点睛】本题是一次函数综合题，考查了矩形的性质、用待定系数法确定一次函数的解析式、相似三角形的判定与性质等知识；本题难度较大，综合性强，特别是（2）、（3）中，需要证明三角形相似或三角形全等才能得出结果．3.如图，在平面直角坐标系中，矩形OACB 的顶点O 在坐标原点，顶点A、B 分别在x 轴、y 轴的正半轴上，OA＝3，OB＝4，D 为边OB 的中点．（1）点D 的坐标为（0，2）；（2）若E 为边OA 上的一个动点，当△CDE 的周长最小时，求点E 的坐标．【思路点拨】由于C、D 是定点，则CD 是定值，如果△CDE 的周长最小，即DE+CE 有最小值．为此，作点D 关于x 轴的对称点D′，当点E 在线段CD′上时，△CDE 的周长最小．【解析】解：（1）∵OB＝4，D为边OB的中点，∴OD＝2，∴D（0，2），故答案为：（0，2）；（2）如图，作点D 关于x 轴的对称点D′，连接CD′与x 轴交于点E，连接DE．若在边OA 上任取点E′与点E 不重合，连接CE′、DE′、D′E′由DE′+CE′＝D′E′+CE′＞CD′＝D′E+CE＝DE+CE，可知△CDE 的周长最小．∵在矩形 OACB 中，OA ＝3，OB ＝4，D 为 OB 的中点，∴BC ＝3，D ′O ＝DO ＝2，D ′B ＝6，∵OE ∥BC ， O E D ะO ∴Rt △D ′OE ∽Rt △D ′BC ，有B C = D ะB ，∴OE ＝1，∴点 E 的坐标为（1，0）．【点睛】此题主要考查轴对称﹣﹣最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是三角形两边之和大于第三边．考点四 坐标系中四边形周长最小问题【方法点拨】已知两线段为定值，通过平移的方法，运用“将军饮马”模型求另外两线段和最小 71. 如图，当四边形 PABN 的周长最小时，a 的值为 ． 4【思路点拨】作 B 关于 x 轴的对称点 C ，连结 CN ，作平行四边形 PNCD ，因为 AB 、PN 为定值 所以 PA +BN 最小即可 因为 BN ＝CN ＝PD 所以只要 AP +PD 最小 作直线 AD 交 x 轴于 Q ，当 P 与 Q 重合时，AP +PD ＝AD 最小．【解析】解：作 B 关于 x 轴的对称点 C ，连结 CN ，作平行四边形 PNCD ，44∵AB 、PN 为定值∴PA +BN 最小即可∵BN ＝CN ＝PD∴只要 AP +PD 最小作直线 AD 交 x 轴于 Q ，当 P 与 Q 重合时，AP +PD ＝AD 最小∵A （1，3）、D （2，﹣1）∴直线 AD 为：y ＝﹣4x +7 当 y ＝0 时，x = 7， 7 ∴Q 为（4，0） ∵P 、Q 重合∴a = 7． 【点睛】本题考查轴对称﹣最短问题，平行四边形的性质、一次函数的应用等知识，解题的关键是学会构建平行四边形，利用对称解决最短问题，属于中考常考题型．2. 在平面直角坐标系中，矩形 OACB 的顶点 O 在坐标原点，顶点 A 、B 分别在 x 轴、y 轴的正半轴上，OA ＝3，OB ＝4，D 为边 OB 的中点．若 E 、F 为边 OA 上的两个动点，且 EF ＝2，当四边形 CDEF 的周长 1 最小时，求点 E 、F 的坐标分别为 （ 3 7 ，0），（ 3，0） ，并在图中画出示意图．【思路点拨】由于 DC 、EF 的长为定值，如果四边形 CDEF 的周长最小，即 DE +FC 有最小值．为此， 作点 D 关于 x 轴的对称点 D '，在 CB 边上截取 CG ＝2，当点 E 在线段 D ′G 上时，四边形 CDEF 的周长最小．【解析】解：如图，作点 D 关于 x 轴的对称点 D '，在 CB 边上截取 CG ＝2，连接 D 'G 与 x 轴交于点 E ， 在 EA 上截取 EF ＝2，∵GC ∥EF ，GC ＝EF ，∴四边形 GEFC 为平行四边形，有 GE ＝CF ． 又∵DC 、EF 的长为定值，∴此时得到的点 E 、F 使四边形 CDEF 的周长最小，∵OE ∥BC ， O E D ะO ∴Rt △D 'OE ∽Rt △D 'BG ，有B G = D ะB ．∴OE = D ะO ·B G = D ะO ·(B C —C G ) = 2×1 = 1 D ะB D ะB 6 3 ∴OF ＝OE +EF = 1 +2= 7．3 317 ∴点 E 的坐标为（ 3 1，0），点 F 的坐标为（ 3 7 ，0）．故答案为：（3，0），（3，0）．【点睛】此题主要考查轴对称﹣﹣最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是三角形两边之和大于第三边．考点五 其它最值问题【方法点拨】根据具体题型求最值 1．若一次函数 y ＝kx +b ，当﹣2≤x ≤6 时，函数值的范围为﹣11≤y ≤9， 则此一次函数的解析式为 y = 5 x — 6 或 y =— 5 x + 4 ．2 2【思路点拨】根据函数自变量的取值范围用待定系数法求函数解析式．【解析】解：∵y 是 x 的一次函数，当﹣2≤x ≤6 时，﹣11≤y ≤9．2 2 2 2 设所求的解析式为 y ＝kx +b ，分两种情况考虑：（1）将 x ＝﹣2，y ＝﹣11 代入得：﹣11＝﹣2k +b ，将 x ＝6，y ＝9 代入得：9＝6k +b ，联立解得：k = 5，b ＝﹣6，则函数的解析式是 y = 5x ﹣6；（2）将 x ＝6，y ＝﹣11 代入得：﹣11＝6k +b ，将 x ＝﹣2，y ＝9 代入得：9＝﹣2k +b ，联立解得：k =— 5，b ＝4，则函数的解析式是 y =— 5x +4． 综上，函数的解析式是 y = 5x ﹣6 或 y =— 5x +4． 2 2 故答案为：y = 5x ﹣6 或 y =— 5x +4 2 2【点睛】本题要注意利用一次函数自变量的取值范围，来列出方程组，求出未知数，写出解析式．2. 如图，在平面直角坐标系中，已知点 M （2，﹣3）、N （6，﹣3），连接 MN ，如果点 P 在直线 y ＝﹣x +1上，且点 P 到直线 MN 的距离不小于 1，那么称点 P 是线段 MN 的“疏远点”．（1） 判断点 A （2，﹣1）是否是线段 MN 的“疏远点”，并说明理由；（2） 若点 P （a ，b ）是线段 MN 的“疏远点”，求 a 的取值范围；（3） 在（2）的前提下，用含 a 的代数式表示△MNP 的面积 S △MNP ，并求 S △MNP 的最小值．【思路点拨】（1）求出 A 到 MN 的距离，再判断即可；（2） 根据“疏远点”的意义求出 b 的范围，再代入求出 a 的范围即可；（3） 根据“疏远点”的意义得出 S MNP = 1 ×4×|﹣a +1﹣（﹣3）|，再去掉绝对值符号即可． △ 2【解析】解：（1）点A（2，﹣1）是线段MN的“疏远点”，并说明理由理由是：∵M（2，﹣3）、N（6，﹣3），A（2，﹣1），∴A 到直线MN 的距离为﹣1﹣（﹣3）＝2＞1，∵点P到直线MN的距离不小于1，那么称点P是线段MN的“疏远点”，∴点A（2，﹣1）是线段MN的“疏远点”；（2）∵点P（a，b）是线段MN的“疏远点”，M（2，﹣3）、N（6，﹣3），∴|b﹣（﹣3）|≥1，∴b≥﹣2 或b≤﹣4，代入y＝﹣x+1 得：﹣a+1≥﹣2 或﹣a+1≤﹣4，解得：a≤3 或a≥5，即 a 的取值范围是a≤3 或a≥5；（3）∵M（2，﹣3）、N（6，﹣3），∴MN＝6﹣2＝4，∴S =1 ×4×|﹣a+1﹣（﹣3）|= — 2a + 8(a＜4)△MNP 2，2a — 8(a＞4)∵a≤3 或a≥5，∴S△MNP的最小值是2．【点睛】本题考查了一次函数图象上点的特征，一次函数的性质等知识点，能根据“疏远点”的意义列出算式是解此题的关键．3.对某一个函数给出如下定义：若存在实数M＞0，对于任意的函数值y，都满足﹣M≤y≤M，则称这个函数是有界函数，在所有满足条件的M 中，其最小值称为这个函数的边界值．例如，图中的函数是有界函数，其边界值是1．（1）函数y＝x+1（﹣4≤x≤2）是不是有界函数？若是有界函数，求其边界值；（2）若函数y＝﹣x+1（a≤x≤b，b＞a）的边界值是2，且这个函数的最大值也是2，求b 的取值范围．(x — O)2 + (O — 1)2【思路点拨】（1）根据有界函数的定义即可得出函数 y ＝x +1（﹣4≤x ≤2）是有界函数，再代入 x ＝﹣4和 x ＝2 即可得出其边界值；（2）根据一次函数的性质可得出函数 y ＝﹣x +1 是单减函数，结合函数的最大值为 2 即可得出 a 的值， 再代入 b 的值结合有界函数的定义以及该函数的边界值即可得出关于 b 的一元一次不等式组，解不等式组即可得出 b 的取值范围；【解析】解：（1）根据有界函数的定义知，函数 y ＝x +1（﹣4≤x ≤2）是有界函数．∵﹣4+1＝﹣3，2+1＝3，∴y ＝x +1（﹣4＜x ≤2）边界值为 3．（2）∵k ＝﹣1＜0，∴函数 y ＝﹣x +1 的图象是 y 随 x 的增大而减小，∴当 x ＝a 时，y ＝﹣a +1＝2，解得：a ＝﹣1；当 x ＝b 时，y ＝﹣b +1，— 2 ≤— b + 1 ≤ 2∴ b ＞a ，a =— 1∴﹣1＜b ≤3；【点睛】本题考查了一次函数的性质、有界函数的定义以及解一元一次不等式组，解题的关键是：（1）根据有界函数的定义判断一个函数是否为有界函数；（2）找出关于 b 的一元一次不等式组．4. 请阅读下述材料，并解答问题例：说明代数式 x 2 + 1 + (x — 3)2 + 4的几何意义，并求它的最小值．解： 在平面直角坐标系中， 已知两点 P 1 （ x 1 ， y 1 ）， P 2 （ x 2 ， y 2 ） 则这两点间的距离公式为：P 1P 2=所以原式= +如图建立直角坐标系，点 P （x ，0）是 x 轴上一点，则 (x — O)2 + (O — 1)2可以看成点 P 与点 A （0，1） (x 1 — x 2)2 + (y 1 — y 2)2(x — 3)2 + (O — 2)2(x — 1)2 + 1 的距离， (x — 3)2 + (O — 2)2可以看成点 P 与点 B （3，2）的距离，所以原代数式的值可以看成线段 PA 与 PB 的长度之和，它的最小值就是 PA +PB 的最小值．设点 A 关于 x 轴的对称点为 A ′，则 PA ＝PA ′， 因此，求 PA +PB 的最小值，只需求 PA ′+PB 的最小值，由两点之间，线段最短可得，PA ′+PB 的最小值为线段 A ′B 的长度．为求 A ′B 我们可以构造直角三角形 A ′CB ，因为 A ′C ＝3，CB ＝3，所以 A ′ B ＝3 2，即原式的最小值为 3 2解答问题：（1）代数式 + (x — 2)2 + 9的值可以看成平面直角坐标系中点 P （x ，0）与点 A （1，1）、点 B （2，3） 的距离之和（填写点 B 的坐标）；（2）代数式 x 2 + 49 + x 2 — 12x + 37的最小值为 10 ．【思路点拨】（1）模仿例题即可解决问题；（2）用转化的思想思考问题即可；【解析】解：（1）由题意可知，点 B 坐标为（2，3）；故答案为（2，3）．（2） x 2 + 49 + x 2 — 12x + 37 = x 2 + 72 + (x — 6)2 + 12，求 x 2 + 49 + x 2 — 12x + 37的最小值，相当于在 x 轴上找一点 P （x ，0），使得 P 到 A （0，7），B （6，1）的距离之和的最小值，设点 A 关于 x 轴的对称点为 A ′，则 PA ＝PA ′，因此，求 PA +PB 的最小值，只需求 PA ′+PB 的最小值， 由两点之间，线段最短可得，PA ′+PB 的最小值为线段 A ′B 的长度．为求 A ′B 我们可以构造直角三角形 A ′CB ，因为 A ′C ＝6，CB ＝8，所以 A ′B ＝10，即原式的最小值为 10．故答案为 10．【点睛】本题考查轴对称﹣最短问题，勾股定理等知识，解题的关键是学会用数形结合的思想解决问题，属于中考常考题型．5.如图1，在平面直角坐标系中，点D 的横坐标为4，直线l1：y＝x+2 经过点D，分别与x、y 轴交于点A、B两点．直线l2：y＝kx+b经过点D及点C（1，0）．（1）求出直线l2 的解析式．（2）在直线l2 上是否存在点E，使△ABE 与△ABO 的面积相等，若存在，求出点E 的坐标，若不存在，请说明理由．（3）如图2，点P为线段AD上一点（不含端点），连接CP，一动点H从点C出发，沿线段CP以每秒2 个单位的速度运动到P，再沿线段PD 以每秒2 2个单位的速度运动到D 后停止，求P 点在整个运动过程的最少用时．【思路点拨】（1）利用C，D 两点坐标代入y＝kx+b，解方程组即可解决问题；（2）存在．如图1 中，作OE∥AB 交CD 于E．由AB∥OE，可得S△ABE＝S△ABO，构建方程组求出点E 坐标即可；（3）如图2 中，作DM∥AC，PH⊥DM 于H，CH′⊥DM 于H′交AD 于P′．由题意P 点在整个运2 2 2动过程的时间t = PC+ PD = 1 PC + PD MDA ＝∠BAO ＝45°，推出PH = P D t = 1PC +PH ）， 2 2（ 2 ），易知∠ 2，推出 2（ 根据此线段最短可知，当点 P 与 P ′，点 H 与 H ′共线时，t 的值最小，最小值= 1CH ′； 【解析】解：（1）由题意 A （﹣2，0），B （0，2），D （4，6），C （1，0），则 有 k + b = O ，4k + b = 6解 得 k = 2 ，b =— 2∴直线 l 2 的解析式为 y ＝2x ﹣2．（ 2 ） 存 在 ． ① 当 点 E 在 线 段 CD 上 时 ， 如 图 1 中 ， 作 OE ∥ AB 交 CD 于E ．∵AB ∥OE ，∴S △ABE ＝S △ABO ，∵直线 OE 的解析式为 y ＝x ，y = x 由 y = 2x — 2 ∴E （2，2）．，解得 x = 2， y = 2②当点 E ′在线段 CD 的延长线上时，由 y = x + 4 ，解得 x = 6 ，∴E ′（6，10）．y = 2x — 2y = 1O 综上所述，满足条件的点 E 坐标为（2，2）或（6，10）．（3）如图 2 中，作 DM ∥AC ，PH ⊥DM 于 H ，CH ′⊥DM 于 H ′交 AD 于 P ′．2 2 2 22由题意 P 点在整个运动过程的时间 t =PC + PD = 1（PC + PD 2 2 2∵A （﹣2，0），B （0，2），∴OA ＝OB ，∴∠MDA ＝∠BAO ＝45°，∴PH =PD ∴t = 1（PC +PH ）， 根据此线段最短可知，当点 P 与 P ′，点 H 与 H ′共线时，t 的值最小，最小值= 1CH ′＝3s∴P 点在整个运动过程的最少用时为 3s ．【点睛】本题考查一次函数综合题、待定系数法、平行线的性质、等高模型、垂线段最短等知识，解题的关键是灵活运用所学知识解决问题，学会用转化的思想思考问题，属于中考压轴题．， ），。
线段和差的最值问题ppt课件
▪ ——求线段和差的最值
.
1.常见的几何最值问题有：线段最值问 题， 线段和差最值问题，周长最值问题、 面积 最值问题等；
2.几何最值问题的基本原理。 ①两点之间线段最短 ②垂线段最短 ③三角形两边之差小于第三边 ④利用函数关系求最值
.
一、两条线段和的最小值
已知：直线m外两点A,B，在直线m上求 一点P，使PA+PB最小；
点A为 y 轴正半轴上的一点，⊙A经过点B和点O,直线BC交⊙A
与点D。
（1）求点D的坐标； （2）过O，C，D三点作抛物线，在抛物线的对称轴上是否存在 一点P,使线段PO与PD之差最大？若存在，请求出这个最大值和
点P的坐标。若不存在，请说明理由。
y
B
A
D
O
Cx
.
当P运动到E时，PA ＋PB最小
当Q运动到F时， QD－QC最大
.
.
明理由.
.
第一步 寻找、构造几何模型
要求四边形MNFE F/
F
的周长最小？
N
E
M
E/
把三条线段转移 到同一条直线上 . 就好了！
第二步 计算——勾股定理
E'F' 3242 5
EF 1222 5
因此四 M边 N的 F 形E 周长的5最 5小 . .
练习：如图,四边形ABCD是正方形,△ABE是
长的最小值为（B ）
B .2
C、
D、
A、
.
如图，在边长为2的菱形ABCD中，∠A＝60°M是AD 边的中点，N是AB边上的一动点，将△AMN沿MN 所在直线翻折得△A′MN，连接A′C，则A′C长度的最 小值是多少？
一次函数图像与性质习题PPT课件
.
1
1、判断下列一次函数图象所在象限
1 y 5 x 1
2 y 2 x 9
7
3 y 0 .5 x 1 .8
4 y 3x 7
.
2
2.根据一次函数图象确定k，b的取值范围
①
②
y
y
③
y
ox
k>o, b=o
④y
o
x
k<0, b<0
⑤y
o
x
0
x
o
x
k>o, b>0
y⑥
象限 象限 象限 象限 象限 象限
性质
y随x的增大而增大
y随x的增大而减小
.本节课所学要记住，完成 4
1.函数y=－2x+1经过 一、二、四 象限
2．一次函数y=2x-1的图象大致是（ B ）
y
y
y
y
Ox
Ａ．
O x
B．
.
Ox
C．
Ox
Ｄ．
5
•
3.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,
2
o
A
x 2
3.一次函数y=x+2的图像不经过第_四___象限
4.点P（a,b）点Q（c,d）是一次函数y=-4x+3图像 上的两个点，且a<c，则b与d的大小关系是_b_>_d_
.
19
1、直线y=2x+1与y=3x-1的交点P的坐标为_(2_,_5_)，点P到x轴的距 离为____5___，点P到y轴的距离为___2___。
（3）设另一条直线与此一次函数图象交于 (1，m)点，且与y轴交点的纵坐标是6，求这条直 线的解析式．
线段及差最值问题
专题一.线段和（差）的最值问题【知识依据】1．线段公理——两点之间，线段最短；2．对称的性质——①关于一条直线对称的两个图形全等；②对称轴是两个对称图形对应点连线的垂直平分线；3．三角形两边之和大于第三边；4．三角形两边之差小于第三边；5、垂直线段最短。
一、已知两个定点：1、在一条直线m 上，求一点P ，使PA+PB 最小；（1）点A 、B 在直线m 两侧：（2）点A 、B 在直线同侧：A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ，使PA+PQ+QB 最小。
（1）两个点都在直线外侧：P m A B m A B m A BPm A B A'n m A B Q P n m A B P'Q'（2）一个点在内侧，一个点在外侧：（3）两个点都在内侧：（4）、台球两次碰壁模型变式一：已知点A 、B 位于直线m,n 的内侧，在直线n 、m 分别上求点D 、E 点，使得围成的四边形ADEB 周长最短.变式二：已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.n m A B QP n m A B B'Q P nm A B B'A' n m A B m n A B E D m n A B A'B'm n A P Q m n A A'二、一个动点，一个定点：（一）动点在直线上运动： 点B 在直线n 上运动，在直线m 上找一点P ，使PA+PB 最小（在图中画出点P 和点B ）1、两点在直线两侧：2、两点在直线同侧：（二）动点在圆上运动：点B 在⊙O 上运动，在直线m 上找一点P ，使PA+PB 最小（在图中画出点P 和点B ）1、点与圆在直线两侧：2、点与圆在直线同侧：m n A P m n A B m n A Pm n A A'B m O A P'P m O B A B' m O A P m O A B A'三、已知A 、B 是两个定点，P 、Q 是直线m 上的两个动点，P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点，使得PA+PQ+QB 的值最小。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。