第九章 钢筋混凝土杆塔承载力计算分解
钢筋混凝土环形截面电杆构件的计算

抗裂验算时截面上混凝土的平均应力
输电杆塔结构及其基础设计
(3)在荷载的短期及长期效应组合下的抗裂验算边缘的混凝土法向应力应 按式(4 - 56a) ~式(4 - 58b)计算。
轴心受拉构件
受弯构件
偏心受拉和偏心受压构件
输电杆塔结构及其基础设计
(4) 阶段允许出现裂缝的预应力混凝土电杆,在荷载的短期效应组合下, 最大裂缝宽度可按式(4 - 59)和式(4 - 60)计算。
8 0.911 0.881 0.854 0.825 0.797 0.756 0.700 0.643 0.590 0.503 0.416 0.329 0.245 0.163 0.093
9 0.908 0.878 0.852 0.823 0.793 0.750 0.。695 0.637 0.585 0.494 0.408 0.320 0.238 0.157 0.087
(5)构件验算截面的开裂弯矩值和轴力值(抗裂强度),按下列公式计算。 1)受弯构件 2)偏心受压构件
3)偏心受拉构件
输电杆塔结构及其基础设计
4.4.4 变形验算
(1)构件在正常使用状态下的挠度,可根据构件的 刚度用结构力学的方法计算。(2) 预应力混凝土 电杆的短期刚度B2,可按下列公式计算。
1) 要求不出现裂缝的构件
一次张拉:0.08 con
输电杆塔结构及其基础设计
(4)由于混凝土收缩、徐变引起的预应力损失 L5可按式(4 - 34)计算为
45 220 p L
L5
fcu
1 15
(4 - 34)
p
Ap
con
L1 L3 L4 A Ap E 1
预应力总损失
钢筋混凝土梁承载力计算公式

钢筋混凝土梁承载力计算公式
钢筋混凝土梁的承载力可以根据以下公式计算:
1. 极限弯矩的计算公式:
M = 0.87 * f_y * A_s * d
其中,M为梁的极限弯矩,f_y为钢筋的屈服强度,A_s为钢筋的截面面积,d为梁的有效高度。
2. 极限抗弯承载力的计算公式:
V = 0.36 * f_ck * b * d
其中,V为梁的极限抗弯承载力,f_ck为混凝土的抗压强度,b为梁的宽度,d为梁的有效高度。
3. 混凝土梁的最大承载力为极限弯矩和极限抗弯承载力中的较小值。
请注意,以上公式仅适用于一般情况下的钢筋混凝土梁,具体的承载力计算还需要考虑其他因素,例如梁的几何形状、支座条件等。
对于特殊情况,需要进行更为详细和复杂的承载力计算。
混凝土结构承载力计算公式修改版知识分享

混凝土结构承载力计算公式修改版2b表5.2.4 受弯构件受压区有效翼缘计算宽度'f注:1,表中b为梁的腹板厚度;2,如肋形梁在跨内设有间距小于纵肋间距的横肋时,可不考虑表中情况3的规定;h且加腋的长度b h不大于3h h时,其翼缘3,加腋的T形、I形和倒L形截面,当受压区加腋的高度h h不小于'f计算宽度可按表中情况3的规定分别增加2b h(T形、I形截面)和b h(倒L形截面);4,独立梁受压区的翼缘板在荷载作用下经验算沿纵肋方向可能产生裂缝时,其计算宽度应取腹板宽度b。
O.10;2,板类受弯构件(不包括悬臂板)的受拉钢筋,当采用强度等级400Mpa、500Mpa的钢筋时,其最小配筋百分率应允许采用0.15和45f t/f y中的较大值;3,偏心受拉构件中的受压钢筋,应按受压构件一侧纵向钢筋考虑;4,受压构件的全部纵向钢筋和一侧纵向钢筋的配筋率以及轴心受拉构件和小偏心受拉构件一侧受拉钢筋的配筋率应按全截面面积计算;5,受弯构件、大偏心受拉构件一侧受拉钢筋的配筋率应按全截面面积扣除受压翼缘面积(b f-b)h f后的截面面积计算;6,当钢筋沿构件截面周边布置时,“一侧纵向钢筋”系指沿受力方向两个对边中的一边布置的纵向钢筋;9.2.9梁中箍筋的配置应符合下列规定:1,按承载力计算不需要箍筋的梁,当截面高度h大于300mm时,应沿梁全长设置构造箍筋;当截面高度h=150~300mm时,可仅在构件端部l0/4范围内设置构造箍筋,l为跨度。
但当在构件中部l/2范围内有集中荷载作用时,则应沿梁全长设置箍筋。
当截面高度h<150mm时,可以不设置箍筋。
2,截面高度大于800mm的梁,箍筋不宜小于8mm;对截面高度不大于800mm的梁,不宜小于6mm。
梁中配有计算需要的纵向受压钢筋时,箍筋直径尚不应小于d/4,d为受压钢筋最大直径。
3,梁中箍筋的最大间距宜符合表9.2.9的规定;当V大于0.7ft bh+0.05Np0时,箍筋的配筋率ρsv [(ρsv=Asv/(bs)]尚不应小于0.24ft/fyv。
钢筋混凝土受拉构件承载力计算课件

若x>0.85ξbh0时,取x=0.85ξbh0代入式(6-8)复核承载 力,当式(6-8)满足时,截面承载力满足要求,否则不满 足要求。
图3–28 输水涵洞截面与A-A截面配筋图
解:
(1)判别偏心受拉构件类型 h0 =h-as = 550-60= 490mm
e0 = M/N = 36.4/338.8 = 0.107m = 107mm <h/2-as = 550/2-60 = 215mm
属于小偏心受拉构件。 (2)计算纵向钢筋As和As′
e0≤h/2-as时,称为小偏心受拉。如图6-4(b)所示。
因此,只要拉力N作用在钢筋As与As′之间,不管偏心距 大小如何,构件破坏时均为全截面受拉,拉力由As与As′共 同承担,构件受拉承载力取决于钢筋的抗拉强度。
可见,轴向拉力是作用在钢筋As和As′之外还是作用在 As和As′之间,是划分大小偏心受拉的界限。
轴心受拉构件破坏时截面的应力状态如图6-2所示。按照承 载力极限状态设计原则及内力平衡条件可得:
K N ≤ fy As
K N ≤ fy As
式中N——轴向拉力设计值;
K——承载力安全系数;
As——全部纵向受拉钢筋截面面积。
受拉钢筋截面面积按式(6-1)计算得:
As = KN/fy
(6-2)
注意:轴心受拉构件的钢筋用量并不完全由强度要求决定,
在许多情况下,裂缝宽度对纵筋用量起决定作用。
案例6-1
某2级水工建筑物,压力水管内半径r=800mm,管 壁厚120mm,采用C25混凝土和HRB335级钢筋,水 管内水压力标准值pk=0.2N/mm2,承载力安全系数K =1.20,试进行配筋计算。
混凝土承载能力计算原理

混凝土承载能力计算原理一、概述混凝土承载能力是指混凝土构件在受到外力作用下所能承受的最大荷载。
混凝土承载能力的计算是建筑工程设计中的重要环节,设计师需要根据工程的实际情况,正确计算出混凝土构件的承载能力,以确保工程的安全性和稳定性。
本文将从混凝土承载力的定义、计算方法和影响因素等方面详细介绍混凝土承载能力的计算原理。
二、混凝土承载力的定义混凝土承载力是指混凝土构件在受到外力作用下所能承受的最大荷载。
混凝土承载力可以分为两种,即极限状态承载力和使用状态承载力。
极限状态承载力是指混凝土构件在超过其承载能力后发生破坏的荷载。
在设计中通常采用的是极限状态承载力。
使用状态承载力是指混凝土构件在正常使用状态下所能承受的最大荷载。
使用状态承载力的计算需要考虑混凝土的变形情况。
三、混凝土承载力的计算方法混凝土承载力的计算方法主要有极限状态设计法和使用状态设计法两种。
1. 极限状态设计法极限状态设计法是指在混凝土构件达到破坏状态之前,荷载和强度的比值达到一个预定值时,即为达到了极限状态。
在设计中,通常采用的是混凝土的极限状态承载力来进行计算。
混凝土构件的极限状态承载力可以通过以下公式进行计算:Rn = φR x Ac x f'c其中,Rn为混凝土构件的极限状态承载力,φR为承载能力系数,Ac 为混凝土构件的横截面积,f'c为混凝土的抗压强度。
2. 使用状态设计法使用状态设计法是指在混凝土构件在正常使用状态下所能承受的最大荷载。
使用状态设计法的计算需要考虑混凝土的变形情况。
混凝土构件的使用状态承载力可以通过以下公式进行计算:Rn = φR x Ac x f'c x η其中,Rn为混凝土构件的使用状态承载力,φR为承载能力系数,Ac 为混凝土构件的横截面积,f'c为混凝土的抗压强度,η为混凝土的变形系数。
四、影响混凝土承载力的因素混凝土承载力的大小受到多种因素的影响,包括混凝土的强度、构件的几何形状、荷载作用的方式等。
钢筋混凝土构件受压构件承载力计算

轴心受压、偏心受压和受弯构件截面极限应力状态
’
构件截面应力随偏心距变化
矩形截面偏心受压
偏
心 受
计算基本假定
重心轴
压 平截面假定
构
计算中和轴
件 不考虑混凝土的抗拉作用
正
实际中和轴
截 混凝土和钢筋的应力应变关系
面
承 受压区混凝土采用等效矩形应力图形。 载
力 x 2 a 时,受压钢筋达到抗压设计强度。
偏
心
受
N与M线性关系
压
N与M曲线关系
构
dN/dM=0
件
纵
向
弯
曲
的
影
响
短柱、长柱和细长柱 e0相同、长细比不同时Nu的变化
长细比增加,附加弯矩增大, 长柱承载力Nu降低。(同轴压)
偏
偏心距增大系数法是一个传统的方法,使
心
用方便,在大多数情况下具有足够的精度,至
受 压
今被各国规范所采用。
构
式(5-11)是由两端铰支、计算长度为l0 、
x) 2
f cbx f y As
KV
Vu
0.7 ftbh0
1.25 f yv
Asv s
h0
fy Asb sins
1.正截面承载力(N、M)
单
KN
Nu
fcbx
f
' y
As
s
As
向 偏
KNe
Nue
fcbx h0
x 2
f
' y
As'
算
推导
适筋、超筋、界限破坏时的截面平均应变图
第九章 钢筋混凝土杆塔承载力计算

197第九章 钢筋混凝土杆塔承载力计算钢筋混凝土杆塔广泛应用在110kV 及以下的输电线路中,电杆的外径受制造、运输、安装等条件限制,使之在承载力和稳定性方面也受到限制。
为了保证杆塔有足够的承载力和稳定性,杆塔总高一般不超过20m 。
因此,在计算杆塔在特定计算情况各计算点的荷载设计值时,一般不需考虑高度的影响。
输电线路大部分为直线杆。
耐张、转角及终端等电杆,通称为耐张型或特种杆。
特种杆应当能够承受断线荷载,以限制事故波及范围。
在导线紧线时,还用特种杆做锚杆并承受较大的安装荷载。
所有特种杆都安装拉线,以承受外部荷载。
第一节 不打拉线直线拔梢单杆不打拉线的直线拔梢单杆(以下简称拔梢单杆) ,具有结构简单、施工方便、运行维护简单、占地面积小、对机耕影响不大等优点,被广泛应用在110kV 及以下的输电线路中。
拔梢单杆的主要缺点是电杆的抗扭性能差,荷载较大时杆顶容易倾斜,故一般用于LGJ-150以下的导线及平地或丘陵地带较为适宜,荷载较大的重冰区不宜采用。
一、正常运行情况的计算拔梢单杆的锥度为1/75,由于不打拉线,故采用深埋式基础,以保证电杆基础的稳定可靠。
这种杆型的主杆属于一端固定,另一端为自由的变截面压弯构件。
电杆正常运行情况的受力,可按纯弯构件计算。
由于杆顶挠度,考虑增加12%~15%的弯矩,如图9-1所示,主杆任意截面x-x 处的弯矩M x ,可按下式计算:11223(1)[(2)]x M m P h P h h P Z =++++ (9-1) 式中 M x —主杆x-x 截面处的弯矩,N.m ; P 1—地线风压荷载设计值,N ; P 2—导线风压荷载设计值,N ;Py —计算截面x-x 以上的杆身风压对x-x 截面处产生的弯矩,N.m ; 图9-1 拔梢单杆 m —由于杆顶挠度和垂直荷载产生的附加弯矩系数,一般取0.12~0.15。
计算截面x-x 以上主杆档风面积为一等腰梯形,杆身风压为22001.4()0.875()1.62150x z s z s D D v h P B h Bv D h μμμμ+==+ (9-2)x-x 截面以上杆身风压合力作用点,距截面x-x 处的高度y 为 002()3x x D D h y D D +=+故计算截面x-x 的杆身(按锥度为1/75)风压弯矩为22200000023(/225)0.8750.875()()150331502(/150)x z s z s x D D D h h h h Py Bv D h Bv D h D D D h μμμμ++=+⨯⨯=+⨯++2200.4375()225z s h Bv h D μμ=⨯+(9-3)为简化计算,杆身风压P 的作用点,可考虑距截面x-x 的高度为h /2,则杆身风压弯矩可变为下式: 2200.4375()150z s z h Py B h v D μμβ=+ (9-4)式中 μz —风压高度变化系数,按地面粗糙度类别和离地面或水面的高度Z (m)用指数公式计算:A 类指近海海面、海岛、海岸、湖岸及沙漠地区,μz =0.794h 0.24,1.00≤μz μz ≤3.12;B 类指田野、乡村、丛林、丘陵以及房屋比较稀疏的乡镇和城市郊区,μz =0. 478Z 0.32,1.00≤μz ≤3.12;C 类指有密集建筑群的城市市区,μz =0.224Z 0.44,0.74≤μz ≤3.12;D 类指有密集建筑群且房屋较高的城市市区,μz =0.08Z 0.60,0.62≤μz ≤3.12。
第九章:钢筋混凝土受弯构件承载力计算
拉区纵向受力钢筋屈服。然后受压区混凝土被压碎,钢筋 和混凝土的强度都得到充分利用。这种破坏在破坏前有明 显的塑性变形和裂缝预兆。破坏不是突然发生的,呈塑性 性质(图9-11b)。
9-11
界限破坏:适筋破坏的特例, 当ρ=ρmax时,当受拉钢筋
少筋破坏和超筋破坏都具有脆性性质,破坏前无明显预兆 。破坏时将造成严重后果,材料的强度得不到充分利用。因此 应避免将受弯件设计成少筋构件和超筋构件,只允许设计成适 筋构件。在后面的讨论中,我们将所讨论的范围限制在适筋构 件范围以内,并且将通过控制配筋率或控制相对受压区高度等 措施使设计成为适筋构件。
梁内箍筋数量由抗剪计算和构造要 求确定。
箍筋分开口和封闭两种形式(如图 a)。箍筋的肢数有单肢、双肢和四肢 (如图b)。
箍筋的形式和肢数
(a) 箍筋的形式;(b)
腰筋 拉筋
板的构造规定
1 截面尺寸
板的承载力应满足荷载、刚度和抗力的要求。
现浇板的厚度h取10mm倍数数,从刚度条件出发,
不需作挠度验算的板的厚度与跨度的最小比值(h/l)应按表
可采用HRB335(Ⅱ级钢筋)。
3 混凝土保护层及钢筋间净距
混凝土保护层的作用是防止钢筋锈蚀、防火
和保证钢筋与混凝土的紧密粘结,故梁、板的受
力钢筋均应有足够的混凝土保护层。
保护层厚度主要取决于构件使用环境、构件
类型、混凝土强度等级、受力钢筋直径等因素的
混凝土保护层应从钢筋的外边缘算起。具体
数值按表3-5采用,但同时也不应小于受力钢筋的
第九章 钢筋混凝土受弯构件承载力计算
9.1基本构造规定
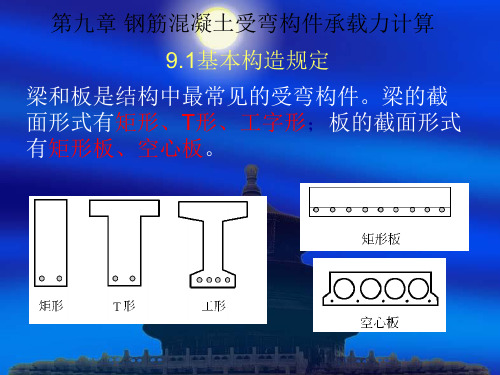
梁和板是结构中最常见的受弯构件。梁的截 面形式有矩形、T形、工字形;板的截面形式 有矩形板、空心板。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
197第九章 钢筋混凝土杆塔承载力计算钢筋混凝土杆塔广泛应用在110kV 及以下的输电线路中,电杆的外径受制造、运输、安装等条件限制,使之在承载力和稳定性方面也受到限制。
为了保证杆塔有足够的承载力和稳定性,杆塔总高一般不超过20m 。
因此,在计算杆塔在特定计算情况各计算点的荷载设计值时,一般不需考虑高度的影响。
输电线路大部分为直线杆。
耐张、转角及终端等电杆,通称为耐张型或特种杆。
特种杆应当能够承受断线荷载,以限制事故波及范围。
在导线紧线时,还用特种杆做锚杆并承受较大的安装荷载。
所有特种杆都安装拉线,以承受外部荷载。
第一节 不打拉线直线拔梢单杆不打拉线的直线拔梢单杆(以下简称拔梢单杆) ,具有结构简单、施工方便、运行维护简单、占地面积小、对机耕影响不大等优点,被广泛应用在110kV 及以下的输电线路中。
拔梢单杆的主要缺点是电杆的抗扭性能差,荷载较大时杆顶容易倾斜,故一般用于LGJ-150以下的导线及平地或丘陵地带较为适宜,荷载较大的重冰区不宜采用。
一、正常运行情况的计算拔梢单杆的锥度为1/75,由于不打拉线,故采用深埋式基础,以保证电杆基础的稳定可靠。
这种杆型的主杆属于一端固定,另一端为自由的变截面压弯构件。
电杆正常运行情况的受力,可按纯弯构件计算。
由于杆顶挠度,考虑增加12%~15%的弯矩,如图9-1所示,主杆任意截面x-x 处的弯矩M x ,可按下式计算:11223(1)[(2)]x M m P h P h h P Z =++++ (9-1) 式中 M x —主杆x-x 截面处的弯矩,N.m ; P 1—地线风压荷载设计值,N ; P 2—导线风压荷载设计值,N ;Py —计算截面x-x 以上的杆身风压对x-x 截面处产生的弯矩,N.m ; 图9-1 拔梢单杆 m —由于杆顶挠度和垂直荷载产生的附加弯矩系数,一般取0.12~0.15。
计算截面x-x 以上主杆档风面积为一等腰梯形,杆身风压为22001.4()0.875()1.62150x z s z s D D v h P B h Bv D h μμμμ+==+ (9-2)x-x 截面以上杆身风压合力作用点,距截面x-x 处的高度y 为 002()3x x D D h y D D +=+故计算截面x-x 的杆身(按锥度为1/75)风压弯矩为22200000023(/225)0.8750.875()()150331502(/150)x z s z s x D D D h h h h Py Bv D h Bv D h D D D h μμμμ++=+⨯⨯=+⨯++2200.4375()225z s h Bv h D μμ=⨯+(9-3)为简化计算,杆身风压P 的作用点,可考虑距截面x-x 的高度为h /2,则杆身风压弯矩可变为下式: 2200.4375()150z s z h Py B h v D μμβ=+ (9-4)式中 μz —风压高度变化系数,按地面粗糙度类别和离地面或水面的高度Z (m)用指数公式计算:A 类指近海海面、海岛、海岸、湖岸及沙漠地区,μz =0.794h 0.24,1.00≤μz μz ≤3.12;B 类指田野、乡村、丛林、丘陵以及房屋比较稀疏的乡镇和城市郊区,μz =0. 478Z 0.32,1.00≤μz ≤3.12;C 类指有密集建筑群的城市市区,μz =0.224Z 0.44,0.74≤μz ≤3.12;D 类指有密集建筑群且房屋较高的城市市区,μz =0.08Z 0.60,0.62≤μz ≤3.12。
198μs —构件的体型系数,环形截面电杆取0.7;B —覆冰时风荷载增大系数,5mm 冰区取1.1,10mm 冰区取1.2。
βz —杆塔风荷载调整系数,对杆塔本身,当杆塔全高不超过60m 时应按照表9-1对全高采用一个系 数,当杆塔全高超过60m 时应按现行国家规范GB50009《建筑结构荷载规范》的规定采用由 下到上逐段增大的数值,但其加权平均值不应小于1.6;对单柱拉线杆塔不应小于1.8;设计基 础时,当杆塔全高不超过60m 时应取1.0,全高超过60m 时,应采用由下到上逐段增大的数值, 但其加权平均值不应小于1.6取1.3;D 0— D x —主杆x-x 处的外径,m ; v —计算风速,m/s ;P —计算截面x-x 以上主杆杆身风压,N ; h —计算截面x-x 以上主杆高度,m 。
电杆在正常运行情况下,各截面除了受弯矩作用以外,还受剪力和主拉应力的作用。
截面x-x 所受剪力V x 为 V x =P+P 1+3P 2 (9-5) 式中符号意义同前。
构件截面x-x 处的最大主拉应力为: 1.2x x x V tD σ= (9-6)式中V x 和D x 分别为计算截面x-x 的剪力和外径。
在实际计算杆身弯矩时,一般应分别计算主杆的A 点、B点和C 点的弯矩,还应计算主杆分段和杆内抽钢筋处的弯矩。
以便选配钢筋和杆段。
二、断导线情况的计算由于电杆不打拉线,所以电杆的长细比很大,在断线张力T 的作用下,将使杆顶发生很大的位移,致使一侧地线拉紧,另一侧地线放松,从而产生地线支持力ΔT ,图9-2所示为断线情况电杆的受力图。
这时对电杆截面x-x 处产生的弯矩,除顺线方向的荷载(ΔT 和T )引起的弯矩M zx 以外,还有不平衡垂直荷载引起的弯矩M qx ,故截面x-x 的总弯矩为x M = (9-7) 当计算主杆强度时,应按最不利情况考虑。
取断线发生在上导线或下导线,且地线有最小支持力∆T min 或最大支持力∆T max 时,取其中弯矩较大者。
如图9-2所示的荷载及几何尺寸,对电杆任意截面产生的弯矩为x M = (9-8) 图9-2 拔梢单杆断线情况 当计算下横担以上主杆各截面强度时,应取断线发生在下导线左边相,且取地线有最大支持力∆T max时,这时,主杆A 点的最大弯矩为A M = (9-9)式中 M x —任意截面x-x 处的总弯矩,N.m ; T —断线张力,N ;ΔT min —地线最小支持力,N ;199G 1—地线重量设计值,N ;G 2’—断线相导线重量设计值,N 。
G 2—未断线相导线重量设计值,N ;断导线时电杆还受扭矩M n 和剪力V 的作用,可分别按下式计算:扭矩 断上导线时 M n =Tb 断下导线时 M n =Ta (9-10) 剪力 断线点以上截面 V=ΔT max 断线点以下截面 V=T-ΔT min (9-11)求得电杆截面的扭矩和剪力后,可按前章所述,校验主拉应力和计算螺旋钢筋规格。
三、电杆配筋及强度验算当已知作用在电杆的弯矩后,即可按前述的式(8-53)求出电杆所需配筋和设计弯矩。
第二节 拔梢门型直线杆为了增加电杆横线路方向的强度,拔梢门型直线杆一般装有钢筋混凝土叉梁或角钢叉梁,不打拉线,采用深埋式基础,导线横担采用平面桁架横担,杆型如图9-3所示。
这种杆型占地面积较少,有较大的承载能力,断边导线时,导线横担起杠杆作用,使两根主杆只承受反力而没有扭矩,这就克服了拔梢单杆抗扭性能差的弱点,故在110kV 线路普遍采用。
一、正常运行情况主杆受力计算带叉梁的双杆,其结构属于超静定体系。
电杆在土中的嵌固情况,电杆的刚度、节点构造等都影响受力分配,因此,要十分准确地计算电杆受力是困难的,目前工程上采用下述的近似计算方法。
假定地面以下1/3埋深处为电杆的嵌固点。
在水平荷载作用下,从叉梁的下节点3到嵌固点4之间的一段主杆,存在一个由正弯矩过渡到负弯矩的反弯点,反弯点的弯矩等于零,称为零力矩点,该点只承受轴向力和剪力,可视为一个铰接点。
只要确定了零力矩点的位置,则零力矩点以上及以下的主杆均成为静定结构,这时可用图9-4所示的受力计算图形、用静定方法计算。
图9-3 拔梢门型直线杆 图9-4 拔梢门型电杆受力计算图形 图9-5 带叉梁门型杆弯矩图形 对等径电杆,零力矩点的位置在点3、4的中央(0-0处),即图9-3中的h 5/2处。
对拔梢杆可认为零力矩点距点3、4的距离h 3和h 4分别与主杆点3、4的断面系数W 3和W 4成正比。
即 3344h W h W =,333434h W h h W W =++3353343434()W W h h h h W W W W =+=++ 对环形截面的断面系数可按下式计算 44()32D d W Dπ-= (9-12)式中D 和d 分别为环形截面的外径和内径,mm 。
200零力矩点的位置确定之后,即可按图9-4,用下式求零力矩点处的水平反力R P 和垂直反力R V[]121123222P R P P P P ==++∑ (9-13) []1123212312()3()2V R PZ P h h h h P h h h b=+++++++ (9-14) 式中 P 和PZ 为零力矩点以上杆身风压及其对零力矩点的弯矩。
考虑两杆受力的不均匀性,主杆各点弯矩按下式计算:M 1=0.55(2P 1h+2P 1Z 1) (9-15) M 2=0.55[2P 1(h+h 1)+3P 2h 1+ 2P 2Z 2] (9-16) M 3=1.05R P h 3 (9-17) M 4=1.05(R P h 4+P 4Z 4) (9-18) 式中 P 1Z 1及P 2Z 2—分别为点1、2以上杆身风压对该点的弯矩(N.m ); P 4Z 4—为h 4处杆身风压对嵌固点4的弯矩(N.m );0.55、1.05—为主杆外弯矩分配系数。
弯矩图形如图9-5所示,从图中看出:由于叉梁的存在,显著地减少了主杆的弯矩。
二、断导线情况主杆受力计算对门型直线双杆,在正常运行情况及断线情况下主杆的受力分配如表9-2所示。
表9-2所列双杆直线杆主柱的受力分配是由理论和实验研究得出的。
对无地线直线双杆,当边导线断线时,离断线相近的B 柱,几乎承受全部断线相导线张力,而远离断线相的A 柱,则几乎不承受断线相导线张力。
因此,B 柱的分配系数m B =1,A 柱的分配系数m A =0。
如果两主柱为刚性结构,如双柱自立式铁塔,顺线路方向有拉线的直线双杆,则以横担和电杆的接触点为支点按简支梁求支点反力。
由各力对支点B 的力矩和为零,即Ta-R A b =0,得R A =Ta /b=m A T ,m A =a /b ;由各力对支点A 的力矩和为零,即T (a+b )-R B b =0,得R B =T (a+b )/b=m B T ,m B =(a+b )/b 。
对于有地线无顺线路方向拉线的钢筋混凝土直线双杆,顺线路方向的刚度较小,地线只能起一部分支201持作用,故分配系数应乘以折减系数0.85,即m A =0.85a /b ,m B =0.85(a+b )/b 。
