杆塔耐雷水平计算办法

110kv耐雷水平

110kv耐雷水平110kv耐雷水平是指110kv线路在遭受雷击时能够承受的雷电过电压水平。

耐雷水平是评估线路防雷保护能力的重要指标之一，对于保障电力系统的安全稳定运行具有重要意义。

本文将从以下几个方面详细介绍110kv耐雷水平的含义、影响因素、计算方法和提高措施。

一、110kv耐雷水平的含义110kv耐雷水平是指110kv线路在遭受雷击时，能够承受的雷电过电压水平。

耐雷水平的高低直接影响到线路的防雷保护效果。

当线路遭受雷击时，雷电过电压会超过线路的绝缘水平，导致线路跳闸或设备损坏等后果，严重时甚至会影响到电力系统的稳定运行。

因此，提高110kv线路的耐雷水平对于保障电力系统的安全稳定运行具有重要意义。

二、影响110kv耐雷水平的因素影响110kv耐雷水平的因素有很多，主要包括以下几个方面：1．雷电活动的强度和频度：雷电活动的强度和频度是影响线路耐雷水平的重要因素。

一般来说，雷电活动强烈的地区，线路的耐雷水平相对较低。

2．线路绝缘水平：线路绝缘水平是决定线路耐雷水平的关键因素。

绝缘水平低的线路容易发生闪络，导致线路跳闸或设备损坏。

3．杆塔高度和地形条件：杆塔高度和地形条件也会对线路的耐雷水平产生影响。

高杆塔和复杂地形条件的线路更容易遭受雷击，因此其耐雷水平相对较低。

4．防雷保护措施：防雷保护措施的采取和效果也会对线路的耐雷水平产生影响。

例如，安装避雷器、架设耦合地线等措施可以提高线路的耐雷水平。

三、110kv耐雷水平的计算方法110kv耐雷水平的计算方法主要包括以下几种：1．统计法：根据多年的雷电活动情况和线路跳闸记录，统计出线路的耐雷水平。

这种方法简单易行，但准确度相对较低。

2．模拟法：通过模拟雷电过电压对线路的影响，计算出线路的耐雷水平。

这种方法需要建立模型并进行大量计算，但可以得到较为准确的结果。

3．工程法：根据经验公式和相关参数，计算出线路的耐雷水平。

这种方法在实际工程中应用较为广泛，但准确度受到参数选择的影响。

杆塔耐雷水平计算办法

精心整理
杆塔耐雷水平计算方法
一、反击耐雷水平按式（1）计算
()
110%
501av gv
t a SU
h K h L k h R k U I ⎪⎪⎫ ⎛-+⎪⎪⎫ ⎛-+-=
ββ式（1）式（1av h h f
gv
h h f a h t
h ——杆塔高度，m
K ——导线与地线间的几何耦合系数
几种典型线路的几何耦合系数0K 见表1
表1典型线路的几何耦合系数0K
t L t L '
t L 表β表k ——电晕下的耦合系数，01K k k =，其中1k 为雷击塔顶时的电晕校正系数，取
值如表4 表4电晕校正系数
R
SU
U
50
%
式（5）
例：忻侯Ⅰ线108＃塔型如下图，杆塔接地电阻为10Ω，导线弧垂6.6米，地线弧垂4.5米
（1）避雷线平均高度：
（2）导线平均高度：(这里计算与上述表达式不一致)
（3）双避雷线对外侧导线的几何耦合系数：
（4）电晕下的耦合系数：
（5
（6
（7
＝
（8。

超(特)高压输电线路耐雷性能计算方法综述

超(特)高压输电线路耐雷性能计算方法综述杜颖【摘要】针对超(特)高压输电线路的反击耐雷性能、绕击耐雷性能特点,比较分析了采用规程法、行波法、蒙特卡洛法、故障树法、电磁暂态程序(electro-magnetic transient program, EMTP)法来计算反击耐雷水平的具体过程、优缺点,以及采用规程法、电气几何模型法、改进电气几何模型法、输电线路雷电绕击的先导发展模型法、输电线路绕击概率模型法来计算绕击耐雷水平的具体过程、优缺点,并提出今后超(特)高压输电线路耐雷性能的研究工作应放在雷击线路的传播过程和机理上,寻找更合理的计算模型和方法.【期刊名称】《广东电力》【年(卷),期】2010(023)009【总页数】6页(P15-20)【关键词】超(特)高压输电线路;反击耐雷水平;绕击耐雷水平【作者】杜颖【作者单位】广东省电力设计研究院,广东,广州,510663【正文语种】中文【中图分类】TM863超(特)高压输电线路结构尺寸大,线路及杆塔高度大幅度地提高。

受高等级线路运行电压等因素影响,输电线路的引雷能力增大,导致输电线路被雷电击中的概率大大提高,所以,对超(特)高压输电线路进行防雷研究是超(特)高压输电线路设计的一项重要工作。

由于超(特)高压输电线路结构尺寸增加,线路、杆塔波阻抗分布、计算及雷电暂态响应特性更为复杂,为了更进一步研究超(特)高压输电线路的反击耐雷性能,必须重新建立符合超(特)高压输电线路特点的反击耐雷性能研究模型。

对于超(特)高压输电线路,其绝缘水平较高,绕击成为超(特)高压输电线路跳闸的主要原因,降低输电线路绕击跳闸率是降低超(特)高压输电线路跳闸率最有利的途径之一。

因此,建立更符合雷电发展规律的超(特)高压输电线路绕击研究模型是超(特)高压输电线路防雷研究的迫切需求。

1 超(特)高压输电线路反击耐雷性能计算方法1.1 规程法文献[1]规定:绝缘子串的耐受电压由导线感应电压和悬挂点塔身电压叠加而成。

线路直击雷过电压与耐雷水平

有避雷线时线路应有的耐雷水平
额定电压(kV)
35
110
220
330
500
耐雷水平I1(kA) 雷电流超过I1的概率(%)
20～30 40～75 75～110 100～150 125～175
59～46 35～14 14～6
7～2
3.8～1
2、雷击避雷线档距中央：
根据模拟试验和实际运行经验，雷击避雷线档距中由央于的半概径率较较小小的(避10雷%线)。的强烈电晕衰减作用，使过电压波传播到杆塔时，已不足以使绝缘子串闪络标，准通规常定只，需只要要考按虑经雷验击公避式雷S线＝对0.导01线2l+的1确反定击档问距题。中央导、地线间的空气间距S，一般不会发生避雷线对导线的反击故障。
Riit
Lt
dit dt
(Rii Lt
di ) dt
Lt为杆塔等值电感，雷电流波前陡度di/dt=I/T1，塔顶电位幅值为：
U top Ri I Lti / T1 I Ri Lt / T1
注：不同类型杆塔的等值电感不同，见表7-1；不同电压等级及避雷线数目的β也不同，见表7-2
谢谢观看！ 2020
(2) 导线电位和绝缘子串上的电压：
雷击塔顶时，与塔顶相连的避雷线也有相同的电位 utop。负极性的雷电波沿杆塔及避雷线传播时，由于避雷线与导线之间的电磁耦合作用，在导线上将产生耦合电压kutop，其极性与雷电流极性相同。
另一方面，由塔顶向雷云发展的正极性雷电波，引起空间电磁场的迅速变化，又使导线上出现与雷电流极性相反的正的感应过电压 U g ahc (1 k) 。
提高雷击塔顶时耐雷水平的措施：
（1）一般高度杆塔（小于40m），冲击接地电阻上压降是塔顶电位的主要成分，因此降低接地电阻可以有效地减小塔顶电位和提高耐雷水平；（2）增大耦合系数k；（3）加强线路绝缘（提高U50%）。

杆塔耐雷水平计算方法

杆塔耐雷水平计算方法一、反击耐雷水平按式（1）计算()6.216.210%501av av gvt t a SUh K h h L k h h R k U I ⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-+-=ββ 式（1）式（1）中：av h ——导线的平均高度，ma av f h h ⨯-=321 式（2）式（2）中：1h ——导线挂线点高度 a f ——导线弧垂gvh ——地线的平均高度，mg gv f h h ⨯-=322 式（3）式（3）中：2h ——地线挂线点高度 g f ——地线弧垂a h ——导线横担对地高度，m th ——杆塔高度，mK ——导线与地线间的几何耦合系数几种典型线路的几何耦合系数0K 见表1表1 典型线路的几何耦合系数0Kt L ——杆塔电感，H μ't t L h =t L 式（4）式（4）中 t h ——杆塔高度，m't L ——单位杆塔电感，m /H μ，取值见表2表2 典型杆塔的波阻抗和电感β——杆塔分流系数，取值见表3表3 杆塔分流系数k ——电晕下的耦合系数，01K k k =，其中1k 为雷击塔顶时的电晕校正系数，取值如表4表4 电晕校正系数SU R ——杆塔接地电阻，实测后应考虑1.4～1.8倍的季节系数%50U ——50％放电冲击电压二、绕击耐雷水平Z%502U I =式（5）式（5）Z ——波阻抗，一般取100Ω。

例：忻侯Ⅰ线108＃塔型如下图，杆塔接地电阻为10Ω，导线弧垂6.6米，地线弧垂4.5米（1）避雷线平均高度：()m h b 325.4325.36=⨯-=（2）导线平均高度：(这里计算与上述表达式不一致)()m h d 1.246.6325.433=⨯--=（3）双避雷线对外侧导线的几何耦合系数：184.01022.2164ln 10005.4322ln36.129.736.121.56ln7.19.77.11.56ln 22222222220=++⨯+++++=K（4）电晕下的耦合系数：k ＝k 1k 0＝1.28×0.2＝0.256（5）杆塔电感：L t ＝36.5×0.5＝18.25(μH)（6）雷击杆塔时分流系数：β＝0.88（7）雷击杆塔时耐雷水平(当用FXBW4-500/160时)：()6.21.242.01.243216.225.1888.0256.05.3633788.0256.0121001⨯⎪⎭⎫⎝⎛⨯-+⨯⨯⎪⎭⎫⎝⎛-+⨯⨯-=I＝136.507(kA)（8）雷绕击于导线时的耐雷水平：)(2110021002kA I ==经计算可看出，108＃杆塔（ZB2-33）雷击塔顶时的耐雷水平为136.507kA ，绕击耐雷水平为21kA 。

雷击杆塔顶时耐雷水平的计算

雷击杆塔顶时耐雷水平的计算I1：雷击杆塔顶时的耐雷水平；kAU50％：绝缘子串50％冲击放电电压；kVk：导线与地线间的耦合系数；k＝k1×k0k1：电晕校正系数；查表2-7-9k0：导线和地线间的几何耦合系数；查表2-7-8β：杆塔分流系数；查表2-7-4R su：杆塔冲击接地电阻；Ωh a：横担对地高度；mh t：杆塔高度；mL t：杆塔电感；μHh gv：地线的平均高度；mh av：导线的平均高度；mP1:超过雷电流幅值I1的概率；logP1=-I1/88I2：雷绕击导线时的耐雷水平；kA；I2=U50％/100P2:超过雷电流幅值I2的概率；logP2=-I2/88b：两根地线之间的距离；mN：每年每100km线路的雷击次数；N=0.28(b+4h av)η：建弧率；η=(4.5E0.75-14)×10-2g:击杆率；查表2-7-2θ：杆塔上地线对外侧导线的保护角；°Pθ：平原线路绕击率；lgPθ=θ×(h)0.5/86-3.9Pθ'：山区线路绕击率；lgPθ'=θ×(h)0.5/86-3.35h：地线在杆塔上的悬挂点高度；mP3：雷击档距中央的避雷线时，雷电流超过耐雷水平的概率。

由于发生这种闪络的情况极少，其值一般可U（kV）n k1k0kβR su h a h t L t h1f1h gv h2f2 12022 1.250.2370.296250.881027381924818.67381312016 1.250.2370.296250.881227381924818.67381312016 1.250.2370.296250.881427381924818.67381312016 1.250.2370.296250.881627381924818.67381312016 1.250.2370.296250.881827381924818.67381312016 1.250.2370.296250.882027381924818.673813 12016 1.250.2370.296250.882227381924818.673813 12016 1.250.2370.296250.882427381924818.673813 12016 1.250.2370.296250.882627381924818.673813 12016 1.250.2370.296250.882827381924818.673813 12016 1.250.2370.296250.883027381924818.673813 12016 1.250.2370.296250.883227381924818.673813 12016 1.250.2370.296250.883427381924818.673813的情况极少，其值一般可不予计算。

线路直击雷过电压及耐雷水平讲义

输电线路的直击雷过电压以及防护一、直击雷过电压
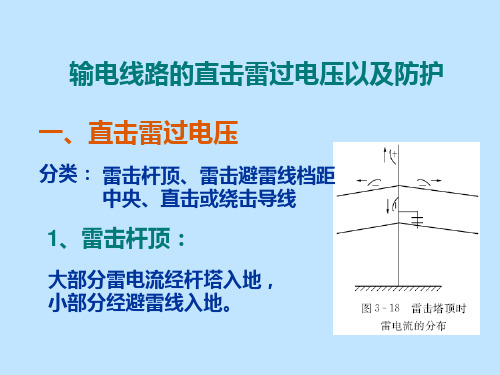
分类：雷击杆顶、雷击避雷线档距中央、直击或绕击导线
1、雷击杆顶：
大部分雷电流经杆塔入地，小部分经避雷线入地。
(1) 塔顶电位：设雷电流i为斜角波头，波头T1，幅值I，陡度a，流过杆塔的电流为 it i at （β为分流系数）则塔顶电位为
(2) 导线电位和绝缘子串上的电压：雷击塔顶时，与塔顶相连的避雷线也有相同的电位 utop。负极性的雷电波沿杆塔及避雷线传播时，由于避雷线与导线之间的电磁耦合作用，在导线上将产生耦合电压kutop，其极性与雷电流极性相同。另一方面，由塔顶向雷云发展的正极性雷电波，引起空间电磁场的迅速变化，又使导线上出现与雷电 ahc (1 k ) 。流极性相反的正的感应过电压 U g 于是，导线电位就等于避雷线电位产生的耦合电压与雷电流引起的感应过电压之和： uc kutop ahc (1 k )
u top dit di Ri it Lt ( Ri i Lt ) dt dt
Lt为杆塔等值电感，雷电流波前陡度di/dt=I/T1，塔顶电位幅值为：
U top Ri I Lt i / T1 I Ri Lt / T1
注：不同类型杆塔的等值电感不同，见表7-1；不同电压等级及避雷线数目的β也不同，见表7-2
提高雷击塔顶时耐雷水平的措施：（1）一般高度杆塔（小于40m），冲击接地电阻上压降是塔顶电位的主要成分，因此降低接地电阻可以有效地减小塔顶电位和提高耐雷水平；（2）增大耦合系数k；（3）加强线路绝缘（提高U50%）。为了减少反击，必须提高线路的耐雷水平。标准中规定，雷击塔顶时应有的耐雷水平I1为：
有避雷线时线路应有的耐雷水平

线路直击雷过电压及耐雷水平资料

中央导、地线间的空气间距S，一般不会发生避雷线对导线的反击故障。
3、直击或绕击：
装设避雷线的线路，仍有雷绕过避雷线击于导线的可能
发生绕击的概率称为绕击率Ka Ka与避雷线保护角α、杆塔高度h及线路通过地区的地形地貌有关。山区线路因地面附近电场受山坡地形影响，绕击率约为平原线路的3倍。虽然绕击率很小，但一旦发生绕击，产生的雷过电压很高，即使是绝缘水平很高的超高压线路也往往难免闪络。 (1) 雷击点电压幅值：研究表明，雷电流通道具有分布参数特征，其波阻抗用Z0表示。
令 U Lj U 50% ，即可求得雷击塔顶反击时的耐雷水平I1，即影响I1的因素：
I1
U 50% Lt hc (1 k ) Ri T T 1 1
杆塔分流系数β，杆塔等值电感Lt，杆塔冲击接地电阻Ri，耦合系数k和绝缘子串的U50%冲击放电电压。
此即国标中用来估算绕击时过电压的近似公式
(2) 绕击时的耐雷水平：令 U A U 50% ，可得绕击时的耐雷水平I2：I 2
U 50%
100
例如：采用13片XP-70型绝缘子的220kV线路绝缘子串的U50%≈1200kV，可求得其I2＝12 kA ，大于I2的雷电流出现概率P1≈73.1%。同理110、500kV线路绕击时耐雷水平分别只有7、27.4kA，雷电流幅值超过7、27.4kA的概率分别为83.3%、48.8%！
反击：本来是地（低）电位的物体，由于某种原因导致其电位（绝对值）突然升高，当其与周围导体的电压超过了该间隙的击穿电压或表面放电电压时，发生的击穿或闪络现象。
绝缘子串上电压幅值为： (3) 耐雷水平：
U j

输电线路防雷保护计算

输电线路防雷保护计算01class1. 雷电参数1.1 雷电活动频度雷暴日雷暴日T d是一年中发生雷电的天数，以听到雷声为准，在一天内只要听到过雷声，无论次数多少，均计为一个雷暴日。

雷暴小时雷暴小时T h是一年中发生雷电放电的小时数，在一个小时内只要有一次雷电，即计为一个雷电小时。

一个雷暴日折合三个雷暴小时。

少雷区年均雷暴日数不超过15d或地面落雷密度不超过0.78次/（km2·a）的地区。

注：《建筑物电子信息系统防雷技术规范》（GB 50343-2012）规定少雷区年平均雷暴日在25d及以下的地区。

中雷区年平均雷暴日数超过15d 但不超过40d 或地面落雷密度超过0.78次/（km2·a）但不超过2.78次/（km2·a）的地区。

注：《建筑物电子信息系统防雷技术规范》（GB 50343-2012）规定中雷区年平均雷暴日大于25d ，不超过40d 的地区。

多雷区年平均雷暴日数超过40d 但不超过90d 或地面落雷密度超过2.78次/（km2·a）但不超过7.98次/（km2·a）的地区。

强雷区年平均雷暴日数超过90d 或地面落雷密度超过7.98次/（km2·a）以及根据运行经验雷害特殊严重的地区。

1.2 地面落雷密度地面落雷密度表示每平方公里地面在一个雷暴日受到的平均雷击次数。

用γ表示（次/km2·雷暴日）。

我国标准对T d＝40的地区，取＝0.07 。

1.3 雷电流幅值雷电流是指雷击于接地良好的目标时泄入大地的电流。

雷电流的幅值（I）一般都是在塔上或避雷针上用磁钢棒测出的。

一般地区，雷电流幅值超过I的概率可按下式计算：lg P=-I/8802class2. 防雷保护计算2.1 线路落雷次数每100km线路的年落雷次数N L按下式计算：式中：N L——线路落雷次数[次/（100km·a）]；Ng——地闪密度[次/(km2·a)]，对年平均雷暴日数为40d的地区暂取2.78次/(km2·a)；h T——杆塔高度(m)；b——两根底下之间的距离(m)。

浅谈交流35kV输电线路反击耐雷性能

浅谈交流35kV输电线路反击耐雷性能雷击是一种很常见的自然灾害，对于电线线路有很大的影响。

当电线线路遇到雷击的时候，很容易造成线路跳闸停电事故，当雷电击到输电线路的时候，会沿着输电线路的传播，进而进入到变电所中，成为危害变电所运营安全的一个重要原因。

因此，在线路架设以及保护的过程中应该重视输电电路的雷击防护问题。

当前对110kV以上输电线路进行了很多研究，对于35kV的研究则相对少一些。

但是在我国的很多线路中，采用的都是35kV输电线路和中性点不接地的运行方式，而且没有架设避雷线，在使用过程中很容易出现安全隐患。

1 35kV输电线路反击耐雷特性计算方法1.1 反击耐雷水平的计算在我国很多35kV的输电线路中，Z型塔比较常见，如图1所示：如图1所示，对于我们日常生活中比较常见的Z型塔，一旦出现雷电现象时，一般都会首先击中杆塔的顶部，当雷电流达到了一定的数值，就会使得图1中的A相绝缘子出现闪络的情况，然后紧接着B相线路也会出现闪絡现象，因为A 相导线出现闪络现象之后会产生分流的作用，因此可以将其看作是避雷线。

如图2所示的等值电路可以计算出杆塔的电位大小，其中各个参数代表的含义不相同：Lt指的是杆塔的等值电感；Rg指的是杆塔的冲击接地电阻；it指的是流经杆塔入地的雷电流；Zc指的是杆塔两侧A相一档导线并联的等值波阻抗；iA指的是流经线路A相导线的电流。

一旦被雷电击中，各个部位的电阻大小是不相同的，一般说来，被雷击中的部位对地电阻比雷电通道的波阻抗相对要低一些，所以我们在计算电流以及电压的过程中就可以相对地忽略雷电通道波阻抗的影响，输电线路中的电流i可以看成是可以看成是从输电线路的杆塔顶端的A点注入的。

如果杆塔中的雷电流出现了斜角波形，其幅值为I，波头为πf，波头陡度为α。

因此就可以得到一个具体的计算雷电电流的公式：i=αt。

当杆塔出现雷击现象的时候，很多电流都会通过输电线路中被击中的杆塔进入到地面，一小部分会通过闪络的A相绝缘子、A 相导线等支路入地。

耐雷水平计算详细公式1

K0 I1 I2 P1 P2
0.1735 179.2094 36.5225 0.9195% 38.4567% 1.8 11.7650 0.151818896 8.6986 0.2664% 0.6064 1/6 0.0d Hg Hc Hg Hc a b r1 d13~ d13 d23~ d23 d12~ d12 K0 Lt Lg Ri β U50% K1 β Ri h呼 h塔 Lt Hg Hc
几何耦合系数反击耐雷水平(KA) 雷绕击导线时的耐雷水平(KA) 雷电流超过I1的概率雷电流超过I2的概率地线挂点与导线挂点的水平距离地线挂点与导线挂点的垂直距离保护角(弧度) 保护角(度) 绕击率建弧率击杆率(平原取1/6；山地取1/4）跳闸率(40个雷暴日)(次/100KM·年) 跳闸率(80个雷暴日)(次/100KM·年)
耐雷水平计算
使用时请注意:1、使用之前请做好备份；2、不要改动黄色框中数据；3 、红色字体为报告中需填写内容，摘录时请勿复制。地线最低点应力导线最低点应力地线自重比载导线自重比载雷击杆塔前侧档距雷击杆塔后侧档距雷击杆塔垂直档距塔高呼高绝缘子结构高度(mm) 绝缘子有效片数绝缘子实际片数绝缘子有效串长(米) 绝缘子实际串长(米) 地线连接金具长(米) 实测接地电阻地线弧垂导线弧垂地线平均高度导线平均高度地线平均高度(米) 导线平均高度(米) 导地线水平间距(米) 地线间距(米) 地线半径(米) 导线与较近地线影象间距导线与较近地线实际间距导线与较远地线影象间距导线与较远地线实际间距地线影象间距地线间距(米) 几何耦合系数铁塔电感杆塔两侧相邻档避雷线的电感并联值冲击接地电阻分流系数冲击放电电压电晕下的耦合系数分流系数冲击接地电阻杆塔呼高杆塔塔高铁塔电感地线平均高度导线平均高度 δb δd Gb Gd L前 L后 L h塔 h呼 228.5000 53.5000 0.077817 0.030319 734.0000 730.0000 732.0000 58.8000 54.0000 195.0000 35.0000 37.0000 6.8250 7.2150 0.2500 15.0000 22.8099 37.9575 43.3434 21.4800 43.3434 21.4800 1.8000 14.0000 0.0057 64.8484 21.9374 66.7212 26.9750 87.8101 14.0000 0.1735 29.4000 307.4377 12.0000 0.8723 3652.2500 0.2221 0.8723 12.0000 54.0000 58.8000 29.4000 43.3434 21.4800

杆塔耐雷水平计算方法

杆塔耐雷水平计算方法
1.杆塔耐雷水平概述
2.固定系数法
固定系数法是指根据将不同的雷电参数转化为固定的数值系数，结合
杆塔的结构参数进行计算。

根据天津市规定，固定系数法的计算公式如下：-杆塔雷电冲击可承受过流I(kA)=αS(Lxσ-λ)
-杆塔雷电冲击绕组电压U(kV)=αS(Lxσ-λ)
其中，α为雷势系数，取1.15；S为杆塔横截面积（单位：m²）；L
为杆塔高度（单位：m）；σ为大地电阻率（单位：Ω.m）；λ为杆塔附
近的基本层次雷电过程的雷电平均充电量（单位：C/m²）。

3.概率法
概率法是指根据雷电的概率分布进行统计分析，计算杆塔在不同概率
水平下的耐雷水平。

IEEE指南中介绍的概率法包括以下几个步骤：-确定雷电信号的概率分布
-选择阻抗模型
-进行雷电流和雷电绕组电压的计算
概率法的计算结果更加准确，能够更好地反映实际情况。

其优点是能
够根据具体雷电活动的特点，对杆塔进行更加精细的耐雷设计和计算。

4.其他影响因素
在杆塔耐雷水平的计算中，还需考虑以下因素：
-线路的输电能力：根据线路参数和设计要求，计算雷电过电压通过线路的能力。

-地面接地系统：合理设计接地系统，减小杆塔接地电阻，提高杆塔的抗雷性能。

-环境因素：考虑杆塔的周围环境，如空气离子浓度、湿度等对线路的影响，合理选择防雷强度等级。

综上所述，杆塔耐雷水平的计算方法可以采用固定系数法或概率法，其中概率法的计算结果更准确。

在计算中还需综合考虑线路的输电能力、接地系统和环境因素等。

通过合理的耐雷设计和计算，可以保证杆塔的安全运行和电力系统的可靠性。

配网线路杆塔防雷性能指标评价

所示。
２计算原理
雷击线路的跳次数与线路可能受雷击的次数有
密切的关系。通常地面落雷密度＝０．０１５，若取每年
４０个雷暴 ¨作为标准值，此１３寸，每年１００ｋｎ线路受到ｉ的雷击次数为：Ｎ＝４０× ０．０１５× ｈ＝０．６ｈ次／（１００ｋｍ・４０雷电口）（ｈ为避雷线平均高度，在无避雷线时施的保护效果及技术经济性进行研究，提出有针对性的配电线路防雷保护实施方案，是目前配电线路防雷工作中亟待解决的问题。
进入程序主界面图２，点击程序“ 信息管理 ” 菜单选择“ 编辑杆塔 ” 下拉选项进入信息录入界丽，如图３
１０２
《电气开关》（２０１７．Ｎｏ．３）
文章编号：１００４—２８９Ｘ（２０１７）０３— ０１０２— ０３
配网线路杆塔防雷性能指标评价
贤昌华
（广西电网有限责任公司崇左凭祥供电局，广西凭祥
摘
５３２６００）
ｐｏｔｒｅｃｔｉｏｎｍｅａｓｕｒｅｓ，ａｎｄｔｈｅｃｏｒｒｅｓｐｏｎｄｉｎｇｌｉｎｅｌｉｇｈｔｎｉｎｇｐｒｏｔｅｃｔｉｏｎｃｏｎｓｔｒｕｃｔｉｏｎｓｃｈｅｍｅ，ｐｒｏｔｅｃｔｉｏｎｏｆｄｉｓｔｉｂｕｒｔｉｏｎｎｅｔ・ｗｏｒｋｌｉｇｈｔｎｉｎｇｐｒｏｔｅｃｔｉｏｎｅｆｆｅｃｔｉｎｔｏｆｕｌｌｐｌａｙａｒｅａｎｌｙａｚｅｄｉｎｔｈｉｓｐａｐｅｒ．Ａｃｃｏｒｄｉｎｇｔｏｔｈｅｌｉｇｈｔｎｉｎｇｐｒｏｔｅｃｔｉｏｎｍｅａｓｕｒｅｓｏｆ

7-4 直击雷过电压和耐雷水平

20
1000～ 2000
25
2000 以上
30

小结：有避雷线线路直击雷的三种情况 ①雷击杆塔塔顶； ②雷击避雷线档距中央； ③雷电绕过避雷线击于导线；
雷击杆塔塔顶时的过电压和耐雷水平为
I1
U 50% Lgt hd (1 K ) ( Rch ) 2.6 2.6
平原
山丘
1/4
1/3
1/6
1/4
3
1. 塔顶电位
雷击杆塔时，雷电流分布和等值电路如下图所示
U td Rchigt Lgt
digt
diL RchiL Lgt dt dt
式中： igt iL ，为分流系数，对于不同电压等级
值可由表7-3查得。一般长度档距的杆塔，
4
线路额定电压（kV） 110 220 330（500）
雷击杆塔时的过电压和耐雷水平
有避雷线线路直击雷的三种情况
｛
①雷击杆塔塔顶； ②雷击避雷线档距中央； ③雷电绕过避雷线击于导线；
2
一、雷击杆塔时的过电压
雷击杆塔的次数与避雷线的根数和经过地区的地形有
关，雷击杆塔次数与雷击输电线路总次数之比称为击杆率 g
，DL/T 620—1997标准，击杆率g可采用表8-5所列数据。避雷线根数 1 2
2. 导线电位和线路绝缘子串上的电压
当塔顶电位为 U td 时，则与塔顶相连的避雷线上也将
有 U td 的电位，由于避雷线与导线间的耦合作用，导线上
将产生耦合电压 kU td ，此电压与雷电流同极性。此外，由于雷电通道电磁场的作用，根据式(7-5)在导线上还有感应电压 - hd (1 k ) ，此电压与雷电流极性相反，所以导线电位 U d 的幅值为：

杆塔耐雷水平计算方法

杆塔耐雷水平计算方法杆塔耐雷水平计算方法一、反击耐雷水平按式（1）计算()6.216.210%501av av gvt t a SUh K h h L k h h R k U I ⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-+-=ββ 式（1）式（1）中：av h ——导线的平均高度，ma av f h h ⨯-=321 式（2）式（2）中：1h ——导线挂线点高度 a f ——导线弧垂gvh ——地线的平均高度，mg gv f h h ⨯-=322 式（3）式（3）中：2h ——地线挂线点高度 g f ——地线弧垂a h ——导线横担对地高度，m th ——杆塔高度，mK ——导线与地线间的几何耦合系数几种典型线路的几何耦合系数0K 见表1表1 典型线路的几何耦合系数0Kk ——电晕下的耦合系数，01K k k =，其中1k 为雷击塔顶时的电晕校正系数，取值如表4表4 电晕校正系数SU R ——杆塔接地电阻，实测后应考虑1.4～1.8倍的季节系数%50U ——50％放电冲击电压二、绕击耐雷水平Z%502U I =式（5）式（5）Z ——波阻抗，一般取100Ω。

例：忻侯Ⅰ线108＃塔型如下图，杆塔接地电阻为10Ω，导线弧垂6.6米，地线弧垂4.5米（1）避雷线平均高度：()m h b 325.4325.36=⨯-=（2）导线平均高度：(这里计算与上述表达式不一致)()m h d 1.246.6325.433=⨯--=（3）双避雷线对外侧导线的几何耦合系数：184.01022.2164ln 10005.4322ln36.129.736.121.56ln7.19.77.11.56ln 22222222220=++⨯+++++=K（4）电晕下的耦合系数：k ＝k 1k 0＝1.28×0.2＝0.256（5）杆塔电感：L t ＝36.5×0.5＝18.25(μH)（6）雷击杆塔时分流系数：β＝0.88（7）雷击杆塔时耐雷水平(当用FXBW4-500/160时)：()6.21.242.01.243216.225.1888.0256.05.3633788.0256.0121001⨯⎪⎭⎫⎝⎛⨯-+⨯⨯⎪⎭⎫⎝⎛-+⨯⨯-=I＝136.507(kA)（8）雷绕击于导线时的耐雷水平：)(2110021002kA I ==经计算可看出，108＃杆塔（ZB2-33）雷击塔顶时的耐雷水平为136.507kA ，绕击耐雷水平为21kA 。

线路直击雷过电压及耐雷水平

提高雷击塔顶时耐雷水平的措施：
（1）一般高度杆塔（小于40m），冲击接地电阻上压降是塔顶电位的主要成分，因此降低接地电阻可以有效地减小塔顶电位和提高耐雷水平；（2）增大耦合系数k；（3）加强线路绝缘（提高U50%）。
为了减少反击，必须提高线路的耐雷水平。标准中规定，雷击塔顶时应有的耐雷水平I1为：
由于半径较小的BLX的强烈电晕衰减作用，使过电压波传播到杆塔时，已不足以使绝缘子串闪络，通常只需要考虑雷击BLX对导线的反击问题。
标准规定，只要按经验公式S＝0.012l+1确定档距中央导、地线间的空气间距S，一般不会发生BLX 对导线的反击故障。
3、直击或绕击：
装设BLX的线路，仍有雷绕过BLX击于导线的可能
(4.5E 0.75 14) 10 2
建弧率η取决于沿绝缘子串或空气间隙的平均工作电压梯度E，也与闪络瞬间工频电压瞬时值和去游离条件有关。
2、雷击跳闸率的计算
线路总的雷击跳闸率n为雷击杆塔跳闸率n1和绕击跳闸率n2之和，即n=n1+n2
经验公式： n1=N·g·P1·η n2=N·Pa·P2·η
110
0.83 1.18－ 2.01
三、输电线路防雷措施
220
500
0.25
0.43－ 0.95
0.081 0.17－0.42
自学总结
自学要点：（1）BLX在线路防雷中的作用？（2）Ri的影响？（3）消弧线圈在防雷中怎么起作用？
思考题
7-3 补充思考题：
1、耐雷水平的含义？影响耐雷水平的因素主要有哪些？ 2、线路防雷措施主要有哪些？
发生绕击的概率称为绕击率Ka
Ka与避雷线保护角α、杆塔高度h及线路通过地区的地形地貌有关。