切线长定理公开课
合集下载
初中数学北师大版九年级下册第三单元第7课《切线长定理》优质课公开课教案教师资格证面试试讲教案
初中数学北师大版九年级下册第三单元第7课《切线长定理》优质课公开课教案教师资格证面试试讲教案
初中数学北师大版九年级下册第三单元第7课《切线长定理》优质课公开课教案教师资格证面试试讲教案
1教学目标
1. 使学生理解切线长定义.
2. 使学生掌握切线长定理,并能初步运用.
3. 通过本节教学,进一步培养学生的动手操作能力和创新意识.
4. 学生在猜想、探索、验证切线长定理活动中通过相互间的合作与交流,进一步发展学生合作交流的能力和数学表达能力.
5. 通过分析问题、解决问题的过程,激发学生学数学的兴趣,使学生积极参与、体验成功. 2学情分析
本节课是在学习了切线的性质和判定的基础之上,继续对切线的性质的研究,是在垂径定理之后对圆的对称性又一次的认识.体现了图形的认识、图形的变换、图形的证明的有机结合.在习题和内切圆的计算中体现了把复杂问题转化为简单问题后解决问题,从而滲透转化思想和方程思想,提高应用意识.
3重点难点
切线长定理的探究
4教学过程
4.1第一学时
4.1.1教学活动
活动1【导入】创设情景，引入新课
问题:有一天,同学们去王老师家做客,王老师正在洗锅,就问:谁能测出这个锅盖的半径,就可以得到一根雪糕,同学们都跃跃欲试,但老师家里只有一个曲尺,到底谁能得到这根雪糕呢?。
北师大版九年级数学下册切线长定理市公开课一等奖省优质课获奖课件
C D
A
B
第12页
6、已知：在△ABC中，BC＝14cm，AC＝ 9cm，AB＝13cm，BC，AC，AB分别与⊙O 切于点D、E、F，求AF，BD和CE长。
A
F
E
O
B
DC第13页 Nhomakorabea切线长： 从圆外一点引圆切线，这个点与切点间
线段长称为切线长。
切线长定理： 从圆外一点能够引圆两条切线，它们切
线长相等。这一点和圆心连线平分这两条切 线夹角。
OC D
P
（1）图中相互垂直关系 3有
对，分别是
B
OA PA,OB PB,OP AB
（2）图中直角三角形有 6 个，分别是
等腰三角形有 2 个，分别是
（3）图中全等三角形 3 对，分别是
（4）假如半径为3cm，PO=6cm，则点P到⊙ O切线长
为 3 3cm，两切线夹角等于
度60
第9页
3、已知：如图，P为⊙O外一点，PA，PB为
A
O B
P
第5页
例2、如图，过半径为6cm⊙O外一点P作圆切 线PA、PB，连结PO交⊙O于F，过F作⊙O切 线分别交PA、PB于D、E，假如PO＝10cm， 求△PED周长。
AD
OF
P
E B
第6页
例3、 已知四边形ABCD边AB、BC、CD、DA 分别与⊙O相切于P、Q、M、N， 求证：AB+CD=AD+BC。
⊙O切线，A和B是切点，BC是直径。∠C＝
50，
①求∠APB度数
②求证：AC∥OP。 C
A
O
P
B
第10页
4、如图，Δ ABC内切圆分别和BC，AC，AB切
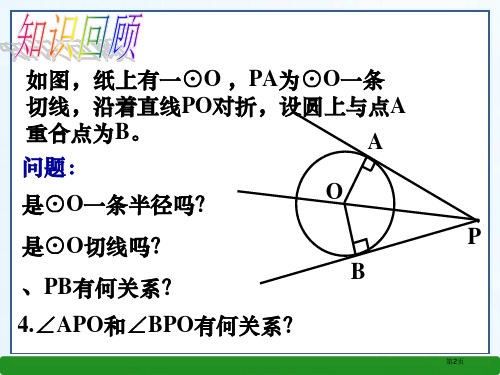
A
B
第12页
6、已知：在△ABC中，BC＝14cm，AC＝ 9cm，AB＝13cm，BC，AC，AB分别与⊙O 切于点D、E、F，求AF，BD和CE长。
A
F
E
O
B
DC第13页 Nhomakorabea切线长： 从圆外一点引圆切线，这个点与切点间
线段长称为切线长。
切线长定理： 从圆外一点能够引圆两条切线，它们切
线长相等。这一点和圆心连线平分这两条切 线夹角。
OC D
P
（1）图中相互垂直关系 3有
对，分别是
B
OA PA,OB PB,OP AB
（2）图中直角三角形有 6 个，分别是
等腰三角形有 2 个，分别是
（3）图中全等三角形 3 对，分别是
（4）假如半径为3cm，PO=6cm，则点P到⊙ O切线长
为 3 3cm，两切线夹角等于
度60
第9页
3、已知：如图，P为⊙O外一点，PA，PB为
A
O B
P
第5页
例2、如图，过半径为6cm⊙O外一点P作圆切 线PA、PB，连结PO交⊙O于F，过F作⊙O切 线分别交PA、PB于D、E，假如PO＝10cm， 求△PED周长。
AD
OF
P
E B
第6页
例3、 已知四边形ABCD边AB、BC、CD、DA 分别与⊙O相切于P、Q、M、N， 求证：AB+CD=AD+BC。
⊙O切线，A和B是切点，BC是直径。∠C＝
50，
①求∠APB度数
②求证：AC∥OP。 C
A
O
P
B
第10页
4、如图，Δ ABC内切圆分别和BC，AC，AB切
《切线长定理》课件精品 (公开课)2022年数学PPT
三角形角平分线的这个 性质，你还记得吗？
三圆角心形I应三是条三角角平形分的线三交条 为什么呢？
于角一平点分，线这的一交点与. 三角 形的三边距离相等.
做一做
已知：△ABC.
求作：和△ABC的各边都相切的圆.
A
N
作法： 1.作∠B和∠C的平分线BM和 CN，交点为O. 2.过点O作OD⊥BC.垂足为D. M 3.以O为圆心，OD为半径作 圆O.
∴PA = PB ，∠OPA=∠OPB
∴△PAB是等腰三角形，PM为顶角的平分线 ∴OP垂直平分AB.
想一想：若延长PO交⊙O于点C， A
连结CA、CB，你又能得出什么
C
O.
新的结论?并给出证明.
P
CA=CB
B
证明：∵PA，PB是⊙O的切线,点A，B是切点，
∴PA = PB ，∠OPA=∠OPB.
证明：∵PA切☉O于点A， O.
P
∴ OA⊥PA.
B
同理可得OB⊥PB.
∵OA=OB，OP=OP， ∴Rt△OAP≌Rt△OBP， ∴PA=PB，∠APO=∠BPO.
想一想：若连结两切点A、B，AB交
A
OP于点M.你又能得出什么新的结论? O. M
并给出证明.
P
OP垂直平分AB.
B
证明：∵PA，PB是⊙O的切线,点A，B是切点
24.2 直线和圆的位置关系
第3课时 切线长定理
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.掌握切线长的定义及切线长定理.（重点） 2.初步学会运用切线长定理进行计算与证明. （难点）
导入新课
情境引入 同学们玩过空竹和悠悠球吗？在空竹和悠悠球的旋转的那一 瞬间，你能从中抽象出什么样数学图形？
三圆角心形I应三是条三角角平形分的线三交条 为什么呢？
于角一平点分，线这的一交点与. 三角 形的三边距离相等.
做一做
已知：△ABC.
求作：和△ABC的各边都相切的圆.
A
N
作法： 1.作∠B和∠C的平分线BM和 CN，交点为O. 2.过点O作OD⊥BC.垂足为D. M 3.以O为圆心，OD为半径作 圆O.
∴PA = PB ，∠OPA=∠OPB
∴△PAB是等腰三角形，PM为顶角的平分线 ∴OP垂直平分AB.
想一想：若延长PO交⊙O于点C， A
连结CA、CB，你又能得出什么
C
O.
新的结论?并给出证明.
P
CA=CB
B
证明：∵PA，PB是⊙O的切线,点A，B是切点，
∴PA = PB ，∠OPA=∠OPB.
证明：∵PA切☉O于点A， O.
P
∴ OA⊥PA.
B
同理可得OB⊥PB.
∵OA=OB，OP=OP， ∴Rt△OAP≌Rt△OBP， ∴PA=PB，∠APO=∠BPO.
想一想：若连结两切点A、B，AB交
A
OP于点M.你又能得出什么新的结论? O. M
并给出证明.
P
OP垂直平分AB.
B
证明：∵PA，PB是⊙O的切线,点A，B是切点
24.2 直线和圆的位置关系
第3课时 切线长定理
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.掌握切线长的定义及切线长定理.（重点） 2.初步学会运用切线长定理进行计算与证明. （难点）
导入新课
情境引入 同学们玩过空竹和悠悠球吗？在空竹和悠悠球的旋转的那一 瞬间，你能从中抽象出什么样数学图形？
切线长定理(共33张)PPT课件
a,AC＝b, AB＝c,⊙O为Rt△ABC的内切圆. 求：
Rt△ABC的内切圆的半径 r.
解：设Rt△ABC的内切圆与三边相切于D、E、F，
连结OD、OE、OF则OA⊥AC，OE⊥BC，OF⊥AB。
A
∵ ⊙O与Rt△ABC的三边都相切
∴AD＝AF,BE＝BF,CE＝CD
F
设AD= x , BE= y ,CE＝ r
∠OAC=∠OBC=∠APC=∠BPC
（3）写出图中所有相等的线段
OA=OB=OD=OE, PA-=PB, AC=BC, AE=BE
-
12
例题1
已知：如图,PA、PB是⊙O的切线，切点分别是
A、B，Q为AB上一点，过Q点作⊙O的切线，交
PA、PB于E、F点，已知PA=12CM，求△PEF的周
长。
易证EQ=EA, FQ=FB,
OP垂直平分AB
切线长定理为证明线段相等，角
相等，弧相等，垂直关系提供了理论
依据。必须掌握并能- 灵活应用。
21
练习.如图，△ABC中,∠C =90º,它的
内切圆O分别与边AB、BC、CA相切
于点D、E、F，且BD=12，AD=8，
求⊙O的半径r.
A
D
F O
B
EC
-
22
思考
三角形的内切圆的有关计算
OP垂直平分AB
OM
P
A 证明：∵PA，PB是⊙O的切线,点A，B是切点
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形，PM为顶角的平分线
∴OP垂直平分AB
-
10
若延长PO交⊙O于点C，连结CA、CB，你又 能得出什么新的结论?并给出证明.
九年级数学下册24.2圆的切线长定理全国公开课一等奖百校联赛微课赛课特等奖PPT课件
刺猬和松鼠童话作文
刺猬和松鼠童话作文
在森林中住着一对好朋友------刺猬和松鼠，它们亲密无间，每天形影不离，可在以前，松鼠最讨厌的就是刺猬了！
松鼠讽刺地对刺猬说：“瞧瞧你身上长满了刺，一靠近你，就会被刺到，谁愿意跟你做朋友，一起玩呀？你在看看我，漂亮的皮毛蓬松的大尾巴，多招人喜欢呀！”
刺猬看着松鼠得意的样子，温和地说：真心希望和我做朋友的人是不会在乎我的外表！虽然我浑身长满刺，但我有一颗善良的`心！”
“你永远只能在地上爬行，而我呢？因为有一条能做降落伞的尾巴，所以能在树上自由自在的跳来跳去，一溜烟儿，就无影无踪了！还能够欣赏美丽的风景呢！”松鼠摇着大尾巴得意地说道。
“虽然我的刺很锋利，但是我能用它搬运果实，”刺猬不紧不慢地说，“而且还能防卫敌人呢！”
就在这时候，一只豹子正静悄悄地靠近它们，只见它纵身一跃，向刺猬冲来！刺猬突然缩成一个长满刺的大肉球，豹子想用前爪拨开，可是无从下爪。
豹子愤怒了，此时的松鼠已经吓呆了，眼睛瞪得老大！刺猬大喊：“松鼠你快逃呀！”就在这千钧一发之时，松鼠摇着它的大尾巴轻轻地跃上一棵大树，豹子紧随其后，抓住了它的大尾巴，松鼠不敢犹豫，用尽九牛二虎之力挣脱了豹子的利爪，跳到了更高的树杈上。
劫后余生的松鼠气喘吁吁地跳上了树杈，豹子看两头都占不到便宜，只好灰溜溜地走了。
松鼠感激地对刺猬说：“如果没有你的提醒，我就死定了，非常感谢你！”说完扑进了刺猬的怀里！刺猬开心地笑了。
北师大版《切线长定理》ppt公开课课件3
谢谢合作！ 三画、一应 画用：新画知圆，O,体在验圆成外功取一点P，过点P作圆O的切线PA,切点为A。
2、你有哪些好的经验可推广？ 1（、三填）空、：圆如的图外1切0，四P边A、形P的B性分质别与⊙O相切于点A、B， ∴2、PA你=P有B哪，些∠好AP的O经=∠验B可PO推. 广？ （41）既是然指点一条P到线⊙段O的的长切度线。长可以用两条不同的线段的长来表示，那么这两条线段之间一定存在着某种关系，是什么关系呢？ 例②题两1个：端已点知一如个图是，切R点t△，A一BC个的是两圆条外直已角知边点A。C=10，BC=24，⊙O 是△ABC 的内切圆，切点分别为D,E,F，求⊙O 的半径。 3（、1）为了是测指量一一条个线圆段形的锅 长盖度的。半径，某同学采用了如下办法：将锅盖平放在水平桌面上，用一个锐角为30°的三角板和一个刻度尺，按 图四中、所 梳示理的小方结法，得盘到点相收关获数据，进而可求得锅盖的半径，若测得PA=5cm，则锅盖的半径长是多少？ （34）如既图然2点，P思到考⊙：O的点切P到线⊙长O可的以切用线两长条可不以同用的三线条段或的三长条来以表上示不，同那的么线这段两的条长线来段表之示间吗一？定这存样在的着线某段种最关多系可，以是有什几么条关？系为呢什？么？ （线4段）P既A或然线点段P到PB⊙O的切线长可以用两条不同的线段的长来表示，那么这两条线段之间一定存在着某种关系，是什么关系呢？ ②（两3）个若端P点A=一4，个A是O切=点3，，则一P个O是= 圆外；已知点。 变式12：如图，5，P△是A⊙BOC外的一内点切，圆P⊙AO与与PB分C，别C⊙AO,A切B分于别A、相B切两于点点，DD，E也E，是F⊙，O且的A切B线=9，cm切,B点C为=1C4，cmP,AC=AP=B1=35ccmm,求，A求F,△BDP,DCEE的的周长长。。 画二一、画合：作画学圆习O，,在探圆究外新取知一点P，过点P作圆O的切线PA,切点为A。 ②两个端点一个是切点，一个是圆外已知点。
2、你有哪些好的经验可推广？ 1（、三填）空、：圆如的图外1切0，四P边A、形P的B性分质别与⊙O相切于点A、B， ∴2、PA你=P有B哪，些∠好AP的O经=∠验B可PO推. 广？ （41）既是然指点一条P到线⊙段O的的长切度线。长可以用两条不同的线段的长来表示，那么这两条线段之间一定存在着某种关系，是什么关系呢？ 例②题两1个：端已点知一如个图是，切R点t△，A一BC个的是两圆条外直已角知边点A。C=10，BC=24，⊙O 是△ABC 的内切圆，切点分别为D,E,F，求⊙O 的半径。 3（、1）为了是测指量一一条个线圆段形的锅 长盖度的。半径，某同学采用了如下办法：将锅盖平放在水平桌面上，用一个锐角为30°的三角板和一个刻度尺，按 图四中、所 梳示理的小方结法，得盘到点相收关获数据，进而可求得锅盖的半径，若测得PA=5cm，则锅盖的半径长是多少？ （34）如既图然2点，P思到考⊙：O的点切P到线⊙长O可的以切用线两长条可不以同用的三线条段或的三长条来以表上示不，同那的么线这段两的条长线来段表之示间吗一？定这存样在的着线某段种最关多系可，以是有什几么条关？系为呢什？么？ （线4段）P既A或然线点段P到PB⊙O的切线长可以用两条不同的线段的长来表示，那么这两条线段之间一定存在着某种关系，是什么关系呢？ ②（两3）个若端P点A=一4，个A是O切=点3，，则一P个O是= 圆外；已知点。 变式12：如图，5，P△是A⊙BOC外的一内点切，圆P⊙AO与与PB分C，别C⊙AO,A切B分于别A、相B切两于点点，DD，E也E，是F⊙，O且的A切B线=9，cm切,B点C为=1C4，cmP,AC=AP=B1=35ccmm,求，A求F,△BDP,DCEE的的周长长。。 画二一、画合：作画学圆习O，,在探圆究外新取知一点P，过点P作圆O的切线PA,切点为A。 ②两个端点一个是切点，一个是圆外已知点。
34第三课时切线长定理用课件
22cm
知识小结
直角三角形的外接圆与内切圆
1.直角三角形外接圆的圆心(外心)在__________，半径为___________.
2.直角三角形内切圆的圆心(内心)在__________，半径r=___________.
a
b
c
斜边中点
斜边的一半
三角形内部
课前训练
1、已知，如图，PA、PB是⊙O的两条切线，A、B为切点.直线 OP 交 ⊙O 于点 D、E，交 AB 于 C.（1）写出图中所有的垂直关系；（2）如果 PA = 4 cm , PD = 2 cm , 求半径 OA的长.
练习
(1)如图PA、PB切圆于A、B两点， 连结PO，则 度。
P
B
O
A
二、填空
25
（3）如图，PA、PB、DE分别切⊙O于A、B、C，DE分别交PA，PB于D、E，已知P到⊙O的切线长为8CM，则Δ PDE的周长为（ ）
A
A 16cm
D 8cm
C 12cm
B 14cm
D
C
B
E
A
P
例2、如图，过半径为6cm的⊙O外一点P作圆的切线PA、PB，连结PO交⊙O于F，过F作⊙O切线分别交PA、PB于D、E，如果PO＝10cm， 求△PED的周长。
数学探究
思考：连结AB，则AB与PO有怎样的位置关系？ 为什么？
（2）填空：AB+CD AD+BC（>,<,=)
=
DN=DP，AP=AL，BL=BM，CN=CM
比较圆的内接四边形的性质：
圆的内接四边形：角的关系
圆的外切四边形：边的关系
练习四 已知：△ABC是⊙O外切三角形，切点为D，E，F。若BC＝14 cm ，AC＝9cm，AB＝13cm。求AF，BD，CE。
知识小结
直角三角形的外接圆与内切圆
1.直角三角形外接圆的圆心(外心)在__________，半径为___________.
2.直角三角形内切圆的圆心(内心)在__________，半径r=___________.
a
b
c
斜边中点
斜边的一半
三角形内部
课前训练
1、已知，如图，PA、PB是⊙O的两条切线，A、B为切点.直线 OP 交 ⊙O 于点 D、E，交 AB 于 C.（1）写出图中所有的垂直关系；（2）如果 PA = 4 cm , PD = 2 cm , 求半径 OA的长.
练习
(1)如图PA、PB切圆于A、B两点， 连结PO，则 度。
P
B
O
A
二、填空
25
（3）如图，PA、PB、DE分别切⊙O于A、B、C，DE分别交PA，PB于D、E，已知P到⊙O的切线长为8CM，则Δ PDE的周长为（ ）
A
A 16cm
D 8cm
C 12cm
B 14cm
D
C
B
E
A
P
例2、如图，过半径为6cm的⊙O外一点P作圆的切线PA、PB，连结PO交⊙O于F，过F作⊙O切线分别交PA、PB于D、E，如果PO＝10cm， 求△PED的周长。
数学探究
思考：连结AB，则AB与PO有怎样的位置关系？ 为什么？
（2）填空：AB+CD AD+BC（>,<,=)
=
DN=DP，AP=AL，BL=BM，CN=CM
比较圆的内接四边形的性质：
圆的内接四边形：角的关系
圆的外切四边形：边的关系
练习四 已知：△ABC是⊙O外切三角形，切点为D，E，F。若BC＝14 cm ，AC＝9cm，AB＝13cm。求AF，BD，CE。
切线长定理公开课
（3）连结圆心和圆外一点
练习：PA、PB是⊙O的两条切线，A、B为切点，
直线OP交于⊙O于点D、E，交AB于C。
A
（1）写出图中所有的垂直关系
E OA⊥PA，OB ⊥PB，AB ⊥OP
O
CD
P
（2）写出图中所有的全等三角形
B
△AOP≌ △BOP， △AOC≌ △BOC， △ACP≌ △BCP （3）写出图中所有的等腰三角形
A
=PA+PB P =7+7
·O E
=14 cm
C B
活动 三
下图是一张三角形的铁皮，如何在它的上面截下一块圆形的 用料，并且使圆的面积尽可能大呢？
A
A
·l
B
C
B
C
假设符合条件的圆已经作出，那么它应当与三 角形的三边都相切，这个圆的圆心到三角形的距 离都等于半径，如何找到圆心？
A
B
C
三角形的三条角平分线交于一点，并且这个点到三条边 的距离相等，因此，如图，分别作出∠B、∠C的平分线 BM和CN，设他们相交于点I，那么点I到AB、BC、CA的距 离都相等，以点I为圆心，点I到BC的距离ID为半径做圆， 则⊙I与△ABC的三条边都相切.
2、已知PA、PB与⊙O相切
于点A、B，⊙O的半径为2
A
（1）若四边形OAPB的周
长为10，则PA= 3 。
（2）若∠APB=60°，
2 30
4° 2
则PA= 2 3。
B
思考
已知：PA、PB分别与⊙O切于点AB，连接AB交OP
于点M，那么OP除了平分∠APB以外，还有什么作用？
请说明理由。
A
(1)OP垂直平分AB
九年级数学切线长定理(市区公开课)
O
过圆外一点作圆的切线，这点和 切点之的线段的长，叫做这点到 圆的切线长。
思考：切线与切线长有区别吗？
O
观察与猜想：你认为图中有哪些
相等的数量？
A
O
P
B
1、验证与推理：你有办法确定咱 们的猜想吗？ 2、结论表达：你会用语言或数学 的符号表达吗？
切线长定理：
从圆外一点引圆的两条切线，它们的切 线长相等，这一点和圆心的连线平分两条 切线的夹角。
实际应用
例2 已知：如图, △ABC的内切圆⊙O 与BC 、CA、 AB 分别相交于点D 、 E 、 F ，且AB＝9厘米，BC ＝14厘 米,CA ＝13厘米,求AF、BD、CE的长。
A E F B D O C
已知在直角三角形中AB=10，AC=6.求 它的内接圆的半径。
A 10
6
C
B
1、圆的切线的定义是什么？ 2、圆的切线有哪些判定方法？ 3、你能过圆上一点作出圆的切线吗？ 能说出作图的步骤吗？理论依据是 什么？
作图的步骤： 1、连接OA; 2、过点A作直线l⊥OA.
O
ห้องสมุดไป่ตู้ 1、你能过圆外一点作出圆的切线吗？
2、能说出作图的步骤吗？ 3、理论依据是什么？ 4、过圆外一点能
作几条圆的切线 吗？
人教版九年级数学--切线长定理公开课课件
A
·
B
p
切线长定理：
从圆外一点可以引圆的两条切线，切线长相等， 这一点和圆心的连线平分两条切线的夹角。
o
探究：切线长定理的拓展 A
E
O
C
D
P
B 相等线段： AP=BP,AO=BO,AC=BC ⌒ ⌒ ⌒ ⌒ 相等的弧： AD=BD， AE=BE 相等的角： ∠APO=∠BPO，∠AOP=∠BOP， ACP= ∠BCP 垂直关系： ∠ AO ⊥PA,AB ⊥ OP,BO ⊥ BP
6、从圆外一点引圆的两条切线，它们的切线长相等，
圆心和这一点的连线平分两条切线的夹角。
切线长定理：从圆外一点引圆的两条切线， 它们的切线长相等，圆心和这一点的连线平分两 条切线的夹角。
你还有什么疑惑？
课本P101 第5，6，11，12题
牛刀小试：
1.如图所示,PA、PB分别切⊙O于A、B， 若PA=6cm，∠APB=60 °
A
(1)则PB=
6cm ；
O B
M
P
° (2)则∠APO= 30 ， ∠AOB= 120 ； (3)AB= 6cm ； (4）半径OA= 2 3 ；
例1：已知：如图，PA、PB是⊙O的切线，切点 分别是A、B，Q为弧AB上一点，过Q点作⊙O的切线， 交PA、PB于E、F点，已知PA=12cm，∠P=700， （1）求证：EF=AE+BF （2）求△PEF的周长； （3）求∠EOF的度数。
A
△PEF的周长为24cm EOF 550
P
E
O
Q
F B
如图，已知：在△ABC中，∠B＝90°，O是 AB上一点，以O为圆心，OB为半径的圆交AB于 点E，交AC于切点D。求证：DE∥OC
·
B
p
切线长定理：
从圆外一点可以引圆的两条切线，切线长相等， 这一点和圆心的连线平分两条切线的夹角。
o
探究：切线长定理的拓展 A
E
O
C
D
P
B 相等线段： AP=BP,AO=BO,AC=BC ⌒ ⌒ ⌒ ⌒ 相等的弧： AD=BD， AE=BE 相等的角： ∠APO=∠BPO，∠AOP=∠BOP， ACP= ∠BCP 垂直关系： ∠ AO ⊥PA,AB ⊥ OP,BO ⊥ BP
6、从圆外一点引圆的两条切线，它们的切线长相等，
圆心和这一点的连线平分两条切线的夹角。
切线长定理：从圆外一点引圆的两条切线， 它们的切线长相等，圆心和这一点的连线平分两 条切线的夹角。
你还有什么疑惑？
课本P101 第5，6，11，12题
牛刀小试：
1.如图所示,PA、PB分别切⊙O于A、B， 若PA=6cm，∠APB=60 °
A
(1)则PB=
6cm ；
O B
M
P
° (2)则∠APO= 30 ， ∠AOB= 120 ； (3)AB= 6cm ； (4）半径OA= 2 3 ；
例1：已知：如图，PA、PB是⊙O的切线，切点 分别是A、B，Q为弧AB上一点，过Q点作⊙O的切线， 交PA、PB于E、F点，已知PA=12cm，∠P=700， （1）求证：EF=AE+BF （2）求△PEF的周长； （3）求∠EOF的度数。
A
△PEF的周长为24cm EOF 550
P
E
O
Q
F B
如图，已知：在△ABC中，∠B＝90°，O是 AB上一点，以O为圆心，OB为半径的圆交AB于 点E，交AC于切点D。求证：DE∥OC
切线长定理公开课(很好用)
解得
因此 A
x
F
x
9
9﹣x
13
E O B 9﹣x D 13﹣x
X=4 AE=4 cm BD=5 cm CE=9 cm
C 13﹣x
14
例题：如图， △ABC的内切圆⊙O与BC、CA、AB分别
相切于点D、E、F，且AB=9cm,BC=14cm，CA=13cm，求 AE、BD、CE的长。
解：设AE=x (cm), 则AF=x (cm) 设CD=y，则CE=y 由题意得
(1) 解：
(2) △OAP ≌△ OBP , △OCA≌△OCB E △ACP≌△BCP. (3) 设 OA = x cm , 则 PO = PD + x = 2 + x (cm) 在 Rt△OAP 中，由勾股定理，得 PA 2 + OA 2 = OP 2 即 4 2 + x 2 = (x + 2 ) 2 解得 x = 3 cm
再探索
例1 已知，如图，PA、PB是⊙O的两条切线，A、B为切点.
直线 OP 交 ⊙O 于点 D、E，交 AB 于 C. （1）写出图中所有的垂直关系； （2）写出图中所有的全等三角形. （3）如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长. OA⊥PA , OB⊥PB , OP⊥AB O A C D P
B
所以，半径 OA 的长为 3 cm.
练一练
已知：两个同心圆PA、PB是大圆的两条切线， PC、PD是小圆的两条切线，A、B、C、D为切点。 求证：AC=BD
A P B
C O· D
反思：在解决有
关圆的切线长的问 题时，往往需要我 们构建基本图形。
（1）分别连结圆心和切点
因此 A
x
F
x
9
9﹣x
13
E O B 9﹣x D 13﹣x
X=4 AE=4 cm BD=5 cm CE=9 cm
C 13﹣x
14
例题：如图， △ABC的内切圆⊙O与BC、CA、AB分别
相切于点D、E、F，且AB=9cm,BC=14cm，CA=13cm，求 AE、BD、CE的长。
解：设AE=x (cm), 则AF=x (cm) 设CD=y，则CE=y 由题意得
(1) 解：
(2) △OAP ≌△ OBP , △OCA≌△OCB E △ACP≌△BCP. (3) 设 OA = x cm , 则 PO = PD + x = 2 + x (cm) 在 Rt△OAP 中，由勾股定理，得 PA 2 + OA 2 = OP 2 即 4 2 + x 2 = (x + 2 ) 2 解得 x = 3 cm
再探索
例1 已知，如图，PA、PB是⊙O的两条切线，A、B为切点.
直线 OP 交 ⊙O 于点 D、E，交 AB 于 C. （1）写出图中所有的垂直关系； （2）写出图中所有的全等三角形. （3）如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长. OA⊥PA , OB⊥PB , OP⊥AB O A C D P
B
所以，半径 OA 的长为 3 cm.
练一练
已知：两个同心圆PA、PB是大圆的两条切线， PC、PD是小圆的两条切线，A、B、C、D为切点。 求证：AC=BD
A P B
C O· D
反思：在解决有
关圆的切线长的问 题时，往往需要我 们构建基本图形。
（1）分别连结圆心和切点
最新冀教版九年级数学下29.4切线长定理ppt公开课优质课件
拓展提升
A F O · B
直角三角形的两直角边分别是3cm ,4cm,试问： （1）它的外接圆半径是 2.5 径是 1 cm？ cm;内切圆半 D
C E 解：如图，△ABC的外接圆直径为AB,而由勾股定理可得 AB=5cm,故外接圆半径为2.5cm.连接AO,BO,CO.设△ABC的内
接圆半径为r，由面积公式可得：S△ABC=S△AoB+S△AoC+S△BoC ,
已知：△ABC.
求作：和△ABC的各边都相切的圆. 作法：
A
1.作∠B和∠C的平分线BM和CN， 交点为O.
M
O
N
2.过点O作OD⊥BC.垂足为D. 3.以O为圆心，OD为半径作圆O. ⊙O就是所求的圆.
C
B
D
概念学习
1.与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形内切圆的圆心叫做三角形的内心.
A
P
线平分两条切线的夹角.）
几何语言: PA、PB分别切⊙O于A、B ∠OPA=∠OPB
注意
B PA = PB
切线长定理为证明线段相等、角相等提供了新的方法.
拓展结论
PA、PB是⊙O的两条切线，A、
B为切点，直线OP交⊙O于点D、 E，交AB于C. （1）写出图中所有的垂直关系； OA⊥PA，OB ⊥PB，AB ⊥OP. （2）写出图中与∠OAC相等的角； E
⑴ △PDE的周长是 14
⑵ ∠DOE= 70°.
；
D P A
C
E B
O
例2 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、 E、F，且AB=13cm，BC=14cm，CA=9cm，求AF、BD、CE 的长.
九年级数学切线长定理(市区公开课)
学习方法分享
归纳总结法
在学习切线长定理时，要善于归纳总结，将分散的知识点串联起来， 形成完整的知识体系。
图形结合法
在解题过程中，要注重图形与文字的结合，通过画图来辅助理解和 分析问题。
举一反三法
在学习切线长定理的应用时，要学会举一反三，通过类似问题的解答， 培养解题思维和技巧。
下一步学习计划
巩固提高
结合具体案例，分析切线长定理在实际问题中的应用方法和效果。
小组合作：设计实验方案并展示成果
小组分工
明确小组成员的分工，如 负责绘制图形、测量数据、 记录结果等。
设计实验方案
小组讨论并确定实验方案， 包括实验目的、实验步骤、 所需工具等。
展示成果
将实验过程和结果整理成 报告或PPT，向全班同学 展示，并接受老师和同学 的提问和评价。
推导与证明
利用切线长定理及其推论、相似 三角形的性质等知识点进行推导 和证明，得出正确的结论。
检查与反思
检查解题过程是否严谨、结论 是否正确，并进行反思和总结
。
典型错误分析及避免方法
忽视切线长定理的前提条件
错误理解题意
在使用切线长定理时，必须明确切线与半 径垂直且切线长相等的前提条件，否则会 导致错误结论。
九年级数学切线长定理市区公开课
目录
• 引言 • 切线长定理基本概念 • 切线长定理应用举例 • 切线长定理相关题型解析 • 实验操作与探究 • 课程总结与回顾
01 引言
课程背景与目的
课程背景
九年级数学是中学数学的重要阶段， 而切线长定理是几何部分的核心内容 之一。本市区公开课旨在帮助学生深 入理解切线长定理及其应用。
地理测量
在地理测量中，可以利用切线长 定理来计算地球表面上两点之间 的距离，或者测量某些地理特征 （如山峰、河流）的高度和宽度。
《切线长定理》教学课件
通过切线长定理，我们可以解决一些复杂的几何问题，如 求圆的切线方程、证明与切线有关的定理等。同时，切线 长定理也是数学竞赛中一些难题和压轴题的解题关键。
PART 04
切线长定理的拓展
REPORTING
WENKU DESIGN
相关定理的介绍
切线长定理
切线与弦的性质定理
切线长定理是几何学中的一个基本定 理，它指出从圆外一点引圆的两条切 线，它们的切线长相等。
定理内容
切线长定理的内容是，一个三角 形的三条外接圆的切线长度相等 。
重要性及应用
重要性
切线长定理是几何学中的基础定理之 一，它在证明其他几何定理、解决几 何问题以及理解几何概念等方面具有 重要作用。
应用
切线长定理在几何学、三角学、解析 几何等领域都有广泛的应用，例如在 解决三角形面积问题、三角形外接圆 问题等方面都有重要的应用。
切线与弦的性质定理是关于切线与弦 的关系的定理，它包括切线与弦的距 离、切线与弦的平行关系等。
切线性质定理
切线性质定理是关于切线的性质和性 质的定理，它包括切线的性质、切线 与半径的关系等。
相关定理的证明
切线长定理的证明
切线长定理可以通过圆周角定理、三角形中位线定理等几何定理 进行证明。
切线性质定理的证明
定理的推论
总结词：丰富多样
详细描述：根据切线长定理，我们可以推导出多个重要的几何结论。例如，当两个圆相切时，它们的切线长度相等；当一个 圆与一个直线相切时，圆心到直线的距离等于圆的半径；当一个圆与一个斜线相切时，圆心到斜线的垂足与圆心和切点的连 线形成一个直角三角形等。
PART 03
切线长定理的应用
定理证明
切线长定理可以通过勾股定理进行 证明，利用圆的性质和勾股定理的 逆定理来推导。
PART 04
切线长定理的拓展
REPORTING
WENKU DESIGN
相关定理的介绍
切线长定理
切线与弦的性质定理
切线长定理是几何学中的一个基本定 理，它指出从圆外一点引圆的两条切 线，它们的切线长相等。
定理内容
切线长定理的内容是，一个三角 形的三条外接圆的切线长度相等 。
重要性及应用
重要性
切线长定理是几何学中的基础定理之 一，它在证明其他几何定理、解决几 何问题以及理解几何概念等方面具有 重要作用。
应用
切线长定理在几何学、三角学、解析 几何等领域都有广泛的应用，例如在 解决三角形面积问题、三角形外接圆 问题等方面都有重要的应用。
切线与弦的性质定理是关于切线与弦 的关系的定理，它包括切线与弦的距 离、切线与弦的平行关系等。
切线性质定理
切线性质定理是关于切线的性质和性 质的定理，它包括切线的性质、切线 与半径的关系等。
相关定理的证明
切线长定理的证明
切线长定理可以通过圆周角定理、三角形中位线定理等几何定理 进行证明。
切线性质定理的证明
定理的推论
总结词：丰富多样
详细描述：根据切线长定理，我们可以推导出多个重要的几何结论。例如，当两个圆相切时，它们的切线长度相等；当一个 圆与一个直线相切时，圆心到直线的距离等于圆的半径；当一个圆与一个斜线相切时，圆心到斜线的垂足与圆心和切点的连 线形成一个直角三角形等。
PART 03
切线长定理的应用
定理证明
切线长定理可以通过勾股定理进行 证明，利用圆的性质和勾股定理的 逆定理来推导。
《切线长定理》PPT课件 人教版九年级数学
切线长定理
A 从圆外一点可以引圆的两条切线，
它们的切线长相等，这一点和圆心的
连线平分两条切线的夹角.
O
P
几何语言: PA，PB分别切⊙O于A，B
B PA = PB ∠OPA=∠OPB
切线长定理为证明线段相 等、角相等提供新的方法.
探究：PA、PB是⊙O的两条切线，
A
A、B为切点，直线OP交于⊙O于
O P
∵∠BAC=25°, ∴∠BAP=65°. C 又∵PA＝PB, ∴∠BAP=∠ABP=65°.
B
∴∠P=180°-∠BAP-∠ABP=50°.
7.如图，一个油桶靠在直立的墙边，量得WY =0.65m， 并且XY⊥WY，这个油桶底面半径是多少?为什么？
解：设圆心为O，连接OW，OX. ∵YW，YX均是⊙O的切线， ∴OW⊥WY，OX⊥XY， 又∵XY⊥WY, ∴∠OWY＝∠OXY＝∠WYX＝90°， ∴四边形OWYX是矩形，又∵OW=OX. ∴四边形OWYX是正方形. ∴OW=WY=0.65m. 即这个油桶底面半径是0.65m.
CA ＝13，求AF，BD，CE的长.
解：设AF=x,则AE=x,
A
CD=CE=AC-AE=13-x,
E
BD=BF=AB-AF=9-x.
F
由BD+CD=BC,可得
(13-x)+(9-x)=14.解得，x=4. B
D
C
因此，AF=4，BD=5，CE=9.
随堂练习 1.如图，△ABC的内切圆⊙O与BC，CA，AB分 别相切于点D，E，F，且AB=11cm，BC=14cm， CA=13cm，则AF的长为( C ) A.3cm B.4cm C.5cm D.9cm
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解：∵点O是△ABC的内心
A
解：∴∵∠点OOB是C△= A1B∠CA的BC内心
ቤተ መጻሕፍቲ ባይዱ
1 12 ∠O∴C∠BO=B12C∠=AC2∠BABC=30°
OO
∴∴∠∠∠OBBCOOBCC=======111211∠18888180A0000°0°°°°C°B---- -=1∠∠2134OO∠00(BBA°°∠CCBA-C--B40∠∠C-°OO+CC12∠BB∠AACCBB)
4、如图，PA、PB、DE分别切⊙O于A、B、C，DE分 别交PA，PB于D、E，已知P到⊙O的切线长为8CM， 则ΔPDE的周长为（ A ）
A.16cm
B.14cm C.12cm
D.8cm
AD
C
P
BE
活动二：
思考
一张三角形的铁皮，如何在它上面截下一块圆 形的用料，并且使圆的面积尽可能大呢？
A
B C
13﹣x
BD=5 cm
B O
9﹣x
D 14
13﹣x
CE=9 cm
C
例题：如图， △ABC的内切圆⊙O与BC、CA、AB分别
相切于点D、E、F，且AB=9cm,BC=14cm，CA=13cm，求 AE、BD、CE的长。
解：设AE=x (cm), 则AF=x (cm)
设CD=y，则CE=y 设BD=z，则BF=y
相切于点D、E、F，且AB=9cm,BC=14cm，CA=13cm，求 AE、BD、CE的长。
解：设AE=x (cm), 则AF=x (cm)
CD=CE=AC﹣AE=13﹣x
BD=BF=AB﹣AF=9﹣x ∵ BD+CD=BC
A
x
x F9
9﹣x
∴（13﹣x）+（9﹣x）=14 13 E
解得 X=4 因此 AE=4 cm
B
C
=180°- 12 (180°- ∠A)=180°- 70°=110°
2
小结
1. 切线长定理
2.如何作三角形的内切圆？
3.三角形的内心的性质 4.区分三角形的内切圆和外接圆，三角 形的内心和外心。
求证： PA PB,APO BPO
A
O
p
B
切线长定理 从圆外一点引圆的两条切线，它们 的切线长相等，圆心和这一点的连线平分两条切 线的夹角。
请你们结合图形用
A
数学语言表达定理
O
B PA、PB分别切⊙O于A、B, 连结PO
p
PA = PB ∠OPA=∠OPB
牛刀小试
1、如图，PM、PN都是圆O的切线，则
（1）图中相等的线段有 OM=ON PM=PN
（2）图中相等的角有 ∠ MPO= ∠ NPO ∠ POM= ∠ PON
∠ OMP= ∠ ONP
2、如图PA、PB切圆于A、B两点，APB 50 连结PO，
则 APO 25 度。
A
O
P
B
3、如图，PA、PB分别切⊙O于点A、B，点E是 ⊙O上一点，且∠AEB=60°,则∠ P= 60°度．
探索
这是一位同学运动完后放的篮球，如果截它的 平面，那么你能从中发现什么几何知识呢？
P
A
B
地面
墙
经过圆外一
点可以有两
P
条直线与圆 相切
活动一：怎样画圆O的切线？
作法：1、在圆周上取一点A，连接AO； 2、过点A作AO的垂线。
A P
O
B
思考：切线长 和切线的区别
和联系？
切线长：在经过圆外一点的圆的切线上，
三角形的内切圆：
与三角形各边都相切的圆叫做三角形的内切圆
三角形的内心：三角形的内切圆的圆心
（即三角形三条角平分线的交点）
A
B O
C
C
C
．o A
．o
A
B
B
三角形外接圆
外接圆圆心：
三角形内切圆
内切圆圆心：
三角形三边垂直平分线的交点。 三角形三个内角平分线的交点。
例题：如图， △ABC的内切圆⊙O与BC、CA、AB分别
牛刀小试
1、如图，Δ ABC的内切圆分别和BC，AC，AB切于D，E，F； 如果AF=2cm,BD=7cm,CE=4cm,则BC= 11,cAmC= 6AcBm=
9cm
A
2 F
E 4
7
C
B
D
练一练
2、如图，△ABC中，∠ AB∠CA=6=04°0°，∠ACB=80 °，点O
是△ABC的内心，求∠ BOC的度数。
这点和切点之间的线段的长。
A
P O
B
小结：切线是直线，不可以度量；切线长是 指切线上的一条线段的长，可以度量。
动手量一量：
测量切线长PA、PB的长度，并比较大小 测量∠1、 ∠2的度数，并比较大小。
A
O
1
2
p
B
你能不能用所学的几何知识证明刚才的结论？
已知：如图，P为⊙ O外一点，PA、PB为⊙ O的切线，A、B为切点，连结PO
由题意得
A
x y
y z
13 14
(1) (2)
z x 9 (3)
x
x F9
z
13 E
B
O
(1)+(2)+(3)得: x+y+z=18 (4)
z
(4)-(1)得 z=5 (4)-(2)得 x=4
y
D 14
(4)-(1)得 y=9
y
因此AE=4 cm BD=5 cm CE=9 cm C