几何体上最短路径问题
勾股定理的应用(最短路径问题)(2)
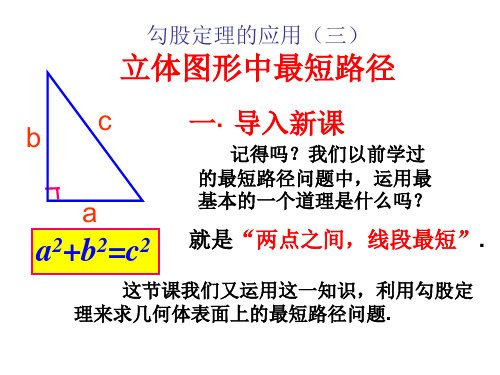
AB= 32+32 = 18=3 2;
(2)经过前(后)面和右(左)面;
AB= 52 +12 = 26 ;
32
(3)经过左(右)面和上(下)底面.
AB 22 42 20 2 5 .
A
3
26
B
A
3
1
25
B
2
1
C B 1
2C
B 2
A
3
2
A1
3
C
Q 3 2 2 5 26 最短路程是3 2 .
四)阶梯(组合几何体)问题
如图是一个三级台阶,它的每一级的长宽和高分别为20dm、
3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂
蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短
路程是2__5________dm.
A
20
C
A
20
3
23
2
32B3源自2 BAB= AC2+BC2 = 202+152 = 625=25 dm
C1
(三条棱长如图所 示),问怎样走路
最短路程是5.
A1 D
1 B1
C
线最短?最短路线 长为多少?
A
A1
5
b2
4
a A1
41
37
B141c
B
A
如果长方形的长、宽、高分别是a、b、c(a>b>c),
你能求出蚂蚁从顶点A1到C的最短路径吗?
练习2:如图,长方体的长为15 cm,宽为 10 cm,高为
20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从 点 A爬到点B,需要爬行的最短距离是_______2c5m.
几何体上最短路径问题
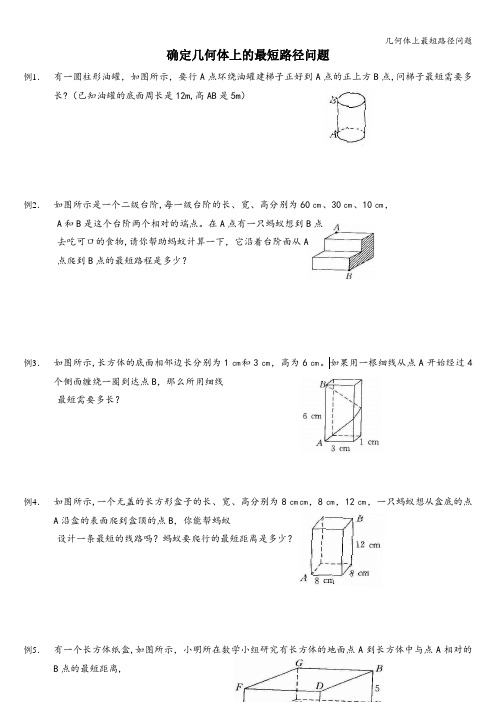
确定几何体上的最短路径问题例1.有一圆柱形油罐,如图所示,要行A点环绕油罐建梯子正好到A点的正上方B点,问梯子最短需要多长?(已知油罐的底面周长是12m,高AB是5m)例2.如图所示是一个二级台阶,每一级台阶的长、宽、高分别为60㎝、30㎝、10㎝,A和B是这个台阶两个相对的端点。
在A点有一只蚂蚁想到B点去吃可口的食物,请你帮助蚂蚁计算一下,它沿着台阶面从A点爬到B点的最短路程是多少?例3.如图所示,长方体的底面相邻边长分别为1㎝和3㎝,高为6㎝。
如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要多长?例4.如图所示,一个无盖的长方形盒子的长、宽、高分别为8㎝㎝,8㎝,12㎝,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,你能帮蚂蚁设计一条最短的线路吗?蚂蚁要爬行的最短距离是多少?例5.有一个长方体纸盒,如图所示,小明所在数学小组研究有长方体的地面点A到长方体中与点A相对的B点的最短距离,若长方体的底面长为12,宽为,高为5,请帮助该小组求出有A点到B点的最短距离.(21。
592≈466,18。
442≈340)变式训练1.有一只蚂蚁要从一个圆柱形玻璃杯的点A爬到点B处,如图所示,已知杯子高8㎝,点B距杯口3㎝(杯口在上),杯子底面半径为4㎝,蚂蚁沿表面从A点爬到B点的最短距离是多少?( 取3)2.如图所示,MN表示一条铁路,A,B分别表示两个城市,它们到铁路所在直线MN的垂直距离分别为AA1=20km,BB1=40km,且A1B1=80km.现要在A1,B1之间设一个中转站P,使两个城市到中转站的距离的和最短.请你设计一个方案确定P点的位置,并求出这个最短距离。
3.如图1-6,圆柱形玻璃杯,高为12㎝,底面周长为18㎝,在杯内离杯底4㎝的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4㎝与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为多少?5.同学们为学校国庆晚会设计了一个圆柱形灯罩,然后在侧面上缠绕红色彩纸如图(1)所示。
3.3勾股定理的应用举例——立体图形中最短路径问题

归●纳5:、圆柱答展开转化为平面图形,利用两点之间
线段最短找到最短路径,然后运用勾股定理求
解。圆柱体的展开图是一个长方形,但需要注
意展开后点的位置的确定。
变式训练:最短路径问题——圆柱
1、有一圆柱形糖罐, 底面周长是12厘米,高AB是5厘米,蚂蚁从
BC
=
16
×
1 2
= 8,
由勾股定理得
AB2= AC2+ BC2=1100
∴AB=10(m) .
最短路径问题——长方体
如图:长方体的长、宽、高分别是12,8,30,在 AB中点C处有一滴蜜糖,一只小虫从E处爬到C处去 吃,有无数种走法,则最短路程是( )
A.15
B.25
C.35
D.45
最短路径问题——长方体 例3.如图是一块长,宽,高分别是 4cm,2cm和1cm的长方体木块一只 蚂蚁要从长方体木块的一个顶点A 处,沿着长方体的表面到长方体上 和A相对的顶点B处吃糖,那么它需 要爬行的最短路径的长是(B )
因为每个面的 大小相同,展 开后长方形的 长宽不变,所 以结果相同。
ቤተ መጻሕፍቲ ባይዱ
无论什么立方体,都必须通过展开后得到平面图形,利用两点 之间线段最短得到最短的距离,再运用勾股定理求出结果。
课堂总结:
知识:立体图形中的最短路径问题
转化
方法:1、展开; 平面图形
2、找起点、终点 3、运用两点之间线段最短找到最短路径; 4、运用勾股定计算。 5、答
勾股定理的应用 立体图形中最短路径问题
立体图形中的最短路径
最短路径问题——圆柱
B
例1、有一个圆柱,它 我怎 的高为12cm,底面半径为 么走
几何体表面的最短路线问题

体顶点A处有一个蚂蚁,现要向顶点B爬行,求最短
路线长.
B
7
侧面展 开图
左
B
3
3 A5
A7
5
AB2 (5 7)2 32 153
B 结论:
AB最短 b c 2 a 2 `
A
长:a, 宽:b, 高:c 且a > b > c > 0
第三项:爬柱子
比赛规则:在圆柱侧面从A走到B,所走路线最 短者获胜.
5
12
立体图形
转化 展开
平面图形
数学思想:转化思想
数学原理:两点之间线段最短
当堂检测:
1.如图,蚂蚁从台阶A处爬到B处它的最短距离是( B ).
A 20 B 25 C 30 D 35
2.如图,长方体的底面边长分别为2cm和4cm,高为5cm,若一只
蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短
2
如图,台阶的长、宽、高分别是30,2,8,求 从A到B所走的的最短距离是 50 .
第二项:翻方块
比赛规则:在方体表面从A走到B,所走路线最 短者获胜.
B
A
如图,方块是边长为1的正方体,求从A到B所走
的最短路线长是
。
第二项:翻方块
如图,方块是边长为1的正方体,求从A到B所走
的最短路线长是
。
B
B
B
答:最短距离是20厘米
路径长为 13
cm.
3.有一个长方体,它的长、宽、高分别为10cm,6cm,12cm.在
顶点A处有一只蚂蚁,它想吃到与顶点A相对的顶点B的食物.已知蚂 蚁沿长方体表面爬行的速度是3cm/s,问蚂蚁能否在7秒内获取到食物? 并说明理由.
几何体最短路径--勾股定理12.22

A.20cm
B.2 10 cm
C.6cm D.无法确定
2O
蛋糕 B
2
A
圆柱(锥)中的半径2cm,一只蚂蚁从
点A沿侧面爬到点B处吃食,要爬行的最短路程( 取3)
是( B)
A.20cm
B. 2 10 cm
2O
蛋糕 B
C.6cm D.无法确定
周长的一半
C6
B
2
A
求解几何体的最短路线长
一、正方体中的最值问题
例1、如图,边长为1的正方体中,一只蚂蚁从顶点A出
发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3
(B) √5
(C)2 (D)1
B C
A
C
2
B
1
A
分析: 由于蚂蚁是沿正方体的外表面爬行的, 故需把正方体展开成平面图形(如图).
二、长方体中的最值问题
D1 A1 D
A
4
C1
1 B1 C
2 B
如果长方形的长、宽、高分别是a、b、c (a>b>c),你能求出蚂蚁从顶点A到C1 的最短路径吗?
从A到C1的最短路径是
小 结: 最短路径问题把几何体适当
展开成平面图形,再利用“两点 之间线段最短”,或点到直线 “垂线段最短”等性质来解决问 题。
②
C
2
A
4
B
AC1 =√42+32 =√25 =5 ;
A1
A
4
B1
C1
1
B2 C
AC1 =√62+12 =√37 ;
D D1
C1
2
③
A 1 A1
4
B1
AC1 =√52+22 =√29 .
08 立体图形上的最短路径问题
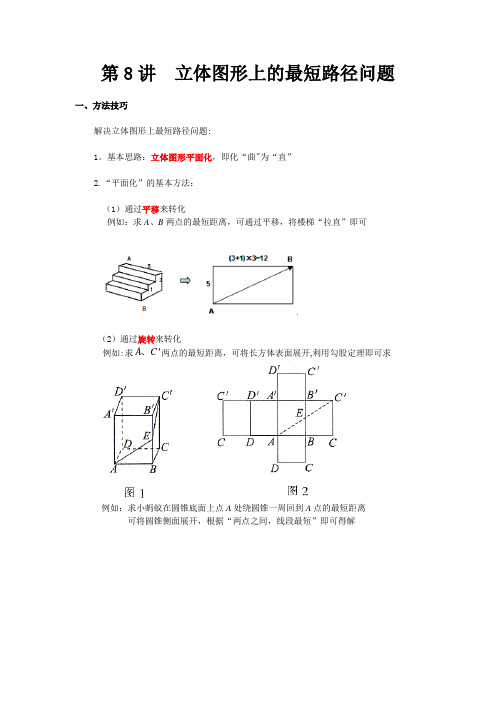
第8讲 立体图形上的最短路径问题一、方法技巧解决立体图形上最短路径问题:1。
基本思路:立体图形平面化,即化“曲"为“直”2.“平面化”的基本方法:(1)通过平移来转化例如:求A 、B 两点的最短距离,可通过平移,将楼梯“拉直”即可(2)通过旋转来转化例如:求'A C 、两点的最短距离,可将长方体表面展开,利用勾股定理即可求例如:求小蚂蚁在圆锥底面上点A 处绕圆锥一周回到A 点的最短距离 可将圆锥侧面展开,根据“两点之间,线段最短”即可得解(3)通过轴对称来转化例如:求圆柱形杯子外侧点B到内侧点A的最短距离,可将杯子(圆柱)侧面展开,作点A关于杯口的对称点'A,根据“两点之间,线段最短”可知'A B即为最短距离3.储备知识点:(1)两点之间,线段最短(2)勾股定理4。
解题关键:准确画出立体图形的平面展开图二、应用举例类型一通过平移来转化【例题1】如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A 和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想要到B点去吃可口的食物,请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?【答案】13cm【解析】试题分析:只需将其展开便可直观得出解题思路,将台阶展开得到的是一个矩形,蚂蚁要从B 点到A 点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.试题解析:解:展开图如图所示,2251213AB cm =+=所以,蚂蚁爬行的最短路线是13cm类型二 通过旋转来转化【例题2】如下图,正四棱柱的底面边长为5cm ,侧棱长为8cm ,一只蚂蚁欲从正四棱柱底面上的A 点沿棱柱侧面到点C'处吃食物,那么它需要爬行的最短路径的长是多少?【答案】cm 412【解析】试题分析:解这类题应将立体图形展开,转化为平面图形,把空间两点的距离转化为平面上两点间的距离,利用“同一平面内两点间的最短路线是连接这两点的线段”进行计算.试题解析:解:如图1,设蚂蚁爬行的路径是AEC'(在面ADD'A’上爬行是一样的).将四棱柱剪开铺平使矩形AA’B’B 与BB’C’C 相连,连接AC’,使E 点在AC'上(如图2))(412810')('2222cm CC BC AB AC =+=++=所以这只蚂蚁爬行的最短路径长为cm 412【难度】一般【例题3】如下图所示,圆柱形玻璃容器高18cm ,底面周长为60cm ,在外侧距下底1cm 的点S 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm 的点F 处有一苍蝇,试求蜘蛛捕获苍蝇充饥所走的最短路线的长度.【答案】34cm【解析】试题分析:展开后连接SF ,求出SF 的长就是捕获苍蝇的最短路径,过点S 作SE CD ⊥于E ,求出SE 、EF ,根据勾股定理求出SF 即可。
专题1.4 勾股定理中的最短路径问题(教师版)
专题1.4 勾股定理中的最短路径问题1、熟练掌握勾股定理的最短路径问题(主要包含:长方体、圆柱、圆锥、将军饮马等)。
2、解决实际问题时,要善于构造直角三角形,把实际问题抽象成几何问题.知识点01 最短路径问题平面展开图-最短路径问题几何体中最短路径基本模型如下:基本思路:将立体图形展开成平面图形,利用两点之间线段最短确定最短路线,构造直角三角形,利用勾股定理求解。
【知识拓展1】圆柱有关的最短路径问题【微点拨】计算跟圆柱有关的最短路径问题时,要注意圆柱的侧面展开图为矩形,利用两点之间线段最短结合勾股定理进行求解,注意展开后两个端点的位置,有时候需要用底面圆的周长进行计算,有时候需要用底面圆周长的一半进行计算。
要点总结:1)运用勾股定理计算最短路径时,按照展开—定点—连线—勾股定理的步骤进行计算;2)缠绕类题型可以求出一圈的最短长度后乘以圈数。
例1.(2022·山东青岛·八年级期末)如图,一个圆桶,底面直径为16cm ,高为18cm ,则一只小虫从下底点A 处爬到上底B 处再回到A 处,则小虫所爬的最短路径长是( )(p 取3)A.60cm B.40cm C.30cm D.20cm【答案】A【分析】先将圆柱的侧面展开为一矩形,而矩形的长就是底面周长的一半,高就是圆柱的高,再根据勾股定理就可以求出其值.【详解】解:展开圆柱的侧面如图,根据两点之间线段最短就可以得知AB最短.由题意,得AC=3×16÷2=24,在Rt△ABC中,由勾股定理,得30AB===cm.∵一只小虫从下底点A处爬到上底B处再回到A处,∴最短路径长为60cm.故选:A.【点睛】本题考查了圆柱侧面展开图的运用,两点之间线段最短的运用,勾股定理的运用.在解答时将圆柱的侧面展开是关键.【即学即练】1.(2022·吉林长春·八年级期末)如图,有一个圆柱,底面圆的直径AB=24pcm,高BC=10cm,在BC的中点P处有一块蜂蜜,聪明的蚂蚁能够找到距离食物的最短路径,则蚂蚁从点A爬到点P的最短路程为_____cm.【答案】13【分析】化“曲”为“平”,在平面内,得到两点的位置,再根据两点之间线段最短和勾股定理求解即可.【详解】将圆柱体的侧面展开,如图所示:AB=12底面周长=12×p×24p=12(cm),BP=12BC=5(cm),所以AP(cm),故蚂蚁从A点爬到P点的最短距离为13cm,故答案为:13.【点睛】本题考查最短距离问题,化“曲”为“平”,在平面内,利用两点之间线段最短和勾股定理是常用求解方法.2.(2022·浙江金华初三月考)如图,圆柱底面半径为4pcm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )A.24cm B.30cm C.cm D.cm【答案】B【分析】要求圆柱体中两点之间的最短路径,最直接的作法,就是将圆柱体展开,然后利用两点之间线段最短解答.【解析】解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB;即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短;∵圆柱底面半径为4pcm,∴长方形的宽即是圆柱体的底面周长:2π×4p=8cm;又∵圆柱高为18cm,∴小长方形的一条边长是6cm;根据勾股定理求得AC=CD=DB=10cm;∴AC+CD+DB=30cm;故选:B.【点睛】本题主要考查了圆柱的计算、平面展开−−路径最短问题.圆柱的侧面展开图是一个长方形,此长方形的宽等于圆柱底面周长,长方形的长等于圆柱的高.本题就是把圆柱的侧面展开成长方形,“化曲面为平面”,用勾股定理解决.【知识拓展2】长方体有关的最短路径问题想【微点拨】计算跟长方体有关的最短路径问题时,要熟悉长方体的侧面展开图,利用两点之间线段最短结合勾股定理进行求解,注意长方体展开图的多种情况和分类讨论。
勾股定理--与最短路径问题
17.1(11)勾股定理--与最短路径问题一.【知识要点】1.两点之间线段最短:⑴将军饮马型;⑵几何体上两点最短型2.垂线段最短型3.造桥选址型二.【经典例题】1.如图一个圆柱,底圆周长10cm ,高4cm ,一只蚂蚁沿外壁爬行,要从A 点爬到B 点,则最少要爬行 cm .2.如图一个圆柱,底圆周长10cm ,高4cm ,点B 距离上边缘1cm,一只蚂蚁沿外壁爬行,要从A 点爬到B 点,则最少要爬行 cm .3.如图,圆柱形容器中,高为0.4m ,底面周长为1m ,在容器内壁..离容器底部0.3m 的点B 处有一蚊子,此时一只壁虎正好在容器外壁..,与蚊子相对..的点A 处,求壁虎捕捉蚊子的最短距离(容器厚度忽略不计).4.编制一个底面半径为6cm 、高为16cm 的圆柱形花柱架,需用沿圆柱表面绕织一周的竹条若干根,如图中的111AC B ,222,A CB ,则每一根这样的竹条的长度最少是__________.5.如图,圆柱底面半径为cm ,高为9cm ,点A 、B 分别是圆柱两底面圆周上的点,且A 、B在同一高上,用一根棉线从A 点顺着圆柱侧面绕3圈到B 点,则这根棉线的长度最短为______.6.一只蚂蚁从长为4cm,宽为3 cm ,高是5 cm 的长方体纸箱的A 点沿纸箱爬到B 点,那么它所行的最短路线的长是____________cm 。
7.已知 A (1,1)、B (4,2).P 为 x 轴上一动点,求 PA+PB 的最小值.8.如图是一个三级台阶,它的每一级的长、宽和高分别为20 dm,3 dm,2 dm ,A 和B 是这个台阶两个相对的端点,A 点有一只蚂蚁,想到B 点去吃可口的食物,则蚂蚁沿着台阶面爬到B 点的最短路程是__________dm.2A B三.【题库】【A 】1.如图,一个长方体盒子,一只蚂蚁由A 出发,在盒子的表面上爬到点C 1,已知AB=7cm ,BC=CC 1=5 cm ,则这只蚂蚁爬行的最短路程是________.2.如图是一个三级台阶,它的每一级的长、宽和高分别为9、3和1,A 和B 是这个台阶两个相对的端点,A 点有一只蚂蚁,想到B 点去吃可口的食物,则这只蚂蚁沿着台阶面爬行的最短路程是________.3.如图,∠ABC =30°,点D 、E 分别在射线BC 、BA 上,且BD =2,BE =4,点M 、N 分别是射线BA 、BC 上的动点,当DM +MN +NE 最小时,(DM +MN +NE )2的值为( )A 、20B 、26C 、32D 、36【B 】1.如图所示,正方形 ABCD 的面积为 12,△ABE 是等边三角形,点 E 在正方形 ABCD 内,在对角线 AC 上有一点 P ,使 PD+PE 的和最小,则这个最小值为( ) A.23 B. 26 C.3 D.6A 1B 1C 1D 1 A B C D2.如图,一个无盖的长方体长、宽、高分别为8cm 、8cm 、12cm ,一只蚂蚁从A 爬到C 1,怎样爬路线最短,最短路径是多少?3.如图,在Rt ABC ∆中,90,45,2B BCA AC ︒︒∠=∠==,点D 在BC 边上,将ABD ∆沿直线AD 翻折,点B 恰好落在AC 边上的点E 处,若点P 是直线AD 上的动点,连接,PE PC ,则PEC ∆的周长的最小值为( )A .22-B .2C .21+D .14.如图,已知圆柱底面的周长为4dm ,圆柱高为2dm ,在圆柱的侧面上,过点A 和点C 嵌有一圈金属丝,则这圈金属丝的周长最小为( )A .4dmB .2dmC .2dmD .4dm8cm 8cm12cm【C 】 1.(8分)如图,要在河边修建一个水泵站,分别向张村A 和李庄B 送水,已知张村A. 李庄B 到河边的距离分别为2km 和7km ,且张、李二村庄相距13km.(1)水泵应建在什么地方,可使所用的水管最短?请在图中设计出水泵站的位置;(2)如果铺设水管的工程费用为每千米1500元,为使铺设水管费用最节省,请求出最节省的铺设水管的费用为多少元?2.已知直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD=2,BC=DC=5,点P 在BC 上移动,则当PA+PD 取最小值时,PA+PD 长为( )A .8 B.4+15 C .152 D .1723.如图,在边长为 2 的菱形 ABCD 中,∠ABC =60°,若将△ACD 绕点 A 旋转,当 AC ′、AD ′分别与 BC 、CD 交于点 E 、F ,则△CEF 的周长的最小值为( )A.2B.23C.2+3D. 44.如图,在矩形ABCD 中,AB =5,BC =8,点E 是BC 中点,点F 是边CD 上的任意一点,则△AEF 的周长最小时值为( )A .17B .21C .13+41 D. 13+345.如图,四边形ABCD 中,∠BAD=120°,∠B=∠D=90°,在BC 、CD 上分别找一点M 、N ,使△AMN 周长最小时,则∠AMN+∠ANM 的度数为( )。
八上几何最短路径问题
八上几何最短路径问题
嘿,小伙伴们!今天咱们来唠唠八上几何最短路径问题。
简单来说呢,这就是让咱们在各种几何图形里,找出从一个点到另一个点的最短路线。
比如说,在一个三角形里,从一个顶点到对边上的某个点,怎么走距离最短。
这可不是随便走走就行的哦,得用咱们的聪明才智好好琢磨琢磨。
常见的类型
1. 两点之间线段最短
这可是最基本的啦。
比如说,给你两个点 A 和 B,那直接把它们连起来的线段就是最短的路径。
2. 直线同侧两定点到直线上一动点距离之和最小
就像在一条直线的同侧有两个固定的点 P 和 Q,然后在这条直线上找一个动点 M,让 PM + QM 的和最小。
这种情况就得作其中一个点关于直线的对称点,然后连接另一个点和对称点,与直线的交点就是咱们要找的动点啦。
解题方法和技巧
1. 画图很重要
先把题目里的几何图形画清楚,把关键的点和线标出来,这样能让咱们思路更清晰。
2. 利用对称性质
遇到那种同侧两定点的问题,对称可是个好帮手,能把问题变得简单不少。
3. 多做练习题
熟能生巧嘛,做得多了,碰到类似的问题就能很快找到思路啦。
几何最短路径问题虽然有点小复杂,但是只要咱们认真思考,多练习,肯定能轻松拿下!加油哦小伙伴们!。
求解几何体的最短路经长之——正方体、长方体中的最值问题
求解几何体的最短路经长之——正方体、长方体中的最值问题【正方体】如图,边长为1厘米的正方体中,一只瓢虫从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是?两点之间直线最短!图中是一个立体图形,应当把它展开!展开之后连接A和C,即最短路径。
已知AB为1厘米,BC为正方体的两个棱长即2厘米,根据勾股定理,求得最短路径为√5厘米。
结论:展开正方体中的最短路径为两个正方形组成的长方形的对角线长【长方体】如图是一块长,宽,高分别是4厘米、5厘米、3厘米的长方体木块,一只瓢虫要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是?想一想,该如何展开呢?有三种情况!第一种:把我们所看到的前面和上面组成一个平面,如下图展开的长方形两边分别是4厘米和8厘米(3+5=8),根据勾股定理,AB长√80厘米第二种:把我们看到的左面与上面组成一个平面,如下图展开的长方形两边分别是5厘米和7厘米(3+4=7),根据勾股定理,AB长√74厘米第三种:把我们所看到的前面和右面组成一个平面,如下图展开的长方形两边分别是3厘米和9厘米(5+4=9),根据勾股定理,AB长√90厘米三种情况比较而言,最短的是第二种,即最短距离是√74厘米结论:长方体中的最值问题,将长方体按三种方式展开,比较最短的走法。
练习题:1,如图是一个棱长为4厘米的正方体盒子,一只蚂蚁在AE的中点M处,它到CD的中点N 的最短路线是多少?2,如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点B处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?答案:1. 2√10厘米2. 5厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
确定几何体上的最短路径问题
例1.有一圆柱形油罐,如图所示,要行A点环绕油罐建梯子正好到A点的正上方B点,问梯子最短需要多长?(已知油罐的底面周长是12m,高AB是5m)
例2.如图所示是一个二级台阶,每一级台阶的长、宽、高分别为60㎝、30㎝、10㎝,A和B是这个台阶两个相对的端点。
在A点有一只蚂蚁想到B点
去吃可口的食物,请你帮助蚂蚁计算一下,它沿着台阶面从A
点爬到B点的最短路程是多少?
例3.如图所示,长方体的底面相邻边长分别为1㎝和3㎝,高为6㎝.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线
最短需要多长?
例4.如图所示,一个无盖的长方形盒子的长、宽、高分别为8㎝㎝,8㎝,12㎝,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,你能帮蚂蚁
设计一条最短的线路吗?蚂蚁要爬行的最短距离是多少?
例5.有一个长方体纸盒,如图所示,小明所在数学小组研究有长方体的地面点A到长方体中与点A相对的B点的最短距离,
若长方体的底面长为12,宽为,高
为5,请帮助该小组求出有A点到
B点的最短距离。
(21.592≈466,18.442≈340)
变式训练
1.有一只蚂蚁要从一个圆柱形玻璃杯的点A爬到点B处,如图所示,已知杯子高8㎝,点B距杯口3㎝(杯口在上),杯子底面半径为4㎝,蚂蚁沿表面
从A点爬到B点的最短距离是多少?( 取3)
2.如图所示,MN表示一条铁路,A,B分别表示两个城市,它们到铁路所在直线MN的垂直距离分别为AA1=20km,BB1=40km,且A1B1=80km。
现要在A1,B1之间设一个中转站P,使两个城市到中转站的距离的和最短。
请你设计一个方案确定P点的位置,并求出这个最短距离。
3.如图1-6,圆柱形玻璃杯,高为12㎝,底面周长为18㎝,在杯内离杯底4㎝的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4㎝与
蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为多少?
5.同学们为学校国庆晚会设计了一个圆柱形灯罩,然后在侧面上缠绕
红色彩纸如图(1)所示。
已知圆筒高108㎝,周长36㎝,如果在
表面缠绕彩纸4圈,应需彩纸多长?
6.如图所示,李俊的家在高楼的第15层,一天他去买竹竿,如果
电梯的长、宽、高分别是1.2m、1.2m、2.1m,则他所买的竹竿
的最大长度是多少?
7.将一根24㎝的筷子,置于底面直径为5㎝,高为12㎝的圆柱形水杯中(如图),设筷
子露在杯子外面的长为h㎝,则h的取值范围是。
