《高等数学第一章》PPT课件
合集下载
高数一章9节ppt课件
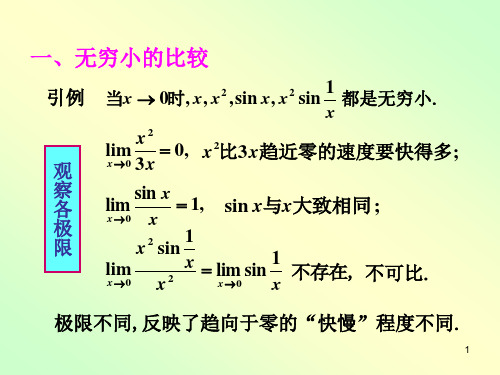
用等价无穷小可给出函数的近似表达式:
因若 lim 1, 则有 o( ).
tan x x o( x), e x 1 x o( x)
14
思考题
1.任何两个无穷小量都可以比较吗？
2. 比较下列各对无穷小的阶 1) x 1时, 1 x 与1 x . 1 x 2) x 0时, 1 x 1 x与sin x tan x.
同阶无穷小.
3
因 lim x0
1
cos x2
x
=
1 2
,所以当x
0时,1
cos
x是
关于x的二阶无穷小.
因lim sin x =1,所以当x 0时,sin x与x是等价 x0 x
无穷小,即sin x x ( x 0).
4
n 1 x 1 1 x. n
5
二、等价无穷小的性质
定理1 o( ).
12
例7 求 lim tan x sin x . x0 sin3 2 x
错 解 当x 0时, tan x ~ x, sin x ~ x.
原式
x x lim x0 (2 x)3
0.
正确解法如下:
解 当x 0时, sin 2x ~ 2x,
tan x sin x tan x(1 cos x) ~ 1 x3 ,
1 x 1 x 是比sinx tanx低阶的无穷小.
17
见例1
1
解 当x 0,(1 x2 )3 1
1 x2 ,cos x 1
1 x2
3
2
所以
1
(1 x2 )3 1
lim
lim
1 x2 3
x0 cos x 1
x0 1 x2
2
2 3
《高等数学》电子课件(同济第六版)01第一章第1节函数
复合函数的实际应用
复合函数在数学、物理、工程等领域有广 泛的应用。
反函数
反函数的定义
反函数是原函数关于y=x对称的函数。
反函数的性质
反函数具有原函数的性质，如连续性、可导性等。
反函数的求导法则
反函数的求导法则与原函数有关，可以通过交换x和y的导数来实现。
反函数的应用
反函数在数学、物理、工程等领域有广泛的应用，如解方程、优化问题等。
函数单调性的定义
如果对于函数的定义域内的任意两个数$x_1$和$x_2$，当$x_1 < x_2$时，都 有$f(x_1) leq f(x_2)$（或$f(x_1) geq f(x_2)$），则称函数在该区间内单调递 增（或单调递减）。
单调性的判定方法
通过比较函数在不同区间内的增减性，可以判断函数的单调性。此外，导数也 是判断函数单调性的重要工具，如果函数在某区间内的导数大于0，则函数在该 区间内单调递增；如果导数小于0，则函数单调递减。
04
函数的图像与性质
函数的图像
函数图像的概念
函数图像是表示函数值的点在平面上 的集合。通过函数图像，我们可以直 观地了解函数的形态和变化趋势。
函数图像的绘制方法
绘制函数图像通常需要确定函数的定 义域和值域，然后根据函数的解析式 ，在坐标系上标出对应的点，最后用 光滑的曲线将它们连接起来。
函数的单调性
答案与解析
$|x|$ 是偶函数。
$x^3$ 是奇函数。
判断下列函数是否为奇函 数或偶函数
01
03 02
答案与解析
$frac{1}{x}$ 是奇函数。
解析：奇函数的定义是对于定义域内的任意 $x$，都有 $f(-x) = -f(x)$；偶函数的定义是对 于定义域内的任意 $x$，都有 $f(-x) = f(x)$。 根据这些定义，可以判断出 $x^3$、$|x|$ 和 $frac{1}{x}$ 的奇偶性。
复合函数在数学、物理、工程等领域有广 泛的应用。
反函数
反函数的定义
反函数是原函数关于y=x对称的函数。
反函数的性质
反函数具有原函数的性质，如连续性、可导性等。
反函数的求导法则
反函数的求导法则与原函数有关，可以通过交换x和y的导数来实现。
反函数的应用
反函数在数学、物理、工程等领域有广泛的应用，如解方程、优化问题等。
函数单调性的定义
如果对于函数的定义域内的任意两个数$x_1$和$x_2$，当$x_1 < x_2$时，都 有$f(x_1) leq f(x_2)$（或$f(x_1) geq f(x_2)$），则称函数在该区间内单调递 增（或单调递减）。
单调性的判定方法
通过比较函数在不同区间内的增减性，可以判断函数的单调性。此外，导数也 是判断函数单调性的重要工具，如果函数在某区间内的导数大于0，则函数在该 区间内单调递增；如果导数小于0，则函数单调递减。
04
函数的图像与性质
函数的图像
函数图像的概念
函数图像是表示函数值的点在平面上 的集合。通过函数图像，我们可以直 观地了解函数的形态和变化趋势。
函数图像的绘制方法
绘制函数图像通常需要确定函数的定 义域和值域，然后根据函数的解析式 ，在坐标系上标出对应的点，最后用 光滑的曲线将它们连接起来。
函数的单调性
答案与解析
$|x|$ 是偶函数。
$x^3$ 是奇函数。
判断下列函数是否为奇函 数或偶函数
01
03 02
答案与解析
$frac{1}{x}$ 是奇函数。
解析：奇函数的定义是对于定义域内的任意 $x$，都有 $f(-x) = -f(x)$；偶函数的定义是对 于定义域内的任意 $x$，都有 $f(-x) = f(x)$。 根据这些定义，可以判断出 $x^3$、$|x|$ 和 $frac{1}{x}$ 的奇偶性。
《高等数学第一章》PPT课件
若函数f ( x)在[ x0 , b)内有定义,且f ( x0 0) f ( x0 ),
则
称f
(
x
)在
点x
处右
0
连续.
定理 函数 f ( x)在 x0 处连续 是函数 f ( x)在 x0
处既左连续又右连续.
例2
讨论函数
f
(x)
x 2,
x
2,
x 0, x 0,
一、函数的连续性
1.函数的增量
设函数 f ( x)在U ( x0 )内有定义, x U ( x0 ), x x x0 , 称为自变量在点 x0的增量.
y f ( x) f ( x0 ),称为函数 f ( x)相应于x的增量.
y
y
y f (x)
y f (x)
★
f
(
x)
1, 1,
当x是有理数时, 当x是无理数时,
在定义域 R内每一点处都间断, 但其绝对值处 处连续.
判断下列间断点类型:
y
y f x
x1 o
x2
x3
x
例8 当a取何值时,
函数
f
(x)
cos a
x, x,
x 0, 在 x 0处连续. x 0,
解 f (0) a,
y
解 f (0 0) 0, f (0 0) ,
x 1为函数的第二类间断点.
o
x
这种情况称为无穷间 断点.
例7 讨论函数 f ( x) sin 1 在 x 0处的连续性. x
解 在x 0处没有定义,
且 lim sin 1 不存在. x0 x
高等数学第一章复习课ppt课件.ppt
3.极限的性质
定理 设 lim f ( x) A,lim g( x) B,则 (1) lim[ f ( x) g( x)] A B; (2) lim[ f ( x) g( x)] A B; (3) lim f ( x) A , 其中B 0. g(x) B
推论1 如果lim f ( x)存在,而c为常数,则 lim[cf ( x)] c lim f ( x).
1 o 1
x
(5) 函数的周期性:
设函数 f(x) 的定义域为D，如果存在一个不为零的
数l,使得对于任一 x D,有 x l D .且 f(x+l)=f(x)
恒成立,则称f(x)为周期函数,l 称为 f(x) 的周期.（通
常说周期函数的周期是指其最小正周期）.
T 1
y
y x [x]
1
o
1
x
3.反函数
由y f ( x)确定的y f 1( x)称为反函数.
y sinh x
4.隐函数
y f 1( x) ar sinh x
由方程F ( x, y) 0所确定的函数 y f ( x)称为隐函数.
5.反函数与直接函数之间的关系
设函数f ( x)是一一对应
函数, 则
y y f 1( x)
3.连续的充要条件
定理 函数f ( x)在 x0 处连续 是函数f ( x)在 x0 处 既左连续又右连续.
4.间断点的定义
函数f ( x)在点x0处连续必须满足的三个条件: (1) f ( x)在点x0处有定义;
(2) lim f ( x)存在; x x0
(3) lim x x0
f (x)
f ( x0 ).
2.函数的性质
高等数学第一章的总结-PPT
n
1
lim
n
n2 n2
lim n1
1
n2
1
lim n
n
1
n2
n2
1
2
n2
1
n
1
例:
lim
1
1
(e n
2
en
n
en
)
n n
1
e
x
d
x
e 1
0
1
n
1
解：原式
lim
n
1 n
e
n
(1
e
1
n
)
(1
e) lim
n
n
1
1en
1en
1
(1 e) lim ln(1 u) (1 e) lim ln(1 u) u e 1.
)x
e
两个重要极限
(1) lim sin 1
0
(2) lim ( 1 1 ) e
1
或 lim(1 ) e
0
注: 代表相同的表达式
思考与练习
填空题 ( 1～4 )
1. lim sin x __0___ ;
x x
3. lim xsin 1 _0___ ;
x0
x
2. lim xsin 1 __1__ ;
从此时刻以后 0 x x0 0 x x0
f (x)
f (x) A
x x0
x x0 0
思考题
x
sin
1 x
,
试问函数 f ( x) 10,
5
x2,
x0 x 0在x 0处
x0
的左、右极限是否存在？当 x 0 时， f ( x) 的
高等数学-第1章课件
x x0
三、函数极限的性质
第三节 极限的运算
一、极限的运算法则
法则1 法则2
x x0
lim[ f ( x) g ( x)] lim f ( x) lim g ( x) A B
x x0 x x0 x x0 x x0
x x0
lim[ f ( x ) g ( x )] lim f ( x ) lim g ( x ) A B
第 一 章 函 数 ︑ 极 限 与 连 续
目录
第一节 函数
第二节 极限
第三节 极限的运算 第四节 无穷小与无穷大 第五节 函数的间断性与连续点 第六节 初等函数的连续性
第一节 函数
一、集合、区间与邻域
1.集合
集合（简称集）是具有某种共同性质的事物的全 体，组成集合的单一事物称为该集合的元素。
有限集合 有限个元素构成 北京户籍人口
° a
• a •
a°Leabharlann a3.邻域设 x0, δ R, 其中δ > 0,以 x0为中心,以δ 为半径,长为 2δ的
开区间. 即
( x0 , x0 ) { x x x0 , 0}
称为点 x0 的 δ 邻域 , 记为U(x0 , δ ).
2
x0
x0
x0
集合的运算及关系
由所有属于集合A或属于集合B的元 并集 素所组成的集合，称为集合A与B的 并集 交集 差集 由属于集合A且属于集合B的所有元 素组成的集合，称为A与B的交集
由所有属于集合A 而不属于集合B 的 元素组成的集合
A∪B A∪B={x|x∈A,或 x∈B}
A∩B A-B
A∩B={x|x∈A,且 x∈B} A-B={x|x∈A,且 xB}
三、函数极限的性质
第三节 极限的运算
一、极限的运算法则
法则1 法则2
x x0
lim[ f ( x) g ( x)] lim f ( x) lim g ( x) A B
x x0 x x0 x x0 x x0
x x0
lim[ f ( x ) g ( x )] lim f ( x ) lim g ( x ) A B
第 一 章 函 数 ︑ 极 限 与 连 续
目录
第一节 函数
第二节 极限
第三节 极限的运算 第四节 无穷小与无穷大 第五节 函数的间断性与连续点 第六节 初等函数的连续性
第一节 函数
一、集合、区间与邻域
1.集合
集合（简称集）是具有某种共同性质的事物的全 体，组成集合的单一事物称为该集合的元素。
有限集合 有限个元素构成 北京户籍人口
° a
• a •
a°Leabharlann a3.邻域设 x0, δ R, 其中δ > 0,以 x0为中心,以δ 为半径,长为 2δ的
开区间. 即
( x0 , x0 ) { x x x0 , 0}
称为点 x0 的 δ 邻域 , 记为U(x0 , δ ).
2
x0
x0
x0
集合的运算及关系
由所有属于集合A或属于集合B的元 并集 素所组成的集合，称为集合A与B的 并集 交集 差集 由属于集合A且属于集合B的所有元 素组成的集合，称为A与B的交集
由所有属于集合A 而不属于集合B 的 元素组成的集合
A∪B A∪B={x|x∈A,或 x∈B}
A∩B A-B
A∩B={x|x∈A,且 x∈B} A-B={x|x∈A,且 xB}
高等数学 第一部分 函数、极限与连续 课件ppt
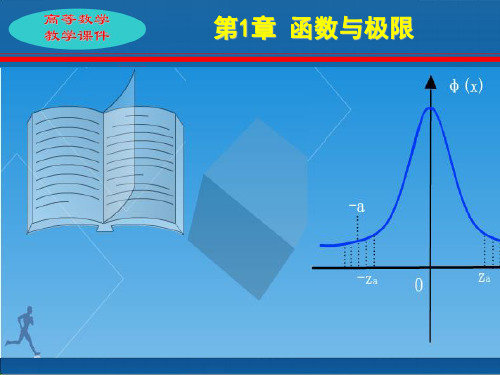
a 1 时，y log a x 单调递增， y
y logax (a 1)
0 a 1时y， log a x 单调递减。 o
x
y logax (0 x 1)
1-1 函数
4. 三角函数
正弦函数：y sin x
定义域：(,)．
值 域：[1,1] ．
单调性：
在
2
2k , 2
2k
单调增加；2
1-1 函数
函数的表示法
1）以数学式子表示函数的方法叫公式法如： y x2, y cos x 公式法的优点是便于理论推导和计算．
2）以表格形式表示函数的方法叫表格法，它是 将自变量的值与对应的函数值列为表格，如三角函 数表、对数表等，表格法的优点是所求的函数值容 易查得．
3）以图形表示函数的方法叫图形法或图象法， 这种方法在工程技术上应用很普遍，其优点是直观 形象，可看到函数的变化趋势．
4
2
3
（2） y sin x cosx 的周期T 2
（3） y cos 2x tan x 的周期T 3 ．
3 3 6
1-1 函数
4．有界性
定义 1.6 设函数 y f (x) 的定义域为 D，如果存在 一个正常数 M，使得对于任意的 x D ，都有| f (x) | M , 则称函数 y f (x) 在 D 上有界．如果不存在这样的正常 数 M，即对任意的正常数 M，都存在某个点 x0 D ，使 得| f (x0 ) | M , 则称函数 y f (x) 在 D 上无界．
2k ,
3
2
2k
单调减少．
奇偶性：奇函数．
周期性：周期函数．
有界性：有界函数．
余弦函数：y cosx
1-1 函数
大一高数上_PPT课件_第一章
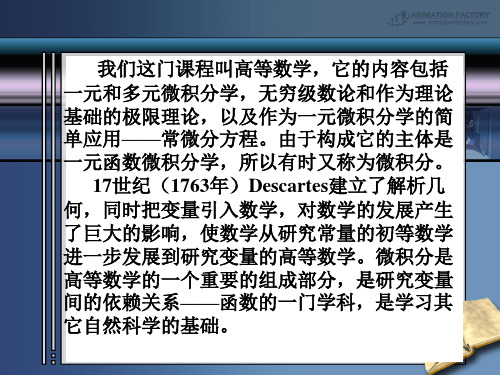
几个数集:
R表示所有实数构成的集合，称为实数集。
Q表示所有有理数构成的集合，称为有理集。 Z表示所有整数构成的集合，称为整数集。 N表示所有自然数构成的集合, 称为自然数集。 子集: 若xA，则必有xB，则称A是B 的子集, 记 为AB（读作A包含于B）。 显然，N Z ，Z Q ，Q R 。
的上方。
y y=f(x) O x
y=K2
如果存在数 M,使对任一 xX，有 | f(x) |M， 则称函数f(x)在X上有界；如果这样的M不存在， 则称函数f(x)在X上是无界函数，就是说对任何M ，总存在 x1X，使|f(x)|>M。 有界函数的图形特点： 函数y = f(x)的图形在直线y = - M和y = M y 的之间。
高等数学研究的主要对象是函数，主要研 究函数的分析性质（连续、可导、可积等）和 分析运算（极限运算、微分法、积分法等）。 那么高等数学用什么方法研究函数呢？这个方 法就是极限方法，也称为无穷小分析法。从方 法论的观点来看，这是高等数学区别于初等数 学的一个显著标志。 由于高等数学的研究对象和研究方法与初 等数学有很大的不同，因此高等数学呈现出 以下显著特点：
周期函数的图形特点：
y
y=f(x)
-2l
-l
O
l
2l
x
四、反函数与复合函数
1. 反函数 设函数y=f(x)的定义域为D，值域为W。 对于任一数值 yW，D上可以确定唯一数值 x 与 y 对应，这个数值 x 适合关系 f(x)=y。
如果把 y看作自变量，x 看作因变量，按 照函数的定义就得到一个新的函数，这个 新函数称为函数y=f(x)的反函数，记作 x=f -1(y)。
什么样的函数存在反函数？
《高等数学》PPT课件-第一章极限
②逆命题不成立：有界列不一定收敛. ③数列有界是收敛的必要条件(不充分).
2.1.2 函数极限 【数列极限】
【函数的极限】 有
—— 整标函数 两大类情形
【直观定义】在x→∞时，函数值f (x)无限接近于一 个确定的常数A ,称A为f (x)当x→∞时的极限. 记作
[两种特殊情况]
[定理] [例如]
注意 无穷多个无穷小的代数和未必是无穷小.
定理3 有界函数与无穷小的乘积是无穷小. 推论1 在同一过程中,有极限的变量与无穷小的乘 积是无穷小. 推论2 常数与无穷小的乘积是无穷小. 推论3 有限个无穷小的乘积也是无穷小.
都是无穷小
2.3.2无穷大
绝对值无限增大的变量称为无穷大.
特殊情形：正无穷大，负无穷大．
[极限存在定理] [例1] [证]
左右极限存在但不相等, [注] 一般而言, 分段函数的极限要分左右极限考察.
2.1.3函数极限的性质
1.[唯一性]
2.[ 局部有界性]
[定理2]
3.[ 保号性] [定理3]
2.2 极限运算法则
定理
推论1
常数因子可以提到极限记号外面. 推论2
2.3 无穷小量与无穷大量
注意 （1）无穷大是变量,不能与很大的数混淆;
（3）无穷大是一种特殊的无界变量,但是无 界变量未必是无穷大.
2.3.3无穷小与无穷大的关系
定理4 在同一过程中,无穷大的倒数为无穷小; 恒不为零的无穷小的倒数为无穷大.
意义 关于无穷大的讨论,都可归结为关于无穷小 的讨论.
2.3.4 无穷小量的比较
二、极限
2.1 极限的定义
2.1.1 数列极限
截丈问题： “一尺之棰，日截其半，万世不竭”
2.1.2 函数极限 【数列极限】
【函数的极限】 有
—— 整标函数 两大类情形
【直观定义】在x→∞时，函数值f (x)无限接近于一 个确定的常数A ,称A为f (x)当x→∞时的极限. 记作
[两种特殊情况]
[定理] [例如]
注意 无穷多个无穷小的代数和未必是无穷小.
定理3 有界函数与无穷小的乘积是无穷小. 推论1 在同一过程中,有极限的变量与无穷小的乘 积是无穷小. 推论2 常数与无穷小的乘积是无穷小. 推论3 有限个无穷小的乘积也是无穷小.
都是无穷小
2.3.2无穷大
绝对值无限增大的变量称为无穷大.
特殊情形：正无穷大，负无穷大．
[极限存在定理] [例1] [证]
左右极限存在但不相等, [注] 一般而言, 分段函数的极限要分左右极限考察.
2.1.3函数极限的性质
1.[唯一性]
2.[ 局部有界性]
[定理2]
3.[ 保号性] [定理3]
2.2 极限运算法则
定理
推论1
常数因子可以提到极限记号外面. 推论2
2.3 无穷小量与无穷大量
注意 （1）无穷大是变量,不能与很大的数混淆;
（3）无穷大是一种特殊的无界变量,但是无 界变量未必是无穷大.
2.3.3无穷小与无穷大的关系
定理4 在同一过程中,无穷大的倒数为无穷小; 恒不为零的无穷小的倒数为无穷大.
意义 关于无穷大的讨论,都可归结为关于无穷小 的讨论.
2.3.4 无穷小量的比较
二、极限
2.1 极限的定义
2.1.1 数列极限
截丈问题： “一尺之棰，日截其半，万世不竭”
高等数学基础PPT第一章
返回
1.1函数的概念与特性—函数
返回
1.1函数的概念与特性—函数
返回
1.1函数的概念与特性—函数
返回
1.1函数的概念与特性—函数的几种简单性态
返回
1.1函数的概念与特性—函数的几种简单性态
返回
1.1函数的概念与特性—函数的几种简单性态
返回
1.1函数的概念与特性—函数的几种简单性态
返回
1.2初等函数与建立函数关系式—初等函数
返回
1.2初等函数与建立函数关系式ห้องสมุดไป่ตู้初等函数
返回
1.2初等函数与建立函数关系式— 建立函数关系式举例
返回
1.2初等函数与建立函数关系式— 建立函数关系式举例
返回
本章结束
请选择: 重学一遍 退出
高等数学基础
第一章 函数及其图形
主讲:
函数及其图形
函数的概念与特性
集合与区间 函数 函数的几种简单性态
初等函数与建立函数关系式
初等函数 建立函数关系式举例
退出
1.1函数的概念与特性--集合与区间
返回
1.1函数的概念与特性--集合与区间
返回
1.1函数的概念与特性--集合与区间
返回
1.1函数的概念与特性--集合与区间
高数上册第一章第一节映射与函数一.ppt
预备知识
一.区间和邻域
⑴【区间】是指介于某两个实数之间的全体实数. 这两个实数叫做区间的端点.
a,b R,且a b.
开区间 ( a , b ) x a x b
oa
b
x
闭区间 [ a , b ] x a x b
oa
b
x
半开区间 无限区间
有限区间
无限区间
oa
x
ob
x
区间长度的定义:
y (1)x a
• (0,1)
y ax (a 1)
3.【对数函数】 y loga x (a 0, a 1) y ln x
y log a x
(1,0)
•
(a 1)
y log 1 x
a
4.【三角函数】
正弦函数 y sin x
y sin x
余弦函数 y cos x
y cos x
【说明】通常 f 称为外层函数，g 称为内层函数.
2【注意】 1）构成复合函数的条件 g(D) D1 不可少.
（即：内层函数在复合函数定义域D内的值域g(D) 一定包含在外层函数的定义域D1内）
例如 y arcsin u, u 2 x2; y arcsin(2 x2 )
2）复合函数可以由两个以上的函数经过复合构成.
D : (,), 奇函数.
② 双曲余弦chx e x e x 2
D : (,), 偶函数.
y chx
y 1ex 2
y shx
y 1ex 2
③
双 曲 正 切 thx
shx chx
ex ex
ex ex
D : (,) 奇函数, 有界函数,
【双曲函数常用公式】
sh( x y) shxchy chxshy; ch( x y) chxchy shxshy; ch2 x sh2 x 1;
一.区间和邻域
⑴【区间】是指介于某两个实数之间的全体实数. 这两个实数叫做区间的端点.
a,b R,且a b.
开区间 ( a , b ) x a x b
oa
b
x
闭区间 [ a , b ] x a x b
oa
b
x
半开区间 无限区间
有限区间
无限区间
oa
x
ob
x
区间长度的定义:
y (1)x a
• (0,1)
y ax (a 1)
3.【对数函数】 y loga x (a 0, a 1) y ln x
y log a x
(1,0)
•
(a 1)
y log 1 x
a
4.【三角函数】
正弦函数 y sin x
y sin x
余弦函数 y cos x
y cos x
【说明】通常 f 称为外层函数，g 称为内层函数.
2【注意】 1）构成复合函数的条件 g(D) D1 不可少.
（即：内层函数在复合函数定义域D内的值域g(D) 一定包含在外层函数的定义域D1内）
例如 y arcsin u, u 2 x2; y arcsin(2 x2 )
2）复合函数可以由两个以上的函数经过复合构成.
D : (,), 奇函数.
② 双曲余弦chx e x e x 2
D : (,), 偶函数.
y chx
y 1ex 2
y shx
y 1ex 2
③
双 曲 正 切 thx
shx chx
ex ex
ex ex
D : (,) 奇函数, 有界函数,
【双曲函数常用公式】
sh( x y) shxchy chxshy; ch( x y) chxchy shxshy; ch2 x sh2 x 1;
高数一章6节ppt课件
分子次数等 于分母次数
时, 分母
分子
分子分母同除以 x3 , 则
“ 抓大头”
42
lim
x
3x3 7x3
4x2 5x2
2 3
lim
x
3 7
x 5
x
x3 3
x3
这是因为lim x
a xn
a lim x
1 xn
a
lim
x
1 n x
0.
10
例8 求 lim 3x2 2x 1 . x 2x3 x2 5
( x x2
x
2) 1
1
通分化作商的极限
14
例12 求 lim x 1 . x1 x 1
解 方法 1 令 u x , 则 lim u 1, x1 x 1 u2 1 u1 x 1 u1
所以原式 lim(u 1) 2 u1
方法2 lim x 1 lim ( x 1)( x 1)
x2 lim
x2 x 2
x22
lim
x 7 3 x2
x22 x73
2
3
13
例11
求
lim(
x 1
x
3 3
1
1 ). x1
解 lim( 3 1 ) x1 x3 1 x 1
lim
x1
3
(x2 (x3
x 1)
1)
lim ( x 2)( x 1) x1 ( x3 1)
lim
x 1
由定理1，推论1及推论2 4
定理3的(1), (2)可以分别推广到有限个函数的 代数和,相乘的情形.
推论1 若lim f ( x) A，c为常数，则
lim[cf ( x)] c lim f ( x) cA
高等数学第一章-课件2.ppt
一 函数的连续性
1.函数在点x0的连续性
函数连续的概念源于对几何曲线的直观分析,粗略地 说,如果函数是连续的,那么它的图像是一条连绵不断的曲 线,当然我们不能满足于这种直观的认识,我们需要用数学 的语言给出它的精确定义。
第四节
考察如图1-21所示的函数图像。
图1-21
第四节
故函数f(x)在点 x=0处连续,如图 1-22所示。
图1－20
第二节 极
四 无穷小量与无穷大量
1.无穷小量
定义1－9 若函数f(x)在自变量的某一变化过程中 的极限为零,则称该函数为自变量在此变化过程中的无 穷小量,简称无穷小。通常函数极限有x→+∞,x→- ∞, x→∞,x→x0 + ,x→x0 -,x→x0这六种情形。因此,只简 单地说函数是无穷小量是不确切的,还必须指出x的趋近 方式。
fξ=0。 该推论表明方程fx=0在 a,b内有实根。其几何解释如 图1-26所示。
图1-26
Thank You!
第一章 函数、极限与连续
第一节 函数
第二节 极限
第三节
极限的运算
第四节
初等函数的连续性Leabharlann 第五节 闭区间上连续函数的性质
第一节 函数
一 函数
1.函数的概念
定义1－1 给定两个实数集D和E，若有一个对应法则f，使 得对每个x∈D，都有唯一确定的值y∈E与之对应，则称f是定义 在数集D上的函数，记作y=f(x) ，x∈D。其中，x称为自变量，y 称为因变量，D称为函数fx的定义域，全体函数值的集合E称为函 数的值域.如果在D中任取某一个数值x0，与之对应的y的数值y0， 称为函数f(x)在点x0处的函数值，记作y0=f(x)0 。
1.函数在点x0的连续性
函数连续的概念源于对几何曲线的直观分析,粗略地 说,如果函数是连续的,那么它的图像是一条连绵不断的曲 线,当然我们不能满足于这种直观的认识,我们需要用数学 的语言给出它的精确定义。
第四节
考察如图1-21所示的函数图像。
图1-21
第四节
故函数f(x)在点 x=0处连续,如图 1-22所示。
图1－20
第二节 极
四 无穷小量与无穷大量
1.无穷小量
定义1－9 若函数f(x)在自变量的某一变化过程中 的极限为零,则称该函数为自变量在此变化过程中的无 穷小量,简称无穷小。通常函数极限有x→+∞,x→- ∞, x→∞,x→x0 + ,x→x0 -,x→x0这六种情形。因此,只简 单地说函数是无穷小量是不确切的,还必须指出x的趋近 方式。
fξ=0。 该推论表明方程fx=0在 a,b内有实根。其几何解释如 图1-26所示。
图1-26
Thank You!
第一章 函数、极限与连续
第一节 函数
第二节 极限
第三节
极限的运算
第四节
初等函数的连续性Leabharlann 第五节 闭区间上连续函数的性质
第一节 函数
一 函数
1.函数的概念
定义1－1 给定两个实数集D和E，若有一个对应法则f，使 得对每个x∈D，都有唯一确定的值y∈E与之对应，则称f是定义 在数集D上的函数，记作y=f(x) ，x∈D。其中，x称为自变量，y 称为因变量，D称为函数fx的定义域，全体函数值的集合E称为函 数的值域.如果在D中任取某一个数值x0，与之对应的y的数值y0， 称为函数f(x)在点x0处的函数值，记作y0=f(x)0 。
《高等数学》课件第1章
2
(3) y e2sin3 x2 解 (1) y是由y=sinu与u=2x (2) y是由y=u2、u=tanv及 v x
(3) 表格法.变量间的函数关系通过列表形式反映出来. 例 如，火车时刻表就是利用列表的方法，把进(出)站火车的车 次与时间的函数关系表示出来.这种表示方法使得自变量 与因变量的对应关系一目了然.
4. 某市电话局规定市话的收费标准为：当月所打电话次数 不超过30次时，只收月租费10元；超过30次时，每次加收 0.20元.则电话费y和用户当月所打电话次数x的关系可用下面 的形式给出：
有arccos(－x)=π－arccosx成立.
图 1-8
图 1-9
反正切函数y=arctanx的图形如图1-10所示，其定义域是
x∈(－∞，+∞)，值域是
y
π 2
,
π 2
，该函数是单调增加
的，是奇函数，即arctan(－x)=-arctanx.
图 1-10
反余切函数y=arccotx的图形如图1-11所示，其定义域是 x∈(－∞，+∞)，值域是y∈(0，π)，该函数是单调减少的， 且有arccot(－x)=π－arccotx成立.
第一章 函数的极限与连续
1.1 函数及其性质 1.2 初等函数 1.3 数学模型方法概述 1.4 极限的概念 1.5 极限的运算 1.6 函数的连续性 本章小结
1.1 函数及其性质
1.1.1 函数
函数是微积分学研究的对象.虽然在中学已经学习了函数 的概念， 但是在以后的学习中我们不再是进行简单的重复， 而是要从全新的视角对函数进行描述并重新分类.
邻域是一个经常应用到的概念. 以点x0为中心的任何开 区间称为点x0的邻域，记作N(x0).
(3) y e2sin3 x2 解 (1) y是由y=sinu与u=2x (2) y是由y=u2、u=tanv及 v x
(3) 表格法.变量间的函数关系通过列表形式反映出来. 例 如，火车时刻表就是利用列表的方法，把进(出)站火车的车 次与时间的函数关系表示出来.这种表示方法使得自变量 与因变量的对应关系一目了然.
4. 某市电话局规定市话的收费标准为：当月所打电话次数 不超过30次时，只收月租费10元；超过30次时，每次加收 0.20元.则电话费y和用户当月所打电话次数x的关系可用下面 的形式给出：
有arccos(－x)=π－arccosx成立.
图 1-8
图 1-9
反正切函数y=arctanx的图形如图1-10所示，其定义域是
x∈(－∞，+∞)，值域是
y
π 2
,
π 2
，该函数是单调增加
的，是奇函数，即arctan(－x)=-arctanx.
图 1-10
反余切函数y=arccotx的图形如图1-11所示，其定义域是 x∈(－∞，+∞)，值域是y∈(0，π)，该函数是单调减少的， 且有arccot(－x)=π－arccotx成立.
第一章 函数的极限与连续
1.1 函数及其性质 1.2 初等函数 1.3 数学模型方法概述 1.4 极限的概念 1.5 极限的运算 1.6 函数的连续性 本章小结
1.1 函数及其性质
1.1.1 函数
函数是微积分学研究的对象.虽然在中学已经学习了函数 的概念， 但是在以后的学习中我们不再是进行简单的重复， 而是要从全新的视角对函数进行描述并重新分类.
邻域是一个经常应用到的概念. 以点x0为中心的任何开 区间称为点x0的邻域，记作N(x0).
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
由定义2知
函f数 (x)在 x0处连 . 续h Nhomakorabea5
3.单侧连续
若f(函 x )在 (a ,x 数 0 ] 内有 ,且 f(x 0 定 0 ) f(x 义 0 ), 则 f(x ) 称 在 x 0 处 点左 ; 连续
若f(函 x )在 [x 0 ,b 数 ) 内有 ,且 f(x 0 定 0 ) f(x 义 0 ), 则 f(x ) 称 在 x 0 处 点右 . 连续
x x0
f (x)
f ( x0 )
那末就称函数 f ( x) 在点x0 连续.
""定义 :
0,0,使x当 x0时 , 恒f有 (x)f(x0).
h
4
例1 试证函 f(x数 )xsin1x, x0, 在x0 0, x0,
处连. 续
证 limxsin10,
x0
x
又f(0)0, lim f(x)f(0), x 0
设 xx0 x,
yf(x )f(x 0),
x 0 就 x 是 x 0 , y 0 就 f ( x ) 是 f ( x 0 ).
h
3
定义 2 设函数 f ( x) 在U ( x0 )内有定义,如果
函数 f ( x) 当x x0 时的极限存在,且等于它在
点
x
0
处的函数值
f
(
x 0
)
,即
lim
二 、 f ( x )在 ( , 1 )与 ( 1 , )内连续 , x 1 为 跳 跃 间
断点.
三、1、 x 1为第 一类间断点；
2、 x k 为可去间断点 , 2
x k(k 0)为第二类间断点.
f1( x )
x tan
x
,
x
k,k
2
1 , x 0
(k 0,1,2, ) ,
h
23
思考题解答 f(x)在 x0连 续 ， x l ix0m f(x)f(x0)
且 0 f ( x ) f ( x 0 ) f ( x ) f ( x 0 )
x l ix0m f(x)f(x0) x l x i0fm 2 (x ) x l x i0fm (x ) x l x i0fm (x ) f2(x0) 故 |f ( x ) |、 f 2 ( x ) 在 x 0 都 连 续 .
x 0
x 0
lifm (x ) li(a m x )a,
x 0
x 0
要 f ( 0 0 ) 使 f ( 0 0 ) f ( 0 ) ,a1 ,
故当且a仅 1时 当 , 函f数 (x)在 x0处连 . 续
h
20
三、小结
1.函数在一点连续必须满足的三个条件; 2.区间上的连续函数; 3.间断点的分类与判别;
连续函数的图形是一条连续而不间断的曲线.
例如,有理函(数 , 在 ) 内 区 是 间 连 . 续
h
8
例3 证 函 明 y s 数 x i在 n ( 区 , ) 内 间 .连
证 任x 取 (, ) ,
y six n x )( sx i n 2si nxcoxs(x)
2
2
cosx(x)1, 则y2sinx.
0
0
0
f(x)的跳跃.间断点
例4
讨论f(函 x) 1 数 x x ,,
x0,在 x0处的.连 x0,
解 f(00)0, f(00)1,
y
f( 0 0 ) f( 0 0 ),
x0为函数的跳跃间.断点 o
x
h
11
2.可去间断点如果 f(x)在点 x0处的极限 , 存
但lx ixm 0 f(x)Af(x0),或f(x)在点 x0处无定 义则称 x0为 点函f数 (x)的可去间 . 断点
间断点的类型，如果是可去间断点，则补充或改变
函数的定义使它连续 .
1、
f
(x
)
x
3
1, x x, x
1在 1
x R
上
.
2、 f (x) x ,在 x R 上 . tan x
四 、 讨 论 函 数 f ( x ) lim 1 x 2 n 的 连 续 性 ， 若 有 间 断 n 1 x 2n
例6 讨论函 f(x) 数 1 x, x0,在 x0处的连 . 续
x, x0,
y
解 f(00)0, f(00),
x1为函数的第二类间. 断点 o x 这种情况称为无穷断间点.
h
15
例7 讨论f(函 x)s数 i1 n在 x0处的连 . 续 x
解 在x0处没有,定义
且limsin1不存.在 x0 x
h
24
但反之不成立.
例
f(x)1,1,
x0 x0
在 x 0 0 不 连 续
但 |f ( x ) | 、 f 2 ( x ) 在 x 0 0 连 续
h
25
练习题
一、填空题：
1、指 出 y x 2 1 在 x 1 是 第 _______类 间 x2 3x 2
断点；在 x 2 是第_____类间断点 .
2、指 出 y x 2 x 在 x 0 是 第 ________ 类 间 x ( x 2 1)
断点；在 x 1 是第______类间断点；在 x 1
是第_____类间断点 .
x, x 1
二、研究函数 f (x)
的连续性，并画出函数
1, x 1
的图形 .
h
26
三、指出下列函数在指定范围内的间断点，并说明这些
间断点
第一类间断点:可去型,跳跃型. 第二类间断点:无穷型,振荡型.
(见下图)
h
21
第y
一
可去型
类
间
断
点
o x0
x
y
第 二 类 间 断o 点
x0
x
无穷型
h
y
o
x0
y
o
跳跃型 x
x 振荡型
22
思考题
若 f(x)在 x0连 续 ， 则 |f(x)|、 f2(x)在 x0是 否 连 续 ？ 又 若 |f(x)|、 f2(x)在 x0连 续 ， f(x)在 x0是 否 连 续 ？
例5 讨论函数
f
(
x)
2 1,
x,
0 x 1, x1
1 x , x 1,
在 x 1处的连续性 .
y y1x
2 y2 x
1
o1
x
h
12
解 f(1)1,
f(10)2, f(10)2,
lim f(x)2 f(1), x 1
x 0为函数的可去间.断点
注意 可去间断点只要改变或者补充间断处函 数的定义, 则可使其变为连续点.
2
2
对任,意 当 的 0时 , 有 si n,
故y2sin xx, 当 x 0 时 , y 0 . 2
即 函 y 数 six 对 n x 任 (,意 )都 是 . 连
h
9
二、函数的间断点
函数 f(x)在点 x0处连续必须满条 足件 :的三
(1)f(x)在x点 0处有;定义
(2)limf(x)存在 ; xx0
点，判断其类型 .
五 、 试 确 定 a,b 的 值 ,使 f (x) e x b ， ( x a )( x 1 )
（ 1 ） 有 无 穷 间 断 点 x 0 ；（ 2 ） 有 可 去 间 断 点 x 1 .
h
27
练习题答案
一 、 1、 一 类,二 类 ； 2、 一 类,一 类 ,二类 .
x 0
x 0
右连续但不左连续 ,
故函 f(x)在 数x点 0处不 . 连续
h
7
4.连续函数与连续区间
在区间上每一点都连续的函数,叫做在该区间上 的连续函数,或者说函数在该区间上连续.
如果函数在(a开 ,b)内 区连 间 , 续 并且在左端 xa处右连 , 在 续右端 x点 b处左连 , 则 续称 函数 f(x)在闭区 [a,b间 ]上连. 续
x0为第二类间. 断点
这种情况称为的振荡断间点.
注意 不要以为函数的间断点只是个别的几个点.
h
16
y sin 1 x
h
17
★ 狄利克雷函数
yD(x)10,,
当x是有理,数时 当x是无理,数时
在定义域R内每一点处都间断,且都是第二类间 断点.
★
f(x)xx,,
当x是有理,数时 当x是无理,数时
仅在x=0处连续, 其余各点处处间断.
h
28
f2( x )
x tan 0,x
,x k,k x k
2
(k
0 , 1, 2 ,
).
2
x, x 1
四、
f
(
x
)
0
,
x
0
x 1 和 x 1 为 第 一 类 间 断 点 .
x, x
1
五 、 (1)a 0,b 1;
(2)a 1,b e .
h
29
h
18
★
f(x)11,,
当x是有理,数时 当x是无理,数时
在定义域 R内每一点处都间断, 但其绝对值处 处连续.
判断下列间断点类型:
y
yfx
x1 o
x2
x3
h
x
19
例8 当 a取何,值时
函数 f(x) a cox xs,,
x0, x0,
在 x0处连 . 续
解 f(0)a,
lim f(x)lic m o xs1,
h
2
2.连续的定义
定义 1 设函数 f ( x )在U ( x0 ) 内有定义,如