湖北省黄石市2017-2018学年高二数学10月月考试题文及答案
湖北省黄石市部分高中2017-2018学年高二上学期第一次月考数学试卷(理科)(重点班)Word版含解析

湖北省黄石市高中2017-2018学年高二上学期第一次月考试卷数学(理科)一、选择题(本大共题12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的).1.设命题甲:△ABC的一个内角为60°,命题乙:△ABC的三内角的度数成等差数列.那么()A.甲是乙的充分条件,但不是必要条件B.甲是乙的必要条件,但不是充分条件C.甲是乙的充要条件D.甲不是乙的充分条件,也不是乙的必要条件2.已知关于某设备的使用年限x(年)和所支出的费用y(万元),有如表所示的统计资料:根据上表提供的数据,求出了y关于x的线性回归方程为=1.23x+0.08,那么统计表中t的值为()A.5.5 B.5.0 C.4.5 D.4.83.若干人站成一排,其中为互斥事件的是()A.“甲站排头”与“乙站排头”B.“甲站排头”与“乙站排尾”C.“甲站排头”与“乙不站排头”D.“甲不站排头”与“乙不站排头”4.若“A+B”发生的概率为0.6,则,同时发生的概率为()A.0.6 B.0.36 C.0.24 D.0.45.下列命题中,真命题是()A.B.∀x∈(3,+∞),x2>2x+1C.∃x∈R,x2+x=﹣1 D.6.某流程图如图所示,现输入如下四个函数,则可以输出的函数是()A.f(x)=B.f(x)=ln(﹣x)C.f(x)=D.f(x)=7.某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100],若低于60分的人数是15人,则该班的学生人数是()A.45 B.50 C.55 D.608.若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为()A.B.C.D.9.已知p:∀x∈[1,2],x2﹣a≥0,q:方程x2+2ax+2﹣a=0有实数解,若p且q为真命题,则实数a的取值范围是()A.a≤﹣2或a=1 B.a≤2或1≤a≤2 C.a≥1 D.﹣2≤a≤110.在△ABC中,“sin(A﹣B)cosB+cos(A﹣B)sinB≥1”是“△ABC是直角三角形”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件11.已知函数f(x)=x+,g(x)=2x+a,若∀x1∈[,3],∃x2∈[2,3],使得f(x1)≥g (x2),则实数a的取值范围是()A.a≤1 B.a≥1 C.a≤0 D.a≥012.设点(a,b)是区域内的随机点,函数y=ax2﹣4bx+1在区间[1,+∞)上是增函数的概率为()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分)13.命题:对∀x∈R,x3﹣x2+1≤0的否定是.14.将参加数学竞赛的1000名学生编号如下:0001,0002,0003,…,1000,按系统抽样的方法从中抽取一个容量为50的样本,如果在第一组抽得的编号是0015,则在第21组抽得的编号是.15.从甲、乙、丙三个厂家生产的同一种产品中各抽取8件产品,对其使用寿命(单位:年)跟踪调查结果如下:甲:3,4,5,6,8,8,8,10;乙:4,6,6,6,8,9,12,13;丙:3,3,4,7,9,10,11,12.三个厂家在广告中都称该产品的使用寿命是8年,请根据结果判断厂家在广告中分别运用了平均数、众数、中位数中的哪一种集中趋势的特征数:甲,乙,丙.16.在一次跳伞训练中,甲、乙两位学员各跳一次,设命题p是“甲降落在指定范围”,q是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.运行如图所示的程序框图,当输入实数x的值为﹣3时,输出的函数值为12,当输入实数x的值为1时,输出的函数值为2.(1)求函数f(x)的解析式;(2)当输出结果为80时,求输入的x的值.18.设命题p:实数x满足x2﹣4ax+3a2<0,q:x2+2x﹣8>0,且¬p是¬q的必要不充分条件,求实数a的取值范围.19.农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)甲:9,10,11,12,10,20乙:8,14,13,10,12,21(Ⅰ)绘出所抽取的甲、乙两种麦苗株高的茎叶图;(Ⅱ)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.20.某个体服装店经营某种服装在某周内获得利润y(单位:元)与该周每天销售这种服装件数x之间有如下一组数据:已知(1)求;(2)求纯利润y与每天销售件数x的回归方程;(3)估计每天销售10件这种服装时,纯利润是多少元?21.甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头,它们在一昼夜内任何时刻到达是等可能的.(1)已知甲船上有男女乘客各3名,现从中任选3人出来做某件事情,求所选出的人中恰有一位女乘客的概率;(2)如果甲船的停泊时间为4小时,乙船的停泊时间为2小时,求它们中的任何一条船不需要等待码头空出的概率.22.已知P={x|x2﹣8x﹣20≤0},S={x|1﹣m≤x≤1+m}(1)是否存在实数m,使x∈P是x∈S的充要条件,若存在,求出m的取值范围;(2)是否存在实数m,使x∈P是x∈S的必要条件,若存在,求出m的取值范围.湖北省黄石市高中2017-2018学年高二上学期第一次月考数学试卷(理科)参考答案与试题解析一、选择题(本大共题12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的).1.设命题甲:△ABC的一个内角为60°,命题乙:△ABC的三内角的度数成等差数列.那么()A.甲是乙的充分条件,但不是必要条件B.甲是乙的必要条件,但不是充分条件C.甲是乙的充要条件D.甲不是乙的充分条件,也不是乙的必要条件【考点】等差关系的确定.【分析】根据三角形内角和180°,△ABC的一个内角为60°,另外两个角的和是120°,满足等差中项的特点,△ABC的三内角的度数成等差数列,等差中项是60°.【解答】解:∵△ABC的一个内角为60°,∴另外两个角的和是120°,∴三个角满足等差数列;∵△ABC的三内角的度数成等差数列,∴等差中项是60°,故选C2.已知关于某设备的使用年限x(年)和所支出的费用y(万元),有如表所示的统计资料:根据上表提供的数据,求出了y关于x的线性回归方程为=1.23x+0.08,那么统计表中t的值为()A.5.5 B.5.0 C.4.5 D.4.8【考点】线性回归方程.【分析】由题意可得,的值,由回归方程过点(,)可得t值.【解答】解:由题意可得=(2+3+4+5+6)=4,=(2.2+3.8+t+6.5+7.0)=3.9+0.2t,由回归方程过点(,)可得3.9+0.2t=1.23×4+0.08,解得t=5.5故选:A.3.若干人站成一排,其中为互斥事件的是()A.“甲站排头”与“乙站排头”B.“甲站排头”与“乙站排尾”C.“甲站排头”与“乙不站排头”D.“甲不站排头”与“乙不站排头”【考点】互斥事件与对立事件.【分析】根据不能同时发生的两个事件,叫互斥事件,依次判断.【解答】解:根据互斥事件不能同时发生,判断A是互斥事件;B、C、D中两事件能同时发生,故不是互斥事件;故选A.4.若“A+B”发生的概率为0.6,则,同时发生的概率为()A.0.6 B.0.36 C.0.24 D.0.4【考点】相互独立事件的概率乘法公式.【分析】利用对立事件概率计算公式求解.【解答】解:∵“A+B”发生的概率为0.6,∴,同时发生的概率:P()=1﹣P(A+B)=1﹣0.6=0.4.故选:D.5.下列命题中,真命题是()A.B.∀x∈(3,+∞),x2>2x+1C.∃x∈R,x2+x=﹣1 D.【考点】四种命题的真假关系.【分析】利用含有量词命题真假的判断方法判断各个命题的真假.充分考虑特称命题与全称命题真假判断的方法.【解答】解:B项是正确的.∀x∈(3,+∞),x2﹣(2x+1)=(x﹣1)2﹣2>2>0,由于对∀x∈R,sinx+cosx≤,故A 错误,方程x2+x+1=0无实根,故C项错误;对于∀x∈(,π)tanx<0<sinx,故D错误.故选B.6.某流程图如图所示,现输入如下四个函数,则可以输出的函数是()A.f(x)=B.f(x)=ln(﹣x)C.f(x)=D.f(x)=【考点】程序框图.【分析】本题的框图是一个选择结构,其算法是找出即是奇函数存在零点的函数,由此规则对四个选项进行比对,即可得出正确选项.【解答】解:由框图知,其算法是输出出即是奇函数存在零点的函数,A中,函数f(x)=不能输出,因为此函数没有零点;A不正确.B中,函数f(x)=ln(﹣x)可以输出,∵f(﹣x)=lg(+x)=﹣f(x)发现,函数是奇函数且当x=0时函数值为0,故B正确;C中,函数f(x)=,不能输出,因为不存在零点;C不正确.D中,函数f(x)=,不能输出,因为它是偶函数,不是奇函数,D不正确.故选B.7.某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100],若低于60分的人数是15人,则该班的学生人数是()A.45 B.50 C.55 D.60【考点】频率分布直方图.【分析】由已知中的频率分布直方图,我们可以求出成绩低于60分的频率,结合已知中的低于60分的人数是15人,结合频数=频率×总体容量,即可得到总体容量.【解答】解:∵成绩低于60分有第一、二组数据,在频率分布直方图中,对应矩形的高分别为0.005,0.01,每组数据的组距为20则成绩低于60分的频率P=(0.005+0.010)×20=0.3,又∵低于60分的人数是15人,则该班的学生人数是=50.故选:B.8.若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为()A.B.C.D.【考点】互斥事件的概率加法公式.【分析】设“甲或乙被录用”为事件A,则其对立事件表示“甲乙两人都没有被录取”,先求出,再利用P(A)=1﹣P()即可得出.【解答】解:设“甲或乙被录用”为事件A,则其对立事件表示“甲乙两人都没有被录取”,则==.因此P(A)=1﹣P()=1﹣=.故选D.9.已知p:∀x∈[1,2],x2﹣a≥0,q:方程x2+2ax+2﹣a=0有实数解,若p且q为真命题,则实数a的取值范围是()A.a≤﹣2或a=1 B.a≤2或1≤a≤2 C.a≥1 D.﹣2≤a≤1【考点】命题的真假判断与应用.【分析】先求出命题p,q下的a的取值:由命题p得,a≤x2,所以只要让a小于等于x2的最小值即可;由命题q得,△≥0,这样即可求得命题p,q下的a的取值.根据p且q为真命题,得到p,q都是真命题,所以对在命题p,q下求得的a的取值求交集即可.【解答】解:命题p:∀x∈[1,2],x2﹣a≥0,∴a≤x2,∵x2在[1,2]上的最小值为1,∴a≤1;命题q:方程x2+2ax+2﹣a=0有实数根;∴△=4a2﹣4(2﹣a)≥0,解得a≤﹣2,或a≥1;∵p且q为真命题,∴p,q都是真命题.∴a的取值范围是即a∈{a|a≤﹣2,或a=1}.故选A.10.在△ABC中,“sin(A﹣B)cosB+cos(A﹣B)sinB≥1”是“△ABC是直角三角形”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】结合两角和的正弦公式,利用充分条件和必要条件的定义进行判断.【解答】解:由sin(A﹣B)cosB+cos(A﹣B)sinB≥1得sin(A﹣B+B)≥1,即sinA≥1,∴sinA=1,即A=,此时“△ABC是直角三角形,当B=时,满足△ABC是直角三角形,但sinA≥1不成立,∴“sin(A﹣B)cosB+cos(A﹣B)sinB≥1”是“△ABC是直角三角形”的成立的充分不必要条件,故选:A.11.已知函数f(x)=x+,g(x)=2x+a,若∀x1∈[,3],∃x2∈[2,3],使得f(x1)≥g (x2),则实数a的取值范围是()A.a≤1 B.a≥1 C.a≤0 D.a≥0【考点】全称命题.【分析】由∀x1∈[,3],都∃x2∈[2,3],使得f(x1)≥g(x2),可得f(x)在x1∈[,3]的最小值不小于g(x)在x2∈[2,3]的最小值,构造关于a的不等式,可得结论.【解答】解:当x1∈[,3]时,由f(x)=x+得,f′(x)=,令f′(x)>0,解得:x>2,令f′(x)<0,解得:x<2,∴f(x)在[,2]单调递减,在(2,3]递增,∴f(2)=4是函数的最小值,当x2∈[2,3]时,g(x)=2x+a为增函数,∴g(2)=a+4是函数的最小值,又∵∀x1∈[,3],都∃x2∈[2,3],使得f(x1)≥g(x2),可得f(x)在x1∈[,3]的最小值不小于g(x)在x2∈[2,3]的最小值,即4≥a+4,解得:a≤0,故选:C.12.设点(a,b)是区域内的随机点,函数y=ax2﹣4bx+1在区间[1,+∞)上是增函数的概率为()A.B.C.D.【考点】几何概型.【分析】作出不等式组对应的平面区域,根据概率的几何概型的概率公式进行计算即可得到结论.【解答】解:作出不等式组内对应的平面区域如图:对应的图形为△OAB,其中对应面积为S=×4×4=8,若f(x)=ax2﹣4bx+1在区间[1,+∞)上是增函数,则满足a>0且对称轴x=≤1,即,结合条件,可得对应的平面区域为△OBC,由,解得a=,b=,∴对应的面积为S1==,∴根据几何概型的概率公式可知所求的概率为=,故选:A.二、填空题(本大题共4小题,每小题5分,共20分)13.命题:对∀x∈R,x3﹣x2+1≤0的否定是.【考点】命题的否定.【分析】根据已知中的原命题,结合全称命题否定的方法,可得答案.【解答】解:命题:对∀x∈R,x3﹣x2+1≤0的否定是,故答案为:14.将参加数学竞赛的1000名学生编号如下:0001,0002,0003,…,1000,按系统抽样的方法从中抽取一个容量为50的样本,如果在第一组抽得的编号是0015,则在第21组抽得的编号是0415.【考点】系统抽样方法.【分析】因为系统抽样是先将总体按样本容量分成k=段,再间隔k取一个,所以只需找到k 的值,就可计算第21个号码为多少.【解答】解:∵系统抽样是先将总体按样本容量分成k=段,再间隔k取一个.又∵现在总体的个体数为1000,样本容量为50,∴k=20,∴若第一个号码为0015,则第21个号码为0015+20×20=0415.故答案为:0415.15.从甲、乙、丙三个厂家生产的同一种产品中各抽取8件产品,对其使用寿命(单位:年)跟踪调查结果如下:甲:3,4,5,6,8,8,8,10;乙:4,6,6,6,8,9,12,13;丙:3,3,4,7,9,10,11,12.三个厂家在广告中都称该产品的使用寿命是8年,请根据结果判断厂家在广告中分别运用了平均数、众数、中位数中的哪一种集中趋势的特征数:甲众数,乙平均数,丙中位数.【考点】众数、中位数、平均数.【分析】分别计算三组数据的众数、平均数和中位数,比较即可.【解答】解:甲厂家生产的产品,众数是8,平均数是6.5,中位数是7;乙厂家生产的产品,众数是6,平均数是8,中位数是7;丙厂家生产的产品,众数是3,平均数是7.375,中位数是8;三个厂家在广告中都称该产品的使用寿命是8年,则甲用众数,乙用平均数,丙用中位数.故答案为:乙众数、平均数、中位数.16.在一次跳伞训练中,甲、乙两位学员各跳一次,设命题p是“甲降落在指定范围”,q是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为(¬p)∨(¬q).【考点】逻辑联结词“或”.【分析】由命题P和命题q写出对应的¬p和¬q,则命题“至少有一位学员没有降落在指定范围”即可得到表示.【解答】解:命题p是“甲降落在指定范围”,则¬p是“甲没降落在指定范围”,q是“乙降落在指定范围”,则¬q是“乙没降落在指定范围”,命题“至少有一位学员没有降落在指定范围”包括“甲降落在指定范围,乙没降落在指定范围”或“甲没降落在指定范围,乙降落在指定范围”或“甲没降落在指定范围,乙没降落在指定范围”三种情况.所以命题“至少有一位学员没有降落在指定范围”可表示为(¬p)V(¬q).故答案为:(¬p)∨(¬q)三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.运行如图所示的程序框图,当输入实数x的值为﹣3时,输出的函数值为12,当输入实数x的值为1时,输出的函数值为2.(1)求函数f(x)的解析式;(2)当输出结果为80时,求输入的x的值.【考点】程序框图.【分析】(1)根据输入实数x的值为﹣3时,输出的函数值为12,当输入实数x的值为1时,输出的函数值为2,求得a、b,可得函数f(x)的解析式;(2)当输出结果为80时,根据分段函数,求输入的x的值.【解答】解:(1)由程序框图知,∵输入x=﹣3<0,输出f(﹣3)=﹣3b=12,∴b=﹣4.∵输入x=1≥0,输出f(1)=a﹣1=2,∴a=3.∴f(x)=.(2)由(1)知:①当x<0时,f(x)=﹣4x=80,∴x=﹣20;②当x≥0时,f(x)=3x﹣1=80,∴x=4.综上,输入的x的值为4或﹣20.18.设命题p:实数x满足x2﹣4ax+3a2<0,q:x2+2x﹣8>0,且¬p是¬q的必要不充分条件,求实数a的取值范围.【考点】必要条件、充分条件与充要条件的判断;命题的否定.【分析】由题意可得p是q的充分不要条件,设A={x|x2﹣4ax+3a2<0},B={x|x2+2x﹣8>0},分当a<0、当a>0、当a=0三种情况,分别求得实数a的取值范围,再取并集,即得所求.【解答】解:∵¬p是¬q的必要不充分条件,∴p是q的充分不要条件.设A={x|x2﹣4ax+3a2<0}={x|3a<x<a,a<0},B={x|x2+2x﹣8>0}={x|x<﹣4,或x>2},由题意可得A⊊B.当a<0时,可得a≤﹣4.当a>0时,可得a≥2.当a=0时,A=∅,满足A⊊B.综上可得,实数a的取值范围为{a|a≤﹣4,或a≥2,或a=0}.19.农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)甲:9,10,11,12,10,20乙:8,14,13,10,12,21(Ⅰ)绘出所抽取的甲、乙两种麦苗株高的茎叶图;(Ⅱ)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.【考点】茎叶图;极差、方差与标准差.【分析】(Ⅰ)根据数据作出对应的茎叶图.(Ⅱ)根据平均数和方差的公式,计算出平均数和方差,并根据平均数和方差作出判断.【解答】解:(Ⅰ)茎叶图如图所示:(Ⅱ),,方差,因为,所以乙种麦苗平均株高较高,因为,所以甲种麦苗长的较为正常.20.某个体服装店经营某种服装在某周内获得利润y(单位:元)与该周每天销售这种服装件数x之间有如下一组数据:已知(1)求;(2)求纯利润y与每天销售件数x的回归方程;(3)估计每天销售10件这种服装时,纯利润是多少元?【考点】线性回归方程.【分析】(1)利用平均数公式,可求;(2)求出利用最小二乘法来求线性回归方程的系数的量,求出横标和纵标的平均数,求出系数,可得回归方程;(3)由回归直线方程预测,只需将x=10代入求解即可.【解答】解:(1)==6,==;(2)b=≈4.75,≈79.86﹣4.75×6=51.36,∴纯利润y与每天销售件数x的回归方程=4.75x+51.36;(3)x=10,=98.86,估计每天销售10件这种服装时,纯利润是98.86元.21.甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头,它们在一昼夜内任何时刻到达是等可能的.(1)已知甲船上有男女乘客各3名,现从中任选3人出来做某件事情,求所选出的人中恰有一位女乘客的概率;(2)如果甲船的停泊时间为4小时,乙船的停泊时间为2小时,求它们中的任何一条船不需要等待码头空出的概率.【考点】几何概型;列举法计算基本事件数及事件发生的概率.【分析】(1)利用列举法进行求解即可.(2)利用几何概型求出对应的面积进行求解即可.【解答】解:记男乘客分别为1,2,3,记女乘客分别为4,5,6,从中任取3人有123,124,125,126,134,135,136,145,146,156,234,235,236,245,246,256,345,346,356,456,共20种取法,其中恰含一女乘客的有124,125,126,134,135,136,234,235,236共9种,∴所求概率P=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2)当甲船的停泊时间为4小时,乙船的停泊时间为2小时,两船不需等待码头空出,则满足x﹣y≥2或y﹣x≥4.设在上述条件时“两船不需等待码头空出”为事件B,画出区域如图:,P(B)===.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣22.已知P={x|x2﹣8x﹣20≤0},S={x|1﹣m≤x≤1+m}(1)是否存在实数m,使x∈P是x∈S的充要条件,若存在,求出m的取值范围;(2)是否存在实数m,使x∈P是x∈S的必要条件,若存在,求出m的取值范围.【考点】必要条件、充分条件与充要条件的判断.【分析】(1)由于x∈P是x∈S的充要条件,则集合P与集合S相等;(2)由于x∈P是x∈S的必要条件,则S⊆P.再结合集合关系求出实数m即可.【解答】解:由于P={x|x2﹣8x﹣20≤0}={x|﹣2≤x≤10},(1)要使x∈P是x∈S的充要条件,则P=S,即,而此方程组无解,则不存在实数m,使x∈P是x∈S的充要条件;(2)要使x∈P是x∈S的必要条件,则S⊆P,①当S=φ时,1﹣m>1+m,即m<0满足题意;②当S≠φ时,则1﹣m≤1+m,得m≥0,要使S⊆P,即有,得m≤3,即得0≤m≤3,综上可得,当实数m≤3时,使x∈P是x∈S的必要条件.。
湖北省黄石市数学高二上学期文数第一次月考试卷
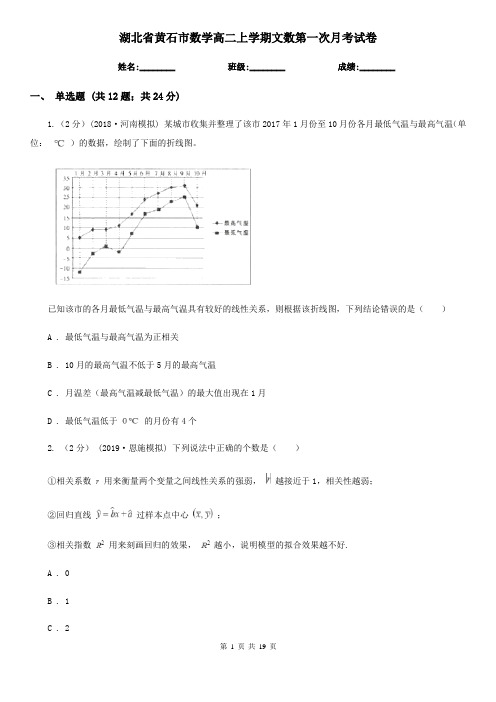
湖北省黄石市数学高二上学期文数第一次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)(2018·河南模拟) 某城市收集并整理了该市2017年1月份至10月份各月最低气温与最高气温(单位:)的数据,绘制了下面的折线图。
已知该市的各月最低气温与最高气温具有较好的线性关系,则根据该折线图,下列结论错误的是()A . 最低气温与最高气温为正相关B . 10月的最高气温不低于5月的最高气温C . 月温差(最高气温减最低气温)的最大值出现在1月D . 最低气温低于的月份有4个2. (2分)(2019·恩施模拟) 下列说法中正确的个数是()①相关系数用来衡量两个变量之间线性关系的强弱,越接近于1,相关性越弱;②回归直线过样本点中心;③相关指数用来刻画回归的效果,越小,说明模型的拟合效果越不好.A . 0B . 1C . 23. (2分) (2020高一下·吉林期中) 如图是调查某学校高三年级男女学生是否喜欢数学的等高条形图,阴影部分的高表示喜欢数学的频率.已知该年级男生女生各500名(所有学生都参加了调查),现从所有喜欢数学的同学中按分层抽样的方式抽取32人,则抽取的男生人数为()A . 16B . 32C . 24D . 84. (2分) (2017高二上·伊春月考) 4830与3289的最大公约数为()A . 11B . 35C . 23D . 135. (2分)(2016·海南模拟) 已知具有线性相关的两个变量x,y之间的一组数据如表:x01234y 2.2 4.3 4.5 4.8t且回归方程是 =0.95x+2.6,则t=()A . 6.7B . 6.6C . 6.56. (2分) (2019高二上·尚志月考) 用秦九韶算法求多项式在时的值时,其中的值为()A .B .C .D .7. (2分) (2018高二上·宜昌期末) 对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本中的中位数、众数、极差分别是A . 46,45,56B . 46,45,53C . 47,45,56D . 45,47,538. (2分)在UNTIL语句的一般形式“LOOP UNTIL M”中,M表示()A . 循环变量B . 循环体C . 终止条件D . 终止条件为真9. (2分)若程序框图如右图所示,则该程序运行后输出k的值是()A . 5B . 6C . 7D . 810. (2分)某中学高三(1)班有学生55人,现按座位号的编号采用系统抽样的方法选取5名同学参加一项活动,已知座位号为5号、16号、27号、49号的同学均被选出,则被选出的5名同学中还有一名的座位号是()A . 36B . 37C . 38D . 3911. (2分)把一颗骰子掷两次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数为b,则方程组只有一组解的概率为()A .B .C .D .12. (2分) (2016高二下·邯郸期中) 将8个不同的小球放入3个不同的小盒,要求每个盒子中至少有一个球,且每个盒子里的球的个数都不同,则不同的放法有()种.A . 2698B . 2688C . 1344D . 5376二、填空题 (共4题;共4分)13. (1分) (2019高二上·江门月考) 广东某家具厂为游泳比赛场馆生产观众座椅,质检人员对该厂的2500套座椅进行抽查,共抽检了100套,发现有5套次品,试问该厂所产的2500套座椅中大约有________套次品.14. (1分) (2018高一下·河南月考) 已知一组样本数据按从小到大的顺序排列为-1,0,4. ,这组数据的平均数与中位数均为5,则其方差为________.15. (1分) (2019高二下·吉林期末) 如图,在菱形中,,,以该菱形的4个顶点为圆心的扇形的半径都为 .若在菱形内随机取一点,则该点取自黑色部分的概率是________.16. (1分)(2019·长宁模拟) 若甲、乙两位同学随机地从门课程中选修门,则两人选修的课程中恰有门相同的概率为________.三、解答题 (共6题;共55分)17. (5分)将十进制数30化为二进制.18. (10分)(2020·镇江模拟) 定义:若数列满足所有的项均由构成且其中-1有m个,1有p 个,则称为“ ﹣数列”.(1)为“ ﹣数列” 中的任意三项,则使得的取法有多少种?(2)为“ ﹣数列” 中的任意三项,则存在多少正整数对使得且的概率为 .19. (10分) (2019高二下·昭通月考) 新个税法于2019年1月1日进行实施.为了调查国企员工对新个税法的满意程度,研究人员在地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中 .(1)求的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)(2)若按照分层抽样从,中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在的概率.20. (10分) (2018高一下·河南月考) 某商店对新引进的商品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:定价 (元)99.29.49.69.810销量(件)1009493908578(1)求回归直线方程;(2)假设今后销售依然服从(Ⅰ)中的关系,且该商品金价为每件5元,为获得最大利润,商店应该如何定价?(利润=销售收入-成本)参考公式: .21. (10分) (2019高一下·梧州期末)(1)任意向轴上这一区间内投掷一个点,则该点落在区间内的概率是多少?(2)已知向量,,若,分别表示一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足的概率.22. (10分) (2019高二上·莆田月考) 一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取一个,求(1)连续取两次都是白球的概率;(2)若取一个红球记2分,取一个白球记1分,取一个黑球记0分,连续取三次分数之和为4分的概率.(本小题基本事件总数较多不要求列举,但是所求事件含的基本事件要列举)参考答案一、单选题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共6题;共55分)答案:17-1、考点:解析:答案:18-1、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、答案:21-2、考点:解析:答案:22-1、答案:22-2、考点:解析:。
2017-2018学年高二数学10月月考试题(含解析)(1)

一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 在中,内角,,所对的边分别为,,,若,,则的面积是()
A. B. C. D.
【答案】C
【解析】试题分析:
,
,故选C.
考点:余弦定理.
【易错点睛】本题主要考查了余弦定理,三角形面积公式.解三角形问题的两重性:①作为三角形问题,它必须要用到三角形的内角和定理,正弦、余弦定理及其有关三角形的性质,及时进行边角转化,有利于发现解题的思路;②它毕竟是三角变换,只是角的范围受到了限制,因此常见的三角变换方法和原则都是适用的,注意“三统一”(即“统一角、统一函数、统一结构”)是使问题获得解决的突破口.
2. 在中,若,,则的值为()
A. B. C. D.
【答案】D
【解析】试题分析:由正弦定理得,因此得,所以,即.
.
考点:正弦定理和余弦定理的应用.
3. 以下关于正弦定理或其变形的叙述错误的是()
A. 在中,
B. 在中,若,则
C. 在中,若,则,若,则都成立
D. 在中,
【答案】B
【解析】由正弦定理易知A,C,D正确,对于B,由sin2A=sin2B,可得A=B或,即A=B或,所以a=b或,故B错误
4. 如图,测量河对岸的塔高时可以选与塔底在同一水平面内的两个测点与,测得
,,,并在点测得塔顶的仰角为,则塔高等于()
A. B. C. D.
【答案】D
【解析】在中,
由正弦定理得,解得
在中,
5. 已知数列的前项和为,且,则()
A. B. C. D.
【答案】D。
2017-2018学年高二上学期10月月考数学试题(文科)(解析版)17

高二(上)10月月考数学试卷(文科)一.选择题:(本大题共12个小题,每小题5分,共60分,在每小题所给出的四个选项中只有一项是符合题目要求的).1.(5分)圆(x+2)2+y2=5关于原点(0,0)对称的圆的方程为()A.(x﹣2)2+y2=5B.x2+(y﹣2)2=5 C.(x+2)2+(y+2)2=5 D.x2+(y+2)2=52.(5分)设x,y∈R,则“x≥2且y≥2”是“x2+y2≥4”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件3.(5分)椭圆的左右焦点为F1,F2,一直线过F1交椭圆于A,B两点,则△ABF2的周长为()A.32 B.16 C.8 D.44.(5分)已知命题p:∀x>0,ln(x+1)>0;命题q:若a>b,则a2>b2,下列命题为真命题的是()A.p∧q B.p∧¬q C.¬p∧q D.¬p∧¬q5.(5分)已知点P(a,b)(ab≠0)是圆x2+y2=r2内的一点,直线m是以P为中点的弦所在直线,直线l的方程为ax+by=r2,那么()A.m∥l,且l与圆相交 B.m⊥l,且l与圆相切C.m∥l,且l与圆相离 D.m⊥l,且l与圆相离6.(5分)已知椭圆C:=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,则C的离心率为()A.B.C.D.7.(5分)已知P为椭圆上的一点,M,N分别为圆(x+3)2+y2=1和圆(x﹣3)2+y2=4上的点,则|PM|+|PN|的最小值为()A.5 B.7 C.13 D.158.(5分)平面内到点(1,1)的距离为1且到点(1,4)的距离为2的直线有()条.A.1 B.2 C.3 D.49.(5分)若关于x的方程﹣kx﹣3+2k=0有且只有两个不同的实数根,则实数k的取值范围是()A.B.C.D.10.(5分)设椭圆的离心率为,右焦点为F(c,0),方程ax2+bx﹣c=0的两个实根分别为x1和x2,则点P(x1,x2)()A.必在圆x2+y2=2内B.必在圆x2+y2=2上C.必在圆x2+y2=2外D.以上三种情形都有可能11.(5分)已知椭圆T:+=1(a>b>0)的离心率为,过右焦点F且斜率为k(k>0)的直线与T相交于A,B两点,若=3,则k=()A.1 B.C.D.212.(5分)已知椭圆C:=1,点M1,M2...M5为其长轴AB 的 6 等分点,分别过这五点作斜率为k(k≠0)的一组平行线,交椭圆C于P1,P2 (10)则10条直线AP1,AP2…AP10的斜率乘积为()A.B.C.D.二、填空题:(本大题共4个小题,每小题5分,共20分,把答案填在答题卷上的相应位置).13.(5分)若点P(2,﹣1)为圆(x﹣1)2+y2=25的弦AB的中点,则直线AB 的方程是.14.(5分)若命题“∃x∈R,使x2+(a﹣1)x+1<0”是假命题,则实数a的取值范围为.15.(5分)在平面直角坐标系xOy中,已知△ABC顶点A(﹣3,0)和C(3,0)顶点B在椭圆上,则=.16.(5分)已知以T=4为周期的函数f(x)=,其中m >0.若方程3f(x)=x恰有5个实数解,则m的取值范围为.三、解答题:(本大题共6个小题,共70分,解答应写出文字说明、证明过程和演算步骤)17.(10分)已知m>0,p:(x+1)(x﹣5)≤0,q:1﹣m≤x≤1+m.(1)若p是q 的充分条件,求实数m的取值范围;(2)若m=5,“p∨q”为真命题,“p∧q”为假命题,求实数x的取值范围.18.(12分)已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.求:(1)顶点C的坐标;(2)直线BC的方程.19.(12分)椭圆ax2+by2=1与直线x+y﹣1=0相交于A,B两点,C是AB的中点,若|AB|=2,OC的斜率为,求椭圆的方程.20.(12分)平面上两点A(﹣1,0),B(1,0),在圆C:(x﹣3)2+(y﹣4)2=4上取一点P,(Ⅰ)x﹣y+c≥0恒成立,求c的范围(Ⅱ)从x+y+1=0上的点向圆引切线,求切线长的最小值(Ⅲ)求|PA|2+|PB|2的最值及此时点P的坐标.21.(12分)求过两圆x2+y2+2x+8y﹣8=0,x2+y2﹣4x﹣4y﹣2=0的交点且面积最小的圆的方程.22.(12分)已知椭圆,四点中恰有三点在椭圆上.(1)求C的方程;(2)设直线l不经过P2点且与C相交于A、B两点,若直线P1A与P2B直线的斜率的和为﹣1,证明:l过定点.高二(上)10月月考数学试卷(文科)参考答案与试题解析一.选择题:(本大题共12个小题,每小题5分,共60分,在每小题所给出的四个选项中只有一项是符合题目要求的).1.(5分)圆(x+2)2+y2=5关于原点(0,0)对称的圆的方程为()A.(x﹣2)2+y2=5 B.x2+(y﹣2)2=5 C.(x+2)2+(y+2)2=5 D.x2+(y+2)2=5【分析】求出对称圆的圆心坐标即可求得结果.【解答】解:圆(x+2)2+y2=5的圆心(﹣2,0),关于(0,0)对称的圆心坐标(2,0)所求圆的方程是(x﹣2)2+y2=5.故选A.【点评】本题考查圆和圆的位置关系,对称问题,是基础题.2.(5分)设x,y∈R,则“x≥2且y≥2”是“x2+y2≥4”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【分析】由“x≥2且y≥2”推出“x2+y2≥4”可证明充分性;由满足“x2+y2≥4”可举出反例推翻“x≥2且y≥2”,则证明不必要性,综合可得答案.【解答】解:若x≥2且y≥2,则x2≥4,y2≥4,所以x2+y2≥8,即x2+y2≥4;若x2+y2≥4,则如(﹣2,﹣2)满足条件,但不满足x≥2且y≥2.所以“x≥2且y≥2”是“x2+y2≥4”的充分而不必要条件.故选A.【点评】本题主要考查充分条件与必要条件的含义.3.(5分)椭圆的左右焦点为F1,F2,一直线过F1交椭圆于A,B两点,则△ABF2的周长为()A.32 B.16 C.8 D.4【分析】先由椭圆方程求得长半轴,而△ABF2的周长为AB+BF2+AF2,由椭圆的定义求解即可.【解答】解:∵椭圆∴a=4,b=,c=3根据椭圆的定义∴AF1+AF2=2a=8∴BF1+BF2=2a=8∵AF1+BF1=AB∴△ABF2的周长为4a=16故选B【点评】本题主要考查椭圆的定义的应用,应用的定义的基本特征,是与焦点有关.4.(5分)已知命题p:∀x>0,ln(x+1)>0;命题q:若a>b,则a2>b2,下列命题为真命题的是()A.p∧q B.p∧¬q C.¬p∧q D.¬p∧¬q【分析】由对数函数的性质可知命题p为真命题,则¬p为假命题,命题q是假命题,则¬q是真命题.因此p∧¬q为真命题.【解答】解:命题p:∀x>0,ln(x+1)>0,则命题p为真命题,则¬p为假命题;取a=﹣1,b=﹣2,a>b,但a2<b2,则命题q是假命题,则¬q是真命题.∴p∧q是假命题,p∧¬q是真命题,¬p∧q是假命题,¬p∧¬q是假命题.故选B.【点评】本题考查命题真假性的判断,复合命题的真假性,属于基础题.5.(5分)已知点P(a,b)(ab≠0)是圆x2+y2=r2内的一点,直线m是以P为中点的弦所在直线,直线l的方程为ax+by=r2,那么()A.m∥l,且l与圆相交 B.m⊥l,且l与圆相切C.m∥l,且l与圆相离 D.m⊥l,且l与圆相离【分析】由P在圆内,得到P到圆心距离小于半径,利用两点间的距离公式列出不等式a2+b2<r2,由直线m是以P为中点的弦所在直线,利用垂径定理得到直线OP与直线m垂直,根据直线OP的斜率求出直线m的斜率,再表示出直线l 的斜率,发现直线m与l斜率相同,可得出两直线平行,利用点到直线的距离公式表示出圆心到直线l的距离,利用得出的不等式变形判断出d大于r,即可确定出直线l与圆相离.【解答】解:∵点P(a,b)(ab≠0)在圆内,∴a2+b2<r2,∵k OP=,直线OP⊥直线m,∴k m=﹣,∵直线l的斜率k l=﹣=k m,∴m∥l,∵圆心O到直线l的距离d=>=r,∴l与圆相离.故选C.【点评】此题考查了直线与圆的位置关系,涉及的知识有:两点间的距离公式,点到直线的距离公式,两直线垂直、平行时直线斜率满足的关系,直线与圆的位置关系由d与r的大小来判断,当d>r时,直线与圆相离;当d<r时,直线与圆相交;当d=r时,直线与圆相切(其中d为圆心到直线的距离,r为圆的半径).6.(5分)已知椭圆C:=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,则C的离心率为()A.B.C.D.【分析】以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,可得原点到直线的距离=a,化简即可得出.【解答】解:以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,∴原点到直线的距离=a,化为:a2=3b2.∴椭圆C的离心率e===.故选:A.【点评】本题考查了椭圆的标准方程及其性质、直线与圆相切的性质、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.7.(5分)已知P为椭圆上的一点,M,N分别为圆(x+3)2+y2=1和圆(x﹣3)2+y2=4上的点,则|PM|+|PN|的最小值为()A.5 B.7 C.13 D.15【分析】由题意可得:椭圆的焦点分别是两圆(x+3)2+y2=1和(x﹣3)2+y2=4的圆心,再结合椭圆的定义与圆的有关性质可得答案.【解答】解:依题意可得,椭圆的焦点分别是两圆(x+3)2+y2=1和(x﹣3)2+y2=4的圆心,所以根据椭圆的定义可得:(|PM|+|PN|)min=2×5﹣1﹣2=7,故选B.【点评】本题考查圆的性质及其应用,以及椭圆的定义,解题时要认真审题,仔细解答,注意公式的合理运用.8.(5分)平面内到点(1,1)的距离为1且到点(1,4)的距离为2的直线有()条.A.1 B.2 C.3 D.4【分析】在坐标平面内,与点A(1,1)距离为1的直线为圆(x﹣1)2+(y﹣1)2=1的切线,同理可得在坐标平面内,与点B(1,4)距离为2的直线为圆(x﹣1)2+(y﹣4)2=4的切线,故所求直线为两圆的公切线.【解答】解:在坐标平面内,与点A(1,1)距离为1的直线为圆(x﹣1)2+(y ﹣1)2=1的切线,同理可得在坐标平面内,与点B(1,4)距离为2的直线为圆(x﹣1)2+(y﹣4)2=4的切线,故所求直线为两圆的公切线,∵|AB|==3=1+2,∴两圆外切,公切线由3条,故选:C.【点评】本题考查了圆的标准方程及其位置关系、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.9.(5分)若关于x的方程﹣kx﹣3+2k=0有且只有两个不同的实数根,则实数k的取值范围是()A.B.C.D.【分析】先将方程根的情况转化为一个半圆与一条直线交点的情况,再用数形结合,先求出相切时的斜率,再得到有两个交点的情况.【解答】解:将方程转化为:半圆,与直线y=kx+3﹣2k有两个不同交点.当直线与半圆相切时,有k=∴半圆与直线y=kx+3﹣2k有两个不同交点时.直线y=kx+3﹣2k=k(x﹣2)+3,一定过(2,3),由图象知直线过(﹣2,0)时直线的斜率k取最大值为k∈故选D【点评】本题主要考查用解析几何法来解决方程根的情况,关键是能够转化为一些特定的曲线才能用数形结合求解.10.(5分)设椭圆的离心率为,右焦点为F(c,0),方程ax2+bx﹣c=0的两个实根分别为x1和x2,则点P(x1,x2)()A.必在圆x2+y2=2内B.必在圆x2+y2=2上C.必在圆x2+y2=2外D.以上三种情形都有可能【分析】由题意可求得c=a,b=a,从而可求得x1和x2,利用韦达定理可求得+的值,从而可判断点P与圆x2+y2=2的关系.【解答】解:∵椭圆的离心率e==,∴c=a,b==a,∴ax2+bx﹣c=ax2+ax﹣a=0,∵a≠0,∴x2+x﹣=0,又该方程两个实根分别为x1和x2,∴x1+x2=﹣,x1x2=﹣,∴+=﹣2x1x2=+1<2.∴点P在圆x2+y2=2的内部.故选A.【点评】本题考查椭圆的简单性质,考查点与圆的位置关系,求得c,b与a的关系是关键,属于中档题.11.(5分)已知椭圆T:+=1(a>b>0)的离心率为,过右焦点F且斜率为k(k>0)的直线与T相交于A,B两点,若=3,则k=()A.1 B.C.D.2【分析】设A(x1,y1),B(x2,y2),根据求得y1和y2关系根据离心率设,b=t,代入椭圆方程与直线方程联立,消去x,根据韦达定理表示出y1+y2和y1y2,进而根据y1和y2关系求得k.【解答】解:A(x1,y1),B(x2,y2),∵,∴y1=﹣3y2,∵,设,b=t,∴x2+4y2﹣4t2=0①,设直线AB方程为,代入①中消去x,可得,∴,,解得,故选B【点评】本题主要考查了直线与圆锥曲线的综合问题.此类题问题综合性强,要求考生有较高地转化数学思想的运用能力,能将已知条件转化到基本知识的运用.12.(5分)已知椭圆C:=1,点M1,M2...M5为其长轴AB 的 6 等分点,分别过这五点作斜率为k(k≠0)的一组平行线,交椭圆C于P1,P2 (10)则10条直线AP1,AP2…AP10的斜率乘积为()A.B.C.D.【分析】解法一:设直线P1P2的方程为x=my+t,代入椭圆方程,利用韦达定理及直线的斜率公式,当t 分别取、、0、、时,代入即可求得10条直线AP1,AP2…AP10的斜率乘积;解法二:利用椭圆的性质可得得•=•=﹣=﹣.及其椭圆的对称性可得=,=,进而得出答案.【解答】解(法一):设其中的任一等分点为M(t,0),过M(t,0)的直线交椭圆于点P1(x1,y1)、P2(x2,y2),不妨设直线P1P2的方程为x=my+t,则与椭圆方程联立可得:,整理后可得(m2+2)y2+2mty+t2﹣2=0.从中可以得到,所以.当t 分别取、、0、、时,算出斜率的乘积为=(﹣)5=﹣.故选D.解法二::如图所示,由椭圆的性质可得•=•=﹣=﹣.由椭圆的对称性可得=,=,∴•=﹣,同理可得k AP3•=•=•=•=﹣.∴直线AP1,AP2,…,AP10这10条直线的斜率乘积=(﹣)5=﹣.故选D.【点评】本题考查椭圆的标准方程,直线与椭圆的位置,椭圆的性质,直线的斜率公式,考查计算能力,属于中档题.二、填空题:(本大题共4个小题,每小题5分,共20分,把答案填在答题卷上的相应位置).13.(5分)若点P(2,﹣1)为圆(x﹣1)2+y2=25的弦AB的中点,则直线AB 的方程是x﹣y﹣3=0.【分析】求出圆心C的坐标,得到PC的斜率,利用中垂线的性质求得直线AB 的斜率,点斜式写出AB的方程,并化为一般式.【解答】解:圆(x﹣1)2+y2=25的圆心C(1,0),点P(2,﹣1)为弦AB的中点,PC的斜率为=﹣1,∴直线AB的斜率为1,点斜式写出直线AB的方程y+1=1×(x﹣2),即x﹣y﹣3=0,故答案为:x﹣y﹣3=0.【点评】本题考查直线和圆相交的性质,线段的中垂线的性质,用点斜式求直线的方程的方法.14.(5分)若命题“∃x∈R,使x2+(a﹣1)x+1<0”是假命题,则实数a的取值范围为﹣1≤a≤3.【分析】先求出命题的否定,再用恒成立来求解【解答】解:命题“∃x∈R,使x2+(a﹣1)x+1<0”的否定是:““∀x∈R,使x2+(a﹣1)x+1≥0”即:△=(a﹣1)2﹣4≤0,∴﹣1≤a≤3故答案是﹣1≤a≤3【点评】本题通过逻辑用语来考查函数中的恒成立问题.15.(5分)在平面直角坐标系xOy中,已知△ABC顶点A(﹣3,0)和C(3,0),顶点B在椭圆上,则=.【分析】由正弦定理和椭圆的定义可知=,即可.【解答】解:由椭圆方程得:a=5,b=4,c=3.∵三角形ABC顶点A(﹣3,0)和C(3,0),顶点B在椭圆上,∴BC+AB=2a=10,∴由正弦定理可知=故答案为:.【点评】本题考查正弦定理和椭圆的定义,考查学生分析解决问题的能力,正确运用正弦定理和椭圆的定义是关键.属于中档题.16.(5分)已知以T=4为周期的函数f(x)=,其中m>0.若方程3f(x)=x恰有5个实数解,则m的取值范围为.【分析】根据对函数的解析式进行变形后发现当x∈(﹣1,1],[3,5],[7,9]上时,f(x)的图象为半个椭圆.根据图象推断要使方程恰有5个实数解,则需直线y=与第二个椭圆相交,而与第三个椭圆不公共点.把直线分别代入椭圆方程,根据△可求得m的范围.【解答】解:∵当x∈(﹣1,1]时,将函数化为方程x2+=1(y≥0),∴实质上为一个半椭圆,其图象如图所示,同时在坐标系中作出当x∈(1,3]得图象,再根据周期性作出函数其它部分的图象,由图易知直线y=与第二个椭圆(x﹣4)2+=1(y≥0)相交,而与第三个半椭圆(x﹣8)2+=1 (y≥0)无公共点时,方程恰有5个实数解,将y=代入(x﹣4)2+=1 (y≥0)得,(9m2+1)x2﹣72m2x+135m2=0,令t=9m2(t>0),则(t+1)x2﹣8tx+15t=0,由△=(8t)2﹣4×15t (t+1)>0,得t>15,由9m2>15,且m>0得m,同样由y=与第三个椭圆(x﹣8)2+=1 (y≥0)由△<0可计算得m<,综上可知m∈(,)故答案为:(,)【点评】本题主要考查了函数的周期性.采用了数形结合的方法,很直观.三、解答题:(本大题共6个小题,共70分,解答应写出文字说明、证明过程和演算步骤)17.(10分)已知m>0,p:(x+1)(x﹣5)≤0,q:1﹣m≤x≤1+m.(1)若p是q 的充分条件,求实数m的取值范围;(2)若m=5,“p∨q”为真命题,“p∧q”为假命题,求实数x的取值范围.【分析】(1)求出p的范围,根据集合的包含关系得到关于m的不等式组,求出m的范围即可;(2)求出q为真时的x的范围,通过讨论p,q的真假,得到关于x的不等式组,解出即可.【解答】解:(1)由题知p:﹣1≤x≤5.因为p 是q 的充分条件,所以[﹣1,5]是[1﹣m,1+m]的子集,所以解得m≥4.所以实数m 的取值范围是[4,+∞).(2)当m=5 时,q:﹣4≤x≤6,依题意得,p 与q 一真一假.当p 真q 假时,有无解;当p 假q 真时,有解得﹣4≤x<﹣1 或5<x≤6.所以实数x 的取值范围为[﹣4,﹣1)∪(5,6].【点评】本题考查了集合的包含关系,考查充分必要条件以及分类讨论思想,是一道中档题.18.(12分)已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.求:(1)顶点C的坐标;(2)直线BC的方程.【分析】(1)设C(m,n),利用点与直线的位置关系、相互垂直的直线斜率之间的关系即可得出;(2)利用中点坐标公式、点斜式即可得出.【解答】解:(1)设C(m,n),∵AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.∴,解得.∴C(4,3).(2)设B(a,b),则,解得.∴B(﹣1,﹣3).∴k BC==∴直线BC的方程为y﹣3=(x﹣4),化为6x﹣5y﹣9=0.【点评】本题考查了点与直线的位置关系、相互垂直的直线斜率之间的关系、中点坐标公式、点斜式,考查了计算能力,属于基础题.19.(12分)椭圆ax2+by2=1与直线x+y﹣1=0相交于A,B两点,C是AB的中点,若|AB|=2,OC的斜率为,求椭圆的方程.【分析】方法一:利用点差法,求得=k OC=,代入b=a.利用弦长公式求得()2﹣4•=4.则a=,∴b=;方法二:将直线方程代入椭圆方程利用弦长公式=1.①OC的斜率为,∴=.代入①,即可求得a和b的值,求得椭圆方程.【解答】解:方法一:设A(x1,y1),B(x2,y2),代入椭圆方程并作差,得a(x1+x2)(x1﹣x2)+b(y1+y2)(y1﹣y2)=0.而=﹣1,=k OC=,代入上式可得b=a.再由|AB|=|x2﹣x1|=|x2﹣x1|=2,其中x1,x2是方程(a+b)x2﹣2bx+b﹣1=0的两根.故()2﹣4•=4.将b=a代入,得a=,∴b=.∴所求椭圆的方程是;方法二:由,整理得(a+b)x2﹣2bx+b﹣1=0.设A(x1,y1),B(x2,y2),则|AB|==•.∵|AB|=2,∴=1.①设C(x,y),则x==,y=1﹣x=.∵OC的斜率为,∴=.代入①,得a=,b=.∴椭圆方程为.【点评】本题考查椭圆的标准方程的求法,直线与椭圆的位置关系,弦长公式,考查计算能力,属于中档题.20.(12分)平面上两点A(﹣1,0),B(1,0),在圆C:(x﹣3)2+(y﹣4)2=4上取一点P,(Ⅰ)x﹣y+c≥0恒成立,求c的范围(Ⅱ)从x+y+1=0上的点向圆引切线,求切线长的最小值(Ⅲ)求|PA|2+|PB|2的最值及此时点P的坐标.(Ⅰ)由x﹣y+c≥0,得c≥y﹣x,由圆的参数方程得c≥4+2sinθ﹣3﹣2cosθ,【分析】即可求c的范围;(Ⅱ)求出圆心C到直线x+y+1=0的距离为,利用勾股定理求切线长的最小值;(Ⅲ)设出的是PP(a,b),使要求的式子转化为求圆上的点到原点的距离问题,利用数形结合法求最值.【解答】解:(Ⅰ)由x﹣y+c≥0,得c≥y﹣x,由圆的参数方程得c≥4+2sinθ﹣3﹣2cosθ,所以(Ⅱ)圆心C到直线x+y+1=0的距离为,切线长的最小值为(Ⅲ)设P(a,b),则|PA|2+|PB|2=2a2+2b2+2,a2+b2为圆C:(x﹣3)2+(y﹣4)2=4上的点到原点的距离平方,所以最小值为20,;最大值为100,.【点评】本题考查圆的参数方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.21.(12分)求过两圆x2+y2+2x+8y﹣8=0,x2+y2﹣4x﹣4y﹣2=0的交点且面积最小的圆的方程.【分析】求出圆x2+y2+2x+8y﹣8=0和x2+y2﹣4x﹣4y﹣2=0的圆心和半径,写出两圆圆心所在直线方程,再求出公共弦所在直线方程,两直线交点为面积最小的圆的圆心,再求出该圆的半径即可.【解答】解:圆x2+y2+2x+8y﹣8=0化为(x+1)2+(y+4)2=25,圆心坐标为(﹣1,﹣4),半径为5;圆x2+y2﹣4x﹣4y﹣2=0化为(x﹣2)2+(y﹣2)2=10,圆心坐标为(2,2),半径为;两圆圆心所在直线方程为,化为一般式是2x﹣y﹣2=0,…①公共弦所在直线方程为x+2y﹣1=0,…②解①②组成的方程组,得,∴面积最小的圆的圆心坐标为(1,0);又点(1,0)到(﹣1,﹣4)的距离为d==,∴该圆的半径为r=,∴所求圆系中面积最小的圆的方程为(x﹣1)2+y2=5.【点评】本题考查了两圆的位置关系应用问题,也考查了求圆的方程应用问题,是综合题.22.(12分)已知椭圆,四点中恰有三点在椭圆上.(1)求C的方程;(2)设直线l不经过P2点且与C相交于A、B两点,若直线P1A与P2B直线的斜率的和为﹣1,证明:l过定点.【分析】(1)根据椭圆的对称性,得到P2,P3,P4三点在椭圆C上.把P2,P3代入椭圆C,求出a2=4,b2=1,由此能求出椭圆C的方程.(2)当斜率不存在时,不满足;当斜率存在时,设l:y=kx+b,(b≠1),与椭圆方程联立,得(1+4k2)x2+8kbx+4b2﹣4=0,由此利用根的判别式、韦达定理、直线方程,结合已知条件能证明直线l过定点(2,﹣1).【解答】解:(1)根据椭圆的对称性,得到P2,P3,P4三点在椭圆C上.把P2,P3代入椭圆C,得,得出a2=4,b2=1,由此椭圆C的方程为.证明:(2)①当斜率不存在时,设l:x=m,A(m,y A),B(m,﹣y A),∵直线P2A与直线P2B的斜率的和为﹣1,=﹣1解得m=2,此时l过椭圆右顶点,不存在两个交点,故不满足.②当斜率存在时,设l:y=kx+b,(b≠1),A(x1,y1),B(x2,y2),联立,整理,得(1+4k2)x2+8kbx+4b2﹣4=0,…①∵直线P2A与P2B直线的斜率的和为﹣1,∴==…②①代入②得:又b≠1,∴b=﹣2k﹣1,此时△=﹣64k,存在k,使得△>0成立,∴直线l的方程为y=kx﹣2k﹣1,当x=2时,y=﹣1,∴l过定点(2,﹣1).【点评】本题考查椭圆方程的求法,考查椭圆、直线方程、根的判别式、韦达定理、直线方程位置关系等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想,是中档题.21。
湖北省黄石市高二数学10月月考试卷

湖北省黄石市高二数学10月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)(2018·郑州模拟) 已知数列的前项和为,,,且,记,则()A .B .C .D .2. (2分) (2020高二上·天津期末) 正方体 ,点 , 分别是,的中点,则与所成角的余弦值为()A .B .C .D .3. (2分)在正方形SG1G2G3中,E、F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE、SF及EF 把这个正方形折成一个四面体,使G1、G2、G3三点重合,重合后的点记为G,那么,在四面体S﹣EFG中必有()A . SG⊥△EFG所在平面B . SD⊥△EFG所在平面C . GF⊥△SEF所在平面D . GD⊥△SEF所在平面4. (2分)两等角的一组对应边平行,则A . 另一组对应边平行B . 另一组对应边不平行C . 另一组对应边也不可能垂直D . 以上都不对5. (2分)(2013·湖北理) 曲线y=1+与直线y=k(x-2)+4有两个交点,则实数k的取值范围是()A . (0,)B . (,+∞)C . (,]D . (,]6. (2分)圆心坐标为(2,-1)的圆在直线x-y-1=0上截得的弦长为,那么这个圆的方程为()A . (x-2)2+(y+1)2=4B . (x-2)2+(y+1)2=2C . (x-2)2+(y+1)2=8D . (x-2)2+(y+1)2=167. (2分)(2016·绍兴模拟) 如图,面ABC⊥α,D为AB的中点,|AB|=2,∠CDB=60°,P为α内的动点,且P到直线CD的距离为,则∠APB的最大值为()A . 30°B . 60°C . 90°D . 120°8. (2分) (2017高三上·南充期末) 设α,β是两个不同的平面,a,b是两条不同的直线,下列四个命题中正确的命题是()A . 若a∥α,b∥α,则a∥bB . 若a∥α,b∥β,a∥b,则α∥βC . 若a⊥α,a⊂β,则α⊥βD . 若a,b在α内的射影相互垂直,则a⊥b9. (2分)直线l:4x+y﹣4=0,下列曲线:x2=﹣y,﹣x2=1, + =1,其中与直线l只有一个公共点的个数为()A . 0B . 1C . 2D . 310. (2分)(2018·泉州模拟) 已知直线:,圆: .若对任意,存在被截得弦长为,则实数的取值范围是()A .B .C .D .11. (2分)(2017·新余模拟) 我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式1+ 中“”即代表无数次重复,但原式却是个定值,它可以通过方程1+ =x求得x= .类比上述过程,则 =()A . 3B .C . 6D . 212. (2分)(2017·滨州模拟) 已知双曲线E:(a>0,b>0)的右顶点为A,抛物线C:y2=8ax 的焦点为F,若在E的渐近线上存在点P使得PA⊥FP,则E的离心率的取值范围是()A . (1,2)B . (1, ]C . (2,+∞)D . [ ,+∞)二、填空题 (共4题;共4分)13. (1分)已知x>0,y>0且2x+y=2,则的最小值为________14. (1分)(2017·运城模拟) 四棱锥P﹣ABCD底面是一个棱长为2的菱形,且∠DAB=60°,各侧面和底面所成角均为60°,则此棱锥内切球体积为________.15. (1分) (2017高二上·哈尔滨月考) 椭圆的左焦点为,直线与椭圆相交于点、,当的周长最大时,的面积是________.16. (1分)已知各项都为正数的等比数列中,a2•a4=4,a1+a2+a3=14,则满足的最大正整数n的值为________.三、解答题 (共6题;共60分)17. (10分)已知点P(0,﹣1),椭圆C: + =1(a>b>0),椭圆的左右焦点分别为F1 , F2 ,若三角形PF1F2的面积为1,且a2 , b2的等比中项为2 .(1)求椭圆C的标准方程;(2)若椭圆C上有A,B两点,使△PAB的重心为F1,求直线AB的方程.18. (10分) (2016高二下·韶关期末) 等比数列{an}的各项均为正数,且a2﹣a1=6,9a32=a2a6 .(1)求数列{an}的通项公式;(2)若bn=log3a1+log3a2+…+log3an,数列{ }的前n项和Tn,求证:Tn<2.19. (10分) (2019高二下·上海月考) 如图,正三棱柱的底面边长为4,侧棱长为1.(1)求二面角的大小;(2)若过的截面与底面成30°的二面角,求此截面的面积.20. (10分)已知圆O:x2+y2=4及一点P(﹣1,0),Q在圆O上运动一周,PQ的中点M形成轨迹C.(1)求轨迹C的方程;(2)若直线PQ的斜率为1,该直线与轨迹C交于异于M的一点N,求△CMN的面积.21. (10分) (2017高二上·张家口期末) 如图四棱锥E﹣ABCD中,四边形ABCD为平行四边形,△BCE为等边三角形,△ABE是以∠A为直角的等腰直角三角形,且AC=BC.(Ⅰ)证明:平面ABE⊥平面BCE;(Ⅱ)求二面角A﹣DE﹣C的余弦值.22. (10分) (2017高二上·南昌月考) 已知椭圆的一个顶点为A(0,-1),焦点在x轴上。
湖北省黄石市数学高二上学期文数10月月考试卷

湖北省黄石市数学高二上学期文数10月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)已知a<b,则下列不等式正确的是()A .B .C .D .2. (2分)等差数列{an}中,a1=2,公差d=3则{an}的通项公式为()A . .an=3n﹣1B . an=2n+1C . .an=2n+3D . .an=3n+23. (2分)(2018·滨海模拟) 在中,,,则角()A .B .C . 或D .4. (2分)在中,已知,,A=30°,则()A .B .C .D .5. (2分)设M是椭圆上的一点,为焦点,且,则的面积为()A .B .C .D . 166. (2分)已知等差数列中,,,则前10项和()A . 55B . 155C . 350D . 4007. (2分) (2017高三上·漳州期末) 等差数列{an}中,Sn是前n项和,且S3=S8 , S7=Sk ,则k的值为()A . 4B . 11C . 2D . 128. (2分)已知等比数列{an}满足a1=, a3a5=4(a4-1),则a2=()A . 2B . 1C .D .9. (2分) (2020高三上·长春月考) 若数列中的项按一定规律变化,则实数最有可能的值是()A .B .C .D .10. (2分)已知等差数列的首项为a,公差为b,等比数列的首项为b,公比为a,其中且,则a的值为()A . 2B . 1C . 4D . 311. (2分)已知正整数a1 , a2 ,…,a2016成等比数列,公比q∈(1,2),则a2016取最小值时,q=()A .B .C .D .12. (2分)(2014·福建理) 等差数列{an}的前n项和为Sn ,若a1=2,S3=12,则a6等于()A . 8B . 10C . 12D . 14二、填空题 (共4题;共4分)13. (1分)(2017·天津) 若a,b∈R,ab>0,则的最小值为________.14. (1分) (2017高一下·彭州期中) 若关于x的不等式﹣ +2x>﹣mx的解集为 {x|0<x<2},则m=________.15. (1分)若变量 x,y满足约束条件,则z=3x+y的最小值为________16. (1分) (2016高三上·洛阳期中) 等差数列{an}中,Sn为其前n项和,若a5=10,S5=30,则 + ++…+ =________.三、解答题 (共6题;共50分)17. (10分) (2019高二上·烟台期中) 设函数 .(1)若函数在处取得极值,求的值;(2)若不等式对任意都成立,求实数的取值范围.18. (5分)在△ABC中,内角A,B,C所对的边分别为a,b,c,且4sinAsinC﹣4cos2=﹣2.求角B的大小19. (10分) (2016高三上·湖北期中) 数列{an}的前n项和Sn=3n2+2n+1.(1)求{an}的通项公式;(2)令bn=an2n,求{bn}的前n项和Tn.20. (5分) (2016高二上·吉林期中) 某生产甲,乙两种产品,生产这两种产品每吨需要的煤,电以及每吨产品的产值如表所示.若每天配给该厂的煤至多56吨,供电至多45千瓦,问该厂如何安排生产,使该厂日产值最大?用煤/吨用电/千瓦产值/万元甲种产品728乙种产品351121. (10分) (2016高二上·九江期中) 已知x,y满足不等式组,求(1) z=x+2y的最大值;(2) z=x2+y2﹣10y+25的最小值.22. (10分) (2019高一上·丰台期中) 已知函数.(1)若,求不等式的解集;(2)若不等式的解集为,求实数的取值范围.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共50分) 17-1、17-2、18-1、19-1、19-2、20-1、21-1、21-2、22-1、22-2、。
湖北省黄石市有色第一中学2017-2018学年高二上学期10月月考数学(文)试题 Word版含答案
2017-2018学年度上学期有色一中十月月考数学试卷(高二文科)一.选择题:(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合{|1A x =-≤x ≤2},B=},04|{2R x x x x ∈>-,则)(B C A R ⋂=( )A.[1,2]B.[0,2]C. [1,4]D.[0,4]2.已知ABC △中,a =b =60B =,那么角A 等于( )A .45 B .60 C . 60120或 D .45135或3.已知向量(2,3)a =,(1,2)b =-,若4ma b +与2a b -共线,则m 的值为( )1.2A .2B 1.2C - .2D - 4. 已知实数y x ,满足约束条件04340x x y y >⎧⎪+≤⎨⎪≥⎩,则2z y x =-的最小值是( )A .1-B .0C .1D .835.某几何体的三视图如图所示,则它的体积是( )A .283π-B .83π- C .82π- D .23π6.设{}n a 是公差为正数的等差数列,若12315a a a ++=,12380a a a =,则111213a a a ++=( )A 、75B 、90C 、105D 、1207. 直线 L 1:(1)3ax a y +-=, L 2:(1)(23)2a x a y -++= 互相垂直,则a 的值为 ( )A .-3B .1C . 0 或32-D .1或-3 8. 用a 、b 、c 表示三条不同的直线,y 表示平面,给出下列: ①若a ∥b , b ∥c ,则a ∥c ;②若a ⊥b ,b ⊥c ,则a ⊥c ; ③若a ∥y ,b ∥y ,则a ∥b ;④若a ⊥y ,b ⊥y ,则a ∥b . 正确的是( )A.①②B.①④C.②③D.③④9. 若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为( )A .120°B .150°C .180°D .240°10. 椭圆2214924x y +=上一点P 与椭圆的两个焦点12,F F 的连线互相垂直,则12PF F ∆的面积为( )A.20B.22C.24D.25 11.不等式2162a bx x b a+<+对任意,(0,)a b ∈+∞恒成立,则实数x 的取值范围是 ( ) A .(2,0)- B .(,2)(0,)-∞-+∞ C .(,4)(2,)-∞-+∞ D .(4,2)-12. 过椭圆22194x y +=上一点M 作圆222x y +=的两条切线,点,A B 为切点.过 ,A B 的直线l 与x 轴,y 轴分别交于,P Q 两点,则POQ ∆的面积的最小值为( )A.12 B. 23 C .1 D. 43二.填空题:(本大题共4小题,每小题5分,共20分.请将答案填在答题卡对应题号.......的位置上. 答错位置,书写不清,模棱两可均不得分. )13. 已知{}n a 是等比数列,22a =, 434a a -=,则此数列的公比q =______ 14.长方体的一个顶点上三条棱长分别是3、4、5,且它的8个顶点都在同一球面上, 则这个球的表面积是15.在长方体1111ABCD A B C D -中,3AB BC ==,14AA =则异面直线1A D 与1AB 所成角的余弦值 。
高二数学10月月考试题理word版本
2017-2018学年度高二上期十月月考数学试题(理科)注意事项:1.本试卷分第Ⅰ卷和第Ⅱ卷两个部分。
2. 本堂考试120分钟,满分150分。
3.答题前,考生务必先将自己的姓名、班级、考号、座位号填写在答题卷的密封线内。
4.考试结束后,将所有答题卷和机读卡交回。
第Ⅰ卷(60分)一.选择题:(本大题共12个小题,每小题5分,共60分,在每小题所给出的四个选项中只有一项是符合题目要求的)。
1.圆22(2)5++=x y 关于原点对称的圆的方程是(A )A. 22(2)5-+=x y B. 22(-2)5+=x y C. 22(2)(2)5+++=x y D. 22(2)5++=x y2.设,、∈x y R 则“2≥x 且2≥y ”是“224+≥x y ”的( A ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.即不充分也不必要条件3.椭圆221167+=x y 的左右焦点分别为12,F F ,一直线过交椭圆于A ,B 两点, 则 2∆ABF 的周长为 ( B )A.32B.16C. 8D. 44. 已知命题:0,ln(1)0p x x ∀>+>;命题22:,q a b a b >>若则,下列命题为真命题的是( B )A 、p ∧qB 、p ∧¬qC 、¬p ∧qD 、¬p ∧¬q5.已知点M (a,b )(ab ≠0),是圆222+=x y r 内一点,直线m 是以M 为中点的弦所在的 直线,直线的方程是2+=ax by r ,则( C ) A.∥m 且与圆相交 B.⊥m 且与圆相切C.∥m 且与圆相离D.⊥m 且与圆相离6. 已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为( A )A .3B .3C .3D .137.已知为椭圆22=12516x y +上的一点,M N 、分别为圆2231()x y ++=和圆2()3x -+24y =上的点,则PM PN +的最小值为( B ) A .5 B .7 C .13 D .158.平面内到点(1,1)的距离为1且到点(1,4)的距离为2的直线有( C )条。
湖北省黄石市数学高二上学期理数10月月考试卷
湖北省黄石市数学高二上学期理数10月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2019高二上·成都期中) 下列说法正确的是()A . 命题“3能被2整除”是真命题B . 命题“ ,”的否定是“ ,”C . 命题“47是7的倍数或49是7的倍数”是真命题D . 命题“若都是偶数,则是偶数”的逆否命题是假命题2. (2分)设A为圆(x-1)2+y2=1上的动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程是()A . (x-1)2+y2=4B . (x-1)2+y2=2C . y2=2xD . y2=-2x3. (2分) (2017高二下·黄陵开学考) “a=b”是“直线y=x+2与圆(x﹣a)2+(y﹣b)2=2相切”的()A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分又不必要条件4. (2分)椭圆的两焦点之间的距离为()A .B .C .D .5. (2分) (2016高二下·福建期末) 命题p:∃x∈N,x3<x2;命题q:∀a∈(0,1)∪(1,+∞),函数f(x)=loga(x﹣1)的图象过点(2,0),则下列命题是真命题的是()A . p∧qB . p∨¬qC . ¬p∧qD . ¬p∧¬q6. (2分)抛物线的焦点F恰好是双曲线的右焦点,且它们的交点的连线过点F,则双曲线的离心率为()A .B .C . 3D .7. (2分)偶函数f(x)满足f(x-2)=f(x+2),且在时,则关于x的方程,在上解的个数是()A . lB . 2C . 3D . 48. (2分) (2016高二上·临川期中) 已知点P(x,y)在椭圆x2+4y2=4上,则 x2+2x﹣y2的最大值为()A . ﹣2B . 7C . 2D . ﹣19. (2分)已知f(x)=x﹣sinx,命题p:∃x∈(0,),f(x)<0,则()A . p是假命题,¬p:∀x∈(0,),f(x)≥0B . p是假命题,¬p:∃x∈(0,),f(x)≥0C . p是真命题,¬p:∀x∈(0,),f(x)≥0D . p是真命题,¬p:∃x∈(0,),f(x)≥010. (2分) (2018高三上·昭通期末) 椭圆C:的右焦点为F,右顶点为A,抛物线x2=4by 的焦点为B,且.则椭圆C的离心率为()A .B .C .D .11. (2分) (2017高二上·南阳月考) 已知为椭圆的两个焦点,为椭圆上一点且,则此椭圆离心率的取值范围是()A .B .C .D .12. (2分)线段∣AB∣=4,∣PA∣+∣PB∣=6,M是AB的中点,当P点在同一平面内运动时,PM的长度的最小值是()A . 2B .C .D . 5二、填空题 (共4题;共4分)13. (1分) (2016高二上·黄陵期中) 已知α、β是不同的两个平面,直线a⊂α,直线b⊂β,命题p:a 与b没有公共点;命题q:α∥β,则p是q的________条件.14. (1分) (2017高二上·邢台期末) 椭圆的右顶点和上顶点分别为A和B,右焦点为F.若|AF|、|AB|、3|BF|成等比数列,则该椭圆的离心率为________.15. (1分)(2017·福建模拟) 已知双曲线﹣ =1(a>0,b>0)的右焦点为F2 ,过F2作其中一条渐近线的垂线,分别交y轴和该渐近线于M,N两点,且 =3 ,则 =________.16. (1分) (2017高一下·盐城期中) 若圆x2+y2=4 与圆x2+y2﹣2mx+m2﹣1=0相外切,则实数m=________.三、解答题 (共6题;共45分)17. (5分)已知,(1)求命题的否定;命题的否定;(2)若为真命题,求实数的取值范围.18. (10分) (2015高二上·海林期末) 已知命题p:x2﹣8x﹣20>0,q:x2﹣2x+1﹣m2>0(m>0),若p 是q的必要不充分条件,求实数m的取值范围.19. (10分) (2017高二上·太原月考) 已知抛物线的焦点为,是抛物线上横坐标为4,且位于轴上方的点,到抛物线准线的距离等于5,过作垂直于轴,垂足为,的中点为.(1)求抛物线的方程;(2)若过作,垂足为,求点的坐标.20. (5分) (2016高三上·定州期中) 如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B,P在单位圆上,且B(﹣,),∠AOB=α.(1)求的值;(2)若四边形OAQP是平行四边形,(i)当P在单位圆上运动时,求点O的轨迹方程;(ii)设∠POA=θ(0≤θ≤2π),点Q(m,n),且f(θ)=m+ n.求关于θ的函数f(θ)的解析式,并求其单调增区间.21. (5分) (2017高二上·牡丹江月考) 已知双曲线的渐近线方程为:,右顶点为 .(Ⅰ)求双曲线的方程;(Ⅰ)已知直线与双曲线交于不同的两点,且线段的中点为,当时,求的值。
湖北省黄石市2017_2018学年高二数学10月月考试题文201710190172
湖北省黄石市2017-2018学年高二数学10月月考试题文一、选择题(本大题共12小题,共60分)1.下列命题是真命题的是()A.“若x=2,则(x-2)(x-1)=0”B.“若x=0,则xy=0”的否命题C.“若x=0,则xy=0”的逆命题D.“若x>1,则x>2”的逆否命题2.已知a∈R,b∈R,则“a>b”是“”成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件3. 已知圆的方程为x2+y2-4x+2y-4=0,则圆的半径为()A.3B.9C.D.±34.已知命题p:∀x>0,总有(x+1)e x>1,则¬p为()A.∃x0≤0,使得(x0+1)e≤1B.∃x0>0,使得(x0+1)e≤1C.∀x>0,总有(x+1)e x≤1D.∀x≤0,总有(x+1)e x≤15. 已知命题p:∃x∈R,x2-x+1≥0.命题q:若a2<b2,则a<b,下列命题为真命题的是()A.p∧qB.p∧¬qC.¬p∧qD.¬p∧¬q6.若直线l1:ax+2y+6=0与直线l2:x+(a-1)y+a2-1=0垂直,则a=()A.2B.C.1D.-27.经过圆C:(x+1)2+(y-2)2=4的圆心且斜率为1的直线方程为()A.x-y+3=0B.x-y-3=0C.x+y-1=0D.x+y+3=08.对于a∈R,直线(x+y-1)-a(x+1)=0恒过定点P,则以P为圆心,为半径的圆的方程是()A. x2+y2+2x+4y=0B.x2+y2+2x-4y=0C.x2+y2-2x+4y=0D.x2+y2-2x-4y=09.过圆x2+y2-4x+my=0上一点P(1,1)的圆的切线方程为()A.2x+y-3=0B.2x-y-1=0C.x-2y-1=0D.x-2y+1=010.已知点M是直线3x+4y-2=0上的动点,点N为圆(x+1)2+(y+1)2=1上的动点,则|MN|的最小值为()A. B.1 C. D.11.已知点P(x,y)的坐标满足x2+y2-2y=0,则的取值范围是()A. B. 或C. D. 或12.已知圆M:x2+y2-2ay=0(a>0)截直线x+y=0所得线段的长度是2,则圆M与圆N:(x-1)2+(y-1)2=1的位置关系是()A.内切B.相交C.外切D.相离二、填空题(本大题共4小题,共20分)13.命题“若a=-1,则a2=1”的逆否命题是______ .14.已知命题,命题q:x2-(2a+1)x+a(a+1)≤0,若¬p是¬q的必要而不充分条件,则实数a的取值范围是______ .15.由直线y=x+1上一点向圆x2-6x+y2+8=0引切线,则切线长的最小值为______ .16.若直线ax-by+1=0平分圆C:x2+y2+2x-4y+1=0的周长,则ab的取值范围是______ .三、解答题(本大题共6小题,共70分)17.已知圆心为C的圆经过三个点O(0,0)、A(1,3)、B(4,0)(1)求圆C的方程;(2)求过点P(3,6)且被圆C截得弦长为4的直线的方程.18.命题p:方程x2-x+a2-6a=0有一正根和一负根.命题q:函数y=x2+(a-3)x+1的图象与x轴有公共点.若命题“p∨q”为真命题,而命题“p∧q”为假命题,求实数a的取值范围.19.已知曲线C的方程是:x2+y2-2x-4y+m=0,点P(3,-1).(1)若m=1,直线l过点P且与曲线C只有一个公共点,求直线l的方程;(2)若曲线C表示圆且被直线x+2y+5=0截得的弦长为2 ,求实数m的值.20.如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AB,BC的中点,点F在侧棱BB1上,且A1F⊥B1D,求证:(Ⅰ)直线DE∥平面A1C1F;(Ⅱ)B1D⊥平面A1C1F.2x 21. 设p:实数x满足x2-4ax+3a2<0,其中a≠0,命题q:实数x满足2xx 60 2x 8(1)若a=1,且p∧q为真,求实数x的取值范围;(2)若p是q的必要不充分条件,求实数a的取值范围.- 3 -22.已知圆C:(x+2)2+y2=5,直线l:mx-y+1+2m=0,m∈R.(1)求证:对m∈R,直线l与圆C总有两个不同的交点A、B;(2)求弦AB的中点M的轨迹方程,并说明其轨迹是什么曲线;(3)是否存在实数m,使得圆C上有四点到直线l的距离为?若存在,求出m的范围;若不存在,说明理由.黄石三中高二年级文科10月月考试卷答案和解析【答案】1.A2.D3.C4.B5.C6.B7.A8.B9.D 10.C 11.B 12.B13.“若a2≠1,则a≠-1”14.15.16.17.解:(1)设圆的方程为x2+y2+D x+E y+F=0.圆C经过三个点O(0,0)A(1,3)B(4,0),所以解得D=-4,E=-2,F=0,所以圆C的方程x2+y2-4x-2y=0.(2)①过点P(3,6)且被圆C截得弦长为4的直线的斜率不存在,此时x=3,满足题意.②当过点P(3,6)且被圆C截得弦长为4的直线的斜率存在时设为k,直线方程为y-6=k(x-3).则,解得k= ,所求直线方程为:12x-5y-6=0.故所求直线方程为:x=3或12x-5y-6=0.18.解:若方程x2-x+a2-6a=0有一正根和一负根,则,解得0<a<6.即p:0<a<6.若函数y=x2+(a-3)x+1的图象与x轴有公共点.则判别式△≥0,即(a-3)2-4≥0,解得a≥5或a≤1.即q:a≥5或a≤1.命题“p∨q”为真命题,而命题“p∧q”为假命题,则命题p,q为一真,一假.若p真q假,则1<a<5.若p假q真,则a≥6或a≤0.综上实数a的取值范围是a≥6或a≤0或1<a<5.19.解:(1)m=1时,曲线C的方程是:(x-1)2+(y-2)2=4,表示圆心为(1,2),半径为2的圆,∵直线l过点P且与曲线C只有一个公共点,∴直线l与圆相切.①当直线l的斜率不存在时,直线l的方程为:x=3.②当直线l的斜率存在时,设直线l的方程为:y=k(x-3)-1.即kx-y-3k-1=0.⇒k=- ,直线l的方程为:5x+12y-3=0.综上所述所求直线l的方程为:x=3,5x+12y-3=0.(2)曲线C的方程配方得:(x-1)2+(y-2)2=5-m,若方程表示圆则5-m>0⇒m<5.圆心到直线x+2y+5=0距离d= ,根据圆的弦长公式2 ,⇒2 ,⇒m=-2020.证明:(Ⅰ)∵D,E分别为AB,BC的中点,∴DE为△ABC的中位线,∴DE∥AC,∵ABC-A1B1C1为棱柱,∴AC∥A1C1,∴DE∥A1C1,∵A1C1⊂平面A1C1F,且DE⊄平面A1C1F,∴DE∥平面A1C1F;(Ⅱ)由题意,A1C1⊥平面A1B,B1D⊂平面A1B,∴B1D⊥A1C1,∵A1F⊥B1D,A1F∩A1C1=A1,∴B1D⊥平面A1C1F.21.解:(1)由x2-4ax+3a2<0,得(x-3a)(x-a)<0,当a=1时,解得1<x<3,即p为真时,实数x的取值范围是1<x<3,…(1分)由,得2<x≤3,即q为真时,实数x的取值范围是2<x≤3,…(3分)若p∧q为真,则p真且q真,…(4分)∴实数x的取值范围是(2,3).…(5分)(2)p是q的必要不充分条件,即q⇒p,且p推不出q,设A={x|p(x)},B={x|q(x)},则A⊉B,…(7分)又B=(2,3],当a>0时,A=(a,3a);a<0时,A=(3a,a),∴当a>0时,有,解得1<a≤2;…(9分)当a<0时,A∩B=∅,不合题意;∴实数a的取值范围是(1,2].…(10分)22.解:(1)圆C:(x+2)2+y2=5,的圆心为C(-2,0),半径为,所以圆心C到直线l:mx-y+1+2m=0的距离.所以直线l与圆C相交,即直线l与圆C总有两个不同的交点;…(4分)(2)设中点为M(x,y),因为直线l:mx-y+1+2m=0恒过定点(-2,1),当直线l的斜率存在时,,又,k AB•k MC=-1,所以,化简得.…(6分)当直线l的斜率不存在时,中点M(-2,0)也满足上述方程.…(7分)所以M的轨迹方程是,它是一个以为圆心,以为半径的圆.…(8分)(3)假设存在直线l,使得圆上有四点到直线l的距离为,由于圆心C(-2,0),半径为,则圆心C(-2,0)到直线l的距离为化简得m2>4,解得m>2或m<-2.…(12分)【解析】1. 解:对于A,若x=2,则(x-2)(x-1)=0显然成立,A正确.对于B,“若x=0,则xy=0”的否命题是:“若x≠0,则xy≠0”,当y=0时,xy=0,∴B不正确;对于C,“若x=0,则xy=0”的逆命题:“若xy=0,则x=0”,也可能是y=0,∴C不正确;对于D,“若x>1,则x>2”的逆否命题,∵原命题与逆否命题有相同的真假性,原命题显然不正确,∴D不正确;故选:A.利用函数的零点判断A的正误;通过命题的否命题,判断B的正误;判断命题的逆命题的真假判断C的正误;利用原命题的真假与逆否命题的真假相同判断D的正误;本题考查命题的真假的判断,考查函数的零点,四种命题的真假关系,基本知识的应用.2. 解:令a=1,b=-1,则a>b,而>,不是充分条件,若,即<0,∴或,即a,b同号时:a>b,a,b异号时:a<b,不是必要条件,故选:D.根据充分必要条件的定义分别判断其充分性和必要性即可.本题考查了充分必要条件,考查不等式问题,是一道基础题.3. 解:圆x2+y2-4x+2y-4=0,即(x-2)2+(y+1)2=9,故此圆的半径为3,故选:A.圆x2+y2-4x+2y-4=0,即(x-2)2+(y+1)2=9,由此可得圆的半径.本题主要考查把圆的一般方程化为标准方程,求圆的半径,属于中档题.4. 解:根据全称命题的否定为特称命题可知,¬p为∃x0>0,使得(x0+1)e≤1,故选:B.据全称命题的否定为特称命题可写出命题p的否定.本题主要考查了全称命题的否定的写法,全称命题的否定是特称命题.5. 解:命题p:∃x=0∈R,使x2-x+1≥0成立.故命题p为真命题;当a=1,b=-2时,a2<b2成立,但a<b不成立,故命题q为假命题,故命题p∧q,¬p∧q,¬p∧¬q均为假命题;命题p∧¬q为真命题,故选:B.先判断命题p,q的真假,进而根据复合命题真假的真值表,可得答案.本题以命题的真假判断与应用为载体,考查了复合命题,特称命题,不等式与不等关系,难度中档.6. 解:直线l1:ax+2y+6=0,l2:x+(a-1)y+a2-1=0,且l1⊥l2,∴a•1+2(a-1)=0;解得:a=.故选:B.根据直线l1与l2垂直,A1•A2+B1•B2=0,列出方程求出a的值.本题考查了直线方程的应用问题,考查了两条直线互相垂直的应用问题,是基础题目.7. 解:由题意知,直线过点(-1,2),斜率为1,代入点斜式得,y-2=x+1,即直线方程为x-y+3=0.故选A.由题意先求出圆心C的坐标,再代入点斜式方程,再化为一般式方程.本题重点考查了直线的点斜式方程,最后要化为一般式方程,这是容易忽视的地方.8. 解:联解,可得x=-1,y=2∴直线(x+y-1)-a(x+1)=0恒过定点P(-1,2)因此以P为圆心,为半径的圆的方程是(x+1)2+(y-2)2=5化成一般式可得x2+y2+2x-4y=0 故选:B联解直线x+y-1=0与x+1=0的方程,可得直线(x+y-1)-a(x+1)=0恒过定点P(-1,2).由圆的标准式方程,写出圆的方程再化成一般式方程,可得本题答案.本题给出直线经过定点P,求以P为圆心且为半径的圆.着重考查了直线的方程、圆的方程和直线与圆的位置关系等知识,属于基础题.9. 解:∵圆x2+y2-4x+my=0上一点P(1,1),可得1+1-4+m=0,解得m=2,圆的圆心(2,-1),过(1,1)与(2,-1)直线斜率为-2,∴过(1,1)切线方程的斜率为,则所求切线方程为y-1=(x-1),即x-2y+1=0.故选:D.求出圆的方程,求出圆心与已知点确定直线方程的斜率,利用两直线垂直时斜率的乘积为-1求出过此点切线方程的斜率,即可确定出切线方程.此题考查了直线与圆的位置关系,涉及的知识有:两直线垂直时斜率满足的关系,以及直线的点斜式方程,找出切线方程的斜率是解本题的关键.10. 解:∵圆心(-1,-1)到直线3x+4y-2=0的距离d= =,r=1,∴|MN|min=d-r=-1=.故选C.求出圆心到直线的距离d,由d-r即可求出|MN|的最小值.此题考查了直线与圆相交的性质,涉及的知识有:圆的标准方程,点到直线的距离公式,根据题意得出d-r为|MN|最小值是解本题的关键.11. 解:由题意可得,点P(x,y)在圆C:x2+(y-1)2=1上,而表示圆上的点(x,y)与点M(0,-1)连线的斜率,如图所示:设MA MB和圆C相切,切点分别为A,B,由于半径CA=1,MC=2,∴∠CMA=∠CMB=30°,故MA的斜率为tan60°=M,B的斜率为tan(90°+30°=)-,∴μ≥,或μ≤-,故选:B.由题意得,点P(x,y)在圆C:x2+(y-1)2=1上,而表示圆上的点(x,y)与点M连线的斜率,如图,根据半径CA=1,MC=2,可得∠CMA=∠CMB=30°,可得MA的斜率和MB的斜率,从而求得μ的范围.本题主要考查斜率公式、直线和圆的位置关系,体现了数形结合的数学思想,属于中档题.12. 解:圆的标准方程为M:x2+(y-a)2=a2(a>0),则圆心为(0,a),半径R=a,圆心到直线x+y=0的距离d= ,∵圆M:x2+y2-2ay=0(a>0)截直线x+y=0所得线段的长度是2,∴2=2,∴a= ,则圆心为M(0,),半径R= ,圆N:(x-1)2+(y-1)2=1的圆心为N(1,1),半径r=1,则MN= ,∵R+r= +1,R-r= -1,∴R-r<<R+r,即两个圆相交.故选:B.根据直线与圆相交的弦长公式,求出a的值,结合两圆的位置关系进行判断即可.本题主要考查直线和圆相交的应用,以及两圆位置关系的判断,根据相交弦长公式求出a的值是解决本题的关键.13. 解:命题的逆否命题为“若a2≠1,则a≠-1”,故答案为“若a2≠1,则a≠-1”根据逆否命题的定义进行求解即可.本题主要考查逆否命题的求解,根据四种命题之间的关系是解决本题的关键.14. 解:命题q等价于:(x-a)[x-(a+1)]≤0解得:a≤x≤a+1另:¬p是¬q的必要而不充分条件等价于q是p的必要而不充分条件即p⊆q,q⊊p故,解得根据原命题与其逆否命题等价;再由小集合推出大集合求解.此题要灵活掌握命题间的关系,准确求解二次不等式.因式分解解二次不等式是首选思路.15. 解:将圆方程化为标准方程得:(x-3)2+y2=1,得到圆心(3,0),半径r=1,∵圆心到直线的距离|AB|=d= =2 ,∴切线长的最小值|AC|= = .故答案为.将圆的方程化为标准方程,找出圆心坐标与半径r,求出圆心到直线y=x+1的距离,利用切线的性质及勾股定理求出切线长的最小值即可.此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,以及勾股定理,熟练掌握公式及定理是解本题的关键.16. 解:∵直线ax-by+1=0平分圆C:x2+y2+2x-4y+1=0的周长,∴直线ax-by+1=0过圆C的圆心(-1,2),∴有a+2b=1,∴ab=(1-2b)b=-2(b-)2+≤,∴ab的取值范围是.故答案为:.依题意知直线ax-by+1=0过圆C的圆心(-1,2),故有a+2b=1,再利用ab=(1-2b)b=-2(b-)2+,求得ab的取值范围.本题主要考查直线和圆的位置关系,配方法的应用,属于基础题.17.(1)设出圆的一般式方程,利用圆上的三点,即可求圆C的方程;(2)通过过点P(3,6)且被圆C截得弦长为4的直线的斜率不存在推出方程判断是否满足题意;直线的斜率存在是利用圆心距与半径的关系,求出直线的斜率,即可解得直线的方程.本题考查圆的一般式方程的求法,直线与圆的位置关系的应用,考查计算能力.18.先求出命题p,q的等价条件,然后利用命题“p∨q”为真命题,而命题“p∧q”为假命题,求实数a的取值范围.本题主要考查复合命题与简单命题的真假关系的应用,要求熟练掌握.19.(1)m=1时,曲线C表示圆,直线l过点P且与曲线C只有一个公共点,即直线l与圆相切,①当直线l的斜率不存在时,直线l的方程为:x=3.②当直线l的斜率存在时,设直线l的方程为:y=k(x-3)-1.由圆心到直线距离等于半径求得k.(2)曲线C的方程配方得:(x-1)2+(y-2)2=5-m,若方程表示圆则m<5.根据圆的弦长公式2 ,⇒m的值.本题考查了圆的方程、直线与圆的位置关系,弦长公式,属于中档题.20.(Ⅰ)通过证明DE∥AC,进而DE∥A1C1,据此可得直线DE∥平面A1C1F1;(Ⅱ)证明B1D⊥A1C1,利用A1F⊥B1D,A1F∩A1C1=A1,即可证明B1D⊥平面A1C1F.本题考查线面平行、垂直的证明,考查学生分析解决问题的能力,正确运用线面平行、垂直的判定定理是关键.21.(1)由x2-4ax+3a2<0,得(x-3a)(x-a)<0,p为真时,实数x的取值范围是1<x<3,q为真时,实数x的取值范围是2<x≤3,p∧q为真,则p真且q真,由此能求出实数x的取值范围.(2)p是q的必要不充分条件,设A={x|p(x)},B={x|q(x)},则A⊉B,由此能求出实数a的取值范围.复合命题p∧q的真假由命题p,q共同决定,当两命题中有一个是真命题时复合后为真命题,由若p是q的必要不充分条件可得集合p是集合q的真子集.22.(1)圆心C到直线l:mx-y+1+2m=0的距离,可得:对m∈R,直线l 与圆C总有两个不同的交点A、B;(2)设中点为M(x,y),利用k AB•k MC=-1,即可求弦AB的中点M的轨迹方程,并说明其轨迹是什么曲线;(3)利用圆心C(-2,0)到直线l的距离为,求出m的范围.本题考查点到直线的距离公式,直线的一般式方程,轨迹方程,直线和圆的方程的应用,考查转化思想,考查分析问题解决问题的能力,计算能力,是中档题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖北省黄石市2017-2018学年高二数学10月月考试题文一、选择题(本大题共12小题,共60分)1.下列命题是真命题的是()A.“若x=2,则(x-2)(x-1)=0”B.“若x=0,则xy=0”的否命题C.“若x=0,则xy=0”的逆命题D.“若x>1,则x>2”的逆否命题2.已知a∈R,b∈R,则“a>b”是“”成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件3. 已知圆的方程为x2+y2-4x+2y-4=0,则圆的半径为()A.3B.9C.D.±34.已知命题p:∀x>0,总有(x+1)e x>1,则¬p为()A.∃x0≤0,使得(x0+1)e≤1B.∃x0>0,使得(x0+1)e≤1C.∀x>0,总有(x+1)e x≤1D.∀x≤0,总有(x+1)e x≤15. 已知命题p:∃x∈R,x2-x+1≥0.命题q:若a2<b2,则a<b,下列命题为真命题的是()A.p∧qB.p∧¬qC.¬p∧qD.¬p∧¬q6.若直线l1:ax+2y+6=0与直线l2:x+(a-1)y+a2-1=0垂直,则a=()A.2B.C.1D.-27.经过圆C:(x+1)2+(y-2)2=4的圆心且斜率为1的直线方程为()A.x-y+3=0B.x-y-3=0C.x+y-1=0D.x+y+3=08.对于a∈R,直线(x+y-1)-a(x+1)=0恒过定点P,则以P为圆心,为半径的圆的方程是()A. x2+y2+2x+4y=0B.x2+y2+2x-4y=0C.x2+y2-2x+4y=0D.x2+y2-2x-4y=09.过圆x2+y2-4x+my=0上一点P(1,1)的圆的切线方程为()A.2x+y-3=0B.2x-y-1=0C.x-2y-1=0D.x-2y+1=010.已知点M是直线3x+4y-2=0上的动点,点N为圆(x+1)2+(y+1)2=1上的动点,则|MN|的最小值为()A. B.1 C. D.11.已知点P(x,y)的坐标满足x2+y2-2y=0,则的取值范围是()A. B.或C. D.或12.已知圆M:x2+y2-2ay=0(a>0)截直线x+y=0所得线段的长度是2,则圆M与圆N:(x-1)2+(y-1)2=1的位置关系是()A.内切B.相交C.外切D.相离二、填空题(本大题共4小题,共20分)13.命题“若a=-1,则a2=1”的逆否命题是 ______ .14.已知命题,命题q:x2-(2a+1)x+a(a+1)≤0,若¬p是¬q的必要而不充分条件,则实数a的取值范围是 ______ .15.由直线y=x+1上一点向圆x2-6x+y2+8=0引切线,则切线长的最小值为 ______ .16.若直线ax-by+1=0平分圆C:x2+y2+2x-4y+1=0的周长,则ab的取值范围是 ______ .三、解答题(本大题共6小题,共70分)17.已知圆心为C的圆经过三个点O(0,0)、A(1,3)、B(4,0)(1)求圆C的方程;(2)求过点P(3,6)且被圆C截得弦长为4的直线的方程.18.命题p:方程x2-x+a2-6a=0有一正根和一负根.命题q:函数y=x2+(a-3)x+1的图象与x轴有公共点.若命题“p∨q”为真命题,而命题“p∧q”为假命题,求实数a的取值范围.19.已知曲线C的方程是:x2+y2-2x-4y+m=0,点P(3,-1).(1)若m=1,直线l过点P且与曲线C只有一个公共点,求直线l的方程;(2)若曲线C表示圆且被直线x+2y+5=0截得的弦长为2,求实数m的值.20.如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AB,BC的中点,点F在侧棱BB1上,且A1F⊥B1D,求证:(Ⅰ)直线DE∥平面A1C1F;(Ⅱ)B1D⊥平面A1C1F.21. 设p :实数x 满足x 2-4ax +3a 2<0,其中a ≠0,命题q :实数x 满足⎪⎩⎪⎨⎧>-+≤--0820622x x x x (1)若a =1,且p ∧q 为真,求实数x 的取值范围;(2)若p 是q 的必要不充分条件,求实数a 的取值范围.22.已知圆C :(x +2)2+y 2=5,直线l :mx -y +1+2m =0,m ∈R.(1)求证:对m ∈R,直线l 与圆C 总有两个不同的交点A 、B ;(2)求弦AB 的中点M 的轨迹方程,并说明其轨迹是什么曲线; (3)是否存在实数m ,使得圆C 上有四点到直线l 的距离为?若存在,求出m 的范围;若不存在,说明理由.黄石三中高二年级文科10月月考试卷答案和解析【答案】1.A2.D3.C4.B5.C6.B7.A8.B9.D 10.C 11.B 12.B13.“若a2≠1,则a≠-1”14.15.16.17.解:(1)设圆的方程为x2+y2+D x+E y+F=0.圆C经过三个点O(0,0)A(1,3)B(4,0),所以解得D=-4,E=-2,F=0,所以圆C的方程x2+y2-4x-2y=0.(2)①过点P(3,6)且被圆C截得弦长为4的直线的斜率不存在,此时x=3,满足题意.②当过点P(3,6)且被圆C截得弦长为4的直线的斜率存在时设为k,直线方程为y-6=k(x-3).则,解得k=,所求直线方程为:12x-5y-6=0.故所求直线方程为:x=3或12x-5y-6=0.18.解:若方程x2-x+a2-6a=0有一正根和一负根,则,解得0<a<6.即p:0<a<6.若函数y=x2+(a-3)x+1的图象与x轴有公共点.则判别式△≥0,即(a-3)2-4≥0,解得a≥5或a≤1.即q:a≥5或a≤1.命题“p∨q”为真命题,而命题“p∧q”为假命题,则命题p,q为一真,一假.若p真q假,则1<a<5.若p假q真,则a≥6或a≤0.综上实数a的取值范围是a≥6或a≤0或1<a<5.19.解:(1)m=1时,曲线C的方程是:(x-1)2+(y-2)2=4,表示圆心为(1,2),半径为2的圆,∵直线l过点P且与曲线C只有一个公共点,∴直线l与圆相切.①当直线l的斜率不存在时,直线l的方程为:x=3.②当直线l的斜率存在时,设直线l的方程为:y=k(x-3)-1.即kx-y-3k-1=0.⇒k=-,直线l的方程为:5x+12y-3=0.综上所述所求直线l的方程为:x=3,5x+12y-3=0.(2)曲线C的方程配方得:(x-1)2+(y-2)2=5-m,若方程表示圆则5-m>0⇒m<5.圆心到直线x+2y+5=0距离d=,根据圆的弦长公式2,⇒2,⇒m=-2020.证明:(Ⅰ)∵D,E分别为AB,BC的中点,∴DE为△ABC的中位线,∴DE∥AC,∵ABC-A1B1C1为棱柱,∴AC∥A1C1,∴DE∥A1C1,∵A1C1⊂平面A1C1F,且DE⊄平面A1C1F,∴DE∥平面A1C1F;(Ⅱ)由题意,A1C1⊥平面A1B,B1D⊂平面A1B,∴B1D⊥A1C1,∵A1F⊥B1D,A1F∩A1C1=A1,∴B1D⊥平面A1C1F.21.解:(1)由x2-4ax+3a2<0,得(x-3a)(x-a)<0,当a=1时,解得1<x<3,即p为真时,实数x的取值范围是1<x<3,…(1分)由,得2<x≤3,即q为真时,实数x的取值范围是2<x≤3,…(3分)若p∧q为真,则p真且q真,…(4分)∴实数x的取值范围是(2,3).…(5分)(2)p是q的必要不充分条件,即q⇒p,且p推不出q,设A={x|p(x)},B={x|q(x)},则A⊉B,…(7分)又B=(2,3],当a>0时,A=(a,3a);a<0时,A=(3a,a),∴当a>0时,有,解得1<a≤2;…(9分)当a<0时,A∩B=∅,不合题意;∴实数a的取值范围是(1,2].…(10分)22.解:(1)圆C:(x+2)2+y2=5,的圆心为C(-2,0),半径为,所以圆心C到直线l:mx-y+1+2m=0的距离.所以直线l与圆C相交,即直线l与圆C总有两个不同的交点;…(4分)(2)设中点为M(x,y),因为直线l:mx-y+1+2m=0恒过定点(-2,1),当直线l的斜率存在时,,又,k AB•k MC=-1,所以,化简得.…(6分)当直线l的斜率不存在时,中点M(-2,0)也满足上述方程.…(7分)所以M的轨迹方程是,它是一个以为圆心,以为半径的圆.…(8分)(3)假设存在直线l,使得圆上有四点到直线l的距离为,由于圆心C(-2,0),半径为,则圆心C(-2,0)到直线l的距离为化简得m2>4,解得m>2或m<-2.…(12分)【解析】1. 解:对于A,若x=2,则(x-2)(x-1)=0显然成立,A正确.对于B,“若x=0,则xy=0”的否命题是:“若x≠0,则xy≠0”,当y=0时,xy=0,∴B不正确;对于C,“若x=0,则xy=0”的逆命题:“若xy=0,则x=0”,也可能是y=0,∴C不正确;对于D,“若x>1,则x>2”的逆否命题,∵原命题与逆否命题有相同的真假性,原命题显然不正确,∴D不正确;故选:A.利用函数的零点判断A的正误;通过命题的否命题,判断B的正误;判断命题的逆命题的真假判断C的正误;利用原命题的真假与逆否命题的真假相同判断D的正误;本题考查命题的真假的判断,考查函数的零点,四种命题的真假关系,基本知识的应用.2. 解:令a=1,b=-1,则a>b,而>,不是充分条件,若,即<0,∴或,即a,b同号时:a>b,a,b异号时:a<b,不是必要条件,故选:D.根据充分必要条件的定义分别判断其充分性和必要性即可.本题考查了充分必要条件,考查不等式问题,是一道基础题.3. 解:圆x2+y2-4x+2y-4=0,即(x-2)2+(y+1)2=9,故此圆的半径为3,故选:A.圆x2+y2-4x+2y-4=0,即(x-2)2+(y+1)2=9,由此可得圆的半径.本题主要考查把圆的一般方程化为标准方程,求圆的半径,属于中档题.4. 解:根据全称命题的否定为特称命题可知,¬p为∃x0>0,使得(x0+1)e≤1,故选:B.据全称命题的否定为特称命题可写出命题p的否定.本题主要考查了全称命题的否定的写法,全称命题的否定是特称命题.5. 解:命题p:∃x=0∈R,使x2-x+1≥0成立.故命题p为真命题;当a=1,b=-2时,a2<b2成立,但a<b不成立,故命题q为假命题,故命题p∧q,¬p∧q,¬p∧¬q均为假命题;命题p∧¬q为真命题,故选:B.先判断命题p,q的真假,进而根据复合命题真假的真值表,可得答案.本题以命题的真假判断与应用为载体,考查了复合命题,特称命题,不等式与不等关系,难度中档.6. 解:直线l1:ax+2y+6=0,l2:x+(a-1)y+a2-1=0,且l1⊥l2,∴a•1+2(a-1)=0;解得:a=.故选:B.根据直线l1与l2垂直,A1•A2+B1•B2=0,列出方程求出a的值.本题考查了直线方程的应用问题,考查了两条直线互相垂直的应用问题,是基础题目.7. 解:由题意知,直线过点(-1,2),斜率为1,代入点斜式得,y-2=x+1,即直线方程为x-y+3=0.故选A.由题意先求出圆心C的坐标,再代入点斜式方程,再化为一般式方程.本题重点考查了直线的点斜式方程,最后要化为一般式方程,这是容易忽视的地方.8. 解:联解,可得x=-1,y=2∴直线(x+y-1)-a(x+1)=0恒过定点P(-1,2)因此以P为圆心,为半径的圆的方程是(x+1)2+(y-2)2=5化成一般式可得x2+y2+2x-4y=0故选:B联解直线x+y-1=0与x+1=0的方程,可得直线(x+y-1)-a(x+1)=0恒过定点P(-1,2).由圆的标准式方程,写出圆的方程再化成一般式方程,可得本题答案.本题给出直线经过定点P,求以P为圆心且为半径的圆.着重考查了直线的方程、圆的方程和直线与圆的位置关系等知识,属于基础题.9. 解:∵圆x2+y2-4x+my=0上一点P(1,1),可得1+1-4+m=0,解得m=2,圆的圆心(2,-1),过(1,1)与(2,-1)直线斜率为-2,∴过(1,1)切线方程的斜率为,则所求切线方程为y-1=(x-1),即x-2y+1=0.故选:D.求出圆的方程,求出圆心与已知点确定直线方程的斜率,利用两直线垂直时斜率的乘积为-1求出过此点切线方程的斜率,即可确定出切线方程.此题考查了直线与圆的位置关系,涉及的知识有:两直线垂直时斜率满足的关系,以及直线的点斜式方程,找出切线方程的斜率是解本题的关键.10. 解:∵圆心(-1,-1)到直线3x+4y-2=0的距离d==,r=1,∴|MN|min=d-r=-1=.故选C.求出圆心到直线的距离d,由d-r即可求出|MN|的最小值.此题考查了直线与圆相交的性质,涉及的知识有:圆的标准方程,点到直线的距离公式,根据题意得出d-r为|MN|最小值是解本题的关键.11. 解:由题意可得,点P(x,y)在圆C:x2+(y-1)2=1上,而表示圆上的点(x,y)与点M(0,-1)连线的斜率,如图所示:设MA MB和圆C相切,切点分别为A,B,由于半径CA=1,MC=2,∴∠CMA=∠CMB=30°,故MA的斜率为tan60°=,MB的斜率为tan(90°+30°)=-,∴μ≥,或μ≤-,故选:B.由题意得,点P(x,y)在圆C:x2+(y-1)2=1上,而表示圆上的点(x,y)与点M 连线的斜率,如图,根据半径CA=1,MC=2,可得∠CMA=∠CMB=30°,可得MA的斜率和MB的斜率,从而求得μ的范围.本题主要考查斜率公式、直线和圆的位置关系,体现了数形结合的数学思想,属于中档题.12. 解:圆的标准方程为M:x2+(y-a)2=a2(a>0),则圆心为(0,a),半径R=a,圆心到直线x+y=0的距离d=,∵圆M:x2+y2-2ay=0(a>0)截直线x+y=0所得线段的长度是2,∴2=2,∴a=,则圆心为M(0,),半径R=,圆N:(x-1)2+(y-1)2=1的圆心为N(1,1),半径r=1,则MN=,∵R+r=+1,R-r=-1,∴R-r<<R+r,即两个圆相交.故选:B.根据直线与圆相交的弦长公式,求出a的值,结合两圆的位置关系进行判断即可.本题主要考查直线和圆相交的应用,以及两圆位置关系的判断,根据相交弦长公式求出a的值是解决本题的关键.13. 解:命题的逆否命题为“若a2≠1,则a≠-1”,故答案为“若a2≠1,则a≠-1”根据逆否命题的定义进行求解即可.本题主要考查逆否命题的求解,根据四种命题之间的关系是解决本题的关键.14. 解:命题q等价于:(x-a)[x-(a+1)]≤0解得:a≤x≤a+1另:¬p是¬q的必要而不充分条件等价于q是p的必要而不充分条件即p⊆q,q⊊p故,解得根据原命题与其逆否命题等价;再由小集合推出大集合求解.此题要灵活掌握命题间的关系,准确求解二次不等式.因式分解解二次不等式是首选思路.15. 解:将圆方程化为标准方程得:(x-3)2+y2=1,得到圆心(3,0),半径r=1,∵圆心到直线的距离|AB|=d==2,∴切线长的最小值|AC|==.故答案为.将圆的方程化为标准方程,找出圆心坐标与半径r,求出圆心到直线y=x+1的距离,利用切线的性质及勾股定理求出切线长的最小值即可.此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,以及勾股定理,熟练掌握公式及定理是解本题的关键.16. 解:∵直线ax-by+1=0平分圆C:x2+y2+2x-4y+1=0的周长,∴直线ax-by+1=0过圆C的圆心(-1,2),∴有a+2b=1,∴ab=(1-2b)b=-2(b-)2+≤,∴ab的取值范围是.故答案为:.依题意知直线ax-by+1=0过圆C的圆心(-1,2),故有a+2b=1,再利用ab=(1-2b)b=-2(b-)2+,求得ab的取值范围.本题主要考查直线和圆的位置关系,配方法的应用,属于基础题.17.(1)设出圆的一般式方程,利用圆上的三点,即可求圆C的方程;(2)通过过点P(3,6)且被圆C截得弦长为4的直线的斜率不存在推出方程判断是否满足题意;直线的斜率存在是利用圆心距与半径的关系,求出直线的斜率,即可解得直线的方程.本题考查圆的一般式方程的求法,直线与圆的位置关系的应用,考查计算能力.18.先求出命题p,q的等价条件,然后利用命题“p∨q”为真命题,而命题“p∧q”为假命题,求实数a的取值范围.本题主要考查复合命题与简单命题的真假关系的应用,要求熟练掌握.19.(1)m=1时,曲线C表示圆,直线l过点P且与曲线C只有一个公共点,即直线l与圆相切,①当直线l的斜率不存在时,直线l的方程为:x=3.②当直线l的斜率存在时,设直线l的方程为:y=k(x-3)-1.由圆心到直线距离等于半径求得k.(2)曲线C的方程配方得:(x-1)2+(y-2)2=5-m,若方程表示圆则m<5.根据圆的弦长公式2,⇒m的值.本题考查了圆的方程、直线与圆的位置关系,弦长公式,属于中档题.20.(Ⅰ)通过证明DE∥AC,进而DE∥A1C1,据此可得直线DE∥平面A1C1F1;(Ⅱ)证明B1D⊥A1C1,利用A1F⊥B1D,A1F∩A1C1=A1,即可证明B1D⊥平面A1C1F.本题考查线面平行、垂直的证明,考查学生分析解决问题的能力,正确运用线面平行、垂直的判定定理是关键.21.(1)由x2-4ax+3a2<0,得(x-3a)(x-a)<0,p为真时,实数x的取值范围是1<x<3,q 为真时,实数x的取值范围是2<x≤3,p∧q为真,则p真且q真,由此能求出实数x的取值范围.(2)p是q的必要不充分条件,设A={x|p(x)},B={x|q(x)},则A⊉B,由此能求出实数a的取值范围.复合命题p∧q的真假由命题p,q共同决定,当两命题中有一个是真命题时复合后为真命题,由若p是q的必要不充分条件可得集合p是集合q的真子集.22.(1)圆心C到直线l:mx-y+1+2m=0的距离,可得:对m∈R,直线l与圆C总有两个不同的交点A、B;(2)设中点为M(x,y),利用k AB•k MC=-1,即可求弦AB的中点M的轨迹方程,并说明其轨迹是什么曲线;(3)利用圆心C(-2,0)到直线l的距离为,求出m的范围.本题考查点到直线的距离公式,直线的一般式方程,轨迹方程,直线和圆的方程的应用,考查转化思想,考查分析问题解决问题的能力,计算能力,是中档题.。
