无穷小的比较
合集下载
七节无穷小的比较-精品

lim(1+o()) 1,
因此~.
例2 因为当 x0时 , six~ nx , ta x~ n x ,
arx c~x s,i1 n co x~ s 1x 2. 当 x 0 时 有 2
sixn xo (x ), taxn xo(x), arx cs x io (n x ),1coxs1x2o(x2).
解 在x0处没有,定义
且limsin1不存.在 x0 x
y sin 1 x
x0为第二类间. 断点
这种情况称为的振荡断间点.
注意 可去间断点只要改变或者补充间断处函 数的定义, 则可使其变为连续点. 在此例中, 令f(1)2, 则f(x)2 x, 0x1,
1x, x1,
在x1处的连.续
跳跃间断点 如果 f(x)在点 x0处,左 右极限都
存在 ,但f(x0)f(x0),则称x0为 点函f(数 x)的
taxnsinx为x的三阶无 . 穷小
定理 1 与是等价无穷小必 的要 的条 充件 分 为o().
证 必要性 设~,
lim
lim
1
0,
因 此 o ( ) , 即 o ( ) .
充分性 设 o().
lim limo()
f (x0)
那么就称函 y 数f (x)在点x0连续。
""定义 :
0,0,使x当 x0时 , 恒f有 (x)f(x0).
例1 试证函 f(x数 )xsin1x, x0, 在x0 0, x0,
处连. 续
证 limxsin10,
x0
x
又f(0)0, lim f(x)f(0), x 0
高数 无穷小比较

求极限的又一种方法, 注意适用条件.
思考题
任何两个无穷小都可以比较吗?
思考题解答
不能.
例当 x 时
1 sin x 都是无穷小量 f ( x ) , g( x ) x x g( x ) lim sin x 不存在且不为无穷大 但 lim x f ( x ) x
x
1 ln(1 u)
1 u
1 1. ln e
即,当 x 0 时, e 1,
x ~ ln(1 x ).
常用等价无穷小:当x 0时,
x ~ sin x ~ tan x ~ arcsin x ~ arctan x
x ~ ln(1 x ) ~ e x 1
1 2 1 cos x ~ x , 2 1 a n 1 x 1 ~ x , (1 x ) 1 ~ ax ( a 0) n
n
1 x 1 ( n 1 x )n 1 lim lim 1 x 0 x 0 1 x x[ n (1 x ) n1 n (1 x ) n 2 1] n n n 1 lim x 0 n (1 x ) n1 n (1 x ) n 2 1 1 n 当 x 0 时, 1 x 1 ~ x . n
充分性 设 o( ).
称 是 的主要部分.
o( ) o( ) lim lim lim (1+ ) 1, ~ .
意义:用等价无穷小可给出函数的近似表达式. 例如, 当x 0时,
sin x ~ x ,
sin x x o( x ),
第八节 无穷小的比较
• 一、无穷小的比较 • 二、等价无穷小代换 • 三、小结 思考题
一、无穷小的比较
思考题
任何两个无穷小都可以比较吗?
思考题解答
不能.
例当 x 时
1 sin x 都是无穷小量 f ( x ) , g( x ) x x g( x ) lim sin x 不存在且不为无穷大 但 lim x f ( x ) x
x
1 ln(1 u)
1 u
1 1. ln e
即,当 x 0 时, e 1,
x ~ ln(1 x ).
常用等价无穷小:当x 0时,
x ~ sin x ~ tan x ~ arcsin x ~ arctan x
x ~ ln(1 x ) ~ e x 1
1 2 1 cos x ~ x , 2 1 a n 1 x 1 ~ x , (1 x ) 1 ~ ax ( a 0) n
n
1 x 1 ( n 1 x )n 1 lim lim 1 x 0 x 0 1 x x[ n (1 x ) n1 n (1 x ) n 2 1] n n n 1 lim x 0 n (1 x ) n1 n (1 x ) n 2 1 1 n 当 x 0 时, 1 x 1 ~ x . n
充分性 设 o( ).
称 是 的主要部分.
o( ) o( ) lim lim lim (1+ ) 1, ~ .
意义:用等价无穷小可给出函数的近似表达式. 例如, 当x 0时,
sin x ~ x ,
sin x x o( x ),
第八节 无穷小的比较
• 一、无穷小的比较 • 二、等价无穷小代换 • 三、小结 思考题
一、无穷小的比较
高等数学无穷小的比较

x0
1 x
不存在.
不可比.
极限不同, 反映了趋向于零的“快慢”程度不 同.
定义:设,是同一过程中的两个无穷小,且 0.
(1) 如果lim 0,就说是比高阶的无穷小,
记作 o();
(2) 如果 lim C(C 0), 就说与是同阶的无穷小;
特殊地 如果lim 1,则称与是等价的无穷小;
2
e x 1 ~ x, 1 cos x ~ 1 x2 . 2
n 1 x 1~ 1 x n
(1 x) 1 ~ x
注 1. 上述10个等价无穷小(包括反、对、幂、
指、三)必须熟练掌握
2.将x换成f ( x) 0都成立
用等价无穷小可给出函数的近似表达式:
lim 1, lim 0, 即 o(),
记作 ~ ;
(3) 如果lim C(C 0,k 0),就说是的k阶的 k
无穷小.
例1 证明:当x 0时,4x tan3 x为x的四阶无穷小.
解
4x tan3
lim
x0
x4xBiblioteka tan 4 lim(x0 x
x)3
4,
故当x 0时,4x tan 3 x为x的四阶无穷小.
例2 当x 0时,求tan x sin x关于x的阶数.
x
(sin x
x
x
cos
1 x
)
1 2
例7. 证明: 当
时,
~
证:
an bn (a b) (an1 an2b bn1)
~
机动 目录 上页 下页 返回 结束
例8
求 lim ( x1
x 1)(3 x 1)(n x 1) ( x 1)n1
解 令u x 1 则x 1 u
1 x
不存在.
不可比.
极限不同, 反映了趋向于零的“快慢”程度不 同.
定义:设,是同一过程中的两个无穷小,且 0.
(1) 如果lim 0,就说是比高阶的无穷小,
记作 o();
(2) 如果 lim C(C 0), 就说与是同阶的无穷小;
特殊地 如果lim 1,则称与是等价的无穷小;
2
e x 1 ~ x, 1 cos x ~ 1 x2 . 2
n 1 x 1~ 1 x n
(1 x) 1 ~ x
注 1. 上述10个等价无穷小(包括反、对、幂、
指、三)必须熟练掌握
2.将x换成f ( x) 0都成立
用等价无穷小可给出函数的近似表达式:
lim 1, lim 0, 即 o(),
记作 ~ ;
(3) 如果lim C(C 0,k 0),就说是的k阶的 k
无穷小.
例1 证明:当x 0时,4x tan3 x为x的四阶无穷小.
解
4x tan3
lim
x0
x4xBiblioteka tan 4 lim(x0 x
x)3
4,
故当x 0时,4x tan 3 x为x的四阶无穷小.
例2 当x 0时,求tan x sin x关于x的阶数.
x
(sin x
x
x
cos
1 x
)
1 2
例7. 证明: 当
时,
~
证:
an bn (a b) (an1 an2b bn1)
~
机动 目录 上页 下页 返回 结束
例8
求 lim ( x1
x 1)(3 x 1)(n x 1) ( x 1)n1
解 令u x 1 则x 1 u
无穷小的比较
§1.8 无穷小的比较
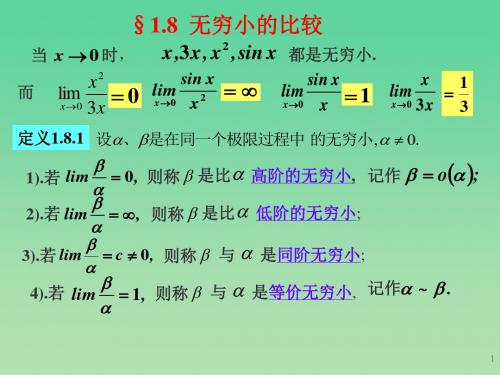
当 x 0 时, x ,3x , x2 , sin x 都是无穷小.
而
lim
x0
x2 3x
0
sin x
lim
x0
x2
sin x
lim
x0
x
1
lim x 1 x0 3x 3
定义1.8.1 设、是在同一个极限过程中 的无穷小, 0.
1).若
lim
x0 x u0 ln(1 u)
3
定理1.8.1 设
f1(x) ~
f2 (x),g1(x)
~
g2 (x),且lim
f2 (x) 存在, g2 ( x)
则 lim f1(x) lim f2 (x)
g1 ( x)
g2 ( x)
证
lim
f1 ( x) g1 ( x)
lim
f1 ( x) f2 ( x)
4
例3.
求
lim
x0
sin2x x3 3x
.Leabharlann 解 当 x 0 时,sin2x ~ 2x
lim x0
sin2x x3 3x
lim
x0
2x x3 3x
lim
x0
2 x2 3
2 3
.
例4.
求 lim (ex 1)sinx . x0 1 cosx
解
当
x
0 时,ex
f2 ( x) g2 ( x)
g2 ( x) g1 ( x)
lim f1(x) lim f2 (x) lim g2 (x) lim f2 (x)
当 x 0 时, x ,3x , x2 , sin x 都是无穷小.
而
lim
x0
x2 3x
0
sin x
lim
x0
x2
sin x
lim
x0
x
1
lim x 1 x0 3x 3
定义1.8.1 设、是在同一个极限过程中 的无穷小, 0.
1).若
lim
x0 x u0 ln(1 u)
3
定理1.8.1 设
f1(x) ~
f2 (x),g1(x)
~
g2 (x),且lim
f2 (x) 存在, g2 ( x)
则 lim f1(x) lim f2 (x)
g1 ( x)
g2 ( x)
证
lim
f1 ( x) g1 ( x)
lim
f1 ( x) f2 ( x)
4
例3.
求
lim
x0
sin2x x3 3x
.Leabharlann 解 当 x 0 时,sin2x ~ 2x
lim x0
sin2x x3 3x
lim
x0
2x x3 3x
lim
x0
2 x2 3
2 3
.
例4.
求 lim (ex 1)sinx . x0 1 cosx
解
当
x
0 时,ex
f2 ( x) g2 ( x)
g2 ( x) g1 ( x)
lim f1(x) lim f2 (x) lim g2 (x) lim f2 (x)
高等数学 无穷小比较

2 n1x1~1x, (1 x )a 1 ~ a(a x 0 )
n ax 1 ~ xlna(a0)
例3 求limtan22x. x0 1coxs
解
当 x 0时 ,1co x~ s1x2, 2
ta 2 x ~ n 2 x .
原式
(2x)2 lim
x0
1 x2
8.
2
若未定式的分子或分母为若干个因子的乘积,则 可对其中的任意一个或几个无穷小因子作等价无
limsinx 1, x0 x
即 six~ n x (x 0 ).
当 x 0时 si, x n与 x是等价 . 无穷
例1 证:当 明 x 0 时 ,tax nsix为 nx的三阶 .
证明: lx im 0tanxx3sinx x l i0m taxn(1 x 3cox)s lx i0(m c1o xs sx ixn 1x c2o x)s lx i0c m 1o xlx s i0s m x ixn lx i01 m x c2o x s 12 ,
(3)如l果 im C0,就 说 与 是同阶;的
特殊 如 地 l果 im , 1,则称 与 是等价;的
记 作 ~;
(4 )如 li果 m k C 0 ,k 0 ,就是 说 的 k阶的 .
例如, limx2 0,
x0 3x
即 x2o (3 x )(x 0 ).
当 x 0时x, 2是3 比 x高阶的; 无穷
例5 求lim taxnsin x. x 0 si3n2x
错解 当 x 0 时 ,ta x ~ n x , sixn ~x.
原式limxx
x0 (2x)3
0.
解 当 x0时 , si2n x~2x, 1coxs~1x2,
n ax 1 ~ xlna(a0)
例3 求limtan22x. x0 1coxs
解
当 x 0时 ,1co x~ s1x2, 2
ta 2 x ~ n 2 x .
原式
(2x)2 lim
x0
1 x2
8.
2
若未定式的分子或分母为若干个因子的乘积,则 可对其中的任意一个或几个无穷小因子作等价无
limsinx 1, x0 x
即 six~ n x (x 0 ).
当 x 0时 si, x n与 x是等价 . 无穷
例1 证:当 明 x 0 时 ,tax nsix为 nx的三阶 .
证明: lx im 0tanxx3sinx x l i0m taxn(1 x 3cox)s lx i0(m c1o xs sx ixn 1x c2o x)s lx i0c m 1o xlx s i0s m x ixn lx i01 m x c2o x s 12 ,
(3)如l果 im C0,就 说 与 是同阶;的
特殊 如 地 l果 im , 1,则称 与 是等价;的
记 作 ~;
(4 )如 li果 m k C 0 ,k 0 ,就是 说 的 k阶的 .
例如, limx2 0,
x0 3x
即 x2o (3 x )(x 0 ).
当 x 0时x, 2是3 比 x高阶的; 无穷
例5 求lim taxnsin x. x 0 si3n2x
错解 当 x 0 时 ,ta x ~ n x , sixn ~x.
原式limxx
x0 (2x)3
0.
解 当 x0时 , si2n x~2x, 1coxs~1x2,
第六节--无穷小的比较精选全文完整版

例2 当x 0时,求 tan x sin x关于x的阶数.
解 tan x sin x tanx(1 cos x) tan x 2sin2 x .
lim
x0
tan
x x3
sin
x
tan x lim( x0 x
2 s in2 x2
x 2
)
1, 2
2
tan x sin x为x的三阶无穷小.
(1 x)a 1 ~ a x (a 0), (n 1 x 1 ~ 1 x ) n
二、等价无穷小替换
定理(等价无穷小替换定理)
设
~ ,
~
且
lim
存在
,则
lim
lim
.
证 lim lim( )
lim
lim lim
lim
.
类似地,乘法也有等价无穷小替换定理,即 若 ~ ,
(2) 若是 x 的无穷小 , 常取 1 为基本无穷小 ; x
如果 lim x0
xk
C(C
0, k
0) , 就说当 x
0时
是 x 的 k 阶无穷小.
例1 证明 :当x 0时,4x tan 3 x为x的四阶无穷小.
解
lim
x0
4x
tan3 x4
x
4 lim x0
tan x
x
3
4,
故当x 0时,4x tan 3 x为x的四阶无穷小.
解 原式 lim
1 cos x
x0 x(1 cos x )(1 cos x )
1
1 cos x
lim
2 x0 x(1 cos x )
1 lim
1 x2 2
2 x0 x 1 x
07第一章 第7节 无穷小的比较

2 2
极限不同, 反映了趋向于零的“快慢”程度不 同.
2
定义:设, 是同一过程中的两个无 穷小, 且 0.
(1) 如果 lim 0, 就说 是比高阶的无穷小 , 记作 o( );
(2) 如 果lim , 就 说是 比低 阶 的 无 穷 小 ;
(4) 如 果lim 1, 则 称与是 等 价 的 无 穷 小 ; 记 作 ~ ;
3
(3) 如果 lim C (C 0), 就说与是同阶的无穷小;
(5) 如 果lim k C (C 0, k 0), 就 说是的k阶 的
无穷小 .
如 : x 3 o( x 2 ) ( x 0); 3
在x 3时,x 2 9和x 3是同阶无穷小;
15
思考题
任何两个无穷小量都可以比较吗?
16
思考题解答
不能.
例当 x 时
1 sin x 都是无穷小量 f ( x ) , g( x ) x x g( x ) lim sin x 不存在且不为无穷大 但 lim x f ( x ) x
故当 x 时 f x ) 和 g( x ) 不能比较.
3 6 2 3 6 2
12
例8 xlim( x 7 x 2 x )
5 5 4
7 2 lim x(5 1 5 1) x x x
t
1 7 t 2t 1 lim t 0 0 t 1 5 (7t 2t ) 7 lim 5 t 0 0 t 5
故当x 0时,4 x tan 3 x为x的四阶无穷小 .
例2 当x 0时, 求 tan x sin x关于x的阶数.
tan x sin x tan x 1 cos x 1 解 lim lim( ) , 3 2 x 0 x 0 x x 2 x
极限不同, 反映了趋向于零的“快慢”程度不 同.
2
定义:设, 是同一过程中的两个无 穷小, 且 0.
(1) 如果 lim 0, 就说 是比高阶的无穷小 , 记作 o( );
(2) 如 果lim , 就 说是 比低 阶 的 无 穷 小 ;
(4) 如 果lim 1, 则 称与是 等 价 的 无 穷 小 ; 记 作 ~ ;
3
(3) 如果 lim C (C 0), 就说与是同阶的无穷小;
(5) 如 果lim k C (C 0, k 0), 就 说是的k阶 的
无穷小 .
如 : x 3 o( x 2 ) ( x 0); 3
在x 3时,x 2 9和x 3是同阶无穷小;
15
思考题
任何两个无穷小量都可以比较吗?
16
思考题解答
不能.
例当 x 时
1 sin x 都是无穷小量 f ( x ) , g( x ) x x g( x ) lim sin x 不存在且不为无穷大 但 lim x f ( x ) x
故当 x 时 f x ) 和 g( x ) 不能比较.
3 6 2 3 6 2
12
例8 xlim( x 7 x 2 x )
5 5 4
7 2 lim x(5 1 5 1) x x x
t
1 7 t 2t 1 lim t 0 0 t 1 5 (7t 2t ) 7 lim 5 t 0 0 t 5
故当x 0时,4 x tan 3 x为x的四阶无穷小 .
例2 当x 0时, 求 tan x sin x关于x的阶数.
tan x sin x tan x 1 cos x 1 解 lim lim( ) , 3 2 x 0 x 0 x x 2 x
无穷小的比较

ln(1 x) ~ x, 1 x 1~ 1x
2
e x 1 ~ x, 1 cos x ~ 1 x2 . 2
n 1 x 1~ 1 x n
(1 x) 1 ~ x
注 1. 上述10个等价无穷小(包括反、对、幂、
指、三)必须熟练掌握
2.将x换成f ( x) 0都成立 QQ:815373296
用等价无穷小可给出函数的近似表达式:
无穷小的比较
一、无穷小的比较
例如, 当x 0时, x, x 2 , sin x, x 2 sin 1 都是无穷小.
lim x 2 0,
x
x 2比3 x要快得多;
观 x0 3x
察 各 极 限
lim sin x 1,
sin x与x大致相同;
x0 x
lim
x0
x 2 sin x2
1 x
lim sin
x cos
1
x
1 110 1
22
2
例7
求 lim ( x1
x 1)(3 x 1)(n x 1) ( x 1)n1
解 令u x 1 则x 1 u
由(1 u) 1 ~ u得
QQ:815373296
I lim ( u0
1 u 1)(3 1 u 1)(n 1 u 1) un1
1u 1u 1 u
lim 2 u0
3
n
un1
1 n!
关于1∞型极限的求法
lim[ f ( x)]g( x) lim f ( x) 1, lim g( x)
lim[ f ( x)]g( x) lime g( x)ln f ( x) elim g( x)ln f ( x)
QQ:815373296
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方法,会用等价无穷小求极限。
教学重点:用等价无穷小求极限
教学过程:
一、讲授新课:
在第三讲中我们讨论了无穷小的和、差、积的情况,对于其商会出现不同的情况,例如: ( 为常数, 为自然数)
可见对于 取不同数时, 与 趋于0的速度不一样,为此有必要对无穷小进行比较或分类:
定理4:设函数 在点 连续,且 ,函数 在 点连续,那么,复合函数 在点 处连续。
注3:定理3、4说明 与 的次序可交换。
注4:在定理3中代入 ,即得定理4。
【例1】 由于 ( 为正整数)在 上严格单调且连续,由定理2,其反函数 在 上也严格单调且连续,进而:对于有理幂函数 ( 为正整数)在定义上是连续的。
综合以上结果,得:基本初等函数在其定义域内都是连续的,由基本初等函数的连续性,及定理1~4,即得:
结论:一切初等函数在其定义区间内都是连续的。
注1:定义区间为包含在定义域内的区间;
2:在§1.9,我们是用极限来证明连续,现在可利用函数的连续来求极限。
【例3】 。
【例4】 。
【例5】
。
三、课堂练习:
四、布置作业:
定理2(反函数的连续性):如果 在区间 上单值,单增(减),且连续,那么其反函数 也在对应的区间 上单值,单增(减),且连续。
注1: 亦为 的反函数,如上知: 在 上有上述性质。
定理3:设 当 时的极限存在且等于 ,即 ,又设 在 处连续,那么,当 时,复合函数 的极限存在,且等于 ,即 。
注2:可类似讨论 时的情形。
6:用等价无穷小可以简化极限的运算,事实上,有:
定理:若 均为 的同一变化过程中的无穷小,且 ,及 ,那么 。
【例2】求 。
解:因为当 时,
所以 。
【例3】求
解:因为当 时, ,
所以 原式 。
7:在目前,常用当 时,等价无穷小有:
;
8:用等价无穷小代换适用于乘、除,对于加、减须谨慎!
二、课堂练习:
三、布置作业:
注 1:高阶无穷小不具有等价代换性,即: ,但 ,因为 不是一个量,而是高阶无穷小的记号;
2:显然(iv)是(iii)的特殊情况;
3:等价无穷小具有传递性:即 ;
4:未必任意两个无穷小量都可进行比较,例如:当 时, 与 既非同阶,又无高低阶可比较,因为 不存在;
5:对于无穷大量也可作类似的比较、分类;
第七节无穷小的比较
教学目的:使学生掌握无穷小的比较方法,会用等价无穷小求极限。
教学重点:用等价无穷小求极限
教学过程:
一、讲授新课:
在第三讲中我们讨论了无穷小的和、差、积的情况,对于其商会出现不同的情况,例如: ( 为常数, 为自然数)
可见对于 取不同数时, 与 趋于0的速度不一样,为此有必要对无穷小进行比较或分类:
第九节连续函数的运算与初等函数的连续性
教学目的:使学生了解连续函数的性质和初等函数的连续性;并会应用函数的连续性求函数的极限
教学重点:应用函数的连续性求函数的极限
教学过程:
一、复习函数的连续性定义、间断点的分类
二、讲解新课:
(一)连续函数的运算
定理1(连续函数的四则运算法则):若 均在 连续,则 及 (要求 )都在 连续。
定义:设 与 为 在同一变化过程中的两个无穷小,
(v)若 ,就说 是比 高阶的无穷小,记为 ;
(vi)若 ,,就说 是比 低阶的无穷小;
(vii)若 ,,就说 是比 同阶的无穷小;
(viii)若 ,就说 与 是等价无穷小,记为 。
【例1】当 时, 是 的高阶无穷小,即 ;反之 是 的低阶无穷小; 与 是同阶无穷小; 与 是等价无穷小,即 。
注 1:高阶无穷小不具有等价代换性,即: ,但 ,因为 不是一个量,而是高阶无穷小的记号;
2:显然(iv)是(iii)的特殊情况;
3:等价无穷小具有传递性:即 ;
4:未必任意两个无穷小量都可进行比较,例如:当 时, 与 既非同阶,又无高低阶可比较,因为 不存在;
5:对于无穷大量也可作类似的比较、分类;
【例2】求
解:因为 ,及 在 点连续,故由定理3,原式
。
(二) 初等函数的连续性
我们已知道 在其定义域内是连续的,由定理2知 和 在其定义域也是连续的。
可证明指数函数 ,在其定义域 内是严格单调且连续的,进而有对数函数 在其定义域 是连续的。
又 ( 为常数),由定理4知: 在 内是连续的,当 取有理数时,见例1,总之 在定义域内是连续的。
6:用等价无穷小可以简化极限的运算,事实上,有:
定理:若 均为 的同一变化过程中的无穷小,且 ,及 ,那么 。
【例2】求 。
解:因为当 时,
所以 。
【例3】求
解:因为当 时, ,
所以 原式 。
7:在目前,常用当 时,等价无穷小有:
;
8:用等价无穷小代换适用于乘、除,对于加、减须谨慎!
二、课堂练习:
三、布置作业:
定义:设 与 为 在同一变化过程中的两个无穷小,
(i)若 ,就说 是比 高阶的无穷小,记为 ;
(ii)若 ,,就说 是比 低阶的无穷小;
(iii)若 ,,就说 是比 同阶的无穷小;
(iv)若 ,就说 与 是等价无穷小,记为 。
【例1】当 时, 是 的高阶无穷小,即 ;反之 是 的低阶无穷小; 与 是同阶无穷小; 与 是等价无穷小,即 。
教学重点:用等价无穷小求极限
教学过程:
一、讲授新课:
在第三讲中我们讨论了无穷小的和、差、积的情况,对于其商会出现不同的情况,例如: ( 为常数, 为自然数)
可见对于 取不同数时, 与 趋于0的速度不一样,为此有必要对无穷小进行比较或分类:
定理4:设函数 在点 连续,且 ,函数 在 点连续,那么,复合函数 在点 处连续。
注3:定理3、4说明 与 的次序可交换。
注4:在定理3中代入 ,即得定理4。
【例1】 由于 ( 为正整数)在 上严格单调且连续,由定理2,其反函数 在 上也严格单调且连续,进而:对于有理幂函数 ( 为正整数)在定义上是连续的。
综合以上结果,得:基本初等函数在其定义域内都是连续的,由基本初等函数的连续性,及定理1~4,即得:
结论:一切初等函数在其定义区间内都是连续的。
注1:定义区间为包含在定义域内的区间;
2:在§1.9,我们是用极限来证明连续,现在可利用函数的连续来求极限。
【例3】 。
【例4】 。
【例5】
。
三、课堂练习:
四、布置作业:
定理2(反函数的连续性):如果 在区间 上单值,单增(减),且连续,那么其反函数 也在对应的区间 上单值,单增(减),且连续。
注1: 亦为 的反函数,如上知: 在 上有上述性质。
定理3:设 当 时的极限存在且等于 ,即 ,又设 在 处连续,那么,当 时,复合函数 的极限存在,且等于 ,即 。
注2:可类似讨论 时的情形。
6:用等价无穷小可以简化极限的运算,事实上,有:
定理:若 均为 的同一变化过程中的无穷小,且 ,及 ,那么 。
【例2】求 。
解:因为当 时,
所以 。
【例3】求
解:因为当 时, ,
所以 原式 。
7:在目前,常用当 时,等价无穷小有:
;
8:用等价无穷小代换适用于乘、除,对于加、减须谨慎!
二、课堂练习:
三、布置作业:
注 1:高阶无穷小不具有等价代换性,即: ,但 ,因为 不是一个量,而是高阶无穷小的记号;
2:显然(iv)是(iii)的特殊情况;
3:等价无穷小具有传递性:即 ;
4:未必任意两个无穷小量都可进行比较,例如:当 时, 与 既非同阶,又无高低阶可比较,因为 不存在;
5:对于无穷大量也可作类似的比较、分类;
第七节无穷小的比较
教学目的:使学生掌握无穷小的比较方法,会用等价无穷小求极限。
教学重点:用等价无穷小求极限
教学过程:
一、讲授新课:
在第三讲中我们讨论了无穷小的和、差、积的情况,对于其商会出现不同的情况,例如: ( 为常数, 为自然数)
可见对于 取不同数时, 与 趋于0的速度不一样,为此有必要对无穷小进行比较或分类:
第九节连续函数的运算与初等函数的连续性
教学目的:使学生了解连续函数的性质和初等函数的连续性;并会应用函数的连续性求函数的极限
教学重点:应用函数的连续性求函数的极限
教学过程:
一、复习函数的连续性定义、间断点的分类
二、讲解新课:
(一)连续函数的运算
定理1(连续函数的四则运算法则):若 均在 连续,则 及 (要求 )都在 连续。
定义:设 与 为 在同一变化过程中的两个无穷小,
(v)若 ,就说 是比 高阶的无穷小,记为 ;
(vi)若 ,,就说 是比 低阶的无穷小;
(vii)若 ,,就说 是比 同阶的无穷小;
(viii)若 ,就说 与 是等价无穷小,记为 。
【例1】当 时, 是 的高阶无穷小,即 ;反之 是 的低阶无穷小; 与 是同阶无穷小; 与 是等价无穷小,即 。
注 1:高阶无穷小不具有等价代换性,即: ,但 ,因为 不是一个量,而是高阶无穷小的记号;
2:显然(iv)是(iii)的特殊情况;
3:等价无穷小具有传递性:即 ;
4:未必任意两个无穷小量都可进行比较,例如:当 时, 与 既非同阶,又无高低阶可比较,因为 不存在;
5:对于无穷大量也可作类似的比较、分类;
【例2】求
解:因为 ,及 在 点连续,故由定理3,原式
。
(二) 初等函数的连续性
我们已知道 在其定义域内是连续的,由定理2知 和 在其定义域也是连续的。
可证明指数函数 ,在其定义域 内是严格单调且连续的,进而有对数函数 在其定义域 是连续的。
又 ( 为常数),由定理4知: 在 内是连续的,当 取有理数时,见例1,总之 在定义域内是连续的。
6:用等价无穷小可以简化极限的运算,事实上,有:
定理:若 均为 的同一变化过程中的无穷小,且 ,及 ,那么 。
【例2】求 。
解:因为当 时,
所以 。
【例3】求
解:因为当 时, ,
所以 原式 。
7:在目前,常用当 时,等价无穷小有:
;
8:用等价无穷小代换适用于乘、除,对于加、减须谨慎!
二、课堂练习:
三、布置作业:
定义:设 与 为 在同一变化过程中的两个无穷小,
(i)若 ,就说 是比 高阶的无穷小,记为 ;
(ii)若 ,,就说 是比 低阶的无穷小;
(iii)若 ,,就说 是比 同阶的无穷小;
(iv)若 ,就说 与 是等价无穷小,记为 。
【例1】当 时, 是 的高阶无穷小,即 ;反之 是 的低阶无穷小; 与 是同阶无穷小; 与 是等价无穷小,即 。
