冲击波基本理论
冲击波的原理

冲击波的原理
冲击波是一种具有高能量的波动,它在自然界和工程领域中都有着重要的应用。
冲击波的产生和传播过程涉及到多个物理学原理,下面我们将对冲击波的原理进行详细的介绍。
首先,冲击波是由高速流体或者固体物体与介质相互作用产生的一种波动。
当
一个物体以超音速速度移动时,它会在前方形成一个高压区域,而在后方形成一个低压区域,这种不连续的压力变化就形成了冲击波。
冲击波的传播过程中,会产生非常高的压力和温度。
这种高压高温的特性使得
冲击波在医疗领域中有着广泛的应用,比如用于肾结石碎石术、心脏瓣膜治疗等。
此外,冲击波还可以被用于材料加工、岩石破碎等工程领域。
冲击波的传播速度是非常快的,通常可以达到音速的数倍甚至数十倍。
这种高
速传播的特性使得冲击波在一些特定的应用中具有独特的优势,比如在爆炸物品中,冲击波可以传播得非常快,从而产生更大的破坏力。
冲击波的产生和传播过程中,涉及到了流体动力学、热力学、声学等多个物理
学原理。
通过对这些原理的深入研究和理解,我们可以更好地控制和利用冲击波的特性,从而为医疗、工程等领域提供更多的应用可能性。
总的来说,冲击波是一种具有高能量的波动,它在医疗和工程领域中有着广泛
的应用。
通过对冲击波的原理进行深入的研究和理解,我们可以更好地掌握和利用它的特性,为人类社会的发展和进步做出更大的贡献。
冲击波的原理

冲击波的原理引言冲击波是一种经常被用来描述爆炸、火箭发射和喷气飞机突破音障时发生的现象。
它具有独特的物理特性和广泛的应用领域。
本文将深入探讨冲击波的原理,包括形成机制、传播规律和影响因素等方面,希望能对读者对冲击波的理解有所帮助。
冲击波的形成机制冲击波是由于某种外部力量(如爆炸、高速运动等)在介质中传播时产生的一种传播形式。
冲击波的形成机制主要有以下几种:超声速流体流动形成的冲击波当流体在流动过程中的速度超过声速时,就会形成超声速流动。
在超声速流动中,流体分子受到压缩,密度增加,速度减小。
当超声速流动突然遇到障碍物时,流体会被迫减速,并形成高密度的区域。
随后,流体分子由于惯性作用再次加速,速度超过了声速,从而形成了冲击波。
爆炸形成的冲击波爆炸是冲击波形成的主要原因之一。
当爆炸物爆炸时,爆炸产生的高温和高压气体通过空气中的传播,使空气发生剧烈扰动,从而形成冲击波。
爆炸冲击波是一种高能量的波动,对周围环境产生破坏性影响。
冲击波的传播规律冲击波在传播过程中会产生一系列规律和特性,以下是冲击波的传播规律的主要内容:Hugoniot关系Hugoniot关系是描述冲击波与介质相互作用的基本规律。
根据Hugoniot关系,冲击波的压力和密度之间存在一定的关系,即当冲击波通过介质时,压力和密度会同时发生变化。
这种变化的规律与介质的物理性质和状态有关。
激波和弱激波冲击波可以分为激波和弱激波两种类型。
激波是一种非线性的冲击波,它具有非常高的压力和密度变化。
而弱激波是指冲击波的压力和密度变化较小,它的传播速度相对较慢。
冲击波的传播速度冲击波的传播速度取决于介质的物理性质和状态。
在气体中,冲击波的传播速度通常大于声速,而在固体中,冲击波的传播速度通常小于声速。
不同介质的传播速度会导致冲击波的形态和传播规律发生变化。
冲击波的影响因素冲击波的形成和传播受到多种因素的影响,以下列举了一些主要的影响因素:爆炸能量爆炸产生的能量是冲击波形成和传播的主要驱动力。
3.3炸药的爆轰理论
炸药径向间隙效应
视频1 视频2
可采取选用爆速大的炸药和大直径药 卷及坚固外壳等措施,实现稳定爆轰。
视频1
视频2
七、爆速的测定方法
炸药的爆速是衡量炸药爆炸性能的重 要标志量,也是目前可以比较准确测定的 一个爆轰参数。
测量方法 (1)导爆索法 (2)电测法 (3)高速摄影法
视频1 视频2
l
h
导爆索法测爆速
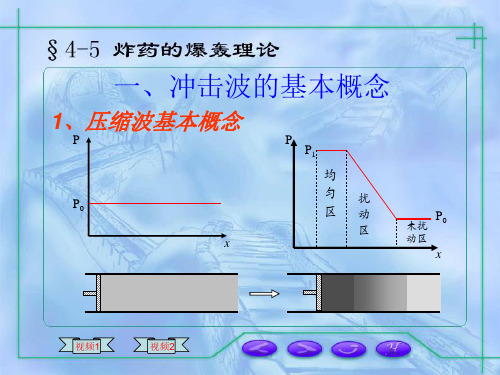
一、冲击波的基本概念
1、压缩波基本概念
P P
P1
P0 x
均 匀 区
扰 动 区
未扰 动区
P0 x
视频1
视频2
在无限长气筒活塞右侧充满压力为P0 的气体,当活塞在F力的作用下向右运动 时,活塞右侧气体存在三个区域: 压力为P1的均匀区 压力介于P1与P0之间的扰动区 压力仍为P0的未扰动区
视频1
视频2
视频1 视频2
2
1 0
使介质运动的力是波阵面两边的压力差 PH P0 在单位时间内流进波阵面的介质质量为 0 ( D u0 ) 其速度的变化为 ( D u 0 ) ( D u H ) u H u 0 根据动量守恒定律有:
PH P0 0 ( D u 0 )( u H u 0 )
已反应的药包
视频1 视频2
未反应的药包
1)炸药达到稳定爆轰前有 一个不稳定的爆炸区。
2)在特定的条件下,每种 炸药都会有一个不变的炸 药特征爆速Di。 3) 每种炸药都存在一个最 小的临界爆速Dc。波速低 于Dc后,冲击波将衰减为 音波而导致爆轰熄灭。
炸药包在冲击波激发下的爆轰过程
视频1 视频2
(2)爆轰波模型
H ( D u H )[ E H
冲击波的工作原理

冲击波的工作原理冲击波是一种高能量、高速度的压缩波,它具有破坏性和穿透性,被广泛应用于医学、工程、军事等领域。
冲击波的工作原理涉及到物理学、化学等多个学科,下面将从多个角度详细介绍。
一、物理学原理1.1 声波传播冲击波是一种特殊的声波,它是由声源在介质中产生的压缩性脉冲。
当声源发出脉冲时,其能量会在介质中以声速传播。
在传播过程中,介质分子会受到振动,形成密度变化和压力变化的波动。
1.2 压缩效应当声速足够大时,介质分子之间的相互作用力不可忽略。
这时候,在传播过程中产生的密度变化和压力变化会引起介质分子之间的相互碰撞和摩擦,从而导致温度升高和能量增加。
这种现象称为压缩效应。
1.3 超音速流动当声速超过介质中声音传播的极限速度时,即超过马赫数1时,介质中的气体分子会发生超音速流动。
这时候,由于声波的传播速度高于气体分子的平均速度,因此声波能够将介质中的气体分子加速到超音速。
二、化学原理2.1 氧化反应冲击波在产生过程中需要一定的能量,这些能量来自于爆炸或者燃烧等化学反应。
例如,在医学上使用的冲击波产生器通常采用电火花放电或者化学爆炸来产生冲击波。
2.2 燃烧反应在军事领域,常常使用高爆药来产生冲击波。
高爆药是一种含有大量可燃物质和氧化剂的混合物,当其受到外界刺激时,内部可燃物质和氧化剂会发生剧烈的燃烧反应,从而释放出大量能量。
三、应用领域3.1 医学领域在医学领域中,冲击波被广泛应用于治疗尿路结石、骨折等多种疾病。
治疗过程中,冲击波能够将高能量的压缩波传递到患者身体内部,从而破碎结石或者加速骨折愈合。
3.2 工程领域在工程领域中,冲击波被应用于清洗和切割等多种场合。
例如,在航空航天领域中,冲击波被用于清洗发动机内部的积碳和沉积物;在建筑领域中,冲击波被用于切割混凝土和金属等材料。
3.3 军事领域在军事领域中,冲击波被应用于武器系统和防御系统。
例如,在导弹攻击时,防御系统可以利用冲击波来摧毁导弹;在地雷清除时,工程师可以利用冲击波来引爆地雷。
冲击波基本理论

*
*
⑥ 压缩波:波阵面到达之处,介质的状态(P、ρ、T)参数增加的波称压缩波,波的传播方向与介质运动方向相同。(图5.1) ⑦ 膨胀波(稀疏波):波阵面到达之处,介质的状态(P、ρ、T)参数减小的波称膨胀波,波的传播方向与介质运动方向相反。 (下图5.2)
*
*
完全气体,量热完全气体与等熵关系 (补物理化学知识) 理想气体(完全气体perfect gas):不考虑分子间的作用力和分子的体积情况下,一种理想化后的气体。它满足: PV=nRT, e=e(T)和Cv=Cv(T) 世上无理想气体,热完全气体是真实气体在一定温度,压力范围内的近似,即近似看成理想气体来处理。 对于热完全气体,有: de=CvdT=Cv(T)dT ,dh=CpdT=Cp(T)dT,e=e(T) ,h=h(T) 可近似认为一定温度范围内,Cv,Cp , ( Cp- Cv =R)保持不变。 但一般说来, Cv=Cv(T) , Cp=Cp(T)
hePV
feTS
ghTS
=+
=-
=-
*
*
将(2)的第一式、(4)、(5)、(6)与(7)的4个式子比较有: —(8) 又因为: ( ) 所以:
*
*
而 类似有: 代入(11)的第1式: (12) (10),(12)就是熵函数的一般表达式(微分形式),也可以写成积分形式: (13)
*
*
等熵关系的建立: 一般地: (1) 对可逆过程: (2) 比较(1)和(2)有: (3)
(2)
(1)
(22)
*
*
又由Maxwell关系: (23) 故有: (24) 对理想气体: 故: , 代入(24)式: (25) 由定义(比热比): 故:
冲击波 原理

冲击波原理
冲击波是一种可以产生强烈动能的波动现象。
它是由某种能量的突然释放引起的,比如爆炸、闪电等。
冲击波通常会在空气、水或固体介质中传播。
冲击波的传播原理可以解释为以下几个步骤:
1. 能量释放:冲击波通常是由某种能量的突然释放引起的。
例如,当爆炸物瞬间释放了大量的化学能量时,就会产生爆炸冲击波。
2. 波动传播:能量的突然释放会在周围介质中引起气体或液体的振动。
这些振动以波的形式向外传播,形成了冲击波。
3. 波前和波后:冲击波中有两个特殊的区域,即波前和波后。
波前是冲击波的前沿边界,表示能量释放的位置。
波后是冲击波的后沿边界,表示波浪传播的方向。
4. 压缩区和展开区:冲击波传播过程中,介质颗粒会发生密集的压缩和膨胀。
在波前的前方,介质会被强烈压缩成高密度状态,形成压缩区。
而在波后的后方,介质会迅速膨胀,形成展开区。
5. 高压和低压:冲击波的传播过程中,引起的压力变化会导致介质中形成高压区和低压区。
在波前的前方,介质颗粒由于受到压缩而形成高压区。
而在波后的后方,由于膨胀作用,介质颗粒形成低压区。
冲击波的强烈动能可以对物体产生破坏作用,如破碎建筑物、损坏设备等。
因此,在实际应用中,需要合理控制冲击波的传播,以确保安全。
冲击波的原理对于研究爆炸、地震等现象,以及开发冲击波技术具有重要意义。
冲击波原理

冲击波原理
冲击波,又称激波,是一种突然而强烈的压力波,它的产生和传播对于许多领
域都具有重要意义,如医学、航空航天、地质勘探等。
冲击波原理是指冲击波在产生和传播过程中所遵循的物理规律和特性。
本文将对冲击波原理进行详细阐述,以便读者对其有更深入的了解。
冲击波的产生是由于某种突然的能量释放所引起的,比如爆炸、气体快速压缩、超声波等。
这种能量释放会导致介质中的压力迅速升高,从而形成冲击波。
冲击波的传播则是由于介质中的粒子在受到压力作用下发生振动,从而将能量传递给周围的粒子,使得冲击波向外扩散。
冲击波的传播速度通常非常快,可以达到音速以上甚至是超音速。
冲击波具有很强的能量,它可以对物体产生巨大的压力和破坏力。
在医学上,
冲击波被用于肾结石碎石术、心脏瓣膜手术等治疗方法中。
在航空航天领域,冲击波的特性对于超音速飞行器的设计和飞行具有重要影响。
在地质勘探中,冲击波可以通过地震勘探技术来获取地下结构的信息。
冲击波的产生和传播受到介质的性质和外界条件的影响。
介质的密度、弹性模量、粘度等都会影响冲击波的产生和传播速度。
而外界条件如温度、压力、湿度等也会对冲击波的传播产生影响。
因此,研究冲击波的原理不仅需要深入了解物理学和流体力学知识,还需要考虑介质和外界条件的影响。
总的来说,冲击波原理是一个复杂而又有趣的物理现象,它的研究不仅有助于
我们更好地理解自然界的规律,还可以为医学、航空航天、地质勘探等领域的发展提供重要的理论基础。
希望本文能够帮助读者对冲击波原理有一个更清晰的认识,激发大家对这一领域的兴趣,促进相关领域的进一步发展和应用。
《冲击波基本理论》教案

《冲击波基本理论》教案教案:冲击波基本理论教学目标:1.了解冲击波的定义和基本特征;2.掌握计算冲击波的基本方法;3.了解冲击波在不同领域中的应用。
教学重点:1.冲击波的定义和基本特征;2.计算冲击波的基本方法。
教学难点:1.冲击波的计算方法;2.冲击波在不同领域中的应用。
教学内容:一、引入(10分钟)1.引导学生回忆并复习上节课所学的波动理论知识。
2.提问:你们知道什么是冲击波吗?有什么特点?二、理论讲解(30分钟)1.定义:冲击波是指波运动中由于载波在介质中传播速度突然改变而形成的一种特殊波动现象。
2.特点:-载波改变速度突然;-载波在介质中传播方向不可逆;-载波传播过程中的能量集中在一些区域。
三、计算方法演示(40分钟)1.讲解流线与冲击波的关系,解释冲击波的传播过程。
2.讲解计算冲击波形成的条件和方法,并通过示例进行演示。
四、应用举例(30分钟)1.介绍冲击波在航空航天领域的应用,如超音速飞行器的设计与控制。
2.介绍冲击波在地质勘探领域的应用,如地震波的传播与勘探。
3.介绍冲击波在医学领域的应用,如激光碎石、冲击波治疗等。
五、小结与讨论(10分钟)1.总结冲击波的基本理论和计算方法。
2.提出问题:你认为冲击波还有哪些其他应用场景?教学方法:1.授课讲解结合示例演示;2.学生小组讨论;3.提问与回答。
教学资源:1.演示PPT;2.示例计算题;3.相关实验数据。
评价与反馈:1.讲解明了,条理清晰;2.学生参与讨论积极,对冲击波的掌握较好;3.需要加强实例的举例和应用的讲解。
1.《波动与振动基础理论》;2.《冲击波理论与应用》;3.《声学原理与应用》。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)T
S
?
?
(
?f ?T
)V
?
?
(
?g ?T
)
P
—(8)
又因为: de
?
(
?e ?S
)V
dS
?
(
?e ?V
)
S
dV
de ? TdS ? P d
( e ? e(S,V) )
所以:
(
?
(
?e ?S
)
V
?V
)
S
?
?T (?V )S
?
(
?
(
?e
?V ?S
)
S
)V
?
?
(
? ?
P S
)
V
2020/7/2
10
即:(
(因为
,
CV
?
de dT
?
1 2
fR
)
所以: ? ? 1 ? R ? f ? 2
CV
f
对单原子分子气体:f ? 3,
CV
?
3 R
2
, ? ? 1.67
对双原子分子气体:
f ?5
,C V
?
5 R
2
, ? ? 1.4
对三原子分子气体: f ? 6 ,CV ? 3R , ? ? 1.33
——γ为多方指数或绝热指数adiabatic exponent)自 由度解释:决定一个物体位置所需要的独立坐标数,这里指的 是热力学自由度亦称准自由度,不同于一般的力学自由度。
⑦ 膨胀波(稀疏波):波阵面到达之处,介质的状 态( P、ρ、 T)参数减小的波称膨胀波,波的传播方向 与介质运动方向相反。 (下图5.2)
2020/7/2
3
? ⑧ 音波:介质质点在原来的位置振动,而波 向左右传播,这种波称音波,音波是弱压缩波 或膨胀波的合成。 ⑨ 冲击波:是波面以突跃面的形式在弹性介 质中传播的压缩波,波阵面上介质的状态参数 变化是突跃的。 ⑩ 爆轰波:是含有化学反应能量支持的冲击
7
Hale Waihona Puke 等熵关系的建立: 一般地:
S ? S(T,V)
e ? e(T,V)
dS
?
( ?S ?T
)V
dT
?
( ?S ?V
)T
dV
对可逆过程: de ? TdS ? P
de
?
( ?e ?T
)V
dT
?
( ?e ?V
)T
dV(1)
?dTV(
?S ?T
)
V
dT
?
?S T(?V )T
dV
?
P
d
? T ( ?S ) ? dT ? [T ( ?S )T ? P ]dV
2 冲击波基本理论
? 2.1一维等熵流动 ? 2.2正冲击波基本关系式*# ? 2.3冲击波雨贡纽曲线及冲击波的性质 ? 2.4冲击波的正反射 ? 2.5冲击波的斜反射
2020/7/2
1
2.1一维等熵流动
2.1.1波的基本概念 (复习)
① 波:在弹性介质中,某个局部受到作用后,由于物 质点的相互作用,由近及远地使物质质点陆续发生扰动, 这种扰动在介质的传播就称为波。常见的如:水波,音 波,电磁波 ···
?T
?V
(2)
比较(1)和(2)有:
?e ( ?T )V
?
?S T (?T )V
(3)
2020/7/2
8
heP?V? feTS?? ghT?S?
对焓、 Helmholtz自由能、 Gibbs自由焓的表达式分别微分:
dh ? de ? PdV ? VdP ? TdS ? V
df ? de ? d (TS) ? ? P ? SddV
?T ?V
)
S
?
? ( ?P ?S
)V
类似有:
?P ( ?T )V
?
?S ( ?V )T
?T ( ?P )S
?
?V ( ?S ) P
?V ( ?T ) P
?
?
(
?S ?P
)
T
——(9)(Maxwell关系)
将(9)的第二式代入(1)的第一式有:
dS
?
?S (?T )V
dT
?
?P ( ?T
)V
dV
[ (1)的第一式dS
dP
,dh
?
?h (?T )P
dT
?
?h (?P )T
dP
(11)
11
而
dh
?
TdS
?
VdP
?
?S T( ?T ) P
dT
?
[T
(
?S ?P
)
T
?
V]dP
?S 类似有:T ( ? T ) P
?
?h (?T )P
② 波阵面:介质的原始状态与扰动状态的交界面称波 阵面
③ 纵波与横波: 波阵面移动方向与介质质点振动方向平行的波称纵波。 波阵面移动方向与介质质点振动方向垂直的波称横波。 ④ 波速:波阵面在介质中传播的速度。 ⑤ 波的传播方向:波阵面的移动方向。
2020/7/2
2
⑥ 压缩波:波阵面到达之处,介质的状态( P、ρ、 T)参数增加的波称压缩波,波的传播方向与介质运动方 向相同。(图 5.1)
(4)
(5)
dg ? dh ? d (TS) ? V ? SddP
(6)
而:e ? e(S,V ) ,h ? h(S, P ),g ? g(P,T) , f ? f (V,T)
de
?
?e (?S )V
dS
?
?e ( ?V )S
dV
dh
?
?h (?S )P
dS
?
?h ( ?P
)S
dP
dg
?
( ?g ?P
世上无理想气体,热完全气体 是真实气体在一定温度,压力
范围内的近似,即近似看成理想气体来处理。
对于热完全气体,有: de=CvdT=Cv(T)dT ,dh=CpdT=Cp(T)dT,e=e(T) ,h=h(T)
可近似认为一定温度范围内,Cv,Cp ,
=R)保持不变。 但一般说来, Cv=Cv(T) , Cp=Cp(T)
波,因为有化学反应能量的支持,因此爆轰波 所以具有稳定的传播特性。
2020/7/2
4
完全气体,量热完全气体与等熵关系 (补物理化学 知识)
理想气体(完全气体perfect gas):不考虑分子间的作用力和分 子的体积情况下,一种理想化后的气体。它满足:
PV=nRT, e=e(T)和Cv=Cv(T)
?
?S (?T )V
dT
?
?S ( ?V )T
dV
]
又由(3)式:(
?S ?T
)
V
?
(
?e ?T
)
V
T ? CV T
,代入上式:
有:
dS
?
CV dT T
?
(
?P ?T
)V
dV
(10)
若 S ? S(T, P) , h ? h (T , P )
dS2?020(/7??/2TS
)P
dT
?
( ?S ?P
)T
)T
dP
?
( ?g ?T
)P
dT
2020/7/2
df
?
?f (?V )T
dV ?
?f ( ?T )V dT
——(7)
9
将(2)的第一式、(4)、(5)、(6)与(7)的4个式子
比较有:
T
?
?e (?S )V
?
?h ( ?S ) P
P
?
?
(
?e ?V
)
S
?
?
(
?f ?V
)
T
V
?
(
?h ?P
)
S
?
(
?g ?P
2020/7/2
( Cp- Cv
5
多方气体就是指量热完全气体 (calorically perfect
gas) :
Cp , Cv ,
保持不变的完全气体。
ee==CCvv(T(T)),,hh==CCp(pT(T) )
2020/7/2
6
CV ? f 2 R f:分子平动和转动的总自由度(不包括振动)
