正多边形与圆 知识点+例题+练习(非常好 分类全面)
正多边形和圆练习题

正多边形和圆练习题1、如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是()A.4???B.5??C.6??D.72、下面给出五个命题(1(2(3(4(5)正nA.2个B.3个C.4个D.5个3A.B.C.D.4、如果一个正三角形与一个正六边形的面积相等,那么它们的周长之比是()A.1:2B.:2C.:2D.:3?5、正nA.4B.2C.4D.2?6①弦AB②弦AC③弧AC=④∠ABC.②③④D.①②③?7、以半径为1的圆内接正三角形、正方形、正六边形的边长为三边作三角形,则()A.这个三角形是等腰三角形B.这个三角形是直角三角形C.这个三角形是锐角三角形D.不能构成三角形?8、如图,一正方形同时外切和内接于两个同心圆,当小圆的半径为r时,大圆的半径为()A.rB.1.5rC.rD.2r?9ABC心距的倍D10A.2:1B.:C.:D.3:111()A.B.C.D .?12、一个平面封闭图形内(含边界)任意两点距离的最大值称为该图形的“直径”,封闭图形的周长与直径之比称为图形的“周??”,下面四个平面图形(依次为正三角形、正方形、正六边形、圆)的周率从左到右依次记为a 1,a 2,a 3,a 4,则下列关系中正确的是( )A .a 4>a 2>a 1B .a 4>a 3>a 2C .a 1>a 2D .a 2>a 3?13A .6B .12C .D .14A . . . 或15(3(??)A .1 16、正六边形的内切圆与外接圆面积之比是(??) A .B .C .D . 17、圆内接正三角形的边心距与半径的比是(??).A .2:1B .1:2C .D .18、如果正多边形的中心角是36°,那么这个正多边形的边数是 ? .19、O是正五边形ABCDE的中心,则∠AOB的度数为?.20、如图,若干全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环还需个五边形.?21、正六边形的边长为a,面积为S,那么S关于a的函数关系式是??.22、如果正六边形的边长为a,那么它的外接圆的半径r=?.23、正四边形的半径与边心距的比等于??.24、已知正三角形的边长为a,那么它的内切圆与外接圆组成的圆环的面积S=?.25262728,则正八边形的面积为??? cm230313233形A(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是多少?(2)边长为1cm的正三角形被一个半径为r的圆所覆盖,r的最小值是多少?(3)半径为1cm的圆被边长为a的正方形所覆盖,a的最小值是多少?(4)半径为1cm的圆被边长为a的正三角形所覆盖,a的最小值是多少?34、如图,分别是正方形、正五边形和正六边形,(1)试分别计算这三种正多边形的相邻两条对角线的夹角的度数;(235“接近度”(1.于是,|180﹣m|①若n=3②若③当“(2n边形的“定义为.分别计算n边36、(1证明:在∵△ABC是正三角形∴AB=CB∵∠1和∠2的同弧圆周角∴∠1=∠2∴△ABE≌△CBP(2)如图2,四边形ABCD是⊙O的内接正方形,点P为上一动点,求证:PA=PC+PB.(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.?37、已知正方形ABCD的边心距OE=cm,求这个正方形外接圆⊙O的面积.?38、下图是一个正六边形.请你对它进行研究,并写出你的研究结论(至少6个,不得雷同,不必证明)?3940、图1B在小(1(2。
24.3正多边形和圆知识梳理与同步练习人教版2024—2025学年九年级上册

24.3正多边形和圆知识梳理与同步练习人教版2024—2025学年九年级上册知识点1 正多边形的相关概念(1)正多边形:各边相等、各角也相等的多边形叫做正多边形。
(2)正多边形和圆:把一个圆n等分,依次联接各等分点所得的多边形是这个圆的内接正多边形,这个圆是这个正多边形的外接圆。
正多边形的外接圆的圆心叫做正多边形的中心。
(3)正多边形是对称图形。
当n为奇数时,是轴对称图形;当n为偶数时,既是轴对称图形,又是中心对称图形。
(4)与正多边形有关的概念:正多边形的中心:正多边形的外接圆的圆心;正多边形的半径:正多边形的外接圆的半径;正多边形的中心角:正多边形每一条边所对的外接圆的圆心角。
正n边形的每个中心角都等于360/n,正n边形的每个内角都等于【(n-2)×180】/n.正多边形的边心距:正多边形的中心到正多边形一条边的距离。
例题1.圆的半径扩大一倍,则它的相应的圆内接正n边形的边长与半径之比( )A.扩大了一倍B.扩大了两倍C.扩大了四倍D.没有变化例题2.正五边形共有__________条对称轴,正六边形共有__________条对称轴. 例题3.正n边形是对称图形,它的对称轴有条。
例题4.正n边形的每个内角是,每个中心角是。
例题5.如图,已知正六边形的外接圆半径为4,求这个正六边形的边长、周长、面积.知识点2 正多边形的计算1.正多边形的中心是这个正多边形的外接圆的圆心,也是内切圆的圆心;2.联接中心和正多边形的各顶点,所得线段都是外接圆的半径,相邻两条半径的夹角是中心角;3.在正n 变形中,分别经过各顶点的这些半径将这个正n 边形分成n 个全等的等腰三角形,每个等腰三角形的腰是正n 边形的半径,底边是正n 边形的边,顶角是正n 边形的中心角;底边上的高是正n 边形的内切圆的半径,它的长是正n 边形的边心距;注:正多边形半径R 和边长a 、边心距r 之间的数量关系式例题 6.司南是我国古代辨别方向用的一种仪器.其早在战国时期就已被发明,是现在所用指南针的始祖.如图,司南中心为一圆形,圆心为点O ,直径为20,根据八个方位将圆形八等分(图2中点A ~H ),过点E 作⊙O 的切线与AG 的延长线交于点M ,连接EG .(1)相邻两个方位 间所夹的圆心角的度数为 .(2)求AG 的长.(3)求ME 的长.2222⎪⎭⎫ ⎝⎛+=a r R例题7.如图,在正六边形ABCDEF中,P是BC的中点,点Q在CD上,且CQ =1,DQ=3,求∠APQ的度数.例题8.正六边形ABCDEF的边长为4,求对角线AC的长和正六边形的面积.例题9.如图,正方形ABCD内接于⊙O,M为弧AD中点,连接BM,CM.(1)求证:BM=CM;(2)连接OB、OM,求∠BOM的度数.课堂同步练习1.一个正方形、一个正五边形和一个正六边形组成了如图所示的图形,则∠ABF的度数为()A.18°B.20°C.22°D.24°2.如图,点A,B,C,D,E,F是圆O上的六等分点,已知圆O的半径是2.则图中阴影部分的面积是()A.B.C.D.3.刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若⊙O的半径为1,则这个圆内接正十二边形的面积为()A.1B.3C.πD.2π4.如图,等边三角形ABC和正方形DEFG均内接于⊙O,若EF=2,则BC的长为()A.B.C.D.5.下列说法正确的是()A.经过三个不同的点可以画一个圆B.平分弦的直径,平分这条弦所对的弧C.每条边都相等的圆内接多边形是正多边形D.如果两条弦相等,那么它们所对的圆周角也相等6.如图,正六边形螺帽的边长是a cm,这个扳手开口的距离是3cm,a的值是()A.B.C.D.17.蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点P,Q,M均为正六边形的顶点.若点P,Q的坐标分别为,(0,﹣3),则点M的坐标为.8.如图,边长为1的正六边形ABCDEF内接于⊙O,则图中阴影部分的面积为.(结果保留π)9.如图,已知正方形ABCD内接于⊙O,点E在上,则∠BEC的度数为°.10.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=20°,则这个正多边形的边数为.11.如图,在⊙O中,AB=AC,∠B=70°,∠C度数是.12.在一个正多边形中,一个内角是与它相邻的一个外角的3倍.(1)求这个多边形的边数;(2)求这个多边形的每一个外角的度数.13.如图,正六边形ABCDEF的半径为5.(1)求对角线AC的长;(2)求这个正六边形的周长与面积.14.如图,正五边形ABCDE内接于⊙O,连结AC,BD交于点F.(1)求证:AB=AF.(2)若⊙O的半径为10,求正五边形ABCDE的面积(结果精确到0.1,参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73).15.如图,在正五边形ABCDE中,连结AC,AD,CE,CE交AD于点F.(1)求∠CAD的度数.(2)已知AB=2,求DF的长.16.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则(1)⊙O的直径长为;(2)△AMN周长的最小值是.。
2020年九年级数学上册专题24.3正多边形和圆(讲练)【含解析】

2020年九年级数学上册专题24.3正多边形和圆(讲练)一、知识点1.正多边形与圆(1)正多边形的有关概念:边长(a)、中心(O)、中心角(∠AOB)、半径(R))、边心距(r),如图所示①.(2)特殊正多边形中各中心角、长度比:中心角=120° 中心角=90° 中心角=60°,△BOC 为等边△a:r:R=2:1:2 a:r:R=2::2 a:r:R=2:2二、标准例题:例1:如图,正六边形ABCDEF 内接于⊙O ,连接BD .则∠CBD 的度数是()A .30°B .45°C .60°D .90°【答案】A【解析】∵在正六边形ABCDEF 中,∠BCD ==120°,BC =CD,(62)1806-⨯∴∠CBD =(180°﹣120°)=30°,12故选:A .总结:本题考查的是正多边形和圆、等腰三角形的性质,三角形的内角和,熟记多边形的内角和是解题的关键.例2:如图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形翻折起来后,就能形成一个圆形桌面(可以近似看作正方形的外接圆),正方形桌面与翻折成圆形桌面的面积之比最接近( )A .B .C .D .45342312【答案】C【解析】连接AC ,设正方形的边长为a ,∵四边形ABCD 是正方形,∴∠B=90°,∴AC 为圆的直径,a ,,223π=≈故选C.总结:本题考查的是正多边形和圆,掌握圆周角定理、正方形的性质是解题的关键.例3:如图,正六边形ABCDEF 内接于⊙O ,BE 是⊙O 的直径,连接BF ,延长BA ,过F 作FG ⊥BA ,垂足为G .(1)求证:FG是⊙O的切线;(2)已知FG =,求图中阴影部分的面积.【答案】(1)见解析;(2) 图中阴影部分的面积为.83π【解析】(1)证明:连接OF ,AO ,∵AB =AF =EF ,∴,AB AF EF ==∴∠ABF =∠AFB =∠EBF =30°,∵OB =OF ,∴∠OBF =∠BFO =30°,∴∠ABF =∠OFB ,∴AB ∥OF ,∵FG ⊥BA ,∴OF ⊥FG ,∴FG 是⊙O 的切线;(2)解:∵,AB AF EF ==∴∠AOF =60°,∵OA =OF ,∴△AOF 是等边三角形,∴∠AFO =60°,∴∠AFG =30°,∵FG =,∴AF =4,∴AO =4,∵AF ∥BE ,∴S △ABF =S △AOF ,∴图中阴影部分的面积=.260483603ππ⨯=总结:此题考查切线的判定,等边三角形的判定,扇形面积,解题关键在于利用等弧对等角三、练习1.如图,正六边形的边长为2,分别以点为圆心,以为半径作扇形,扇形ABCDEF ,A D ,AB DCABF .则图中阴影部分的面积是( )DCE A .B .C .D.43π83π-43π-43π【答案】B 【解析】解:∵正六边形的边长为2,ABCDEF ∴正六边形的面积是:,,ABCDEF ()22sin 606622︒⨯⨯=⨯=120FAB EDC ∠=∠=∴图中阴影部分的面积是:,21202823603ππ⨯⨯-⨯=故选:B .2.有一个正五边形和一个正方形边长相等,如图放置,则的值是()1∠A .B .C .D .15︒18︒20︒9︒【答案】B 【解析】解:正五边形的内角的度数是1(52)1801085︒︒⨯-⨯=正方形的内角是90°,则∠1=108°-90°=18°.故选:B .3.如图,已知正方形的顶点、在上,顶点、在内,将正方形绕点逆ABCD A B O C D O ABCD A 时针旋转,使点落在上.若正方形的边长和的半径均为,则点运动的路径长为D O ABCD O 6cm D ()A .B .C .D .2cmπ32cm πcm π12cm π【答案】C 【解析】解:设圆心为O ,连接AO ,BO , OF ,∵AB=6,AO=BO=6,∴AB=AO=BO,∴三角形AOB 是等边三角形,∴∠OAB=60°∵AF=AO=FO=6,∴△FAO 是等边三角形,∴∠OAF=60°∠FAB=∠OAB+∠OAF =120°,∴∠EAC=120°-90°=30°,∵AD=AB=AF=6,∴点D 运动的路径长为:=π.306180π⨯⨯故选:C .4.如图,在正五边形中,,的延长线交于点,则等于( ).ABCDE AE CD FF ∠A .B .C .D .30°32︒36︒38︒【答案】C 【解析】∵五边形ABCDE 是正五边形,∴∠AED =∠EDC =108°,∴∠FED =∠FDE =72°,由三角形的内角和定理得:∠F =180°﹣72°﹣72°=36°.故选C .5.如图,已知正五边形内接于,连结,则的度数是( )ABCDE O BD ABD ∠A .B .C .D .60︒70︒72︒144︒【答案】C 【解析】∵五边形为正五边形ABCDE ∴()1552180108ABC C ∠=∠=-⨯︒=︒∵CD CB =∴181(8326)010CBD ∠=︒-︒=︒∴72ABD ABC CBD ∠=∠-∠=︒故选:C .6.如图,正六边形的边长为2,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是( )A .B .C .D .π-2π-π+2π+【答案】A【解析】解:6个月牙形的面积之和,2132622πππ⎛=--⨯⨯= ⎝故选:A .7.阅读理如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M 的位置可由∠MOx 的度数θ与OM 的长度m 确定,有序数对(θ,m)称为M 点的“极坐标”,这样建立的坐标系称为“极坐标系”。
2020年人教版九年级数学上册24.3《正多边形和圆》随堂练习(含答案)

2020年人教版九年级数学上册24.3《正多边形和圆》随堂练习基础题知识点1 认识正多边形1.下面图形中,是正多边形的是( )A.矩形 B.菱形C.正方形 D.等腰梯形2.如图,正六边形的每一个内角都相等,则其中一个内角α的度数是( )A.240° B.120° C.60° D.30°3.一个正多边形的一个外角等于30°,则这个正多边形的边数为.4.如图,AC是正五边形ABCDE的一条对角线,则∠ACB= .知识点2 与正多边形有关的计算5.如图,正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )A. 3 B.2 C.2 2 D.2 36.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )A.正三角形 B.正方形C.正五边形 D.正六边形7.若正方形的外接圆半径为2,则其内切圆半径为( )A. 2 B.2 2C.22D.18.边长为6 cm的等边三角形的外接圆半径是.9.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合.若A点的坐标为(-1,0),则点C的坐标为( ).10.将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于 (结果保留根号).知识点3 画正多边形11.如图,甲:①作OD的中垂线,交⊙O于B,C两点;②连接AB,AC,△ABC即为所求的三角形.乙:①以D为圆心,OD长为半径作圆弧,交⊙O于B,C两点;②连接AB,BC,CA,△ABC即为所求的三角形.对于甲、乙两人的作法,可判断( )A.甲、乙均正确 B.甲、乙均错误C.甲正确,乙错误 D.甲错误,乙正确12.图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图2,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).中档题13.正三角形内切圆半径r与外接圆半径R之间的关系为( )A.4R=5r B.3R=4rC.2R=3r D.R=2r14.如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( )A.(2,-3) B.(2,3)C.(3,2) D.(3,-2)15.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )A.22B.32C. 2D. 316.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )A.2a2 B.3a2 C.4a2 D.5a217.如图,圆O与正八边形OABCDEFG的边OA,OG分别交于点M,N,则弧MN所对的圆心角∠MPN的大小为.18.如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10= .19.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.(1)正方形ABCD与正六边形AEFCGH的边长之比为;(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.综合题20.如图1,2,3,…,m,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连接OM,ON.(1)求图1中∠MON的度数;(2)图2中∠MON的度数是,图3中∠MON的度数是;(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).参考答案01 基础题知识点1 认识正多边形1.下面图形中,是正多边形的是(C)A .矩形B .菱形C .正方形D .等腰梯形2.(柳州中考)如图,正六边形的每一个内角都相等,则其中一个内角α的度数是(B)A .240°B .120°C .60°D .30°3.(连云港中考)一个正多边形的一个外角等于30°,则这个正多边形的边数为12.4.(资阳中考)如图,AC 是正五边形ABCDE 的一条对角线,则∠ACB=36°.知识点2 与正多边形有关的计算5.(沈阳中考)如图,正六边形ABCDEF 内接于⊙O ,正六边形的周长是12,则⊙O 的半径是(B)A. 3B .2C .2 2D .2 3 6.(株洲中考)下列圆的内接正多边形中,一条边所对的圆心角最大的图形是(A) A .正三角形 B .正方形 C .正五边形 D .正六边形7.(滨州中考)若正方形的外接圆半径为2,则其内切圆半径为(A)A. 2 B .2 2C.22D .1 8.边长为6 cm 的等边三角形的外接圆半径是23.9.(宁夏中考)如图,将正六边形ABCDEF 放在直角坐标系中,中心与坐标原点重合.若A点的坐标为(-1,0),则点C 的坐标为(12,-32).10.(教材P109习题T6变式)将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于1+2(结果保留根号).知识点3 画正多边形甲:①作OD的中垂线,交⊙O于B,C两点;②连接AB,AC,△ABC即为所求的三角形.乙:①以D为圆心,OD长为半径作圆弧,交⊙O于B,C两点;②连接AB,BC,CA,△ABC即为所求的三角形.对于甲、乙两人的作法,可判断(A)A.甲、乙均正确B.甲、乙均错误C.甲正确,乙错误D.甲错误,乙正确12.(镇江中考改编)图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图2,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).解:如图.02中档题13.正三角形内切圆半径r与外接圆半径R之间的关系为(D)A.4R=5r B.3R=4rC.2R=3r D.R=2r14.(滨州中考)如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是(C)A.(2,-3) B.(2,3)C.(3,2) D.(3,-2)15.(达州中考)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(A)A.22B.32C. 2D. 316.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为(A)A.2a2 B.3a2 C.4a2 D.5a217.(山西中考命题专家原创)如图,圆O与正八边形OABCDEFG的边OA,OG分别交于点M,N,则弧MN所对的圆心角∠MPN的大小为67.5°.18.(连云港中考)如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=75°.19.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.(1)正方形ABCD与正六边形AEFCGH的边长之比为2∶1;(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.解:BE是⊙O的内接正十二边形的一边,理由:连接OA ,OB ,OE ,在正方形ABCD 中,∠AOB=90°,在正六边形AEFCGH 中,∠AOE=60°,∴∠BOE=30°.∵n=360°30°=12, ∴BE 是正十二边形的边.03 综合题20.如图1,2,3,…,m ,M ,N 分别是⊙O 的内接正三角形ABC ,正方形ABCD ,正五边形ABCDE ,…正n 边形ABCDEF …的边AB ,BC 上的点,且BM=CN ,连接OM ,ON.(1)求图1中∠MON 的度数;(2)图2中∠MON 的度数是90°,图3中∠MON 的度数是72°;(3)试探究∠MON 的度数与正n 边形边数n 的关系(直接写出答案).解:(1)连接OA ,OB.∵正三角形ABC 内接于⊙O ,∴OA=OB ,∠OAM=∠OBA=30°,∠AOB=120°.∵BM=CN ,AB=BC ,∴AM=BN.∴△AOM ≌△BON(SAS).∴∠AOM=∠BON.∴∠AOM +∠BOM=∠BON +∠BOM ,即∠AOB=∠MON.∴∠MON=120°.(3)∠MON=360°n.。
(完整版)正多边形与圆练习题
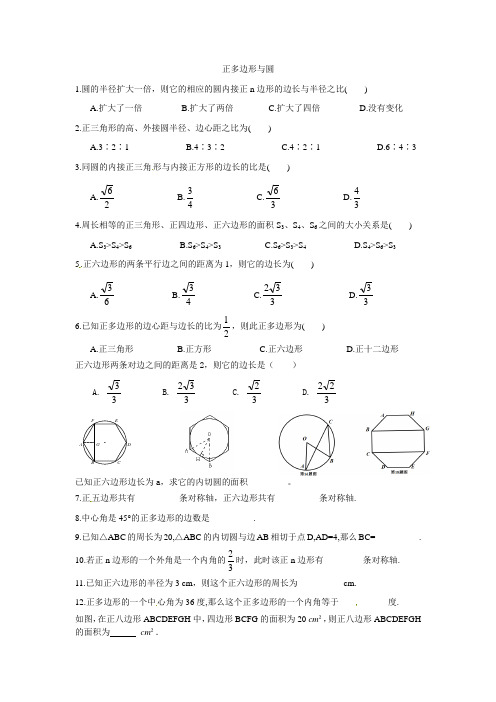
正多边形与圆1.圆的半径扩大一倍,则它的相应的圆内接正n 边形的边长与半径之比( )A.扩大了一倍B.扩大了两倍C.扩大了四倍D.没有变化2.正三角形的高、外接圆半径、边心距之比为( )A.3∶2∶1B.4∶3∶2C.4∶2∶1D.6∶4∶33.同圆的内接正三角形与内接正方形的边长的比是( ) A.26 B.43 C.36 D.34 4.周长相等的正三角形、正四边形、正六边形的面积S 3、S 4、S 6之间的大小关系是( )A.S 3>S 4>S 6B.S 6>S 4>S 3C.S 6>S 3>S 4D.S 4>S 6>S 35.正六边形的两条平行边之间的距离为1,则它的边长为( )A.63B.43C.332D.33 6.已知正多边形的边心距与边长的比为21,则此正多边形为( ) A.正三角形 B.正方形 C.正六边形 D.正十二边形 正六边形两条对边之间的距离是2,则它的边长是( )A. 33B. 233C. 23D. 223已知正六边形边长为a ,求它的内切圆的面积_________。
7.正五边形共有__________条对称轴,正六边形共有__________条对称轴.8.中心角是45°的正多边形的边数是__________.9.已知△ABC 的周长为20,△ABC 的内切圆与边AB 相切于点D,AD=4,那么BC=__________.10.若正n 边形的一个外角是一个内角的32时,此时该正n 边形有_________条对称轴. 11.已知正六边形的半径为3 cm ,则这个正六边形的周长为__________ cm.12.正多边形的一个中心角为36度,那么这个正多边形的一个内角等于___________度.如图,在正八边形ABCDEFGH 中,四边形BCFG 的面积为20 cm ²,则正八边形ABCDEFGH 的面积为 cm ².F EA G DB C如图,在正八边形ABCDEFGH 中,等腰梯形CDEF 的面积是12,则这个八边形的面积为___________ 如图,有一圆内接正八边形ABCDEFGH,若△ADE 的面积为10,则正八边形ABCDEFGH 的面积为 ___________如图,点M 、N 、P 、Q 、G 、H 都在同一直线L 上,四边形ABCD 都是正方形,其边长分别为a 、b 、c 、d,若密封图形总面积是m,其中阴影部分的面积为n,则a ²+b ²+c ²+d ²的值为___________ 直角三角行abc 的两直角边ac 多种等于8cm,bc 等于6cm,以ac,bc 边向三角形外分作正方形acd 与bcfg,再以ab 为边上作正方形abmn,其中n 点落在de 上,bm 交cf 于点t.问:图中阴影部分如图,正六边形ABCDEF 内接于⊙O ,若⊙O 的半径为4,则阴影部分的面积等于 . 为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a ,则阴影部分的面积为______.如图,将边长为a 的正六边形A 1 A 2 A 3 A 4 A 5 A 6在直线l 上由图1的位置按顺时针方向向 作无滑动滚动,当A 1第一次滚动到图2位置时,顶点A 1所经过的路径的长为( ).A .4+233πa B .8+433πa C .4+33πa D .4+236πa如图24-3-6(1)、24-3-6(2)、24-3-6(3)、…、24-3-6(n),M 、N分别是⊙O 的内接正三角形ABC 、正方形ABCD 、正五边形ABCDE 、…、正n 边形ABCDE…的边AB 、BC 上的点,且BM=CN ,连结OM 、ON.图24-3-6。
部编数学九年级上册24.3正多边形和圆(7大题型)2023考点题型精讲(解析版)含答案

24.3 正多边形和圆正多边形的概念 各边相等,各角也相等的多边形是正多边形.正多边形的有关概念 (1)一个正多边形的外接圆的圆心叫做这个正多边形的中心. (2)正多边形外接圆的半径叫做正多边形的半径. (3)正多边形每一边所对的圆心角叫做正多边形的中心角. (4)正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.题型1:正多边形的相关概念1.下列关于正多边形的叙述,正确的是( )A.正九边形既是轴对称图形又是中心对称图形B.存在一个正多边形,它的外角和为720°C.任何正多边形都有一个外接圆D.不存在每个外角都是对应每个内角两倍的正多边形【答案】C【解析】【解答】解:正九边形是轴对称图形,不是中心对称图形,故选项A不正确;任何多边形的外角和都为360°,故选项B不正确;【变式1-1】已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )A.45° B.60° C.75° D.90°【答案】A.【解析】如图,连接OB、OC,则∠BOC=90°,根据圆周角定理,得:∠BPC=∠BOC=45°.故选A.【点评】本题主要考查了正方形的性质和圆周角定理的应用.【变式1-2】如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于( )A.30° B.45° C.55° D.60°【答案】连接OA,OB.根据正方形的性质,得∠AOB=90°.再根据圆周角定理,得∠APB=45°.故选B.正多边形的有关计算 (1)正n边形每一个内角的度数是; (2)正n边形每个中心角的度数是; (3)正n边形每个外角的度数是.注意:要熟悉正多边形的基本概念和基本图形,将待解决的问题转化为直角三角形题型2:正多边形与圆有关的计算-角度2.如图,正五边形ABCDE内接于⊙O,连接AC,则∠BAC的度数是( )A.45°B.38°C.36°D.30°【答案】C【解析】【解答】解:连接OC、OB,如下图:根据正多边形的性质可得:∠BOC=360°5=72°根据圆周角定理可得:∠BAC=12∠BOC=36°故答案为:C【分析】连接OC、OB,根据正多边形的性质可得∠BOC=360°5=72°,再根据圆周角定理求解即可。
正多边形和圆的经典例题

正多边形和圆的经典例题1. 前言嘿,大家好!今天咱们聊聊正多边形和圆的那些事儿。
别紧张,听我慢慢道来,这绝对不是枯燥的数学课,而是一次轻松有趣的数学旅行。
你可能会问,正多边形是什么?那就是像正方形、正六边形那样,边和角都一模一样的形状。
而圆呢,它就像咱们喝水时看到的杯子底部,圆滑得让人觉得舒服。
接下来,我们来探讨一下这些形状之间的关系,还有一些有趣的例子,让你在不知不觉中get到这些知识!2. 正多边形的特点2.1 边和角的对称正多边形最大的特点,就是它的边和角都超级对称,简直像个模特儿站在那儿,姿态优雅!比如,想象一下一个正六边形,就像是蜜蜂的蜂巢,六个边都是相等的,角度也是60度,完全没有一个角敢突出自己,真是团结的好榜样!这就是为什么很多建筑和设计师喜欢用它,显得大方又美观。
2.2 周长和面积的计算再说说正多边形的周长和面积,简单得不要不要的!你只需知道每条边的长度,就可以轻松算出周长,公式就是边长乘以边的数量。
至于面积嘛,正六边形的面积就有点小复杂,不过只需用边长乘以边数,然后再乘以一个常数,记得把它除以2就好。
是不是简单?看吧,数学其实也可以很轻松嘛!3. 圆的魅力3.1 圆的周长和面积说到圆,咱们就不得不提它的周长和面积了。
圆的周长可得靠π(pi)来帮忙,公式是2πr,r是半径。
想象一下,一个大披萨,切下来一片,边缘那一圈就是周长。
而面积呢,则是πr²,听起来高深,其实只要记住这两个公式,就能在朋友面前装得很厉害了!不仅可以计算圆形的游泳池,还能算算自家花园的面积,绝对是个实用的小技能。
3.2 圆和正多边形的关系有趣的是,正多边形和圆之间的关系就像是两位老朋友。
圆的形状是完美的,而正多边形可以通过不断增加边的数量,逐渐接近圆形。
比如,八边形就比六边形更接近圆,十六边形又比八边形更接近,直到你加到无数个边,哦,那简直就是一个圆啊!这种不断变化的过程就像人生,有时候需要不断调整,才能找到最适合自己的方式。
正多边形和圆(知识解读+真题演练+课后巩固)(原卷版)

第06讲 正多边形和圆1. 了解正多边形和圆的有关概念;2. 理解并掌握正多边形半径和边长、边心距、中心角之间的关系,会应用多边形和圆的有关知识画多边形.知识点1 圆内正多边形的计算(1)正三角形在⊙O 中△ABC 是正三角形,有关计算在Rt BOD ∆中进行:::2OD BD OB =;(2)正四边形同理,四边形的有关计算在Rt OAE ∆中进行,::OE AE OA =(3)正六边形同理,六边形的有关计算在Rt OAB ∆中进行,::2AB OB OA =. 知识点2 与正多边形有关的概念1、正多边形的中心正多边形的外接圆的圆心叫做这个正多边形的中心。
2、正多边形的半径正多边形的外接圆的半径叫做这个正多边形的半径。
3、正多边形的边心距正多边形的中心到正多边形一边的距离叫做这个正多边形的边心距。
4、中心角正多边形的每一边所对的外接圆的圆心角叫做这个正多边形的中心角。
知识点3正多边形的对称性1、正多边形的轴对称性正多边形都是轴对称图形。
一个正n边形共有n条对称轴,每条对称轴都通过正n边形的中心。
2、正多边形的中心对称性边数为偶数的正多边形是中心对称图形,它的对称中心是正多边形的中心。
3、正多边形的画法先用量角器或尺规等分圆,再做正多边形。
【题型1 正多边形与圆求角度】【典例1】(2023•青羊区校级模拟)如图,正六边形ABCDEF内接于⊙O,∠ADB的度数是()A.20°B.30°C.45°D.60°【变式1-1】(2023•惠水县一模)如图,边长相等的正五边形、正六边形的一边重合,则∠1的度数为()A.10°B.12°C.20°D.22°【变式1-2】(2022秋•曲周县期末)已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数等于()A.45°B.60°C.35°D.55°【变式1-3】(2023•新市区校级一模)如图,⊙O与正五边形ABCDE的边AB、DE分别相切于点B、D,则劣弧所对的圆心角∠BOD的大小为()A.150°B.144°C.135°D.120°【题型2正多边形与圆求线段长度】【典例2】(2023•龙港市二模)如图,要拧开一个边长为a的正六边形螺帽,则扳手张开的开口b至少为()A.2a B.C.D.【变式2-1】(2023春•鼓楼区校级期中)如图,A、B、C、D为一个正多边形的顶点,若∠ADB=15°,则该正多边形的边数为()A.9B.10C.11D.12【变式2-2】(2022秋•烟台期末)如图,正六边形ABCDEF内接于⊙O,若⊙O 的周长等于6π,则正六边形的边长为()A.B.3C.D.【变式2-3】(2023•苏州二模)如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,过O作OM垂直AB,交AB于点M,则OM的长为.【题型3正多边形与圆求半径】【典例3】(2022秋•巩义市期末)如图,已知⊙O的内接正方形ABCD的边长为1,则⊙O的半径为()A.B.C.1D.【变式3-1】(2022秋•慈溪市期末)如图,正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是()A.1B.C.2D.【变式3-2】(2023•宜春一模)若正方形的边长为8,则其外接圆的半径是.【题型4正多边形与圆求面积】【典例4】(2022秋•呈贡区期末)正六边形的边长为6cm,则该正六边形的内切圆面积为()A.48πcm2B.36πcm2C.24πcm2D.27πcm2【变式4-1】(2023•大冶市一模)如图,有一个亭子,它的地基是边长为4m的正六边形,则地基的面积为()A.4m2B.12m2C.24m2D.24m2【变式4-2】(2023•南山区二模)刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正八边形.若⊙O的半径为1,则这个圆内接正八边形的面积为()A.πB.2πC.D.【变式4-3】(2023•济源一模)如图,正六边形ABCDEF,A(﹣2,0),D(2,0),点P从点A出发,沿A→B→C→D→E→F→A以每秒1个单位长度的速度运动,当运动到第2023秒时,△AOP的面积为()A.B.C.D.1【题型5正多边形与圆求周长】【典例5】(2023•钦州一模)如图,若一个正六边形的对角线AB的长为10,则正六边形的周长()A.5B.6C.30D.36【变式5-1】(2023春•余姚市期中)一个边长为1的正多边形的每个外角的度数是36°,则这个正多边形的周长是()A.1B.10C.5D.【变式5-2】(2022秋•北辰区校级期末)边心距为3的正六边形的周长为()A.18B.C.D.【变式5-3】(2022秋•河西区期末)六个带30°角的直角三角板拼成一个正六边形,直角三角板的最短边为10,求中间正六边形的周长.【题型6正多边形与直角坐标系综合】【典例6】(2023•西和县一模)在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受到中国人的浪漫,如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,“雪花”中心与原点重合,C,F在y轴上,则顶点B 的坐标为()A.(4,2)B.(4,4)C.D.【变式6-1】(2023•洛龙区一模)在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫.如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,﹣3),则顶点C的坐标为()A.)B.C.D.【变式6-2】(2022秋•绵阳期末)如图,在平面直角坐标系中,正六边形OABCDE 的边长是4,则它的内切圆圆心M的坐标是()A.B.C.D.(2,4)1.(2023•临沂)将一个正六边形绕其中心旋转后仍与原图形重合,旋转角的大小不可能是()A.60°B.90°C.180°D.360°2.(2023•内江)如图,正六边形ABCDEF内接于⊙O,点P在上,点Q是的中点,则∠CPQ的度数为()A.30°B.45°C.36°D.60°3.(2023•安徽)如图,正五边形ABCDE内接于⊙O,连接OC,OD,则∠BAE ﹣∠COD=()A.60°B.54°C.48°D.36°4.(2023•自贡)第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角∠ACB=15°,算出这个正多边形的边数是()A.9B.10C.11D.12 5.(2022•绵阳)在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫.如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,﹣3),则顶点C的坐标为()A.(2﹣2,3)B.(0,1+2)C.(2﹣,3)D.(2﹣2,2+)6.(2022•雅安)如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF 的边心距OG为()A.3B.C.D.31.(2022秋•灵宝市期末)边长为4的正方形内接于⊙O,则⊙O的半径是()A.B.2C.2D.4 2.(2023•梁溪区二模)如图所示,A、B、C、D是一个外角为40°的正多边形的顶点.若O为正多边形的中心,则∠OAD的度数为()A.14°B.40°C.30°D.15°3.(2023春•汉寿县期末)若一个正多边形的一个内角的度数为144°,则这个正多边形的边数为()A.7B.8C.9D.10 4.(2023•崆峒区校级三模)平凉市崆峒山塔群是研究院东地区砖石建筑艺术的宝贵实物资料,图①是位于崆峒山灵龟台西的灵秘塔,塔为石基砖砌身,呈六角六面四级阶状尖顶塔,图②是灵秘塔某层的平面示意图,若将其抽象为正六边形,则a的度数为()A.45°B.50°C.60°D.72°5.(2023•玉林一模)如图,在由边长相同的7个正六边形组成的网格中,点A,B在格点上.再选择一个格点C,使△ABC是以AB为腰的等腰三角形,符合点C条件的格点个数是()A.1B.2C.3D.4 6.(2023•夏津县一模)如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是()A.7个B.8个C.9个D.10个7.(2023•咸宁模拟)如图,正五边形ABCDE内接于⊙O,其半径为1,作OF ⊥BC交⊙O于点F,则的长为()A.πB.C.D.8.(2022•青岛)如图,正六边形ABCDEF内接于⊙O,点M在上,则∠CME 的度数为()A.30°B.36°C.45°D.60°9.(2022秋•荔湾区校级期末)如图.点O是正五边形ABCDE的中心,⊙O 是正五边形的外接圆,∠ADE的度数为()A.30°B.32°C.36°D.40°10.(2022•思明区校级二模)如图,正三角形PMN的顶点分别是正六边形ABCDEF三边的中点,则三角形PMN与六边形ABCDEF的面积之比()A.1:2B.1:3C.2:3D.3:8 11.(2022•桐梓县模拟)如图,⊙O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.若FM=4.则点O到FM的距离是()A.4B.C.D.12.(2023春•高邑县期末)定义:如果几个全等的正n边形依次有一边重合,排成一圈,中间可以围成一个正多边形,那么我们称作正n边形的环状连接.如图1,我们可以看作正八边形的环状连接,中间围成一个正方形.(1)若正六边形作环状连接,如图2,中间可以围成的正多边形的边数为;(2)若边长为a的正n边形作环状连接,中间围成的是等边三角形,则这个环状连接的外轮廓长为.(用含a的代数式表示)13.(2023•兴庆区校级一模)如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的中心与原点O重合,AB∥x轴,交y轴于点P.将△OAP绕点O顺时针旋转,每次旋转90°,则第2023次旋转结束时,点A的坐标为.14.(2023•新城区校级二模)如图,已知⊙O的内接正六边形ABCDEF的边心距OM是,则正六边形的边长为.15.(2023•镇江一模)在九年级《数学实验手册》中,我们探究了最小覆盖圆与图形之间的关系.现有如图所示的等边三角形△ABC,边长为3,若分别以顶点A、B、C为圆心作三个等圆,这三个等圆能完全覆盖△ABC,则所作等圆的最小半径是.16.(2023•抚州一模)蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§ 2.6 正多边形与圆
一、概念
知识点1 正多边形及其有关概念
★正多边形:________相等、________也相等的多边形叫做正多边形.
注:边数3
n 的多边形必须同时满足“各边相等”和“各角相等”这两个条件,才能判定它是正多边形.
例1 下列说法正确的是()
A.正三角形不是正多边形
B.平行四边形是正多边形
C.正方形是正多边形
D.各角相等的多边形是正多边形
知识点2 正多边形的对称性(重点)
1.正多边形都是________图形.一个正n边形共有_______条对称轴,每一条对称轴都经过正n边形的_________.
2.一个正多边形,如果有偶数条边,那么它是________________图形,也是_________________图形;如果有奇数条边,那么是_______________图形.
注:(1)如果一个正多边形是中心对称图形,那么它的中心就是对称中心;
(2)正n边形的内角和等于________________,每一个内角都等于___________________,每一个外角都等于_________________.
知识点3 正多边形的判定
例2 如图,在正∆ABC中,E,F,G,H,L,K分别是各边的三等分点,试说明六边形EFGHLK是正六边形.
二、经典题型
题型1 根据正多边形的性质求角
例1 如图,正方形ABCD是O的内接正方形,点P是弧CD上不同于点C的任意一点,则∠BPC等于___________.
题型2 利用正多边形的性质求图形的面积
例 2 如图,正六边形内接于O,O的半径为10,则图中阴影面积_________.
典例精讲:
1. 下列边长为a 的正多边形与边长为a 的正方形组合起来,不能镶嵌成平面
( ) 、(1)正三角形 (2)正五边形 (3)正六边形 (4)正八边形
A .(1)(2)
B .(2)(4)
C .(1)(3)
D .(1)(4)
2. 若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r 3,r 4,r 6,则r 3:r 4:r 6等于( )
A .1:2:3
B .3:2:1
C .1:2:3
D . 3:2:1
3. 已知正六边形ABCDEF 内接于⊙O ,图中阴影部分的面积为312,则⊙O
的半径为______________________.
(第4题) (第5题)
4.如图,正方形ABCD 内接于⊙O ,点E 在AD 上,则∠BEC= .
5.将一块正六边形硬纸片(图1),做成一个底面仍为正六边形且高相等的无盖纸盒(侧面均垂直于底面,见图2),需在每一个顶点处剪去一个四边形,例如图中的四边形AGA /H ,那么∠GA /H 的大小是 度.
O
B C
D
A E
F E D C A O
6.从一个半径为10㎝的圆形纸片上裁出一个最大的正方形,则此正方形的边长为 .
7.如图,若正方形A 1B 1C 1D 1内接于正方形ABCD 的内接圆,则
AB B A 11的值为( )
A .2
1 B .2
2 C .41
D .42。
