2017年中考数学浙江省绍兴市届中考数学试卷(解析版)
2017年中考数学浙江绍兴市届中考数学考试(解析版)

2017年中考数学浙江绍兴市届中考数学考试(解析版)————————————————————————————————作者:————————————————————————————————日期:2017年浙江省绍兴市中考数学试卷一、选择题1、-5的相反数是()A、B、5 C、D、-52、研究表明,可燃冰是一种可替代石油的新型清洁能源。
在我国某海域已探明的可燃冰储存量达150 000 000 000立方米,其中数字150 000 000 000用科学记数法可表示为()A、15×1010B、0.15×1012C、1.5×1011D、1.5×10123、如图的几何体由五个相同的小正方体搭成,它的主视图是()A、B、C、D、4、在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其它均相同,从中任意摸出一个球,则摸出黑球的概率是()A、B、C、D、5、下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:甲乙丙丁平均数(环) 9.14 9.15 9.14 9.15方差 6.6 6.8 6.7 6.6()A、甲B、乙C、丙D、丁6、如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米.则小巷的宽度为()A、0.7米B、1.5米C、2.2米D、2.4米7、均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是()A、B、C、D、8、在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形ABCD是矩形,E是BA 延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA。
若∠ACB=21°,则∠ECD的度数是()A、7°B、21°C、23°D、24°9、矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C 重合,则该抛物线的函数表达式变为()A、y=x2+8x+14B、y=x2-8x+14C、y=x2+4x+3D、y=x2-4x+310、一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是()A、B、C、D、二、填空题11、分解因式:=________.12、如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E.则∠DOE的度数为________.13、如图,Rt△ABC的两个锐角顶点A,B在函数y= (x>0)的图象上,AC//x轴,AC=2.若点A的坐标为(2,2),则点B的坐标为________.14、如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪得行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为________m.15、以Rt△ABC的锐角顶点A为圆心,适当长为半径作弧,与边AB,AC各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A作直线,与边BC交于点D.若∠ADB=60°,点D到AC的距离为2,则AB的长为________.16、如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是________.三、解答题17、计算题。
2017年浙江省绍兴市中考数学试卷

2017年浙江省绍兴市中考数学试卷一、选择题(本大题共10小题,每小题4分,共40分)1.(4分)﹣5的相反数是()A.B.5C.﹣D.﹣52.(4分)研究表明,可燃冰是一种替代石油的新型清洁能源,在我国某海域已探明的可燃冰存储量达150000000000立方米,其中数字150000000000用科学记数法可表示为()A.15×1010B.0.15×1012C.1。
5×1011D.1。
5×10123.(4分)如图的几何体由五个相同的小正方体搭成,它的主视图是()A.B.C.D.4.(4分)在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其他均相同,从中任意摸出一个球,则摸出黑球的概率是()A.B.C.D.5.(4分)下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:甲乙丙丁平均数(环)9。
149。
159.149。
15方差6。
66。
86。
7 6.6根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择()A.甲B.乙C.丙D.丁6.(4分)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0。
7米,顶端距离地面2。
4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为()A.0。
7米B.1。
5米C.2。
2米D.2.4米7.(4分)均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h 随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是()A.B.C.D.8.(4分)在探索“尺规三等分角"这个数学名题的过程中,曾利用了如图.该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是()A.7°B.21°C.23°D.24°9.(4分)矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为()A.y=x2+8x+14B.y=x2﹣8x+14C.y=x2+4x+3D.y=x2﹣4x+310.(4分)一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是()A.B.C.D.二、填空题(本大题共6小题,每小题5分,共30分)11.(5分)分解因式:x2y﹣y=.12.(5分)如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为.13.(5分)如图,Rt△ABC的两个锐角顶点A,B在函数y=(x>0)的图象上,AC∥x轴,AC=2,若点A的坐标为(2,2),则点B的坐标为.14.(5分)如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为m.15.(5分)以Rt△ABC的锐角顶点A为圆心,适当长为半径作弧,与边AB,AC 各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A作直线,与边BC交于点D.若∠ADB=60°,点D到AC的距离为2,则AB 的长为.16.(5分)如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点,若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.三、解答题(本大题共8小题,共80分)17.(8分)(1)计算:(2﹣π)0+|4﹣3|﹣.(2)解不等式:4x+5≤2(x+1)18.(8分)某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.(1)若某月用水量为18立方米,则应交水费多少元?(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?19.(8分)为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如图所示),并用调查结果绘制了图1,图2两幅统计图(均不完整),请根据统计图解答以下问题:(1)本次接受问卷调查的同学有多少人?补全条形统计图.(2)本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.20.(8分)如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.(1)求∠BCD的度数.(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0。
2017年浙江省绍兴市中考数学试卷

2017 年浙江省绍兴市中考数学试卷一、选择题(本大题共10 小题,每题 4 分,共 40 分)1.(4 分)﹣ 5 的相反数是()A.B. 5C.﹣D.﹣ 52.(4 分)研究表示,可燃冰是一种代替石油的新式洁净能源,在我国某海疆已探明的可燃冰储存量达0 立方米,此中数字0 用科学记数法可表示为()A.15×1010B.0.15×1012C. 1.5× 1011D.1.5×10123.(4 分)如图的几何体由五个同样的小正方体搭成,它的主视图是()A.B.C.D.4.(4 分)在一个不透明的袋子中装有 4 个红球和 3 个黑球,它们除颜色外其余均同样,从中随意摸出一个球,则摸出黑球的概率是()A. B. C. D.5.(4 分)下表记录了甲、乙、丙、丁四名射击运动员近来几次选拔赛成绩的平均数和方差:甲乙丙丁均匀数(环)9.149.159.149.15方差 6.6 6.8 6.7 6.6依据表中数据,要从中选择一名成绩好且发挥稳固的运动员参加竞赛,应选择()A.甲B.乙C.丙D.丁6.(4 分)如图,巷子左右双侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7 米,顶端距离地面 2.4 米,假如保持梯子底端地点不动,将梯子斜靠在右墙时,顶端距离地面 2 米,则巷子的宽度为()A.0.7 米B.1.5 米C.2.2 米D.2.4 米7.(4 分)均匀地向一个容器灌水,最后把容器注满,在灌水过程中,水面高度h 随时间 t 的变化规律如下图(图中OABC 为折线),这个容器的形状能够是()A.B.C.D.8.(4 分)在探究“尺规三均分角”这个数学名题的过程中,曾利用了如图.该图中,四边形 ABCD是矩形,E 是 BA 延伸线上一点, F 是 CE上一点,∠ACF=∠AFC,∠ FAE=∠FEA.若∠ ACB=21°,则∠ ECD的度数是()A.7° B.21°C.23°D.24°9.(4 分)矩形 ABCD的两条对称轴为坐标轴,点 A 的坐标为( 2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点 C 重合,则该抛物线的函数表达式变成()A.y=x2+8x+14 B.y=x2﹣8x+14 C. y=x2+4x+3D.y=x2﹣ 4x+310.( 4分)一块竹条编织物,先将其按如下图绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是()A.B.C.D.二、填空题(本大题共 6 小题,每题 5 分,共30 分)11.( 5 分)分解因式:x2y﹣ y=.12.( 5 分)如图,一块含45°角的直角三角板,它的一个锐角极点 A 在⊙O上,边 AB, AC分别与⊙O 交于点D,E,则∠ DOE的度数为.13.( 5 分)如图, Rt△ABC的两个锐角极点A,B 在函数 y=(x> 0)的图象上,AC∥x 轴, AC=2,若点 A 的坐标为( 2,2),则点 B 的坐标为.14.( 5 分)如图为某城市部分街道表示图,四边形ABCD为正方形,点G 在对角线 BD 上, GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为 B→A→G→E,小聪行走的路线为 B→A→D→E→F.若小敏行走的行程为 3100m,则小聪行走的路程为m.15.( 5 分)以 Rt△ABC的锐角极点 A 为圆心,适合长为半径作弧,与边 AB,AC各订交于一点,再分别以这两个交点为圆心,适合长为半径作弧,过两弧的交点与点A 作直线,与边 BC交于点 D.若∠ ADB=60°,点 D 到 AC的距离为 2,则 AB的长为.16.( 5 分)如图,∠ AOB=45°,点 M, N 在边 OA 上, OM=x,ON=x+4,点 P 是边 OB 上的点,若使点 P, M ,N 组成等腰三角形的点 P 恰巧有三个,则 x 的值是.三、解答题(本大题共8 小题,共 80 分)17.( 8 分)(1)计算:(2﹣π)0+| 4﹣3| ﹣.(2)解不等式: 4x+5≤2(x+1)18.( 8 分)某市规定了每个月用水18 立方米之内(含 18 立方米)和用水 18 立方米以上两种不一样的收费标准,该市的用户每个月应交水费y(元)是用水量x(立方米)的函数,其图象如下图.( 1)若某月用水量为18 立方米,则应交水费多少元?( 2)求当 x>18 时, y 对于 x 的函数表达式,若小敏家某月交水费81 元,则这个月用水量为多少立方米?19.( 8 分)为认识本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷检查(问卷检查表如下图),并用检查结果绘制了图 1,图 2 两幅统计图(均不完好),请依据统计图解答以下问题:(1)本次接受问卷检查的同学有多少人?补全条形统计图.(2)本校有七年级同学 800 人,预计双休日参加体育锻炼时间在 3 小时之内(不含 3 小时)的人数.20.( 8 分)如图,学校的实验楼对面是一幢教课楼,小敏在实验楼的窗口 C 测得教课楼顶部 D 的仰角为 18°,教课楼底部 B 的俯角为 20°,量得实验楼与教课楼之间的距离 AB=30m.(1)求∠ BCD的度数.(2)讨教课楼的高 BD.(结果精准到 0.1m,参照数据: tan20 °≈0.36,tan18 °≈ 0.32)21.( 10 分)某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑资料可建围墙的总长为50m.设饲养室长为x(m),占地面积为 y( m2).(1)如图 1,问饲养室长 x 为多少时,占地面积 y 最大?(2)如图 2,现要求在图中所示地点留 2m 宽的门,且仍使饲养室的占地面积最大,小敏说:“只需饲养室长比( 1)中的长多 2m 就行了.”请你经过计算,判断小敏的说法能否正确.22.( 12 分)定义:有一组邻边相等,而且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图 1,等腰直角四边形 ABCD,AB=BC,∠ABC=90°,①若 AB=CD=1, AB∥CD,求对角线 BD 的长.②若 AC⊥BD,求证: AD=CD,(2)如图 2,在矩形 ABCD中,AB=5,BC=9,点 P 是对角线 BD 上一点,且 BP=2PD,过点 P 作直线分别交边 AD, BC于点 E,F,使四边形 ABFE是等腰直角四边形,求 AE 的长.23(.12 分)已知△ ABC,AB=AC,D 为直线 BC上一点,E 为直线 AC上一点,AD=AE,设∠ BAD=α,∠ CDE=β.( 1)如图,若点 D 在线段 BC上,点 E 在线段 AC上.①假如∠ ABC=60°,∠ ADE=70°,那么α= °,β= °,②求α,β之间的关系式.(2)能否存在不一样于以上②中的α,β之间的关系式?若存在,求出这个关系式(求出一个即可);若不存在,说明原因.24.( 14 分)如图 1,已知 ?ABCD,AB∥x 轴, AB=6,点 A 的坐标为( 1,﹣ 4),点 D 的坐标为(﹣ 3,4),点 B 在第四象限,点 P 是?ABCD边上的一个动点.( 1)若点 P 在边 BC上, PD=CD,求点 P 的坐标.( 2)若点 P 在边 AB,AD 上,点 P 对于坐标轴对称的点 Q 落在直线 y=x﹣ 1 上,求点 P 的坐标.( 3)若点 P 在边 AB,AD,CD 上,点 G 是 AD 与 y 轴的交点,如图 2,过点 P作 y 轴的平行线 PM,过点 G 作 x 轴的平行线 GM,它们订交于点 M ,将△ PGM 沿直线PG翻折,当点M 的对应点落在座标轴上时,求点P 的坐标.(直接写出答案)2017 年浙江省绍兴市中考数学试卷参照答案与试题分析一、选择题(本大题共10 小题,每题 4 分,共 40 分)1.(4 分)(2017?绍兴)﹣ 5 的相反数是()A.B. 5C.﹣D.﹣ 55,【解答】解:﹣ 5 的相反数是应选: B.2.(4 分)(2017?绍兴)研究表示,可燃冰是一种代替石油的新式洁净能源,在我国某海疆已探明的可燃冰储存量达0 立方米,此中数字 0 用科学记数法可表示为()A.15×1010 B.0.15×1012 C. 1.5× 1011 D.1.5×1012【解答】解: 0=1.5×1011,应选: C.3.(4 分)(2017?绍兴)如图的几何体由五个同样的小正方体搭成,它的主视图是()A.B.C.D.【解答】解:从正面看第一层是三个小正方形,第二层左侧一个小正方形,应选: A.4.(4 分)(2017?绍兴)在一个不透明的袋子中装有 4 个红球和 3 个黑球,它们除颜色外其余均同样,从中随意摸出一个球,则摸出黑球的概率是()A.B.C.D.【解答】解:∵在一个不透明的袋子中装有除颜色外其余均同样的 4 个红球和3个黑球,∴从中随意摸出一个球,则摸出黑球的概率是.应选 B.5.(4 分)(2017?绍兴)下表记录了甲、乙、丙、丁四名射击运动员近来几次选拔赛成绩的均匀数和方差:甲乙丙丁均匀数(环)9.149.159.149.15方差 6.6 6.8 6.7 6.6依据表中数据,要从中选择一名成绩好且发挥稳固的运动员参加竞赛,应选择()A.甲B.乙C.丙D.丁【解答】解:丁的均匀数最大,方差最小,成绩最稳定,因此选丁运动员参加竞赛.应选 D.6.(4 分)(2017?绍兴)如图,巷子左右双侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为 0.7 米,顶端距离地面 2.4 米,假如保持梯子底端地点不动,将梯子斜靠在右墙时,顶端距离地面 2 米,则巷子的宽度为()A.0.7 米B.1.5 米C.2.2 米D.2.4 米【解答】解:在 Rt△ACB中,∵∠ ACB=90°,BC=0.7米, AC=2.4米,∴AB2=0.72+2.42=6.25.在 Rt△A′BD中,∵∠ A′DB=90,°A′D=2米, BD2+A′D2′2,′ =A B∴BD2 +22=6.25,∴BD2 =2.25,∵BD>0,∴BD=1.5米,∴CD=BC+BD=0.7+1.5=2.2米.应选 C.7.(4 分)(2017?绍兴)均匀地向一个容器灌水,最后把容器注满,在灌水过程中,水面高度h 随时间 t 的变化规律如下图(图中OABC为折线),这个容器的形状能够是()A.B.C.D.【解答】解:灌水量必定,函数图象的走势是稍陡,平,陡;那么速度就相应的变化,跟所给容器的粗细相关.则相应的摆列次序就为D.应选: D.8.(4 分)(2017?绍兴)在探究“尺规三均分角”这个数学名题的过程中,曾利用了如图.该图中,四边形 ABCD是矩形,E 是 BA 延伸线上一点, F 是 CE上一点,∠ ACF=∠ AFC,∠ FAE=∠FEA.若∠ ACB=21°,则∠ ECD的度数是()A.7° B.21°C.23°D.24°【解答】解:∵四边形 ABCD是矩形,∴∠ D=90°,AB∥CD,AD∥BC,∴∠ FEA=∠ECD,∠ DAC=∠ACB=21°,∵∠ ACF=∠AFC,∠ FAE=∠FEA,∴∠ ACF=2∠ FEA,设∠ ECD=x,则∠ ACF=2x,∴∠ ACD=3x,在Rt△ACD中,3x+21°=90°,解得: x=23°;应选: C.9.( 4 分)(2017?绍兴)矩形 ABCD的两条对称轴为坐标轴,点A 的坐标为( 2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点 A 重合,此时抛物线的函数表达式为 y=x2,再次平移透明纸,使这个点与点 C 重合,则该抛物线的函数表达式变成()A.y=x2+8x+14 B.y=x2﹣8x+14 C. y=x2+4x+3D.y=x2﹣ 4x+3【解答】解:∵矩形 ABCD的两条对称轴为坐标轴,∴矩形 ABCD对于坐标原点对称,∵A 点 C 点是对角线上的两个点,∴ A 点、 C 点对于坐标原点对称,∴ C 点坐标为(﹣ 2,﹣ 1);∴抛物线由 A 点平移至 C 点,向左平移了 4 个单位,向下平移了 2 个单位;∵抛物线经过 A 点时,函数表达式为y=x2,∴抛物线经过 C 点时,函数表达式为y=(x+4)2﹣2=x2+8x+14,应选 A.10.( 4 分)(2017?绍兴)一块竹条编织物,先将其按如下图绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是()A.B.C.D.【解答】解:先将其按如下图绕直线MN 翻转 180°,再将它按逆时针方向旋转 90°,所得的竹条编织物是 B,应选 B.二、填空题(本大题共 6 小题,每题 5 分,共 30 分)11.( 5 分)(2017?绍兴)分解因式: x2y﹣ y= y(x+1)(x﹣ 1).【解答】解: x2y﹣y,=y(x2﹣1),=y(x+1)( x﹣ 1),故答案为: y( x+1)( x﹣ 1).12.( 5 分)( 2017?绍兴)如图,一块含 45°角的直角三角板,它的一个锐角极点 A 在⊙ O 上,边 AB,AC分别与⊙ O 交于点 D,E,则∠ DOE的度数为 90° .【解答】解:∵∠ A=45°,∴∠ DOE=2∠A=90°.故答案为: 90°.13.(5 分)(2017?绍兴)如图,Rt△ABC的两个锐角极点A,B 在函数 y=(x> 0)的图象上, AC∥ x 轴, AC=2,若点 A 的坐标为( 2,2),则点 B 的坐标为(4,1).【解答】解:∵点 A(2,2)在函数 y=(x> 0)的图象上,∴2=,得 k=4,∵在 Rt△ ABC中, AC∥ x 轴, AC=2,∴点 B 的横坐标是 4,∴y==1,∴点 B 的坐标为( 4, 1),故答案为:( 4, 1).14.(5 分)(2017?绍兴)如图为某城市部分街道表示图,四边形 ABCD为正方形,点 G在对角线 BD上,GE⊥CD,GF⊥ BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为 B→A→D→E→F.若小敏行走的行程为 3100m,则小聪行走的行程为 4600 m.【解答】解:连结 GC,∵四边形 ABCD为正方形,因此 AD=DC,∠ ADB=∠CDB=45°,∵∠ CDB=45°,GE⊥ DC,∴△ DEG是等腰直角三角形,∴DE=GE.在△ AGD和△ GDC中,∴△ AGD≌△ GDC∴AG=CG在矩形 GECF中, EF=CG,∴EF=AG.∵BA+AD+DE+EF﹣ BA﹣AG﹣GE=AD=1500m.∵小敏共走了 3100m,∴小聪行走的行程为3100+1500=4600(m)故答案为: 460015.(5 分)(2017?绍兴)以 Rt△ABC的锐角极点 A 为圆心,适合长为半径作弧,与边 AB,AC 各订交于一点,再分别以这两个交点为圆心,适合长为半径作弧,过两弧的交点与点 A 作直线,与边 BC交于点 D.若∠ ADB=60°,点 D 到 AC的距离为 2,则 AB 的长为 2 .【解答】解:如图,作 DE⊥AC于 E.由题意 AD 均分∠ BAC,∵DB⊥AB,DE⊥AC,∴DB=DE=2,在 Rt△ADB 中,∵∠ B=90°,∠ BDA=60°,BD=2,∴AB=BD?tan60°=2,故答案为 216.(5 分)(2017?绍兴)如图,∠ AOB=45°,点 M,N 在边 OA 上,OM=x,ON=x+4,点 P 是边 OB 上的点,若使点 P,M,N 组成等腰三角形的点 P 恰巧有三个,则 x 的值是 x=0 或 x=4﹣ 4 或 4<x<4 .【解答】解:分三种状况:①如图 1,当 M 与 O 重合时,即 x=0 时,点 P 恰巧有三个;②如图 2,以 M 为圆心,以 4 为半径画圆,当⊙ M 与 OB 相切时,设切点为C,⊙M 与 OA交于 D,∴MC⊥ OB,∵∠ AOB=45°,∴△ MCO 是等腰直角三角形,∴MC=OC=4,∴OM=4,当 M 与 D 重合时,即 x=OM﹣ DM=4﹣4 时,同理可知:点 P 恰巧有三个;③如图 3,取 OM=4,以 M 为圆心,以 OM 为半径画圆,则⊙ M 与 OB 除了 O 外只有一个交点,此时 x=4,即以∠ PMN 为顶角,MN 为腰,切合条件的点 P 有一个,以 N 圆心,以 MN 为半径画圆,与直线 OB 相离,说明此时以∠ PNM 为顶角,以 MN 为腰,切合条件的点 P 不存在,还有一个是以 NM为底边的切合条件的点P;点 M 沿 OA 运动,到 M1时,发现⊙ M1与直线 OB 有一个交点;∴当 4<x<4 时,圆 M 在挪动过程中,则会与 OB 除了 O 外有两个交点,知足点P 恰巧有三个;综上所述,若使点P,M, N 组成等腰三角形的点 P 恰巧有三个,则x的值是:x=0 或 x=4﹣4 或 4.故答案为: x=0 或 x=4﹣4 或 4.三、解答题(本大题共8 小题,共 80 分)17.( 8 分)(2017?绍兴)( 1)计算:(2﹣π)0+| 4﹣3| ﹣.(2)解不等式: 4x+5≤2(x+1)【解答】解:(1)原式=1 =﹣3;(2)去括号,得 4x+5≤2x+2移项归并同类项得, 2x≤﹣ 3解得 x.18.( 8 分)(2017?绍兴)某市规定了每个月用水 18 立方米之内(含18 立方米)和用水 18 立方米以上两种不一样的收费标准,该市的用户每个月应交水费y(元)是用水量 x(立方米)的函数,其图象如下图.( 1)若某月用水量为 18 立方米,则应交水费多少元?( 2)求当 x>18 时, y 对于 x 的函数表达式,若小敏家某月交水费81 元,则这个月用水量为多少立方米?【解答】解:(1)由纵坐标看出,某月用水量为18 立方米,则应交水费18 元;(2)由 81 元> 45 元,得用水量超出 18 立方米,设函数分析式为 y=kx+b ( x≥18),∵直线经过点( 18,45)(28,75),∴,解得,∴函数的分析式为 y=3x﹣9 (x≥18),当 y=81 时, 3x﹣9=81,解得 x=30,答:这个月用水量为 30 立方米.19.(8 分)(2017?绍兴)为认识本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷检查(问卷检查表如下图),并用检查结果绘制了图1,图 2 两幅统计图(均不完好),请依据统计图解答以下问题:(1)本次接受问卷检查的同学有多少人?补全条形统计图.(2)本校有七年级同学 800 人,预计双休日参加体育锻炼时间在 3 小时之内(不含 3 小时)的人数.【解答】解:(1)40÷25%=160(人)答:本次接受问卷检查的同学有 160 人;D 组人数为: 160×18.75%=30(人)统计图补全如图:(2) 800×=600(人)答:预计双休日参加体育锻炼时间在 3 小时之内(不含 3 小时)的人数为 600 人.20.( 8 分)(2017?绍兴)如图,学校的实验楼对面是一幢教课楼,小敏在实验楼的窗口 C 测得教课楼顶部 D 的仰角为 18°,教课楼底部 B 的俯角为 20°,量得实验楼与教课楼之间的距离AB=30m.(1)求∠ BCD的度数.(2)讨教课楼的高 BD.(结果精准到 0.1m,参照数据: tan20 °≈0.36,tan18 °≈ 0.32)【解答】解:(1)过点 C 作 CE⊥BD,则有∠ DCE=18°,∠ BCE=20°,∴∠ BCD=∠DCE+∠ BCE=18°+20°=38°;(2)由题意得: CE=AB=30m,在 Rt△CBE中, BE=CE?tan20°≈10.80m,在Rt△CDE中, DE=CD?tan18°≈ 9.60m,∴教课楼的高 BD=BE+DE=10.80+9.60≈20.4m,则教课楼的高约为 20.4m.21.( 10 分)(2017?绍兴)某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑资料可建围墙的总长为50m.设饲养室长为 x(m),占地面积为y( m2).(1)如图 1,问饲养室长 x 为多少时,占地面积 y 最大?(2)如图 2,现要求在图中所示地点留 2m 宽的门,且仍使饲养室的占地面积最大,小敏说:“只需饲养室长比( 1)中的长多 2m 就行了.”请你经过计算,判断小敏的说法能否正确.【解答】解:(1)∵ y=x?=﹣( x﹣ 25)2+,∴当 x=25 时,占地面积最大,即饲养室长 x 为 25m 时,占地面积y 最大;(2)∵ y=x?=﹣( x﹣26)2+338,∴当 x=26 时,占地面积最大,即饲养室长 x 为 26m 时,占地面积 y 最大;∵ 26﹣25=1≠2,∴小敏的说法不正确.22.( 12 分)(2017?绍兴)定义:有一组邻边相等,而且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图 1,等腰直角四边形 ABCD,AB=BC,∠ABC=90°,①若 AB=CD=1, AB∥CD,求对角线 BD 的长.②若 AC⊥BD,求证: AD=CD,(2)如图 2,在矩形 ABCD中,AB=5,BC=9,点 P 是对角线 BD 上一点,且 BP=2PD,过点 P 作直线分别交边 AD, BC于点 E,F,使四边形 ABFE是等腰直角四边形,求 AE 的长.【解答】解:(1)①∵ AB=AC=1, AB∥CD,∴S四边形ABCD是平行四边形,∵ AB=BC,∴四边形 ABCD是菱形,∵∠ ABC=90°,∴四边形 ABCD是正方形,∴BD=AC==.(2)如图 1 中,连结 AC、BD.∵ AB=BC,AC⊥BD,∴∠ ABD=∠CBD,∵BD=BD,∴△ ABD≌△ CBD,∴AD=CD.(2)若 EF⊥ BC,则 AE≠EF,BF≠EF,∴四边形 ABFE表示等腰直角四边形,不切合条件.若 EF与 BC不垂直,①当 AE=AB时,如图 2 中,此时四边形 ABFE是等腰直角四边形,∴ AE=AB=5.②当 BF=AB时,如图 3 中,此时四边形 ABFE是等腰直角四边形,∴ BF=AB=5,∵ DE∥BF,∴ DE:BF=PD:PB=1:2,∴ DE=2.5,∴AE=9﹣ 2.5=6.5,综上所述,知足条件的AE的长为 5 或 6.5.23.( 12 分)(2017?绍兴)已知△ ABC,AB=AC,D 为直线 BC上一点, E 为直线AC上一点, AD=AE,设∠ BAD=α,∠ CDE=β.( 1)如图,若点 D 在线段 BC上,点 E 在线段 AC上.①假如∠ ABC=60°,∠ ADE=70°,那么α= 20 °,β= 10 °,②求α,β之间的关系式.(2)能否存在不一样于以上②中的α,β之间的关系式?若存在,求出这个关系式(求出一个即可);若不存在,说明原因.【解答】解:(1)①∵ AB=AC,∠ ABC=60°,∴∠ BAC=60°,∵AD=AE,∠ ADE=70°,∴∠ DAE=180°﹣2∠ADE=40°,∴α=∠BAD=60°﹣40°=20°,∴∠ ADC=∠BAD+∠ABD=60°+20°=80°,∴β=∠CDE=∠ADC﹣∠ ADE=10°,故答案为: 20, 10;②设∠ ABC=x,∠ AED=y,∴∠ ACB=x,∠ AED=y,在△ DEC中, y=β+x,在△ ABD中,α+x=y+β=β+x+β,∴α=2β;(2)①当点 E 在 CA 的延伸线上,点 D 在线段 BC上,如图 1设∠ ABC=x,∠ ADE=y,∴∠ ACB=x,∠ AED=y,在△ ABD中, x+α=β﹣ y,在△ DEC中, x+y+β=180,°∴α=2β﹣ 180°,②当点 E在 CA的延伸线上,点 D 在 CB的延伸线上,如图 2,同①的方法可得α=180﹣°2β.24.( 14 分)( 2017?绍兴)如图 1,已知 ?ABCD,AB∥x 轴, AB=6,点 A 的坐标为( 1,﹣ 4),点 D 的坐标为(﹣ 3, 4),点 B 在第四象限,点 P 是?ABCD边上的一个动点.(1)若点 P 在边 BC上, PD=CD,求点 P 的坐标.(2)若点 P 在边 AB,AD 上,点 P 对于坐标轴对称的点 Q 落在直线 y=x﹣ 1 上,求点 P 的坐标.(3)若点 P 在边 AB,AD,CD 上,点 G 是 AD 与 y 轴的交点,如图 2,过点 P作 y 轴的平行线 PM,过点 G 作 x 轴的平行线 GM,它们订交于点 M ,将△ PGM 沿直线PG翻折,当点M 的对应点落在座标轴上时,求点P 的坐标.(直接写出答案)【解答】解:(1)∵ CD=6,∴点 P 与点 C重合,∴点 P 坐标为( 3,4).(2)①当点 P 在边 AD 上时,∵直线 AD 的分析式为 y=﹣2x﹣2,设 P(a,﹣ 2a﹣ 2),且﹣ 3≤a≤1,若点 P 对于 x 轴的对称点 Q1( a, 2a+2)在直线 y=x﹣1 上,∴ 2a+2=a﹣ 1,解得 a=﹣3,此时 P(﹣ 3, 4).若点 P 对于 y 轴的对称点 Q3(﹣ a,﹣ 2a﹣ 2)在直线 y=x﹣1 上时,∴﹣ 2a﹣2=﹣a﹣1,解得 a=﹣ 1,此时 P(﹣ 1, 0)②当点 P 在边 AB 上时,设 P(a,﹣ 4)且 1≤ a≤ 7,若等P 对于 x 轴的对称点 Q2( a, 4)在直线 y=x﹣1 上,∴4=a﹣1,解得 a=5,此时 P(5,﹣ 4),若点 P 对于 y 轴的对称点 Q4(﹣ a,﹣ 4)在直线 y=x﹣ 1 上,∴﹣ 4=﹣ a﹣1,解得 a=3,此时 P(3,﹣ 4),综上所述,点 P 的坐标为(﹣ 3,4)或(﹣ 1,0)或( 5,﹣ 4)或( 3,﹣ 4).( 3)①如图 1 中,当点 P 在线段 CD上时,设 P(m,4).在 Rt△PNM′中,∵ PM=PM′=6,PN=4,∴NM′==2,在 Rt△OGM′中,∵ OG2+OM′22,=GM′∴22+( 2﹣ m)2 =m2,解得 m=﹣,∴P(﹣, 4)依据对称性可知, P(, 4)也知足条件.②如图 2 中,当点 P 在 AB 上时,易知四边形PMGM′是正方形,边长为2,此时P(2,﹣ 4).③如图 3 中,当点 P 在线段 AD 上时,设 AD 交 x 轴于 R.易证∠M′RG=∠M′GR,推出 M′R=M′G=GM,设 M′R=M′G=GM=x.∵直线 AD 的分析式为 y=﹣2x﹣2,∴R(﹣ 1,0),在 Rt△OGM′中,有 x2=22+(x﹣1)2,解得 x=,∴ P(﹣, 3).点 P 坐标为( 2,﹣ 4)或(﹣, 3)或(﹣, 4)或(, 4).参加本试卷答题和审题的老师有:2300680618;gbl210;sjzx;gsls;弯弯的小河;家有子女;499807835;王学峰;HLing;蓝月梦;CJX;zgm666;463454002;tcm123;fangcao; sks; HJJ;星月相随(排名不分先后)2017年 7月 25日。
(高清版)2017年浙江省绍兴、义乌市中考数学试卷
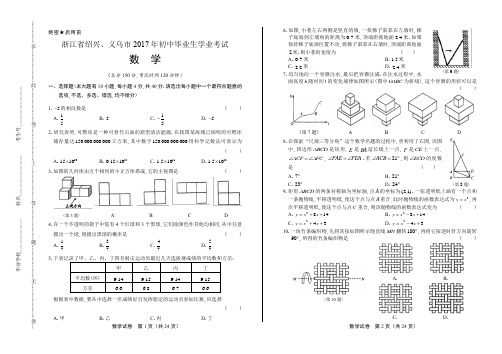
数学试卷 第1页(共24页) 数学试卷 第2页(共24页)绝密★启用前浙江省绍兴、义乌市2017年初中毕业生学业考试数 学(总分150分,考试时间120分钟)一、选择题(本大题有10小题,每小题4分,共40分.请选出每小题中一个最符合题意的选项,不选、多选、错选,均不给分) 1.5-的相反数是( )A .15B .5C .15-D .5-2.研究表明,可燃冰是一种可替代石油的新型清洁能源.在我国某海域已探明的可燃冰储存量达150000000000立方米,其中数字150000000000用科学记数法可表示为( )A .101510⨯B .120.1510⨯C .111.510⨯D .121.510⨯ 3.如图的几何体由五个相同的小正方体搭成,它的主视图是( )(第3题)ABCD4.在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其他均相同,从中任意摸出一个球,则摸出黑球的概率是( )A .17B .37C .47D .575.根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )A .甲B .乙C .丙D .丁6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米.则小巷的宽度为( ) A .0.7米 B .1.5米C .2.2米D .2.4米7.均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h 随时间t 的变化规律如图所示(图中OABC 为折线),这个容器的形状可以是 ( )(第7题)ABCD8.在探索“尺规三等分角”这个数学名题的过程中,曾利用了右图,该图中,四边形ABCD 是矩形,E 是BA 延长线上一点,F 是CE 上一点,ACF AFC ∠=∠,FAE FEA ∠=∠.若21ACB ∠=︒,则ECD ∠的度数是( )A .7︒B .21︒C .23︒D .24︒9.矩形ABCD 的两条对称轴为坐标轴,点A 的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A 重合,此时抛物线的函数表达式为2y x =,再次平移透明纸,使这个点与点C 重合,则该抛物线的函数表达式变为( )A .2814y x x =++B.2814yxx=-+C .243y x x =++D .243y x x =-+10.一块竹条编织物,先将其按如图所示绕直线MN 翻转180︒,再将它按逆时针方向旋转90︒,所得的竹条编织物是( )(第10题)A .B .C .D .(第6题)(第8题) 毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共24页) 数学试卷 第4页(共24页)二、填空题(本大题有6小题,每小题5分,共30分) 11.分解因式:2x y y -= .12.如图,一块含45︒角的直角三角板,它的一个锐角顶点A 在O e 上,边AB ,AC 分别与O e 交于点D ,E .则DOE ∠的度数为 .(第12题)(第13题)(第14题)13.如图,Rt ABC △的两个锐角顶点A ,B 在函数(0)ky x x=>的图象上,AC x ∥轴,2AC =.若点A 的坐标为(2,2),则点B 的坐标为 .14.如图为某城市部分街道示意图,四边形ABCD 为正方形,点G 在对角线BD 上,GE CD ⊥,GF BC ⊥,1500m AD =,小敏行走的路线为B A G E →→→,小聪行走的路线为B A D E F →→→→.若小敏行走的路程为3100m ,则小聪行走的路程为 m .15.以Rt ABC △的锐角顶点A 为圆心,适当长为半径作弧,与边AB ,AC 各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A 作直线,与边BC 交于点D .若60ADB ∠=︒,点D 到AC 的距离为2,则AB 的长为 .16.如图,45AOB ∠=︒,点M ,N 在边OA 上,OM x =,4ON x =+,点P 是边OB 上的点.若使点P ,M ,N 构成等腰三角形的点P 恰好有三个,则x 的值是 .三、解答题(本大题有8小题,共80分.解答需写出必要的文字说明、演算步骤或证明过程)17.(本题8分)(1)计算:0π)|4+-. (2)解不等式:452(1)x x ++≤.18.(本题8分)某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y (元)是用水量x (立方米)的函数,其图象如图所示.(1)若某月用水量18立方米,则应交水费多少元? (2)求当18x >时,y 关于x 的函数表达式.若小敏家某月交水费81元,则这个月用水量为多少立方米?19.(本题8分)为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如下图所示),并用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题.七年级部分同学双休日参加 体育锻炼时间的条形统计图图1七年级部分同学双休日参加 体育锻炼时间的扇形统计图图2(1)本次接受问卷调查的同学有多少人?补全条形统计图.(2)本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.(第16题)数学试卷 第5页(共24页) 数学试卷 第6页(共24页)20.(本题8分)如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C 测得教学楼顶部D 的仰角为18︒,教学楼底部B 的俯角为20︒,量得实验楼与教学楼之间的距离30cm AB =. (1)求BCD ∠的度数. (2)求教学楼的高BD .(结果精确到0.1m .参考数据:tan200.36︒≈,tan180.32︒≈)21.(本题10分)某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50m .设饲养室长为(m)x ,占地面积为2(m )y .(1)如图1,问饲养室长x 为多少时,占地面积y 最大? (2)如图2,现要求在图中所示位置留2m 宽的门,且仍使饲养室的占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m 就行了.”请你通过计算,判断小敏的说法是否正确.图1图222.(本题12分)定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图1,等腰直角四边形ABCD ,AB BC =,90ABC ∠=︒.①若1AB CD ==,AB CD ∥,求对角线BD 的长;②若AC BD ⊥,求证:AD CD =. (2)如图2,在矩形ABCD 中,5AB =,9BC =,点P 是对角线BD 上一点,且2BP PD =,过点P 作直线分别交边AD ,BC 于点E ,F ,使四边形ABFE 是等腰直角四边形.求AE 的长.图1图223.(本题12分)已知ABC △,AB AC =,D 为直线BC 上一点,E 为直线AC 上一点,AD AE =,设BAD α∠=,CDE β∠=. (1)如图,若点D 在线段BC 上,点E 在线段AC 上.①如果60ABC ∠=︒,70ADE ∠=︒,那么α= ︒,β= ︒; ②求α,β之间的关系式. (2)是否存在不同于以上②中的α,β之间的关系式?若存在,求出这个关系式(求出一个即可);若不存在,说明理由.24.(本题14分)如图1,已知□ABCD ,AB x ∥轴,6AB =,点A 的坐标为(1,4)-,点D 的坐标为(3,4)-,点B 在第四象限,点P 是□ABCD 边上的一个动点. (1)若点P 在边BC 上,PD CD =,求点P 的坐标.(2)若点P 在边AB ,AD 上,点P 关于坐标轴对称的点Q 落在1y x =-上,求点P 的坐标.(3)若点P 在边AB ,AD ,CD 上,点G 是AD 与y 轴的交点,如图2,过点P 作y 轴的平行线PM ,过点G 作x 轴的平行线GM ,它们相交于点M ,将PGM △沿直线PG 翻折,当点M 的对应点落在坐标轴上时,求点P 的坐标(直接写出答案).图1图2-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共24页) 数学试卷 第8页(共24页)浙江省绍兴、义乌市2017年初中毕业生学业考试数学答案解析一、选择题 1.【答案】B【解析】5-的相反数是(5)5--=.故选B .【提示】一个数的相反数是在它的前面添加“-”,并化简. 【考点】相反数 2.【答案】C【解析】150000000000一共有12位数,那么12111n =-=,则11150000000000 1.510=⨯,故选:C .【提示】用科学记数法表示数:把一个数字记为10na ⨯的形式(11||0a ≤<,n 为整数).表数学试卷 第9页(共24页) 数学试卷 第10页(共24页)【解析】从正面看到的图形是【考点】解直角三角形的应用 7.【答案】D【解析】从折线图可得,倾斜度:OB OA BC <<,表示水上升的高度的速度:OB OA BC <<,则OB 段所在的容器的底面积最大,OA 段的次之,BC 段的最小,即容器的分布是中等长方体,最大长方体,最小长方体,所以符合这一情况的只有D .故选D .【提示】从折线图的倾斜度出发,根据注水的速度不变,而容器水里的高度除了与时间有关,且与容器里的底面积有关,则底面积越大的,水的高度增加的越慢. 【考点】函数的图象 8.【答案】C【解析】在矩形ABCD 中,AB CD ∥,90BCD ∠=︒,所以FEA ECD ∠=∠,9069ACD ACB ∠=︒-∠=︒,因为ACF AFC ∠=∠,FAE FEA ∠=∠,AFC FAE FEA ∠=∠+∠,所以2ACF FEA ∠=∠,则369ACD ACF ECD ECD ∠=∠+∠=∠=︒,所以23ECD ∠=︒故选C .【提示】由矩形的性质不难得到FEA ECD ∠=∠,9069ACD ACB ∠=︒-∠=︒;根据三角形的外角性质及已知条件不难得出2ACF FEA ∠=∠,即可得ACD ∠被线CE 三等分,则可解出ECD ∠.【考点】三角形的外角性质,矩形的性质 9.【答案】A【解析】如图,(2,1)A ,则可得(21)C --,.由(2,1)A 到(21)C --,,需要向左平移4个单位,向下平移2个单位,则抛物线的函数表达式为2y x =,经过平移与为22(4)2814y x x x =+-=++,故选A .数学试卷 第11页(共24页) 数学试卷 第12页(共24页)【提示】题中的意思就是将抛物线2y x =平移后,点A 平移到了点C ,由A 的坐标不难得出C 的坐标,由平移的性质可得点A 怎样平移到点C ,那么抛物线2y x =,就怎样平移到新的抛物线. 【考点】二次函数的图象 10.【答案】B【解析】绕MN 翻折180︒后,是下面的图形:再逆时针旋转90︒,可得故选B .【提示】绕MN 翻折180︒,本来排在第一行的横纸条排在了第5条,而且5根竖条,分别叠放在它的下、上、上、下、上面,通过这样的分析,确认五根横条的位置,再将其逆时针旋转90︒可得答案. 【考点】翻折变换(折叠问题) 二、填空题11.【答案】(1)(1)y x x +-【解析】原式2(1)(1)(1)y x y x x =-=+- 故答案为(1)(1)y x x +-.【提示】观察整式可得,应选提取公因式y ,再运用平方差公式分解因式.【解析】根据题中的语句作图可得下面的图,过点D作于E,此时,则.交OB两点和;数学试卷第13页(共24页)数学试卷第14页(共24页)此时,数学试卷第15页(共24页)数学试卷第16页(共24页)数学试卷第17页(共24页) 数学试卷 第18页(共24页)204060++所以182038BCD DCE BCE ∠=∠+∠=︒+︒=︒.所以ABDCBD≅△△,所以AD CD=.(2)解:若EF与BC垂直,则AE EF BF EF≠≠,,所以四边形ABFE不是等腰直角四边形,不符合条件;若EF与BC不垂直,①当AE AB=时,如图2,此时四边形ABFE是等腰直角四边形.所以5AE AB==②当BF AB=时,如图3,此时四边形ABFE是等腰直角四边形.所以5BF AB==,因为DE BF∥,所以~PED PFB△△,所以:12DE BF PD PB==::,所以9 2.5 6.5AE=-=综上所述,AE的长为5或6.5【提示】(1)①由1AB CD==,AB CD∥,根据“有一组对边平行且相等的四边形是平行四边形”可得四边形ABCD是平行四边形.由邻边相等AB BC=,有一直角90ABC∠=度,在ABD△中,,所以.数学试卷第19页(共24页)数学试卷第20页(共24页)数学试卷第21页(共24页)数学试卷第22页(共24页)则或;数学试卷 第23页(共24页) 数学试卷 第24页(共24页)方形,所以,则.⎛⎫⎛⎫关于y 轴对称时,相反;)将得到的点Q 的坐标代入直线1y x =-,即可解答; (3)在不同边上,根据图象,点M 翻折后,点M '落在x 轴还是y 轴,可运用相似求解.【考点】平行四边形的性质,翻折变换(折叠问题)。
2017年中考数学浙江省绍兴市届中考数学试卷[解析版]
![2017年中考数学浙江省绍兴市届中考数学试卷[解析版]](https://img.taocdn.com/s3/m/79df6d1cc850ad02de8041d1.png)
2017年浙江省绍兴市中考数学试卷一、选择题1、-5的相反数是()A 、B、5 C 、D、-52、研究表明,可燃冰是一种可替代石油的新型清洁能源。
在我国某海域已探明的可燃冰储存量达150 000 000 000立方米,其中数字150 000 000 000用科学记数法可表示为()A、15×1010B、0.15×1012C、1.5×1011D、1.5×10123、如图的几何体由五个相同的小正方体搭成,它的主视图是()A 、B 、C 、D 、4、在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其它均相同,从中任意摸出一个球,则摸出黑球的概率是()A 、B 、C 、D 、5、下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:()A、甲B、乙C、丙D、丁6、如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米.则小巷的宽度为()A、0.7米B、1.5米C、2.2米D、2.4米7、均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是()A、B、C、D、8、在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA。
若∠ACB=21°,则∠ECD的度数是()A、7°B、21°C、23°D、24°9、矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为()A、y=x2+8x+14B、y=x2-8x+14C、y=x2+4x+3D、y=x2-4x+310、一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是()A、B、C、D、二、填空题11、分解因式:=________.12、如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E.则∠DOE的度数为________.13、如图,Rt△ABC的两个锐角顶点A,B在函数y= (x>0)的图象上,AC//x轴,AC=2.若点A的坐标为(2,2),则点B的坐标为________.14、如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪得行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为________m.15、以Rt△ABC的锐角顶点A为圆心,适当长为半径作弧,与边AB,AC各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A作直线,与边BC交于点D.若∠ADB=60°,点D 到AC的距离为2,则AB的长为________.16、如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N 构成等腰三角形的点P恰好有三个,则x的值是________.三、解答题17、计算题。
浙江省绍兴市2017年数学中考试题

浙江省绍兴市2017年中考数学试题第Ⅰ卷(共60分)一、选择题:本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 的相反数是()A. B. C. D.2. 研究表明,可燃烧是一种可代替石油的新型清洁能源,在我国某海域已探明的可燃烧存储量达立方米,其中数字用科学记数法可表示为()A. B. C. D.3. 如图的几何体由五个相同的小正方体搭成,它的主观图是()A. B. C. D.4. 在一个不透明的袋子中装有个红球和个黑球,它们除颜色外其它均相同,从中任意摸出一个球,則摸出黑球的概率是()A. B. C. D.5. 下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:甲乙丙丁平均数(环)方差根据表中数据,要从中选择―名成绩好且友挥稳定的运动员参加比赛,应选择()A.甲 B.乙 C. 丙 D.丁6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为米,顶端距离地面米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面米.则小巷的宽度为()A.米 B.米 C.米 D.米7. 均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度随时变化规律如图所示(图中为折线),这个容器的形状可以是()5-15515-5-150000000000150000000000101510⨯120.1510⨯111.510⨯121.510⨯43173747579.149.159.149.156.6 6.8 6.7 6.60.72.420.7 1.5 2.2 2.4h tOABCA .B . C. D .8. 在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形是矩形,是延长线上一点,是上一点,.若,则的度数是( )A . B . C. D .9.矩形的两条对称轴为坐标轴,点的坐标为.一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点重合,此时抛物线的函数表达式为,再次平移透明纸,使这个点与点重合,则该抛物线的函数表达式变为 ( )A .B .C. D .10. 一块竹条编织物,先将其按如图所示绕直线翻转,再将它按逆时针方向旋转,所得的竹条编织物是( )A . B . C. D .第Ⅱ卷(共90分)二、填空题(每题5分,满分30分,将答案填在答题纸上)ABCD E BA F CE ,ACF AFC FAE FEA ∠=∠∠=∠21ACB ∠=ECD ∠7 21 23 24ABCD A ()2,1A 2y x =C 2814y x x =++2814y x x =-+243y x x =++243y x x =-+MN 180 9011.分解因式: .12.如图,一块含角的直角三角板,它的一个锐角顶点在上,边分别与交于点,则的度数为 .13.如图,的两个锐角顶点在函数的图象上,轴,.若点的坐标为,则点的坐标为 .14.如图为某城市部分街道示意图,四边形为正方形,点在对角线上,,小敏行走的路线为,小聪行走的路线为.若小敏行走的路程为,则小聪行走的路程为 .15.以的锐角顶点为圆心,适当长为半径作弧,与边各相交于一点,再分别以两个交点为圆心,适当长为半径作弧,过两弧的交点与点作直线,与边交于点.若,点到的距离为,则的长为 .16.如图,,点在边上,,点是边上的点.若使点构成等腰三角形的点恰好有三个,则的值是.2x y y -=45 A O ,AB AC O ,D E DOE ∠R ∆t ABC ,A B ()0k y x x=>//AC x 2AC =A ()2,2B ABCD G BD ,,1500GE CD GF BC AD m ⊥⊥=B A G E →→→B A D E F →→→→3100m m R ∆t ABC A ,AB AC A BC D 60ADB ∠=D AC 2AB 45AOB ∠= ,M N OA ,4OM x ON x ==+P OB ,,P M N P x三、解答题(本大题共8小题,17—20小题,命题8分,第21题10分,第22,23小题12分,第24题14分,共80分.解答应写出文字说明、证明过程或演算步骤.)17. (1)计算:(2)解不等式:.18. 某市规定了毎月用水立方米以内(含立方米)和用水立方米以上两种不同的收费标准.该市的用户毎月应交水费(元)是用水量(立方米)的函数,其图象如图所示.(1)若某月用水量为立方米,则应交水费多少元?(2)求当时,关于的函数表达式.若小敏家某月交水费元,则这个月用水量为多少立方米?19. 为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如图所示),并用调查结果绘绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题.(1)本次接受问卷调查的同学有多少人?补全条形统计图.()04π+-()4521x x+≤+181818y x1818x>y x81(2)本校有七年级同学人,估计双休日参加体育锻炼时间在小时以内(不含小时)的人数.20.如图,学校的实验楼对面是一栋教学楼,小敏在实验楼的窗户测得教学楼顶D 的仰角是 ,教学楼底部的俯角是,量得实验楼与教学楼之间的距离是 .(1)求 的度数.(2)求教学楼的高 .21.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长度为 .设饲养室为长为,占地面积为 .(1)如图 ,问饲养室为长为多少时,占地面积 最大?(2)如图,现要求在图中所示位置留的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多就行了.”请你通过计算,判断小敏的说法是否正确.22.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图 ,等腰直角四边形 .①若 ,对角线 的长.②若 ,求证:.(2)如图 ,矩形 中, 点 是对角线 上一点. 且 ,过点 作直线分别交于点,使四边形 是等腰直角四边形.求 的长.80033C 18︒B 20︒30AB m =BCD ∠BD 50m ()x m ()2y m1x y 22m 2m 1=,90ABCD AB BC ABC ︒∠=,1,AB CD ==AB CD BD AC BD ⊥AD CD =2ABCD 5,9,AB BC ==P BD 2BP PD =P ,AD BC ,E F ABEF AE23.已知为直线上一点,为直线上一点, ,设 .(1)如图,若点在线段上,点在线段上.①如果 那么 , . ②求 之间的关系式.(2)是否存在不同于以上②中的之间的关系式?若存在,求出这个关系式,若不存在,请说明理由.24.如图,已知轴,点 的坐标为 点的坐标为,点在第四象限,点是边上一个动点.(1) 若点在边上,,求点的坐标.(2)若点在边上,点关于坐标轴对称的点 ,落在直线上,求点的坐标.(3) 若点在边上,点是与轴的交点,如图,过点作轴的平行线,过点作轴的平行线,它们相交于点,将沿直线翻折,当点的对应点落在坐标轴上时,求点的坐标(直接写出答案).,,ABC AB AC D ∆=BC E AC AD AE =,BAD CDE ββ∠=∠=D BC E AC 60,70,ABC ADE ︒︒∠=∠==α=βαβ,αβ,1,ABCD AB x 6,AB =A ()1,4,-D ()3,4-B P ABCD P BC PD CD =P P ,AB AD P Q 1y x =-P P ,AB AD CD ,G AD y 2P y PM G x GM M PGM ∆PG M P23. 在平面直角坐标系xOy 中,二次函数的图象与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C 。
2017年浙江省绍兴市中考数学试卷

2017年浙江省绍兴市中考数学试卷一、选择题(本大题共10小题,每小题4分,共40分。
请选出每小题中一个最符合题意的选项,不选、多选、错选,均不给分)1.(4分)﹣5的相反数是()A.B.5 C.﹣ D.﹣52.(4分)研究表明,可燃冰是一种替代石油的新型清洁能源,在我国某海域已探明的可燃冰存储量达150000000000立方米,其中数字150000000000用科学记数法可表示为()A.15×1010B.0.15×1012C.1.5×1011D.1.5×10123.(4分)如图的几何体由五个相同的小正方体搭成,它的主视图是()A.B.C.D.4.(4分)在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其他均相同,从中任意摸出一个球,则摸出黑球的概率是()A.B.C.D.5.(4分)下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择()A.甲B.乙C.丙D.丁6.(4分)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为()A.0.7米B.1.5米C.2.2米D.2.4米7.(4分)均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是()A.B. C. D.8.(4分)在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图.该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是()A.7°B.21°C.23°D.24°9.(4分)矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为()A.y=x2+8x+14 B.y=x2﹣8x+14 C.y=x2+4x+3 D.y=x2﹣4x+310.(4分)一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是()A. B.C.D.二、填空题(本大题共6小题,每小题5分,共30分)11.(5分)分解因式:x2y﹣y=.12.(5分)如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为.13.(5分)如图,Rt△ABC的两个锐角顶点A,B在函数y=(x>0)的图象上,AC∥x轴,AC=2,若点A的坐标为(2,2),则点B的坐标为.14.(5分)如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为m.15.(5分)以Rt△ABC的锐角顶点A为圆心,适当长为半径作弧,与边AB,AC 各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A作直线,与边BC交于点D.若∠ADB=60°,点D到AC的距离为2,则AB 的长为.16.(5分)如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点,若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.三、解答题(本大题共8小题,第17-20小题每小题8分,第21题10分,第22,23小题每小题8分,第24小题14分,共80分,解答需写出必要的文字说明、演算步骤或证明过程)17.(8分)(1)计算:(2﹣π)0+|4﹣3|﹣.(2)解不等式:4x+5≤2(x+1)18.(8分)某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.(1)若某月用水量为18立方米,则应交水费多少元?(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?19.(8分)为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如图所示),并用调查结果绘制了图1,图2两幅统计图(均不完整),请根据统计图解答以下问题:(1)本次接受问卷调查的同学有多少人?补全条形统计图.(2)本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.20.(8分)如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.(1)求∠BCD的度数.(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)21.(10分)某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50m.设饲养室长为x(m),占地面积为y(m2).(1)如图1,问饲养室长x为多少时,占地面积y最大?(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大,小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.22.(12分)定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,①若AB=CD=1,AB∥CD,求对角线BD的长.②若AC⊥BD,求证:AD=CD,(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.23.(12分)已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.(1)如图,若点D在线段BC上,点E在线段AC上.①如果∠ABC=60°,∠ADE=70°,那么α=°,β=°,②求α,β之间的关系式.(2)是否存在不同于以上②中的α,β之间的关系式?若存在,求出这个关系式(求出一个即可);若不存在,说明理由.24.(14分)如图1,已知▱ABCD,AB∥x轴,AB=6,点A的坐标为(1,﹣4),点D的坐标为(﹣3,4),点B在第四象限,点P是▱ABCD边上的一个动点.(1)若点P在边BC上,PD=CD,求点P的坐标.(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x﹣1上,求点P的坐标.(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P 作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM 沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标.(直接写出答案)2017年浙江省绍兴市中考数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题4分,共40分。
2017年浙江省绍兴、义乌市中考数学试卷有答案

数学试卷 第1页(共22页) 数学试卷 第2页(共22页)绝密★启用前浙江省绍兴、义乌市2017年初中毕业生学业考试数 学(总分150分,考试时间120分钟)一、选择题(本大题有10小题,每小题4分,共40分.请选出每小题中一个最符合题意的选项,不选、多选、错选,均不给分) 1.5-的相反数是( ) A .15B .5C .15-D .5-2.研究表明,可燃冰是一种可替代石油的新型清洁能源.在我国某海域已探明的可燃冰储存量达150000000000立方米,其中数字150000000000用科学记数法可表示为( ) A .101510⨯B .120.1510⨯C .111.510⨯D .121.510⨯ 3.如图的几何体由五个相同的小正方体搭成,它的主视图是( )(第3题)ABCD4.在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其他均相同,从中任意摸出一个球,则摸出黑球的概率是( ) A .17B .37C .47D .575.根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )A .甲B .乙C .丙D .丁 6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米.则小巷的宽度为 ( ) A .0.7米 B .1.5米C .2.2米D .2.4米7.均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h 随时间t 的变化规律如图所示(图中OABC 为折线),这个容器的形状可以是 ( )(第7题)ABCD8.在探索“尺规三等分角”这个数学名题的过程中,曾利用了右图,该图中,四边形ABCD 是矩形,E 是BA 延长线上一点,F 是CE 上一点,ACF AFC ∠=∠,FAE FEA ∠=∠.若21ACB ∠=︒,则ECD ∠的度数是( )A .7︒B .21︒C .23︒D .24︒9.矩形ABCD 的两条对称轴为坐标轴,点A 的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A 重合,此时抛物线的函数表达式为2y x =,再次平移透明纸,使这个点与点C 重合,则该抛物线的函数表达式变为( )A .2814y x x =++ B.2814y xx=-+ C .243y x x =++D .243y x x =-+10.一块竹条编织物,先将其按如图所示绕直线MN 翻转180︒,再将它按逆时针方向旋转90︒,所得的竹条编织物是( )(第6题)(第8题) 毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共22页) 数学试卷 第4页(共22页)(第10题)A .B .C .D .二、填空题(本大题有6小题,每小题5分,共30分) 11.分解因式:2x y y -= .12.如图,一块含45︒角的直角三角板,它的一个锐角顶点A 在O 上,边AB ,AC 分别与O 交于点D ,E .则DOE ∠的度数为 .(第12题)(第13题)(第14题)13.如图,Rt ABC △的两个锐角顶点A ,B 在函数(0)ky x x=>的图象上,AC x ∥轴,2AC =.若点A 的坐标为(2,2),则点B 的坐标为 .14.如图为某城市部分街道示意图,四边形ABCD 为正方形,点G 在对角线BD 上,GE CD ⊥,GF BC ⊥,1500m AD =,小敏行走的路线为B A G E →→→,小聪行走的路线为B A D E F →→→→.若小敏行走的路程为3100m ,则小聪行走的路程为 m .15.以Rt ABC △的锐角顶点A 为圆心,适当长为半径作弧,与边AB ,AC 各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A 作直线,与边BC 交于点D .若60ADB ∠=︒,点D 到AC 的距离为2,则AB 的长为 .16.如图,45AOB ∠=︒,点M ,N 在边OA 上,OM x =,4ON x =+,点P 是边OB 上的点.若使点P ,M ,N 构成等腰三角形的点P 恰好有三个,则x 的值是 .三、解答题(本大题有8小题,共80分.解答需写出必要的文字说明、演算步骤或证明过程)17.(本题8分)(1)计算:0π)|4+-.(2)解不等式:452(1)x x ++≤.18.(本题8分)某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y (元)是用水量x (立方米)的函数,其图象如图所示.(1)若某月用水量18立方米,则应交水费多少元? (2)求当18x >时,y 关于x 的函数表达式.若小敏家某月交水费81元,则这个月用水量为多少立方米?19.(本题8分)为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如下图所示),并用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题.七年级部分同学双休日参加 体育锻炼时间的条形统计图图1七年级部分同学双休日参加 体育锻炼时间的扇形统计图(第16题)数学试卷 第5页(共22页) 数学试卷 第6页(共22页)图2(1)本次接受问卷调查的同学有多少人?补全条形统计图.(2)本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.20.(本题8分)如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C 测得教学楼顶部D 的仰角为18︒,教学楼底部B 的俯角为20︒,量得实验楼与教学楼之间的距离30cm AB =. (1)求BCD ∠的度数. (2)求教学楼的高BD .(结果精确到0.1m .参考数据:tan200.36︒≈,tan180.32︒≈)21.(本题10分)某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50m .设饲养室长为(m)x ,占地面积为2(m )y .(1)如图1,问饲养室长x 为多少时,占地面积y 最大? (2)如图2,现要求在图中所示位置留2m 宽的门,且仍使饲养室的占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m 就行了.”请你通过计算,判断小敏的说法是否正确.图1图222.(本题12分)定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图1,等腰直角四边形ABCD ,AB BC =,90ABC ∠=︒. ①若1AB CD ==,AB CD ∥,求对角线BD 的长;②若AC BD ⊥,求证:AD CD =.(2)如图2,在矩形ABCD 中,5AB =,9BC =,点P 是对角线BD 上一点,且2BP PD =,过点P 作直线分别交边AD ,BC 于点E ,F ,使四边形ABFE 是等腰直角四边形.求AE 的长.图1图223.(本题12分)已知ABC △,AB AC =,D 为直线BC 上一点,E 为直线AC 上一点,AD AE =,设BAD α∠=,CDE β∠=. (1)如图,若点D 在线段BC 上,点E 在线段AC 上.①如果60ABC ∠=︒,70ADE ∠=︒,那么α= ︒,β= ︒; ②求α,β之间的关系式. (2)是否存在不同于以上②中的α,β之间的关系式?若存在,求出这个关系式(求出一个即可);若不存在,说明理由.24.(本题14分)如图1,已知□ABCD ,AB x ∥轴,6AB =,点A 的坐标为(1,4)-,点D 的坐标为(3,4)-,点B 在第四象限,点P 是□ABCD 边上的一个动点. (1)若点P 在边BC 上,PD CD =,求点P 的坐标.(2)若点P 在边AB ,AD 上,点P 关于坐标轴对称的点Q 落在1y x =-上,求点P 的坐标.(3)若点P 在边AB ,AD ,CD 上,点G 是AD 与y 轴的交点,如图2,过点P 作y 轴的平行线PM ,过点G 作x 轴的平行线GM ,它们相交于点M ,将PGM △沿直线PG 翻折,当点M 的对应点落在坐标轴上时,求点P 的坐标(直接写出答案).-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共22页) 数学试卷 第8页(共22页)图1图2浙江省绍兴、义乌市2017年初中毕业生学业考试数学答案解析一、选择题 1.【答案】B【解析】5-的相反数是(5)5--=.故选B .【提示】一个数的相反数是在它的前面添加“-”,并化简. 【考点】相反数 2.【答案】C【解析】150000000000一共有12位数,那么12111n =-=,则11150000000000 1.510=⨯,故选:C .【提示】用科学记数法表示数:把一个数字记为10na ⨯的形式(11||0a ≤<,n 为整数).表示绝对值较大的数时,1n =-位数 【考点】科学记数法,表示绝对值较大的数 3.【答案】A【解析】从正面看到的图形是数学试卷 第9页(共22页) 数学试卷 第10页(共22页)【提示】从折线图的倾斜度出发,根据注水的速度不变,而容器水里的高度除了与时间有关,且与容器里的底面积有关,则底面积越大的,水的高度增加的越慢. 【考点】函数的图象 8.【答案】C【解析】在矩形ABCD 中,A B C D ∥,90BCD ∠=︒,所以F E A E C D ∠=∠,9069ACD ACB∠=︒-∠=︒,因为A C F A ∠=∠,FAE FEA ∠=∠,AFC FAE FEA ∠=∠+∠,所以2ACF FEA ∠=∠,则369ACD ACF ECD ECD ∠=∠+∠=∠=︒,所以23ECD ∠=︒故选C .【提示】由矩形的性质不难得到FEA ECD ∠=∠,9069ACD ACB ∠=︒-∠=︒;根据三角形的外角性质及已知条件不难得出2ACF FEA ∠=∠,即可得ACD ∠被线CE 三等分,则可解出ECD ∠.【考点】三角形的外角性质,矩形的性质 9.【答案】A【解析】如图,(2,1)A ,则可得(21)C --,.由(2,1)A 到(21)C --,,需要向左平移4个单位,向下平移2个单位,则抛物线的函数表达式为2y x =,经过平移与为22(4)2814y x x x =+-=++,故选A .【提示】题中的意思就是将抛物线2y x =平移后,点A 平移到了点C ,由A 的坐标不难得出C 的坐标,由平移的性质可得点A 怎样平移到点C ,那么抛物线2y x =,就怎样平移到新的抛物线. 【考点】二次函数的图象 10.【答案】B【解析】绕MN 翻折180︒后,是下面的图形:再逆时针旋转90︒,可得故选B .【提示】绕MN 翻折180︒,本来排在第一行的横纸条排在了第5条,而且5根竖条,分别叠放在它的下、上、上、下、上面,通过这样的分析,确认五根横条的位置,再将其逆时针旋转90︒可得答案. 【考点】翻折变换(折叠问题) 二、填空题11.【答案】(1)(1)y x x +-【解析】原式2(1)(1)(1)y x y x x =-=+- 故答案为(1)(1)y x x +-.【提示】观察整式可得,应选提取公因式y ,再运用平方差公式分解因式. 【考点】因式分解——运用公式法 12.【答案】90︒【解析】DAE ∠与DOE ∠在同一个圆中,且所对的弧都是DE ,则224590D O E D A E ∠=∠=⨯︒=︒. 故答案为90︒.【提示】运用圆周角与圆心角的关系即可解答.数学试卷 第11页(共22页) 数学试卷 第12页(共22页)【解析】根据题中的语句作图可得下面的图,过点D 作于E ,t a nB D ∠由尺规作图-角平分线的作法可得2=,只有3个点P ;数学试卷 第13页(共22页) 数学试卷 第14页(共22页)交OB 两点和;此时,选D的同学有(人),补全条形统计图如下.204060++所以182038BCD DCE BCE∠=∠+∠=︒+︒=︒.502xx-=-最大,即当饲养室长为25m时,占地面积最大.50(212xx--大,即饲养室长为26m时,占地面积最大.因为数学试卷第15页(共22页)数学试卷第16页(共22页),所以ABCD是菱形.度,所以菱形所以ABD CBD≅△△,所以AD CD=.综上所述,AE的长为5或6.5数学试卷第17页(共22页)数学试卷第18页(共22页)在ABD △中,x yαβ+=+,所以2αβ=.(2)解:如图,点E在CA延长线上,点D在线段BC上,设ABC x∠=,ADE y∠=,则ACB x∠=,AED y∠=,在ABD△中,x yαβ+=-,在D E C△中,180x yβ++=︒,所以2180αβ=-︒.注:求出其它关系式,相应给分,如点E在CA的延长线上,点D在CB的延长线上,可得1802αβ=︒-.【提示】(1)①在ADE△中,由70AD AE ADE=∠=︒,,不难求出AED∠和DAE∠;由60AB AC ABC=∠=︒,,可得60BAC C ABC∠=∠=∠=︒,则BAC DAEα=∠-∠,再根据三角形外角的性质可得AED Cβ=∠-∠;②求解时可借助设未知数的方法,然后再把未知数消去的方法,可设ABC x ADE y∠=∠=,;(2)有很多种不同的情况,做法与(1)中的②类似,可求这种情况:点E在CA延长线上,点D在线段BC上.【考点】三角形的外角性质)解:在ABCD中,在边AD上时,由已知得,直线数学试卷第19页(共22页)数学试卷第20页(共22页)数学试卷第21页(共22页) 数学试卷 第22页(共22页)②如下图,当点P 在AD 边上时,设,⎛⎫⎛⎫。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年浙江省绍兴市中考数学试卷一、选择题1、-5的相反数是()A、B、5 C、D、-52、研究表明,可燃冰是一种可替代石油的新型清洁能源。
在我国某海域已探明的可燃冰储存量达150 000 000 000立方米,其中数字150 000 000 000用科学记数法可表示为()A、15×1010B、0.15×1012C、1.5×1011D、1.5×10123、如图的几何体由五个相同的小正方体搭成,它的主视图是()A、B、C、D、4、在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其它均相同,从中任意摸出一个球,则摸出黑球的概率是()A、B、C、D、5、下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:甲乙丙丁平均数(环) 9.14 9.15 9.14 9.15方差 6.6 6.8 6.7 6.6()A、甲B、乙C、丙D、丁6、如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米.则小巷的宽度为()A、0.7米B、1.5米C、2.2米D、2.4米7、均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是()A、B、C、D、8、在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形ABCD是矩形,E是BA 延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA。
若∠ACB=21°,则∠ECD的度数是()A、7°B、21°C、23°D、24°9、矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C 重合,则该抛物线的函数表达式变为()A、y=x2+8x+14B、y=x2-8x+14C、y=x2+4x+3D、y=x2-4x+310、一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是()A、B、C、D、二、填空题11、分解因式:=________.12、如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E.则∠DOE的度数为________.13、如图,Rt△ABC的两个锐角顶点A,B在函数y= (x>0)的图象上,AC//x轴,AC=2.若点A的坐标为(2,2),则点B的坐标为________.14、如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪得行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为________m.15、以Rt△ABC的锐角顶点A为圆心,适当长为半径作弧,与边AB,AC各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A作直线,与边BC交于点D.若∠ADB=60°,点D到AC的距离为2,则AB的长为________.16、如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是________.三、解答题17、计算题。
(1)计算:.(2)解不等式:4x+5≤2(x+1).18、某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.(1)若某月用水量为18立方米,则应交水费多少元?(2)求当x>18时,y关于x的函数表达式.若小敏家某月交水费81元,则这个月用水量为多少立方米?19、为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如下图所示),并用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题.(1)本次接受问卷调查的同学有多少人?补全条形统计图.(2)本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.20、如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶总D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.(结果精确到0.1m。
参考数据:tan20°≈0.36,tan18°≈0.32)(1)求∠BCD的度数.(2)求教学楼的高BD21、某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为为50m.设饲养室长为x(m),占地面积为y(m2).(1)如图1,问饲养室长x为多少时,占地面积y最大?(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大。
小敏说:“只要饲养室长比(1)中的长多2m就行了.”22、定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,①若AB=CD=1,AB//CD,求对角线BD的长.②若AC⊥BD,求证:AD=CD.(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.求AE的长.23、已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.(1)如图,若点D在线段BC上,点E在线段AC上.①如果∠ABC=60°,∠ADE=70°,那么α=________°,β=________°.②求α,β之间的关系式.________(2)是否存在不同于以上②中的α,β之间的关系式?若存在,请求出这个关系式(求出一个即可);若不存在,说明理由.24、如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.(1)若点P在边BC上,PD=CD,求点P的坐标.(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G 作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).答案解析部分一、选择题1、【答案】B【考点】相反数【解析】【解答】解:-5的相反数是-(-5)=5.故选B.【分析】一个数的相反数是在它的前面添加“-”,并化简.2、【答案】C【考点】科学记数法—表示绝对值较大的数【解析】【解答】解:150 000 000 000一共有12位数,那么n=12-1=11,则150 000 000 000= 1.5×1011,故选:C.【分析】用科学记数法表示数:把一个数字记为a×10n的形式(1≤|a|<10,n为整数).表示绝对值较大的数时,n=位数-1.3、【答案】A【考点】简单几何体的三视图【解析】【解答】解:从正面看到的图形是故选A.【分析】主视图是从主视方向看到的图形,也可以说是从正面看到的图形.4、【答案】B【考点】概率的意义,利用频率估计概率【解析】【解答】解:摸出一个球一共有3+4=7种同可能的情况,而抽出一个是黑球的有3种情况,故P(摸出黑球)= .故选B.【分析】用简单的概率公式解答P= ;在这里,n是球的总个数,m是黑球的个数.5、【答案】D【考点】算术平均数【解析】【解答】解:比较四名射击运动员成绩的平均数可得,乙和丁的成绩更好,而乙的方差>丁的方差,所以丁的成绩更稳定些,故选D.【分析】平均数能比较一组数据的平均水平的高低,方差是表示一组数据的波动大小.在这里要选平均数越高为先,再比较方差的大小。
6、【答案】C【考点】解直角三角形的应用【解析】【解答】解:设梯子斜靠在右墙时,底端到右墙角的距离为x米,由勾股定理可得梯子的长度2=0.72+2.42=x2+22,可解得x=1.5,则小巷的宽度为0.7+1.5=2.2(米).故选C.【分析】当梯子斜靠在右墙时,梯子的长度并不改变,而且墙与水平面是垂直的,则可运用勾股定理构造方程解出底端到右墙角的距离.再求小巷的宽度.7、【答案】D【考点】函数的图象【解析】【解答】解:从折线图可得,倾斜度:OB<OA<BC,表示水上升的高度的速度:OB<OA<BC则OB段所在的容器的底面积最大,OA段的次之,BC段的最小,即容器的分布是中等长方体,最大长方体,最小长方体,所以符合这一情况的只有D.故选D.【分析】从折线图的倾斜度出发,根据注水的速度不变,而容器水里的高度除了与时间有关,且与容器里的底面积有关,则底面积越大的,水的高度增加的越慢。
8、【答案】C【考点】三角形的外角性质,矩形的性质【解析】【解答】解:在矩形ABCD中,AB//CD,∠BCD=90°,所以∠FEA=∠ECD,∠ACD=90°-∠ACB=69°,因为∠ACF=∠AFC,∠FAE=∠FEA,∠AFC=∠FAE+∠FEA,所以∠ACF=2∠FEA,则∠ACD=∠ACF+∠ECD=3∠ECD=69°,所以∠ECD=23°故选C.【分析】由矩形的性质不难得到∠FEA=∠ECD,∠ACD=90°-∠ACB=69°;根据三角形的外角性质及已知条件不难得出∠ACF=2∠FEA,即可得∠ACD被线CE三等分,则可解出∠ECD。
9、【答案】A【考点】二次函数的图象【解析】【解答】解:如图,A(2,1),则可得C(-2,-1).由A(2,1)到C(-2,-1),需要向左平移4个单位,向下平移2个单位,则抛物线的函数表达式为y=x2,经过平移与为y=(x+4)2-2= x2+8x+14,故选A.【分析】题中的意思就是将抛物线y=x2平移后,点A平移到了点C,由A的坐标不难得出C的坐标,由平移的性质可得点A怎样平移到点C,那么抛物线y=x2,就怎样平移到新的抛物线.10、【答案】B【考点】翻折变换(折叠问题)【解析】【解答】解:绕MN翻折180°后,是下面的图形:再逆时针旋转90°,可得故选B.【分析】绕MN翻折180°,本来排在第一行的横纸条排在了第5条,而且5根竖条,分别叠放在它的下、上、上、下、上面,通过这样的分析,确认五根横条的位置,再将其逆时针旋转90°可得答案.二、填空题11、【答案】【考点】因式分解-运用公式法【解析】【解答】解:原式= =故答案为.【分析】观察整式可得,应选提取公因式y,再运用平方差公式分解因式.12、【答案】90°【考点】圆心角、弧、弦的关系【解析】【解答】解:∠DAE与∠DOE在同一个圆中,且所对的弧都是,则∠DOE=2∠DAE=2×45°=90°.故答案为90°.【分析】运用圆周角与圆心角的关系即可解答.13、【答案】(4,1)【考点】反比例函数的图象,反比例函数的性质【解析】【解答】解:因为点A(2,2)在函数y= (x>0)的图象上,所以k=2×2=4.则反比函数y= (x>0),因为AC//x轴,AC=2,所以C(4,2).在Rt△ABC中,∠ACB=90°,所以B的横坐标与C的横坐标相同,为4,当x=4时,y= =1,则B(4,1).故答案为(4,1).【分析】运用待定系数法求出k的值,而点B也在反比例函数上,所以只要求出B的横坐标或纵坐标代入函数解析式即可解出,由AC//x轴,AC=2,得到C(4,2),不难得到B的横坐标与C的横坐标相同,可得B的横坐标.14、【答案】4600【考点】全等三角形的判定,正方形的性质【解析】【解答】解:小敏走的路程为AB+AG+GE=1500+(AG+GE)=3100,则AG+GE=1600m,小聪走的路程为BA+AD+DE+EF=3000+(DE+EF).连接CG,在正方形ABCD中,∠ADG=∠CDG=45°,AD=CD,在△ADG和△CDG中,所以△ADG≅△CDG,所以AG=CG.又因为GE⊥CD,GF⊥BC,∠BCD=90°,所以四边形GECF是矩形,所以CG=EF.又因为∠CDG=45°,所以DE=GE,所以小聪走的路程为BA+AD+DE+EF=3000+(GE+AG)=3000+1600=4600(m).故答案为4600.【分析】从两人的行走路线得到他们所走的路程和,可以得到AG+GE=1600m,小聪走的路程为BA+AD+DE+EF=3000+(DE+EF),即要求出DE+EF,通一系列的证明即可得到DE=GE,EF=CG=AG.15、【答案】2【考点】作图—尺规作图的定义【解析】【解答】解:根据题中的语句作图可得下面的图,过点D作DE⊥AC于E,由尺规作图的方法可得AD为∠BAC的角平分线,因为∠ADB=60°,所以∠B=90°,由角平分线的性质可得BD=DE=2,在Rt△ABD中,AB=BD·tan∠ADB=2 .故答案为2 .【分析】由尺规作图-角平分线的作法可得AD为∠BAC的角平分线,由角平分线的性质可得BD=2,又已知∠ADB即可求出AB的值.16、【答案】x=0或x= 或4≤x<4【考点】相交两圆的性质【解析】【解答】解:以MN为底边时,可作MN的垂直平分线,与OB的必有一个交点P1,且MN=4,以M为圆心MN为半径画圆,以N为圆心MN为半径画圆,①如下图,当M与点O重合时,即x=0时,除了P1,当MN=MP,即为P3;当NP=MN时,即为P2;只有3个点P;②当0<x<4时,如下图,圆N与OB相切时,NP2=MN=4,且NP2⊥OB,此时MP3=4,则OM=ON-MN= NP2-4= .③因为MN=4,所以当x>0时,MN<ON,则MN=NP不存在,除了P1外,当MP=MN=4时,过点M作MD⊥OB于D,当OM=MP=4时,圆M与OB刚好交OB两点P2和P3;当MD=MN=4时,圆M与OB只有一个交点,此时OM= MD=4 ,故4≤x<4 .与OB有两个交点P2和P3,故答案为x=0或x= 或4≤x<4 .【分析】以M,N,P三点为等腰三角形的三顶点,则可得有MP=MN=4,NP=MN=4,PM=PN这三种情况,而PM=PN这一种情况始终存在;当MP=MN时可作以M为圆心MN为半径的圆,查看与OB的交点的个数;以N为圆心MN为半径的圆,查看与OB的交点的个数;则可分为当x=0时,符合条件;当0<x<4时,圆M与OB只有一个交点,则当圆N与OB相切时,圆N与OB只有一个交点,符合,求出此时的x值即可;当4≤x时,圆N与OB没有交点,当x的值变大时,圆M会与OB相切,此时只有一个相点,求出此时x的值,则x在这个范围内圆M与OB有两个交点;综上即可求答案.三、解答题17、【答案】(1)解:原式=1+ -4-3 =-3.(2)解:4x+5≤2(x+1)去括号,得4x+5≤2x+2移项合并类项,得2x≤-3解得x≤【考点】二次根式的性质与化简【解析】【分析】(1)所有非零数的0次幂的结果都为1,去绝对值符号时要注意非负性,化简二次根式可运用二次根式的乘法性质.(2)按解不等式的一般解法,去分母,再去括号,再移项并合并同类项,最后系数化为1.18、【答案】(1)解:观察折线图可得当横坐标为18时的点的纵坐标为45,即应交水费为45元.(2)解:设当x>18时,y关于x的函数表达式为y=kx+b,将(18,45)和(28,75)代入可得解得,则当x>18时,y关于x的函数表达式为y=3x-9,当y=81时,3x-9=81,解得x=30.答:这个月用水量为30立方米.【考点】一次函数的应用【解析】【分析】(1)从图中即可得到横坐标为18时的点的纵坐标;(2)运用待定系数法,设y=kx+b,代入两个点的坐标求出k和b,并将y=81时代入求出x的值即可.19、【答案】(1)解:本次接受问卷调查的同学有40÷25%=160(人);选D的同学有160-20-40-60-10=30(人),补全条形统计图如下.(2)解:(人).【考点】扇形统计图,条形统计图【解析】【分析】(1)从条形统计图中,可以得到选B的人数是40,从扇形统计图中可得选B的人数占25%,即可求得;需要求出选D的人数,再补条形统计图.(2)锻炼时间在3小时以内的,即包括选A、B、C的人数;要求出选A、B、C占调查人数的百分比,再乘以七年级总人数即可求出.20、【答案】(1)解:过点C作CD⊥BD于点E,则∠DCE=18°,∠BCE=20°,所以∠BCD=∠DCE+∠BCE=18°+20°=38°.(2)解:由已知得CE=AB=30(m),在Rt△CBE中,BE=CE×tan20°≈30×0.36=10.80(m),在Rt△CDE中,DE=CE×tan18°≈30×0.32=9.60(m),∴教学楼的高BD=BE+DE=10.80+9.60≈20.4(m).答:教学楼的高为20.4m.【考点】解直角三角形的应用-仰角俯角问题【解析】【分析】(1)C观测D的仰角应为CD与水平面的较小的夹角,即∠DCE;C观测B的俯角应为CB与水平线的较小的夹角,即为∠BCE,不难得出∠BCD=∠DCE+∠BCE;(2)易得CE=AB,则由直角三角形的锐角函数值即可分别求得BE和DE,求和即可.21、【答案】(1)解:因为,所以当x=25时,占地面积y最大,即当饲养室长为25m时,占地面积最大.(2)解:因为,所以当x=26时,占地面积y最大,即饲养室长为26m时,占地面积最大.因为26-25=1≠2,所以小敏的说法不正确.【考点】一元二次方程的应用【解析】【分析】(1)根据矩形的面积=长×高,已知长为x,则宽为,代入求出y关于x的函数解析式,配成二次函数的顶点式,即可求出x的值时,y有最大值;(2)长虽然不变,但长用料用了(x-2)m,所以宽变成了,由(1)同理,代入求出y关于x的函数解析式,配成二次函数的顶点式,即可求出x的值时,y有最大值.22、【答案】(1)解:①因为AB=CD=1,AB//CD,所以四边形ABCD是平行四边形.又因为AB=BC,所以□ABCD是菱形.又因为∠ABC=90度,所以菱形ABCD是正方形.所以BD= .②如图1,连结AC,BD,因为AB=BC,AC⊥BD,所以∠ABD=∠CBD,又因为BD=BD,所以△ABD≅△CBD,所以AD=CD.(2)解:若EF与BC垂直,则AE≠EF,BF≠EF,所以四边形ABFE不是等腰直角四边形,不符合条件;若EF与BC不垂直,①当AE=AB时,如图2,此时四边形ABFE是等腰直角四边形.所以AE=AB=5.②当BF=AB时,如图3,此时四边形ABFE是等腰直角四边形.所以BF=AB=5,因为DE//BF,所以△PED~△PFB,所以DE:BF=PD:PB=1:2,所以AE=9-2.5=6.5.综上所述,AE的长为5或6.5.【考点】平行四边形的判定【解析】【分析】(1)①由AB=CD=1,AB//CD,根据“有一组对边平行且相等的四边形是平行四边形”可得四边形ABCD是平行四边形.由邻边相等AB=BC,有一直角∠ABC=90度,所以菱形ABCD是正方形.则BD= ;②连结AC,BD,由AB=BC,AC⊥BD,可知四边形ABCD是一个筝形,则只要证明△ABD≅△CBD,即可得到AD=CD.(2)分类讨论:若EF与BC垂直,明示有AE≠EF,BF≠EF,即EF与两条邻边不相等;由∠A=∠ABC=90°,可分类讨论AB=AE时,AB=BF时去解答.23、【答案】(1)20;10;α=2β(2)解:如图,点E在CA延长线上,点D在线段BC上,设∠ABC=x,∠ADE=y,则∠ACB=x,∠AED=y,在△ABD中,x+α=β-y,在△DEC中,x+y+β=180°,所以α=2β-180°.注:求出其它关系式,相应给分,如点E在CA的延长线上,点D在CB的延长线上,可得α=180°-2β.【考点】三角形的外角性质【解析】【解答】解:(1)①因为AD=AE,所以∠AED=∠ADE=70°,∠DAE=40°,又因为AB=AC,∠ABC=60°,所以∠BAC=∠C=∠ABC=60°,所以α=∠BAC-∠DAE=60°-40°=20°,β=∠AED-∠C=70°-60°=10°;②解:如图,设∠ABC=x,∠ADE=y,则∠ACB=x,∠AED=y,在△DEC中,y=β+x,在△ABD中,α+x=y+β,所以α=2β.【分析】(1)①在△ADE中,由AD=AE,∠ADE=70°,不难求出∠AED和∠DAE;由AB=AC,∠ABC=60°,可得∠BAC=∠C=∠ABC=60°,则α=∠BAC-∠DAE,再根据三角形外角的性质可得β=∠AED-∠C;②求解时可借助设未知数的方法,然后再把未知数消去的方法,可设∠ABC=x,∠ADE=y;(2)有很多种不同的情况,做法与(1)中的②类似,可求这种情况:点E在CA延长线上,点D在线段BC上.24、【答案】(1)解:在□ABCD中,CD=AB=6,所以点P与点C重合,所以点P的坐标为(3,4).(2)解:①当点P在边AD上时,由已知得,直线AD的函数表达式为y=-2x-2,设P(a,-2a-2),且-3≤a≤1,若点P关于x轴对称点Q1(a,2a+2)在直线y=x-1上,所以2a+2=a-1,解得a=-3,此时P(-3,4)。
