ANSYSLS-DYNA数值模拟霍普金森压杆试验
圆环形整形器设计及整形效果的数值模拟

Vol. 11, No. 3Sept. 2020第11卷第3期2020年9月现代应用物理MODERN APPLIED PHYSICS圆环形整形器设计及整形效果的数值模拟高波,彭 刚,王绪财,王 伟,陈春晓,冯家臣,刘 宇(中国兵器工业集团第53研究所,济南250031)摘 要:以大口径霍普金森压杆试验中入射波整形为目的,利用ANSYS/LS-DYNA 软件模 拟并分析了 1 mm 分离式霍普金森压杆试验中圆形整形器受到0100 mm 压杆碰撞后的形变过程,发现圆形整形器存在应力较高的环状区域。
为提高应力均匀性,提出了一种圆环形整 形器设计方案,并对圆环形整形器的整形效果进行了仿真分析。
结果表明,与圆形整形器相比,圆环形整形器应力波波形更加平滑,入射波上升时间更长,有利于试件尽早达到应力均匀。
在混凝土试件压缩试验中,经圆环形整形器作用的反射波为平台波,可基本实现大尺寸混凝土 试件的恒应变率加载。
关键词:分离式霍普金森压杆;圆环形整形器;数值仿真;恒应变率;应力均匀中图分类号:TB332 文献标志码:A DOI :10. 12061/j. issn. 2095 - 6223. 2020. 031002Design of Circular Ring Shaper and Numerical Simulation of Shaping EffectGAO Bo, PENG Gang, WANG Xu-cai, WANG Wei, CHEN Chun-xiao, FENG Jia-chen, LIUYu(Institute 53 of ChinaOrdnance Industry Group , Jinan 250031, China)Abstract : In the test of T100 mm splitting Hopdinson pressure bar , the deformation processof a circular shaper impacted by ^100 mm pressure bar is analyzed by ANSYS/LS-DYNA soft w are. The resu Its show that t h ere is a ring area with high st r ess in the circular shaper.To improve the stress equilibrium, a design scheme of circular ring shaper is put forward, and the effect of the ring shaper is simulated and analyzed. The resuIts show that the stress waveform of the ring shaper is smoother than that of the circular shaper, and the rise time of incident wave is longer. In the compression test of a concrete specimen, the reflecting waveis almost flat which means that the ring shaper can basically realize the dynamic compression cons t a_nt st r ain rale loading on large-sized concre t e specimen.Keywords : splitting Hopkinson pressure bar; circular ring shaper; numerical simulation ;cons t a_nt st r ain rale; st r ess equilibrium大口径分离式霍普金森压杆(splitting Hopkinsonpressure bar, SHPE)装置在混凝土「円及复合材料构件匕呵的动态力学性能研究中广泛应用。
霍普金森压杆实验流程

霍普金森压杆实验流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classicarticles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!霍普金森压杆实验是一种用来研究材料的压缩性质的实验方法,下面是霍普金森压杆实验的流程:1. 准备实验所需材料和设备:实验所需的材料包括被测样品和压杆,设备包括载荷传感器、位移传感器、数据采集系统等。
基于霍普金森压杆系统的动态压痕实验

基于霍普金森压杆系统的动态压痕实验张新;候兵;李玉龙【摘要】设计了基于分离式Hopkinson压杆系统(SHPB)的动态压痕实验装置,使其能够获得动态压痕实验中试样的压痕位移和所受冲击载荷的实验数据,从而得到一种新的材料动态性能测试技术.对3种不同的材料进行了动态压痕实验,得到了材料的动态硬度和率敏感性等动态性能,与采用其他实验技术所测得的性能数据具有很好的一致性,并实现了利用动态压痕的方法获取材料的动态性能.%A new technology for testing dynamic properties of materials was proposed by developing an experimental setup based on a split-Hopkinson pressure bar system. The experimental setup can be used in dynamic indentation experiments to obtain the indentation displacements of materials and the impact load suffered by them. To validate the experimental setup, the ABAQUS/Explicit FE code was used to numerically simulate dynamic indentation experiments. Dynamic indentation experiments were conducted on aluminum alloy LY12, pure titanium and oxygen-free copper. The dynamic properties such as dynamic hardness and rate sensitivity were obtained for these three kinds of materials. The dynamic properties obtained by dynamic indentation experiments are consistent with those by other experimental methods.【期刊名称】《爆炸与冲击》【年(卷),期】2011(031)003【总页数】7页(P256-262)【关键词】固体力学;动态硬度;压痕;SHPB;率敏感性【作者】张新;候兵;李玉龙【作者单位】西北工业大学航空学院,陕西西安710072;西北工业大学航空学院,陕西西安710072;西北工业大学航空学院,陕西西安710072【正文语种】中文【中图分类】O347压痕硬度实验是一种应用广泛的材料性能测试技术,主要思想是强制压迫“较硬”的压头进入“较软”材料的表面,通过记录压入过程中载荷和压痕深度的关系曲线,研究材料抵抗外物侵入的能力,即材料硬度[1]。
ANSYSLS-DYNA数值模拟霍普金森压杆试验资料

A N S Y S L S-D Y N A数值模拟霍普金森压杆试验ANSYS/LS-DYNA数值模拟霍普金森压杆试验1 功能概述大多数材料在强度等力学性质方面都表现出某种程度的加载率或应变率敏感性,高幅值短持续时间脉冲和荷载所引起材料力学性质的应变率效应,对于抗动载的结构设计和分析是非常重要的。
这些动载来至常规武器侵彻与爆炸、偶然爆炸和高速撞击等许多军事和民用事件,对于这些事件的理论分析和数值模拟必须知道材料的高应变率强度、断裂特性和应力-应变关系等本构性质。
要研究材料在脉冲动载作用下的力学性质的实验设备和实验必须模拟类似现场的应变率条件,分离式霍普金森杆被公认为是最常用最有效的研究脉冲动载作用下材料力学性质的实验设备。
数值模拟是一种依靠电子计算机对工程问题和物理问题乃至自然界各类问题进行研究的技术。
它利用材料的本构函数,结合有限元或有限容积的概念,采用数值计算和图像显示的方法,因此具有如下优势:(1)检验理论结果是否正确;(2)弥补实验与观测得不足;(3)利用模拟结果,了解非线性过程中的因果关系与主要物理机制;(4)预测在不同初始条件与边界条件下非线性过程的发展情形;(5)数值模拟成本低,可以带来巨大社会经济效益。
由于很多材料的本构性质已经知道,因此在设计产品时,可以利用材料的本构性质通过仿真来模拟复杂的系统。
ANSYS/LS-DYNA数值模拟霍普金森压杆试验,就是通过ANSYS/LS-DYNA软件来模拟霍普金森压杆实验,通过设置弹丸不同速度,对试件进行研究。
霍普金森压杆实验分为自由式和分离式两种,本仿真采用分离式的办法。
2 原理简介2.1 霍普金森压杆实验简介霍普金森杆实验装置的基本原型最早是由Hopkinson提出的,它可用于测量冲击载荷的脉冲波形。
1949年Kolsky将压杆分成两段,试件置于输入杆和输出杆中间,通过加速的质量块、短杆撞击或炸药爆轰产生加速脉冲,利用这一装置可测量材料在冲击载荷作用下的应力-应变关系。
分离式霍普金森压杆实验技术数值模拟

首先分析试样与压杆不均匀接触的影响。根据实验
经验,考虑试样与压杆不平度分别为0.03/100,
O.05/100,0.1/100三种情形。从试样的前后接触面以及
中间截面的A、B、c三处取出数值模拟应力波波形图,
其中A处是试样最先与压杆接触的一边,c处则是最
后与压杆接触到的一边,B处是A、B正中间的单元。
如图4.36所示。
图4.37至图4_39是不平度0.03/100的试样的模拟
结果,从图中我们观察到尽管对于100mm直径只有
O.Olmm的不平度,在接触瞬间同一截面还是有明显的图4.36:试样不均匀
接触分析波形采集位置
不平度,试样在约一半上升沿内试样不平接触面各点处在不同应变率加载之中。
变对波形的影响。可以发现随着pulse shaper杨氏模量的降低,波的上升沿时明显拉长,杨氏模量的降低较多时波峰会略有降低,而且当杨氏模量降到12GPa 时波的上升段近似直线,波形被改造为近似三角形波。还可以发现硬化模量的改变对波的上升沿时没有改变,其对波形整形的贡献表现在波的上升段曲率上,即波的形状上,也就是说不同的硬化模量会影响在总的上升沿时段内不同阶段波上升的快慢。
4.4试样表面缺陷及与压杆不Leabharlann 匀接触分析4.4.1计算方案
SHPB实验的一维应力假定和均匀性假定要求试样与压杆、压杆与子弹之间共轴撞击并且保持试样均匀受压,这要求子弹与压杆、压杆与试样之间在碰撞时接触面保持均匀接触,试样的表面无缺损。对于大直径试样来说,试样的加工总会存在一些误差,而一些脆性材料例如混凝土、砂浆是由粗骨料和胶凝材料经过水化反应及后期的养护而成,必然会存在初始缺陷;在表面加工过程中,由于加工误差,试样两端面不可能完全平行;同时在加工和运输过程中还极易造成试样边缘剥落。这些初始几何缺陷导致SHPB实验过程中试样与压杆不可能保持在理想的均匀接触状态下共轴撞击,从而试样内各点应力是不均匀的。分析这种由于试样几何缺陷产生的试样受力不均匀对sHPB实验精度的影响程度是十分必要的,有利于实验方法的改进和试样加工精度的确定。本文建立了m100mm大直径实验装置数值模型。分别分析了试样与压杆不均匀接触和试样表面初始缺陷对试样截面应力均匀性的影响。为了突出试样的缺陷和不均匀接触的影响,我们取试样材料等同于压杆材料,试样长50mm,直径100mm,试样网格划分:纵向10等分,径向12等分。接触刚度因子O.8。
子弹长度对SHPB测试影响的ANSYS有限元模拟

1、引言
在航空、航天、汽车、运输、包装及其它军事和民用领域中,工程材料可能遇到象爆炸、 高速碰撞这样的冲击加载情况。 了解材料在冲击加载条件下的力学响应必将大大有助于这些 材料的工程应用和工程设计。此外,数值模拟已在工程设计中发挥着重要作用,而进行数值 模拟的前提是必须首先建立一个基于材料在各种应变率下 (尤其是在动态应变率下) 的精确 应力-应变曲线基础上的本构模型。 所以, 获得一套材料在高应变率下的应力—应变曲线则 成为首要任务。尽管人们已经研制了多种动态实验技术,但是,与准静态实验相比,进行有 效并准确的高应变率下的动态实验依然是一个很大的挑战。 因此, 为得到有效并准确的材料 的应变率相关的应力—应变曲线,研制高效的、精确的高应变率实验装置是非常重要的。 自1949年,Kolsky[1]发明分离式霍普金森压杆(SHPB)以来,它已被普遍认为是测试 多种材料,例如金属[2]、陶瓷[3]、岩石[4]、混凝土[5]、复合材料[6]、橡胶[7]等在高应变率 下力学响应的一种行之有效的实验手段。 分离式霍普金森压杆技术可以获得材料在102-104 1/s应变率范围内的应力-应变曲线。然而,为了获得有效的、精确的实验数据,霍普金森 压杆实验中的一些问题依然需要引起足够的重视。
从上述公式可以看出,高应变率下材料的应力应变关系受诸多因素影响。本文着重讨 论波形整形器尺寸对SHPB测试材料动态应力应变关系的影响,波形整形器材料为黄铜,选 择黄铜的直径为10mm,厚度分别1mm,1.5mm,2mm; 黄铜的厚度为1mm,直径为5mm 和 借助三维非线性动力分析软件ANSYS LS-DYNA详细模拟SHPB 15mm冲击速度均为15 m/s , 实验过程,与实验结果进行对比,验证了有限元模型的正确性,并给出波形整性器对实践应 力应变曲线的影响规律。
霍普金森杆实验技术简介

霍普金森杆实验技术简介霍普金森杆实验技术简介1.材料动态力学性能实验简史在各类工程技术、军事技术和科学研究等广泛领域的一系列实际问题中,甚至就在日常生活中,人们都会遇到各种各样的爆炸/冲击载荷问题,并且可以观察到,物体在爆炸/冲击载荷下的力学响应往往与静载荷下的有显著不同。
了解材料在冲击加载条件下的力学响应必将大大有助于这些材料的工程应用和工程设计。
此外,数值模拟已在工程设计中发挥着重要作用,而进行数值模拟的前提是必须首先建立一个基于材料在各种应变率下(尤其是在动态应变率下)的精确应力-应变曲线基础上的本构模型。
所以,获得一套材料在高应变率下的应力—应变曲线则成为首要任务。
尽管人们已经研制了多种动态实验技术,但是,与准静态实验相比,进行有效并准确的高应变率下的动态实验依然是一个很大的挑战。
因此,为得到有效并准确的材料的应变率相关的应力—应变曲线,研制高效的、精确的高应变率实验装置是非常重要的。
首先,人们知道,固体力学的静力学理论所研究的是处于静力平衡状态下的固体介质,以忽略介质微元体的惯性作用为前提。
这只是在载荷强度随时间不发生显著变化的时候,才是允许和正确的。
而爆炸/冲击裁荷以载荷作用的短历时为其特征,在以毫秒(ms)、微秒(?s)甚至纳秒(ns)计的短暂时间尺度上发生了运动参量(位移、速度、加速度)的显著变化。
在这样的动载荷条件,介质的微元体处于随时间迅速变化着的动态过程中,这是一个动力学问题。
对此必须计及介质微元体的惯性,从而就导致了对应力波传播的研究。
一切固体材料都具有惯性和可变形性,当受到随时间变化着的外载荷的作用时,它的运动过程总是一个应力波传播、反射和相互作用的过程。
在忽略了介质惯性的可变形固体的静力学问题中,只是允许忽略或没有必要去研究这一在达到静力平衡前的应力波的传播和相互作用的过程,而着眼于研究达到应力平衡后的结果而已。
在忽略了介质可变形性的刚体力学问题中,则相当于应力波传播速度趋于无限大,因而不必再予以考虑。
霍普金森压杆实验报告
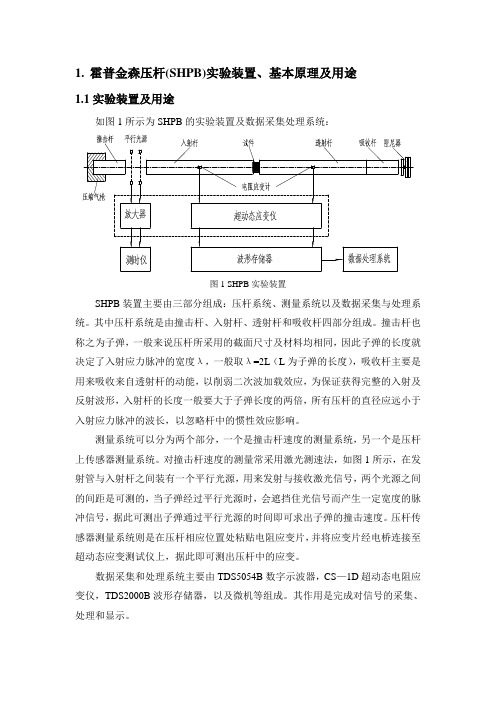
1.1 实验装置及用途
如图 1 所示为 SHPB 的实验装置及数据采集处理系统:
图 1 SHPB 实验装置
SHPB 装置主要由三部分组成:压杆系统、测量系统以及数据采集与处理系 统。其中压杆系统是由撞击杆、入射杆、透射杆和吸收杆四部分组成。撞击杆也 称之为子弹, 一般来说压杆所采用的截面尺寸及材料均相同,因此子弹的长度就 决定了入射应力脉冲的宽度λ,一般取λ=2L(L 为子弹的长度) ,吸收杆主要是 用来吸收来自透射杆的动能, 以削弱二次波加载效应,为保证获得完整的入射及 反射波形, 入射杆的长度一般要大于子弹长度的两倍,所有压杆的直径应远小于 入射应力脉冲的波长,以忽略杆中的惯性效应影响。 测量系统可以分为两个部分,一个是撞击杆速度的测量系统,另一个是压杆 上传感器测量系统。对撞击杆速度的测量常采用激光测速法,如图 1 所示,在发 射管与入射杆之间装有一个平行光源,用来发射与接收激光信号,两个光源之间 的间距是可测的, 当子弹经过平行光源时,会遮挡住光信号而产生一定宽度的脉 冲信号, 据此可测出子弹通过平行光源的时间即可求出子弹的撞击速度。压杆传 感器测量系统则是在压杆相应位置处粘贴电阻应变片, 并将应变片经电桥连接至 超动态应变测试仪上,据此即可测出压杆中的应变。 数据采集和处理系统主要由 TDS5054B 数字示波器,CS—1D 超动态电阻应 变仪,TDS2000B 波形存储器,以及微机等组成。其作用是完成对信号的采集、 处理和显示。
图 6 透射波波形
万试屋 – 材料测试仪器方法资源小站/test_house
2.5 试件应力-应变曲线
工程应力曲线:
图 7 试样的工程应力曲线
工程应变曲线:
图 8 试样的工程应变曲线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ANSYS/LS-DYNA数值模拟霍普金森压杆试验1 功能概述大多数材料在强度等力学性质方面都表现出某种程度的加载率或应变率敏感性,高幅值短持续时间脉冲和荷载所引起材料力学性质的应变率效应,对于抗动载的结构设计和分析是非常重要的。
这些动载来至常规武器侵彻与爆炸、偶然爆炸和高速撞击等许多军事和民用事件,对于这些事件的理论分析和数值模拟必须知道材料的高应变率强度、断裂特性和应力-应变关系等本构性质。
要研究材料在脉冲动载作用下的力学性质的实验设备和实验必须模拟类似现场的应变率条件,分离式霍普金森杆被公认为是最常用最有效的研究脉冲动载作用下材料力学性质的实验设备。
数值模拟是一种依靠电子计算机对工程问题和物理问题乃至自然界各类问题进行研究的技术。
它利用材料的本构函数,结合有限元或有限容积的概念,采用数值计算和图像显示的方法,因此具有如下优势:(1)检验理论结果是否正确;(2)弥补实验与观测得不足;(3)利用模拟结果,了解非线性过程中的因果关系与主要物理机制;(4)预测在不同初始条件与边界条件下非线性过程的发展情形;(5)数值模拟成本低,可以带来巨大社会经济效益。
由于很多材料的本构性质已经知道,因此在设计产品时,可以利用材料的本构性质通过仿真来模拟复杂的系统。
ANSYS/LS-DYNA数值模拟霍普金森压杆试验,就是通过ANSYS/LS-DYNA软件来模拟霍普金森压杆实验,通过设置弹丸不同速度,对试件进行研究。
霍普金森压杆实验分为自由式和分离式两种,本仿真采用分离式的办法。
2 原理简介2.1 霍普金森压杆实验简介霍普金森杆实验装置的基本原型最早是由Hopkinson提出的,它可用于测量冲击载荷的脉冲波形。
1949年Kolsky将压杆分成两段,试件置于输入杆和输出杆中间,通过加速的质量块、短杆撞击或炸药爆轰产生加速脉冲,利用这一装置可测量材料在冲击载荷作用下的应力-应变关系。
Kolsky的工作是一项革命性改进,现代的分离式霍普金森杆都是在其基础上发展而来,所以分离式霍普金森杆也称之为Kolsky杆。
在这半个多世纪的时间里,分离式霍普金森杆实验技术得到了大力的发展,由最初的压缩实验系统发展到拉伸和扭转实验系统甚至是压扭、拉扭复合系统;其测试材料的种类己由金属发展到非金属,由韧性材料到脆性材料;从常温实验发展到高、低温实验;从较低应变率实验发展到较高应变率实验。
另外,由于自由式霍普金森杆技术由于能够实验高过载,已经成为高g值加速度传感器的标准标定实验技术。
2.2 ANSYS/LS-DYNA简介在求解冲击、爆炸问题时,只有采用非线性数值算法才能解决。
广泛使用的有限元程序如LS-DYNA、DYTRAN、ABAQUS和AUTODYN等专长于求解非线性问题。
DYTRAN可用于爆炸、高速侵彻、船体撞击毁损等分析领域,但是在处理冲击问题的接触算法上远不如LS-DYNA全面。
ABAQUS可以分析复杂的固体力学和结构力学系统,特别是能够驾驭非常庞大复杂的问题和模拟高度非线性问题,但是对爆炸和冲击过程的模拟相对不足。
AUTODYN可用于处理几何和材料大变形的非线性瞬态动力分析数值模拟,尤其在弹药工程领域应用广泛,可对聚能射流现象、破甲穿甲弹侵彻靶板的作用机理进行仿真。
LS-DYNA作为世界上最著名的通用显示动力分析程序,能够模拟真实世界的各种复杂问题,特别适合于求解各种二维、三维非线性结构的高速碰撞、爆炸和金属成型等非线性动力冲击问题,同时可以求解传热、流体及流固藕合问题。
1996LSTC公司与ANSYS公司合作推出ANSYS/LS-DYNA,大大增强了LS-DYNA的分析能力。
ANSYS/LS-DYNA程序是功能齐全的几何非线性(大位移、大转动和大应变)、材料非线性(140多种材料动态模型)和接触非线性(50多种)程序。
它以Lagrange算法为主,兼有ALE和Euler 算法;以显式求解为主,兼有隐式求解功能;以结构分析为主,兼有热分析、流体-结构耦合功能;以非线性动力分析为主,兼有静力分析功能(如动力分析前的预应力计算和薄板冲压成型后的回弹计算);军用和民用相结合的通用结构分析非线性有限元程序。
运用ANSYS/LS-DYNA进行数值模拟的一般步骤包括:前处理、求解及后处理。
前处理工作主要包括:算法及有限元单元的选择、材料模型的确定、模型的建立、网格的划分、接触的定义、约束及载荷的施加等步骤,其中前处理工作由ANSYS/PREP7完成。
前处理操作完成后,系统将生成相应的K文件。
此时可根据数值模拟的实际情况来决定是否修改K文件内容。
由于K文件为二进制文件,需采用文本编辑器将K文件打一开、编辑。
K文件修改完毕后,调用LS-DYNA970版求解器进行求解,生成图形文件和时间历程文件。
求解过程结束后,启动后处理程序LS-PREPOST。
LS-PREPOST可读取LS-DYNA的计算结果d3Plot文件,进行计算数据的整理以及二次运算。
3 仿真材料及模型尺寸的选择分离式霍普金森压杆实验包括子弹、输入杆、输出杆及试件。
本仿真采用钨钢作为子弹、输入杆以及输出杆的材料,试件选用5A06-C铝。
数值模拟的模型尺寸如表3.1,数值模拟材料参数如表3.2,表3.3。
表3.1 数值模拟的模型尺寸模型长度l/m 外径∅/m钨钢子弹0.2 1.5×10−2钨钢输入杆 1 1.5×10−2钨钢输出杆0.8 1.5×10−25A06-C铝试件8×10−3 1.3×10−2表3.2 子弹、输入杆、输出杆的材料参数和模型材料密度ρ/kg/m3杨氏模量E/Pa泊松比μ切线模量E T/Pa失效模量E S/Pa模型钨钢子弹7678 2.1E11 0.29 - - Isotropic 钨钢输入杆7678 2.1E11 0.29 - - Isotropic 钨钢输出杆7678 2.1E11 0.29 - - Isotropic表3.3 试件的材料参数和模型材料密度ρ/kg/m3杨氏模量E/Pa泊松比μA/Mpa B/Mpa n c m5A06-C铝试件2680 7.9E10 0.33 235.4 622.3 0.58 0.174 1.05接上表:材料Ef P1 SR Specific HeatFailStressRoomTemp(K)MeltTemp(K)模型5A06-C铝试件1e-6 4.77e-6 -9 294 1050Johnson-Cook上述3个表中采用的是kg-m-s单位制,在建模过程中采用的是cm-g-us单位制,因此需进行单位换算。
4 霍普金森压杆实验LS-DYNA有限元模型建立4.1 创建单元及材料类型首先选择单元类型,由于霍普金森压杆实验中子弹、输入杆、输出杆及试件均为圆柱体且共轴,因此,有限元模型单元类型选用三维实体SOLID164单元,并采用拉格朗日算法。
由于该实验过程时间短,为了方便输入参数以及仿真,本仿真采用cm-g-us 单位制进行建模。
因此,在建模的过程中,对单位进行了换算,将通用的kg-m-s 单位制参数换算成cm-g-us单位制。
另外,为了防止模型尺寸对数值模拟结果的影响,数值模拟过程中实体建模采用全比例尺寸。
为了节省数值计算工作量,采用给弹丸赋值初速度的办法忽略了炮膛和支架,并通过约束输出杆末端的办法忽略吸收杆,同时圆柱体的对称结构,建立了1/4三维实体模型,在后处理的时候还原成圆柱体。
4.2 划分网格在划分网格前,需要给实体模型赋予网格属性,即给实体模型选择之前创建的材料类型和单元类型。
在数值模拟过程中,网格密度太小会产生虚波现象,网格密度太大,对改善波形起的作用不是很大,相反会耗费大量机时。
因此,应该给实体模型选择合适的网格密度。
本仿真选择映射式网格划分有限元模型,并对前人的结果进行分析,不同网格密度的计算结果进行比较,设置了合适的网格数量。
4.3 定义接触LS-DYNA程序中处理接触-碰撞界面主要采用三种不同的算法,即:节点约束法、对称罚函数法和分配参数法。
在此,我采用了最常用的对称罚函数法。
对称罚函数法中接触刚度值K是个重要参数,根据应力波相关知识,弹性波在两个截面相等、波阻抗相同以及互相接触的弹性杆中传播时,应力波在杆的接触处无反射。
这里选择接触刚度值为1.2,此时入射杆上的反射波很微弱。
满足要求。
在数值模拟中,子弹与输入杆之间的接触类型为表面-表面自动接触类型,子弹为接触面,输入杆为目标面。
输入杆与试件之间的接触类型为节点-表面自动接触类型,试件与输出杆之间的接触类型也为节点-表面自动接触类型,由于试件的网格密度较大,所以试件为接触面,输入杆和输出杆为目标面。
4.4 定义对称和子弹速度由于采用了1/4三维实体模型,所以需要对对称面才用对称约束。
另外,由于省略了吸收杆,因此对输出杆末端进行了约束,建立了其z轴无位移约束,x 轴和y轴方向的平动约束和转动约束。
另外,前处理中定义了子弹的速度,并可以通过修改K文件中的*INITIAL-VELOCITY-GENRATION关键字来修改子弹的速度,从而进行不同速度的比较。
4.5 定义求解条件为了求得实验的完整结果,所定义的求解时间应略大于应力波在压杆中完整传播一个来回的时间。
通过查询资料,求解时间设为600us,最终结果达到了预想的要求。
5 实验结果分析图5.1 分离式霍普金森压杆LS-DYNA模型图如图5.1所示,改图为分离式霍普金森压杆LS-DYNA模型,从左到右依次是输出杆、试件、输入杆以及子弹。
通过LS-DYNA建立模型后,输入相关求解条件,然后生成K文件,用LS-DYNA求解器求解,并获得名为3dplot的文件,然后通过LS-DYNA后处理软件LS-Prepost软件分析求解结果。
图5.2 子弹速度为10m/s时试件靠近输入杆一侧的应变弹性波速是材料的基本参数,它可由材料的弹性模量和密度计算得出。
如图5.2所示,当t=184.94us时,试件开始有应变,说明弹性波已经通过输入杆进入试件了,可以计算出数值模拟中弹性波在压杆中的传播速度C0C0=(1/184.94)×106=5407.16m/s图5.3 不同子弹速度下输入杆中点处应变图5.4 不同子弹速度下输入杆中点处应力图5.5 不同子弹速度下输入杆中点出加速度在分离式霍普金森杆数值模拟中,不同子弹速度下,输入杆上应变、应力以及加速度与时间关系如图5.3、图5.4、图5.5所示。
如图5.3,图5.4所示,可以发现:(1)随着子弹速度的增大,入射波应力幅值随之增大;(2)随着子弹速度的增大,入射波的第一峰值点在时间域内的位置不发生变化;(3)入射波近似为矩形波,入射波在刚开始稍有振荡现象,表明波形弥散现象存在,但不是很严重。
