坐标系中的平行四边形ppt课件
合集下载
坐标系中的平行四边形
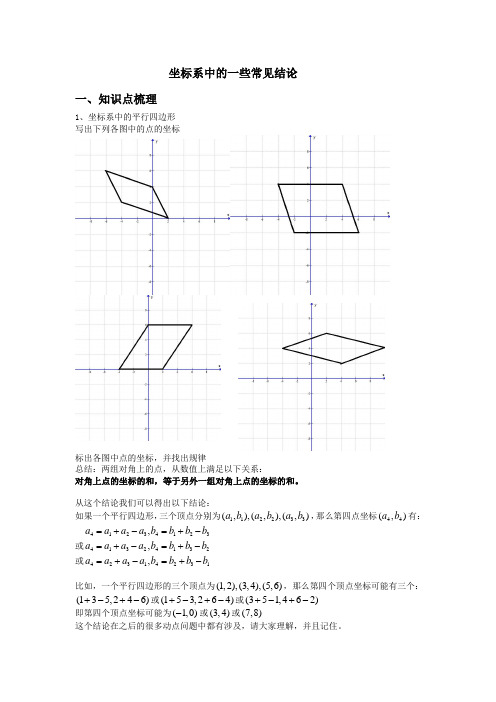
坐标系中的一些常见结论一、知识点梳理1、坐标系中的平行四边形 写出下列各图中的点的坐标标出各图中点的坐标，并找出规律总结：两组对角上的点，从数值上满足以下关系：对角上点的坐标的和，等于另外一组对角上点的坐标的和。
从这个结论我们可以得出以下结论：如果一个平行四边形，三个顶点分别为112233(,),(,),(,)a b a b a b ，那么第四点坐标44(,)a b 有： 41234123,a a a a b b b b =+-=+-或41324132,a a a a b b b b =+-=+-或42314231,a a a a b b b b =+-=+-比如，一个平行四边形的三个顶点为(1,2),(3,4),(5,6)，那么第四个顶点坐标可能有三个： (135,246)+-+-或(153,264)+-+-或(351,462)+-+-即第四个顶点坐标可能为(1,0)-或(3,4)或(7,8)这个结论在之后的很多动点问题中都有涉及，请大家理解，并且记住。
2、坐标系中，中点的表示在坐标系中标出以下各点，并观察，写出它们中点的坐标。
(1,2),(5,4) (1,3),(5,1)-你能得出什么结论？结论：坐标系中，两点坐标为1122(,),(,)a b a b ，那么它们的中点坐标为：1212(,)22a ab b ++3、坐标系中，两条平行线的表达式之间的关系请参照第一页，算出每个平行四边形对边所在直线对应的一次函数，比较它们的k 的关系。
结论：在同一个坐标系中，平行的两条直线，它们的k 相等。
特殊情况：如果两个直线k 都不存在，那么它们也是平行的。
4、坐标系中，知道两点求过这两点的直线的表达式如果一条直线经过点(,),(,)a b c d ，那么这个直线的表达式为：()() d b y x a b c a c a-=-+≠-5、坐标系中，两点之间距离的表示：如果一线段端点为(,),(,)a b c d，那么这条线段长度为：6、坐标系中，两直线垂直，那么这两直线所对应的一次函数表达式的k关系为：121k k=-或者12,k k一个为0，另一个不存在。
平行四边形的判定课件(浙教版)
定理1、一组对边平行且相等的四边形是平行四边形
跟踪练习：已知：线段CD是线段AB经平移所得的像， 连接AD,BC，求证四边形ABCD是平行四边形。
A
D
B
C
证明：∵线段CD是线段AB平移后的像
∴CD∥AB ∴四边形ABCD是平行四边形。
知识回顾
情境：请从下列条件中选取两个作为条件，使得
四边形ABCD是平行四边形
D
F CH
GA E
B
拓展与提高
勇攀高峰
直角坐标系内有平行四边形的三个顶点，它们的坐 标分别是A（2，1）、B（-1，-2）、C（3 , -2 ）， 试找出第四个顶点的位置，并写出它的坐标。
Y轴
（-2，1）D
3 2 1
太棒了！
A（2，1） E（6，1）
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 -1
∴BE=DF(平行四边形的对边分别相等)。
课内练习2
学以致用
已知：如图，在△ABC中，AB=AC,点P是BC上 一点，且PE//AC,PF//AB，问线段PE,PF,AB三 者之间的数量关系。
A
F
E
BP
C
课内练习3
学以致用
已知：如图，在 ABCD中，E，F分别是AB， CD的中点，分别延长BA,DC于G,H,使得AG=CH. 求证：GF//EH
X轴
A
-2
平行四边形的判定方法:
根据定义：两组对边分别平行的四边形叫做平行四边形. 定理1 一组对边平行且相等的四边形是平行四边形. 定理2 两组对边分别相等的四边形是平行四边形. ……
知识回顾
情境：请从下列条件中选取两个作为条件，使得
四边形ABCD是平行四边形
华东师大版八下数学1平行四边形的性质课件
4.如图，在□ ABCD中，AC平分∠DAB，AB=3，则□
ABCD的周长为（ ）
A.6
B.9
C.12
D.15
【解析】选C.∵四边形ABCD是平行四边形, ∴∠DAB=
∠DCB，AB∥CD，AB=CD,AD∥BC，AD=BC.
又∵AC平分∠DAB，∴∠DAC=∠BAC.
∴∠DAC=∠DCA,∴AD=DC.又∵AB=3,
AB+BC+CD+AD=2+4+2+4=12. 答案：12
６.如图，在平面直角坐标系中，□ OBCD的顶点O,B,D
的坐标如图所示，则顶点C的坐标为（ C ）
A. (3,7) B. (5,3) C. (7,3) D. (8,2)
y
D(2,3)
C
O (0,0) B(5,0) x
A
D
1、如图，在 ABCD中，
A:基础知识：
B
C
若∠A=130°，则∠B=__5_0_°__ 、∠C=__1_3_0_°_ 、
∠D=__5_0_°__.
B:变式训练： 若∠A+ ∠C= 200°，则∠A=_1_0_0_°__ 、∠B=__8_0_°__.
２.如图，在□ ABCD中， ∠B=110°，延长AD至点F，
延长CD至点E，连结EF，则∠E+∠F的值为（ ） A.110° B.30° C.50° D.70°
求证： ∠A＝ ∠C， ∠B＝ ∠D。 B
C
证明：∵四边形ABCD是平行四边形（已知）,
∴AB∥CD，AD∥BC（性质１）,
∴∠A+∠D＝180°， ∠A+∠B＝180°（两直线平行，同
旁内角互补）,
平行四边形的判定(2)(课件)-八年级数学下册(人教版)
一组对边平行且相等的四边形是平行四边形吗？
如图，在四边形ABCD中，AB∥CD，AB=CD.
求证：四边形ABCD是平行四边形.
证明：连接AC.
∵ AB∥CD
∴ ∠1=∠2
又∵ AB=CD，AC=CA
∴ △ABC≌△CDA (SAS)
∴ BC=DA
∴ 四边形ABCD的两组对边分别相等，它是平行四边形.
BQ=_________cm；CQ=_________cm.
15-2t
(3)当t为何值时，四边形PDCQ是平行四边形?
解:(3)∵AD//BC
∴当DP=CQ时，四边形PDCQ是平行四边形.
∴12-t=2t
解得t=4
∴t=4s时，四边形PDCQ是平行四边形.
平行四边形判定定理4：一组对边平行且相等的四边形是平行四边形.
t
12-t
AP=_________cm；DP=_________cm；
BQ=_________cm；CQ=_________cm.
2t
15-2t
(1)用含t的代数式表示:
12-t
t
AP=_________cm；DP=_________cm；
2t
BQ=_________cm；CQ=_________cm.
4.如图，在□ABCD中，E，F分别是边BC，AD上的点，有下列条件:
①AE//CF;②BE=FD;③∠1=∠2;④AE=CF.若要添加其中一个条件，使四边
形AECF一定是平行四边形，则添加的条件可以是( B )
A.①②③④
B.①②③
C.②③④
D.①③④
5.已知四边形ABCD，有以下四个条件:①AB//CD;②AB=CD;③BC// AD;④
22.2 平行四边形(2)课件
AD上的点，且AE∥CF
求证：∠BAE ＝ ∠DCF
证明：
∵四边形ABCD是平行四边形，
∴AD∥BC (平行四边形的定义)
∠BAD＝∠DCB
(平行四边形的对角相等）
又∵AE∥CF
是否还有其
∴四边形AECF是平行四边形 （平行四边形的定义）
他的方法？
得∠1＝∠2（平行四边形的对角相等）
∵∠3＝∠BAD－∠1
在□ABCD中，
∴AO=CO，BO=DO（平行四边形的两条对角线互相平分） 性质定理4： 平行四边形是中心对称图形，对称中心是两条对角线的交 点. 2.解平行四边形题目的关键是，要在复杂的图形中找到中心 对称的全等三角形，利用平行四边形的性质证明线段相等
布置作业 练习册 习题22.2(2)
A
B
SAOD SAOB
适时小结：平行四边
10 1 6 1 4 12cm 22
形中有四组面积相等 的三角形。
答： ΔAOD的周长为12cm， ΔAOD和ΔAOB的面积相等。
课堂练习
2.在平面直角坐标系中，□ABCD的对角线的交点
正好与坐标原点重合，且点A、B的坐标分别为A (3，2)、B (– 2，1)，试写出C、D两点的坐标.
有4对.
D
C
△AOD≌△COB
O
△ABD≌△CDB
A
B
Hale Waihona Puke △ACD≌△CAB△AOB≌△COD
学习新知
问2：由这些三角形全等，可得平行四边形的 对角线什么特点？
D
O
A
B
性质定理3： 平行四边形的两条 对角线互相平分.
C
答：AO＝CO,BO＝DO
符号语言：
人教版八年级数学下册期末复习课件：平行四边形 (共47张PPT)
论的个数是
()
• A．2
• B．3
• C．4
• D．5
7．如图，在△ABC 中，AB＝3，AC＝4，BC＝5，P 为边 BC 上一动点，PE⊥
AB 于点 E，PF⊥AC 于点 F，M 为 EF 中点，则 AM 的最小值为
(D )
A．54
B．45
C．53
D．65
8．如图，ABCD 是正方形，E、F 分别是 DC 和 CB 的延长
∠CBF，∴BF平分∠ABC．
• (3)解：△BEF是等腰三角形．理由如下：过 点F作FG⊥BE于点G.∵AD∥BC，FG⊥BE，
BE⊥AD，∴FG∥AD∥BC．∵F为CD的中点，
∴EG＝BG，∴EF＝BF，∴△BEF是等腰三
• ★集训2 特殊平行四边形的性质与判定的相 关计算与证明
• 7．已知四边形ABCD中，对角线AC与BD相A 交于点O，AD∥BC，下列判断中错误的是 ()
D．4 个
(B )
• 二、填空题(每小题5分，共20分)
• 9．已知一个菱形的两条对角线的长分别为 5210和24，则这个菱形的周长为______.
• 10．【湖北武汉中考】以正方形ABCD的边 A30D°或作15等0°边△ADE，则∠BEC的度数是 _______________.
• 11．如图，矩形ABCD的对角2线0 BD的中点为 O，过点O作OE⊥BC于点E，连接OA，已知 AB＝5，BC＝12，则四边形ABEO的周长为 ______.
• 4．如图，在□ABCD中，E、F分别是AB、
DC边上的点，AF与DE相交于点P，BF与CE 相41交于点Q.若S△APD＝16 cm2，S△BQC＝25 cm2，则图中阴影部分的面积为______cm2.
平面直角坐标系中的平行四边形
(1)试求b、c的值，并写出该二次函数表达式；
(2)动点P从A到D，同时动点Q从C到A都以每秒1个单位的速度运动，问：
①当P运动到何处时，有PQ⊥AC?
②当P运动到何处时，四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?
五、中考课堂议练（超越中考p68，2，3）
六、课堂小结作业：超越中考自主训练p70，5
教学章节
第16课平面直角坐标系中四边形
教学内容
平面直角坐标系中四边形
教学年级
9年级
教学课时
1课时
教学目标
1．在掌握平行四边形的判定方法的基础上，能够根据题目的具体情况选择不同的判定方法，解决平面直角坐标系中的四边形存在性问题.
2．经历例题探究过程，初步理解求解平面直角坐标系中四边形存在性问题的一般思路.
设计意图
教
学
过
程
设
计
一、聚集考点
如图，在平行四边形ABCD中，已知A(0,0) B(1,3),D(5,0),(1)你能得出点C的坐标吗？
二、考点互动讲练
1、考点母题
如图，在平行四边形ABCD中，A（x1,y1）B（x2,y2）C（x3,y3）D（x4,y4），AC与BD交于点E，点E的坐标（x,y），说说这些点的坐标有哪些关系。
三、变式训练
如图，抛物线y=14x2-32x-4与x轴交与A，B两点（点B在点A的右侧），与y轴交于点C，连接BC，以BC为一边，点O为对称中心作菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．
（1）求点A、B、C的坐标．
（2）当点P在线段OB上运动时，直线l分别交BD，BC于点M，N．试探究m为何值时，四边形CQMD是平行四边形，此时，请判断四边形CQBM的形状，并说明理由．
(2)动点P从A到D，同时动点Q从C到A都以每秒1个单位的速度运动，问：
①当P运动到何处时，有PQ⊥AC?
②当P运动到何处时，四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?
五、中考课堂议练（超越中考p68，2，3）
六、课堂小结作业：超越中考自主训练p70，5
教学章节
第16课平面直角坐标系中四边形
教学内容
平面直角坐标系中四边形
教学年级
9年级
教学课时
1课时
教学目标
1．在掌握平行四边形的判定方法的基础上，能够根据题目的具体情况选择不同的判定方法，解决平面直角坐标系中的四边形存在性问题.
2．经历例题探究过程，初步理解求解平面直角坐标系中四边形存在性问题的一般思路.
设计意图
教
学
过
程
设
计
一、聚集考点
如图，在平行四边形ABCD中，已知A(0,0) B(1,3),D(5,0),(1)你能得出点C的坐标吗？
二、考点互动讲练
1、考点母题
如图，在平行四边形ABCD中，A（x1,y1）B（x2,y2）C（x3,y3）D（x4,y4），AC与BD交于点E，点E的坐标（x,y），说说这些点的坐标有哪些关系。
三、变式训练
如图，抛物线y=14x2-32x-4与x轴交与A，B两点（点B在点A的右侧），与y轴交于点C，连接BC，以BC为一边，点O为对称中心作菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．
（1）求点A、B、C的坐标．
（2）当点P在线段OB上运动时，直线l分别交BD，BC于点M，N．试探究m为何值时，四边形CQMD是平行四边形，此时，请判断四边形CQBM的形状，并说明理由．
坐标系中的平行四边形共15页
60、人民的幸福是至高无个的法。— —西塞 罗
41、学问是异常珍贵的东西，从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间，才能认识自 己。——德国
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
坐标系中的平行四边形
56、极端的法规，就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要，人们 就不再 配享受 自 了公共 的利益 ；一部 分靠有 害的强 制，一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ，那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
41、学问是异常珍贵的东西，从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间，才能认识自 己。——德国
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
坐标系中的平行四边形
56、极端的法规，就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要，人们 就不再 配享受 自 了公共 的利益 ；一部 分靠有 害的强 制，一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ，那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
y
B1(a,2) B(0,1)
a+2=0+3 ∴a=1 1+b=2+0 ∴b=1
A1(3,b)
0
A(2,0)
x
精品课件
变式一：如图：求点D的坐标,使以A、B、C、 D为顶点的四边形为平行四边形。
(-2,5) D2
y
(3,7）
A
●
D1 (8,9)
● C（6,4）
●
B(1,2)
o
D3 (4,-1)
x
当图形的顶点位置不确定时，
o(A) D(e,0)x 图2
A(a,b) D(e,b)
o
x
图3
（2）在观图察2图中1，,2给,3,出你平能行发四现边平形行A四BC边D形的的顶四点个A，顶B点，的D的坐 标， 写横出坐图标2中,纵的坐顶标点之C间的的坐关标系是吗__？（__c+_e_,_d）_
（3）坐在标图对对，3中角角写，线线出给两两图出个个3平顶顶中行点点的四精的的顶品边课横纵点件形坐坐C的A标标B坐C之之D标和和的是相相顶_（等等_点_e;.-_Aa_，+_c_,Bd_），D的
探究—— 坐标系中平行四边形顶点的问题
精品课件
1.（1）在图1中，给出平行四边形ABCD的顶点A，B，D的 坐标， 写出图1中的顶点C的坐标是___（__5,_2_）_
y
y
y
B(1,2) C（5,2） B(c,d) C（c+e,d）
B(c,d) C（e-a+c,d）
o(A) D(4,0) x 图1
的中点旋转180°，点O落到点B的位置．抛物线
经过y点Aa，x点2 D是2该3抛x物线的顶点．
(1) 求a的值，点B的坐标及顶点D的坐标； (2) 若点P是x轴上一点，以P、A、D为顶点作平行四边形， 该平行四边形的另一顶点F在y轴上．写出点P的坐标(直接写 出答案即可)．
(1, 3 3 )
精品课件
要进行分类讨论。
精品课件
变式二：如图：将△ABC绕AC的中点P旋转 180°，点B落到点 B’的位置，求点B’的坐标；
(8,9)
y
A(C’)
(3,7）● ● P
(B’)
●
B (1,2)
o
● C(A’) （6,4）
x
精品课件
（07中考绍兴24题）如图，在平面直角坐标系中，O为原点，
点A、C的坐标分别为（2，0）、（1， ）．3 将3 △OAC绕AC
探究二:
对角线两个顶点的横坐标之和相等;
对角线两个顶点的纵坐标之和相等.
y
(c,d)B
(Aa,b)
o 图4
C’ (e-a+c,d+m) mC (e-a+c,d)
D’ (e,b+m) m D (e,b)
x
精品课件
归纳与发现
（3）通过对图1，2，3，4的观察，你会发现： 无论 平行四边形ABCD处于直角坐标系中哪个位置，当其顶 点坐标为A（xA，yA），B（ xB ，yB），
(2,0)
解:⑴把A(2,0)代入 yax2 2 3x,
得:a= 3
由题意:OA∥BC,而
OA=2,C(1, 3 3 )
∴B(3, 3 3 )
∵ y 3x22 3x
x+1=2+0
∴顶点D(1, 3)
(2) ∵A(2,0),D(1, 3)
设P(x,0),F(0,y) ①当P→A x+2=1+0
0+0=y- 3
∴ x=-1
Байду номын сангаас
②当P→D： 0-
3 =0+y
x=1
∴ y=- 3 ∴p2(1,0)
③当P→F： x+0=2+1
y+0=0- 3
∴
x=3
y=- 3 ∴p3(3,0)
y= 3
∴p1(-1,0)
∴存在点精p1品(-课1件,0), p2(1,0), p3(3,0)满足条件.
(07义乌）如图，抛物线
yx2 2x与x3轴交A、B两
(-1,0)
精品课件
(2,-3)
精品课件
小结：
一个规律: 坐标系中平行四边形
对角线两个顶点的横坐标之和相等;
对角线两个顶点的纵坐标之和相等.
两种思想：
1.分类讨论思想 2.方程精品思课件 想
精品课件
精品课件
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
精品课件
C（ xC ，yC），D（ xD，yD）时，
则:四个顶点的 横坐标之间的等量关系为 XA+XC=XB+XD； 纵坐标之间的等量关系为 yA+yC=yB+yD .
y
（xB,yB）
（xA,yA）
（xC,yC）
（xD,yD）
o
x
精品课件
1、如图,在平行四边形ABB1A1中A、B的坐标分别 （2,0）,（0,1），则a+b的值为（ A ） A、2 B、3 C、4 D、5
点（A点在B点左侧），直线与抛物
线交于A、C两点 ，其中C点的横坐标为2．
（1）求A、C两点的坐标；
（2）若点G抛物线上的动点，在x轴上是否存在点F， 使A、C、F、G这样的四个点为顶点的四边形是平行 四边形？如果存在，求出所有满足条件的F点坐标； 如果不存在， 请说明理由．
F1(1,0) F2(-3,0) F3(4+ 7,0) F4(4- 7 ,0)
B1(a,2) B(0,1)
a+2=0+3 ∴a=1 1+b=2+0 ∴b=1
A1(3,b)
0
A(2,0)
x
精品课件
变式一：如图：求点D的坐标,使以A、B、C、 D为顶点的四边形为平行四边形。
(-2,5) D2
y
(3,7）
A
●
D1 (8,9)
● C（6,4）
●
B(1,2)
o
D3 (4,-1)
x
当图形的顶点位置不确定时，
o(A) D(e,0)x 图2
A(a,b) D(e,b)
o
x
图3
（2）在观图察2图中1，,2给,3,出你平能行发四现边平形行A四BC边D形的的顶四点个A，顶B点，的D的坐 标， 写横出坐图标2中,纵的坐顶标点之C间的的坐关标系是吗__？（__c+_e_,_d）_
（3）坐在标图对对，3中角角写，线线出给两两图出个个3平顶顶中行点点的四精的的顶品边课横纵点件形坐坐C的A标标B坐C之之D标和和的是相相顶_（等等_点_e;.-_Aa_，+_c_,Bd_），D的
探究—— 坐标系中平行四边形顶点的问题
精品课件
1.（1）在图1中，给出平行四边形ABCD的顶点A，B，D的 坐标， 写出图1中的顶点C的坐标是___（__5,_2_）_
y
y
y
B(1,2) C（5,2） B(c,d) C（c+e,d）
B(c,d) C（e-a+c,d）
o(A) D(4,0) x 图1
的中点旋转180°，点O落到点B的位置．抛物线
经过y点Aa，x点2 D是2该3抛x物线的顶点．
(1) 求a的值，点B的坐标及顶点D的坐标； (2) 若点P是x轴上一点，以P、A、D为顶点作平行四边形， 该平行四边形的另一顶点F在y轴上．写出点P的坐标(直接写 出答案即可)．
(1, 3 3 )
精品课件
要进行分类讨论。
精品课件
变式二：如图：将△ABC绕AC的中点P旋转 180°，点B落到点 B’的位置，求点B’的坐标；
(8,9)
y
A(C’)
(3,7）● ● P
(B’)
●
B (1,2)
o
● C(A’) （6,4）
x
精品课件
（07中考绍兴24题）如图，在平面直角坐标系中，O为原点，
点A、C的坐标分别为（2，0）、（1， ）．3 将3 △OAC绕AC
探究二:
对角线两个顶点的横坐标之和相等;
对角线两个顶点的纵坐标之和相等.
y
(c,d)B
(Aa,b)
o 图4
C’ (e-a+c,d+m) mC (e-a+c,d)
D’ (e,b+m) m D (e,b)
x
精品课件
归纳与发现
（3）通过对图1，2，3，4的观察，你会发现： 无论 平行四边形ABCD处于直角坐标系中哪个位置，当其顶 点坐标为A（xA，yA），B（ xB ，yB），
(2,0)
解:⑴把A(2,0)代入 yax2 2 3x,
得:a= 3
由题意:OA∥BC,而
OA=2,C(1, 3 3 )
∴B(3, 3 3 )
∵ y 3x22 3x
x+1=2+0
∴顶点D(1, 3)
(2) ∵A(2,0),D(1, 3)
设P(x,0),F(0,y) ①当P→A x+2=1+0
0+0=y- 3
∴ x=-1
Байду номын сангаас
②当P→D： 0-
3 =0+y
x=1
∴ y=- 3 ∴p2(1,0)
③当P→F： x+0=2+1
y+0=0- 3
∴
x=3
y=- 3 ∴p3(3,0)
y= 3
∴p1(-1,0)
∴存在点精p1品(-课1件,0), p2(1,0), p3(3,0)满足条件.
(07义乌）如图，抛物线
yx2 2x与x3轴交A、B两
(-1,0)
精品课件
(2,-3)
精品课件
小结：
一个规律: 坐标系中平行四边形
对角线两个顶点的横坐标之和相等;
对角线两个顶点的纵坐标之和相等.
两种思想：
1.分类讨论思想 2.方程精品思课件 想
精品课件
精品课件
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
精品课件
C（ xC ，yC），D（ xD，yD）时，
则:四个顶点的 横坐标之间的等量关系为 XA+XC=XB+XD； 纵坐标之间的等量关系为 yA+yC=yB+yD .
y
（xB,yB）
（xA,yA）
（xC,yC）
（xD,yD）
o
x
精品课件
1、如图,在平行四边形ABB1A1中A、B的坐标分别 （2,0）,（0,1），则a+b的值为（ A ） A、2 B、3 C、4 D、5
点（A点在B点左侧），直线与抛物
线交于A、C两点 ，其中C点的横坐标为2．
（1）求A、C两点的坐标；
（2）若点G抛物线上的动点，在x轴上是否存在点F， 使A、C、F、G这样的四个点为顶点的四边形是平行 四边形？如果存在，求出所有满足条件的F点坐标； 如果不存在， 请说明理由．
F1(1,0) F2(-3,0) F3(4+ 7,0) F4(4- 7 ,0)