第7章2恒定磁场

合集下载

大学物理第7章恒定磁场(总结)

磁场对物质的影响实验
总结词
磁场对物质的影响实验是研究磁场对物质性质和行为影响的实验，通过观察物质在磁场中的变化，可以深入了解物质的磁学性质和磁场的作用机制。
详细描述
在磁场对物质的影响实验中，常见的实验对象包括铁磁性材料、抗磁性材料和顺磁性材料等。通过观察这些材料在磁场中的磁化、磁致伸缩等现象，可以研究磁场对物质内部微观结构和宏观性质的影响。此外，还可以通过测量物质的磁化曲线和磁滞回线等参数，进一步探究物质的磁学性质和磁畴结构。
毕奥-萨伐尔定律
02
描述了电流在空间中产生的磁场分布，即电流元在其周围空间
产生的磁场与电流元、距离有关。
磁场的高斯定理
03
表明磁场是无源场，即穿过任意闭合曲面的磁通量恒等于零。
磁场中的电流和磁动势
安培环路定律
描述了电流在磁场中所受的力与电流、磁动势之间的关系，即磁场中的电流所受的力与电流、磁动势沿闭合回路的线积分成正比。
磁流体动力学
研究磁场对流体运动的影响，如磁场对流体流动的导向、加速和减速作用。
磁力
磁场可以产生磁力，对物体进行吸引或排斥，可以用于物体的悬浮、分离和搬运等。
磁电阻
某些材料的电阻会受到磁场的影响，这种现象称为磁电阻效应，可以用于电子器件的设计。
磁场的工程应用
1 2
磁悬浮技术
利用磁场对物体的排斥力，实现物体的无接触悬浮，广泛应用于高速交通、悬浮列车等领域。
磁动势
描述了产生磁场的电流的量，即磁动势等于产生磁场的电流与线圈匝数的乘积。
磁阻
描述了磁通通过不同材料的难易程度，即磁阻等于材料磁导率与材料厚度的乘积。
磁场中的力
安培力

大学物理稳恒磁场的基本性质

7 – 3 稳恒磁场的基本性质
第七章稳恒磁场
四安培环路定理的应用举例
例1 求长直密绕螺线管内磁场
解 1 ) 对称性分析螺旋管内为均匀场 , 方向沿
轴向, 外部磁感强度趋于零，即 B 0 .
7 – 3 稳恒磁场的基本性质
第七章稳恒磁场
2 ) 选回路 L .
磁场 B 的方向与
电流 I 成右螺旋.
s
B dS B dS
S
S
-Br 2
7 – 3 稳恒磁场的基本性质
第七章稳恒磁场
例如图载流长直导线的电流为 I ,
形面积的磁通量.
解先求
试求通过矩 B ，对变磁场
B
给B出dΦ后0I 积分求BΦ// S
I
l
2π x dΦ BdS
0I
ldx

M
NB
++++++++++++
P
LO

B dl B dl B dl BPM
B MN 0nMNI B 0nI
无限长载流螺线管内部磁场处处相等 , 外部磁场为零.
7 – 3 稳恒磁场的基本性质
第七章稳恒磁场
例3 无限长载流圆柱体的磁场
I
解 1）对称性分析 2）选取回路
RR

rR
Bdl l
0I
L
2π rB 0I
B 0I
2π r
r B
0 r R
l
B
d
l

0
π π

7第七章稳恒磁场课件

稳恒磁场是涡旋场，静电场不是涡旋场。
例题： P237 7-19
电场与磁场比较
力线
电场起于正电荷止于负电荷不形成闭合曲线
高斯定理
S
E

dS

10（s内）qi
磁场
无头无尾闭合曲线

B dS 0
S

环路定理 E dl 0 L

B dl L
0 I
enB
B
s s

通过任意面元dS的磁通量： d B dS
穿过整个曲面S的磁通量为：

d B dS
S
S
B cosdS
S
B
dS

B
规定：外法线方向为正
（1）当 < 90°时： 0
s
（2）当 > 90°时： 0
B Bx L dBx dBsin

0IR 4 r3
2 R dl 0
0
2
R2I r3

0
2
(R2
R2I x2)3/2

Idl

r
dB
o
P
R
x
*
x
I
方向：图示沿x轴正向，即沿圆电流的轴线，与电流的环绕方向成右手螺旋关系。
如果令x＝0，则圆电流圆心O处的磁感应强度的大小为
第七章稳恒磁场
第七章稳恒磁场
7-1 磁感应强度磁场的高斯定理 7-2 安培定律 7-3 毕奥-萨伐尔定律 7-4 安培环路定律
7-1 磁感应强度磁场的高斯定理
一.磁感应强度
1. 磁场

恒定磁场

1恒定磁场1．真空中位于'r点的点电荷q的电位的泊松方程为（）2．由（）可知，无界空间中的恒定磁场由恒定磁场的散度和旋度方程共同决定3．恒定磁场在自由空间中是（）场4．磁通连续性定律公式物理意义：穿过任意闭和面的磁通量为（）。

即进入闭和面S的磁力线数与穿出闭和面S的磁力线数（），磁力线是闭和的5．安培环路定律公式物理意义：磁感应强度B沿任意闭和路径l的线积分，（）穿过路径l所围面积的总电流与的乘积6．一个载流的小闭和圆环称为（）7．电流环的面积与电流的乘积，称为（）8．在远离偶极子处，磁偶极子和电偶极子的场分布是（）的，但在偶极子附近，二者场分布（）9．磁力线是（）的，电力线是间断的10．介质在磁场作用下会产生（）11．磁化引起的分子电流、原子电流相当于（）12．磁偶极子产生（）磁场，叠加于原场之上，使磁场发生变化。

磁化的结果使介质中的合成磁场可能减弱，也可能增强13．介质磁性能分类：（）磁性介质，（）磁性介质，铁磁性及亚铁磁性介质14．（）磁性介质：二次磁场与外加磁场方向相反，导致介质中合成磁场减弱15．（）磁性介质：二次磁场与外加磁场方向相同，导致介质中合成磁场增强16．铁磁性及亚铁磁性介质：在（）作用下，磁化现象非常显著17．在无传导电流的均匀介质中，束缚电流体密度为（）18．只有磁场强度为零或磁场强度与介质表面相垂直的区域，束缚电流面密度为（）19．磁感应强度通过某一表面的通量称为（）20．与某电流交链的磁通量称为（）21．导线回路的总自感等于内、外自感之（）22．单位导线回路的内自感为（）23．磁场问题的基本变量是场源变量和两个基本的场变量：磁感应强度和磁场强度。

实验证明：磁场的两个基本变量之间的关系为（）24．磁通量连续性方程微分形式：（）25．安培力可以用磁能量的空间变化率称（）来计算26．自由空间中一半径为a的无限长导体圆柱，其中均匀流过电流I，求导体内外的磁感应强度27．一段长为L的导线，当其中有电流I通过时，求空间任一点的矢量磁位及磁感应强度28．磁导率为，内外半径分别为a，b的无限长空心导体圆柱，其中存在轴向均匀电流密度，求各处磁场强度和磁化电流密度。

第7章稳恒磁场(比奥萨法尔定律).

−
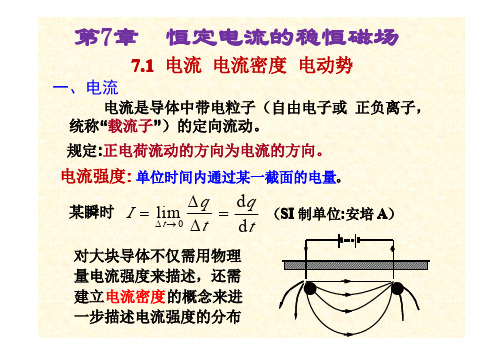
µ0I 4π R1
例3 载流直螺线管的磁场
如图所示，有一长为l , 半径为R的载流密绕直螺线管，螺线管的总匝数为N，通有电流I. 设把螺线管放在真空中，求管内轴线上一点处的磁感强度 .
dB = µ0R2dI
R
O
p*
dx x
x
++++++ +++++++ +
2（x2 + R2）3/2 dI = NI dx
�
q
�
在
�� v⊥ B
方向上受力
F = qv×B
7.4 电流和运动电荷的磁场
一、毕奥 — 萨伐尔定律及其应用
� 静电场：源(电荷) → E
�
� dE
=
1 4 πε0
⋅
dq r2
� er
磁场：源(电流) �
电流元：Idl :
→
� dB
=
B µ0
⋅
� Idl
× rˆ
4π r2
大小:
dB
=
µ0 4π
⋅
Idl sinθ r2
方向: 满足右手螺旋法则
∫ ∫ 真空中的磁导率: �
叠加原理 B =
µ0d=B�4π=×14µ0π0-7亨I利dlr�·米2× -rˆ1(H·m-1)
二、运动电荷的磁场
电流的磁场本质是运动电荷磁场
电产从流生毕元的萨磁定Id律场l�导：出dB�运=动µ电04I荷dπl�r的×3 磁r� 场
S：电流元横截面积
∫ B = µ 0 I θ 2 sin θdθ
4π r0 θ1
= 4µπ0rI0（cosθ1 − cosθ2）

第七章恒定电流的磁场

Bb Ba a
Bc
b
c
B
B dS
d m B dS
磁通量，定义为： m S
等于通过该面积的磁感线的条数， SI单位：Wb(韦伯) 1Wb=1T〃m
大学物理第三次修订本
第7章恒定电流的磁场直线电流的磁力线
通电螺线管的磁力线
I
圆电流的磁力线
I
I
I
大学物理第三次修订本
m B dS
磁场的高斯定律：
S
B
穿过任意闭合曲面的磁通量为零
BdS 0
磁场是无源场。
大学物理第三次修订本
第7章恒定电流的磁场
一、安培环路定理静电场磁场
7.4 安培环路定理
I
l
E dl 0 Bdl
r
永磁体为什么具有磁性？
安培指出：天然磁性（如永磁体）的产生也是由于磁体内部有电流流动。分子电流
I
n
N
大学物理第三次修订本
S
第 7章恒定电流的磁场基本磁现象
电流电流磁体电流
I1
I2
F
I
N I
F
F
S
磁体磁体
S N
磁场
电流磁体 I
N
S
运动电荷
磁场
大学物理第三次修订本
单位（SI）：A/m2
例：金属中的电流密度（载流子为电子）为：
J env
载流子的平均速度
二、恒定电流：导体内各处电流密度不随时间改变的电流称为---恒定电流。
大学物理第三次修订本
第7 章恒定电流的磁场基本磁现象磁性：具有能吸引铁磁物资（Fe、Co、Ni）的一种特性。磁体：具有磁性的物体。磁极：磁性集中的区域。 1、永磁体及其特性同极相斥异极相吸

恒定磁场分析

真空中本构关系
7
求证：
证明:
∫
ur r B ds = 0
Q
ur µ B= 0 4π
∫
r ur Id l × R R3
r r u r r µ0 Idl × eR r ∴ ∫ B ds = ∫ ∫ c R2 d s s 4π
又Q
uv ur uv uv ur uv A× B C = A B×C
23
2、磁偶极子的标量位（解释P116）磁偶极子的标量位（解释）在无源区域（在无源区域（只有无源 ∇ × H = J＝0 uu r 区域才定义标量位）：区域才定义标量位）： ∇×H =0 uu r H = −∇ ϕ m 由下面式子
P ( r ,θ , 0 )
µ0 µ0 1 A = p m × e r = − p m × ∇ 2 4πr 4π r B、幂级数近似）与求电偶极子类似的方法（余弦定理、幂级数近似）可以得到磁偶极子的矢量位和标量位：磁偶极子的矢量位和标量位：
µ0 µ0 1 A= p m × er = − p m × ∇ 2 4πr 4π r
的距离，是标量。其中 r 为场点 P 到磁偶极子中心 O 的距离，是标量。
这表明恒定磁场是无散有旋场，这表明恒定磁场是无散有旋场，无散有旋场传导电流是其旋涡源。传导电流是其旋涡源。
13
5－2、内、外半径分别为 a、b 的无限长空心圆柱中，均匀－、、的无限长空心圆柱中，分布着轴向电流求柱内、外的磁场强度。 I ，求柱内、外的磁场强度。
解：使用圆柱坐标系。电流密度沿轴线方向为使用圆柱坐标系。
12
3、真空（介质）中磁场的基本方程：真空（介质）中磁场的基本方程：
∫sB • d s = 0 , ∇•B =0 , ∇×H = J ∫c H • d l = I B = µ0H B = µH

大学物理第7章恒定磁场试题及答案.docx

第7章恒定磁场一、选择题1.磁场可以用下述哪一种说法来定义？[](A)只给电荷以作用力的物理量(B)只给运动电荷以作用力的物理量(C)贮存有能量的空间(D)能对运动电荷作功的物理量2.空间某点磁感应强度的方向，在下列所述定义中错误的是[](A)小磁针N极在该点的指向(B)运动正电荷在该点所受最大的力与其速度的矢积的方向(C)电流元在该点不受力的方向(D)载流线圈稳定平稳时，磁矩在该点的指向3.下列叙述中错误的是[](A) 一根给定的磁力线上各点处的B的大小一定相等一(B)一根给定的磁力线上各点处的〃的方向不一定相同(C)均匀磁场的磁力线是一组平行直线(D)载流长直导线周围的磁力线是一组同心圆坏4.下列关于磁力线的描述中正确的是[](A)条形磁铁的磁力线是从N极到S极的(B)条形磁铁的磁力线在磁铁内部是从S极到N极的(C)磁力线是从N极出发终止在S极的曲线(D)磁力线是不封闭的曲线5.下列叙述中不能正确反映磁力线性质的是[](A)磁力线是闭合曲线(B)磁力线上任一点的切线方向为运动电荷的受力方向(C)磁力线与载流回路彖环一样互相套连(D)磁力线与电流的流向互相服从右手定则6.关于磁场之I'可的相互作用有下列说法,其屮正确的是[](A)同性磁极相吸，异性磁极相斥(B)磁场屮小磁针的磁力线方向只有与磁场磁力线方向一致时,才能保证稳定平稳(C) 小磁针在非均匀磁场中一定向强磁场方向运动 (D) 在涡旋电场中，小磁针沿涡旋电场的电场线运动7. 一电荷放置在行驶的列车上，相对于地面来说，电荷产生电场和磁场的情况将是[](A) (B)只只产生产生电场磁场(C)既产生电场，又产生磁场 (D)既不产生电场，又不产生磁场 T7-1-7图8. 通以稳恒电流的长直导线，在其周阖产生电场和磁场的情况将是 [](A)只产生电场 (B) 只产生磁场(C) 既产生电场，又产生磁场 (D) 既不产生电场，乂不产生磁场9. 在电流元I d/激发的磁场中，若在距离电流元为r 处的磁感应强度为d B .则下列叙述中正确的是(C) dB 一的方向垂直于/d 乙与[组成的平面二T7-1-9图 (D) dB 的方向为(-厂)方向10. 决定长直螺线管中磁感应强度大小的因素是 [](A)通入导线中的电流强度 (B)螺线管的体积(C)螺线管的直径(D)与上述各因素均无关一-11. 磁场的高斯定理B-dS= 0,说明S[](A)穿入闭合曲血的磁感应线的条数必然等于穿出的磁感应线的条数(B) 穿入闭合曲面的磁感应线的条数不等于穿出的磁感应线的条数[](A) d B 一的方向与r 方向相同一(B) dB 的方向与/d/方向相同 dl(C) 一根磁感应线可以终止在闭合曲面内 (D) 一根磁感应线不可能完全处于闭合曲面内13. 磁场中的高斯路理JJ BdS= 0说明了磁场的性质之一是[](A)磁场力是保守力(B)磁力线可能闭合 (C)磁场是无源场(D)磁场是无势场14. 若某空间存在两无限长直载流导线，空间的磁场就不存在简单的对称性.此时该磁场的分布[](A)可以直接用安培环路定理来计算 (B) 只能用安培环路定理来计算 (C) 只能用毕奥-萨伐尔定律来计算(D) 可以用安培环路定理和磁场的叠加原理求出15.对于安培环路定律I ,在下面说法中正确的是[](A)H 只是穿过闭合环路的电流所激发,与环路外的电流无关(B)是环路内、外电流的代数和(C) 安培环路定律只在具有高度对称的磁场中才成立(D) 只有磁场分布具有高度对称性时,才能用它直接计算磁场强度的人小16. 在圆形电流的平面内取一同心圆形坏路，由于环路内无电流穿过，所以§H・d/[](A)圆形环路上各点的磁场强度为零(B) 圆形环路上各点的磁场强度方向垂直于环路平面 (C) 圆形坏路上各点的磁场强度方向指向圆心 (D) 圆形环路上各点的磁场强度方向为该点的切线方向12.安培环路定律/说明了磁场的性质之一是[](A)磁力线是闭合曲线(C)磁场是无源场(B)磁场力是保守力 (D)磁场是无势场17.下述情况中能用安培坏路定律求磁感应强度的是[](A) 一段载流直导线 (C) 一个环形电流(B) 无限长直线电流 (D) 任意形状的电流1& 取一闭合积分回路L,使三根载流导线穿过L 所围成的面.现改变三根导线之间的相互间隔，但不越出积分回路，则[](A)回路厶内的》/不变，厶上各点的8不变(B)回路厶内的工/不变,L 上各点的B 改变变，厶上各点的B 不变 (D)冋路厶内的》/改变，厶上各点的B 改变19.边长为L 的一个正方形线圈屮通有电流/,则线圈中心的磁感应强度的大小将](A)与厶成正比 (B)与厶成反比(C)与厶无关(D)与厶*成正比T7-1-19图 20. 一无限长直圆柱体，半径为沿轴向均匀流有电流. 磁感应强度大小为Bi,圆柱体外(r>R )感应强度大小为B2,则有[1(A) 31、均与厂成正比设圆柱体内(r<R )的 (B) B 、、B 2均与厂成反比(C) B\与F •成反比,与厂成正比(D) B 1与F •成正比，〃2与r 成反比 T7-1-20图21.如T7-1-21图所示，两根载有相同电流的无限长直导线，分别通过x 】 = l 和兀2=3的点，且平行于尹轴.由此可知,磁感一应强度B 为零的地方是 O12 3 x T7-1-21 图[](A) x=2的直线上(B) x>2的区域(C) x<l 的区域 (D)不在平而内22・一个半径为R 的圆形电流厶其圆心处的磁场强度大小为[1(A)4R (B)(C) 0(D)— 2R23. 有一个圆形冋路1及一个正方形冋路2,圆的直径和正方形回路的边长相等，二者屮通有大小相等的电流，它们在各自屮心产生的磁感应强度的大小之比BJB.为[](A) 0.90(B) 1.00(C) 1.11 (D) 1.2224. 一载有电流I 的细导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管(R = 2r ),两螺线管单位长度上的匝数相等•两螺线管屮的磁感应强度大小B R 和B r 应满足关系[](A) B R =2 B 丫 r(D) B R = 4 B r25. 两根载有相同电流的通电导线，彼此之间的斥力为F.如果它们的电流均增加一倍,相互之间的距离也加倍,则彼此之间的斥力将为变为FF[](A)—(B)— (C)F (D) 2F4226. 两束阴极射线(电子流)，以不同的速率向同一方向发射，则两束射线间[](A)存在三种力：安培力、库仑力和洛仑兹力 (B) 存在二种力:库仑力和洛仑兹力 (C) 存在二种力：安培力和洛仑兹力 (D) 只存在洛仑兹力27. 可以证明，无限接近长直电流处(r->0)的B 为--有限值.可是从毕一萨定律得到的长直电流的公式屮得出，当尸一0时B-8.解释这一矛盾的原因是 [](A)毕一萨定律得出的过程不够严密(B) 不可能存在真正的无限长直导线 (C) 当尸一0 口寸，毕一萨定律已不成立 (D) 毕一萨定律是一个近似理论28. 运动电荷受洛仑兹力后，其动能、动量的变化情况是[](A)动能守恒(B)动量守恒(C)动能、动量都守恒(D)动能、动量都不守恒29. 运动电荷垂直进入均匀磁场后，下列各量中不守恒是T7亠23图(B)B R =B 「 (C) 2B R =B[](A)动量(B)关于圆心的角动量(C)动能(D)电荷与质量的比值30. —电量为g 的带电粒子在均匀磁场中运动，下列说法中正确的是 [](A)只要速度大小相同,粒子所受的洛仑兹力就相同(B) 在速度不变的前提下，若电荷q 变为一么则粒子受力反向，数值不变 (C) 粒子进入磁场后，其动能和动量都不改变 (D) 洛仑兹力与速度方向垂直,所以其运动轨迹是圆31. 一个长直螺线管通有交流电，把一个带负电的粒子沿螺线管的轴线射入管屮，粒子将在管屮作 ](A)圆周运动 (B)沿管轴来回运动(C)螺旋线运动 (D)匀速直线运动T7-1-31图32. 一束正离子垂直射入一个均匀磁场与均匀电场互相平行且同向的区域.结果表明离子束在一与入射束垂直放置的荧光屏上产生一条抛物线,则所有粒子有相同的 [](A)动能(B)质量(C)电量(D)荷质比 T7-1-32图33. 质量为〃?、电量为g 的带电粒子，以速度v 沿与均匀磁场E 成g 角方向射入磁场，英轨迹为一螺旋线.若要增大螺距，应34. 在一个由南指向北的匀强磁场中，一束电子垂直地向下通过_B此 (C) [ ] (A)磁场，受到由由磁场对西下指向上指向它东的作用力的力•向耳V® 0 0T7-1-34 图—11 11 111[](A)增大磁场B (C)减小速度v (B)减少磁场B _(D) 增加夹角q(B)(D)由由北东指向指向南西35. 一电子在垂直于一均匀磁场方向作半径为R 的圆周运动，电子的速度为v ，忽略电子产生的磁场，则此轨道内所包圉面积的磁通量为x BxnmvRT7亠35图36. 一带电粒子垂直射入均匀磁场中，如果粒子质量增大到原来的两倍，入射速度增大到两倍，磁场的磁感应强度增大到4倍，忽略粒子运动产生的磁场，则粒子运动轨迹所包围范围内的磁通量增大到原来的1 1 [](A)2 倍 (B)4 倍(C)2 倍(D)4倍37. 一电子以速度丿垂直地入射到一磁感应强度为B 的均匀磁场中•忽略其电子产生的磁场,此时电子在磁场中运动的轨道所圉面积的磁通量 [](A)正比于3,正比于v 2 (B)反比于B,反比于v 2(C) 正比于5正比于v(D)反比于5反比于v38. 图中六根无限长导线相互绝缘，通过的电流均为/,区域I 、II 、均为相等的正方形.问哪个区域垂直指向里的磁通量最大？1(B) II 区/ III IV (C)III 区(D) IV 区T7-1-38 图39. 在某均匀磁场中放置有两个平面线圈,其面积S]二2S2,通有电流人二2/2,它们所受的最大磁力矩之比M 2为[](A)1 (B)2 (C)4 (D) 1/440. 有一由N 匝细导线绕成的平而正三角形线圈，边长为°,通有电流/,置于均匀外磁场3中.当线圈平面的法向与外磁场同向时，线圈所受到的磁力矩大小为 [](A) 3Na 岳/ 2(B) 3Na 炼 /4[](A)eR 2(B) emR (C)——eR(D)兀u41.一直径为2.0cm、匝数为300匝的圆线圈，放在5xl0'2T的磁场中，当线圈内通过10mA的电流时，磁场作用于线圈的最大磁力矩为[](A) 4.7 N.m (B) 4.7xlO'2N.m(C) 4.7x1 O'5 N.m (D) 4.7x10-4 N.m42.有一直径为8 cm的线圈，共12匝，通以电流5 A.现将此线圈置于磁感应强度为0.6 T的匀强磁场屮，则[](A)作用在线圈上的最大磁力矩为M=18N.m(B)作用在线圈上的最大磁力矩为M=1.8N.m(C)线圈正法线与B成30。

第7章稳恒磁场

o
L
P
x
结论任意平面载流导线在均匀磁场中所受的力，与其始点和终点相同的载流直导线所受的磁场力相同.
42
二物理学均匀磁场对载流线圈的作用力矩
将平面载流线圈放入均匀磁场中，
da边受到安培力大小:
Fda
Il
2
B
sin(
2
)
bc边受到安培力大小:
Fbc
Il 2 B
sin(
2
)
o
Fda
d
a
I
l1
qvB m v2 R
m qBR v
70 72 73 74 76
质谱仪的示意图
锗的质谱
30
物理学
霍耳效应
31
物理学
B
霍耳电压 Fm
UH
RH
IB d
b
d
vd+
+ ++
+q
+
- - - - - I
UH
Fe
qEH qvd B I qnvd S qnvdbd
EH vd B U H vd Bb
× ×
××0
粒子做匀速圆周运动
物理学
(3)
0与B成角
// 0 cos
0 sin
R m m0 sin
qB
qB
•
0 //
B
B
T 2R 2m qB
螺距 h ： h //T 0 cos T 2m0 cos
qB
h //
0
q R
物理学
例题1 :请根据磁感应强度的方向规定，给出下列情况运动电荷的受力方向：
B
c
en

电流与磁场

B dB 0
0 I dl R B B// d B cos 4 π r2 r
0 IR 4 π r3
2π R
0 IR2 d l 2( R 2 x 2 ) 0
3
2
§7-3 毕奥-萨伐尔定律 2π R Rdl 0 B 0 4 π R2 x2
I
解：dI I dl I Rd I d . . . dl . R R . . . 0 dI 0 I . d . dB d . R 2 . 2R 2 R
P B Bx dBx dBcos
2 2

x
dB
2
2
由于对称性
Idl
r
dB
dB
r
Idl
r
Idl
I
§7-3 毕奥-萨伐尔定律
第7章电流与磁场
电流元在a，b，c处 dB 方向
dB 0
c
⊙
b
Idl r

a
第7章电流与磁场 §7-3 毕奥-萨伐尔定律与点电荷电场公式比较：相同之处：都是元场源产生场的公式场强都与 r 2 成反比不同之处：公式的来源不同方向不同二、毕奥—萨伐尔定律应用举例恒定磁场的计算：选取电流元Idl或某些典型电流分布为积分元由毕-萨定律写出积分元的磁场dB及方向建立坐标系，将dB分解为分量式，对每个分量积分(统一变量、确定上下积分限)。分析对称性。求出总磁感应强度大小、方向，对结果进行分析
§7-2 恒定磁场和磁感应强度二、磁场磁感强度
第7章电流与磁场
1. 磁场(magnetic field) 运动电荷磁场运动电荷

第七章恒定磁场-习题解答

第七章、稳恒磁场
7-3 如图所示，一无限长载流绝缘直导线弯成如附图所示的
形状。求使o点的磁感应强度为零的半径a和b的比值。
解该载流系统由三部分组成，o点的磁感
应强度为载有相同电流的无限长直导线
及两个半径分别为a和b的圆环分别在该
处激发的磁感应强度的矢量和。设磁场方向以垂直纸面向内为正，向外为负。
方向垂直纸面向里。（2）由磁矩定义
方向垂直纸面向里。
第七章、稳恒磁场
7-20 质谱仪的构造原理如图所示。离子源S提供质量为M、
电荷为q的离子。离子初速很小，可以看作是静止的，然后经
过电压U的加速，进入磁感应强度为B的均匀磁场，沿着半圆
周运动，最后到达记录底片P上。测得离子在P上的位置到入
口处A的距离为x。试证明该离子的质量为：M ? qB 2 x 2 。
或由磁感应线是闭合曲线，也可推知
??
Φaefd
?
? Φabcd
?
0.24Wb
? Φ ? ?B?dS ? 0
第七章、稳恒磁场
7-9 一个非均匀磁场磁感应强度的变化规律为B=ky（k为常量），方向垂直纸面向外。磁场中有一边长为a的正方形线框，其位置如图所示。求通过线框的磁通量。
解在线框内坐标为y处取一长为a宽为 dy的矩形面积元dS，在dS中磁场可认为是均匀的，则通过dS的磁通量
? I2l
? 0 I1
2πx1
I2l
? ?7.2?
F2 10?4
? B2I2l N
?
? 0 I1
2πx2
I2l
负号表示合力方向水平向左。
第七章、稳恒磁场
习题7-16 一长直导线通有电流I =20A，另一导线ab通有电流I?=10A，两者互相垂直且共面，如图所示。求导线ab所受的作用力和对o点的力矩。

大学物理第七章稳恒磁场习题答案

第七章稳恒磁场习题7-1 一个半径为r 的半球面如图放在均匀磁场中，通过半球面的磁通量为多少？解：取平面S ’与半球面S 构成闭合曲面，根据高斯定理有 0m mS mS ΦΦΦ'=+=2cos mS mS r E ΦΦπα'=-=-球面外法线方向为其正方向7-2 如图所示，几种载流导线在平面内分布，电流均为I ，它们在点O 的磁感应强度各为多少？08IR μ垂直画面向外0022II RR μμπ-垂直画面向里 00+42I IR Rμμπ垂直画面向外 7-3 如图所示，两根导线沿半径方向引向铁环上的A ，B 两点，并在很远处与电源相连。

已知圆环的粗细均匀，求环中心O 的磁感应强度。

解：如图所示，圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生，但∞A 和∞B 在O 点产生的磁场为零。

且θ-πθ==21221R R I I 电阻电阻 1I 产生1B 方向⊥纸面向外πθπμ2)2(2101-=R I B2I 产生2B 方向⊥纸面向里πθμ22202R I B =∴1)2(2121=-=θθπI I B B 有0210=+=B B B7-4 如图所示，已知地球北极地磁场磁感强度B 的大小为6.0×10－5T 。

如设想此地磁场是由地球赤道上一圆电流所激发的，此电流有多大？流向如何？（已知圆电流轴线上北极点的磁感强度()R IRR IR B 24202/32220μμ=+=）解：9042 1.7310A RBI μ==⨯方向如图所示7-5 有一同轴电缆，其尺寸如题图所示．两导体中的电流均为I ，但电流的流向相反，导体的磁性可不考虑。

试计算以下各处的磁感应强度：（1）r<R 1；（2）R 1<r<R 2；（3）R 2<r<R 3；（4）r>R 3。

解：同轴电缆的电流分布具有轴对称性在电缆各区域中磁感应线是以电缆轴线为对称轴的同心圆。

大学物理学第五版马文蔚高等教育出版社磁场2

L
(7-19)
讨论： (1) 式中各量的含义： B ～环路上各点的磁感应强度。由环路内、外电流共同产生的。 I ～穿过环路内的电流的代数和。注意 I 的正负的确定方法。 L1 I2 I1 L2 I
I1

L3 L4
I2
① B d l 0 ( 2 I 2 I1 ) L1 ③ B d l 0 ( I1 I 2 )
n1 O
n2
7-4 毕奥-萨伐尔定律（Biot-Savart law）四.运动电荷的磁场
L
E
r
•P
+++ ++++ + ++++ +++ +++ +++ ++++++++ ++++ ++++ + ++ + ++ + +++ + ++ + +++ + ++ ++ ++ + + + +++ ++ ++ + + ++++ I d l e r +++ + ++++ +++++++++ + +++++ ++++++ +++d B 0 + + + + +++++ +++ +++ ++ ++ + + + + + + + (7-12c) 2 4 r dl S 运动电荷 q 产生的磁场导体单位体积内电荷数 n dB 0 (qnvS)dl B dl内电荷数: dN= nSdl sin 2 dN 4r (nSdl ) 0 I d l 0 dB sin vq sin 2 2 4 r 4 r 方向与 d B 同向，仍为 I d l r 。 q 的平均速度 v 取dl = v dt 0 qv r (7-15a) 矢量式：B 3 则电流元体积dV = Sdl = Svdt 4 r 0 qv er dN=ndV=nSvdt 此体积内电荷数： B (7-15b) 2 4 r dq qdN q(nSvdt) 说明： B 的方向垂直于 v 和 I qnvS 所确定的平面。 dt dt dt r

大学物理课后选择与作业答案

第七章恒定磁场7 －1 两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管，两个螺线管的长度相同，R ＝2r ，螺线管通过的电流相同为I ，螺线管中的磁感强度大小B R 、B r 满足（）（A ） r R B B 2= （B ） r R B B = （C ） r R B B =2 （D ）r R B B 4=分析与解在两根通过电流相同的螺线管中，磁感强度大小与螺线管线圈单位长度的匝数成正比．根据题意，用两根长度相同的细导线绕成的线圈单位长度的匝数之比21==R r n n r R 因而正确答案为（C ）。

7 －2 一个半径为r 的半球面如图放在均匀磁场中，通过半球面的磁通量为（）（A ）B r 2π2 （B ） B r 2π （C ）αB r cos π22（D ） αB r cos π2分析与解作半径为r 的圆S ′与半球面构成一闭合曲面，根据磁场的高斯定理，磁感线是闭合曲线，闭合曲面的磁通量为零，即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量；S B ⋅=m Φ．因而正确答案为（D ）．7 －3 下列说法正确的是（）（A ）闭合回路上各点磁感强度都为零时，回路内一定没有电流穿过（B ）闭合回路上各点磁感强度都为零时，回路内穿过电流的代数和必定为零（C ）磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度必定为零（D ）磁感强度沿闭合回路的积分不为零时，回路上任意一点的磁感强度都不可能为零分析与解由磁场中的安培环路定律，磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度不一定为零；闭合回路上各点磁感强度为零时，穿过回路的电流代数和必定为零。

因而正确答案为（B ）．7 －4 在图（ａ）和（ｂ）中各有一半径相同的圆形回路L1 、L2 ，圆周内有电流I1 、I2 ，其分布相同，且均在真空中，但在（ｂ）图中L2 回路外有电流I3 ，P 1 、P 2 为两圆形回路上的对应点，则（）（A ） ⎰⎰⋅=⋅21L L d d l B l B ，21P P B B =（B ） ⎰⎰⋅≠⋅21L L d d l B l B ，21P P B B =（C ） ⎰⎰⋅=⋅21L L d d l B l B ，21P P B B ≠（D ） ⎰⎰⋅≠⋅21L L d d l B l B ，21P P B B ≠分析与解由磁场中的安培环路定律，积分回路外的电流不会影响磁感强度沿回路的积分；但同样会改变回路上各点的磁场分布．因而正确答案为（C ）．*7 －5 半径为R 的圆柱形无限长载流直导体置于均匀无限大磁介质之中，若导体中流过的恒定电流为I ，磁介质的相对磁导率为μｒ（μｒ＜1），则磁介质内的磁化强度为（）（A ）()r I μr π2/1-- （B ） ()r I μr π2/1- （C ） r I μr π2/- （D ） r μI r π2/分析与解利用安培环路定理可先求出磁介质中的磁场强度，再由M ＝（μｒ－1）H求得磁介质内的磁化强度，因而正确答案为（B ）．7 －15 如图所示，载流长直导线的电流为I ，试求通过矩形面积的磁通量．分析由于矩形平面上各点的磁感强度不同，故磁通量Φ≠BS ．为此，可在矩形平面上取一矩形面元d S ＝l d x ［图（ｂ）］，载流长直导线的磁场穿过该面元的磁通量为x l xlμΦd π2d d 0=⋅=S B 矩形平面的总磁通量ΦΦ⎰=d解由上述分析可得矩形平面的总磁通量⎰==211200ln π2d π2d d d d Il μx l x l μΦ 7 －16 已知10 mm 2裸铜线允许通过50 A 电流而不会使导线过热．电流在导线横截面上均匀分布．求：（1）导线内、外磁感强度的分布；（2）导线表面的磁感强度．分析可将导线视作长直圆柱体，电流沿轴向均匀流过导体，故其磁场必然呈轴对称分布，即在与导线同轴的圆柱面上的各点，B 大小相等．方向与电流成右手螺旋关系．为此，可利用安培环路定理，求出导线表面的磁感强度．解（1）围绕轴线取同心圆为环路L ，取其绕向与电流成右手螺旋关系，根据安培环路定理，有∑⎰=⋅=⋅I μB 0πr 2d l B在导线内r ＜R ， 2222πππRr r R I I ==∑，因而 202πRIrμB =在导线外r ＞R ，I I =∑，因而rIμB 2π0=磁感强度分布曲线如图所示．（2）在导线表面磁感强度连续，由I ＝50 A ，m 1078.1π/3-⨯==s R ，得T 106.52π30-⨯==RIμB 7 －25 霍尔效应可用来测量血流的速度，其原理如图所示．在动脉血管两侧分别安装电极并加以磁场．设血管直径为d ＝2.0 mm ，磁场为B ＝0.080 T ，毫伏表测出血管上下两端的电压为U H ＝0.10 mV ，血流的流速为多大？分析血流稳定时，有H qE B q =v由上式可以解得血流的速度．解依照分析m/s 63.0===dBU B E HH v 7 －29 如图（ａ）所示，一根长直导线载有电流I 1 ＝30 A ，矩形回路载有电流I 2 ＝20 A ．试计算作用在回路上的合力．已知d ＝1.0 cm ，b ＝8.0 cm ，l ＝0.12 m ．分析矩形上、下两段导线受安培力F 1 和F 2 的大小相等，方向相反，对不变形的矩形回路来说，两力的矢量和为零．而矩形的左右两段导线，由于载流导线所在处磁感强度不等，所受安培力F 3 和F 4 大小不同，且方向相反，因此线框所受的力为这两个力的合力．解由分析可知，线框所受总的安培力F 为左、右两边安培力F 3 和F 4 之矢量和，如图（ｂ）所示，它们的大小分别为dlI I μF π22103=()b d lI I μF +=π22104故合力的大小为()N 1028.1π2π2321021043-⨯=+-=-=b d lI I μd l I I μF F F 合力的方向朝左，指向直导线．第八章电磁感应电磁场8 －1 一根无限长平行直导线载有电流I ，一矩形线圈位于导线平面内沿垂直于载流导线方向以恒定速率运动（如图所示），则（）（A ）线圈中无感应电流（B ）线圈中感应电流为顺时针方向（C ）线圈中感应电流为逆时针方向（D ）线圈中感应电流方向无法确定分析与解由右手定则可以判断，在矩形线圈附近磁场垂直纸面朝里，磁场是非均匀场，距离长直载流导线越远，磁场越弱．因而当矩形线圈朝下运动时，在线圈中产生感应电流，感应电流方向由法拉第电磁感应定律可以判定．因而正确答案为（B ）．8 －2 将形状完全相同的铜环和木环静止放置在交变磁场中，并假设通过两环面的磁通量随时间的变化率相等，不计自感时则（）（A ）铜环中有感应电流，木环中无感应电流（B ）铜环中有感应电流，木环中有感应电流（C ）铜环中感应电动势大，木环中感应电动势小（D ）铜环中感应电动势小，木环中感应电动势大分析与解根据法拉第电磁感应定律，铜环、木环中的感应电场大小相等，但在木环中不会形成电流．因而正确答案为（A ）．8 －3 有两个线圈，线圈1 对线圈2 的互感系数为M 21 ，而线圈2 对线圈1的互感系数为M 12 ．若它们分别流过i 1 和i 2 的变化电流且ti t i d d d d 21<，并设由i 2变化在线圈1 中产生的互感电动势为ε12 ，由i 1 变化在线圈2 中产生的互感电动势为ε21 ，下述论断正确的是（）．（A ）2112M M = ，1221εε= （B ）2112M M ≠ ，1221εε≠ （C ）2112M M =， 1221εε<（D ）2112M M = ，1221εε<分析与解教材中已经证明M21 ＝M12 ，电磁感应定律t i M εd d 12121=；tiM εd d 21212=．因而正确答案为（D ）．8 －4 对位移电流，下述四种说法中哪一种说法是正确的是（）（A ）位移电流的实质是变化的电场（B ）位移电流和传导电流一样是定向运动的电荷（C ）位移电流服从传导电流遵循的所有定律（D ）位移电流的磁效应不服从安培环路定理分析与解位移电流的实质是变化的电场．变化的电场激发磁场，在这一点位移电流等效于传导电流，但是位移电流不是走向运动的电荷，也就不服从焦耳热效应、安培力等定律．因而正确答案为（A ）．8 －5 下列概念正确的是（）（A ）感应电场是保守场（B ）感应电场的电场线是一组闭合曲线（C ） LI Φm =，因而线圈的自感系数与回路的电流成反比（D ） LI Φm =，回路的磁通量越大，回路的自感系数也一定大分析与解对照感应电场的性质，感应电场的电场线是一组闭合曲线．因而正确答案为（B ）．8 －6 一铁心上绕有线圈100匝，已知铁心中磁通量与时间的关系为()Wb π100sin 100.85t Φ⨯=，求在s 100.12-⨯=t 时，线圈中的感应电动势．分析由于线圈有N 匝相同回路，线圈中的感应电动势等于各匝回路的感应电动势的代数和，在此情况下，法拉第电磁感应定律通常写成tψt ΦN ξd d d d -=-=，其中ΦN ψ=称为磁链．解线圈中总的感应电动势()()t tΦNξπ100cos 51.2d d =-= 当s 100.12-⨯=t 时，V 51.2=ξ．8 －7 有两根相距为d 的无限长平行直导线，它们通以大小相等流向相反的电流，且电流均以tId d 的变化率增长．若有一边长为d 的正方形线圈与两导线处于同一平面内，如图所示．求线圈中的感应电动势．分析本题仍可用法拉第电磁感应定律tΦξd d -=来求解．由于回路处在非均匀磁场中，磁通量就需用⎰⋅=S ΦS B d 来计算（其中B 为两无限长直电流单独存在时产生的磁感强度B 1与B 2 之和）．为了积分的需要，建立如图所示的坐标系．由于B 仅与x 有关，即()B B x =，故取一个平行于长直导线的宽为ｄx 、长为d 的面元ｄS ，如图中阴影部分所示，则x d S d d =，所以，总磁通量可通过线积分求得（若取面元y x S d d d =，则上述积分实际上为二重积分）．本题在工程技术中又称为互感现象，也可用公式tlM E M d d -=求解．解1 穿过面元ｄS 的磁通量为()x d xIμx d d x I μΦd π2d π2d d d d 0021-+=⋅+⋅=⋅=S B S B S B因此穿过线圈的磁通量为()43ln π2d π2d π2d 02020Id μx x Id μx d x Id μΦΦd d dd=-+==⎰⎰⎰再由法拉第电磁感应定律，有tI d μt ΦE d d 43ln π2d d 0⎪⎭⎫ ⎝⎛=-= 解2 当两长直导线有电流I 通过时，穿过线圈的磁通量为43ln π20dI μΦ=线圈与两长直导线间的互感为43ln π20d μI ΦM ==当电流以tld d 变化时，线圈中的互感电动势为 tI d μt I ME d d 43ln π2d d 0⎪⎭⎫ ⎝⎛=-= 试想：如线圈又以速率v 沿水平向右运动，如何用法拉第电磁感应定律求图示位置的电动势呢？此时线圈中既有动生电动势，又有感生电动势．设时刻t ，线圈左端距右侧直导线的距离为ξ，则穿过回路的磁通量()ξf ΦS,1d =⋅=⎰S B ，它表现为变量I 和ξ的二元函数，将Φ代入tΦE d d -= 即可求解，求解时应按复合函数求导，注意，其中v =t ξd d ，再令ξ＝d 即可求得图示位置处回路中的总电动势．最终结果为两项，其中一项为动生电动势，另一项为感生电动势．8 －13 如图（ａ）所示，金属杆AB 以匀速12.0m s -=⋅v 平行于一长直导线移动，此导线通有电流I ＝40A ．求杆中的感应电动势，杆的哪一端电势较高？分析本题可用两种方法求解．（1）用公式()l B d ⋅⨯=⎰lE v 求解，建立图（a ）所示的坐标系，所取导体元x l d d =，该处的磁感强度xIμB π20=．（2）用法拉第电磁感应定律求解，需构造一个包含杆AB 在内的闭合回路．为此可设想杆AB 在一个静止的形导轨上滑动，如图（ｂ）所示．设时刻t ，杆AB 距导轨下端CD 的距离为y ，先用公式⎰⋅=SΦS B d 求得穿过该回路的磁通量，再代入公式tΦE d d -=，即可求得回路的电动势，亦即本题杆中的电动势．解1 根据分析，杆中的感应电动势为()V 1084.311ln 2πd 2πd d 50m1.1m 1.00-⨯-=-=-==⋅⨯=⎰⎰vv v I μx x μxl E ABAB l B 式中负号表示电动势方向由B 指向A ，故点A 电势较高．解2 设顺时针方向为回路AB CD 的正向，根据分析，在距直导线x 处，取宽为ｄx 、长为y 的面元ｄS ，则穿过面元的磁通量为x y xIμΦd 2πd d 0=⋅=S B 穿过回路的磁通量为11ln 2πd 2πd 0m1.1m 1.00⎰⎰-===SIyμx y x I μΦΦ回路的电动势为V 1084.32πd d 11ln 2πd d 500-⨯-=-=-=-=Iyμt y x I μt ΦE 由于静止的形导轨上电动势为零，所以V 1084.35-⨯-==E E AB式中负号说明回路电动势方向为逆时针，对AB 导体来说，电动势方向应由B 指向A ，故点A 电势较高．8 －14 如图（ａ）所示，在“无限长”直载流导线的近旁，放置一个矩形导体线框，该线框在垂直于导线方向上以匀速率v 向右移动，求在图示位置处，线框中感应电动势的大小和方向．分析本题亦可用两种方法求解．其中应注意下列两点：1．当闭合导体线框在磁场中运动时，线框中的总电动势就等于框上各段导体中的动生电动势的代数和．如图（ａ）所示，导体eh 段和fg 段上的电动势为零［此两段导体上处处满足()0l B =⋅⨯d v ］，因而线框中的总电动势为()()()()hg ef hgef gh ef E E E -=⋅⨯-⋅⨯=⋅⨯+⋅⨯=⎰⎰⎰⎰l B l B l B l B d d d d v v v v 其等效电路如图（ｂ）所示．2．用公式tΦE d d -=求解，式中Φ是线框运动至任意位置处时，穿过线框的磁通量．为此设时刻t 时，线框左边距导线的距离为ξ，如图（c ）所示，显然ξ是时间t 的函数，且有v =t ξd d ．在求得线框在任意位置处的电动势E （ξ）后，再令ξ＝d ，即可得线框在题目所给位置处的电动势．解1 根据分析，线框中的电动势为hg ef E E E -=()()⎰⎰⋅⨯-⋅⨯=hgef l B l B d d v v ()⎰⎰+-=2201000d 2πd 2πl l l l d I μl d I μv v ()1202πl d I I μ+=1vI 由E ef ＞E hg 可知，线框中的电动势方向为efgh ．解2 设顺时针方向为线框回路的正向．根据分析，在任意位置处，穿过线框的磁通量为 ()()ξl ξξx Il μdx ξx Il μΦl 120020ln π2π21++=+=⎰ 相应电动势为 ()()1120π2d d l ξξl l I μt ΦξE +=-=v 令ξ＝d ，得线框在图示位置处的电动势为()1120π2l d d l l I μE +=v 由E ＞0 可知，线框中电动势方向为顺时针方向．8 －19 截面积为长方形的环形均匀密绕螺绕环，其尺寸如图（ａ）所示，共有N 匝（图中仅画出少量几匝），求该螺绕环的自感L ．分析如同电容一样，自感和互感都是与回路系统自身性质（如形状、匝数、介质等）有关的量．求自感L 的方法有两种：1．设有电流I 通过线圈，计算磁场穿过自身回路的总磁通量，再用公式IΦL =计算L ．2．让回路中通以变化率已知的电流，测出回路中的感应电动势E L ，由公式t I E L L d /d =计算L ．式中E L 和t I d d 都较容易通过实验测定，所以此方法一般适合于工程中．此外，还可通过计算能量的方法求解．解用方法1 求解，设有电流I 通过线圈，线圈回路呈长方形，如图（ｂ）所示，由安培环路定理可求得在R 1 ＜r ＜R 2 范围内的磁场分布为xNI μB π20= 由于线圈由N 匝相同的回路构成，所以穿过自身回路的磁链为12200ln π2d π2d 21R R hI N μx h x NI μN N ψS R R ==⋅=⎰⎰S B 则1220ln π2R R h N μI ψL = 若管中充满均匀同种磁介质，其相对磁导率为μr ，则自感将增大μr 倍．第九章振动9-1 一个质点作简谐运动，振幅为A ，起始时刻质点的位移为2A -，且向x 轴正方向运动，代表此简谐运动的旋转矢量为（）题９-１图分析与解（b ）图中旋转矢量的矢端在x 轴上投影点的位移为－A /2，且投影点的运动方向指向O x 轴正向，即其速度的x 分量大于零，故满足题意．因而正确答案为（b ）．9-2 已知某简谐运动的振动曲线如图（a ）所示，则此简谐运动的运动方程为（）()()()()()()()()cm π32π34cos 2D cm π32π34cos 2B cm π32π32cos 2C cm π32π32cos 2A ⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡-=t x t x t x t x题９-２图分析与解由振动曲线可知，初始时刻质点的位移为 –A /2，且向x 轴负方向运动．图（ｂ）是其相应的旋转矢量图，由旋转矢量法可知初相位为3/π2．振动曲线上给出质点从–A /2 处运动到+A 处所需时间为1 s ，由对应旋转矢量图可知相应的相位差3/π4Δ=，则角频率()1s 3/π4Δ/Δ-==t ω，故选（D ）．本题也可根据振动曲线所给信息，逐一代入方程来找出正确答案．9-3 两个同周期简谐运动曲线如图（a ）所示， x 1 的相位比x 2 的相位（）（A ）落后2π （B ）超前2π （C ）落后π （D ）超前π 分析与解由振动曲线图作出相应的旋转矢量图（b ）即可得到答案为（b ）．题９-３图9-4 当质点以频率ν 作简谐运动时，它的动能的变化频率为（）（A ） 2v （B ）v （C ）v 2 （D ）v 4 分析与解质点作简谐运动的动能表式为()ϕωω+=t A m E k 222sin 21，可见其周期为简谐运动周期的一半，则频率为简谐运动频率ν的两倍．因而正确答案为（C ）． 9-5 图（a ）中所画的是两个简谐运动的曲线，若这两个简谐运动可叠加，则合成的余弦振动的初相位为（）（A ） π23 （B ）π21 （C ）π （D ）0 分析与解由振动曲线可以知道，这是两个同振动方向、同频率简谐运动，它们的相位差是π（即反相位）．运动方程分别为t A x ωcos 1=和()πcos 22+=t ωA x ．它们的振幅不同．对于这样两个简谐运动，可用旋转矢量法，如图（b ）很方便求得合运动方程为t A x ωcos 21=．因而正确答案为（D ）．9-7 若简谐运动方程为()()m π25.0π20cos 10.0+=t x ，求：（1）振幅、频率、角频率、周期和初相；（2）s 2=t 时的位移、速度和加速度．分析可采用比较法求解．将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较，即可求得各特征量．运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t 值后，即可求得结果．解（1）将()()m π25.0π20cos 10.0+=t x 与()ϕω+=t A x cos 比较后可得：振幅A ＝0.10m ，角频率1s π20-=ω，初相ϕ＝0.25π，则周期s 1.0/π2==ωT ，频率Hz /1T =v ．（２）s 2=t 时的位移、速度、加速度分别为()m 1007.7π25.0π40cos 10.02-⨯=+=t x()-1s m 44.4π25.0π40sin π2d /d ⋅-=+-==t x v()-22222s m 1079.2π25.0π40cos π40d /d ⋅⨯-=+-==t x a9-8 一远洋货轮，质量为m ，浮在水面时其水平截面积为S ．设在水面附近货轮的水平截面积近似相等，水的密度为ρ，且不计水的粘滞阻力，证明货轮在水中作振幅较小的竖直自由运动是简谐运动，并求振动周期．分析要证明货轮作简谐运动，需要分析货轮在平衡位置附近上下运动时，它所受的合外力F 与位移x 间的关系，如果满足kx F -=，则货轮作简谐运动．通过kx F -=即可求得振动周期k m ωT /π2/π2==．证货轮处于平衡状态时［图（a ）］，浮力大小为F ＝mg ．当船上下作微小振动时，取货轮处于力平衡时的质心位置为坐标原点O ，竖直向下为x 轴正向，如图（b ）所示．则当货轮向下偏移x 位移时，受合外力为∑'+=F P F其中F '为此时货轮所受浮力，其方向向上，大小为gSx mg gSx F F ρρ+=+='题９-８图则货轮所受合外力为kx gSx F P F -=-='-=∑ρ式中gS k ρ=是一常数．这表明货轮在其平衡位置上下所作的微小振动是简谐运动．由∑=t x m F 22d d /可得货轮运动的微分方程为 0d d 22=+m gSx t x //ρ令m gS /ρω=2，可得其振动周期为 gS ρm πωT /2/π2==9-12 一放置在水平桌面上的弹簧振子，振幅A ＝2.0 ×10-2 m ，周期T ＝0.50ｓ．当t ＝0 时，（1）物体在正方向端点；（2）物体在平衡位置、向负方向运动；（3）物体在x ＝-1.0×10-2m 处，向负方向运动；（4）物体在x ＝-1.0×10-2 m 处，向正方向运动．求以上各种情况的运动方程．分析在振幅A 和周期T 已知的条件下，确定初相φ是求解简谐运动方程的关键．初相的确定通常有两种方法．（1）解析法：由振动方程出发，根据初始条件，即t ＝0 时，x ＝x 0 和v ＝v 0 来确定φ值．（2）旋转矢量法：如图（a ）所示，将质点P 在Ox 轴上振动的初始位置x 0 和速度v 0 的方向与旋转矢量图相对应来确定φ．旋转矢量法比较直观、方便，在分析中常采用．9-28 已知两同方向、同频率的简谐运动的运动方程分别为()()m π75.010cos 05.01+=t x ；()()m π25.010cos 06.02+=t x ．求：（1）合振动的振幅及初相；（2）若有另一同方向、同频率的简谐运动()()m 10cos 07033ϕ+=t x .，则3ϕ为多少时，x 1 ＋x 3 的振幅最大？又3ϕ 为多少时，x 2 ＋x 3 的振幅最小？题9-28 图分析可采用解析法或旋转矢量法求解.由旋转矢量合成可知，两个同方向、同频率简谐运动的合成仍为一简谐运动，其角频率不变；合振动的振幅()12212221cos 2ϕϕ-++=A A A A A ，其大小与两个分振动的初相差12ϕϕ-相关．而合振动的初相位()()[]22112211cos cos sin sin arctan ϕϕϕϕϕA A A A ++=/解（1）作两个简谐运动合成的旋转矢量图（如图）．因为2/πΔ12-=-=，故合振动振幅为 ()m 1087cos 2212212221-⨯=-++=.ϕϕA A A A A 合振动初相位()()[]rad1.48arctan11cos cos sin sin arctan 22112211==++=ϕϕϕϕϕA A A A / （2）要使x 1 ＋x 3 振幅最大，即两振动同相，则由π2Δk =得,...2,1,0,π75.0π2π213±±=+=+=k k k要使x 1 ＋x 3 的振幅最小，即两振动反相，则由()π12Δ+=k 得 (),...2,1,0,π25.1π2π1223±±=+=++=k k k题9-12 图解由题给条件知A ＝2.0 ×10-2 m ，1s π4/2-==T ω，而初相φ可采用分析中的两种不同方法来求．解析法：根据简谐运动方程()ϕω+=t A x cos ，当0t =时有()ϕω+=t A x cos 0，sin 0ωA -=v ．当（1）A x =0时，1cos 1=ϕ，则01=ϕ；（2）00=x 时，0cos 2=ϕ，2π2±=，因00<v ，取2π2=；（3）m 100120-⨯=.x 时，50cos 3.=ϕ，3π3±= ，由00<v ，取3π3=；（4）m 100120-⨯-=.x 时，50cos 4.-=ϕ，3ππ4±= ，由00>v ，取3π44=．旋转矢量法：分别画出四个不同初始状态的旋转矢量图，如图（b ）所示，它们所对应的初相分别为01=ϕ，2π2=，3π3=，3π44=．振幅A 、角频率ω、初相φ均确定后，则各相应状态下的运动方程为（1）()m t πcos4100.22-⨯=x （2）()()m /2πt π4cos 100.22+⨯=-x （3）()()m /3πt π4cos 100.22+⨯=-x （4）()()m /3π4t π4cos 100.22+⨯=-x 第十章波动10-1 图（a ）表示t ＝0 时的简谐波的波形图，波沿x 轴正方向传播，图（b ）为一质点的振动曲线．则图（a ）中所表示的x ＝0 处振动的初相位与图（b ）所表示的振动的初相位分别为（）题10-1 图（Ａ）均为零（Ｂ）均为2π （Ｃ）均为2π- （Ｄ） 2π 与2π- （Ｅ） 2π-与2π 分析与解本题给了两个很相似的曲线图，但本质却完全不同．求解本题要弄清振动图和波形图不同的物理意义．图（a ）描述的是连续介质中沿波线上许许多多质点振动在t 时刻的位移状态．其中原点处质点位移为零，其运动方向由图中波形状态和波的传播方向可以知道是沿y 轴负向，利用旋转矢量法可以方便的求出该质点振动的初相位为π/2．而图（b ）是一个质点的振动曲线图，该质点在t ＝0 时位移为0，t ＞0 时，由曲线形状可知，质点向y 轴正向运动，故由旋转矢量法可判知初相位为－π/2，答案为（D ）．10-2 机械波的表达式为()()m π06.0π6cos 05.0x t y +=，则（）（Ａ）波长为100 ｍ（Ｂ）波速为10 ｍ·ｓ-1（Ｃ）周期为1/3 ｓ（Ｄ）波沿x 轴正方向传播分析与解波动方程的一般表式为⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=ϕωu x t A y cos ，其中A 为振幅，φ为初相，u 为波速．x /u 前的“-”表示波沿x 轴正向传播，“+”表示波沿x 轴负向传播．因此将原式写为()()()m 100/π6cos 05.0x t y +=和一般式比较可知（Ｂ）、（Ｄ）均不对．而由ω＝2π/T ＝6πｓ-1 可知T ＝（1/3）ｓ．则λ＝uT ＝33.3 m ，因此（Ａ）也不对．只有（Ｃ）正确．10-3 一平面简谐波，沿x 轴负方向传播，角频率为ω，波速为u ．设4T t =时刻的波形如图（a ）所示，则该波的表达式为（） ()()()()⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=πωπωπωπωu x t A y u x t A y u x t A y u x t A y cos B 2cos C 2cos B cos A题10-3 图分析与解因为波沿x 轴负向传播，由上题分析知（Ａ）、（B ）表式不正确．找出（C ）、（D ）哪个是正确答案，可以有很多方法．这里给出两个常用方法．方法一：直接将t ＝T /4，x ＝0 代入方程，那么对（C ）有y 0 ＝A 、对（D ）有y 0 ＝0，可见（D ）的结果与图一致．方法二：用旋转矢量法求出波动方程的初相位．由图（a ）可以知道t ＝T /4 时原点处质点的位移为0，且向y 轴正向运动，则此时刻的旋转矢量图如图（b ）所示．要求初相位，只要将该时刻的旋转矢量反转（顺时针转）Δφ＝ω·Δt ＝ω·T /4 ＝π/2，如图（b ）所示，即得φ0 ＝π．同样得（D ）是正确答案．题10-4 图10-4 如图所示，两列波长为λ的相干波在点P 相遇．波在点S 1 振动的初相是φ1 ，点S 1 到点P 的距离是r 1 ．波在点S 2的初相是φ2 ，点S 2 到点P 的距离是r 2 ，以k 代表零或正、负整数，则点P 是干涉极大的条件为（）()()()()()()πλπϕϕπλπϕϕπϕϕπk r r k r r k k r r 22A 22A 2A A 211212121212=-+-=-+-=-=-// 分析与解 P 是干涉极大的条件为两分振动的相位差π2Δk =，而两列波传到P 点时的两分振动相位差为()λr r /π2Δ1212---=，故选项（D ）正确．10-5 在驻波中，两个相邻波节间各质点的振动（）（A ）振幅相同，相位相同（B ）振幅不同，相位相同（C ）振幅相同，相位不同（D ）振幅不同，相位不同分析与解驻波方程为t λx A y v π2cos π2cos 2=，因此根据其特点，两波节间各点运动同相位，但振幅不同．因此正确答案为（B ）．10-8 波源作简谐运动，其运动方程为()m t πcos240100.43-⨯=y ，它所形成的波形以30ｍ·ｓ-1 的速度沿一直线传播．（1）求波的周期及波长；（2）写出波动方程．分析已知波源运动方程求波动物理量及波动方程，可先将运动方程与其一般形式()ϕω+=t cos A y 进行比较，求出振幅A 、角频率ω及初相φ0 ，而这三个物理量与波动方程的一般形式()[]0cos ϕω+-=u x t A y /中相应的三个物理量是相同的．再利用题中已知的波速u 及公式ω＝2πν ＝2π／T 和λ＝u T 即可求解．解（1）由已知的运动方程可知，质点振动的角频率1s π240-=ω．根据分析中所述，波的周期就是振动的周期，故有 s 1033.8/π23-⨯==ωT波长为λ＝uT ＝0.25 ｍ（２）将已知的波源运动方程与简谐运动方程的一般形式比较后可得A ＝4.0 ×10-3m ，1s π240-=ω，φ0 ＝0故以波源为原点，沿x 轴正向传播的波的波动方程为()[]()()m π8π240cos 100.4/cos 30x t u x t ωA y -⨯=+-=-10-10 波源作简谐运动，周期为0.02ｓ，若该振动以100m·ｓ-1 的速度沿直线传播，设t ＝0时，波源处的质点经平衡位置向正方向运动，求：（1）距波源15.0ｍ和5.0 m 两处质点的运动方程和初相；（2）距波源为16.0 m 和17.0m 的两质点间的相位差．分析（1）根据题意先设法写出波动方程，然后代入确定点处的坐标，即得到质点的运动方程．并可求得振动的初相．（2）波的传播也可以看成是相位的传播．由波长λ的物理含意，可知波线上任两点间的相位差为Δφ＝2πΔx ／λ．解（1）由题给条件1s m 100s 020-⋅==u T ,.，可得 m 2;s m π100/π21==⋅==-uT λT ω当t ＝0 时，波源质点经平衡位置向正方向运动，因而由旋转矢量法可得该质点的初相为φ0 ＝－π／2（或3π／2）．若以波源为坐标原点，则波动方程为()[]2/π100π100cos --=x/t A y距波源为x 1 ＝15.0 m 和x 2 ＝5.0 m 处质点的运动方程分别为()()π5.5t π100cos π15.5t π100cos 21-=-=A y A y它们的初相分别为φ10 ＝－15.5π和φ10 ＝－5.5π（若波源初相取φ0＝3π/2，则初相φ10 ＝－13.5π，φ10 ＝－3.5π．）（2）距波源16.0m 和17.0 m 两点间的相位差()π/π2Δ1212=-=-=λx x10-13 如图所示为一平面简谐波在t ＝0 时刻的波形图，求（1）该波的波动方程；（2） P 处质点的运动方程．题10-13 图分析（1）根据波形图可得到波的波长λ、振幅A 和波速u ，因此只要求初相φ，即可写出波动方程．而由图可知t ＝0 时，x ＝0 处质点在平衡位置处，且由波的传播方向可以判断出该质点向y 轴正向运动，利用旋转矢量法可知φ＝－π/2．（2）波动方程确定后，将P 处质点的坐标x 代入波动方程即可求出其运动方程y P ＝y P （t ）．解（1）由图可知振幅A ＝0.04 ｍ，波长λ＝0.40 ｍ，波速u ＝0.08ｍ·ｓ-1 ，则ω＝2π/T ＝2πu /λ＝（2π/5）ｓ-1 ，根据分析已知φ＝－π/2，因此波动方程为()m 208.05π20.04cos y ⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-=πx t（2）距原点O 为x ＝0.20ｍ处的P 点运动方程为 ()m 2520.04cos y ⎥⎦⎤⎢⎣⎡+=ππ10-18 有一波在介质中传播，其波速u ＝1.0 ×103m·s -1 ，振幅A ＝1.0 ×10-4 m ，频率ν ＝1.0 ×103Hz ．若介质的密度为ρ ＝8.0×102 kg·m -3 ，求：（1）该波的能流密度；（2） 1 min 内垂直通过4.0 ×10-4m 2 的总能量．解（1）由能流密度I 的表达式得2522222m W 10581221-⋅⨯===.v uA uA I ρπωρ （2）在时间间隔Δt ＝60 s 内垂直通过面积S 的能量为J 107933⨯=∆⋅=∆⋅=.t IS t P W10-20 如图所示，两相干波源分别在P 、Q 两点处，它们发出频率为ν、波长为λ，初相相同的两列相干波．设PQ ＝3λ/2，R 为PQ 连线上的一点．求：（1）自P 、Q 发出的两列波在R 处的相位差；（2）两波在R 处干涉时的合振幅．题10-20 图分析因两波源的初相相同，两列波在点R 处的相位差Δφ仍与上题一样，由它们的波程差决定．因R 处质点同时受两列相干波的作用，其振动为这两个同频率、同振动方向的简谐运动的合成，合振幅ϕ∆++=cos 2212221A A A A A ．解（1）两列波在R 处的相位差为πλr 3/Δπ2Δ==（2）由于π3Δ=，则合振幅为21212221cos32A A A A A A A -=++=π第十一章光学11-1 在双缝干涉实验中，若单色光源S 到两缝S 1 、S 2 距离相等，则观察屏上中央明条纹位于图中O 处，现将光源S 向下移动到图中的S ′位置，则（）（A ）中央明纹向上移动，且条纹间距增大（B ）中央明纹向上移动，且条纹间距不变（C ）中央明纹向下移动，且条纹间距增大（D ）中央明纹向下移动，且条纹间距不变分析与解由S 发出的光到达S 1 、S 2 的光程相同，它们传到屏上中央O 处，光程差Δ＝0，形成明纹．当光源由S 移到S ′时，由S ′到达狭缝S 1 和S 2 的两束光产生了光程差．为了保持原中央明纹处的光程差为0，它会向上移到图中O ′处．使得由S ′沿S 1 、S 2 狭缝传到O ′处的光程差仍为0．而屏上各级条纹位置只是向上平移，因此条纹间距不变．因此正确答案为（B ）．。

第7章-稳定磁场-2(3)

M 的作用。
这一力矩使分子磁矩转向外磁场的方向
B0
pm M
B0
M = pm B
as
. . . . . .
磁化面电流 as
I
l
B0
分子电流
M
这些分子磁矩对应的分子电流在磁介质内部流向相反，它们的磁作用相互抵消；而在表面流向相同，形成一层磁化（束缚）电流，该磁化电流产生的磁场就是介质磁化后所产生的附加磁场，其方向与原磁场方向相同。
B dS 0
S
2. 有介质存在时的安培环路定理
B dl o I I s
L
o I M dl
L

B L o M dl I
定义“磁场强度”
H
B
o
硬磁材料：
磁滞回线较宽，剩余磁感应强度和矫顽力都比较大。 B
H
适合于制造永磁体
矩磁材料：
磁滞回线接近于矩形，剩余磁感应强度 Br接近于饱和磁感应强度Bs。 B
H
适合于制作记录磁带及计算机的记忆元件。
2. 磁畴
铁磁质内部相邻原子的磁矩会在一个微小的区域内形成方向一致、排列非常整齐的 “自发磁化区”，称为磁畴。磁畴大小：
( N : 匝数 )
NI 得： H = 2π r =nI B = H = 0 r nI
r
[例题2]一无限长载流圆柱体，通有电流I ，设电流 I 均匀分布在整个横截面上。柱体的磁导率为μ，柱外真空。求：柱内外各区域的磁场强度和磁感应强度。解：
1. r < R
H .dl = H 2π r = I ´ μ l r2 = R2 I

恒定磁场习题

B
设M线圈p平m 面B与B成pm6B0°sin角30，则 1P.m5与7 B1成03-20N°角m ，方圈有向法力：线矩力转矩向A将与驱B平使行线O
第七章恒定磁场
解：在圆盘上任取一微元 dq 2rdr 圆盘以ω匀速转动相当于产生一圆电流。
or R
dI dq rdr
T 微元在P点产生的磁感应强度大小为：
dB

0r 2dI
2(r
2

x2
3
)2
B
R
dB
0
0q 2R2
(
R2 2x2 R2 x2
2x)
第七章恒定磁场
恒定磁场习题课选讲例题
物理学教程（第二版）
例一无限长载流 I 的导线，中部弯成如图所示的四分之一圆周 AB，圆心为O，半径为R，则在O点处的磁感应强度的大小为
（A）
0I
2πR
（B）
0 I (1
4πR
π) 2
（C）
0I
4R
（D）
0 I (1
4πR
π) 2
A
R
B
O
第七章恒定磁场
物理学教程（第二版）
有一带电球壳，内、外半径分别为a和b，电荷体密度r = A /
r，在球心处有一点电荷Q，证明当A = Q / ( 2a2 )时，球壳
区域内的场强的大小与r无关．
r
证：用高斯定理求球壳内场强：

E d S E 4r 2 S
Q
r dV
V
/0
恒定磁场习题课选讲例题
物理学教程（第二版）
圆弧形例载流有导一线半径bc为,按a图，示流方过式稳置恒于电均流匀为外I磁的场1B4