椭圆双曲线方程知识汇总
圆椭圆双曲线抛物线知识点汇总

圆椭圆双曲线抛物线知识点汇总一、圆椭圆双曲线抛物线的定义1. 圆:圆是平面上到定点距离相等的所有点的集合。
圆由圆心和半径唯一确定。
2. 椭圆:椭圆是平面上到两个定点的距离之和为常数的所有点的集合。
椭圆由两个焦点和两个半轴唯一确定。
3. 双曲线:双曲线是平面上到两个定点的距离之差为常数的所有点的集合。
双曲线由两个焦点和两个实轴唯一确定。
4. 抛物线:抛物线是平面上到定点距离等于到定直线的距离的所有点的集合。
抛物线由焦点和直线唯一确定。
二、圆椭圆双曲线抛物线的方程1. 圆:圆的标准方程为(x-a)² + (y-b)² = r²,其中圆心为(a, b),半径为r。
2. 椭圆:椭圆的标准方程为x²/a² + y²/b² = 1,其中a和b分别为x轴和y轴上的半轴长。
3. 双曲线:双曲线的标准方程为x²/a² - y²/b² = 1或者y²/a² - x²/b² = 1,取决于焦点的位置。
4. 抛物线:抛物线的标准方程为y² = 4ax或者x² = 4ay,取决于抛物线开口的方向。
三、圆椭圆双曲线抛物线的性质1. 圆:圆的直径是圆上任意两点之间的最大距离,且所有直径相等。
2. 椭圆:椭圆的离心率介于0和1之间,离心率越接近0,椭圆越接近于圆。
3. 双曲线:双曲线分为两支,每一支的焦点到定点的距离之差相等。
4. 抛物线:抛物线的焦点在抛物线上方,开口方向取决于系数a的正负号。
四、圆椭圆双曲线抛物线的应用1. 圆:在几何中常常与角度和三角函数结合,用于描述正弦和余弦函数的周期性。
2. 椭圆:在天体力学中用于描述行星轨道的形状,以及通信中的极化椭圆。
3. 双曲线:在光学和电磁学中用于描述折射和反射现象。
4. 抛物线:在物理学中用于描述自由落体运动和抛物线运动。
椭圆与双曲线知识点集合
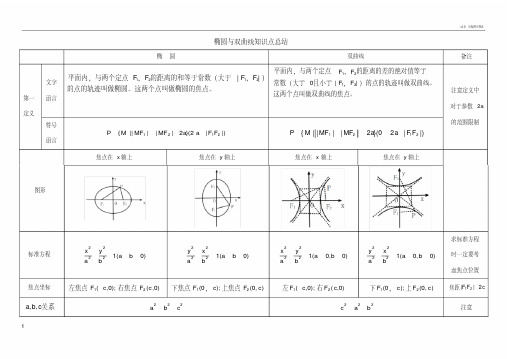
x0 2 a2
y02 b2
1
点P在椭圆 C外
| PF1 | | PF2 | 2a
面积 S b2 cot ( 2
F1PF2 )
已知点(P
x0 , y0)和双曲线
C:x a
2 2
y2 b2
1(a
b
0);
F1, F2是双曲线的两焦点,则
x02 a2
y0 2 b2
1
点 P在双曲线两支间
| PF1 | | PF2 | 2a
2
焦点弦为通径时最短,长为 2b a
左 | AB | |2a e(x 1 x2 )|; 右 | AB | |2a e(x 1 x2 )|
下 | AB | |2a e( y 1 y2 )|; 上 | AB | |2a e( y 1 y2 )|
2
同侧焦点弦为通径时最短,长为 2b a
异侧焦点弦为实轴时最短,长为 2a;
F 是椭圆的一个焦点。 l 叫做焦点 F 对应的准线。
焦点在 x 轴上
焦点在 y 轴上
| x | a, y R
| y | a,x R
左 A1 ( a,0); 右 A2 (a,0)
下 A1( a,0); 上 A2 (a,0)
渐近线 y
b x
a
a
渐近线 y
x
b
实轴 A1 A2; 实轴长 2a;虚轴 B1B2; 虚轴长 2b
1 1 k2
( y1 y2) 2 4 y1y2
2
2
已知点(P x0, y0)在椭圆 C:ax2
y b2
1(a
b
0)上; 则
则过(P x0, y0)的椭圆 C的切线方程为
x0 a2
高中椭圆双曲线抛物线知识点汇总

高中椭圆双曲线抛物线知识点汇总一、椭圆的定义和基本特性1. 椭圆的定义:椭圆是平面上到两定点F1和F2的距离之和为常数2a (a>0)的点P的轨迹。
2. 椭圆的基本特性:椭圆有两条对称轴,长轴和短轴,焦点到中心的距离为c,满足c²=a²-b²,离心率e的定义为e=c/a。
3. 椭圆的标准方程:椭圆的标准方程为x²/a²+y²/b²=1(a>b>0),中心在原点,长轴与x轴平行。
二、双曲线的定义和基本特性1. 双曲线的定义:双曲线是平面上到两定点F1和F2的距离之差为常数2a的点P的轨迹。
2. 双曲线的基本特性:双曲线有两条对称轴,两个顶点,离心率e的定义为e=c/a。
3. 双曲线的标准方程:双曲线的标准方程为x²/a²-y²/b²=1(a>0,b>0),中心在原点,x²项系数为正。
三、抛物线的定义和基本特性1. 抛物线的定义:抛物线是平面上到定点F与直线l的距离相等的点P 的轨迹。
2. 抛物线的基本特性:抛物线有焦点F和直线l两个重要元素,焦点到顶点的距离为p,离心率e的定义为e=1。
3. 抛物线的标准方程:抛物线的标准方程为y²=2px(p>0),焦点在y轴上。
四、椭圆双曲线抛物线的性质比较1. 焦点、离心率和轴与方程的关系:椭圆的焦点在轴上,双曲线的焦点在中心轴的延长线上,抛物线的焦点在轴上。
2. 直线与曲线的关系:椭圆是对称轴与任意直线的交点个数有限,双曲线是对称轴与任意直线的交点有两个,抛物线是对称轴与任意直线的交点有且仅有一个。
3. 其他性质:椭圆和双曲线是封闭曲线,抛物线是开口向上或者向下的曲线。
五、高中数学中的应用1. 物理中的应用:椭圆、双曲线和抛物线在经典力学、电磁学等物理学科中有着重要的应用,比如行星轨道、抛物线运动等。
双曲线和椭圆的知识点

双曲线和椭圆的知识点一、双曲线的定义和基本性质双曲线是平面上的一种曲线,由两个相交的直线割成两个分支。
它的定义式为x^2/a^2-y^2/b^2=1或y^2/b^2-x^2/a^2=1,其中a和b为正实数。
双曲线有以下基本性质:1. 双曲线关于x轴、y轴对称;2. 双曲线有两条渐近线,即与x轴和y轴夹角趋近于0或π/2的直线;3. 双曲线在两条渐近线处无界;4. 双曲线分为左右两个分支,左分支开口向左,右分支开口向右;5. 双曲线在x=a和x=-a处有垂直渐近线。
二、椭圆的定义和基本性质椭圆是平面上一条封闭弧形,其所有点到两个定点之距离之和等于定长(即椭圆长轴),定义式为(x-h)^2/a^2+(y-k)^2/b^2=1或(x-h)^2/b^2+(y-k)^2/a^2=1,其中(h,k)为椭圆中心坐标,a和b为长短半轴长度。
椭圆有以下基本性质:1. 椭圆关于x轴、y轴对称;2. 椭圆有两条主轴,即长轴和短轴,交于椭圆中心;3. 椭圆的离心率为e=c/a,其中c为焦点到中心的距离;4. 椭圆上任意一点P(x,y)到焦点F1和F2的距离之和等于椭圆长轴长度;5. 椭圆在x=h处有垂直渐近线。
三、双曲线和椭圆的参数方程双曲线的参数方程为x=acosht,y=bsinht或x=asect,y=btant,其中t为参数。
这两种参数方程对应左右两个分支。
椭圆的参数方程为x=h+acosθ,y=k+bsinθ或x=h+bsinθ,y=k+acosθ,其中θ为参数。
四、双曲线和椭圆的焦点双曲线有两个焦点F1(ae,0)和F2(-ae,0),其中e为离心率。
椭圆也有两个焦点F1(h+ae,k)和F2(h-ae,k),其中a、b、h、k、e均已定义。
五、双曲线和椭圆的面积双曲线面积公式为S=abπ,其中a和b分别为左右两个分支的半轴长度。
椭圆面积公式为S=abπ,其中a和b分别为长轴和短轴长度。
六、双曲线和椭圆的应用1. 双曲线在物理学中有许多应用,如描述电磁波传播、天体运动等。
双曲线椭圆抛物线知识总结

双曲线椭圆抛物线知识总结双曲线、椭圆和抛物线是二次曲线的三种特殊情况。
它们在数学和物理等领域中有广泛应用,下面是它们的一些基本特点和公式总结。
1. 双曲线:- 定义:双曲线是平面上一组点,使得到两个固定点的距离之差等于一个常数的点的轨迹。
- 方程:标准方程为(x/a)^2 - (y/b)^2 = 1,其中a和b为正常数。
- 焦点和准线:双曲线有两个焦点和两条准线。
焦点是曲线上的特殊点,准线是曲线上的两条无限远直线。
- 对称轴和顶点:双曲线有对称轴和顶点。
对称轴是曲线的对称中线,顶点是曲线的极值点。
- 对称性:双曲线是关于对称轴对称的,即左右对称。
2. 椭圆:- 定义:椭圆是平面上一组点,使得到两个固定点的距离之和等于一个常数的点的轨迹。
- 方程:标准方程为(x/a)^2 + (y/b)^2 = 1,其中a和b为正常数。
- 焦点和准线:椭圆有两个焦点和两条准线。
焦点是曲线上的特殊点,准线是曲线上的两条无限远直线。
- 对称轴和顶点:椭圆有对称轴和顶点。
对称轴是曲线的对称中线,顶点是曲线的极值点。
- 对称性:椭圆是关于对称轴对称的,即左右对称。
3. 抛物线:- 定义:抛物线是平面上一组点,使得到一个固定点的距离与到一条固定直线的距离相等的点的轨迹。
- 方程:标准方程为y = ax^2 + bx + c,其中a、b和c为常数,a ≠ 0。
- 焦点和准线:抛物线有一个焦点和一条准线。
焦点是曲线上的特殊点,准线是曲线上的无限远直线。
- 对称轴和顶点:抛物线有对称轴和顶点。
对称轴是曲线的对称中线,顶点是曲线的极值点。
- 对称性:抛物线是关于对称轴对称的,即左右对称。
以上是双曲线、椭圆和抛物线的基本知识总结,它们的性质和公式还有更多深入的内容,如离心率、焦距、直径等,可作为进一步学习的参考。
椭圆双曲线知识点总结

椭圆知识点【知识点1】椭圆的概念:在平面内到两定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫椭圆.这两定点叫做椭圆的焦点,两焦点间的距离叫做焦距.当动点设为M 时,椭圆即为点集P ={}12|2M MF MF a += 注意:若)(2121F F PF PF =+,则动点P 的轨迹为线段21F F ;若)(2121F F PF PF <+,则动点P 的轨迹无图形。
【知识点2】椭圆的标准方程焦点在x 轴上椭圆的标准方程: ()222210x y a b a b += >>,焦点坐标为(c ,0),(-c ,0)焦点在y 轴上的椭圆的标准方程为:()222210x y a b b a+= >>焦点坐标为(0,c ,)(o ,-c )【知识点3】椭圆的几何性质:规律:(1)椭圆焦点位置与x 2,y 2系数间的关系:焦点在分母大的那个轴上.(2)椭圆上任意一点M 到焦点F 的所有距离中,长轴端点到焦点的距离分别为最大距离和最小距离,且最大距离为a +c ,最小距离为a -c .(3)在椭圆中,离心率22222221a b a b a a c a c e -=-===(4)椭圆的离心率e 越接近1椭圆越扁;e 越接近于0,椭圆就接近于圆; (5)离心率公式:在21PF F ∆中,α=∠21F PF ,β=∠12F PF ,()βαβαsin sin sin ++=e二、椭圆其他结论标准方程()222210x y a b a b += >> ()222210x y a b b a += >> 图形性质范围 a x a -≤≤b y b -≤≤对称性 对称轴:坐标轴 对称中心:原点顶点A 1(-a,0), A 2(a,0)B 1(0,-b ),B 2(0,b )A 1(0,-a ),A 2(0,a )B 1(-b,0),B 2(b,0)轴 长轴A 1A 2的长为2a ;短轴B 1B 2的长为2b焦距 ∣F 1F 2 |=2c离心率 e=ca∈(0,1) a ,b ,c 的关系c 2=a 2-b 21、若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y ya b+=若已知切线斜率K ,切线方程为222b k a kx y +±=2、若000(,)P x y 在椭圆22221x y a b +=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+= 3、椭圆22221x y a b+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点θ=∠21PF F ,则椭圆的焦点角形的面积为2tan221θb S PF F =∆4、以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5、过焦点的弦中,通径(过焦点且与焦点所在坐标轴垂直的弦)最短ab 226、过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF 。
高中数学中的椭圆与双曲线知识点总结

高中数学中的椭圆与双曲线知识点总结在高中数学中,椭圆与双曲线是解析几何部分的重要内容,它们具有独特的性质和广泛的应用。
下面让我们一起来详细了解一下这两个重要的数学概念。
一、椭圆椭圆是平面内到定点 F1、F2 的距离之和等于常数(大于|F1F2|)的动点轨迹。
1、椭圆的标准方程当焦点在 x 轴上时,椭圆的标准方程为:\(\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\)(\(a > b > 0\)),其中\(a\)为椭圆的长半轴长,\(b\)为椭圆的短半轴长,\(c\)满足\(c^2 = a^2 b^2\),\(c\)为半焦距,焦点坐标为\((\pm c, 0)\)。
当焦点在 y 轴上时,椭圆的标准方程为:\(\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1\)(\(a > b > 0\)),焦点坐标为\((0, \pm c)\)。
2、椭圆的性质(1)对称性:椭圆关于 x 轴、y 轴和原点对称。
(2)范围:对于\(\frac{x^2}{a^2} +\frac{y^2}{b^2} =1\),\(a \leq x \leq a\),\(b \leq y \leq b\)。
(3)离心率:椭圆的离心率\(e =\frac{c}{a}\)(\(0 < e < 1\)),离心率反映了椭圆的扁平程度,\(e\)越接近 0,椭圆越接近圆;\(e\)越接近 1,椭圆越扁。
3、椭圆的焦半径设椭圆上一点\(P(x_0, y_0)\),焦点为\(F_1\)、\(F_2\),则\(|PF_1| = a + ex_0\),\(|PF_2| = a ex_0\)。
4、椭圆的切线方程若点\(P(x_0, y_0)\)在椭圆\(\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\)上,则过点\(P\)的切线方程为\(\frac{x_0x}{a^2} +\frac{y_0y}{b^2} = 1\)。
圆锥曲线(椭圆,双曲线,抛物线)的定义方程和性质知识总结

椭圆的定义、性质及标准方程1. 椭圆的定义:⑴第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
⑵第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ,则动点M 的轨迹叫做椭圆。
定点F 是椭圆的焦点,定直线l 叫做椭圆的准线,常数e 叫做椭圆的离心率。
说明:①若常数2a 等于2c ,则动点轨迹是线段12F F 。
②若常数2a 小于2c ,则动点轨迹不存在。
2.3. 椭圆上的任一点和焦点连结的线段长称为焦半径。
焦半径公式:椭圆焦点在x 轴上时,设12F F 、分别是椭圆的左、右焦点,()00P x y ,是椭圆上任一点,则10PF a ex =+,20PF a ex =-。
推导过程:由第二定义得11PF e d =(1d 为点P 到左准线的距离), 则211000a PF ed e x ex a a ex c ⎛⎫==+=+=+ ⎪⎝⎭;同理得20PF a ex =-。
简记为:左“+”右“-”。
由此可见,过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数。
22221x y a b +=;若焦点在y 轴上,则为22221y x a b+=。
有时为了运算方便,设),0(122n m m ny mx ≠>=+。
双曲线的定义、方程和性质1. 定义(1)第一定义:平面内到两定点F 1、F 2的距离之差的绝对值等于定长2a (小于|F 1F 2|)的点的轨迹叫双曲线。
说明:①||PF 1|-|PF 2||=2a (2a <|F 1F 2|)是双曲线;若2a=|F 1F 2|,轨迹是以F 1、F 2为端点的射线;2a >|F 1F 2|时无轨迹。
②设M 是双曲线上任意一点,若M 点在双曲线右边一支上,则|MF 1|>|MF 2|,|MF 1|-|MF 2|=2a ;若M 在双曲线的左支上,则|MF 1|<|MF 2|,|MF 1|-|MF 2|=-2a ,故|MF 1|-|MF 2|=±2a ,这是与椭圆不同的地方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
椭圆双曲线知识汇总
基本专题:
(1)求曲线的标准方程 方法一:待定系数法 方法二、求c b a ,,
(2)判断曲线的类型 12
2=+B
y A x 类型 022=++C By Ax 类型
(3)定义的应用 判断所求轨迹的点的性质
(4)求曲线的离心率 要求曲线离心率,找出关系消去b ,化简之后变成e ,注意范围取正值 (5)中点弦问题 点差法(设而不求)
(6)焦点三角形 (正弦定理、余弦定理的应用)
(7)弦长公式 |
|1||11||1||2
122
122m k y y k
x x k AB ∆+=-+=-+=
(8)最值问题 注意几何意义
(9)圆锥曲线应用题 读题--->反复读题--->建立模型--->求解结果--->写出结论 (10)圆锥曲线的位置关系 (点在曲线外/内/上)(直线:联立,化简,判断△)
椭圆知识专题练习
专题一、求椭圆标准方程 根据下列条件求椭圆的方程
(1)焦距是8,到焦点的距离是10
(2)焦点坐标是(0,32-)和(0,32),且经过点(6,5-)
(3)长轴长是短轴长的三倍,椭圆经过点)0,3(P (4)长轴和短轴的和等于20,焦距等于54,焦点在y 轴;
(5)椭圆过定点)2,2
23
(,)3
62,3(-
(6)过)3,2(-且与椭圆36492
2
=+y x 有共同焦点 (7)椭圆与直线01=-+y x 的交点的横坐标是0和5
8
(8)焦距等于12,离心率等于0.6,焦点在x 轴 (9)已知)0,5(),0,5(B A -,ABC ∆的周长是26,求ABC ∆的顶点C 的轨迹方程。
(10)
和已知点)0,6(B )0,6(-C ,过点B 的直线l 与过点C 的直线m 相交于点A ,设直线l 的斜率为1k ,直线m 的斜率为2k ,如果9
421-=⋅k k ,求点A 的轨迹
方程。
(11)ABC ∆中,已知))0,2(),0,2(-B A ,且
|||,||,|BC AB AC 成等差数列,求C 的轨迹方程
(12)与⊙2)2(:2
2=++y x C 内切,且过点)0,2(A ;
(13)与⊙9)3(:2
2
1=++y x C 外切,且与⊙
1)3(:2
22=+-y x C 内切;
专题二、判断曲线性质
(1)曲线1352
2=-+-k
y k x 中,k 取何值时,该曲线表
示的分别是(1)圆(2)椭圆(3)焦点在x 轴的椭圆(4) 焦点在y 轴的椭圆(5)双曲线
(2)曲线1)3()5(2
2
=-+-y k x k 中,k 取何值时,该曲线表示的分别是(1)圆(2)椭圆(3)焦点在x 轴的椭圆(4) 焦点在y 轴的椭圆(5)双曲线
专题三、求离心率
(1)若椭圆的长轴长、短轴长、焦距成等差数列,则
其离心率
(2)若椭圆的长轴长、短轴长、焦距成等比数列,
则其离心率 (3)椭圆的一个顶点与两焦点组成一个等边三角形,则椭圆的离心率是 。
(4)若椭圆短轴的一个端点与两个焦点连线互相垂直,则椭圆的离心率为 。
(5)椭圆122
22=+b
y a x 的左右焦点1F ,2F ,线段1F 2F 被
点)0,2
(b ,分为3:5两段,则椭圆离心率
(7)正六边形ABCDEF 的四个顶点在椭圆上,点D A ,为椭圆的左右焦点,则椭圆离心率 (6) O 为原点, 椭圆
)0(12
22
2>>=+b a b y a x
的左焦点1F ,过1F 作垂直于长轴的直线交椭圆于
P 点,B A ,分别为椭圆与坐标轴正半轴的交点,
若AB OP //,则椭圆离心率
专题四、焦点三角形
1、点P 在椭圆14
92
2=+y x 上 (1)21F PF ∆的周长是 ;
21F PF ∆面积的最大值
(2)连接1PF 延长交椭圆于Q ,则2
P Q F
∆的周长是 ,
2PQF ∆的面积是
(3)x 取何值时,21F PF ∆为直角三角形?
(4)若︒=∠6021PF F , 则=∆21F PF S ;点P 到x 轴的距离是 ;
(5)与两焦点21,F F 的连线所成的α=∠21PF F ; 求证:三角形21F PF ∆的面积是2
tan
2
α
b
(6)求21PF F ∠取到最大值时,点P 坐标 (7)若︒=∠6021PF F ,离心率的范围 (8)||||21PF PF ⋅最大时,点P 坐标 (9)︒=∠1521F PF ,︒=∠7512F PF 时,离心率是。
