立体几何图形操作步骤
高中数学第八章立体几何初步8.1基本立体图形教案第二册

8.1 基本几何图形第1课时棱柱、棱锥、棱台立体几何是研究三维空间中物体的形状、大小、位置关系的一门数学学科,而三维空间是人们生存发展的现实空间,学习立体几何对我们更好地认识客观世界,更好地生存与发展具有重要意义。
在立体几何初步部分,学生将先从对空间几何体观察入手、认识空间图形;再以长方体为载体,直观认识和理解空间点、线、面的位置关系。
本节内容既是义务教育阶段“空间与图形”课程的延续和提高,也是后续研究空间点、线、面位置关系的基础,既巩固了前面所学的内容,又为后面内容的学习做了知识上和方法上的准备,在教材中起着承前启后的作用。
课程目标1.通过对实物模型的观察,归纳认知简单多面体——棱柱、棱锥、棱台的结构特征.2.能运用棱柱、棱锥、棱台的结构特征来判断、描述现实生活中的实物模型.3.与平面几何体的有关概念、图形和性质进行适当类比,初步学会用类比的思想分析问题和解决问题.数学学科素养1。
数学抽象:多面体与旋转体等概念的理解;2.逻辑推理:棱柱、棱锥、棱台的结构特点;3.直观想象:判断空间几何体;4。
数学建模:通过平面展开图将空间问题转化为平面问题解决,体现了转化的思想方法.重点:掌握棱柱、棱锥、棱台的结构特征;难点:棱柱、棱锥和棱台的侧面展开图问题.教学方法:以学生为主体,小组为单位,采用诱思探究式教学,精讲多练。
教学工具:多媒体。
一、情景导入在平面几何中,我们认识了三角形,正方形,矩形,菱形,梯形,圆,扇形等平面图形。
但我们知道在我们周围存在着各种各样的物体,它们都占据着空间的一部分.如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些抽象出来的空间图形就叫做空间几何体.那么对空间中各种各样的几何体,我们如何认识它们的结构特征?对空间中不同形状、大小的几何体我们如何理解它们的联系和区别?要求:让学生自由发言,教师不做判断.而是引导学生进一步观察.研探。
二、预习课本,引入新课阅读课本97-100页,思考并完成以下问题1、什么是空间几何体?什么是多面体与旋转体?2、多面体包含哪些图形?这些图形是怎样定义的?又有什么结构特点?要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
高二解析几何立体几何知识点

高二解析几何立体几何知识点一、知识概述《解析几何与立体几何知识点》①基本定义:- 解析几何:简单说就是用代数方法来研究几何图形。
就是把图形放在坐标系里,通过点的坐标、方程等代数的东西来描述图形的形状、位置啥的。
比如一条直线,我们可以用方程y = kx + b来表示它,其中k 是斜率,b是截距,这样就把直线这个几何对象用代数方程表示出来了。
- 立体几何:这是研究空间里的图形形状、大小、位置关系的学科。
像我们周围的房子、盒子,都是立体几何研究的对象。
在立体空间中有很多元素,比如点、线、面,它们之间有着各种各样的关系。
②重要程度:- 解析几何:在高二数学里特别重要的一部分,它是连接代数和几何的桥梁。
像在物理里的运动轨迹分析,还有工程绘图等很多地方都能用得上。
很多实际问题通过建立解析几何模型就好解决多了。
- 立体几何:对于培养空间想象能力那可太有帮助了。
无论是建筑设计,还是机械制造等领域,都需要立体几何的知识。
对于了解三维世界物体间的关系不可或缺。
③前置知识:- 解析几何:得对代数基础有一定掌握,像函数、方程这些知识。
比如说要有解方程的能力,因为解析几何里经常要解各种直线、曲线的方程。
还得了解坐标的概念和基本运算。
- 立体几何:平面几何知识那肯定是要有的。
像三角形的性质、平行四边形的性质等,因为很多立体图形都是由平面图形构成的。
还得有基本的空间感知能力,虽然可以通过后天培养,但要是对空间有点感觉那学起来就轻松些。
④应用价值:- 解析几何:可以用来分析行星的轨道,就像科学家用它来计算火星探测器的飞行轨迹等。
还能在计算机图形处理中有很大用途,比如游戏里的3D建模等都会用到。
- 立体几何:建筑设计的时候得考虑各个房间、各种结构在空间里的情况,就是立体几何知识的应用。
还有在雕塑创作时,雕塑家要考虑形状、比例、空间布局等,这都是立体几何干的事儿。
二、知识体系①知识图谱:- 解析几何:是代数与几何融合的部分。
在高二数学知识里是函数、方程等代数知识往几何方向的延伸。
如何画立体图形

如何画立体图形立体图形在我们生活中无处不在,我们要要发挥我们的创造力,可以让画板为我们表现出丰富多彩的立体几何图形的。
一、立体几何图形的制作在空间里我们常用到的几何体有长方体、正方体、棱锥、棱台、圆锥和圆台等。
下面以正三棱锥为例,详细介绍下立体几何图形的制作画法。
设计标准:(1)能够反映正三棱锥的的几何性质,(2)能让其旋转。
设计的核心:解决正三角形在底面上的旋转。
为了使图形的直观性更强,我让一个三角形顶点在同一个椭圆上旋转,这样可以更好的表现出空间图形的立体感。
主要步骤:(1)画出椭圆上旋转的三角形。
用圆工具画一圆并在圆上任取一点C ,测算角CAB 的度数。
。
用线段工具。
作两条线段DE 和FG 并测算其长度。
。
利用三个测量值,计算出的值,选择二测算值,并在图表菜单中选择绘出(x,y ).这时画板中出现点J 。
。
标识中心A ,让点C 分别旋转120度和240度得到C`和C``,并分别测算角C`AB 和角C``AB ,然后通过上述画点J 的方法得到K ,L 。
。
连接三个点便生成了一个在底面可以旋转的三角形。
定义点C 在圆A 上旋转的动画,随着点C 的运动,三角形JKL 也开始旋转。
(2)构造棱锥。
将点A 平移到竖直的上方若干单位得到点A`。
(也可以标识一个向量,让点A 按着标识的向量来平移,这样能达到控制棱锥的高度的目的)。
。
构造线段JA`、KA`,LA`得到三棱锥的侧棱。
AA`为三棱锥的高,在此基础上我们再画出三棱锥的有关要素,例如高及三个重要的直角三角形。
类似的,我们可以得到圆柱、圆锥、圆台等几何图形。
另外,我们可以发挥几何画板动画的功能让我们的几何图形旋转起来,旋转的好处有二,一是在旋转的过程中选取最佳的识图视角,从而提高学生的识图能力;二是可以看到平面图形旋转成旋转体的生成过程,加强知识发生的过程的教学,变“知识重现”为“意义建构”,以往这部分内容的教学是引导学生展开“想象”,但对那些想象能力相对薄弱的学生来说,其中的困难可想而知。
立体几何全部教案.

⽴体⼏何全部教案.第⼀章:空间⼏何体1.1.1柱、锥、台、球的结构特征⼀、教学⽬标1.知识与技能(1通过实物操作,增强学⽣的直观感知。
(2能根据⼏何结构特征对空间物体进⾏分类。
(3会⽤语⾔概述棱柱、棱锥、圆柱、圆锥、棱台、圆台、球的结构特征。
(4会表⽰有关于⼏何体以及柱、锥、台的分类。
2.过程与⽅法(1让学⽣通过直观感受空间物体,从实物中概括出柱、锥、台、球的⼏何结构特征。
(2让学⽣观察、讨论、归纳、概括所学的知识。
3.情感态度与价值观(1使学⽣感受空间⼏何体存在于现实⽣活周围,增强学⽣学习的积极性,同时提⾼学⽣的观察能⼒。
(2培养学⽣的空间想象能⼒和抽象括能⼒。
⼆、教学重点、难点重点:让学⽣感受⼤量空间实物及模型、概括出柱、锥、台、球的结构特征。
难点:柱、锥、台、球的结构特征的概括。
三、教学⽤具(1学法:观察、思考、交流、讨论、概括。
(2实物模型、投影仪四、教学思路(⼀创设情景,揭⽰课题1.教师提出问题:在我们⽣活周围中有不少有特⾊的建筑物,你能举出⼀些例⼦吗?这些建筑的⼏何结构特征如何?引导学⽣回忆,举例和相互交流。
教师对学⽣的活动及时给予评价。
2.所举的建筑物基本上都是由这些⼏何体组合⽽成的,(展⽰具有柱、锥、台、球结构特征的空间物体,你能通过观察。
根据某种标准对这些空间物体进⾏分类吗?这是我们所要学习的内容。
(⼆、研探新知1.引导学⽣观察物体、思考、交流、讨论,对物体进⾏分类,分辩棱柱、圆柱、棱锥。
2.观察棱柱的⼏何物件以及投影出棱柱的图⽚,它们各⾃的特点是什么?它们的共同特点是什么?3.组织学⽣分组讨论,每⼩组选出⼀名同学发表本组讨论结果。
在此基础上得出棱柱的主要结构特征。
(1有两个⾯互相平⾏;(2其余各⾯都是平⾏四边形;(3每相邻两上四边形的公共边互相平⾏。
概括出棱柱的概念。
4.教师与学⽣结合图形共同得出棱柱相关概念以及棱柱的表⽰。
5.提出问题:各种这样的棱柱,主要有什么不同?可不可以根据不同对棱柱分类?请列举⾝边具有已学过的⼏何结构特征的物体,并说出组成这些物体的⼏何结构特征?它们由哪些基本⼏何体组成的?6.以类似的⽅法,让学⽣思考、讨论、概括出棱锥、棱台的结构特征,并得出相关的概念,分类以及表⽰。
几何画板课件制作之立体几何

立体几何在几何画板中绘制固定椭圆椭圆是数学中常见的一种图形,接下来我们看看如何在几何画板中绘制固定椭圆。
1.新建一个几何画板文件,选择“直线工具”,在绘图区域内画出线段AB,选择“构造”—“中点”命令,画出线段A B的中心C。
如下图所示。
依次选中点C、点A,选择“构造”—“以2.选择“箭头工具”,圆心和圆周上的点绘圆”命令,绘制出以点C为圆心经过点A的圆C。
如下图所示。
在圆周上绘制出点D。
选择“箭头工具”,3.选择“点工具”,绘制出线段AB 选中点D和线段AB,选择“构造”—“垂线”命令,的垂线,并使线段AB和AB垂线的交点为E。
如下图所示。
4.选中圆C和直线DE,选择“显示”—“隐藏路径对象”命令,隐藏圆C和直线DE。
5.选择“线段工具”,绘制处线段DE。
选择“构造”—“中点”命令,绘制出线段DE的中点F。
如下图所示。
依次选中点D、点F,选择“构造”—“轨6.选择“箭头工具”,迹”命令,绘制出椭圆。
如下图所示。
7.选中点D、点E、点F、线段DE,选择“显示”—“隐藏对象”命令,隐藏点D、点E、点F、线段DE。
如下图所示。
8.选择“文件”—“保存”命令即可。
几何画板中球体的绘制方法球体如何在几何画板中绘制呢?接下来我们就一同看一看几何画板中球体的绘制。
1.新建一个几何画板文件。
选择“线段工具”,绘制出线段AB的中点。
AB,选择“构造”—“中点”命令,绘制出线段2.选择箭头工具,选中点C、点A,选择“构造”—“以圆心和圆周上的点绘圆”命令,绘制出圆C。
如下图所示。
3.选中点C、线段AB,选择“构造”—“垂线”命令,绘制出线段AB的中垂线。
点击线段AB的中垂线与圆C的交点,作出交点D、交点E。
如下图所示。
4.选择线段AB,选择“构造”—“线段上的点”命令,绘制出线段AB上的点F。
如下图所示。
5.选中点D、点F、点E,然后选择“构造”—“过三点的弧”命令,绘制出弧DFE。
如下图所示。
6.选中点F、弧DFE,选择“构造”—“轨迹”命令即可。
word中怎么画立体几何图形

如何在Word中画立体几何图形唐顺友出数学试卷时,看见某个立体几何题很好,但又不知道怎么把图弄在试卷上,有的老师用几何画板或用扫描仪把资料中的图形扫描,处理后再复制到Word中,这种做法存在画图效果不佳、效率低、图形修改时较麻烦等缺点。
而Word的画图工具,便能快速画出精致的立体几何图形,而且打印效果特别好,看后给人一种心情舒畅的感觉。
一、打开作图工具(视图→工具栏→绘图)具体操作:先必须把有关的图形工具请到工具栏上。
点击“视图→工具栏→绘图”,绘图工具栏便在界面下边显示出来。
二、设置作图工具1.去掉画布,目的是:避免每次画图时,都自动创建画布的麻烦事出现。
(工具→选项→常规→插入自选图形时自动创建画布):具体操作:在“工具→选项”这一菜单中,有个常规页,切换到这个页面后,在其中有个“插入自选图形时自动创建画布”选项,如果这个选项前面打“√”,则:单击之,取消这一选项,注:如果不设置也可以,每次画图时把画的图形拖出画布,然后把画布删除即可(选中画布,按回车键),要增加图形时选中已经画好的图形,再点击要增加的图形,也可以避免出现画布,操作相对来说要麻烦点。
2.设置间距,目的是:用鼠标移动图形时,较好地控制图形的大小以及搬动到预定地方。
(文件→页面设置→文档网格→绘图网格→会弹对话框→网格设置→水平间距”、“垂直间距”设置为0.01→确认→确认)具体操作:在“文件→页面设置”菜单中有个“文档网格”页面,切换到这个页面后,左下角有个“绘图网格”按钮,点击这个按钮时,会弹出一个设置对话框,在其中的“网格设置”的“水平间距”、“垂直间距”设置为0.01(取这一设置的最小值)。
如果不进行这个操作,移动图形时可能出现线条交接间隔过大,位置要向某个地方移动一点点,却不听使唤。
三、基本作图技巧1.画线段具体操作:点击左下方工具栏中的线条工具“”,在相应位置作图即可。
2.画虚线具体操作:先画线段,选中线段后,点击点击左下方工具栏中的虚线工具“”,选择需要的虚线类型单击即可。
立体几何初步知识点全总结

立体几何初步知识点全总结一、空间几何体的结构。
1. 棱柱。
- 定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
- 分类:- 按底面多边形的边数分为三棱柱、四棱柱、五棱柱等。
- 直棱柱:侧棱垂直于底面的棱柱。
正棱柱:底面是正多边形的直棱柱。
- 性质:- 侧棱都相等,侧面是平行四边形。
- 两个底面与平行于底面的截面是全等的多边形。
- 过不相邻的两条侧棱的截面(对角面)是平行四边形。
2. 棱锥。
- 定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
- 分类:- 按底面多边形的边数分为三棱锥、四棱锥、五棱锥等。
- 正棱锥:底面是正多边形,且顶点在底面的射影是底面正多边形的中心的棱锥。
- 性质:- 正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高)。
- 棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。
3. 棱台。
- 定义:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫做棱台。
- 分类:由三棱锥、四棱锥、五棱锥等截得的棱台分别叫做三棱台、四棱台、五棱台等。
- 性质:- 棱台的各侧棱延长后交于一点。
- 棱台的上下底面是相似多边形,侧面是梯形。
4. 圆柱。
- 定义:以矩形的一边所在直线为轴旋转,其余三边旋转所成的曲面所围成的几何体叫做圆柱。
- 性质:- 圆柱的轴截面是矩形。
- 平行于底面的截面是与底面全等的圆。
5. 圆锥。
- 定义:以直角三角形的一条直角边所在直线为轴旋转,其余两边旋转所成的曲面所围成的几何体叫做圆锥。
- 性质:- 圆锥的轴截面是等腰三角形。
- 平行于底面的截面是圆,截面半径与底面半径之比等于顶点到截面距离与圆锥高之比。
6. 圆台。
- 定义:用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台。
第07章 立体几何图形的制作(1)
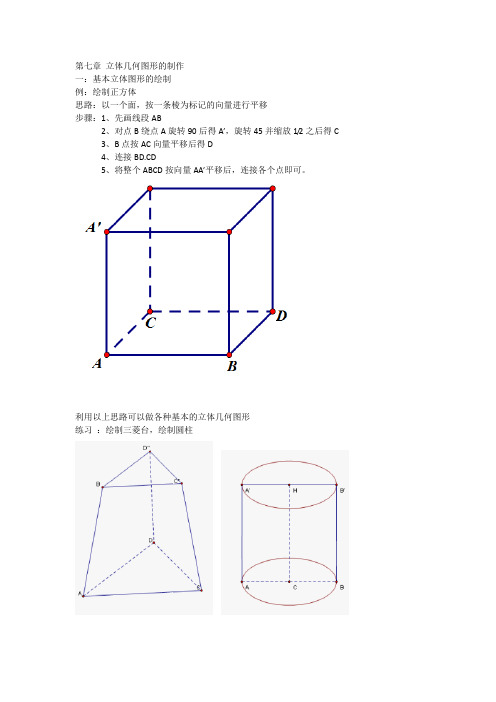
第七章立体几何图形的制作一:基本立体图形的绘制例:绘制正方体思路:以一个面,按一条棱为标记的向量进行平移步骤:1、先画线段AB2、对点B绕点A旋转90后得A’,旋转45并缩放1/2之后得C3、B点按AC向量平移后得D4、连接BD.CD5、将整个ABCD按向量AA’平移后,连接各个点即可。
利用以上思路可以做各种基本的立体几何图形练习:绘制三菱台,绘制圆柱二:正方体的展开动画步骤:1、画线段AB2、双击点A,以A为中心,选中点B,执行“变换,旋转”得B’3、连接AB’,把B’旋转-45得到AB’’4、构造AB’’的中点C,依次选择点A、B’,标记向量AB’,选中点C,“变换,平移”后得到点C’,连接B’C’和CC’5、依次选中点A、B,执行“变换,标记向量”标记向量AB。
选中四边形AB’C’C,执行“变换,平移”,得到四边形BB’’’C’’’C’’’’。
连接B’B’’’,C’C’’’,CC’’’’完成后得到正方体6、双击点A,标记点A为中心,选中点B,执行“变换,旋转”,角度为180,绘制点D,依次选中A,B’和D,执行“构造,圆上的弧”命令,构造出弧B’D,在弧B’D上绘点E,依次选中点E,A。
执行“构造,以圆心和圆周上的点做圆”,绘制圆E。
双击E,以E为中心点,选中点A,执行“变换,旋转”,旋转角度为180,绘制出点A’,选中点A’,执行“变换,旋转”,旋转角度为-90,绘制出点A’’。
7、依次选中点E,A’’和A’,执行“构造,圆上的弧”,构造弧A’A’’。
在弧A’A’’上取一点F,依次选中点B’和C’。
执行“变换,标记向量”,标记出向量B’C’,选中点E,F。
执行“变换,平移”,按向量平移出点E’和F’。
连接AE,EF,FF’,F’E’,EE’。
这样就完成了上底面和左侧面的展开制作。
8、连接B’’C’,选中B’’C’,构造中点G,过点G做B’’C’的垂线,交AB’与H,依次选中H,B’’和C’,执行“构造,圆上的弧”,构造出弧B’’C’,在此弧上任取一点I,依次选中点C和C’’’’。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实训二、制作几何球体(2学时)
【实训目的】:
1.掌握图层的基本操作
2.掌握图层的种类,会建立各种图层
3.掌握运用基本的形状如立体图形、基本规则形状、圆角矩形、圆角四边形,自定义图形,直线在图层上的相关的操作
4.掌握在图层上进行字体设计
【实训重难点】:
掌握运用基本的形状如立体图形、基本规则形状、圆角矩形、圆角四边形,自定义图形,直线在图层上的相关的操作。
【实训教学手段】:
教师讲解实验内容及要求,学生进行实验训练
【实训内容】:
1.制作球体、制作圆柱体、制作圆锥体、制作立方体、制作圆环、制作投影与倒影、2.完成综合布局
【操作步骤】:
1、制作球体
(1)启动photoshop软件
(2)执行菜单命令“文件”--“新建”,建立一个图像文件:400*400像素,分辨率280像素/英寸,RGB模式,背景白色。
(3)添加背景色。
单击“渐变”工具,再单击上方的“渐变编辑器”,打开渐变编辑对话框。
(4)设置线性渐变,从黑(R=0,G=0,B=0)到蓝(R=41,G=83,B=169).
(5)回到工具面板,选择“渐变”工具,由上至下拉出渐变色.
(6)执行菜单命令“窗口”--“图层”打开图层面板,新建图层1。
(7)回到工具面板,将“矩形选框工具“换成”椭圆选框工具“, 按shift键,在图层1画一个正圆。
(8)按照开始所讲的立体规律做一个渐变色,选择颜色块可以进行色彩的编辑。
如图2。
(9)回到工具面板,将“线性渐变”切换到“径向渐变”。
图1
(10)在图层1的选区中,由圆的高光部位斜向下方拉出渐变。
图2
(11)取消浮动,一个立体感的球体就呈现在你眼前。
最后存盘:文件--另存为--圆球。
图3
2、制作圆柱体
(1)在层面板关闭球体层,建一个新层圆柱,回到工具面板,选取矩形选框工具,在新层上画一个长方形的选区。
(2)选择渐变工具,进行渐变编辑。
图4
(3)在方形选区内从左至右进行渐变,然后取消浮动。
图5
(4)圆柱的立体关系如下图:
图6
(5)新建层2,做圆柱的透视效果。
图7
(6)选择层2,在圆柱的上部画一个椭圆选区。
(7)选择前景色为灰色,红框中是颜色的RGB值。
图8
(8)填充,注意不要取消浮动。
图9
(9)回到圆柱层,按键盘上的向下方向键,将选区向下移动。
(10)选择矩形选框工具,按键盘上的shift键进行加选。
图10
(11)选择菜单命令“选择”--“反向”进行反选,然后按键盘上的Delete键,删除不需要的部分,完成圆柱体的制作。
图11
(12)选择菜单命令“选择”--“反向”进行反选,然后按键盘上的Delete键,删除不需要的部分,完成圆柱体的制作。
图12
(13)如果你想得到一个空心体的圆筒,方法是:
a.在层面板上使层2的椭圆浮动(选择――载入选区――确定),
b.新建层3,
c.进行相反方向的渐变,
图13
(14)最后存盘,取名:圆柱体。
3、制作圆锥体
(1)建新层,命名:圆锥,画一个渐变的矩形,编辑--变换--透视。
图14
(2)点击右上方小方块平行移到中心,使左右两个方块在中心重叠。
图15
(3)在锥形的下方画一个椭圆选区。
图16
(4)在工具面板选择矩形工具,按Shift键进行加选.
图17
(5)执行菜单命令“选择”――“反向”,然后按Delete键删除多余的部分.
图18 (6)圆锥体的制作就完成了。
存盘。
图19 4、制作立方体
立方体在光线下,将产生不同的明暗面。
图20
(1)建新层:立方体,按shift键画正方形,填充灰。
图21
(2)复制这一层,“图象”--“调整”--“亮度/对比度”,设置如图:
图22
(3)将调整后的这一层复制,“图象”――“调整”――“亮度/对比度”。
图23
(4)调整立方体的透视效果,将暂不需要的层关闭。
(5)在立方体层执行“编辑”--“自由变换”,在菜单栏的下一栏设置变换的数值,然后按“回车”完成。
图24
(6)激活“立方体副本层”,自由变换,设置如图:
图25
图26
(7)激活“立方体副本2层",自由变换设置如图:
图27
(8)激活另外两层,分别移动到合适的位置。
图28
如果你觉得各个面的角度不好调节,也可手动修改,直到满意为止。
最后将三个层合并,存盘。
5、制作环形体
(1)建新层,画正圆,填充灰。
图29 (2)在中心画小圆,按Delete键删除。
图30 (3)按住Ctrl+D键,点取消选区。
(4)添加图层样式-斜面和浮雕,并设置相应的参数。
图31
(5)好了,一个圆环到此完成,保存。
图32
六、制作投影与倒影
(1)以前做好的球体没有删掉吧,如果删了就再做一个,全当是又练习了一回。
(2)复制球体层,按向下的方向键将复制的球体移动到适当位置,垂直翻转,稍微模糊一点,降低透明度。
倒影做完了,就怎么简单。
图33
(3)再复制一个球体层,放在球体层下,选择扭曲变换工具将其变形。
3.按住Ctrl 键不放点击层面板眼睛旁的方框,使投影变为选区。
4.填充黑色,高斯模糊,降低透明度,球体的投影便完成了。
图34
7、综合布局
我们的球体、圆柱、圆桶、锥体、圆环、立方体都还在吧,好!将它们分别缩小,加上阴影,摆好位置,做这一步的时候要细心哦。
若要看起来美观些,可分别调整上你喜欢的色调.。
