自动控制原理5.3 系统开环频率特性
合集下载
自动控制原理_第5章_3

5.3 控制系统的频率特性
在绘制各个典型环节频率特性的基础上, 可以绘制控制系统的频率特性。
5.3.1 控制系统开环频率特性的Nyquist图
一个控制系统的开环传递函数可以写成典型
环节的连乘积形式。
1
举例 一个开环传递函数为
K ( s 1) G( s) 2 2 s(T1s 1)(T2 s 2 T2 s 1)
27
2
对于非单位反馈系统, 在其开环频率特性幅值
G( j)H ( j) 很大的频段内, 闭环频率特性
1 ( j ) H ( j )
即近似等于反馈环节频率特性的倒数。
对于开环放大倍数 K 很大的闭环系统,在低频段
具有这个特点。
28
3
对于非单位反馈系统, 一般来说, 其开环
频率特性的高频段幅值很小。在这一频段内, 闭环
1
当 0 时,放大环节、惯性环节、振荡环节、
一阶微分环节、二阶微分环节的幅角均为 00 。
。 只有积分环节, 0 时,相角为 900 当
如果开环传递函数中含有 v 个积分环节,开环频率 特性的Nyquist图在 0 的起始处幅角为 v 900 。
6
2
当 0 时, 放大环节的幅值为 K ,
21
[例5-5] 控制系统的开环传递函数为
10( s 1) G( s) s(2.5s 1)(0.04s 2 0.24s 1)
绘制系统的渐近开环对数幅频特性和相频特性。
22
100 Magnitude (dB)
Asymptotic Bode Diagram
-20dB/dec
50
20
频率特性近似等于系统前向通道的频率特性。 一般来说,闭环系统在高频段内显示这一性质。 在工程实践中, 当开环幅频特性
在绘制各个典型环节频率特性的基础上, 可以绘制控制系统的频率特性。
5.3.1 控制系统开环频率特性的Nyquist图
一个控制系统的开环传递函数可以写成典型
环节的连乘积形式。
1
举例 一个开环传递函数为
K ( s 1) G( s) 2 2 s(T1s 1)(T2 s 2 T2 s 1)
27
2
对于非单位反馈系统, 在其开环频率特性幅值
G( j)H ( j) 很大的频段内, 闭环频率特性
1 ( j ) H ( j )
即近似等于反馈环节频率特性的倒数。
对于开环放大倍数 K 很大的闭环系统,在低频段
具有这个特点。
28
3
对于非单位反馈系统, 一般来说, 其开环
频率特性的高频段幅值很小。在这一频段内, 闭环
1
当 0 时,放大环节、惯性环节、振荡环节、
一阶微分环节、二阶微分环节的幅角均为 00 。
。 只有积分环节, 0 时,相角为 900 当
如果开环传递函数中含有 v 个积分环节,开环频率 特性的Nyquist图在 0 的起始处幅角为 v 900 。
6
2
当 0 时, 放大环节的幅值为 K ,
21
[例5-5] 控制系统的开环传递函数为
10( s 1) G( s) s(2.5s 1)(0.04s 2 0.24s 1)
绘制系统的渐近开环对数幅频特性和相频特性。
22
100 Magnitude (dB)
Asymptotic Bode Diagram
-20dB/dec
50
20
频率特性近似等于系统前向通道的频率特性。 一般来说,闭环系统在高频段内显示这一性质。 在工程实践中, 当开环幅频特性
自动控制原理第5章(3)
故对数幅频特性为 L (ω ) = 20 lg
1 (Tω ) 2 + 1
= −20 lg (Tω ) 2 + 1
在时间常数T已知时,可以在ω从0变化到∞的范围内,逐点求出L(ω) 值,从而绘制出精确的对数幅频特性曲线,但十分费时。在工程中,一 般采用渐近线近似的方法,这已经满足大多数情况下的要求。
1.低频段 在Tω<<1(或ω<<1/T)的区段,可以近似地认为Tω≈0, 从而有 L (ω ) = −20 lg (T ω ) 2 + 1 ≈ −20 lg1 = 0 故在频率很低时,对数幅频特性可以近似用零分贝线表示, 这称为低频渐近线。
对数相频特性为ϕ(ω) = -arctanTω。 为了近似绘制相频特性,选择确定以下几个点。
同时,由于惯性环节的 相位与频率呈反正切函数 关系,所以,对数相频特 性曲线将对应于ω=1/T及 ϕ (ω)=-45° 这 一 点 对 称,可以清楚地看出在整 个频率范围内,ϕ(ω)呈滞 后持续增加的趋势,极限 为-90°。
L(ω ) = 20 lg A(ω ) = 20 lg (τω ) 2 + 1
对数相频特性为
ϕ(ω)=arctan(τω)
按照与惯性环节相似的作图方法画图。
L(ω ) = 20 lg A(ω ) = 20 lg (τω ) 2 + 1
1. 低频段 在Tω<<1(或ω<<1/T) 的区段,对数幅频特性可以近 似用零分贝线表示,为低频渐 近线。 2.高频段 在Tω>>1(或 ω >>1/T) 的区段,可以近似地认为高频 渐近线是一条斜线, 斜率为 20dB/dec, 当 频 率 变 化 10倍频时,L(ω)变化20dB。 转折频率为ωT=1/T。
自动控制原理(第三版)第五章频率响应法

频段的两条直线组成的折线近似表示, 如图5-18的渐近线所
示。 这两条线相交处的交接频率ω=1/T, 称为振荡环节的无阻尼
自然振荡频率。在交接频率附近, 对数幅频特性与渐近线存在
一定的误差, 其值取决于阻尼比ζ的值, 阻尼比越小, 则误差越大, 如表5-4所示。当ζ<0.707时, 在对数幅频特性上出现峰值。根
一个单位长度。设对数分度中的单位长度为L, ω0为参考点, 则 当ω以ω0为起点, 在10倍频程内变化时, 坐标点相对于ω0的距离
为表5-1中的第二行数值乘以L。
第五章 频 率 响 应 法
图 5-4 对数分度和线性分度
第五章 频 率 响 应 法
表 5-1 10倍频程内的对数分度
第五章 频 率 响 应 法
第五章 频 率 响 应 法
图 5-7 比例环节的伯德图
第五章 频 率 响 应 法
2. 积分环节 积分环节的频率特性为
其幅频特性和相频特性为
(5.18)
(5.19)
由式(5.19)可见,它的幅频特性与角频率ω成反比, 而相频特性恒
为-90°。对数幅频特性和相频特性为
(5.20)
第五章 频 率 响 应 法
T), 则有
因此有
这表明φ(ω)是关于ω=1/T, φ(ω)=-45°这一点中心对称的。 用
MATLAB画出的惯性环节的伯德图如图5-14所示(T=1)。
第五章 频 率 响 应 法
图 5-14 MATLAB绘制的惯性环节的伯德图
第五章 频 率 响 应 法
5. 一阶微分环节 一阶微分环节的频率特性为 幅频特性和相频特性为
即 所以, 惯性环节的奈氏图是圆心在(0.5, 0), 半径为0.5的半圆 (
见图5-12)。 对数幅频特性和相频特性为
示。 这两条线相交处的交接频率ω=1/T, 称为振荡环节的无阻尼
自然振荡频率。在交接频率附近, 对数幅频特性与渐近线存在
一定的误差, 其值取决于阻尼比ζ的值, 阻尼比越小, 则误差越大, 如表5-4所示。当ζ<0.707时, 在对数幅频特性上出现峰值。根
一个单位长度。设对数分度中的单位长度为L, ω0为参考点, 则 当ω以ω0为起点, 在10倍频程内变化时, 坐标点相对于ω0的距离
为表5-1中的第二行数值乘以L。
第五章 频 率 响 应 法
图 5-4 对数分度和线性分度
第五章 频 率 响 应 法
表 5-1 10倍频程内的对数分度
第五章 频 率 响 应 法
第五章 频 率 响 应 法
图 5-7 比例环节的伯德图
第五章 频 率 响 应 法
2. 积分环节 积分环节的频率特性为
其幅频特性和相频特性为
(5.18)
(5.19)
由式(5.19)可见,它的幅频特性与角频率ω成反比, 而相频特性恒
为-90°。对数幅频特性和相频特性为
(5.20)
第五章 频 率 响 应 法
T), 则有
因此有
这表明φ(ω)是关于ω=1/T, φ(ω)=-45°这一点中心对称的。 用
MATLAB画出的惯性环节的伯德图如图5-14所示(T=1)。
第五章 频 率 响 应 法
图 5-14 MATLAB绘制的惯性环节的伯德图
第五章 频 率 响 应 法
5. 一阶微分环节 一阶微分环节的频率特性为 幅频特性和相频特性为
即 所以, 惯性环节的奈氏图是圆心在(0.5, 0), 半径为0.5的半圆 (
见图5-12)。 对数幅频特性和相频特性为
自动控制原理课件17 5-3对数频率特性

所以低频段过点 A( 1, L() 20lg K) 或 ( N K , L() 0)
系统开环对数频率特性的特点(2)
• 2)开环对数幅频特性经过一个转折频率,其斜率要发生 变化,其高频段最终的斜率为-20*(n-m)dB/dec,开环对 数相频特性最终相角为-(n-m)*900。 3)开环对数幅频特性曲线与横坐标轴的交点频率,称为 截止频率或穿越频率,用wc表示。 即在该频率下,L(w)=0
L1 ( )
0
0.1 0.2
0.5 1
10
1
-1 -0.7
2 3
-0.3 0
L4 () L3 ()
1
L2 ()
L() L1()L2 ()L3()L4 ()L5 ()
L1() 20lg 6.25
L2
(
)
20
lg
1 s
6.25 Wk (s) s(5s 1)(2s 1)(s 1)
L3
(
)
20
lg
1 5s
§ 5-3对数频率特性
二.典型环节的对数频率特性
(一)比例环节 W ( j) K Ke j0 L() 20lg K,() 0
0.1 1 Ψ(ω)
10 ω ω
L(w是) 一条等高度等于 的20直lg线k
K>1时 L() ;0 K<1时, L(;) 0
K=1时 L() 0
相频特性是一条 () 直0线0 。
L(2 ) L(1) 20lg 2T (20lg 1T ) 20(lg2T lg 1T )
20 lg
2 1
20lg10
20dB dec
为一斜率为-20dB/dec的直线。
这样其对数幅频特性可用两条渐近线近似表示
系统开环对数频率特性的特点(2)
• 2)开环对数幅频特性经过一个转折频率,其斜率要发生 变化,其高频段最终的斜率为-20*(n-m)dB/dec,开环对 数相频特性最终相角为-(n-m)*900。 3)开环对数幅频特性曲线与横坐标轴的交点频率,称为 截止频率或穿越频率,用wc表示。 即在该频率下,L(w)=0
L1 ( )
0
0.1 0.2
0.5 1
10
1
-1 -0.7
2 3
-0.3 0
L4 () L3 ()
1
L2 ()
L() L1()L2 ()L3()L4 ()L5 ()
L1() 20lg 6.25
L2
(
)
20
lg
1 s
6.25 Wk (s) s(5s 1)(2s 1)(s 1)
L3
(
)
20
lg
1 5s
§ 5-3对数频率特性
二.典型环节的对数频率特性
(一)比例环节 W ( j) K Ke j0 L() 20lg K,() 0
0.1 1 Ψ(ω)
10 ω ω
L(w是) 一条等高度等于 的20直lg线k
K>1时 L() ;0 K<1时, L(;) 0
K=1时 L() 0
相频特性是一条 () 直0线0 。
L(2 ) L(1) 20lg 2T (20lg 1T ) 20(lg2T lg 1T )
20 lg
2 1
20lg10
20dB dec
为一斜率为-20dB/dec的直线。
这样其对数幅频特性可用两条渐近线近似表示
自动控制原理-5.3 控制系统的频率特性

-2.67k
Im
→
0
Re
=0
16
5.3.2 开环伯德图
开环对数幅频特性和开环对数相频特性分别为
n
n
n
Lk () 20 lg A() 20 lg Ai () 20 lg Ai () Li ()
i 1
i 1
i 1
n
( ) i ( ) i 1
与实轴的交点:
令 Im() = 0 求出 x 代入 Re(x)
(4) 由起点出发,绘制曲线大致形状。
6
m
k (is 1)
= 设开环传递函数G(s)H(s)
i1
s n (Tjs 1)
相频特性:
j1
φ(ω)=-υ×90o+Σim=a1 rtan(ωτi)-jΣn=-1aυ rtan(ωTj )
例5-3 已知系统开环传函为 k
Gk (s) (T1s 1)(T2s 1) 试绘制系统的开环幅相曲线。 解:系统开环频率特性
Gk
(
j
)
T1T2
(
j
k 1 T1
)(
j
1 T2
)
-1/T2
-1/T1
j (1)Gk (j0) = k0
(2)Gk (j) = 0180
() = 90 arctanT
2
A() T 1
() = 90 arctanT
1 (T )2
T
0 0.1 0.3 1.0 2.0 5.0 ∞
A() 0 0.0995 0.288 0.707 0.895 0.982 1
()(°) 90 84.3 73.3 45 30 11.3 0
自动控制原理

L( ) L1 ( ) L2 ( ) Ln ( ) ( ) ( ) ( ) ( ) 1 2 n
可见,开环对数幅频特性等于各环节对数幅频特性 之和;系统开环相频等于各环节相频之和。 将各环节对数幅频特性用其渐近线代替,以及对数 运算的优点(乘除运算对数化后变为加减),可以 很容易绘制出开环对数频率特性。
图5-19
例 5-2的Bode图
例 已知系统的开环传递函数,试绘制系统的 开环Bode图。
系统开环包括了五个典型环节
ω2=2 rad/s
ω4=0.5 rad/s
ω5=10 rad/s
例 绘制开环传递函数
K G( s) (1 s)(1 10s)
的零型系统的Bode图。
解 系统开环对数幅频特性和相频特性分别
解 系统开环频率特性
10 G ( j ) H ( j ) (1 j )(1 j 0.1 ) 10(1 0.12 2 ) 10 1.1 j 2 2 2 (1 )(1 0.1 ) (1 2 )(1 0.1 2 )
ω 由0→∞变化时,找几个特殊点:
设反馈控制系统如图5-21所示,其开环传递 函数为: G(s)H(s) 开环频率特性为: G(jω)H(jω) 在绘制开环极坐标曲线时,可将G(jω)H(jω) 写成实频和虚频形式 G(jω)H(jω) = p(ω) + jθ(ω)
图5-21 反馈控制系统
或写成极坐标形式
G( j ) H ( j ) A( )e j ( )
2. 系统开环对数幅频特性有如下特点
①
低频段的斜率为-20νdB/dec,ν为开环系统中所包 含的串联积分环节的数目。
可见,开环对数幅频特性等于各环节对数幅频特性 之和;系统开环相频等于各环节相频之和。 将各环节对数幅频特性用其渐近线代替,以及对数 运算的优点(乘除运算对数化后变为加减),可以 很容易绘制出开环对数频率特性。
图5-19
例 5-2的Bode图
例 已知系统的开环传递函数,试绘制系统的 开环Bode图。
系统开环包括了五个典型环节
ω2=2 rad/s
ω4=0.5 rad/s
ω5=10 rad/s
例 绘制开环传递函数
K G( s) (1 s)(1 10s)
的零型系统的Bode图。
解 系统开环对数幅频特性和相频特性分别
解 系统开环频率特性
10 G ( j ) H ( j ) (1 j )(1 j 0.1 ) 10(1 0.12 2 ) 10 1.1 j 2 2 2 (1 )(1 0.1 ) (1 2 )(1 0.1 2 )
ω 由0→∞变化时,找几个特殊点:
设反馈控制系统如图5-21所示,其开环传递 函数为: G(s)H(s) 开环频率特性为: G(jω)H(jω) 在绘制开环极坐标曲线时,可将G(jω)H(jω) 写成实频和虚频形式 G(jω)H(jω) = p(ω) + jθ(ω)
图5-21 反馈控制系统
或写成极坐标形式
G( j ) H ( j ) A( )e j ( )
2. 系统开环对数幅频特性有如下特点
①
低频段的斜率为-20νdB/dec,ν为开环系统中所包 含的串联积分环节的数目。
自动控制原理第5章_线性控制系统的频率特性分析法

5. 2控制系统开环传递函数的对数频率特性
5.2.2 系统伯德图的绘制
开环对数幅频渐近特性曲线的绘制步骤: (1)把系统开环传递函数化为标准形式,即化为典型环节的传递函
数乘积,分析它的组成环节; (2)确定一阶环节、二阶环节的转折频率,由小到大将各转折频率
标注在半对数坐标图的频率轴上; (3)绘制低频段渐近特性线; (4)以低频段为起始段,从它开始每到一个转折频率,折线发生转
开环极点的个数。
5. 4 频域稳定判据与系统稳定性
5.4.4 控制系统的相对稳定性
开环频率特性 G( j)H( j)在剪切频率 c处所对应的相角与 180 之差称为相角裕度,记为 ,按下式计算
(c ) (180 ) 180 (c )
开环频率特性 G( j)H的( 相j)角等于 时所1对80应的角频率称为相
闭环系统稳定的充要条件是,当 由 0 时0,开 环奈奎斯 特曲线逆时针方向包围( )点 周1, j。0 是具P有2 正实部P 的开 环极点的个数。 需注意,若开环传递函数含有 v 个积分环节,所谓 由 0 0 ,指的 是由 0 0 0 ,此时奈 奎斯特曲线需顺时针增补 v 角度的无穷大半径的圆弧。
5. 4 频域稳定判据与系统稳定性
5.4.1 奈奎斯特稳定判据
若闭环系统在[ s]右半平面上有 个P开环极点,当 从 变化到
时,奈奎斯特曲线 G( j对)H点( j) 的包围1周, j数0 为 ( 为逆时N针,
为顺N 时 0针),则系统N<在0[ ]右半平面上的闭环极点s的个数为 。
折,斜率变化规律取决于该转折频率对应的典型环节的种类; (5)如有必要,可对上述折线渐近线加以修正,一般在转折频率处
自动控制原理频率特性及其表示法ppt课件

系统中的储能元件引起的。
实际系统具有“低通”滤波器特性 实际系统的输出量都随频率的升高而出现失真,
幅值衰减。
频率特性可应用到某些非线性系统的分析中去
自动控制原理
13
1 频率特性的基本概念
频率特性的求取
根据定义求取 对已知系统的微分方程,把正弦输入函数代
入,求出其稳态解,取输出稳态分量与输入正弦 量的复数比即可得到。
系统频率特性能间接地揭示系统的动态特性和 稳态特性,可简单迅速地判断某些环节或参数对系 统性能的影响,指出系统改进方向。
频率特性可以由实验确定,这对于难以建立动 态模型的系统来说,很有用处。
自动控制原理
2
5.1 频率特性及其表示法
1 频率特性的基本概念 2 频率特性的表示
自动控制原理
3
5.1 频率特性及其表示法
5.1 频率特性及其表示法 5.2 典型环节的频率特性 5.3 系统开环频率特性的绘制 5.4 用频率特性分析控制系统的稳定性 5.5 系统瞬态特性和开环频率特性的关系 5.6 闭环系统频率特性 5.7 系统瞬态特性和闭环频率特性的关系
自动控制原理
1
第5章 频域分析法
频率特性是控制系统在频域中的一种数学模 型,是研究自动控制系统的一种工程方法。
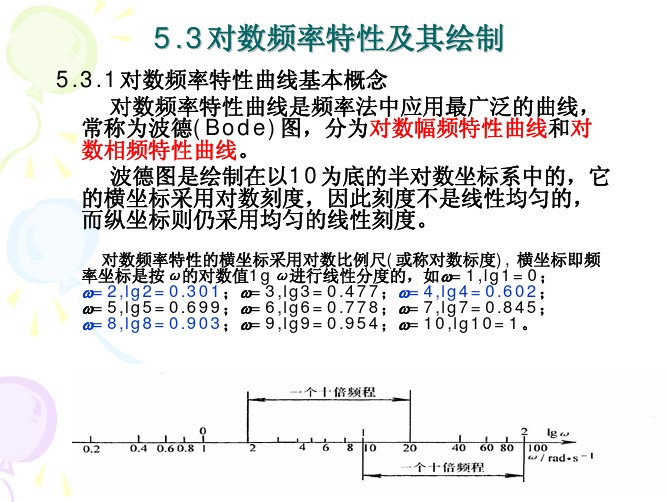
这个单位长度代表10倍频的距离,称之为 “十倍频”或“十倍频程”。
❖ 纵坐标用普通比例尺标度。
自动控制原理
21
A()
100
A
增 10
加
10 1
倍
0.1 0.01
自动控制原理
对数频率特性
L()
40
20 L 增加 20 dB
0
_20
_ 40 0.1
实际系统具有“低通”滤波器特性 实际系统的输出量都随频率的升高而出现失真,
幅值衰减。
频率特性可应用到某些非线性系统的分析中去
自动控制原理
13
1 频率特性的基本概念
频率特性的求取
根据定义求取 对已知系统的微分方程,把正弦输入函数代
入,求出其稳态解,取输出稳态分量与输入正弦 量的复数比即可得到。
系统频率特性能间接地揭示系统的动态特性和 稳态特性,可简单迅速地判断某些环节或参数对系 统性能的影响,指出系统改进方向。
频率特性可以由实验确定,这对于难以建立动 态模型的系统来说,很有用处。
自动控制原理
2
5.1 频率特性及其表示法
1 频率特性的基本概念 2 频率特性的表示
自动控制原理
3
5.1 频率特性及其表示法
5.1 频率特性及其表示法 5.2 典型环节的频率特性 5.3 系统开环频率特性的绘制 5.4 用频率特性分析控制系统的稳定性 5.5 系统瞬态特性和开环频率特性的关系 5.6 闭环系统频率特性 5.7 系统瞬态特性和闭环频率特性的关系
自动控制原理
1
第5章 频域分析法
频率特性是控制系统在频域中的一种数学模 型,是研究自动控制系统的一种工程方法。
这个单位长度代表10倍频的距离,称之为 “十倍频”或“十倍频程”。
❖ 纵坐标用普通比例尺标度。
自动控制原理
21
A()
100
A
增 10
加
10 1
倍
0.1 0.01
自动控制原理
对数频率特性
L()
40
20 L 增加 20 dB
0
_20
_ 40 0.1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
20 lg K的
[20 ]的 斜
率线。
20lgK
0
[ 20 ]
1
§5-3 系统开环频率特性
j
lim b0 sm a0 sn
s j
lim b0 a0 snm
s j
lim
b0 a0 nm
[(n
m)
2
]
0[(n m) ] 2
j
0
以确定Байду номын сангаас角度 收敛于原点
§5-3 系统开环频率特性
3. 确定幅相曲线与实轴的交点:
令Im[Gk ( j)] 0,求得,代入Re[Gk ( j)]中即可
s 20lgK为水平线。所以此时
L() 20lg K 20lg 20lg K 20 lg
顺序斜率迭加法(续)
§5-3 系统开环频率特性
当 1时,L() 20lg K,而 20 lg为 1处
过0db的[20 ]的斜率线。
因此低频起
始段为在
1处过
(n
m)
1、 0的起始段:
lim
0
G
j
lim
0
(
K
j
)
K
lim
0
(
)
2
υ =2
j
υ =3
K 0
υ =0
起始段只取决于和K。
不同,起始段的差异很大。
υ =1
§5-3 系统开环频率特性
开环幅相频率特性的绘制(续)
2、 的终止段:
lim G
得到曲线与实轴的交点。
4. 确定曲线与虚轴的交点:
令 Re[Gk ( j)] 0,求得,代入Im[Gk ( j)]中即可。
★ 另外选几个合适的值,得几个点,最后连起来。
例1:已知Gk
10 s(1 0.2s)(1
,绘制极坐标图。 0.05s)
解: 已知n 3, m 0, 1 Gk ( j0) 90
所以只要确定低频起始段的位置和斜率,并能确 定线段转折频率以及转折后线段的斜率变化量,就可 以从低频到高频一气呵成。
(二)顺序斜率迭加法
§5-3 系统开环频率特性
1.低频起始段的确定:
惯性环节、振荡环节、一阶微分环节、二阶微
分环节等的L( ),在 折时全为0dB。所以
最低的转折频率以前(称为低频段),由积分 环节和比例环节决定,即起始段取决于K ,而
1,折1
20
20
3
tg1
20
(4)G4
1 2
s
1:L4
20 lg
1 2
2
1,折2
2
4
tg1
2
L db
40
L
[-20]
20
0 0.1
1
ω)
900
00 -900
§5-3 系统开环频率特性
[+20] L4
L1 [-20]
2
10 20
100
[-20] [-20] L3
代入 Re[G( j )]中:
10 0.2510
10(0.2510)2 0.4
2
即为(0.4, j0)点,
再令Re[Gk ( j )] 0, 求得 (即原点)。
若选 4,则计算出:
G( j4) 1.47 j1.23。
j
1 0.4 0
1
2
二、开环对数频率特性:
§5-3 系统开环频率特性
Gk (s) G1G2G3
Gk ( j) G1 jG2 jG3 j
A1 e j1 A2 e j2 A3 e j3
3
3
ji A e i1
4
L2
1
3
2
环节曲线迭加法(续)
§5-3 系统开环频率特性
最后, L L1 L2 L3 L4 , 1 2 3 4
因为开环传递函数是由若干个典型环节串联而 成,而且典型环节的对数曲线均为不同斜率的直线或 折线,所以迭加后的开环对数频率特性仍为由不同斜 率的线段组成的折线。
§5-3 系统开环频率特性
一、开环幅相频率特性的绘制(极坐标图):
Gk
K1s 12s 1ms 1 s T1s 1T2s 1Tn s 1
b0 s m a0sn
b1sm1 a1sn1
bm1s bm an1s an
Gk ( j) 0 270
§5-3 系统开环频率特性
开环幅相频率特性的绘制(续)
Gk ( j )
j(1
10
j0.2 )(1
j0.05 )
j10(1 j0.2)(1 j0.05)
(1 j0.2)(1 j0.2)(1 j0.05)(1 j0.05)
i
A
e j
i 1
L() 20lg A() 20lg
3
Ai
(
)
3
20
lg
Ai
3
i 1
i 1
i
i 1
开环对数频率特性(续)
§5-3 系统开环频率特性
故系 系统 统开 开环 环对 对数 数相 幅频 频特 特性 性
各环节的对数幅频特性之代数和。 各环节的对数相频特性之代数和。
可见:用对数表示频率特性后,变乘除为加减 .
再利用( )的奇对称性,L 曲线的平移性和
互为镜像等特点,使曲线绘制较容易。
(一)环节曲线迭加法:
例2 :G(s) 100(s 2) 10(0.5s 1),绘制对数频率特性。 s(s 20) s(0.05s 1)
10[0.25 j(1 0.01 2 )] [(0.25)2 (1 0.01 2 )2 ]
令Im[Gk ( j )] 0, 即1 0.01 2 0 2 100 10(取 10)
§5-3 系统开环频率特性
开环幅相频率特性的绘制(续)
解:四个典型环节:
开环对数频率特性(续)
§5-3 系统开环频率特性
(1)G1 10:L1 20lg 10 20db 1 0
(2)G2 1s:L2 20lg 2 90([20]直线)
(3)G3
1 1
:L3 20lg
s1
1 20
2
[20 ]的 斜
率线。
20lgK
0
[ 20 ]
1
§5-3 系统开环频率特性
j
lim b0 sm a0 sn
s j
lim b0 a0 snm
s j
lim
b0 a0 nm
[(n
m)
2
]
0[(n m) ] 2
j
0
以确定Байду номын сангаас角度 收敛于原点
§5-3 系统开环频率特性
3. 确定幅相曲线与实轴的交点:
令Im[Gk ( j)] 0,求得,代入Re[Gk ( j)]中即可
s 20lgK为水平线。所以此时
L() 20lg K 20lg 20lg K 20 lg
顺序斜率迭加法(续)
§5-3 系统开环频率特性
当 1时,L() 20lg K,而 20 lg为 1处
过0db的[20 ]的斜率线。
因此低频起
始段为在
1处过
(n
m)
1、 0的起始段:
lim
0
G
j
lim
0
(
K
j
)
K
lim
0
(
)
2
υ =2
j
υ =3
K 0
υ =0
起始段只取决于和K。
不同,起始段的差异很大。
υ =1
§5-3 系统开环频率特性
开环幅相频率特性的绘制(续)
2、 的终止段:
lim G
得到曲线与实轴的交点。
4. 确定曲线与虚轴的交点:
令 Re[Gk ( j)] 0,求得,代入Im[Gk ( j)]中即可。
★ 另外选几个合适的值,得几个点,最后连起来。
例1:已知Gk
10 s(1 0.2s)(1
,绘制极坐标图。 0.05s)
解: 已知n 3, m 0, 1 Gk ( j0) 90
所以只要确定低频起始段的位置和斜率,并能确 定线段转折频率以及转折后线段的斜率变化量,就可 以从低频到高频一气呵成。
(二)顺序斜率迭加法
§5-3 系统开环频率特性
1.低频起始段的确定:
惯性环节、振荡环节、一阶微分环节、二阶微
分环节等的L( ),在 折时全为0dB。所以
最低的转折频率以前(称为低频段),由积分 环节和比例环节决定,即起始段取决于K ,而
1,折1
20
20
3
tg1
20
(4)G4
1 2
s
1:L4
20 lg
1 2
2
1,折2
2
4
tg1
2
L db
40
L
[-20]
20
0 0.1
1
ω)
900
00 -900
§5-3 系统开环频率特性
[+20] L4
L1 [-20]
2
10 20
100
[-20] [-20] L3
代入 Re[G( j )]中:
10 0.2510
10(0.2510)2 0.4
2
即为(0.4, j0)点,
再令Re[Gk ( j )] 0, 求得 (即原点)。
若选 4,则计算出:
G( j4) 1.47 j1.23。
j
1 0.4 0
1
2
二、开环对数频率特性:
§5-3 系统开环频率特性
Gk (s) G1G2G3
Gk ( j) G1 jG2 jG3 j
A1 e j1 A2 e j2 A3 e j3
3
3
ji A e i1
4
L2
1
3
2
环节曲线迭加法(续)
§5-3 系统开环频率特性
最后, L L1 L2 L3 L4 , 1 2 3 4
因为开环传递函数是由若干个典型环节串联而 成,而且典型环节的对数曲线均为不同斜率的直线或 折线,所以迭加后的开环对数频率特性仍为由不同斜 率的线段组成的折线。
§5-3 系统开环频率特性
一、开环幅相频率特性的绘制(极坐标图):
Gk
K1s 12s 1ms 1 s T1s 1T2s 1Tn s 1
b0 s m a0sn
b1sm1 a1sn1
bm1s bm an1s an
Gk ( j) 0 270
§5-3 系统开环频率特性
开环幅相频率特性的绘制(续)
Gk ( j )
j(1
10
j0.2 )(1
j0.05 )
j10(1 j0.2)(1 j0.05)
(1 j0.2)(1 j0.2)(1 j0.05)(1 j0.05)
i
A
e j
i 1
L() 20lg A() 20lg
3
Ai
(
)
3
20
lg
Ai
3
i 1
i 1
i
i 1
开环对数频率特性(续)
§5-3 系统开环频率特性
故系 系统 统开 开环 环对 对数 数相 幅频 频特 特性 性
各环节的对数幅频特性之代数和。 各环节的对数相频特性之代数和。
可见:用对数表示频率特性后,变乘除为加减 .
再利用( )的奇对称性,L 曲线的平移性和
互为镜像等特点,使曲线绘制较容易。
(一)环节曲线迭加法:
例2 :G(s) 100(s 2) 10(0.5s 1),绘制对数频率特性。 s(s 20) s(0.05s 1)
10[0.25 j(1 0.01 2 )] [(0.25)2 (1 0.01 2 )2 ]
令Im[Gk ( j )] 0, 即1 0.01 2 0 2 100 10(取 10)
§5-3 系统开环频率特性
开环幅相频率特性的绘制(续)
解:四个典型环节:
开环对数频率特性(续)
§5-3 系统开环频率特性
(1)G1 10:L1 20lg 10 20db 1 0
(2)G2 1s:L2 20lg 2 90([20]直线)
(3)G3
1 1
:L3 20lg
s1
1 20
2
