大一物理实验报告 答辩 霍尔效应与应用设计
大一物理实验报告 答辩 霍尔效应与应用设计PPT

借助实验1的数据,进行计算 使用四个数据的平均值时,通过回归法计算出k=2.0123 只使用V1、V2的平均值时,通过回归法计算出k=2.0182 只使用V1、V3的平均值时,通过回归法计算出k=2.0121 只使用V2、V4的平均值时,通过回归法计算出k=2.0125 只使用V3、V4的平均值时,通过回归法计算出k=2.0064
实验内容
1.测量霍耳电压与工作电流,记录数据测绘VH-IS曲线
恒定磁场,保持励磁电流IM=0.50A,调整工作电流IS,记录数据 根据数据画出VH-IS曲线,
VH-IS曲线
通过回归法可计算出k1=2.0123
2.测量霍耳电压与励磁电流IM,记录数据测绘VH-IM曲线
恒定磁场,保持工作电流IS=3..00mA,调整励磁电流IM,记录数据 根据数据画出VH-IM曲线,
【实验目的】 1.通过实验掌握霍尔效应基本原理,了解霍尔 元件的基本结构; 2.学会测量半导体材料的霍尔系数、电导率、 迁移率等参数的实验方法和技术; 3.学会用“对称测量法”消除副效应所产生的 系统误差的实验方法。 4.学习利用霍尔效应测量磁感应强度B及磁场 分布。 5. 探究能否用更少的数据完成实验
②实验使用了直流电,而且会长时间使用装置, 这样做是否会影响实验结果? 有影响,爱廷豪森效应—热电效应引起的附加 电压VE被证明无法消除,但可通过使用交流电减 小误差,即便使用直流电,在非大电流,非强磁 场下,VH >> VE,因此VE可忽略不计 实验中本人将一空闲装置启动后单独放置了半 个小时左右,其读数变化不明显(约0.02mV),
0
非大电流,非强磁场下,VH>> VE,因此VE可略而不计
三、利用霍尔效应原理测量磁场
利用霍尔效应测量磁场是霍尔效应原理的典型应用。 若已知材料的霍尔系数RH,通过测量霍尔电压VH, 即可测得磁场。其关系式是
大物实验报告霍尔效应【霍尔效应及其应用】

大物实验报告霍尔效应【霍尔效应及其应用】霍尔效应是1879年美国物理学家霍尔读研究生期间在做研究载流子导体在磁场中受力作用实验时发现的。
阐述了霍尔效应的原理,霍尔元件的特点和分类以及在各个领域中的应用。
霍尔效应霍尔元件应用一、霍尔效应原理霍尔效应是1879年美国物理学家霍尔读研究生期间在做研究载流子导体在磁场中受力作用实验时发现的。
霍尔效应是载流试样在与之垂直的磁场中由于载流子受洛仑兹力作用发生偏转而在垂直于电流和磁场方向的试样的两个端面上出现等量异号电荷而产生横向电势差UH的现象。
电势差UH称为霍尔电压,EH称为霍尔电场强度。
此时的载流子既受到洛伦兹力作用又受到与洛伦兹力方向相反的霍尔电场力作用,当载流子所受的洛伦兹力与霍尔电场力相等时,霍尔电压保持相对稳定。
二、霍尔元件的特点和分类1.霍尔元件的特点。
霍尔元件的结构牢固,体积小,重量轻,寿命长,安装方便,功耗小,频率高(可达1MHZ),耐震动,不怕灰尘、油污、水汽及盐雾等的污染或腐蚀,调试方便等。
霍尔元件和永久磁体都能在很宽的温度范围(-40℃~1 50℃)、很强的振动冲击条件下工作,且磁场不受一般介质的阻隔。
另外它的变换器组件能够和相关的信号处理电路集成到同一片硅片上,体积小,成本低,且具有较好的抗电磁干扰性能。
2.霍尔元件的分类。
按照霍尔元件的结构可分为:一维霍尔元件、二维霍尔元件和三维霍尔元件。
一维霍尔元件又被称为单轴霍尔元件,它的主要参数是灵敏度、工作温度和频率响应。
运用此类器件时,就可将与适当的小磁钢一起运动的物体的位置、位移、速度、角度等信息以电信号的形式传感出来,达到了自动测量与控制的目的。
二维霍尔元件的结构是二维平面,也被称为平面霍尔元件;三维霍尔元件通常被称为非平面霍尔元件。
霍尔元件按功能可分为:线形元件、开关、锁存器和专用传感器。
三、霍尔效应的应用人们在利用霍尔效应原理开发的各种霍尔元件已广泛应用于精密测磁、自动化控制、通信、计算机、航天航空等工业部门及国防领域。
霍尔效应及其应用实验报告

霍尔效应及其应用实验报告实验报告:
实验目的:
1. 了解霍尔效应的基本原理和特点。
2. 掌握霍尔系数的测定方法及其相关计算。
3. 熟悉霍尔元件的使用,实现霍尔效应的应用。
实验仪器:
霍尔元件、直流电源、稳压电源、数字万用表、模拟万用表、磁通量表、恒流源等实验仪器设备。
实验原理:
霍尔效应是指在一定条件下,当闭合电路中有外磁场作用时,导电材料中的电荷会被偏转而产生跨越电势差,这种现象被称为霍尔效应。
实验步骤:
1. 将实验仪器连接好,保证电路连接正确无误。
2. 将霍尔元件固定到直流电源的输出端,调节稳压电源电压至所需数值。
3. 将恒流源的输出端接入霍尔元件中,调节电流为所需数值。
4. 调节磁通量表与霍尔元件之间的距离,使其达到最佳感应距离。
5. 打开磁场控制开关,测量相应的电势差与电流值,计算出霍尔系数。
实验结果:
根据实验数据计算出的霍尔系数为2.36×10^-14m^3/C。
证明了实验的可靠性以及相关的计算方法的正确性。
实验结论:
霍尔效应是一种非常实用的物理现象,能够在很多方面应用到实际生活中。
通过本次实验的学习,我们掌握了基本的霍尔效应的原理和相关实验方法,可以更深入地理解和应用相关知识。
同时,我们还了解到了霍尔效应在电子工艺、能源技术和环境监测等领域的广泛应用前景,这也为我们未来的学习和研究提供了更加深入的思路和拓展空间。
霍尔效应及其应用实验报告

课程名称:大学物理实验(二)实验名称:霍尔效应及其应用
图3.3 霍尔器件输出特性测量仪器实物图
仪器操作注意事项
1、测试仪开关机前将I S和I M旋钮逆时针转到底,防止输出电流过大;
2、I S和I M接线不可颠倒,以防烧坏霍尔片;
3、式样应置于螺旋线圈/铁芯气隙内磁场均匀处(即尽量处于中心)。
4、电压表调零
,测试仪功能选择置于“V H”,然后调节I M=0.5A,d=0.5mm
K,单位为千高斯/安(KGs/A)
表5.1 V H—I S曲线图
表5.2测绘曲线V H—I M数据记录表
/mV V2/mV V3/mV V4/mV V
Is-B,+Is-B,-Is+B,-Is
-4.52 4.53-4.80
-6.07 6.11-6.36
-7.637.64-7.92
-9.199.20-9.47
-10.7510.76-11.03
-12.3112.32-12.60
图5.2V H—I M曲线图
测量螺线管轴线上磁场分布
图5.3螺线管轴线上磁场分布
I S曲线的数据处理如下
=0.500A,K=3.94(KGS/A)
V H1=V1−V2+V3−V4
4=2.64−(−2.54)+2.55−(−2.63)
4
=2.59(mV)
5.1;
B=KI M=0.394×0.5=0.197(T)。
霍尔效应及其应用实验报告

霍尔效应及其应用实验报告一、实验名称: 霍尔效应原理及其应用二、实验目的:1、了解霍尔效应产生原理;2、测量霍尔元件的H s V I -、H m V I -曲线,了解霍尔电压H V 与霍尔元件工作电流s I 、直螺线管的励磁电流m I 间的关系;3、学习用霍尔元件测量磁感应强度的原理和方法,测量长直螺旋管轴向磁感应强度B 及分布;4、学习用对称交换测量法(异号法)消除负效应产生的系统误差。
三、仪器用具:YX-04型霍尔效应实验仪(仪器资产编号) 四、实验原理:1、霍尔效应现象及物理解释霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力Bf 作用而引起的偏转。
当带电粒子(电子或空穴)被约束在固体材料中,这种偏转就导致在垂直于电流和磁场的方向上产生正负电荷的聚积,从而形成附加的横向电场。
对于图1所示。
半导体样品,若在x方向通以电流sI ,在z方向加磁场B ,则在y方向即样品A、A′电极两侧就开始聚积异号电荷而产生相应的电场HE ,电场的指向取决于样品的导电类型。
显然,当载流子所受的横向电场力E B f f <时电荷不断聚积,电场不断加强,直到E B f f =样品两侧电荷的积累就达到平衡,即样品A、A′间形成了稳定的电势差(霍尔电压)H V 。
设H E 为霍尔电场,v 是载流子在电流方向上的平均漂移速度;样品的宽度为b ,厚度为d ,载流子浓度为n ,则有:s I nevbd= (1-1)因为E H f eE =,B f evB =,又根据E B f f =,则1s s H H H I BI B V E b R ne d d =⋅=⋅= (1-2)其中1/()H R ne =称为霍尔系数,是反映材料霍尔效应强弱的重要参数。
只要测出H V 、B 以及知道sI 和d ,可按下式计算3(/)H R m c :H H s V dR I B =(1-3)BI U K S H H /= (1—4)H K 为霍尔元件灵敏度。
华科大一下 物理实验报告 霍尔效应与应用设计
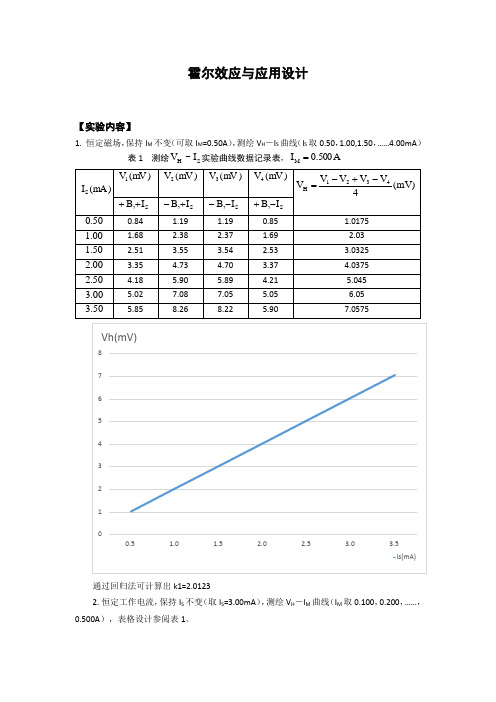
霍尔效应与应用设计【实验内容】1. 恒定磁场,保持I M 不变(可取I M =0.50A ),测绘V H -I S 曲线(I S 取0.50,1.00,1.50,……4.00mA )表1 测绘S H I ~V 实验曲线数据记录表,A 500.0I M =)mA (I S)mV (V 1 )mV (V 2)mV (V 3 )mV (V 4)mV (4V V V V V 4321H -+-=S I ,B ++S I ,B +-S I ,B --S I ,B -+50.0 0.84 1.19 1.19 0.85 1.0175 00.1 1.68 2.38 2.37 1.69 2.03 50.12.513.55 3.54 2.53 3.0325 00.2 3.354.73 4.70 3.37 4.0375 50.2 4.185.90 5.89 4.21 5.045 00.3 5.02 7.08 7.05 5.056.05 50.35.858.268.225.907.0575通过回归法可计算出k1=2.01232. 恒定工作电流,保持I S 不变(取I S =3.00mA ),测绘V H -I M 曲线(I M 取0.100,0.200,……,0.500A ),表格设计参阅表1。
123456780.51.01.52.02.53.03.5 Vh(mV)Is(mA)测绘S H I ~V 实验曲线数据记录表,mA 00.3=S I)mA (M I )mV (V 1 )mV (||2V)mV (V 3 )mV (||4V)mV (4||||4321V V V V V H +++=S I ,B ++S I ,B +-S I ,B --S I ,B -+0.1000 2.23 0.19 0.22 2.20 1.21 0.2000 3.45 1.40 1.42 3.41 2.42 0.3000 4.65 2.61 2.62 4.61 3.6225 0.4000 5.85 3.80 3.84 5.82 4.8275 0.50007.075.025.057.036.0425通过回归法可计算出k2=12.07253.在零磁场下(即I M =0),测量V BC (即σV )。
大一下物理实验【实验报告】 霍尔效应的研究及利用霍尔效应测磁场

东南大学物理实验报告姓名学号指导老师日期座位号报告成绩实验名称:霍尔效应的研究及利用霍尔效应测磁场目录预习报告...................................................2~5 实验目的 (2)实验仪器 (2)实验中的主要工作 (2)预习中遇到的问题及思考 (3)实验原始数据记录 (4)实验报告…………………………………………6~12 实验原理………………………………………………………实验步骤………………………………………………………实验数据处理及分析…………………………………………讨论……………………………………………………………预习报告实验目的:1.了解霍尔效应的基本原理以及有关霍尔元件对材料要求的知识。
2.了解霍尔效应及其消除办法。
3.确定试样的导电类型,载流子浓度以及迁移率。
4.利用霍尔效应测量磁场,并研究载流线圈组的磁场分布。
实验仪器(包括仪器型号):实验中的主要工作:1.霍尔效应的研究:(1)、测量霍尔元件的灵敏度;(2)、测量半导体材料的电导率;(3)、确定所用霍尔元件的电导类型,计算霍尔系数R,载H流子浓度n及载流子迁移率 。
2.利用霍尔效应测磁场:(1)、根据仪器的使用方法调整好测磁实验仪;(2)、测定一对共轴线圈轴线上的磁场分布;(3)、测量长直螺线管轴线上的磁场分布。
①取I=10mA和适当的I M,测量螺线管轴线磁场上的分布,做B-X曲线,并分析结果②测定B=CI M中螺线管常数C预习中遇到的问题及思考:1.霍尔效应实验中有哪些副效应?通过什么方法消除它?答:霍尔元件通常为一矩形薄片,由于材料本身的不均匀以及电压输出的对称性,会在电极位置产生不等位电势差,在研究固体的导电性质时还发现一些热电、热磁效应伴随着霍尔效应一起出现,这样实验中从A、A`测得的电压U并不等于真实的霍尔电压,而是包含了由各种副效应引起的虚假电压。
一般来说附加电压的正负与霍尔原件工作电流及磁感应强度B的方向有关,可以采用对称测量法进行修正。
霍尔效应的应用实验报告
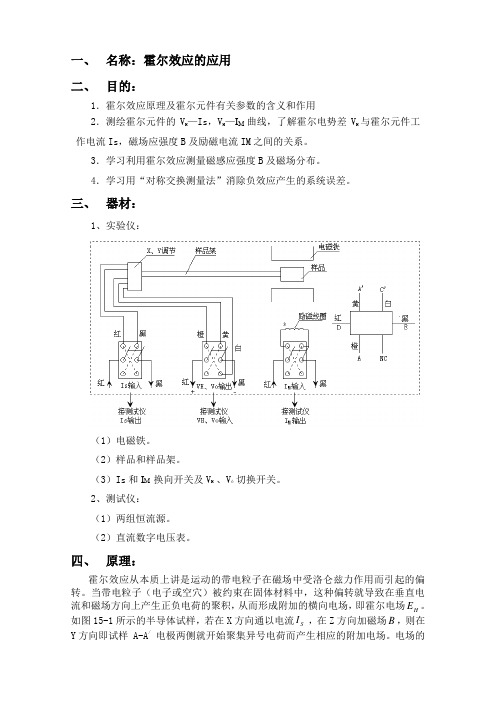
一、名称:霍尔效应的应用二、目的:1.霍尔效应原理及霍尔元件有关参数的含义和作用2.测绘霍尔元件的VH —Is,VH—I M曲线,了解霍尔电势差V H与霍尔元件工作电流Is,磁场应强度B及励磁电流IM之间的关系。
3.学习利用霍尔效应测量磁感应强度B及磁场分布。
4.学习用“对称交换测量法”消除负效应产生的系统误差。
三、器材:1、实验仪:(1)电磁铁。
(2)样品和样品架。
(3)Is和I M 换向开关及V H 、Vó切换开关。
2、测试仪:(1)两组恒流源。
(2)直流数字电压表。
四、原理:霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。
当带电粒子(电子或空穴)被约束在固体材料中,这种偏转就导致在垂直电流和磁场方向上产生正负电荷的聚积,从而形成附加的横向电场,即霍尔电场HE。
如图15-1所示的半导体试样,若在X方向通以电流SI,在Z方向加磁场B,则在Y方向即试样 A-A/ 电极两侧就开始聚集异号电荷而产生相应的附加电场。
电场的指向取决于试样的导电类型。
对图所示的N 型试样,霍尔电场逆Y 方向,(b )的P 型试样则沿Y 方向。
即有)(P 0)()(N 0)(型型⇒>⇒<Y E Y E H H显然,霍尔电场H E 是阻止载流子继续向侧面偏移,当载流子所受的横向电场力H eE 与洛仑兹力B v e 相等,样品两侧电荷的积累就达到动态平衡,故B v e eE H = (1) 其中H E 为霍尔电场,v 是载流子在电流方向上的平均漂移速度。
设试样的宽为b ,厚度为d ,载流子浓度为n ,则bd v ne I S = (2) 由(1)、(2)两式可得:dB I R d BI ne b E V S H S H H ===1 (3) 即霍尔电压H V (A 、A /电极之间的电压)与B I S 乘积成正比与试样厚度d 成反比。
比例系数neR H 1=称为霍尔系数,它是反映材料霍尔效应强弱的重要参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
VH-IM曲线
通过回归法可计算出k2=12.0725
可得到 与仪器标注178 mV/mA·T相差不大
计算KH的不确定度 由于实验没有对同一数据进行多次测量取平均值,没有A 类不确定度,B类不确定度源于仪器的测量误差,已知仪 器的测量准确度为0.5%,取均匀分布
r
r
r
0.0005775 mV/mA·T
一、霍尔效应原理
VH IS
根据霍尔系数RH可进一步确定以下参数
载流子浓度
电导率
迁移率
二、实验中的副效应及其消除方法
(1)不等势电压降V0 (2)爱廷豪森效应—热电效应引起的附加电压VE (3)能斯托效应—热磁效应直接引起的附加电压VN (4)里纪—勒杜克效应—热磁效应产生的温差引起的附加电压VRL
3.在零磁场下(即IM=0),测量VBC(即Vσ )。(IS取0.10, 0.20,0.30……1.00mA)
通过回归法可计算出 k3=766.5455
计算载流子浓度n、电导率、迁移率μ与其不确定度:
UN 、Uσ、Uμ 主要源于所给霍尔 元件尺寸的误差
4.亥姆霍兹线圈单边水平方向磁场分布(IS=3.00mA,IM=0.500A)
影响: 这些都会导致在霍尔效应中作用于霍尔元件的磁
场与相比理论值偏小,产生的霍尔电压VH会偏小。 偏差的大小取决于操作和实验装置的调试,可以
通过采用更精准的装置来减小误差
谢谢!
霍尔效应与应用设计
当电流垂直于外磁场通过导体时,载流子
发生偏转,在垂直于电流和磁场的方向会产生 一附加电场,从而在导体的两端产生电势差,
这一现象就是霍尔效应
霍尔效应的应用在现代汽来自上广泛应用的霍尔器件:ABS 系统中的速度传感器 汽车速度表和里程表 液体物理量检测器 发动机转速传感器。
量子领域的霍尔效应
个小时左右,其读数变化不明显(约0.02mV),
为了严谨,使用装置时最好每十分钟关机冷却一 分钟以上
③记录时需记录V1、V2、V3、V4并求平均值过于
麻烦,能否只用两个电压数据的平均值 完成实
验? 在实验中发现两个电压数据的平均值不但接近
四个电压的平均值,而且与电流之间的回归方程 的斜率似乎也很接近
实验内容
1.测量霍耳电压与工作电流,记录数据测绘VH-IS曲线
恒定磁场,保持励磁电流IM=0.50A,调整工作电流IS,记录数据 根据数据画出VH-IS曲线,
VH-IS曲线
通过回归法可计算出k1=2.0123
2.测量霍耳电压与励磁电流IM,记录数据测绘VH-IM曲线
恒定磁场,保持工作电流IS=3..00mA,调整励磁电流IM,记录数据 根据数据画出VH-IM曲线,
器,输电线等,最好换更场地
②实验使用了直流电,而且会长时间使用装置, 这样做是否会影响实验结果?
有影响,爱廷豪森效应—热电效应引起的附加
电压VE被证明无法消除,但可通过使用交流电减 小误差,即便使用直流电,在非大电流,非强磁 场下,VH >> VE,因此VE可忽略不计
实验中本人将一空闲装置启动后单独放置了半
(|V2|+|V4|)/2= VH + VE (|V3|+|V4|)/2= VH - VN - VRL + VE 由②可以知道实验时VE很小可以忽略,但是这
样做对斜率造成的影响 是否明显呢?
借助实验1的数据,进行计算 使用四个数据的平均值时,通过回归法计算出k=2.0123
只使用V1、V2的平均值时,通过回归法计算出k=2.0182 只使用V1、V3的平均值时,通过回归法计算出k=2.0121 只使用V2、V4的平均值时,通过回归法计算出k=2.0125 只使用V3、V4的平均值时,通过回归法计算出k=2.0064
斜率相差不大,但仍有差异,出于严谨,
不能只使用两个电压数据的平均值进行计算
④实验中还有哪些未考虑到的误差?会有什么影
响?如何处理这些误差? 实验装置不可能达到绝对完美的精准。霍尔元件不
会完美地位于励磁线圈几何中心点上,也不会刚好处于 螺线管的几何轴线上,与磁场也不会完全垂直,线圈、 螺线管不可避免的会有漏磁现象,磁场分布变化也不会 处处平缓
我们无法彻底消除误差,但我们可以减小误
差,只要可以将其减小到我们可以接受的范围, 依旧可以算作排除了误差影响,而用尽可能少的 实验操作减少误差也是实验的重点之一
如果只使用两个电压的平均值
(|V1|+|V2|)/2= VH + VN + VRL + VE (|V1|+|V3|)/2= VH + VE
【实验目的】
1.通过实验掌握霍尔效应基本原理,了解霍尔 元件的基本结构;
2.学会测量半导体材料的霍尔系数、电导率、 迁移率等参数的实验方法和技术;
3.学会用“对称测量法”消除副效应所产生的 系统误差的实验方法。
4.学习利用霍尔效应测量磁感应强度B及磁场 分布。
5. 探究能否用更少的数据完成实验
实验原理
0
非大电流,非强磁场下,VH>> VE,因此VE可略而不计
三、利用霍尔效应原理测量磁场
利用霍尔效应测量磁场是霍尔效应原理的典型应用。 若已知材料的霍尔系数RH,通过测量霍尔电压VH, 即可测得磁场。其关系式是
四、长直通电螺线管轴线上磁感应强度
根据毕奥-萨伐尔定律,对于长度为2L,匝数为N,半径为 R的螺线管离开中心点x处的磁感应强度为
5.通电螺线管轴向磁场分布(IM为500mA,Is为3.00mA))
通电螺线管轴线上磁感应强度
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
理论值
测量值
实验遇到的问题及解决的方法
①是否需要考虑地磁场?
不需要。地磁场过于微弱(50-60μT),对实
验产生的影响完全可以忽略, 但如果周围有产生强磁场的物体,比如变压
