模糊逻辑控制matlab编程仿真(第七组)
模糊控制Matlab仿真
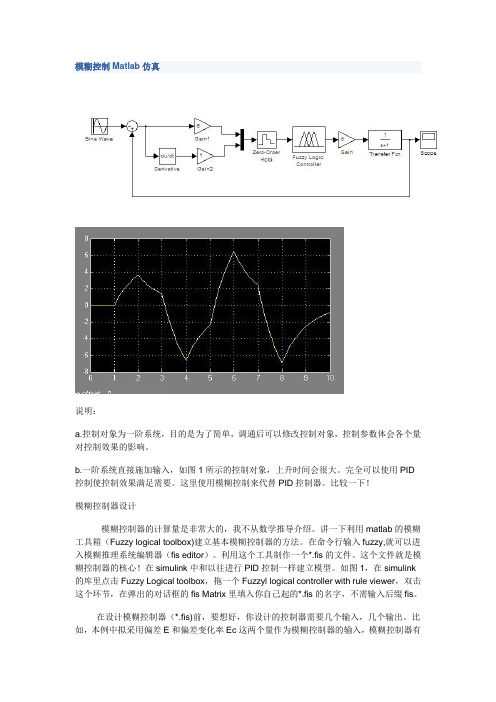
模糊控制Matlab仿真说明:a.控制对象为一阶系统,目的是为了简单,调通后可以修改控制对象,控制参数体会各个量对控制效果的影响。
b.一阶系统直接施加输入,如图1所示的控制对象,上升时间会很大。
完全可以使用PID 控制使控制效果满足需要。
这里使用模糊控制来代替PID控制器。
比较一下!模糊控制器设计模糊控制器的计算量是非常大的,我不从数学推导介绍。
讲一下利用matlab的模糊工具箱(Fuzzy logical toolbox)建立基本模糊控制器的方法。
在命令行输入fuzzy,就可以进入模糊推理系统编辑器(fis editor)。
利用这个工具制作一个*.fis的文件。
这个文件就是模糊控制器的核心!在simulink中和以往进行PID控制一样建立模型。
如图1,在simulink 的库里点击Fuzzy Logical toolbox,拖一个Fuzzyl logical controller with rule viewer,双击这个环节,在弹出的对话框的fis Matrix里填入你自己起的*.fis的名字,不需输入后缀fis。
在设计模糊控制器(*.fis)前,要想好,你设计的控制器需要几个输入,几个输出。
比如,本例中拟采用偏差E和偏差变化率Ec这两个量作为模糊控制器的输入,模糊控制器有一个输出。
很明显,这是利用模糊控制器代替PD控制的。
对应的模糊控制器的设计也要具有两个输入一个输出。
利用matlab的Fuzzy logical toolbox 设计模糊控制器(生成*.fis文件)的关键步骤:a.添加输入输出。
图3.fis编辑器默认的具有一个输出,添加第二个输入,并且分别命名为E,Ec,U。
b.确定隶属函数。
双击黄色和绿色的方框就可以进入隶属函数编辑对话框了。
设置E,Ec 的range为[-6,6],u的range为[-1,1]。
然后每一个变量再添加4个输入隶属函数,总共7个。
matlab提供了11种隶属函数,第一次用选择常用的三角形trimf,区别不大的。
模糊控制在matlab中的实例

模糊控制在matlab中的实例模糊控制(模糊逻辑控制)是一种基于模糊数学理论的控制方法,它可以用于控制系统的稳定性、精度和响应速度等方面的优化。
在MATLAB 中,可以使用模糊逻辑工具箱(FLUS)来应用模糊控制。
以下是一个简单的实例,展示了如何使用 MATLAB 中的模糊逻辑工具箱来对温度控制系统进行控制:首先,我们需要创建一个温度控制系统,该系统将使用模糊控制来控制传感器的读数。
假设我们有四个传感器,分别为温度传感器、湿度传感器、压力和传感器,每个传感器读数为实数。
```matlab% 创建模型T = [120 100 80 50]; % 温度控制器输出R1 = [1.2 0.8 0.4 0.2]; % 湿度控制器输出R2 = [0.9 0.1 0.3 0.5]; % 压力控制器输出R3 = [1.4 0.6 0.2 0.1]; % 传感器误差P1 = [125 125 125 125]; % 温度控制器输入P2 = [100 100 90 80]; % 湿度控制器输入P3 = [85 85 80 75]; % 压力控制器输入F1 = [0.3 0.2 0.1 0.1]; % 温度控制器输出F2 = [0.4 0.3 0.2 0.1]; % 湿度控制器输出F3 = [0.5 0.4 0.3 0.1]; % 压力控制器输出y1 = [100 85 75 60]; % 实际温度y2 = [120 95 80 70]; % 实际湿度y3 = [135 110 90 80]; % 实际压力% 创建模糊控制器go1 = @(t,u,v) if t > 100 then ((1-v)*F1 + v*R1 +(1+v)*R2)/(1-v)*y1 else 0;go2 = @(t,u,v) if t < 50 then ((1-v)*F3 + v*R1 +(1+v)*R2)/(1-v)*y2 else 0;go3 = @(t,u,v) if t == 0 then ((1-v)*F1 + v*R1 +(1+v)*R2)/(1-v)*y3 else 0;% 创建模糊控制器的优化器var = [0 0 0 0];go1(0,:,:) = var;matlab.模糊控制.优化器.LevenbergMarquardt(var,go1);% 运行模糊控制器[t,u,v] = ode45(go1,[0 1],[120 100 80 50],y1);% 输出结果disp(["实际温度:" num2str(t)]);disp(["实际湿度:" num2str(u)]);disp(["实际压力:" num2str(v)]);```在这个例子中,我们使用 MATLAB 中的 ode45 工具箱来拟合温度控制器和湿度控制器的输出响应函数。
MATLAB模糊控制仿真程序

clear all;close all;ts=20;sys1=tf([1],[60,1],'inputdelay',80);%生成或转换传递函数模型dsys1=c2d(sys1,ts,'zoh');%将连续系统离散化[num1,den1]=tfdata(dsys1,'v');%传统PID算法u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;y_1=0;y_2=0;y_3=0;error_1=0;ei=0;for k=1:1:300time(k)=k*ts;rin(k)=40;yout(k)=-den1(2)*y_1+num1(2)*u_5;error(k)=rin(k)-yout(k);ei=ei+error(k)*ts;kp=0.8;ki=0.005;kd=3.0;u(k)=kp*error(k)+kd*(error(k)-error_1)/ts+ki*ei;if u(k)>=110u(k)=110;endif u(k)<=-110u(k)=-110;end%返回PID参数u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);y_3=y_2;y_2=y_1;y_1=yout(k);error_1=error(k);end%获得传递函数模型数据%模糊PID控制系统a=newfis('fuzzf');%创建新的模糊推理系统f1=1;a=addvar(a,'input','e',[-5*f1,5*f1]);%添加e 的模糊语言变量a=addmf(a,'input',1,'NB','trimf',[ -7.5 -5 -2.5]);%添加e 的模糊语言变量的隶属度函数(z型)a=addmf(a,'input',1,'NS','trimf', [-5 -2.5 0]);a=addmf(a,'input',1,'ZE','trimf',[-2.5 0 2.5]);a=addmf(a,'input',1,'PS','trimf',[0 2.5 5]);a=addmf(a,'input',1,'PB','smf',[2.5 5 7.5]);f2=1;a=addvar(a,'input','ec',[-10*f2,10*f2]);%添加ec 的模糊语言变量a=addmf(a,'input',2,'NB','trimf',[-15 -10 -5]);a=addmf(a,'input',2,'NS','trimf',[-10 -5 0]);a=addmf(a,'input',2,'Z','trimf', [-5 -5.551e-017 5]);a=addmf(a,'input',2,'PS','trimf', [0 5 10]);a=addmf(a,'input',2,'PB','smf', [5 10 15]);f3=1.5;a=addvar(a,'output','u',[0*f3,220*f3]);%添加u 的模糊语言变量a=addmf(a,'output',1,'NB','trimf', [-55 -4.441e-016 55]); a=addmf(a,'output',1,'NS','trimf', [0 55 110]);a=addmf(a,'output',1,'Z','trimf', [55 110 165]);a=addmf(a,'output',1,'PS','trimf', [110 165 220]);a=addmf(a,'output',1,'PB','smf',[165 220 275]);rulelist=[1 1 5 1 1; %编辑模糊规则1 2 5 1 1;1 3 5 1 1;1 4 5 1 1;1 5 5 1 1;2 1 5 1 1;2 2 4 1 1;2 3 4 1 1;2 43 1 1;2 5 2 1 1;3 1 5 1 1;3 24 1 1;3 3 3 1 1;3 4 2 1 1;3 5 2 1 1;4 1 4 1 1;4 2 3 1 1;4 3 2 1 1;4 4 2 1 1;4 5 1 1 1;5 1 1 1 1;5 2 1 1 1;5 3 1 1 1;5 4 1 1 1;5 5 1 1 1;]a=addrule(a,rulelist); %添加模糊规则函数showrule(a) %显示模糊规则函数a1=setfis(a,'DefuzzMethod','centroid'); %设置模糊系统特性writefis(a1,'fuzzf'); %保存模糊系统a2=readfis('fuzzf'); %从磁盘读出保存的模糊系统disp('fuzzy Controller table:e=[-5,+5],ec=[-10,+10]');%显示矩阵和数组内容Ulist=zeros(5,5); %全零矩阵for i=1:5for j=1:5e(i)=-4+i;ec(j)=-4+j;Ulist(i,j)=evalfis([e(i),ec(j)],a2); %完成模糊推理计算endendUlist=ceil(Ulist)sys1=tf([1],[60,1],'inputdelay',80);dsys=c2d(sys1,ts,'zoh');[num,den]=tfdata(dsys,'v');U_1=0;U_2=0;U_3=0;U_4=0;U_5=0;Y_1=0;Y_2=0;Y_3=0;e_1=0.0;ec_1=0.0;Error_1=0;Ei=0for k=1:1:300time(k)=k*ts;rin(k)=40;U(k)=evalfis([e_1,ec_1],a2);%完成模糊推理计算Yout(k)=-den(2)*Y_1+num(2)*U_5;Error(k)=rin(k)-Yout(k);ki=0.003; Ei=Ei+Error(k)*ts;U(k)=U(k)+ki*Ei;%返回参数U_5=U_4;U_4=U_3;U_3=U_2;U_2=U_1;U_1=U(k);Y_3=Y_2;Y_2=Y_1;Y_1=Yout(k);e_1=Error(k); ec_1=Error(k)-Error_1;Error_1=Error(k);end%朝正无穷方向取整figure(1); plotfis(a2);figure(2);plotmf(a,'input',1);figure(3);plotmf(a,'input',2);figure(4);plotmf(a,'output',1);figure(1);plot(time,rin,'b',time,yout,'r');xlabel('time(s)');ylabel('rin,yout');figure(2);plot(time,u,'r');xlabel('time(s)');ylabel('u');figure(3);plot(time,rin,'b',time,Yout,'r');xlabel('time(s)');ylabel('rin,yout');figure(4);plot(time,U,'r');xlabel('time(s)');ylabel('u');figure(5); plotfis(a2);figure(6);plotmf(a2,'input',1);figure(7);plotmf(a2,'input',2);figure(8);plotmf(a2,'output',1);。
模糊控制MATLAB仿真
模糊控制MATLAB仿真
实验报告本课程名称:MATLAB模糊控制上机实验
2013~2014学年第⼀学期
⼴东⽯油化⼯学院计算机与电⼦信息学院
实验⽬的:
1、了解MATLAB中各种仿真⼯具。
2、掌握MATLAB仿真⼯具中图形化界⾯以及模糊逻辑⼯具箱函数的仿真⽅法。
上机实验⼀:
设计⼀个温度模糊控制器,具体要求见课本P59要求采⽤下⾯两种MATLAB⼯具进⾏仿真。
1、⼯具箱提供的图形化界⾯
2、模糊逻辑⼯具箱函数
仿真⽅法:
1、采⽤MATLAB语⾔根据具体的控制算法编程
2、利⽤MATLAB提供的模糊逻辑⼯具箱函数
3、利⽤模糊逻辑⼯具箱的图形界⾯与Simulink动态仿真环境
在matlab⼯作窗⼝输⼊:fuzzy+回车或fuzzy + ⽂件名(.fis)进⼊图形界⾯编辑
增加输⼊变量
输⼊mfedit或选择编辑⾪属度函数菜单输⼊误差e的⾪属度函数
输⼊误差变化de的⾪属度函数
输出u的⾪属度函数
输⼊ruleedit,或选择编辑模糊规则菜单
浏览模糊规则
模糊推理输⼊输出曲⾯视图,完成模糊推理系统的构建。
如何利用Matlab进行模糊逻辑控制

如何利用Matlab进行模糊逻辑控制Matlab是一种流行的数学软件,广泛应用于科学和工程领域。
其中一个强大的功能是模糊逻辑控制,它可以帮助人们解决模糊问题。
本文将介绍如何利用Matlab进行模糊逻辑控制,以及其在实际应用中的价值和局限性。
1. 什么是模糊逻辑控制?模糊逻辑控制是一种基于模糊推理的控制方法。
与传统的二值逻辑不同,模糊逻辑可以处理模糊的、不确定的信息。
它将模糊集合和模糊规则引入到控制系统中,使得系统能够根据输入数据和模糊规则进行推理,并输出相应的控制信号。
2. Matlab中的模糊逻辑工具箱Matlab提供了强大的模糊逻辑工具箱,可以用于模糊逻辑控制系统的设计和仿真。
该工具箱包含了模糊集合的定义、模糊规则的建立、模糊控制器的设计等功能。
用户可以通过简单的命令和图形界面进行操作,快速构建模糊逻辑控制系统。
3. 模糊集合的定义模糊集合是模糊逻辑的基础,它用来描述对于一个特定的输入值,它属于某个特定集合的程度。
在Matlab中,我们可以使用模糊集合来定义输入和输出的隶属度函数。
例如,对于一个温度控制系统,我们可以定义一个“冷”的模糊集合和一个“热”的模糊集合,它们分别代表了输入量的不同程度。
4. 模糊规则的建立在模糊逻辑控制系统中,模糊规则用于描述输入和输出之间的关系。
在Matlab 中,我们可以使用模糊规则来定义输入值和输出值之间的映射关系。
例如,对于一个简单的车速控制系统,我们可以定义一个模糊规则,如“如果车速较慢,则增加油门”的规则。
通过组合多个模糊规则,可以构建一个复杂的控制策略。
5. 模糊控制器的设计在Matlab中,我们可以使用模糊控制器对象来设计和实现模糊逻辑控制系统。
模糊控制器对象包含了输入集合、输出集合、模糊规则库等属性,以及推理和解糊过程的方法。
用户可以根据系统需求和实际问题,选择合适的模糊集合、模糊规则和解糊方法,设计出一个有效的模糊控制器。
6. 模糊逻辑控制的应用模糊逻辑控制在实际应用中具有广泛的应用价值。
模糊PID控制器设计及MATLAB仿真_李健

图 1 模糊 PID 控制结构图
PID 参 数 模 糊 自 整 定 是 先 找 出 PID 控 制 器 的 3 个 参 数 Kp、 Ki 和 Kd 与偏差 e 和偏差变化率 ec 之间的模糊关系, 在运行中 通过不断检测 e 和 ec,根据模糊控制规则来对 3 个参量进行在
线修改 ,以 满 足 不 同 e 和 ec 对 控 制 器 参 数 的 不 同 要 求 ,从 而 使
起较大的超调 。 微 分 系 数 Kd 影 响 系 统 的 动 态 特 性 ,Kd 越 大 ,越
能抑制偏差变化,但过大会延长调节时间,降低抗干扰能力。
根 据 参 数 Kp、Ki、Kd 对 系 统 输 出 特 性 的 影 响 情 况 ,可 归 纳 出 系统在被控过程中对于不同的偏差和偏差变化率 , 参数 Kp、Ki、 Kd 的自整定原则:
摘要 将模糊控制器和 PID 控制器结合在一起,构造了一个模糊 PID 控制器,利用模糊推理的方法调整 PID 控制器的参数, 并利用 MATLAB 的 SUMLINK 工具箱,对系统进行仿真,仿真结果表明模糊 PID 控制器能使系统达到满意的控制效果。 关键词:PID 控制器,模糊控制,MATLAB,SIMULINK,系统仿真
1.3 模糊控制算法的确立
PID 参数的整定必须考虑到在不同时刻 3 个参数的作 用 以
及相互之间的互联关系。 模糊自整定 PID 是在 PID 算法的基础
上通过计算当前系统误差 e 和误差变化 ec,利用模糊规则 进 行
模糊推理,查询模糊矩阵表进行参数调整。 参数修正公式:
'
Kp =Kp +(e,ec)p
被控对象具有良好的动、静态性能。
1.2 PID 控制器的确立
通常,PID 控制器的控制算式为:
Matlab中的模糊逻辑控制方法

Matlab中的模糊逻辑控制方法引言模糊逻辑控制(FLC)是一种常用的控制方法,在很多实际应用中得到了广泛的应用。
Matlab作为一种功能强大的数学计算和工程仿真软件,提供了丰富的工具和函数来支持模糊逻辑控制的设计和实现。
本文将介绍Matlab中的模糊逻辑控制方法及其应用。
一、模糊逻辑控制的基本概念模糊逻辑控制是一种基于模糊逻辑原理的控制方法,它可以处理不确定性信息和模糊概念,适用于那些难以建立精确数学模型的控制系统。
模糊逻辑控制系统由四个基本部分组成:模糊化、推理、解模糊和规则库。
1.1 模糊化模糊化是将输入量从实际值转化为模糊集合的过程。
在Matlab中,可以使用fuzzifier函数将实际输入映射到模糊集合上。
模糊集合可以通过一些参数来描述,如三角形型、梯形型、高斯型等。
1.2 推理推理是根据模糊集合的规则进行推导,得到系统的输出。
在Matlab中,可以使用inference函数进行推理。
推理的方法有三种:基于规则的推理、基于模糊集合的推理和基于模型的推理。
根据应用的需求和系统的复杂程度,可以选择不同的推理方法。
1.3 解模糊解模糊是将模糊输出转化为实际值的过程。
在Matlab中,可以使用defuzzifier 函数进行解模糊。
常用的解模糊方法有:最大值法、平均值法、面积法等。
1.4 规则库规则库是模糊逻辑控制系统的核心,它包含了一系列的模糊规则,用来描述输入和输出之间的关系。
在Matlab中,可以使用fuzzy规则对象来定义规则库。
规则库的设计是模糊逻辑控制系统设计中的关键一步,直接影响系统的性能和稳定性。
二、Matlab中的模糊逻辑控制工具箱Matlab提供了专门的工具箱,用于支持模糊逻辑控制系统的设计和实现。
这个工具箱包含了一些常用的函数和工具,能够帮助用户更加方便快捷地进行模糊逻辑控制系统的设计和仿真。
2.1 模糊逻辑控制系统设计工具Matlab的模糊逻辑控制系统设计工具提供了一种用户友好的可视化界面,用于设计和编辑模糊逻辑控制系统。
模糊控制及matlab仿真

模糊控制及matlab仿真1 .实例某个液位控制系统的液体容器中,液体的流出量变化无常,无法建立起数学模型,只能通过控制进液阀门开度调节液位,使容器中的液位保持平衡。
根据积累的操作经验,归纳总结出使液体容器液位保持恒定的下述几条操作规律。
1.如果液位正好,则阀门开度不变;If level is okay then value is no change2.如果液位偏低,则增大阀门开度;If level is low then value is open fast3.如果液位偏高,则减小阀门开度;If level is high then value is close fast4.如果液位正好而进液流速快,则逐渐减小阀门开度;If level is okay and rate is positive then value is close slow5.如果液位正好而进液流速慢,则逐渐增大阀门开度;If level is okay and rate is negation then value is open slow 2. simulink模块及fis文件本系统采用曼达尼模型进行仿真,通过matlab模糊控制编辑器进行控制规则的建立,以及模糊控制器的搭建。
Fis编辑器如下图所示,该控制器为两输入一输出系统。
其中两输入分别为液位高度,及液位变化速率,输出为阀门开度。
“与”算法用求积来表达,“或”算法用代数和来表达,“蕴含”算法用求积来表达,“综合”算法为各条模糊规则结果取并,“清晰化”算法用面积中心法来描述。
隶属函数编辑器液位隶属函数液位变化速率隶属函数阀门开度隶属函数控制规则编写Simulink模块3. 仿真及结果分析液位初始波动与经过阀门调节后系统液位曲线比较。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《智能控制》模糊逼近作业报告组员:李适、郑晓森、匡金龙、沈伟生、武云发黎浩炎、晏开、杜文学、杨晓星目录一、任务及要求 (3)二、系统分析及控制设计原理 (3)三、设计实现 (4)四、仿真验证 (7)五、讨论与分析 (12)一、任务及要求(1)任务设计一个在 上的模糊系统,使其以精度一致地逼近函数()()()()()ππππ2121cos sin cos sin x x x x x g ++=,并进行Matlab 仿真。
(2)要求先进行系统分析,然后给出完整详细的设计过程,可参见P74-75页例5.1和例5.2的仿真实例。
二、系统分析及控制设计原理自适应模糊控制是指具有自适应学习算法的模糊逻辑系统,其学习算法是依靠数据信息调整模糊逻辑系统的参数,且可以保证控制系统的稳定性。
一个自适应模糊控制器可以用一个单一的自适应模糊系统构成,也可以用若干个自适应模糊系统构成。
与传统的自适应控制相比,自适应模糊控制的优越性在于它可以利用操作人员提供的语言性模糊信息,而传统的自适应控制则不能。
这一点对具有高度不确定因素的系统尤其重要。
自适应模糊控制有两种不同形式:一种是直接自适应模糊控制,即根据实际系统性能与理想性能之间的偏差直接设计模糊控制器;另一种是间接自适应模糊控制,即通过在线模糊逼近获得对象的模型,然后根据所得模型在线设计控制器。
三、设计实现(1)模糊系统的设计步骤设二维模糊系统g(x)为集合22211],[],[R U ⊂⨯=βαβα上的一个函数,其解析式形式未知。
假设对任意一个U x ∈,都能得到g(x),则可设计一个逼近g(x)的模糊系统。
模糊系统的设计步骤为:步骤1:在],[i i βα上定义)2,1(=i N i 个标准的,一致的和完备的模糊集i N i i i i A A A A ,...,,,321。
[][]1,11,1-⨯-=U 1.0=ε步骤2:组建21N N M ⨯=条模糊集IF-THEN 规则,即21u i i R :如果1x 为11i A 且2x 为22i A ,则y 为21i i B式中,2211,...,2,1;,...,2,1N i N i ==,将模糊集21i i B 的中心表示为),(),(g 21121221i i i i e e g x x y==式中,j i e 为i x 在模糊集j i A 上的中间值或边界值()2,1;2,1==j i 。
步骤3:采用乘积推理机、单值模糊器和中心平均接模器和中心平均解模糊器,根据21N N M ⨯=规则来构造模糊系统f(x),得()()()()()∑∑∑∑=====11222211112222112111211121)(N i N i i A i A N i N i i A i A i i x x x x yx f μμμμ式中,分子表规则前提之间、规则前提与结论之间的逻辑“与”运算,采用乘积推理机实现;21i i y 采用单值模糊器实现,积隶属度函数最大值(1,0)所对应的横坐标值()2121,i i e e的函数值()2121,g i i e e ;分子与分母相除与中心平均解模糊器算法。
(2)糊系统的逼近精度万能逼近定理表明模糊系统是除以多项函数逼近器,神经网络之外的新的万能逼近器。
模糊系统较之其他逼近器的优势在于它能够有效地利用语言信息能力。
万能逼近是模糊逻辑系统用于非线性系统建模的理论基础,同时也从根本上解释了模糊系统在实际中得到成功应用的原因。
万能逼近定理:令f(x)为上式中二维模糊系统,g(x)为上式中的未知函数,如果g(x)在],[],[2111βαβα⨯=U 上是连续可微的,则模糊系统的逼近精度为2211h x gh x g fg ∞∞∞∂∂+∂∂≤-其中 ()2,1m ax 111=-=+-≤≤i e e h j i j i N j i i式中,无穷维范数∞•定义为函数上界,即)(sup )(x d x d Ux ∈∞=,j i e 为i x 在j i A 个模糊集上的中间值或边界值,j=1和i N j =时为边界值。
由i h 式可知,假设i x 的模糊集的个数为i N ,其变化范围的长度为L ,则模糊系统的逼近精度满足1-=i i i N L h ,即1+=ii i h LN 。
由该定理可得一下结论:①形如f(x)式的模糊系统是万能逼近器,对任意给定的0>ε,都可将1h 和2h 选得足够小,使ε<∂∂+∂∂∞2211g h x g h x 成立,从而保证()()ε<-=-∞∈f g x f x g Ux sup②通过对每个i x 定义更多的模糊集可以得到更为准确的逼近器,即规则越多,所产生的模糊系统越有效。
③为了设计一个具有预定精度的模糊系统,必须知道g(x)关于1x 和2x 的导数边界,即∞∂∂1g x 和∞∂∂2g x 。
同时,在设计过程中,还必须知道g(x)在()()221121,...2,1;,...2,1,21N i N i e e x i i ===处的值。
四.仿真验证设计一个在 上的模糊系统,使其以精度一致地逼近函数()()()()()ππππ2121cos sin cos sin x x x x x g ++=,并进行Matlab 仿真。
原理: 由于由式 可知,当取h 1=0.05,h 2=0.05时,有 1628.0205.0205.0<=⨯+⨯ππ ,满足精度为1要求。
由于L=2,此时模糊集的个数为 取N=21,[][]1,11,1-⨯-=U 1.0=ε()()()ππππππ2cos cos cos sup 2111=+=∂∂∈∞x x x x g Ux ()()()ππππππ2sin sin sin sup 2122=--=∂∂∈∞x x x x gUx 2211h x gh x g f g ∞∞∞∂∂+∂∂≤-211=+=hL N即 和 分别在 上定义11个具有三角隶属函数的模糊集 。
所设计的模糊系统为该模糊系统由1211111=⨯条规则来逼近函数 。
解:根据题目要求,知,L=2,T=0.1,可取h=0.05,N=L/h+1=21 二维函数逼近仿真程序如下所示:%Fuzzy approaching clear all; close all; T=0.1; x1=-1:T:1; x2=-1:T:1;L=2; h=0.05;N=L/h+1;for i=1:1:N %N MF for j=1:1:Ne1(i)=-1+L/(N-1)*(i-1); e2(j)=-1+L/(N-1)*(j-1);gx(i,j)=sin((e1(i))*pi)+cos((e2(j))*pi)+sin(e1(i)*pi)*cos(e2(j)*pi) end enddf=zeros(L/T+1,L/T+1); cf=zeros(L/T+1,L/T+1);for m=1:1:N %u1 change from 1 to N if m==1u1=trimf(x1,[-1,-1,-1+L/(N-1)]); %First u1 elseif m==Nu1=trimf(x1,[1-L/(N-1),1,1]); %Last u1 elseu1=trimf(x1,[e1(m-1),e1(m),e1(m+1)]); endfigure(1); hold on; plot(x1,u1);xlabel('x1');ylabel('Membership function');for n=1:1:N %u2 change from 1 to N1x 2x []1,1-=U j A ()()()()()()∑∑∑∑=====11111121111111211221122121,i i i A i A i i i A i A i i x x x x e e g x f μμμμ()x gif n==1u2=trimf(x2,[-1,-1,-1+L/(N-1)]); %First u2elseif n==Nu2=trimf(x2,[1-L/(N-1),1,1]); %Last u2elseu2=trimf(x2,[e2(n-1),e2(n),e2(n+1)]);endfigure(2);hold on;plot(x2,u2);xlabel('x2');ylabel('Membership function');for i=1:1:L/T+1for j=1:1:L/T+1d=df(i,j)+u1(i)*u2(j);df(i,j)=d;c=cf(i,j)+gx(m,n)*u1(i)*u2(j);cf(i,j)=c;endendendend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%for i=1:1:L/T+1for j=1:1:L/T+1f(i,j)=cf(i,j)/df(i,j);y(i,j)=sin((x1(i))*pi)+cos((x2(j))*pi)+sin(x1(i)*pi)*cos(x2(j)*pi)endendfigure(3);subplot(211);surf(x1,x2,f);title('f(x)');subplot(212);surf(x1,x2,y);title('g(x)');figure(4);surf(x1,x2,f-y);title('Approaching error')程序运行结果:H=0.2 T=0.1图1 的隶属函数图2 的隶属函数1x 2x图3 模糊逼近图4 逼近误差H=0.1 T=0.1图5 H=0.1 T=0.1时运行结果H=0.05 T=0.1图6 H=0.05 T=0.1时运行结果H=0.02 T=0.1图7 H=0.02 T=0.1 时运行结果运算时间过久,将近15分钟图8 H=0.01 T=0.1 时运行结果运算时间过久,超过60分钟图9 H=0.2 T=0.05 时运行结果图10 H=0.1 T=0.05 时运行结果H=0.05 T=0.05图11 H=0.05 T=0.05时运行结果H=0.02 T=0.05图12 H=0.02 T=0.05 时运行结果五.讨论与分析由于由式 可知,当取h 1=0.0075,h 2=0.0075时,有 1.020075.020075.0<⨯+⨯ππ ,满足精度要求。
()()()ππππππ2cos cos cos sup 2111=+=∂∂∈∞x x x x g Ux ()()()ππππππ2sin sin sin sup 2122=--=∂∂∈∞x x x x g Ux 2211h x g h x g f g ∞∞∞∂∂+∂∂≤-H=0.0075时,运行超过30分钟,转而尝试H=0.2,H=0.1,H=0.05,H=0.02,H=0.01,除H=0.2相对误差较大,不过仍在小于0.1范围内。
