叠加定理课件
合集下载
电路与模拟电子技术原理第4章2叠加课件.ppt

反映了动态电路在外加电源为零、单纯 在初始状态作用下所呈现的特征。
零输入响应的形式
t
f (t应与初始状态成线性关系。
14:28:59
13
3.零状态响应
动态电路在初始状态为零(而输入不为零) 时的响应,叫做零状态响应。
反映了动态电路在没有初始状态、单纯在输入 (即外加电源)作用下所呈现的特性。
固有响应,或自由响应(natural response):变化形式取决于电路本身。
f (t)
f () f (0 )
t
f () e
14:28:59
25
4.3.3 暂态响应和稳态响应
一阶电路的完全响应又可以分解为暂 态响应与稳态响应。
暂态响应、瞬态响应:暂时的、瞬间的 分量。
稳态响应
这种叠加实际上是线性电路叠加定理在
“动态元件初始状态可视为激励”这一前 提下的扩展。
14:28:59
15
完全响应(续)
线性动态电路中的完全响应,等于动 态电路本身初始状态激励所产生的响 应(即零输入响应),与外界电源输 入激励所产生的响应(即零状态响应) 的叠加。
14:28:59
16
零输入响应、零状态响应的总结:
iL2(t) iL2() [iL2(0 ) iL2()]e 2
t
25 (0 25)e 2
t
25 25e 2 (A)
(t>0)
14:28:59
8
线性动态电路叠加定理例1(续)
电路中的总响应电流为 iL(t)=iL1(t)+iL2(t)
=
25(A) t
50 25e 2 (A)
(t≤0) (t>0)
uC(0+)=uC(0-)=6(V) 换路后的电路如图421(b)所示。
线性电路的性质叠加定理.2021优秀PPT文档

45.有时候想找人说说话,于是一遍遍翻看手机里的电话簿,却不知道能够给谁发个消息或打个电话,最后还是按下了“清除”。其实很想找个人倾诉一下,却又不知从何说起,最终的最终是什么也不说, 告诉自我,明天就好了。
17.善于利用时间的人,永远找得到充裕的时间。 73.成功的人总是愿意做没成功的人不愿意做的事。 49.不为失败找借口,只为成功找方法。 七、人向前走的过程,应该是慢慢学会做减法的过程。贪念越多,心里装的包袱越多,人越是寸步难行。学会放下,才能走更快更远。
例如
例2 设图中R1 = 2 k,R2 = 1 k,R3 = 3 k, R4 = 0.5 k,Us = 4.5 V,Is = 1 mA。 求电流 I 和电压 U。
解: 电压源单独作用
I1
I 3
Us R1 R3
0.9103 A
0.9
mA
I 2
I4
Us R2 R4
3103 A
3mA
I=I1 + I2 =(0.9+3.0)mA = 3.9 mA
电流源一组 1. 电压源作用,电流源不作用:
U 3 2 3 V 13 2
I 21 3 A 22
2. 电流源作用,电压源不作用:
I 3A
U 31 (3) 9 V
1 3
4
3. 所有电源一起作用:
U U U 3 V 4
I I I 1.5A
例4 图示电路,当us=2V,is=2A,测得i=7A; 当us=0.5V,is=1A,测得i=4A。 问若us=-2.5V,is=2A,i=?
独立电压源单独作用
U x 6 U x U x 2 42
Ux 1.2 V
两独立源共同作用
U x Ux Ux (4 1.2) V 2.8 V
17.善于利用时间的人,永远找得到充裕的时间。 73.成功的人总是愿意做没成功的人不愿意做的事。 49.不为失败找借口,只为成功找方法。 七、人向前走的过程,应该是慢慢学会做减法的过程。贪念越多,心里装的包袱越多,人越是寸步难行。学会放下,才能走更快更远。
例如
例2 设图中R1 = 2 k,R2 = 1 k,R3 = 3 k, R4 = 0.5 k,Us = 4.5 V,Is = 1 mA。 求电流 I 和电压 U。
解: 电压源单独作用
I1
I 3
Us R1 R3
0.9103 A
0.9
mA
I 2
I4
Us R2 R4
3103 A
3mA
I=I1 + I2 =(0.9+3.0)mA = 3.9 mA
电流源一组 1. 电压源作用,电流源不作用:
U 3 2 3 V 13 2
I 21 3 A 22
2. 电流源作用,电压源不作用:
I 3A
U 31 (3) 9 V
1 3
4
3. 所有电源一起作用:
U U U 3 V 4
I I I 1.5A
例4 图示电路,当us=2V,is=2A,测得i=7A; 当us=0.5V,is=1A,测得i=4A。 问若us=-2.5V,is=2A,i=?
独立电压源单独作用
U x 6 U x U x 2 42
Ux 1.2 V
两独立源共同作用
U x Ux Ux (4 1.2) V 2.8 V
高中物理竞赛之电流叠加定理课件

高中物理竞赛专题 之电路叠加原理
1
重点:1、叠加定理的基本内容及注意事项;2、叠加定理的应用;3、戴维南定理的基本内容;4、戴维南等效参数的测试方法;5、戴维南定理的应用。2
4.1 叠加定理一、定理内容在线性电阻电路中有几个独立源共同作用时,各支路的电流(或电压)等于各独立源单独作用时在该 支路产生的电流(或电压)的代数和(叠加)。
根据各支路电流总量参考方向与分量参考方向之 间的关系,可求得支路电流
快速、简便。
7
【例7-2】电路如下图(a)所示。已知r = 2Ω,试用叠加 定理求电流I和电压U。
此题电路中含有受控源,应用叠加定理时 应注意两点:一是受控源不能“不作用”,应始 终保留在电路中;二是受控源的控制量应分别 改为电路中的相应量。
图(b)电路中,只有独立电压源单独作用,列出KVL 方程为
求得I/ = -2 A,
根据叠加定理画出叠加电路图如上图所示。
U/ = -3I/ = 6 V
解:
求得I// = 3 A, U// = 3 (6 - I// ) = 9 V根据各电压、电流的参考方向,最后叠加得到
图(c)电路中,只有独立电流源单独作用,列出 KVL方程为
26
三、参数测量方法n开路电压uOC 的测量方法测量电路如下图所示。
27
n等效电阻RO 的测量方法测量电路如下图所示。
28
本讲小结1、叠加定理适用于有唯一解的任何线性电阻电 路。它允许用分别计算每个独立源产生的电压或电 流,然后相加的方法,求得含多个独立电源的线性 电阻电路的电压或电流。5、戴维南定理和诺顿定理研究的是线性含源单 口网络,它们分别指出了线性含源单口网络的等效电 路模型。应用该两个定理可以简化复杂的含源电路, 从而使电路分析变得简便。
电路原理-叠加定理ppt课件.ppt
– 8
12V + 2
6
+
+
3 U
-
8 3A
6
+
2
3 U
-
(2)对各分电路进行求解 U 12 3 4V 9
U 6 3 3 6V 36
例2 求电压U,电流I
2
1
2
1
I +
+
+
I+
10V
-
3A
++
U 2I --
10V -
2
U
-
+ 1
2I
-
解: (1)画出分电路图
I
+
+
(2)对各分电路进行求解
3. 叠加定理适用范围及要点说明
叠加定理只适用于线性电路, 不适用于非线性电路。
一个独立电源单独作用,其余 独立电源置零。
电压源置零—短路 电流源置零—开路
1
i2
i3
G1
G2
+
is1
us2
–
G3
+= us3
–
1
i2 (1)
i3 (1)
G1
G2
G3
is1
三个电源共同作用
is1单独作用
1
i2 (2)
1
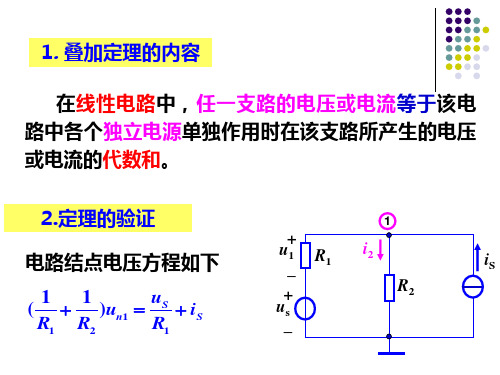
+
u1 R1
i2
–
i3
iS
i2
un1 R2
uS R1 R2
R1iS R1 R2
+ us –
R2
R1
1
R2
uS
R1 R1 R2
iS
i(1)
2
i(2)
2
i (1)
2
R1
叠加定理

ux ?
is1
N
is 2
4-1 叠加定理 解:电路有两个独立源激励,依据电路的叠加 性,设 k1is1 k2is 2 u x 其中 k1,k2 为两个未知的比例系数。 利用已知的条件,可知:
10k1 14k2 100 k1 3 10k1 10k2 20 k2 5
Req 40KΩ //10KΩ 8KΩ
a
8k
用戴维南等效电路置换原 ab端以左的电路部分,如 uoc 图所示。得:
I 4k
12V b
18 I 1.5mA 48
4-3 戴维南定理和诺顿定理 二、诺顿定理
任何线性有源二端网络N,对其外特性而 言,都可以用一个电流源与电阻的并联支路 来代替。其中电流源电流值为有源二端网络 输出端的短路电流 isc ,并联电阻值为该有源 二端网络内所有独立源置零后对应的网络 N 0 在输出端求得的等效输入电阻 Req 。
4-3 戴维南定理和诺顿定理 一、戴维南定理 任何线性有源二端网络N,就其外特性 而言,可以用一个电压源与电阻的串联支 路等效置换,如图所示。
i
i a u b uoc
Req
a
u b
N
4-3 戴维南定理和诺顿定理 其中,电压源的电压值为 该有源二端网络N的开路 电压 uoc ,如图(a)所示; 串联电阻值等于有源二端 网络内部所有独立源不作 用时对应的网络 N 0在输 出端求得的等效输入电 阻 Req ,如图(b)所示。这 样的等效电路称为戴维南 等效电路。
' 1 ' 2
根据叠加定理,得 u3 u3 u3 6 25.6 19.6V
4-1 叠加定理 例4-2:如图所示的线性电阻网络N,当 is1 10A,is 2 14A时,x 100V u
电工学叠加原理 ppt课件

I1'
I
' 3
Us R1 R3
4.5 23
0.9 A
I
' 2
I
' 4
Us R2 R4
4.5 1 0.5
3A
I
'
I1'
I
' 2
(0.9
3)
3.9 A
电流源支路的端电压U′为:
U'
R4
I
' 4
R3
I
' 3
(0.5 3
3 0.9)
1.2V
ppt课件
例3:求下图所示电路中的电流I1、I2和I3
ppt课件
1
求下图所示电路中的电流I1、I2和I3
R1
R3
+ I1
Us1 -
I2 Im1
R2
+ Us2
-
I3 Im2
+ Us3
-
图2.18
ppt课件
2
2.10 网 孔 法
采用网孔电流为电路的变量来列写方 程。
设想在每个网孔中, 都有一个电流沿网孔 边界环流, 这样一个在网孔内环行的假想电 流, 叫做网孔电流。
1
1
1
I +
I′ +
Us -
R2
= Us
Is
-
R2
+
I″
R2
Is
R1
R1
R1
0
0
0
(a)
(b)
(c)
ppt课件
叠加原理.ppt

+
++
I2'
U–S
E –
R1
R3 US'
–
R2
I2
+
R1
R3 IS U–S
(a)
(b) E单独作用
(c) IS单独作用
解:由图(c)
I
2
U
S
R3
RI22
R3
R2
5 IS 5 5
0.5 5
1 0.5A
2.5V
I2
I
2
I
2
1
0.5
0.5A
US
U
S
U
S
5
2.5
7.5V
B
根据叠加原理,I2 = I2´ + I2
解: I2´= I2"=
?1A ?–1A
I2 = I2´ + I2 =
0A
【例题讲解】 I= ? 用叠加原理求:
10 4A
10
10
-
I
20V
+
“恒流源失效” 即令其开路。
解:
10
原电路=
10 10
I´
+
10 10
I"
4A
I'=2A
I"= -1A
I = I'+ I"= 1A
【 重点与难点 】
叠加定理中对不工作电源的处理: 电流源不工作,相当于开路 电压源不工作,相当于短路
例1:电路如图,已知 E =10V、IS=1A ,R1=10 R2= R3= 5 ,试用叠加原理求流过 R2的电流 I2 和理想电流源 IS 两端的电压 US。
叠加定理PPT课件

I I1 R1 + Us - Is - I3 R3 I4 + R4 I2 R2 R1 I′ 1 I′ I ′2 R2 I″ 1 - - I ′3 R3 I′ 4 R4 U′ + I″ I2 ″ R1 Is - I″ 3 R3 I″ 4 U″ R4 + R2
=
+ Us
+
U
(a )
(b )
(c)
电子发 烧友
' 2 ' 4 ' I ' I1' I 2 (0.9 3) 3.9 A
电子发 烧友
第2章 直流电阻电路的分析计算
THANK
YOU
SUCCESS
2019/5/3
第2章 直流电阻电路的分析计算
THANK
YOU
SUCCESS
2019/5/3
图2.27 例2.12图
第2章 直流电阻电路的分析计算
例 2.12(二)
解 (1) 当电压源单独作用时, 电流源开路, 如图2.27(b)所示, 各支路电流分别为
Us 4.5 I I 0.9 A R1 R3 2 3
' 1 ' 3
Us 4.5 I I 3A R2 R4 1 0.5
例 2.12(三)
电流源支路的端电压U′为
U R I R I (0.5 3 3 0.9) 1.2V
' ' 4 4 ' 3 3
电子发 烧友
第2章 直流电阻电路的分析计算
例 2.12(四)
电子发 烧友
第2章 直流电阻电路的分析计算
教学方法
讲授法
电子发 烧友
第2章 直流电阻电路的分析计算
=
+ Us
+
U
(a )
(b )
(c)
电子发 烧友
' 2 ' 4 ' I ' I1' I 2 (0.9 3) 3.9 A
电子发 烧友
第2章 直流电阻电路的分析计算
THANK
YOU
SUCCESS
2019/5/3
第2章 直流电阻电路的分析计算
THANK
YOU
SUCCESS
2019/5/3
图2.27 例2.12图
第2章 直流电阻电路的分析计算
例 2.12(二)
解 (1) 当电压源单独作用时, 电流源开路, 如图2.27(b)所示, 各支路电流分别为
Us 4.5 I I 0.9 A R1 R3 2 3
' 1 ' 3
Us 4.5 I I 3A R2 R4 1 0.5
例 2.12(三)
电流源支路的端电压U′为
U R I R I (0.5 3 3 0.9) 1.2V
' ' 4 4 ' 3 3
电子发 烧友
第2章 直流电阻电路的分析计算
例 2.12(四)
电子发 烧友
第2章 直流电阻电路的分析计算
教学方法
讲授法
电子发 烧友
第2章 直流电阻电路的分析计算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter 2 2.5 叠加原理
一.叠加原理
线性电路:由独立无源元件、独立源、线性受控源组 成的电路。
叠加原理反映了线性电路中响应与激励的关系。
例如单个激励:
i
i us R1 R2
u1
R2 R1 R2
us
+
us
线性关系: u1 us i us
-
+
R1 u1
+
R2 u2
-
Chapter 2
Chapter 2
例 用叠加原理求I 。
+
12 V
-
4Ω 4Ω
2Ω I
6A 1Ω
4Ω 2Ω I'
2A +
12V 4Ω
1Ω
-
4Ω
4Ω
图a
解:12V电压源单独作用(如图a):
I
7
7 //
// 4 4
4
12 2
1
4
28 11
28 4
12 7
2 3
11
Chapter 2
4Ω
2Ω I ''
4Ω 2Ω I'''
4Ω
1Ω
6A
4Ω
1Ω 2A
4Ω
4Ω
图b
图c
6A单独作用(如图b):
I
4
6 8
4 4 // 4 2 1
3
2A单独作用(如图c):
I
1
2 2
1 4 // 4 4 2
9
叠加: I I I I 2 8 2 2.22 339
Chapter 2
例 用叠加原理求4V电压源发出的功率 。
I x Iy
I″
2Ω 2Ω
4V 2I x
叠加: I I I 3 6 3A
4V电压源发出的功率: P 43 12W
谢谢观看! 2020
q
k jisj
i1
j1
其中: p + q = n
ki、kj 均为常数
叠加原理:在线性电路中,任一时刻,任一处的响应等 于各独立源单独作用时,在该处响应的叠加。
Chapter 2
使用叠加定理时应注意: 1.叠加定理只适用于线性电路。 2.叠加定理包含了“加性”和“齐性”两重含义。
3.线性电路中的电压电流响应可叠加,而功率不可叠加。 4.使用叠加定理时,去掉的独立电源应置零,即:电压源 短路,电流源开路。 5.各电源单独作用时,所求电压电流的参考方向应与原电 路参考方向保持一致,这样最后叠加时可直接将各分量相加。 6.叠加时只对独立源产生的响应叠加,受控源应视为电阻。 7.叠加方式是任意的,电源可单独作用,也可分组作用。
解:用叠加原理求电流 I 。
3V电源单独作用:
Ix 2Ω
I 2Ω
4V
Ix I y
I′
3V
2Ix
2Ω 2Ω
I x 3 A Iy 2Ix 3 A
3V
2I x
2
22
I Ix Iy 3A
Chapter 2
4y 2Ix 4 4A 2
I Ix Iy 6A
又例如两个激励: 电源等效变换得下图。
R1
+
us
-
i
is
R2
us + R1
i
s
R1
R2 i
i
R1 R1 R2
us R1
is
us R1 R2
R1 R1 R2
is
i i
即: i k1us k2is
k1、k2为常数
Chapter 2
对n个独立电源的线性电路,响应:
f t
p
kiusi
一.叠加原理
线性电路:由独立无源元件、独立源、线性受控源组 成的电路。
叠加原理反映了线性电路中响应与激励的关系。
例如单个激励:
i
i us R1 R2
u1
R2 R1 R2
us
+
us
线性关系: u1 us i us
-
+
R1 u1
+
R2 u2
-
Chapter 2
Chapter 2
例 用叠加原理求I 。
+
12 V
-
4Ω 4Ω
2Ω I
6A 1Ω
4Ω 2Ω I'
2A +
12V 4Ω
1Ω
-
4Ω
4Ω
图a
解:12V电压源单独作用(如图a):
I
7
7 //
// 4 4
4
12 2
1
4
28 11
28 4
12 7
2 3
11
Chapter 2
4Ω
2Ω I ''
4Ω 2Ω I'''
4Ω
1Ω
6A
4Ω
1Ω 2A
4Ω
4Ω
图b
图c
6A单独作用(如图b):
I
4
6 8
4 4 // 4 2 1
3
2A单独作用(如图c):
I
1
2 2
1 4 // 4 4 2
9
叠加: I I I I 2 8 2 2.22 339
Chapter 2
例 用叠加原理求4V电压源发出的功率 。
I x Iy
I″
2Ω 2Ω
4V 2I x
叠加: I I I 3 6 3A
4V电压源发出的功率: P 43 12W
谢谢观看! 2020
q
k jisj
i1
j1
其中: p + q = n
ki、kj 均为常数
叠加原理:在线性电路中,任一时刻,任一处的响应等 于各独立源单独作用时,在该处响应的叠加。
Chapter 2
使用叠加定理时应注意: 1.叠加定理只适用于线性电路。 2.叠加定理包含了“加性”和“齐性”两重含义。
3.线性电路中的电压电流响应可叠加,而功率不可叠加。 4.使用叠加定理时,去掉的独立电源应置零,即:电压源 短路,电流源开路。 5.各电源单独作用时,所求电压电流的参考方向应与原电 路参考方向保持一致,这样最后叠加时可直接将各分量相加。 6.叠加时只对独立源产生的响应叠加,受控源应视为电阻。 7.叠加方式是任意的,电源可单独作用,也可分组作用。
解:用叠加原理求电流 I 。
3V电源单独作用:
Ix 2Ω
I 2Ω
4V
Ix I y
I′
3V
2Ix
2Ω 2Ω
I x 3 A Iy 2Ix 3 A
3V
2I x
2
22
I Ix Iy 3A
Chapter 2
4y 2Ix 4 4A 2
I Ix Iy 6A
又例如两个激励: 电源等效变换得下图。
R1
+
us
-
i
is
R2
us + R1
i
s
R1
R2 i
i
R1 R1 R2
us R1
is
us R1 R2
R1 R1 R2
is
i i
即: i k1us k2is
k1、k2为常数
Chapter 2
对n个独立电源的线性电路,响应:
f t
p
kiusi
