五年级数学培优讲义
3.4 质数与合数(学霸课堂笔记)-2023-2024学年数学五年级下册同步培优讲义(苏教版)

3.4 质数与合数第一部分学问清单➢一个数,假如只有1和它本身两个因数,那么这样的数叫做质数(或素数)。
如2、3、5都是质数。
➢一个数,假如除了1和它本身还有别的因数,那么这样的数叫做合数。
如4、6、9都是合数。
➢1的因数只有1个。
➢1既不是质数,也不是合数。
➢质数与合数的个数都是无限的,没有最大的质数或合数。
最小的质数是2,最小的合数是4。
其中,2是唯一一个既是偶数又是质数的数。
➢自然数(不包括0)可以分成质数、合数和1三大类。
其次部分典型例题例1:将分别标有1、2、3、4、5的五张卡片放在一个口袋里,从口袋里任意摸出一张,摸后放回,下面()说法是正确的。
A.摸到奇数的可能性比偶数的大B.摸到偶数的可能性最大C.摸到质数的可能性最小D.摸到合数的可能性最大答案:A分析:找出1、2、3、4、5中奇数、偶数、质数、合数的个数,再依据数量的多少进行比较,数量最多的,摸到的可能性最大,数量最少的,摸到的可能性最小,数量相等的,摸到的可能性一样。
详解:五张卡片中奇数有1、3、5共3个;偶数有2、4共2个;质数有2、3、5共3个;合数只有4共1个。
3=3>2>1所以摸到奇数、质数的可能性相等,摸到偶数的可能性居中,摸到合数的可能性最小。
故答案为:A点睛:本题主要考查可能性的大小,找格外数、偶数、质数、合数的个数是解题的关键。
例2:甲数是一个质数,乙数是一个合数,它们的和是11,甲、乙两数相乘的积最小是( ),把这个乘积分解质因数是( )。
答案:18 18=2×3×3分析:一个数只有1和它本身两个因数,这个数叫做质数。
一个数除了1和它本身两个因数,还有其他的因数,这个数叫做合数。
先把11拆分两个数相加,找出符合题意的全部状况,再找出最小的积即可;分解质因数是将合数写成几个质数相乘的形式表示出来。
据此解答。
详解:11=1+10=2+9=3+8=4+7=5+6符合题意的只有2+9、3+8、4+7、5+6;2×9=183×8=244×7=285×6=3018<24<28<3018=2×3×3甲数是一个质数,乙数是一个合数,它们的和是11,甲、乙两数相乘的积最小是18,把这个乘积分解质因数是18=2×3×3。
五年级数学培优讲义

例题1 有两个无盖的长方体水箱,甲水箱里有水,乙水箱空着.从里面量,甲水箱长40厘米,宽32厘米,水面高20厘米;乙水箱长30厘米,宽24厘米,深25厘米.将甲水箱中部分水倒入乙水箱,使两箱水面高度一样,现在水面高多少厘米?1.有一个长方体水箱,从面量长40厘米、宽30厘米、深35厘米,箱中水面高10厘米.放进一个棱长20厘米的正方体铁块后,铁块顶面仍高于水面.这时水面高多少厘米?例2 将表面积分别为54平方厘米、96平方厘米和150平方厘米的三个铁质正方体熔成一个大正方体(不计损耗),求这个大正方体的体积.例题3 长方体不同的三个面的面积分别为10平方厘米、15平方厘米和6平方厘米.这个长方体的体积是多少立方厘米?1,一个长方体,不同的三个面的面积分别是35平方厘米、21平方厘米和15平方厘米,且长、宽、高都是质数,这个长方体的体积是多少立方厘?2,一个长方体的体积是48立方厘米,并且长、宽、高是三个连续的偶数.这个长方体的表面积是多少平方厘米?例题1 一个棱长为6厘米的正方体木块,如果把它锯成棱长为2厘米的正方体若干块,表面积增加多少厘米?1,把一个棱长是5厘米的正方体的六个面涂满红色,然后切成1立方厘米的小正方体,这些小正方体中,一面涂红色的、二面涂红色的、三面涂红色的以及六个面都没有涂色的各有多少个?环形跑道1、小红和小军在周长为400米的环形跑道上进行长跑.小红每分跑40米,小军每分跑60米.(1)两人同时从同一地点出发反向跑步几分钟后第一次相遇?再过几分钟后第二次相遇?(2)两人同时从同一地点同一方向跑步,几分钟第一次追上小红?再过几分钟能第二次追上小红2、小红、小军从环形公路同时同地背向而行.公路长2400米,小红骑一圈要10分钟.如果第一次相遇时小红骑了1440米.(1)小红的速度是每分多少米?(2)出发到第一次相遇用时几分钟?(3)小军骑一圈要多少分钟?再过多久他们第二次相遇?3、在周长为220米的圆形跑道的一条直径的两端,小红、小军骑车分别以6米每秒和5米每秒的速度同时相向出发,在210秒内他们相遇几次?4、小红、小军在操场跑步,小红每分钟跑26米,小军每分钟跑21米,一圈跑道长50米,他们同时从起跑点出发,那么小红第四次超过小军要几分钟?5、在400米的环形跑道上,小红、小军两人分别从A、B两地同时出发,同向而行.4分钟后,小军第一次追上小红,又经过10分钟第二次追上小红.已知小军每分钟走180米,那么小红的速度是多少?A、B两地相距多少米?6、小红、小军在环形跑道跑步,小红每分钟跑250米,小军每分钟跑200米,两人同时同地同向出发,经过45分钟小红追上小军;如果两人同时同地反向出发,经过多少分钟两人相遇?7、(多次相遇)A、B是一条道路的两端点,甲在A点,乙在B点,两人同时出发,相向而行.他们在离点A点100米的C点第一次相遇.甲到达B点后返回A点,乙到达A点后返回B点,两人在离B点80米的D 点第二次相遇.整个过程中,俩人速度不变.求间A、B的距离.1.已知正方形甲的边长为5厘米,正方形乙的边长为4厘米,那么右图阴影部分的面积是多少?2.在正方形ABCD中,AB长4厘米,△BCF比△DEF的面积多2平方厘米,求DF的长3.平行四边形ABCD中,AE=EF=FB,AG=2CG,△GEF的面积是6平方厘米,求平行四边形的面积4.速算与巧算11.计算1+7+3+9.2.计算:1+2+3+4+5+6+7+8+9+10.3.计算34+77+66.4.计算1+3+5+7+9+11+13+15+17+19.5.计算2+4+6+8+10+12+14+16+18+20.6.计算:2+4+6+8+10.7.计算:59+18+41.8.计算:13+14+15+16+17+25.9.计算:22﹣20+18﹣16+14﹣12+10﹣8+6﹣4+2﹣0.速算与巧算21.计算:1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20.2.计算:5+6+7+8+9+10.3.计算:10﹣9+8﹣7+6﹣5+4﹣3+2﹣1.4.计算:1﹣2+3﹣4+5﹣6+7﹣8+9﹣10+11.5.星期天小红家来了7个客人.小红拿出一包糖,里面有35块.小红说:“咱们一共8个人,每人都要分到糖,但每个人分到的糖数不能一样多,谁会分?”结果大家都无法分,你能帮他们分好吗?算得快的奥妙11.用简便方法计算下面各题:(1)9898+203;(2)1308﹣(308﹣149);(3)(4256+125+825)﹣256.2.用简便方法计算下面各题:(1)9+99+999+9999+99999;(2)1﹣2+3﹣4+5﹣6+…﹣1992+1993.算得快的奥妙2444×25.36×11;246×11.2375÷25;52000÷125.看谁算得巧1.38+47.2.19+27+21+13.3.9+19+29+39.除法中的巧算1.用简便方法计算下列各题.(1)825÷25 (2)47700÷900.2.用简便方法计算.(1)(250+165)÷5 (2)(702﹣213﹣414)÷3.3.计算下面各题.(1)525÷7÷5 (2)128×5÷8.4.简便计算下面各题.(1)756÷(7×9)(2)1260÷7÷9.5.简便计算.(1)720×12÷4 (2)125×(8÷2)6.简便计算下面各题.(1)216÷24×6 (2)875000÷(1000÷8)7.巧算下面各题.(1)1326÷39 (3)248×68﹣17×248+248×48(2)520×125 (4)999×99×9.8.98×91.9.96×98速算为.10.93×84速算为.11.(1)97×96(2)95×93(3)98×97(4)99×92(5)88×89(6)95×85.合理分组一、解答题(共5小题,满分0分)1.把2、6、7、8、9和14分别填入括号中,(每个数只能用一次),使两个算式都成立:①+=;②﹣=.2.把2、3、4、5分别填入□中,(每个数只能用一次):□+□﹣□=□3.在1、2、3、4、5之间添上加号(相邻的两个数字可以组成一个数),使他们的和等于60.4.请你把下面钟面用两条直线分成三份,使每份数相加的和都相等:5.把0、1、2、3、7、8、9分别填入□中,使算式成立:□+□=□□﹣□=□□.包含与排除一、填空题1.(3分)课堂上同学们都在复习语文或数学.只复习了语文的占48%,只复习了数学的占只复习了语文的人数的50%,那么,两门功课都复习的占了%.2.(3分)二年级一班共42名同学,其中少先队员33人.这个班男生20人,女生中有4个不是少先队员,男生中有人是少先队员.二、解答题3.某班46人,现调查他们家中电子琴和小提琴的拥有情况.有电子琴的22人,两种琴都没有的14人,只有小提琴的人的个数是两种琴都有的人个数的.那么,只有电子琴的有多少人?4.有三个面积各为30平方厘米的圆,两两重叠的面积分别为5平方厘米、6平方厘米、8平方厘米,三个圆共同重叠的面积为3平方厘米.三个圆共盖住多少平方厘米?5.100个学生只有一人没学过外语,学过英语的有39人,学过法语的有49人,学过俄语的有41人,学过英语也学过法语的有14人,学过英语也学过俄语的有13人,学过法语也学过俄语的有9人.问:三种语言都学过的有多少人?三、解答题6.某校参加数学竞赛有120名男生,80名女生.参加语文竞赛有120名女生,80名男生.已知该校总共有260名学生参加了竞赛,其中有75名男生两科竞赛都参加了,那么只参加数学竞赛而没有参加语文竞赛的女生人数是人.四、解答题7.求1到200的自然数中,所有既不是2的倍数又不是3的倍数的整数共有多少个?8.有2008盏亮着的电灯,各有一个拉线开关控制着.现将其顺序编号为1,2,3,…,2008.将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,拉完后还有几盏灯是亮的?9.东方小学的统计数据表明:学校共有学生1200名,其中男生650名,高年级学生300名,三好学生100名,男生中的三好学生60名,高年级学生中男生160名,高年级女生中三好学生20名,非高年级女生中不是三好学生的400名.试说明:这个统计数据一定有错误.五、解答题10.一个数学测验只有两道题,结果全班有10人全对,第一题有25人做对,第二题有18人做错,那么两道都做错的有人.11.图书馆有中英文的艺术与科技书籍共6000册,其中艺术书共有3060册,中文书有4560册,英文科技书共有840册.那么一共有几本英文书,几本中文艺术书?12.在线段AB上取两个点C、D,已知AB=25,AD=19,CB=17,求CD=.六、解答题13.有三个面积各为20平方厘米的圆纸片放在桌面上.三个纸片共同重叠的面积是8平方厘米,三个纸片盖住桌面的总面积是36平方厘米.那么图中阴影部分的面积之和是多少平方厘米?14.六年级100名同学,每人至少爱好体育、文艺和科学三项中的一项.其中,爱好体育的55人,爱好文艺的56人,爱好科学的51人,三项都爱好的15人,只爱好体育和科学的4人,只爱好体育和文艺的17人.那么有几人只爱好科学和文艺两项?只爱好体育的有几人?15.在1﹣﹣500的所有正整数里,既不是5、也不是7或11的倍数的数共有多少个?16.全班共有50人,不会骑车的有23人,不会滑冰的有35人,两样都会的有4人,那么两样都不会的有多少人?17.某校有120名学生,允许选修A、B、C三门课.选修A的有60人,选修B的有65人,选修C的有55人,兼选A、B的有30人,兼选B、C的有40人,兼选C、A的有35人,而A、B、C都选的人数不详.那么三科都没有选的学生最少有多少人?。
五年级下学期数学培优课部分讲义

五 A 班第四课列方程解应用题一.知识链接1.字母表示运算定律加法互换律: a+b=b+a加法联合律:(a+b)+c=a+(b+c)乘法互换律: ab=ba乘法联合律:(ab) c=a (bc)乘法分派律: (a+b)c=a(bc)2.用字母表示公式长方形面积: s=ab正方形面积:s=a2长方体体积: v=abh正方体体积:v=a3圆的面积: s=πr2圆的周长:c=πd3.含有未知数的等式叫方程。
4.使方程左右两边相等的未知数的值叫方程的解。
5.求方程的解的过程叫解方程。
二.思想训练例: 99999×22222+33333× 33334剖析与解先把 99999 分解为 33333×3,再运用乘法分派律进行简易计算原式= 33333×( 3×22222)+ 33333 ×33334=33333×( 66666+33334)=3333300000练习4444×33331994+997× 997三.经典例题例 1. 两个数相除,商是 8,余数是 11,把被除数、除数、商、余数加起来的和是543. 那么被除数和除数各是多少?例2. 有一个三位数,个位上的数是 5,假如把个位上的数字移到百位上,原百位上的数字移到十位上,原十位上的数字移到个位上,那么所成的新数比原数小108,原数是多少?例 3. 某班学生合买一件纪念品,假如每人出 6 元则多48 元,假如每人出 5 元则少 3 元,求这个班有多少学生?例两地相距 496 千米,甲车从 A 地开往 B 地,每小时行 32 千米。
甲车开出半小时后,乙车从 B 地开往 A 地,每小时行 64 千米。
问乙车开出几小时后与甲车相遇?四.课内练习1.例 1. 两个数相除,商是 18,余数是 13,把被除数、除数、商、余数加起来的和是 652. 那么被除数和除数各是多少?2.一个两位数,十位数字是个位数字的2 倍,将个位数字与十位数字对换,获得一个新的两位数,这两个两位数的和是132,求这个两位数。
五年级上册数学培优奥数讲义-第12讲 平面组合图形1

第12讲平面组合图形1知识与方法1、熟记基本几何图形的特征及有关计算公式:(1)长方形面积公式S=ab;(2)正方形面积公式S=a2;(3)三角形面积公式 S=ah÷2;(4)平行四边形面积公式S=ah;(5)梯形面积公式S=(a+b)h÷2。
2、求平面组合图形面积时,一般是通过分割、拼接、平移或旋转等方法把它分解为若干个基本平面图形。
要注意交叉、重叠图形的情况,做到不重复、不遗漏。
3、计算时还常用到等量代换的知识。
初级挑战1如图,利用房屋的一面墙,用37.5米长的篱笆围成一个梯形菜地,这块菜地的面积是多少平方米?思路引领:根据篱笆的长,可以求出:上底与下底的和是()米,又知梯形的高是()米,则可以求出梯形菜地的面积。
答案:上底+下底:37.5-7.5=30(米),面积=30×6÷2=90(平方米)。
能力探索1求下面图形的面积。
(单位:厘米)答案:上底加下底的和为6厘米,面积为6×6÷2=18(平方厘米)。
初级挑战2如图,两个正方形边长分别为9厘米、6厘米,求图中阴影部分面积。
思路引领:图中阴影部分是一个不规则图形,要求它的面积可用2个正方形的面积减去空白部分的面积。
答案:正方形的面积和:6×6+9×9=117(平方厘米)空白部分的面积:6×(6+9)÷2=45(平方厘米)9×9÷2=40.5(平方厘米)阴影部分面积:117-45-40.5=31.5(平方厘米)能力探索21、求图中阴影部分的面积(单位:厘米)。
答案:整个图形面积4×4+3×3=25(平方厘米);空白三角形面积4×(4+3)÷2=14(平方厘米);阴影面积25-14=11(平方厘米)2、图中的四边形AGBE和CDEF分别是边长6厘米和4厘米的正方形,求阴影部分的面积。
答案:整个图形的面积:6×6+(4+6)×4÷2=56(平方厘米);三角形ABG 面积:6×6÷2=18(平方厘米);三角形CBF面积:(6+4)×4÷2=20(平方厘米);阴影面积:56-18-20=18(平方厘米)。
五年级上册数学培优奥数讲义-第6讲追及问题

第6讲追及问题2知识装备我们在四年级已经学习了追及问题的基本类型,初步掌握了追及问题的基本数量关系及一般的解决问题的思路。
下面我们再把追及问题的基本数量关系整理出来,并进一步研究稍复杂的追及问题。
1、追及问题的基本数量关系:(1)速度差×追及时间=追及路程(路程差)(2)追及路程÷速度差=追及时间(3)追及路程÷追及时间=速度差(根据其中一个速度可以求另一个速度)2、解决稍复杂的追及问题时,一定要弄清下面关系:(1)追及路程、追及时间与速度差是否一一对应。
(2)运动的模式如何?是同时同一方向运动,而出发地点不同;是同一地点不同时间向同一方向运动;是直线运动追及还是环形运动追及;运动速度有没有变化等。
(3)可借助线段图把题目中的已知条件具体化、形象化,便于弄清数量间的对应关系。
(4)借助追及问题的解题思路解决日常生活中的一些其它问题。
初级挑战1大客车每小时行60千米,小轿车每小时行85千米。
两车同时分别从相距250千米的两地同向开出,且大客车在前。
求几小时后小轿车追上大客车?思路引领:根据题意可知这是一道基础追及问题,题目已知了两车的速度差是(),追及路程是()千米,即可求出追及时间。
答案:250÷(85-60)=10(小时)能力探索1甲、乙两车同时分别从A、B两地出发,同向而行,已知甲车在前,乙车在后,甲车的速度是50千米/时,乙车速度是80千米/时,3小时后乙车追上甲车,求A、B两地的距离。
答案:(80-50)×3=90(千米)初级挑战2甲车每小时行驶80千米,走3小时后,乙车出发去追甲车,乙车速度为每小时120千米,多少小时后乙车可追上甲车?思路引领:甲车走3小时走了()千米,当乙车去追甲车时,追及的路程是()千米。
答案:速度差:120-80=40(千米/时)追及路程:80×3=240(千米)追及时间:80×3÷(120-80)=6(小时)能力探索2老王和老张从甲地到乙地开会,老张骑自行车的速度是15千米/小时,老王骑车的速度是25千米/时,老张先出发2小时后,老王才出发,几小时后老王可以追上老张?答案:15×2÷(25-15)=3(小时)中级挑战1A、B两辆货车同时从甲城出发,沿同一条公路送货到乙城。
五年级上册数学培优奥数讲义-第15讲 余数定理

第15讲余数定理知识与方法余数在计算时有三个主要性质,也被称为三个定理,余数问题中非常重要的同余问题以及中国剩余定理,其实就是根据这三个性质来解决问题的,所以这三个性质非常重要。
余数主要有以下三个性质:(1)可加性:a与b的和除以c的余数,等于a、b分别除以c的余数之和。
(2)可减性:a与b的差除以c的余数,等于a、b分别除以c的余数之差。
(3)可乘性:a与b的乘积除以c的余数,等于a、b分别除以c的余数之积(或这个积除以c的余数)。
初级挑战1(1)23÷5=4……()(2)108÷4=2716÷5=3……() 214÷4=53……()39÷5=7……() 322÷4=80……()(3)155÷3=51……()230÷3=76……()385÷3=128……()观察以上每组算式中的被除数和余数,你发现了什么?思维点拨:余数定理一:a与b的和除以c的余数,等于a、b分别除以c的余数之()。
如果余数之和大于除数,那么可以继续除以这个除数得到余数。
答案:(1)3、1、4;(2)2、2;(3)2、2、1发现:三个数除以一个相同的数,如果一个数是其它两个数的和,那么所得的余数也是其它两个数除得的余数的和。
能力探索11、快速计算:(234+123+732)÷3的余数。
2、甲数除以9,商12余3;乙数除以9,商28余6;丙数除以9,商31余5。
(甲数+乙数+丙数)÷9的余数是多少?答案:1、0 2、(3+6+5)÷9=1……5,所以余数是5。
初级挑战2(1)129÷7=18……3 (2)237÷5=47……() 71÷7=10……1 200÷5=4058÷7=8……2 37÷5=7……()(3)93÷4=23……()30÷4=7……()63÷4=15……()观察以上每组算式中的被除数和余数,你发现了什么?思维点拨:余数定理二:a与b的差除以c的余数,等于a、b分别除以c的余数之()。
小学数学五年级数学培优

小学数学五年级数学培优篇一:五年级数学培优因数和倍数第二讲因数和倍数(一)【知识要点】 1.因数和倍数整数a(a?0)乘整数b(b?0)得到整数C,那么a和b叫做C的因数,C叫做a,b的倍数。
2.倍数的特征2的倍数的特征:个位上是0、2,4、6、8的数都是2的倍数。
5的倍数的特征:个位上是0或5的数都是5的倍数。
3的倍数的特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
3.奇数、偶数的意义自然数中,是2的倍数的数叫做偶数;不是2的倍数的数叫做奇数。
【例题讲解】例1、48的全部因数有哪几个?20以内3的倍数有哪几个?例2、一个数既是40的因数,又是5的倍数。
这个数可能是几?例3、在方框里填上适当的数字,使它是2和3的倍数.(1)38□ (2)945□例4、观察下面各数:120 432 115 84130 7579966 2的倍数有既有因数2,又有因数3的数有既有因数3,又有因数5的数有同时是2,3,5的倍数的数是例5、在下面方格内填上适当的数字。
(1)26□4能被2整除,又能被3整除。
(2)412□能被3整除,又能被5整除。
(3)61□□能同时被2、3、5整除。
【巩固练习】A组1、写出下面各数的倍数或因数。
2、填一填。
(1)32的因数有()共()个,其中最小因数是(),最大因数是()。
(2)一个数的倍数的个数是()的,其中最小倍数是()。
(3)24的全部因数从小到大依次为()。
(4)一个数既是15的倍数,又是15的因数,这个数是()。
(5)如果数a能被数b整除(b:*0)a就叫做b的(),b就叫做a的()。
3、连一连。
4、猜数。
(1)它是24的最大因数,这个数是_______。
(2)它的最小倍数是45,这个数是________。
(3)它是l2的倍数,又是24的因数,这个数可能是________。
B组一、填空。
1.自然数按是不是2的倍数,可分为( )和( )。
2.在30、47、28、51、36、41、135、102中是2的倍数的数有( ),是3的倍数的数有( ),是5的倍数的数有( )。
五年级数学培优讲义全
(四)、100以的质数(共 25 个):2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97
(五)奇数+奇数=偶数(如:5+7=12 3+5=8……)
奇数+偶数=奇数(如:1+4=5 7+2=9……)
偶数+偶数=偶数(如:2+4=6 8+6=14……)
奇数×奇数=奇数(如:5×7=35 7×9=63……)
奇数×偶数=偶数(如:5×8=40 7×8=56……)
偶数×偶数=偶数(如: 8×12=96 14×24=336……)
(六)、公因数、最大公因数
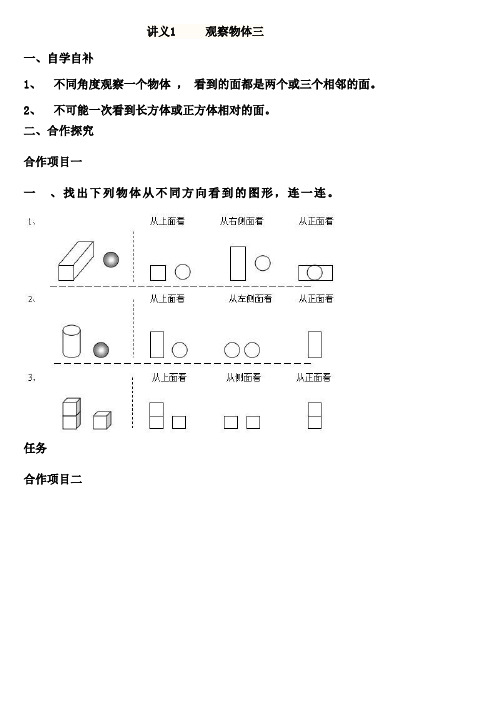
⑵从侧面看是图B的有( )。
⑶从正面和上面看都是图B的有( )。
2他们看到的形状分别是什么?填一填。
3.说出是从哪个方向看到的。
( ) ( ) ( )
( )()()
四、收获大检阅
一、看一看
1、一次最多能看见长方体的( )个面。
2、从( )面看到的图形是 。
3、从( )面看到的图形是 ;从( )面看到的图形是 ;从( )面看到的图形是 。
, 这是由( )个正方体组成的立体模型。【①4 ② 6 ③ 9 】
四、“动手操作”显身手。
下面立体图形从上面、正面和左面看的形状分别是什么?画一画
五、请分别在括号里注明下面四照片是从房子的哪一面拍的。
讲义2 因数与倍数
一、自学自补
(一)、因数和倍数。
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数.又如整数a能被b整除(a÷b=c),那么a就是b的倍数,b就是a的因数。因数和倍数是相互依存的,不能单独存在。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题1 有两个无盖的长方体水箱,甲水箱里有水,乙水箱空着.从里面量,甲水箱长40厘米,宽32厘米,水面高20厘米;乙水箱长30厘米,宽24厘米,深25厘米.将甲水箱中部分水倒入乙水箱,使两箱水面高度一样,现在水面高多少厘米?1.有一个长方体水箱,从面量长40厘米、宽30厘米、深35厘米,箱中水面高10厘米.放进一个棱长20厘米的正方体铁块后,铁块顶面仍高于水面.这时水面高多少厘米?例2 将表面积分别为54平方厘米、96平方厘米和150平方厘米的三个铁质正方体熔成一个大正方体(不计损耗),求这个大正方体的体积.例题3 长方体不同的三个面的面积分别为10平方厘米、15平方厘米和6平方厘米.这个长方体的体积是多少立方厘米?1,一个长方体,不同的三个面的面积分别是35平方厘米、21平方厘米和15平方厘米,且长、宽、高都是质数,这个长方体的体积是多少立方厘?2,一个长方体的体积是48立方厘米,并且长、宽、高是三个连续的偶数.这个长方体的表面积是多少平方厘米?例题1 一个棱长为6厘米的正方体木块,如果把它锯成棱长为2厘米的正方体若干块,表面积增加多少厘米?1,把一个棱长是5厘米的正方体的六个面涂满红色,然后切成1立方厘米的小正方体,这些小正方体中,一面涂红色的、二面涂红色的、三面涂红色的以及六个面都没有涂色的各有多少个?环形跑道1、小红和小军在周长为400米的环形跑道上进行长跑.小红每分跑40米,小军每分跑60米.(1)两人同时从同一地点出发反向跑步几分钟后第一次相遇?再过几分钟后第二次相遇?(2)两人同时从同一地点同一方向跑步,几分钟第一次追上小红?再过几分钟能第二次追上小红2、小红、小军从环形公路同时同地背向而行.公路长2400米,小红骑一圈要10分钟.如果第一次相遇时小红骑了1440米.(1)小红的速度是每分多少米?(2)出发到第一次相遇用时几分钟?(3)小军骑一圈要多少分钟?再过多久他们第二次相遇?3、在周长为220米的圆形跑道的一条直径的两端,小红、小军骑车分别以6米每秒和5米每秒的速度同时相向出发,在210秒内他们相遇几次?4、小红、小军在操场跑步,小红每分钟跑26米,小军每分钟跑21米,一圈跑道长50米,他们同时从起跑点出发,那么小红第四次超过小军要几分钟?5、在400米的环形跑道上,小红、小军两人分别从A、B两地同时出发,同向而行.4分钟后,小军第一次追上小红,又经过10分钟第二次追上小红.已知小军每分钟走180米,那么小红的速度是多少?A、B两地相距多少米?6、小红、小军在环形跑道跑步,小红每分钟跑250米,小军每分钟跑200米,两人同时同地同向出发,经过45分钟小红追上小军;如果两人同时同地反向出发,经过多少分钟两人相遇?7、(多次相遇)A、B是一条道路的两端点,甲在A点,乙在B点,两人同时出发,相向而行.他们在离点A点100米的C点第一次相遇.甲到达B点后返回A点,乙到达A点后返回B点,两人在离B点80米的D 点第二次相遇.整个过程中,俩人速度不变.求间A、B的距离.1.已知正方形甲的边长为5厘米,正方形乙的边长为4厘米,那么右图阴影部分的面积是多少?2.在正方形ABCD中,AB长4厘米,△BCF比△DEF的面积多2平方厘米,求DF的长3.平行四边形ABCD中,AE=EF=FB,AG=2CG,△GEF的面积是6平方厘米,求平行四边形的面积4.速算与巧算11.计算1+7+3+9.2.计算:1+2+3+4+5+6+7+8+9+10.3.计算34+77+66.4.计算1+3+5+7+9+11+13+15+17+19.5.计算2+4+6+8+10+12+14+16+18+20.6.计算:2+4+6+8+10.7.计算:59+18+41.8.计算:13+14+15+16+17+25.9.计算:22﹣20+18﹣16+14﹣12+10﹣8+6﹣4+2﹣0.速算与巧算21.计算:1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20.2.计算:5+6+7+8+9+10.3.计算:10﹣9+8﹣7+6﹣5+4﹣3+2﹣1.4.计算:1﹣2+3﹣4+5﹣6+7﹣8+9﹣10+11.5.星期天小红家来了7个客人.小红拿出一包糖,里面有35块.小红说:“咱们一共8个人,每人都要分到糖,但每个人分到的糖数不能一样多,谁会分?”结果大家都无法分,你能帮他们分好吗?算得快的奥妙11.用简便方法计算下面各题:(1)9898+203;(2)1308﹣(308﹣149);(3)(4256+125+825)﹣256.2.用简便方法计算下面各题:(1)9+99+999+9999+99999;(2)1﹣2+3﹣4+5﹣6+…﹣1992+1993.算得快的奥妙2444×25.36×11;246×11.2375÷25;52000÷125.看谁算得巧1.38+47.2.19+27+21+13.3.9+19+29+39.除法中的巧算1.用简便方法计算下列各题.(1)825÷25 (2)47700÷900.2.用简便方法计算.(1)(250+165)÷5 (2)(702﹣213﹣414)÷3.3.计算下面各题.(1)525÷7÷5 (2)128×5÷8.4.简便计算下面各题.(1)756÷(7×9)(2)1260÷7÷9.5.简便计算.(1)720×12÷4 (2)125×(8÷2)6.简便计算下面各题.(1)216÷24×6 (2)875000÷(1000÷8)7.巧算下面各题.(1)1326÷39 (3)248×68﹣17×248+248×48(2)520×125 (4)999×99×9.8.98×91.9.96×98速算为.10.93×84速算为.11.(1)97×96(2)95×93(3)98×97(4)99×92(5)88×89(6)95×85.合理分组一、解答题(共5小题,满分0分)1.把2、6、7、8、9和14分别填入括号中,(每个数只能用一次),使两个算式都成立:①+=;②﹣=.2.把2、3、4、5分别填入□中,(每个数只能用一次):□+□﹣□=□3.在1、2、3、4、5之间添上加号(相邻的两个数字可以组成一个数),使他们的和等于60.4.请你把下面钟面用两条直线分成三份,使每份数相加的和都相等:5.把0、1、2、3、7、8、9分别填入□中,使算式成立:□+□=□□﹣□=□□.包含与排除一、填空题1.(3分)课堂上同学们都在复习语文或数学.只复习了语文的占48%,只复习了数学的占只复习了语文的人数的50%,那么,两门功课都复习的占了%.2.(3分)二年级一班共42名同学,其中少先队员33人.这个班男生20人,女生中有4个不是少先队员,男生中有人是少先队员.二、解答题3.某班46人,现调查他们家中电子琴和小提琴的拥有情况.有电子琴的22人,两种琴都没有的14人,只有小提琴的人的个数是两种琴都有的人个数的.那么,只有电子琴的有多少人?4.有三个面积各为30平方厘米的圆,两两重叠的面积分别为5平方厘米、6平方厘米、8平方厘米,三个圆共同重叠的面积为3平方厘米.三个圆共盖住多少平方厘米?5.100个学生只有一人没学过外语,学过英语的有39人,学过法语的有49人,学过俄语的有41人,学过英语也学过法语的有14人,学过英语也学过俄语的有13人,学过法语也学过俄语的有9人.问:三种语言都学过的有多少人?三、解答题6.某校参加数学竞赛有120名男生,80名女生.参加语文竞赛有120名女生,80名男生.已知该校总共有260名学生参加了竞赛,其中有75名男生两科竞赛都参加了,那么只参加数学竞赛而没有参加语文竞赛的女生人数是人.四、解答题7.求1到200的自然数中,所有既不是2的倍数又不是3的倍数的整数共有多少个?8.有2008盏亮着的电灯,各有一个拉线开关控制着.现将其顺序编号为1,2,3,…,2008.将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,拉完后还有几盏灯是亮的?9.东方小学的统计数据表明:学校共有学生1200名,其中男生650名,高年级学生300名,三好学生100名,男生中的三好学生60名,高年级学生中男生160名,高年级女生中三好学生20名,非高年级女生中不是三好学生的400名.试说明:这个统计数据一定有错误.五、解答题10.一个数学测验只有两道题,结果全班有10人全对,第一题有25人做对,第二题有18人做错,那么两道都做错的有人.11.图书馆有中英文的艺术与科技书籍共6000册,其中艺术书共有3060册,中文书有4560册,英文科技书共有840册.那么一共有几本英文书,几本中文艺术书?12.在线段AB上取两个点C、D,已知AB=25,AD=19,CB=17,求CD=.六、解答题13.有三个面积各为20平方厘米的圆纸片放在桌面上.三个纸片共同重叠的面积是8平方厘米,三个纸片盖住桌面的总面积是36平方厘米.那么图中阴影部分的面积之和是多少平方厘米?14.六年级100名同学,每人至少爱好体育、文艺和科学三项中的一项.其中,爱好体育的55人,爱好文艺的56人,爱好科学的51人,三项都爱好的15人,只爱好体育和科学的4人,只爱好体育和文艺的17人.那么有几人只爱好科学和文艺两项?只爱好体育的有几人?15.在1﹣﹣500的所有正整数里,既不是5、也不是7或11的倍数的数共有多少个?16.全班共有50人,不会骑车的有23人,不会滑冰的有35人,两样都会的有4人,那么两样都不会的有多少人?17.某校有120名学生,允许选修A、B、C三门课.选修A的有60人,选修B的有65人,选修C的有55人,兼选A、B的有30人,兼选B、C的有40人,兼选C、A的有35人,而A、B、C都选的人数不详.那么三科都没有选的学生最少有多少人?。
