偏微分方程的有限元法ppt课件
合集下载
FEM_有限元法 PPT

优异的解题能力。与其他数值方法相比较,有限 元法在适应场域边界几何形状以及媒质物理性质 变异情况的复杂问题求解上,有突出的优点:不 受几何形状和媒质分布的复杂程度限制;不同媒 质分界面上的边界条件是自动满足的;不必单独 处理第二、三类边界条件;离散点配置比较随意, 通过控制有限单元剖分密度和单元插值函数的选 取,可以充分保证所需的数值计算精度。
❖ 应用范围
广泛地被应用于各种结构工程 成功地用来解决其他工程领域中的问题
➢热传导、渗流、流体力学、空气动力学、土壤力学、 机械零件强度分析、电磁工程问题等等
有限元法
❖ Finite Element Method的缩写,有限单元法,其实际应用 中往往被称为有限元分析(FEA),是一个数值方法解偏微 分方程。FEM是一种高效能、常用的计算方法,它将连续体 离散化为若干个有限大小的单元体的集合,以求解连续体力 学问题。有限元法在早期是以变分原理为基础发展起来的, 所以它广泛地应用于以拉普拉斯方程和泊松方程所描述的各 类物理场中(这类场与泛函的极值问题有着紧密的联系)。 自从1969年以来,某些学者在流体力学中应用加权余数法 中的迦辽金法(Galerkin)或最小二乘法等同样获得了有限元 方程,因而有限元法可应用于以任何微分方程所描述的各类 物理场中,而不再要求这类物理场和泛函的极值问题有所联 系.
❖ FEM是应用于现代复杂机械结构优化设计的非常重要的计算 机辅助分析方法。FEM早期主要应用于航空航天制造、船舶 工业及高端军事领域 。
方法运用的基本步骤
❖ 基本思想:由解给定的泊松方程化为求解泛函的极值问题。
❖ 步骤1:剖分 ❖ 将待解区域进行分割,离散成有限个元素的集合.元素பைடு நூலகம்单
元)的形状原则上是任意的.二维问题一般采用三角形单元 或矩形单元,三维空间可采用四面体或多面体等.每个单元 的顶点称为节点(或结点)。
❖ 应用范围
广泛地被应用于各种结构工程 成功地用来解决其他工程领域中的问题
➢热传导、渗流、流体力学、空气动力学、土壤力学、 机械零件强度分析、电磁工程问题等等
有限元法
❖ Finite Element Method的缩写,有限单元法,其实际应用 中往往被称为有限元分析(FEA),是一个数值方法解偏微 分方程。FEM是一种高效能、常用的计算方法,它将连续体 离散化为若干个有限大小的单元体的集合,以求解连续体力 学问题。有限元法在早期是以变分原理为基础发展起来的, 所以它广泛地应用于以拉普拉斯方程和泊松方程所描述的各 类物理场中(这类场与泛函的极值问题有着紧密的联系)。 自从1969年以来,某些学者在流体力学中应用加权余数法 中的迦辽金法(Galerkin)或最小二乘法等同样获得了有限元 方程,因而有限元法可应用于以任何微分方程所描述的各类 物理场中,而不再要求这类物理场和泛函的极值问题有所联 系.
❖ FEM是应用于现代复杂机械结构优化设计的非常重要的计算 机辅助分析方法。FEM早期主要应用于航空航天制造、船舶 工业及高端军事领域 。
方法运用的基本步骤
❖ 基本思想:由解给定的泊松方程化为求解泛函的极值问题。
❖ 步骤1:剖分 ❖ 将待解区域进行分割,离散成有限个元素的集合.元素பைடு நூலகம்单
元)的形状原则上是任意的.二维问题一般采用三角形单元 或矩形单元,三维空间可采用四面体或多面体等.每个单元 的顶点称为节点(或结点)。
偏微分课程课件12_有限元离散方法(一维问题)

i -1 i
0
0
n1
则 uei Cei u, vei Cei v
n
n
v K u T
ei
ei ei
unvn
v F T ei ei
vn
i 1
i 1
uei Cei u, vei Cei v
vT
n i 1
CT ei
K C ei ei
u
unvn
vT
n i 1
C F T
ei
ei
2
i=1,2,3,4
Ku 0,L 0, un T F 0,L 0,1T
C K C T ei ei ei
xi
Kei
pBT B qN T N dx
xi1
O M M M M N
L 0 0
0
0
L
L L
0 0
k ei i 1,i 1
k ei i ,i 1
k ei i 1,i
k ei i ,i
0 L
0
L
2)转化为变分问题 考虑空间:
V S01 v
b a
v2
dv dx
2
dx
v(a)
0
任取v∈V, 乘方程两边
- d ( p du) qu f , dx dx
-ddx
(
p
du dx
)
qu
v
fv
两边积分
b a
-d dx
(
p
du dx
)
qu
vdx
b a
fvdx
b - d
uh( x)
Nuei , 其中N
xi hi
x
,
x
0
0
n1
则 uei Cei u, vei Cei v
n
n
v K u T
ei
ei ei
unvn
v F T ei ei
vn
i 1
i 1
uei Cei u, vei Cei v
vT
n i 1
CT ei
K C ei ei
u
unvn
vT
n i 1
C F T
ei
ei
2
i=1,2,3,4
Ku 0,L 0, un T F 0,L 0,1T
C K C T ei ei ei
xi
Kei
pBT B qN T N dx
xi1
O M M M M N
L 0 0
0
0
L
L L
0 0
k ei i 1,i 1
k ei i ,i 1
k ei i 1,i
k ei i ,i
0 L
0
L
2)转化为变分问题 考虑空间:
V S01 v
b a
v2
dv dx
2
dx
v(a)
0
任取v∈V, 乘方程两边
- d ( p du) qu f , dx dx
-ddx
(
p
du dx
)
qu
v
fv
两边积分
b a
-d dx
(
p
du dx
)
qu
vdx
b a
fvdx
b - d
uh( x)
Nuei , 其中N
xi hi
x
,
x
有限元法PPT课件

和时间。
如何克服局限性
改进模型
通过更精确地描述实际 结构,减少模型简化带
来的误差。
优化网格生成
采用先进的网格生成技 术,提高网格质量,降
低计算误差。
采用高效算法
采用并行计算、稀疏矩 阵技术等高效算法,提
高计算效率。
误差分析和验证
对有限元法的结果进行误 差分析和验证,确保结果
的准确性和可靠性。
05 有限元法的应用实例
有限元法ppt课件
目 录
• 引言 • 有限元法的基本原理 • 有限元法的实现过程 • 有限元法的优势与局限性 • 有限元法的应用实例 • 有限元法的前沿技术与发展趋势 • 结论
01 引言
有限元法的定义
01
有限元法是一种数值分析方法, 通过将复杂的结构或系统离散化 为有限个简单元(或称为元素) 的组合,来模拟和分析其行为。
有限元法在流体动力学分析中能够处理复杂的流体流动和 压力分布。
详细描述
通过将流体域离散化为有限个小的单元,有限元法能够模 拟流体的流动、压力、速度等状态,广泛应用于航空、航 天、船舶等领域。
实例
分析飞机机翼在不同飞行状态下的气动性能,优化机翼设 计。
热传导分析
总结词
有限元法在热传导分析中能够处理复杂的热传递过程。
实例
分析复杂电磁设备的电磁干扰问题,优化设备性能。
06 有限元法的前沿技术与发 展趋势
多物理场耦合的有限元法
总结词
多物理场耦合的有限元法是当前有限元法的重要发展方向, 它能够模拟多个物理场之间的相互作用,为复杂工程问题提 供更精确的解决方案。
详细描述
多物理场耦合的有限元法涉及到流体力学、热力学、电磁学 等多个物理场的耦合,通过建立统一的数学模型,能够更准 确地模拟多物理场之间的相互作用。这种方法在航空航天、 能源、环境等领域具有广泛的应用前景。
如何克服局限性
改进模型
通过更精确地描述实际 结构,减少模型简化带
来的误差。
优化网格生成
采用先进的网格生成技 术,提高网格质量,降
低计算误差。
采用高效算法
采用并行计算、稀疏矩 阵技术等高效算法,提
高计算效率。
误差分析和验证
对有限元法的结果进行误 差分析和验证,确保结果
的准确性和可靠性。
05 有限元法的应用实例
有限元法ppt课件
目 录
• 引言 • 有限元法的基本原理 • 有限元法的实现过程 • 有限元法的优势与局限性 • 有限元法的应用实例 • 有限元法的前沿技术与发展趋势 • 结论
01 引言
有限元法的定义
01
有限元法是一种数值分析方法, 通过将复杂的结构或系统离散化 为有限个简单元(或称为元素) 的组合,来模拟和分析其行为。
有限元法在流体动力学分析中能够处理复杂的流体流动和 压力分布。
详细描述
通过将流体域离散化为有限个小的单元,有限元法能够模 拟流体的流动、压力、速度等状态,广泛应用于航空、航 天、船舶等领域。
实例
分析飞机机翼在不同飞行状态下的气动性能,优化机翼设 计。
热传导分析
总结词
有限元法在热传导分析中能够处理复杂的热传递过程。
实例
分析复杂电磁设备的电磁干扰问题,优化设备性能。
06 有限元法的前沿技术与发 展趋势
多物理场耦合的有限元法
总结词
多物理场耦合的有限元法是当前有限元法的重要发展方向, 它能够模拟多个物理场之间的相互作用,为复杂工程问题提 供更精确的解决方案。
详细描述
多物理场耦合的有限元法涉及到流体力学、热力学、电磁学 等多个物理场的耦合,通过建立统一的数学模型,能够更准 确地模拟多物理场之间的相互作用。这种方法在航空航天、 能源、环境等领域具有广泛的应用前景。
第六章 第一讲 偏微分方程的有限元法

5.1 泛函与变分原理
数 学 物 理 方 法
5.1.2 变分法
研究泛函极值问题的方法可以归为两类:一类叫直接法,
即直接分析所提出的问题;另一类叫间接法,即把问题 转化为求解微分方程.为讨论间接方法,先介绍变分和 泛函的变分.
Beijing Institute of Technology Deng, Junjun
5.1 泛函与变分原理
数 学 物 理 方 法
类似的例子还可以举出很多,例如,闭合曲线围成的
面积,平面曲线绕固定轴而生成的旋转体积或表面积,
等等,它们也都确定了各自的泛函关系。
这里的函数集合,即泛函的定义域,通常包含要求
y(x)满足一定的边界条件,并且具有连续的二阶导数, 这样的y(x)称为可取函数。
极小值充分条件: J y0 变分: j
j 0 0
0
0
j 0 0
0 是 J 在 y0 处的变分,记为
J
16/76
Beijing Institute of Technology Deng, Junjun
dengjunjun@
15/76
5.1 泛函与变分原理
数 学 物 理 方 法
泛函极值问题转化为一般函数的 j() 极值问题,即:
j J y min!
当 =0时泛函取得极小值J(y0),根据微积分学可知,
泛函在 y0 取得极值的必要条件是
J y0 0 0
变分运算的几条简单法则:
Beijing Institute of Technology Deng, Junjun
dengjunjun@
20/54
5.1 泛函与变分原理
一阶偏微分方程求解方法PPT课件

i 1
i 1
18
19
2019/10/22
4. 加权余量法求解一般化偏微分方程的归纳
n
n
w j[( Ci i ) q] d w*j[ ( Ci i ) s] d 0
i 1
i 1
由于是线性微分算子,故微分、求和、积分次序可调换,代数方程变形:
n
n
{[ w j( i )d]Ci}
{[ w*j ( i )d]Ci}
w jq d
w
* j
s
d
i 1
i 1
n
{[
w j( i )d] [ w*j ( i )d]}Ci
w jq d
w
* j
s
d
i 1
有j个代数方程,
20
通常等于待定系 数个数
4. 加权余量法求解一般化偏微分方程的归纳
n
{[ wj( i )d] [ w*j ( i )d]}Ci wjq d w*j s d
i 1
系数
激励
边界条件
代数方程写成矩阵形式: [K ][C] [F ][b]
在x 0处:()x0=0 在x d处:()xd=10 12
3. 加权余量法--例
3. 加权余数表达式:
Fj(R)
j
R
d
j
R
d,j
1,2
j 1时,得到一个代数方程:
F1(R)
1
R
d
1R
偏微分方程及其求解实例ppt课件
(hn1-2.*h(k,n)+h(k,n-1))./dr.^2);
end plot(r(3:n)./ra,p(k,3:n).*theta.*2./rb)
h hi1 hi1 r i 2r
2h hi1 2hi hi1
r 2
r 2
i
P
1 rb 4
1
r
h r
2h r 2
偏微分方程的求解实例2:
2u A x2
2u B
xy
C
2u y 2
D u x
E u y
Fu
f
x,
y,u,
u x
,
u y
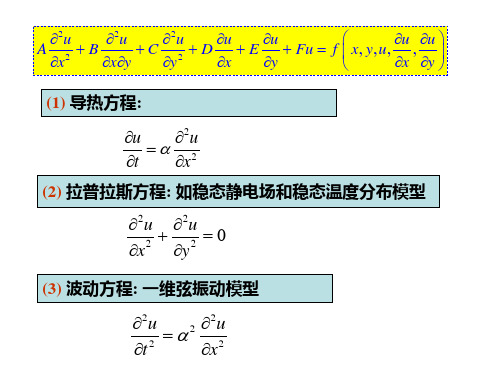
(1) 导热方程:
u 2u
t x2 (2) 拉普拉斯方程: 如稳态静电场和稳态温度分布模型
2u 2u 0
x2 y2
(3) 波动方程: 一维弦振动模型
2u 2 2u
t 2
x2
偏微分方程的边界条件
function PDE1Dd_CrankNicolson % 使用Crank-Nicolson有限差分方法求解一维动态传
热模型
c1 = 100; c2 = 0; a = 10; b = 8; alpha = 2; n = 6; m = 8; U = CrankNicolson(@ic,c1,c2,a,b,alpha,n,m)
h t 3 9c
9c
h3 h33
4h r 4
3
h5 4h4
6h3 4h2 r 4
h1
h t
n
V
r i 2r
2h hi1 2hi hi1
r 2
r 2
i
3h r 3
hi2
2hi1 2hi1 2r 3
偏微分方程的有限元方法67页PPT

偏微分方程ห้องสมุดไป่ตู้有限元方法
11、战争满足了,或曾经满足过人的 好斗的 本能, 但它同 时还满 足了人 对掠夺 ,破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、不应把纪律仅仅看成教育的手段 。纪律 是教育 过程的 结果, 首先是 学生集 体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
13、遵守纪律的风气的培养,只有领 导者本 身在这 方面以 身作则 才能收 到成效 。—— 马卡连 柯 14、劳动者的组织性、纪律性、坚毅 精神以 及同全 世界劳 动者的 团结一 致,是 取得最 后胜利 的保证 。—— 列宁 摘自名言网
15、机会是不守纪律的。——雨果
谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人,越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智,自知者明。胜人者有力,自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
11、战争满足了,或曾经满足过人的 好斗的 本能, 但它同 时还满 足了人 对掠夺 ,破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、不应把纪律仅仅看成教育的手段 。纪律 是教育 过程的 结果, 首先是 学生集 体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
13、遵守纪律的风气的培养,只有领 导者本 身在这 方面以 身作则 才能收 到成效 。—— 马卡连 柯 14、劳动者的组织性、纪律性、坚毅 精神以 及同全 世界劳 动者的 团结一 致,是 取得最 后胜利 的保证 。—— 列宁 摘自名言网
15、机会是不守纪律的。——雨果
谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人,越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智,自知者明。胜人者有力,自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
偏微分方程的有限元法

求解方法
利用有限元法求解弹性力学问题的基本步骤包括建立离散化的数学模型、选择合适的有 限元空间、求解离散化的线性方程组等。
传热学问题
传热学中的偏微分方程
描述热传导、对流、辐射等过程的偏微分方程包括热传导 方程、对流方程等,这些方程描述了温度场的变化规律。
有限元法在传热学中的应用
通过将连续的温度场离散化为有限个单元,有限元法能够 求解复杂的传热学问题,如热传导、对流换热、辐射换热 等。
区域离散
将连续的求解区域离散化为有限 个小的子区域,每个子区域称为
一个有限元。
函数近似
在每个有限元上选择适当的基函数 来近似未知函数,基函数的选择取 决于问题的性质和求解精度要求。
离散化方程
根据微分方程和边界条件,建立离 散化的代数方程组,表示为矩阵形 式。
有限元法的求解过程
线性化
将非线性微分方程转化为线性方程组,以便于求 解。
描述流体运动的偏微分方程包括Navier-Stokes方程、Euler方 程等,这些方程描述了流体的速度、压力、密度等物理量的变
化规律。
有限元法在流体动力学中的应用
通过将连续的流体域离散化为有限个单元,有限元法能够 求解复杂的流体动力学问题,如湍流、非牛顿流体等。
求解方法
利用有限元法求解流体动力学问题的基本步骤包括建立离散化 的数学模型、选择合适的有限元空间、求解离散化的线性方程
组等。
弹性力学问题
弹性力学中的偏微分方程
描述弹性物体变形的偏微分方程包括弹性力学的基本方程、Mindlin-Reissner方程等, 这些方程描述了弹性体的应力、应变等物理量的变化规律。
有限元法在弹性力学中的应用
通过将连续的弹性体离散化为有限个单元,有限元法能够求解复杂的弹性力学问题,如 非线性弹性、复合材料等。
利用有限元法求解弹性力学问题的基本步骤包括建立离散化的数学模型、选择合适的有 限元空间、求解离散化的线性方程组等。
传热学问题
传热学中的偏微分方程
描述热传导、对流、辐射等过程的偏微分方程包括热传导 方程、对流方程等,这些方程描述了温度场的变化规律。
有限元法在传热学中的应用
通过将连续的温度场离散化为有限个单元,有限元法能够 求解复杂的传热学问题,如热传导、对流换热、辐射换热 等。
区域离散
将连续的求解区域离散化为有限 个小的子区域,每个子区域称为
一个有限元。
函数近似
在每个有限元上选择适当的基函数 来近似未知函数,基函数的选择取 决于问题的性质和求解精度要求。
离散化方程
根据微分方程和边界条件,建立离 散化的代数方程组,表示为矩阵形 式。
有限元法的求解过程
线性化
将非线性微分方程转化为线性方程组,以便于求 解。
描述流体运动的偏微分方程包括Navier-Stokes方程、Euler方 程等,这些方程描述了流体的速度、压力、密度等物理量的变
化规律。
有限元法在流体动力学中的应用
通过将连续的流体域离散化为有限个单元,有限元法能够 求解复杂的流体动力学问题,如湍流、非牛顿流体等。
求解方法
利用有限元法求解流体动力学问题的基本步骤包括建立离散化 的数学模型、选择合适的有限元空间、求解离散化的线性方程
组等。
弹性力学问题
弹性力学中的偏微分方程
描述弹性物体变形的偏微分方程包括弹性力学的基本方程、Mindlin-Reissner方程等, 这些方程描述了弹性体的应力、应变等物理量的变化规律。
有限元法在弹性力学中的应用
通过将连续的弹性体离散化为有限个单元,有限元法能够求解复杂的弹性力学问题,如 非线性弹性、复合材料等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y)
y
F
(x, y, y
y)
1 2!
y2
2F
(x, y, y2
y)
2
y
y
2F (x, y, yy
y)
y2
2F (x, y, y2
y)
5.1 泛函与变分原理
J
x1 Fy y Fy y
加权余数法的核心思想是:近似解与解析解相比会存 在误差R,但是可以通过一个准则使R尽量小,求解这个等 式,就可以得到待定常数的值,也就得到了近似解。
第五章 偏微分方程的有限元法
有限元法特点
1. 有限元法的物理意义直观明确,理论完整可靠。 因为变 分原理描述了支配物理现象的物理学中的最小作用原理
(如力学中的最小势能原理)。
泛函的变分
J J ( y y) J ( y)
x1F(x, y y, y y) F(x, y, y)dx x0
5.1 泛函与变分原理
利用二元函数的泰勒展开
F (x, y y, y y)
F
(x,
y,
y)
1 1!
y
F
(x, y, y
自变量为函数,而不是变量。
5.1 泛函与变分原理
例5.1.1 质点在重力作用下,沿一条光滑的从A点到B 点的曲线运动,如图所示。求下落时间最短的曲线。
O
x0
A
x1 x
捷线问题
B y
曲线上任一小段线元长度为:
ds2 dx2 dy2 (1 dy 2 )dx2 dx
ds (1 y2 )dx
y Y(x) y(x) Y(x) y(x) (y)
5.1 泛函与变分原理
5.1.3 泛函的变分
定义最简泛函
J[ y(x)] x1 F(x, y, y)dx x0 F(x,y,y’)称为泛函的“核函数”
最简泛函: 核函数只包含自变量 x、未知函数y(x)以及导数y’(x)
第五章 偏微分方程的有限元法
5.1 泛函与变分原理 5.2 基于变分原理的有限元法 5.3 matlab有限元法工具箱
第五章 偏微分方程的有限元法
有限元法(FEA,Finite Element Analysis,FEM) 有限元法的基本思想是用较简单的问题代替复杂问
题,然后再对简单问题进行求解的数值计算方法。
个域总的满足条件(边界条件),即最终归结为一组多元的
代数方程组,求解代数方程组,就得到待求边值问题的
数值解。
第五章 偏微分方程的有限元法
有限元法--加权余数法
自从1969年以来,某些学者在流体力学中应用加权余 数法中的迦辽金法或最小二乘法等同样获得了有限元方程, 因而有限元法可应用于以任何微分方程所描述的各类物理 场中,而不再要求这类物理场和泛函的极值问题有所联系。
5.1 泛函与变分原理
线元处的质点速度为
v 2gy
ds线元下落时间为
ds 1 y2
dT
dx
v
2gy
O
x0
A
x1 x
B y
从A点到B点的下落时间为
T x1 1 y2 dx J[ y(x)]
x0 2gy
J[ y(x)] min
5.1 泛函与变分原理
5.1.2 函数的变分
有限元法将求解域看成是由许多被称为有限元的小的互 连子域组成,对每一单元假定一个较简单的近似解,然后推 导求解这个域总的满足条件,从而得到问题的解。这个解不 是准确解,而是近似解。有限元不仅计算精度高,而且能适 应各种复杂形状,因而成为行之有效的数值计算方法。
有限元法于上世纪50年代首先在力学领域-----飞机结 构的静、动态特性分析中得到应用,随后很快广泛的应用 于求解热传导、电磁场、流体力学等连续性问题。 有限元法主要用于求解拉普拉斯方程和泊松方程所描述的 各类物理场中。
第五章 偏微分方程的有限元法
有限元法---变分原理
基于变分原理的有限元法是逼近论、偏微分方程、变 分与泛函分析的巧妙结合。
基于变分原理的有限元法以变分原理为基础,把所 要求解的微分方程定解问题,首先转化为相应的变分问 题,即泛函求极值问题;它将求解域看成是由许多称为 有限元的小的互连子域组成,然后利用剖分插值,对每一 单元假定一个合适的(较简单的)近似解,把离散化的变分 问题转化为普通多元函数的极值问题,然后推导求解这
x0
1 2!
Fyy
y2
2Fyy
y
y
Fyy
y2
dx
J 2J
其中
J
x1 x0
Fy y Fy y dx
Fy
F y
Fyy
2F y 2
J J ( y y) J ( y)
2J 1
5.1.1 泛函的定义
泛函通常是指一种定义域为函数,而值域为实数的 “函数”。
设C是函数的集合,B是实数集合。如果对C中的任 一元素y(x),在B中都有一个元素J与之对应,则称J为 y(x)的泛函,记为J[y(x)]。
数学上,通常自变量与因变量间的关系称为函数,
而泛函则是函数集合的函数,也就是函数的函数,即
2. 优异的解题能力。有限元法对边界几何形状复杂以及媒 质物理性质变异等复杂物理问题求解上,有突出优点:
① 不受几何形状和媒质分布的复杂程度限制。 ②不必单独处理第二、三类边界条件。 ③ 离散点配置比较随意,通过控制有限单元剖分密度和 单元插值函数的选取,可以充分保证所需的数值计算精度。
5.1 泛函与变分原理
2
x1
x0
Fyy
y
2 2Fyy y y Fyy
y 2 dx
分别称为泛函的一阶变分和二阶变分。
5.1 泛函与变分原理
泛函取极值的必要条件:一阶变分为零
J 0
性质:对于最简泛函,变分运算可以与积分、微 分运算交换次序
设y(x)是泛泛函J的定义域,则Y(x)与y(x) 之差为函数y(x)的变分。
y Y (x) y(x)
变分δy是x的函数,它不同于函数的
增量Δy。y y x x y x
性质:函数求导与求变分可以交换次序
