2017全国中小学数独比赛北京赛区选拔赛
2017年北京市中小学五人制足球赛竞赛规程.doc

附件12017年北京市中小学五人制足球赛竞赛规程一、比赛名称2017年北京市中小学五人制足球赛二、组织单位主办单位:北京市青少年校园足球工作领导小组办公室承办单位:首都体育学院北京市校园足球协会协办单位:北京最佳拍档营销顾问有限公司三、比赛信息(一)比赛时间2018年1月28日-2月2日(二)比赛地点待定(三)参赛队伍及报名1.参赛队伍由各区教委选派参赛队伍,各区可报小学男队、女队各一支,初中男队、女队各一支,高中男队、女队各一支。
可按学校组队,亦可跨校联合组队,队伍名称为:区名-组别-性别组,如:东城区小学女队。
2.运动员资格(1)运动员必须是有北京市正式学籍的在校学生;(2)小学组仅限五、六年级学生参赛;(3)参赛运动员年龄规定:小学组运动员:出生日期应在2004年9月1日(含)- 2006年8月31日(含);初中组运动员:出生日期应在2001年9月1日(含)- 2004年8月31日(含);高中组运动员:出生日期应在1998年9月1日(含)- 2001年8月31日(含);(4)运动员参赛期间仅能代表一支队伍参赛;不得冒名顶替、弄虚作假,如发现此类情况,经核实后,将取消违规队继续比赛资格及全部比赛成绩,并予以通报批评。
四、报名要求报名截止时间:2017年12月29日16:00。
(一)每支球队参赛运动员限报12名,领队、教练员、队医各1名。
报名后不得更改;(二)各球队须填报参赛报名表(附件2)并加盖区教委公章。
提交参赛运动员学籍卡(复印件)。
(三)报名表提交方式1.报名表扫描件:报名截止时间前,将加盖公章的报名表扫描件、学籍卡扫描件、各参赛运动员一寸白底照片电子版,发送至赛事组委会邮箱:邮件主题为【报名资料】区名-组别-性别组(如【报名资料】东城区小学女队,一寸照片请按报名姓名备注)。
2.报名表纸质版、学籍卡复印件:请各领队在参加领队会当日(2018年1月10日)携带并提交至签到台。
五、资格审查(一)各区教委负责对本区参赛运动员的资格认真审查。
2015 数独比赛 秩序册_0309

2015年北京中小学数独比赛暨第三届北京中小学数独比赛北京市教委《2015年北京市中小学生体育竞赛计划》项目比赛规程时间:2015年4月- 5 月2015年北京中小学数独比赛暨第三届北京中小学数独比赛规程一、组织单位主办单位北京市中小学体育运动协会北京市数独运动协会学而思培优指导单位北京奥运城市发展促进会北京市教育委员会北京市体育局北京广播电视台北京奥运城市发展基金会二、比赛时间及地点1、个人精英赛初赛时间:4月4日地点:北京学而思培优(详见参赛证)2、个人精英赛决赛时间:5月10日地点:光彩体育馆(拟)3、团体赛时间:5月10日地点:光彩体育馆(拟)三、比赛项目1、数独个人精英赛2、数独学校团体赛3、数独王中王表演赛四、比赛组别1、新人组:小学一年级。
不分男女。
2、小学乙组:二至四年级。
不分男女。
3、小学甲组:五至六年级。
不分男女。
4、中学组:初中、高中。
不分男女。
5、个人精英赛严格按规定年级分组。
团体赛低年级选手可参加高年级组别比赛,高年级不能参加低年级组别比赛。
五、比赛办法1、个人精英赛初赛(1)比赛时间:4月4日(下午)14:30-15:00 签到15:00-15:30 第一轮15:45-16:15 第二轮(2)比赛规则比赛共两轮,每轮30分钟,满分100分。
提前交卷不加分。
晋级人数按照四个组别报名人数比例及初赛成绩由高到低晋级。
4月24日前将通知学校领队老师录取结果。
(3)比赛题型(题型说明见附件1)新人组:4宫/6宫/9宫标准数独小学乙组:6宫/9宫标准数独/9宫对角线数独/5字不规则小学甲组:9宫标准数独/对角线数独/7字不规则数独中学组:9宫标准数独/对角线数独/不规则数独2、个人精英赛决赛(1)比赛时间:5月10日(全天)08:00-08:50 比赛签到及检录09:00-09:30 晋级赛第一轮09:45-10:15 晋级赛第二轮10:30-11:00 晋级赛第三轮14:00-14:30 新人组、小学乙组总决赛15:30-16:00 小学甲组、中学组总决赛(2)比赛规则决赛设晋级赛和总决赛,其中晋级赛三轮,总决赛一轮,共四轮。
2017年全国珠心算邀请赛看心算模拟题(学前A组)4套带答案

227 189 76 43 32 210 111 173 29 30
五十一 五十二 五十三 五十四 五十五 五十六 五十七 五十八 五十九
六十
96 50 56 61 23 98 42 73 68 37
43 12 27 -57 -18 53 90 54 -21 40
78 98 40 94 60 17 68 30 92 -56
限时5分钟
计算题 错题
对题
初评
复核
成绩
三十一
9
三十二
1
三十三
4
三十四
6
三十五
6
三十六
1
三十七
1
三十八
4
三十九
5
8
9
3 -3
8
9
2
2
7
7
8
2
5 -5
8
9
5 -2
4
7
1
4
2
4
7
3
6
2
5
9
1
4
7
8
1
4
6
6
7 -2 -7
6
6
9 -3
5
3
8
9
3
3
5
8
1
41
四十一
39
四十二
34
四十三
20
四十四
11
四十五
38
四十六
编号: 201703092
2017年全国珠心算邀请赛看心算模拟题
选手号
学前A组(二)
限时5分钟
计算题 错题
对题
初评
复核
成绩
三十一
2017年4月学而思杯一年级数学试卷解析

2017年第十一届北京学而思综合能力测评(学而思杯)数学试卷(一年级)(考试时间:60分钟,满分200分)一.基础过关(每题8分,共40分)1. 计算:9+19=_______ 8+12—20=_______【考点】计算问题——50以内加减法计算【难度】☆【答案】28,0【分析】第一题为进位加法,可从9中拆一个1给19,和为20,用20+8=28;第二题按照顺序从左到右依次计算。
2. 小朋友,来排队;头向前,站整齐.数一数,共有________个小男孩.【考点】组合问题——图形找规律【难度】☆【答案】24【分析】观察此图,图中小孩按照1,3,5,7,9的顺序进行排列,总人数为1+3+5+7+9=25,其中有一个小女孩,因此小男孩的总人数为25-1=24(个)。
3.《欢乐好声音》电影中的考拉经理决定举办一场盛大的歌唱大赛.很多小动物都来参加比赛,一列队伍中,猪妈妈左边有6只小动物,右边有8只小动物,这列队伍中一共有_______只动物.【考点】应用题问题——排队问题【难度】☆☆【答案】15【分析】排队问题最重要的解决方法就是画图,根据题目的描述画出队列图即可,注意关键词“有几只”,如图:▲为猪妈妈,O代表其他小动物;OOOOOO▲OOOOOOOO 列式6+1+8=15(只)小动物,或者数一数一共有15只小动物。
4. 妈妈送给奇奇一个特别的骰子,六个面分别印有1、2、3、4、5、6不同的点数,当它如图放置时,上面与下面点数的和是6,左面与右面点数的和也是6.那么,后面的点数是______.【考点】图形问题——立体图形【难度】☆☆【答案】3【分析】通过题目叙述6个面的点数分别为1、2、3、4、5、6,上面和下面的点数之和为6,因为上面点数为1所以下面点数为 5,左面和右面的点数和也是6,右面为2所以左面为4,前面为6,排除1,5,2,4,6,所以剩下的后面的点数为3.5.根据下图的规律,判断第10幅图用了______根火柴棒.【考点】图形问题——图形找规律【难度】☆☆【答案】21【分析】观察前3 幅图形会发现,从第二幅图开始每增加一个三角形,都会增加2根火柴棒,则火柴棒的根数就会呈现这样的规律:3,5,7,9,11,13,15,17,19,21。
北京市第4届迎春杯小学数学竞赛决赛试题.doc

北京市第4届迎春杯小学数学竞赛决赛试题1.计算下面的算式,答案保留整数部分,小数部分四舍五入。
33.33332-3.1415926÷0.618≈________。
2.大小两数之和为,大数的倍与小数的2倍之和是16,那么大数是________。
3.某班同学在班主任老师带领下去种树,学生恰好平均分成三组,如果老师与学生每人种树一样多,共种了1073棵,那么平均每人种了________棵树。
4.下面的算式里,相同的汉字代表同一个数字,不同的汉字代表不同的数字。
如果以下三个等式成立:迎迎×春春=杯迎迎杯,数数×学学=数赛赛数,春春×春春=迎迎赛赛。
那么,迎+春+杯+数+学+赛=________。
5.把下面的正方形分割为三种面积不同的小正方形,并且小正方形的个数是8。
(只画出分割线)6.妈妈给小青11.1元,让他去买5斤香蕉、4斤苹果,结果他买的数量给弄颠倒了,从而还剩下0.6元。
那么苹果每斤的售价是________元。
7.把1988表示成28个连续偶数的和,那么其中最大的那个偶数是________。
8.甲、乙、丙三人的平均年龄为42岁,若将甲的岁数增加7岁,乙的岁数扩大2倍,丙的岁数缩小2倍,则三人岁数相等。
丙的年龄为________岁。
9.如图,已知AE=AC,CD=BC,BF=AB,那么,=________。
10.两个数的最大公约数是21,最小公倍数是126。
这两个数的和是________美文欣赏1、走过春的田野,趟过夏的激流,来到秋天就是安静祥和的世界。
秋天,虽没有玫瑰的芳香,却有秋菊的淡雅,没有繁花似锦,却有硕果累累。
秋天,没有夏日的激情,却有浪漫的温情,没有春的奔放,却有收获的喜悦。
清风落叶舞秋韵,枝头硕果醉秋容。
秋天是甘美的酒,秋天是壮丽的诗,秋天是动人的歌。
2、人的一生就是一个储蓄的过程,在奋斗的时候储存了希望;在耕耘的时候储存了一粒种子;在旅行的时候储存了风景;在微笑的时候储存了快乐。
世界数独和谜题锦标赛北京开幕 各国选手拼智力

世界数独和谜题锦标赛北京开幕各国选手拼智力10月12日,第8届世界数独锦标赛和第22届世界谜题锦标赛在北京市昌平区开幕。
这是该智力谜题领域最高级别赛事,首次在中国举办。
来自35个国家和地区的271名数独和谜题高手齐聚一堂,在比拼智力的同时,共享数独和谜题的快乐,共叙友谊。
为了举办一届有特色、高水平的世锦赛,组委会创新赛事组织方式,将中国传统文化元素融入其中,令各国选手和来宾耳目一新。
在宣布赛事开幕后,众人以中国传统击鼓的形式拉开大赛序幕。
世界智力谜题联合会常务理事、匈牙利谜题协会主席乔治·伊斯特万在致辞中表示,世智联非常重视在中国举办国际性赛事,此次数独世锦赛首次来到中国,谜题世锦赛第一次来到亚洲,对增强数独和谜题在中国普及度及参与度,具有里程碑的意义。
据悉,本届世锦赛自今年3月组委会启动报名以来,吸引了众多世界各地的高手前来参赛,其中年龄最小的数独选手仅有10岁。
中国队京13岁中学生出战随着数独这项智力运动在中国的不断普及,越来越多的青少年成为了数独爱好者,中国队也成为本届比赛最年轻的国家队之一。
此次代表中国参赛的中学生“国手”,从2013中盟天隆森林杯中国数独锦标赛上选拔产生。
他们是杭州学军中学15岁的金策、北大附中13岁的孙彻然、人大附中15岁的邱言哲、上海华育中学14岁的陈诺、北京101中学16岁的马梦蕾,他们与桂勇、田健、梁跃组成了本届中国数独代表队,力争在首次设定的18岁以下年龄组比赛中取得好成绩。
题型体现中国元素据介绍,本届赛事注重创新赛题、赛制。
中国首次设计数独世锦赛赛题,题型多达60余种,有些题型为本届大赛所独创,在历届数独世锦赛中未曾出现,赛题总体难度系数达到甚至高于国际数独赛事标准。
除了常规的标准数独、锯齿数独、杀手数独、摩天楼数独等题型外,还有为大赛专门设计的拼图式的数独赛题,并在团体赛中融入魔方的概念,考验团体配合及参赛队整体数独水平,并体现了鲜明的中国元素。
第三届北京中小学数独比赛初赛入围名单(小学甲组)
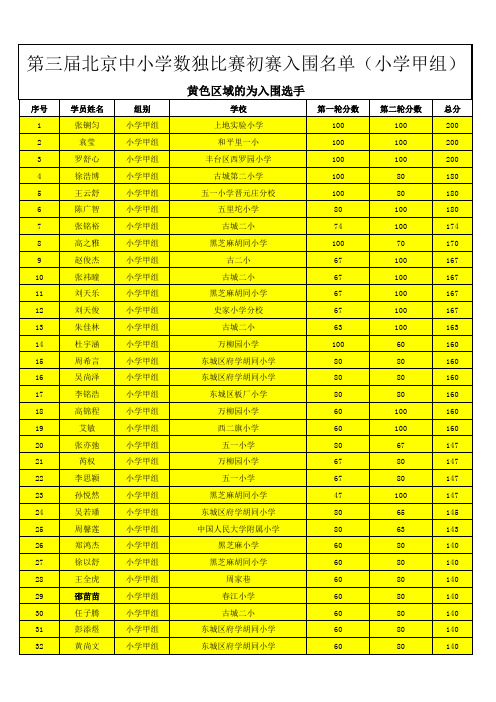
黄色区域的为入围选手序号学员姓名组别学校第一轮分数第二轮分数总分1张锎匀小学甲组上地实验小学100100200 2袁莹小学甲组和平里一小100100200 3罗舒心小学甲组丰台区西罗园小学100100200 4徐浩博小学甲组古城第二小学10080180 5王云舒小学甲组五一小学晋元庄分校10080180 6陈广智小学甲组五里坨小学80100180 7张铭裕小学甲组古城二小74100174 8高之雅小学甲组黑芝麻胡同小学10070170 9赵俊杰小学甲组古二小67100167 10张祎曈小学甲组古城二小67100167 11刘天乐小学甲组黑芝麻胡同小学67100167 12刘天俊小学甲组史家小学分校67100167 13朱佳林小学甲组古城二小63100163 14杜宇涵小学甲组万柳园小学10060160 15周希言小学甲组东城区府学胡同小学8080160 16吴尚泽小学甲组东城区府学胡同小学8080160 17李铭浩小学甲组东城区板厂小学8080160 18高锦程小学甲组万柳园小学60100160 19艾敏小学甲组西二旗小学60100160 20张亦弛小学甲组五一小学8067147 21芮权小学甲组万柳园小学6780147 22李思颍小学甲组五一小学6780147 23孙悦然小学甲组黑芝麻胡同小学47100147 24吴若璠小学甲组东城区府学胡同小学8065145 25周馨莲小学甲组中国人民大学附属小学8063143 26郑鸿杰小学甲组黑芝麻小学6080140 27徐以舒小学甲组黑芝麻胡同小学6080140 28王全虎小学甲组周家巷6080140 29邵苗苗小学甲组春江小学6080140 30任子腾小学甲组古城二小6080140 31彭添煜小学甲组东城区府学胡同小学6080140 32黄尚文小学甲组东城区府学胡同小学6080140黄色区域的为入围选手序号学员姓名组别学校第一轮分数第二轮分数总分33程光霁小学甲组黑芝麻小学6080140 34王言峰小学甲组东城区府学胡同小学6770137 35程子青小学甲组育才学校6770137 36黄琛小学甲组五一小学30100130 37杨传明小学甲组丰台区纪家庙小学6065125 38严骢旭小学甲组春江小学6065125 39闫红红小学甲组丰台区长辛店学校6065125 40孙熠雯小学甲组史家小学分校6065125 41刘靖薇小学甲组朝阳实验小学6065125 42成雪桐小学甲组东城区府学胡同小学6065125 43杨睿小学甲组古城二小4380123 44史非同小学甲组育才学校4380123 45郭京航小学甲组丰台区长辛店学校4380123 46周晓光小学甲组丰台区长辛店学校8040120 47孙岳洋小学甲组丰台五小京铁校区6060120 48马朝阳小学甲组丰台区西罗园小学6060120 49麻屹铭小学甲组古城二小6060120 50刘逸群小学甲组东高地二小6060120 51李佳润小学甲组黑芝麻小学6060120 52姜涵章小学甲组东城区西总布小学6060120 53郭镔慧小学甲组北京市东城区黑芝麻胡同小学6060120 54高麦伦小学甲组西二旗小学6060120 55宗蓓蕾小学甲组丰台区长辛店学校6050110 56张镭小学甲组育才学校6050110 57任意小学甲组春江小学6050110 58多蕙晨小学甲组黑芝麻小学6050110 59李兆妍小学甲组古城二小5060110 60缪一飞小学甲组丰台区西罗园第五小学 4760107 61廉涟小学甲组东城区府学胡同小学4760107 62张世豪小学甲组黑芝麻胡同小学2680106 63姜博远小学甲组万柳园小学6045105 64赵宇宣小学甲组五一小学5450104黄色区域的为入围选手序号学员姓名组别学校第一轮分数第二轮分数总分65秦翔丹小学甲组万柳园小学6043103 66何珺尧小学甲组五一小学6043103 67郑芷兰小学甲组东城区西总布小学4360103 68杨梦雅小学甲组春江小学4360103 69田栋来小学甲组古城二小4360103 70马懿轩小学甲组丰台区西罗园第五小学 4360103 71刘洋小学甲组古城二小4360103 72李宗翰小学甲组黑芝麻胡同小学4360103 73李子墨小学甲组东城区府学胡同小学4360103 74郭芮彤小学甲组东城区板厂小学4360103 75白小鸥小学甲组府学小学4360103 76周飘小学甲组五一小学6040100 77王澍小学甲组黑芝麻小学475097 78王仕湲小学甲组古城第二小学178097 79谷泽萌小学甲组万柳园小学465096 80杨成思小学甲组东城区府学胡同小学603595 81邱实小学甲组板厂小学435093 82肖雨霏小学甲组万柳园小学603090 83魏文萱小学甲组府学胡同小学603090 84李传烨小学甲组史家小学分校603090 85陈炎炎小学甲组周家巷603090 86陈颉小学甲组东城区板厂小学603090 87鄢秋爽小学甲组东城区府学胡同小学306090 88徐弈阳小学甲组育才306090 89魏 一小学甲组周家巷306090 90贾西贝小学甲组学院路306090 91陈心然小学甲组垂杨柳(杨柳校区)306090 92陈俊儒小学甲组北京育才学校306090 93尹姜旭丽小学甲组东城区府学胡同小学434588 94齐悠然小学甲组黑芝麻胡同小学434588 95陈平小学甲组东城区西总布小学434588 96张祖豪小学甲组古城二小602686黄色区域的为入围选手序号学员姓名组别学校第一轮分数第二轮分数总分97张旭小学甲组五里坨小学266086 98杨任宇小学甲组学院路266086 99王英泽小学甲组东城区府学胡同小学266086 100李佩和小学甲组中关村三小266086 101高宇寰小学甲组黑芝麻小学266086 102冯梓航小学甲组东城区府学胡同小学266086 103张子寒小学甲组丰台区长辛店学校671582 104杨梓萌小学甲组丰台区西罗园小学602080 105杨子谦小学甲组东城区府学胡同小学602080 106王赛麒小学甲组育才学校602080 107贵霖娟小学甲组东城特殊教育学校602080 108许超宇小学甲组丰台五小京铁校区305080 109吴思颖小学甲组古城二小433578 110刘京博小学甲组东城区府学胡同小学433578 111张雅小学甲组东城区板厂小学473077 112张江达小学甲组473077 113翟誉秦小学甲组黑芝麻小学473077 114孟佳和小学甲组育才学校473077 115董雨润小学甲组和平里四小473077 116丁梓峰小学甲组古城二小473077 117薛新星小学甲组周家巷601575 118李嘉桐小学甲组万柳园小学453075 119袁锦妲小学甲组东城区府学胡同小学304575 120余梦桓小学甲组万柳园小学304575 121周简文小学甲组灯市口小学433073 122周佳琪小学甲组春江小学433073 123赵佳琦小学甲组向东小学433073 124张泽阳小学甲组古城二小433073 125张墨驰小学甲组芳星园第二小学433073 126张家玮小学甲组春江小学433073 127张楚小学甲组北京市朝阳区白家庄小学433073 128严少擎小学甲组丰台区长辛店学校433073黄色区域的为入围选手序号学员姓名组别学校第一轮分数第二轮分数总分129魏宇童小学甲组古城二小433073 130王乾小学甲组西二旗小学433073 131李梁小学甲组学院路433073 132贾媛媛小学甲组育新小学433073 133何柏旸小学甲组黑芝麻小学433073 134管乐颖小学甲组五里坨小学433073 135邓涵堃小学甲组垂杨柳(杨柳校区)433073 136周宇轩小学甲组东城区板厂小学136073 137王瑞宣小学甲组二十一世纪国际学校136073 138石玉树小学甲组周家巷136073 139卓杰小学甲组春江小学264571 140马思曦小学甲组东城区板厂小学264571 141罗浩洲小学甲组学院路264571 142周飞小学甲组万柳园小学304070 143陈致远小学甲组垂杨柳中心小学金都校区343064 144詹璟仪小学甲组五一小学432063 145史羽蝉小学甲组中关村一小432063 146阮羽亭小学甲组星河实验小学432063 147甘伟豪小学甲组丰台五小京铁校区432063 148安浩诚小学甲组古城二小135063 149郑泓小学甲组学院路471562 150赵子钰小学甲组五一小学471562 151康天赐小学甲组周家巷174562 152陈嘉曦小学甲组丰台一小263561 153余嘉阳小学甲组东城区西总布小学60060 154徐亚芯小学甲组西二旗小学60060 155束孟熹小学甲组东城区府学胡同小学60060 156金灿小学甲组东城区府学胡同小学60060 157郑钰小学甲组东城区府学胡同小学303060 158项成鑫小学甲组蒲黄榆三小303060 159王馨妮小学甲组西二旗小学303060 160王澍凡小学甲组北京市朝阳区白家庄小学303060。
(完整word版)2017年第二十二届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组b卷)

2017年第二十二届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组B 卷)一、填空题(每小题10分,共80分)1.(10分)1111113352015201711111111123345201520162017---++⋯+=⨯⨯⨯⨯⨯⨯ . 2.(10分)甲、乙两车分别从A 、B 两地同时出发,相向而行,出发时甲乙两车的速度比为5:4.出发后不久,甲车发生爆胎,停车更换轮胎后继续前进,并且将速度提高20%,结果在出发后3小时,与乙车相遇在AB 两地中点,相遇后,乙车继续往前行驶,而甲车掉头行驶,当甲车回到A 地时,乙车恰好到达甲车爆胎的位置,那么甲车更换轮胎用了 分钟.3.(10分)在33⨯的网格中(每个格子是个11⨯的正方形)放两枚相同的棋子,每个格子中最多放一枚棋子,共有 种不同的摆放方法.(如果两种放法能够由旋转而重合,则把它们视为同一种摆放方法).4.(10分)小于1000的自然数中,有 个数的数字组成中最多有两个不同的数字. 5.(10分)如图,ABC ∆的面积为100平方厘米,ABD ∆的面积为72平方厘米.M 为CD 边的中点,90MHB ∠=︒,已知20AB =厘米,则MH 的长度为 厘米.6.(10分)一列数1a 、2a ⋯,n a ⋯,记()i S a 为i a 的所有数字之和,如(22)224S =+=,若12017a =,222a =,12()()n n n a S a S a --=+,那么2017a 等于 .7.(10分)一个两位数,其数字和是它的约数,数字差(较大数减去较小数)也是它的约数,这样的两位数的个数共有 个.8.(10分)如图,六边形的六个顶点分别标志为A ,B ,C ,D ,E ,F .开始的时候“华罗庚金杯赛”六个汉字分别位于A ,B ,C ,D ,E ,F 顶点处.将六个汉字在顶点处任意摆放,最终结果是每个顶点处仍各有一个汉字,每个字在开始位置的相邻顶点处,则不同的摆放方法共有种.二、解答下列各题(每小题10分,共40分)9.(10分)平面上有5条不同的直线,这5条直线共形成m个交点,则m有多少个不同的数值?10.(10分)求能被7整除且各位数字均为奇数,各位数字和为2017的最大正整数.11.(10分)从1001,1002,1003,1004,1005,1006,1007,1008,1009中任意选出四个数,使它们的和为偶数,则共有多少种不同的选法.12.(10分)使3251nn++不为最简分数的三位数n之和等于多少.三、解答下列各题(每小题15分,共30分)13.(15分)一个正六边形被剖分成6个小三角形,如图,在这些小三角形的7个顶点处填上7个不同的整数,能否找到一个填法,使得每个小三角形顶点处的3个数都按顺时针方向从小到大排列,如果可以,请给出一种填法;如果不可以,请说明理由.14.(15分)77⨯的方格黑白染色,如果黑格比白格少的列的个数为m,黑格比白格多的行的个数为n,求m n+的最大值.2017年第二十二届“华罗庚金杯”少年数学邀请赛决赛试卷(小高组B 卷)参考答案与试题解析一、填空题(每小题10分,共80分)1.(10分)1111113352015201711111111123345201520162017---++⋯+=⨯⨯⨯⨯⨯⨯ 2034144 . 【分析】观察一下,首先把分子的两个分数变换一下形式,变成两个分数的乘积,恰好能和分母约分,这样就把原来的繁杂的分数变成简单的整数加减运算.【解答】解:1111113352015201711111111123345201520162017---++⋯+⨯⨯⨯⨯⨯⨯ 31532017201513352015201711111111123345201520162017---⨯⨯⨯=++⋯+⨯⨯⨯⨯⨯⨯111122221335572015201711111111132354576201520172016⨯⨯⨯⨯⨯⨯⨯⨯=+++⋯+⨯⨯⨯⨯⨯⨯⨯⨯ 2(24682016)=⨯++++⋯+ (22016)2016222+=⨯⨯20181008=⨯ 2034144=【点评】本题考查了分数的拆项运算知识,本题突破点:把分子拆分成两个分数的乘积形式,从而和分母约分2.(10分)甲、乙两车分别从A 、B 两地同时出发,相向而行,出发时甲乙两车的速度比为5:4.出发后不久,甲车发生爆胎,停车更换轮胎后继续前进,并且将速度提高20%,结果在出发后3小时,与乙车相遇在AB 两地中点,相遇后,乙车继续往前行驶,而甲车掉头行驶,当甲车回到A 地时,乙车恰好到达甲车爆胎的位置,那么甲车更换轮胎用了 52 分钟.【分析】首先分析后半程冲中点到A的过程,求出两人的速度比就可知道路程比,找到爆胎位置.然后再根据原来的速度比求出正常行驶的时间减去爆胎前的时间.最后根据甲前后两次的速度比求出时间比做差即可.【解答】解:依题意可知:甲乙两车的后来速度比:5(120%):43:2+=,甲回来走3份乙走两份路程.得知甲车爆胎的位置是AC的13处.如果不爆胎的甲行驶的时间和速度成反比:设甲行驶的时间为x则有:4:5:3x=,125 x=甲在行驶AC的爆胎位置到中点的正常时间为:121248(1)53155⨯-==(小时);甲乙爆胎前后的速度比为:5:5(120%)5:6+=;路程一定时间和速度成反比:设爆胎后到中点的时间为y则有:86:5:5y=,43y=;修车时间为:121413353315-⨯-=(小时)13605215⨯=(分)故答案为:52分【点评】本题考查对比例应用题的理解和运用,关键是根据不变量判断正反比,找到甲原来不受影响的时间,再和后面的进行比较做差即可,问题解决.3.(10分)在33⨯的网格中(每个格子是个11⨯的正方形)放两枚相同的棋子,每个格子中最多放一枚棋子,共有10种不同的摆放方法.(如果两种放法能够由旋转而重合,则把它们视为同一种摆放方法).【分析】可以分情况讨论,四个顶点的位值一样,正中间的一个方格一个位值,剩下的四个方格位值相同,故可以分次三种情况分别计算不同的摆放方法.【解答】解:根据分析,份三种情况:①当正中间即E处放一颗棋子,然后另一颗棋子放在外围任意一个位置,除去对称性因素,有2种不同的摆放方法,即AE 、BE ;②当两颗棋子都不在正中间E 处时,而其中有一颗在顶点处时,有4种不同摆法,即AB 、AF 、AH 、AD ;③当两颗棋子都在顶点处时,有2种不同摆法,即AC 、AI ;④当两颗棋子都在除顶点和正中间之外的4个方格中,有2种不同摆法,即BD 、BH .综上,共有:242210+++=种不同摆放方法.【点评】本题考查了排列组合,突破点是:分情况讨论,根据不同的位置求出总的不同摆放方法.4.(10分)小于1000的自然数中,有 352 个数的数字组成中最多有两个不同的数字. 【分析】可以先求出有三个同数字的数的个数,再用总数1000减去后就是符合题意“数字组成中最多有两个不同的数字”的个数.【解答】解:根据分析,小于1000的自然数中,有三个不同数字的数有:998648⨯⨯=个, 则最多有两个不同数字的数有:1000648352-=个. 故答案是:352.【点评】本题考查了数的问题,突破点是:先求有三个不同数字的数的个数,用总数减去即可.5.(10分)如图,ABC ∆的面积为100平方厘米,ABD ∆的面积为72平方厘米.M 为CD 边的中点,90MHB ∠=︒,已知20AB =厘米,则MH 的长度为 8.6 厘米.【分析】可以利用面积公式分别求出ABC ∆、ABD ∆的高,而已知20AB =厘米,再利用MH 的中位线性质求出MH 的长度.【解答】解:根据分析,过D ,C 分别作DE AB ⊥交AB 于E ,CF AB ⊥交AB 于F ,如图:ABD ∆的面积11722022DE AB DE ==⨯⨯=⨯⨯,7.2DE ∴=厘米,ABC ∆的面积111002022CF AB CF ==⨯⨯=⨯⨯,10CF ∴=厘米;又11()(7.210)8.622MH DE CF =⨯+=⨯+=厘米.故答案是:8.6.【点评】本题考查了三角形面积,本题突破点是:利用三角形面积公式先求出高,再利用中位线的关系求出MH 的长.6.(10分)一列数1a 、2a ⋯,n a ⋯,记()i S a 为i a 的所有数字之和,如(22)224S =+=,若12017a =,222a =,12()()n n n a S a S a --=+,那么2017a 等于 10 .【分析】首先要分析清楚()i S a 的含义,即i a 是一个自然数,()i S a 表示i a 的数字和,再根据n a 的递推式列出数据并找出规律.【解答】解:()i S a 表示自然数i a 的数字和,又12()()n n n a S a S a --=+,在下表中列出1n =,2,3,4,⋯时的n a 和()n S a ,nn a ()n S a1 2017 102 22 43 145 4 9 9 5 14 56 14 57 10 1 866由上表可以得出:4289a a ==,428()()9S a S a ==;52914a a ==,529()()5S a S a ==;⋯可以得到规律:当4i 时,24i i a a +=,24()()i i S a S a +=, 201732014-=,2014248322÷=⋯,所以:20173222510a a a +===.【点评】本题重点是弄清楚()i S a 的含义,通过地推找到规律,再进行求解.7.(10分)一个两位数,其数字和是它的约数,数字差(较大数减去较小数)也是它的约数,这样的两位数的个数共有 19 个.【分析】首先看所有的10的倍数都是满足条件的,再找出尾数不为0的满足条件的数字即可,数字不多枚举法解决. 【解答】解:枚举法:(1)尾数为0的有:10,20,30,40,50,60,70,80,90. (2)尾数不为0 的有:12,21,24,36,42,45,48,54,63,84. 故答案为:19【点评】本题是考察因数和倍数的关系,同时关键是在枚举过程中按照顺序,可以是数字和也可以是首位数字的大小,问题解决.8.(10分)如图,六边形的六个顶点分别标志为A ,B ,C ,D ,E ,F .开始的时候“华罗庚金杯赛”六个汉字分别位于A ,B ,C ,D ,E ,F 顶点处.将六个汉字在顶点处任意摆放,最终结果是每个顶点处仍各有一个汉字,每个字在开始位置的相邻顶点处,则不同的摆放方法共有 4 种.【分析】显然,只有两种情况,分别讨论,相邻两个字互换,以及顺时针移动一个位值,或逆时针移动一个位值,最后可以求得总的不同的摆放方法. 【解答】解:根据分析,分两类情况:①按顺序移动一个位置,顺时针移动一个位置,有1种不同摆放方法,逆时针移动一个位置,有1种不同摆放方法;②相邻两个位置互换,则共有:2种不同的摆放方法.综上,共有:1124++=种不同摆放方法.故答案是:4.【点评】本题考查排列组合,突破点是:分情况讨论,相邻两个字互换,以及顺时针移动一个位值,或逆时针移动一个位值,最后求和.二、解答下列各题(每小题10分,共40分)9.(10分)平面上有5条不同的直线,这5条直线共形成m个交点,则m有多少个不同的数值?【分析】分情况讨论m的值,有5条直线平行、4条直线平行,三条直线平行,两条直线平行,0条直线平行,五条直线交于一点,四条直线共点,三条直线共点,分别求得m的数值.【解答】解:根据分析,①若5条直线互相平行,则形成的交点为0,故m为0;②若有4条直线互相平行,则交点个数4m=;③若有三条直线互相平行,则5m=,6,7;④若有两条直线互相平行,则5m=,6,7,8,9;⑤若没有直线平行,则1m=,5,6,7,8,9,10.综上,m的可能取值有:0、1、4、5、6、7、8、9、10共9种不同的数值.故答案是:9.【点评】本题考查了组合图形的计数,本题突破点是:分类讨论,确定m的取值的种类.10.(10分)求能被7整除且各位数字均为奇数,各位数字和为2017的最大正整数.【分析】要使整数最大,且每一位数字都是奇数,必须保证整数的位数足够多,且含有尽量多的1;据此分析解答即可.【解答】解:要使整数最大,且每一位数字都是奇数,必须保证整数的位数足够多,且含有尽量多的1.根据能被7整除的数的特征可得,111111是每个数位均为1且能被7整除的最小数. 又有:20176336163357=⨯+=⨯+当有336个111111组成时,因为所有数字之和要是2017,首位数字只能是1,不能被7整除;当有335个111111组成时,前面还需要加上一个正整数,使得它各位数字之和等于7,且这个数最大.满足这个条件的最大整数是13111.说明:我们可以用以下方法,构造一个能被7整除且除了首位数之外,其余数字均为1的数列如下: 21,49021511+=, 7005111211+=, 56005116111+=, 7000611113111+=, 35000611141111+=, 7000041111111111+=, 7000041111111111+=,我们注意到,7000611113111+=是能被7整除且各位数字之和等于7 的最大正整数. 所以,各位数字和为 2017 的最大正整数1311111⋯,其中1的个数是335642014⨯+=,即201311311111⋯个.答:能被7整除且各位数字均为奇数,各位数字和为2017的最大正整数是201311311111⋯个.【点评】本题关键是根据能被7整除的数的特征得到由数字“1”组成的最小数是111111;难点是寻找同时满足数字和是7的最大整数是13111.11.(10分)从1001,1002,1003,1004,1005,1006,1007,1008,1009中任意选出四个数,使它们的和为偶数,则共有多少种不同的选法.【分析】首先分析如果结果是偶数可以分为0,2,4个奇数,把每一种结果加起来即可. 【解答】解:依题意可知:根据四个数的结果是偶数.那么必定是0个奇数,2个奇数或者是4个奇数.在1001,1002,1003,1004,1005,1006,1007,1008,1009奇数的个数为5个,偶数的个数为4个.当0个奇数时有一种情况.当是2个奇数2个偶数时是225460C C=种.当选择4个奇数时有5种.605166++=(种)答:共有66种选择方法.【点评】本题考查对奇偶性的理解和综合运用,同时关键是分类中的排列组合.问题解决.12.(10分)使3251nn++不为最简分数的三位数n之和等于多少.【分析】3251nn++不为最简,表明(51,32)1n n a++=≠,根据辗转相除原理有1|(51)3(32)5a n n≠+⨯-+⨯即1|7a=≠,则a只能等于7,我们可以用51n+尝试来锁定答案,一次尝试可知511n+=或6或11或16或21,因为2137=⨯,所以5121n+=时7|51n+成立,此时n为最小值,且为4,其它值即可顺次找出,只需要将4递加7即可,题中让我们求的是符合条件的三位数,那么最小为102,最大为998,此后利用等差数列求和即可.【解答】解:3251nn++不为最简,表明(51,32)1n n a++=≠,根据辗转相除原理有1|(51)3(32)5a n n≠+⨯-+⨯即1|7a=≠,则a只能等于7,一次尝试可知511n+=或6或11或16或21,因为2137=⨯,所以5121n+=时7|51n+成立,此时n为最小值,且为4,将4递加7即可,符合条件的三位数,那么最小为102,最大为998,102109116998+++⋯+(102998)1292=+⨯÷70950=答:使3251nn++不为最简分数的三位数n之和等于70950.【点评】考查了辗转相除原理,等差数列求和公式,关键是得到符合条件的三位数,最小为102,最大为998.三、解答下列各题(每小题15分,共30分)13.(15分)一个正六边形被剖分成6个小三角形,如图,在这些小三角形的7个顶点处填上7个不同的整数,能否找到一个填法,使得每个小三角形顶点处的3个数都按顺时针方向从小到大排列,如果可以,请给出一种填法;如果不可以,请说明理由.【分析】首先分析最小数字的位置,可以放在圆心出也可以放在外边,两种情况分析即可.【解答】解:依题意可知:分两种情况讨论:假设将最小数放在中心位置,我们只能在外圈顺时针依次从小到达放数字.但是只能满足五个三角形,最后一个三角形无法满足条件.假设将最小的数字放在外圈,然后在周边顺时针依次从小到大放数字,如果想要五个三角形都满足条件,则中心位置必须放大数字,但这样的话,最后一个又不能满足条件.综上所述:不能找到一个填法,使得每个小三角形顶点处的3个数都按顺时针方向从小到大排列.【点评】本题是对凑数谜的理解和运用,关键问题是找最小数字的位置.问题解决.14.(15分)77⨯的方格黑白染色,如果黑格比白格少的列的个数为m,黑格比白格多的+的最大值.行的个数为n,求m n+的值最大.【分析】在m取最大值的条件下n尽量取最大值可使m n【解答】解:根据分析,1黑格和白格的行数7;1列数7,当7⨯=.然后,可以把21个m=时,可以设7列之中黑格个数为3,则黑格总数为:3721黑格在15-行之中每行放4个,第6行放1个,第7行不放.这样就有5行中黑格数量超过白格,所以5+=为最大.如下图1所示:m nn=,从而使得12当6m =时,可以设6列之中黑格个数均为3,其余一列黑格个数为7,这样黑格总数为36725⨯+=.然后,我们使得16-行黑格个数为4个,最后一行只有1个.这样就有6行中黑格数列超过白格,所以6n =,从而使得12m n +=,如图2所示:当5m 时,12m n +.综上,m n +的最大值为12.故答案是:12.【点评】本题考查了最大与最小,本题突破点是:在行数和列数的最小与最大的范围内,确定最大值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、建议参赛选手监护人为学生投保商业意外伤害保险,如发生意外由保险公司承担相应赔偿,其他单位不承担赔偿责任。
监护人签字:
日期:
2017全国中小学数独比赛北京赛区选拔赛
2017北京中小学数独比赛报名表(个人用)
就读学校:
学校地址:区县:
序号
学生姓名
性别
年级
组别
身份证号
监护人姓名
监护人手机
填报人:□教师姓名:手机:
□监护人姓名:手机:
提示:个人报名选手由学生监护人签字后,在学而思培优服务中心提交。
安全责任
1、参赛者需身体健康,不得患有包括但不限于心肌炎等,具有重大安全隐患的器质性疾病;能够有自我管控能力,服从赛事组织,安全参赛。
组别(勾选)
团体
序号
学生姓名
性别
年级
身份证号
联系方式
□新人组
□小学乙组
□小学甲组
□中学组
A队
1
2
3
4
B队
1
2
3
4
组别(勾选)
团体
序号
学生姓名
性别
Байду номын сангаас年级
身份证号
联系方式
□新人组
□小学乙组
□小学甲组
□中学组
A队
1
2
3
4
B队
1
2
3
4
组别(勾选)
团体
序号
学生姓名
性别
年级
身份证号
联系方式
□新人组
□小学乙组
□小学甲组
2017全国中小学数独比赛北京赛区选拔赛
2017北京中小学数独比赛报名表(学校用)
学校全称(盖章):
学校地址:区县:
职务
姓名
性别
手机
邮箱
微信号
项目负责
现场领队
教练
教练
团体赛报名表(每校各组别限报两队,每队限4名学生,可以报多组别,赛前可更换选手。)
选报组别参考:新人组(1年级)小学乙组(2-4年级)小学甲组(5-6年级)中学组
□中学组
A队
1
2
3
4
B队
1
2
3
4
个人赛报名表(个人赛名额不限,表格可以复制后使用,同时报名团体赛和个人赛的学生需两个表格都填写。个人赛初赛入围决赛后将通知学校或家长。)
序号
姓名
性别
年级
组别
身份证号
监护人姓名
监护人手机
提示:纸质报名表由学校领队加盖学校公章后,在领队会上统一提交;个人报名选手由学生监护人签字后,在学而思培优服务中心提交。
安全责任
1、参赛者需身体健康,不得患有包括但不限于心肌炎等,具有重大安全隐患的器质性疾病;能够有自我管控能力,服从赛事组织,安全参赛。
2、学生监护人及参赛单位需认真做好参赛学生健康检查,加强安全教育,制定安全预案,落实安全管理,履行安全职责,确保参赛选手安全。
3、建议参赛选手监护人为学生投保商业意外伤害保险,如发生意外由保险公司承担相应赔偿,其他单位不承担赔偿责任。
