频域分析及典型环节bode图第10讲
合集下载
绘制伯德图
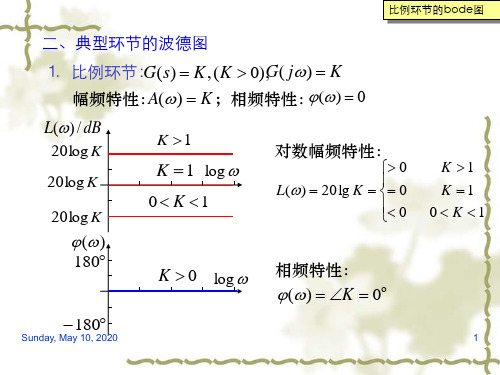
幅频和相频特性为:
A( ) (1 T 2 2 )2 (2 T )2, ( ) tg 1
1 T 1 ,o ,称为转折频率或交换频率。 T
Monday, March 09, 2015
可以用这两段渐近线近似的表示惯性环节的对数幅频特性。
3
惯性环节的Bode图
10 渐近线 0 -10 -20 0° -45° -90° 1 20T
20dB / Dec
图中,红、绿线分别是低频、高频渐近线,蓝线是实际曲线。
T
( )
2.0
-63.4
3.0
-71.5
4.0
-76
5.0
-78.7
7.0
-81.9
10
-84.3
20
-87.1
50
-88.9
100
-89.4
1 1 当 0时, (0) 0;当 时, ( ) ;当 时, () 。 T T 4 2 由图不难看出相频特性曲线在半对数坐标系中对于(0, -45°) 点是斜对称的,这是对数相频特性的一个特点。
当时间常数T 变化时,对数幅频特性和对数相频特性的形状 都不变,仅仅是根据转折频率1/T 的大小整条曲线向左或向 右平移即可。而当增益改变时,相频特性不变,幅频特性上 下平移。
Monday, March 09, 2015 6
振荡环节的频率特性
K Kn 2 ⒋ 振荡环节的频率特性: G( s) 2 2 T s 2Ts 1 s 2 n s n 2
0 L( ) 20 lg K 0 0
K 1 K 1 0 K 1
( )
180
K 0
log
BODE图的讲解

§5.6 利用开环频率特性分析系统的性能
§5.7 利用闭环频率特性分析系统的性能
共二十三页
§5.3
对数(duì shù)频率特性 ( Bode )
Bode图介绍
(jièshào)
共二十三页
§5.3
对数(duì shù)频率特性 ( Bode)(2)
Bode图介绍(jièshào)
横轴 按 lg 刻度,dec “十倍频程”
绘制开环系统(xìtǒng)Bode图的 步骤
⑴ 化G(j)为尾1标准型
⑵ 顺序列出转折频率
例1
G(s)
s(
40(s 0.5) 0.2)( s2 s 1)
100( s 1)
G(s)
0.5
s( s 1)(s2 s 1)
0.2
0.2 惯性环节
0.5 一阶复合微分
1 振荡环节
⑶ 确定低频特性
例1 根据(gēnjù)Bode图确定系统传递函数。
解. 依图有 G(s) K
Ts 1
30
20lg K 30 K 1020 31.6
转折频率 2 1 T T 0.5
G(s)
3.16 s 1
2
• Bode图与Nyquist图之间的对应(duìyìng)
关系: • 截止频率c:G( jc ) 1
最小转折频率之左 的特性或其延长线
基准点 ( 1, L(1) 20lg K ) 斜率 20 v dB dec
⑷ 叠加作图
一阶
二阶
惯性环节 -20dB/dec
复合微分 +20dB/dec
振荡环节 -40dB/dec
复合微分 +40dB/dec
共二十三页
0.2 惯性环节 -20
§5.7 利用闭环频率特性分析系统的性能
共二十三页
§5.3
对数(duì shù)频率特性 ( Bode )
Bode图介绍
(jièshào)
共二十三页
§5.3
对数(duì shù)频率特性 ( Bode)(2)
Bode图介绍(jièshào)
横轴 按 lg 刻度,dec “十倍频程”
绘制开环系统(xìtǒng)Bode图的 步骤
⑴ 化G(j)为尾1标准型
⑵ 顺序列出转折频率
例1
G(s)
s(
40(s 0.5) 0.2)( s2 s 1)
100( s 1)
G(s)
0.5
s( s 1)(s2 s 1)
0.2
0.2 惯性环节
0.5 一阶复合微分
1 振荡环节
⑶ 确定低频特性
例1 根据(gēnjù)Bode图确定系统传递函数。
解. 依图有 G(s) K
Ts 1
30
20lg K 30 K 1020 31.6
转折频率 2 1 T T 0.5
G(s)
3.16 s 1
2
• Bode图与Nyquist图之间的对应(duìyìng)
关系: • 截止频率c:G( jc ) 1
最小转折频率之左 的特性或其延长线
基准点 ( 1, L(1) 20lg K ) 斜率 20 v dB dec
⑷ 叠加作图
一阶
二阶
惯性环节 -20dB/dec
复合微分 +20dB/dec
振荡环节 -40dB/dec
复合微分 +40dB/dec
共二十三页
0.2 惯性环节 -20
《典型环节伯德图》课件

Maya:一汇报人:
稳定性分析
稳定性定义:系统 在受到扰动后能够 恢复到其原始状态 的能力
稳定性分类:稳定、 不稳定、临界稳定
稳定性分析方法: 伯德图分析、奈奎 斯特图分析、根轨 迹分析等
伯德图分析:通过绘制 伯德图,观察系统在不 同频率下的增益和相位 变化,判断系统的稳定 性。
动态性能分析
伯德图:描述系统动态性能的图形工具 频率响应:系统对不同频率信号的响应 相位裕度:系统稳定性的指标 增益裕度:系统放大能力的指标 动态性能分析方法:如根轨迹法、频率响应法等
MATLAB还提供了丰富的函数库,可以方便地进行各种数学计算和仿真。
Simulink软件介绍
软件名称: Simulink
开发商: MathWorks
公司
软件功能:用 于建模、仿真 和分析动态系
统
应用领域:广 泛应用于控制 工程、信号处 理、通信等领
域
软件特点:图 形化界面,易 于操作,支持 多种编程语言
软件版本:最 新版本为 Simulink 2022a
其他绘制软件介绍
AutoCAD:一款专业的CAD软件,可以绘制 各种类型的伯德图
SolidWorks:一款三维设计软件,可以绘制 伯德图
Inventor:一款三维设计软件,可以绘制伯 德图
SketchUp:一款三维设计软件,可以绘制伯 德图
Blender:一款三维设计软件,可以绘制伯德 图
幅频特性的分析
幅频特性的定义:描述信号在频率域上的分布特性 幅频特性的表示方法:通常采用伯德图或奈奎斯特图 幅频特性的应用:用于分析信号的频率响应、滤波器设计等 幅频特性的测量方法:通过频谱分析仪或示波器等仪器进行测量
相频特性的分析
相频特性的定义:描述信号频率与相位之间的关系 相频特性的表示方法:通常用相频特性曲线表示 相频特性的应用:在信号处理、通信等领域有广泛应用 相频特性的测量方法:通过实验或仿真进行测量
稳定性分析
稳定性定义:系统 在受到扰动后能够 恢复到其原始状态 的能力
稳定性分类:稳定、 不稳定、临界稳定
稳定性分析方法: 伯德图分析、奈奎 斯特图分析、根轨 迹分析等
伯德图分析:通过绘制 伯德图,观察系统在不 同频率下的增益和相位 变化,判断系统的稳定 性。
动态性能分析
伯德图:描述系统动态性能的图形工具 频率响应:系统对不同频率信号的响应 相位裕度:系统稳定性的指标 增益裕度:系统放大能力的指标 动态性能分析方法:如根轨迹法、频率响应法等
MATLAB还提供了丰富的函数库,可以方便地进行各种数学计算和仿真。
Simulink软件介绍
软件名称: Simulink
开发商: MathWorks
公司
软件功能:用 于建模、仿真 和分析动态系
统
应用领域:广 泛应用于控制 工程、信号处 理、通信等领
域
软件特点:图 形化界面,易 于操作,支持 多种编程语言
软件版本:最 新版本为 Simulink 2022a
其他绘制软件介绍
AutoCAD:一款专业的CAD软件,可以绘制 各种类型的伯德图
SolidWorks:一款三维设计软件,可以绘制 伯德图
Inventor:一款三维设计软件,可以绘制伯 德图
SketchUp:一款三维设计软件,可以绘制伯 德图
Blender:一款三维设计软件,可以绘制伯德 图
幅频特性的分析
幅频特性的定义:描述信号在频率域上的分布特性 幅频特性的表示方法:通常采用伯德图或奈奎斯特图 幅频特性的应用:用于分析信号的频率响应、滤波器设计等 幅频特性的测量方法:通过频谱分析仪或示波器等仪器进行测量
相频特性的分析
相频特性的定义:描述信号频率与相位之间的关系 相频特性的表示方法:通常用相频特性曲线表示 相频特性的应用:在信号处理、通信等领域有广泛应用 相频特性的测量方法:通过实验或仿真进行测量
典型环节的频率特性
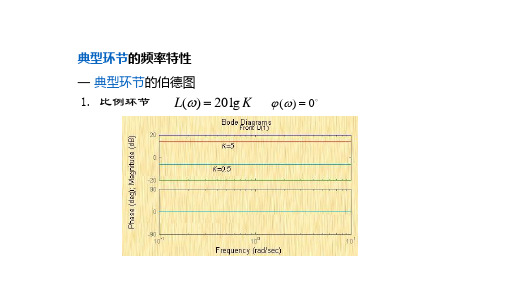
G( j)
1
2
1
j2
2 n
n
n
1 Tn
1 L() 20lg1 0
n
1 L() 20 lg( )2 40 lg
n
n
n
两条渐近线相交于=n,称n为二阶振荡环节的转折频率。
精确幅频特性曲线的形状及其渐近线的误差均与值有关。当值在 某范围时,幅频特性曲线存在峰值,且值越小,对数幅频曲线的 峰值就越大,它与渐近线之间的误差也就越大。
2
1
1 2
0 0.707 系统存在峰值。
0.707 系统不存在峰值
20 18 16 14 12 10
8 6 4 2 0
0 0.2 0.4 0.6 0.8 1
5.时滞环节
0
-100
G( j) ej 1
-200
-300
()
-400
-500
-600
-1
0
1
10
10
10
二 典型环节的奈氏图(极坐标图)
与一阶惯性环节频率特性
30
相反。
0
10-1
100
101
3. 积分、微分环节
L() 20 lg () 90
20
0
-20
-1
0
1
10
10
10
0
-90
-180
-1
0
1
10
10
10
L() 20 lg () 90
20
0
-20
-1
0
1
10
10
10
180
90
0
-1
0
1
10
控制系统的频域分析法

频率特性又称频率响应,是系统(或元件)对不同频率正弦输入信号的响 应特性。
若在如图5.1 所示的线性系统结构的输入端加上图5.2(a)的正弦信号,
设该正弦信号为
r(t) Asint
则其输出响应为
c(t) MAsin(t )
即振幅增加了M倍,相位超前(滞后)了 角。响应曲线如图5.2(b)所
示。
图5.1 系统的结构图
第五章 控制系统的频域分析法
5.1 频率特性的概念
5.1.1 频率特性的基本概念
对于线性定常系统,也可定义系统的稳态输出量与输入量的幅值
之比为幅频特性:定义输出量与输入量的相位差为相频特性。即
幅值频率特性:
A() | G( j) |
相位频率特性:
() G( j)
将幅值频率特性和相位频率特性两者写在一起,可得频率特性或
令s j ,则频率特性为
G(s) 1 Ts 1
G( j) 1 1 j T jT 1 1 (T )2 1 (T )2
幅值频率特性为
A() | G( j) | 1 1 (T )2
相位频率特性为
() G( j) arctanT
第五章 控制系统的频域分析法
5.1 频率特性的概念
5.1.3 频率特性的性质
由此可以看出,振荡环节的频率特性,不仅与 有关,而且还与阻尼比
有关。同惯性环节一样,振荡环节的对数幅频特性也可采用近似的方法绘 制。同样,振荡环节的对数相频特性曲线也可采用近似的作图方法。
第五章 控制系统的频域分析法
5.2 典型环节的伯德图
5.2.6 振荡环节
不同参考值时振荡环节的伯德图如图5.16所示。
幅相频率特性为:
G( j) A()e j() | G( j) |ge jG( j)
如何绘制伯德图.ppt

j?
??
其幅频特性为
1
G ( j? ) ? ?
对数幅频特性是
(5-65) (5-66)
1
20 lg G ( j? ) ? 20 lg ? ? 20 lg ? ?
(5-67)
当 ? ? 0 . 1 时,20 lg G ( j 0 . 1 ) ? ? 20 lg 0 . 1 ? 20 ( dB ) ; 当 ? ? 1 时,20 lg G ( j1) ? ? 20 lg 1 ? 0 ( dB ) ;
当 ? ? 10 时,20 lg G ( j10 ) ? ? 20 lg 10 ? ? 20 ( dB ) 。
6
设 ? ' ? 10 ? ,则有
? 20 lg ? ' ? ? 20 lg 10 ? ? ? 20 ? 20 lg ?
可见,其对数幅频特性是一条 在
dB L(? )
60
(5-68)
ω =1(弧度/秒)处穿过零分贝线
(5-73) (5-74)
? ? 20 lg 1 ? T 2? 2
当 ? ?? 1 时, 20 lg G ( j ? ) ? ? 20 lg 1 ? T 2 ? 2 ? 0 ( dB ) ,
T
当 ? ?? 1 时,20 lg G ( j ? ) ? ? 20 lg 1 ? T 2 ? 2 ? ? 20 lg T ? ( dB )
40
(ω 轴),且以每增加十倍频降
20
? 20 dB / dec
低20分贝的速度( -20dB/dec )
0
0.01
0.1
1
10
?
变化的直线。
? 20
积分环节的相频特性是
? G ( j ? ) ? ? 90 0
频域分析及典型环节bode图第10讲

结论
Ar=1 ω=0.5
2013-12
给稳定的系统输入一个正弦,其稳态输出是与输入 同频率的正弦,幅值随ω而变,相角也是ω的函数。
ω=1
ω=2
ω=2.5
ω=4
9
相角问题
AA ① 稳态输出 迟后于输入的 角度为: B φ= 360o A ②该角度与ω有 关系 , ∴为φ(ω) ③该角度与初始 角度无关 , ∴ …
十倍频程 十倍频程 十倍频程
10 20 30 100
十倍频程
1
0.1
0.2 0.3
2
3
ω(rad/s)
2013-12 25
返回
5.1.2 频率特性的表示方法
倒置的坐标系
2013-12
26
返回
5.1.2 频率特性的表示方法
◆极坐标图(Polar plot),也叫幅相频率特性曲线,其曲线 G ( j ) 可用幅值 G( j) 和相角 ( ) 的向量表示。
p1 , p2 , pn
对稳定系统
n
G(s) 的极点
(5-1)
bi a a C ( s) s j s j i 1 s pi
(5-2)
14
2013-12
5.1
频率特性的概念
a, a 和bi (i 1,2,n)
bi a a (5-2) C ( s) s j s j i 1 s pi
11
5.1
频率特性的概念
2013-12
12
红 —输 入 , 蓝 —全 响 应 , 黑 —稳 态 响 应 6 yss(t)
4
2
u(t ) 2 cos(5t 30)
Sinresponse2order.m
自动控制原理:第六章频域分析法——伯特图及稳定性分析

• 当阻尼系数接近1时,振荡环节具有低通滤波的作用; • 而随着减小,=n=1/T处的幅值迅速增大,表明其对输
入信号中该频率附近分量的放大作用逐渐加强,此时,振
荡环节具有选频作用。
6.4 系统开环频率特性-典型环节的伯德图
40
Bode Diagram
二阶微分环节:
30
20
转折频率 渐近线
L() /(dB)
10 /T
1) 将乘除运算转化为加减运算,因而可通过简单的图像叠加 快速绘制高阶系统的伯德图 ;如 G( j) A1()e j1() A2 ()e , j2 () 则20lgA1()A2()=20lgA1()+20lgA2()
2) 伯德图还可通过实验方法绘制,经分段直线近似整理后, 很容易得到实验对象的频率特性表达式或传递函数.
i 1
i m1 1
v n1
v n1 nv n1 2
( jTl 1)
(1 Tl2 2 2 j lTl )
l v 1
l v n1 1
(6 - 17)
其 中 ,K ,0 i 1,0 l 1, i 0,Tl 0都 为 常 数 。
除此外,也存在某个Tl<0,开环不稳定,但闭环可能仍然 稳定的情况。
1
A(ω)
1 ωT 2 2 2ζωT 2
L() /(dB)
10
0
-10 -20
(1 T 22
j2T)1
0.05 0.1 0.3
-30
0.7
1 -40
180
转折频率 渐近线
135
(ω)
arctan
1
2ζωT
ωT
2
90 45
0
() /()
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p1 , p2 , pn
对稳定系统
n
G(s) 的极点
(5-1)
bi a a C ( s) s j s j i 1 s pi
(5-2)
14
2013-12
5.1
频率特性的概念
a, a 和bi (i 1,2,n)
bi a a (5-2) C ( s) s j s j i 1 s pi
10
B B
2013-12
5.1
设系统结构如图,
频率特性的概念
不 40
由劳斯判据知系统稳定。
给系统输入一个幅值不变频率不断增大的正弦, 曲线如下:
结论:
Ar=1 ω=0.5
2013-12
给稳定的系统输入一个正弦,其稳态输出是与输入
同频率的正弦,幅值随ω而变,相角也是ω的函数。
ω=1
ω=2
Hale Waihona Puke ω=2.5ω=4特点
当输入信号的频率 0 ~ 变化时,向量 G ( j ) 的幅值和相位也随之作相应的变化,其端点在复平面上移 动的轨迹称为极坐标图,奈奎斯特曲线,简称奈氏图 。
奈奎斯特(N.Nyquist)在1932年基于极坐标图阐述了反馈系统的 稳定性 ◆对数幅相图:将构成 G( j) 和 G( j ) 绘制于一图中, 横坐标为 G( j ) 纵坐标为 G( j) ,均为均匀分度。
第5章 线性系统的频域分析法 Frequency-response analysis
本章重点
1.开环频率特性的绘制(包括极坐标图和对数坐标图);
2. 乃奎斯特稳定性判据及其在Bode图中的应用;
3. 对数频率特性和闭环系统性能的关系;
4. 开环频率特性指标;
5. 闭环频率特性指标。
2013-12 3
-1.5 -2
-4 -5
0
0.5
1
1.5
2
2.5
3
0
0.5
1
1.5
2
2.5
3
特点:输出的振幅和相位一般均不同于输入量, 且随着输入信号频率的变化而变化,但在 t 时,输出仍为同频率的正弦函数。 2013-12
8
5.1 频率特性的概念
不
设系统结构如图, 由劳斯判据知系统稳定。
40 40
给系统输入一个幅值不变频率不断增大的正弦, 曲线如下:
5.1
频率特性的概念
输出与输入的相位之差
2013-12
(b)相频特性
20
U o ( s) U o ( j ) 1 1 1 G( s) G( j ) 比较 U i ( s) 1 RCs U i ( j ) 1 RCj 1 Tj
频率特性与传递函数具有十分相的形式,关系为 G ( j ) G ( s ) s j
已知输入 r (t ) A sin(t )
其拉氏变换 R( s )
A s2 2
A为常量,则系统输出为
U ( s) A U ( s) A C ( s ) G ( s ) R( s ) ( s p1 )(s p2 ) ( s pn ) s 2 2 V ( s) s 2 2
数学模型 领域 时域 t 复频域 S 复频域 S 频域 f
常微分方程
线性定常系统
传递函数 方框图 频率特性函数
2013-12
5
第5章 线性系统的频域分析法 Frequency-response analysis 特点
1.频率特性具有明确的物理意义,它可以用实验的 方法来确定,这对于难以列写微分方程式的元部件或 系统来说,具有重要的实际意义。 2.由于频域分析法主要通过开环频率特性的图形对 闭环系统进行分析,因而具有形象直观和计算量少的 特点,即图解分析法。
第10讲
杨湖
线性系统的频域分析法 典型环节的伯特图、极坐标图
2013-12 1
第5章 线性系统的频域分析法 Frequency-response analysis
应用频率特性研究线性系统的经典方法称为频域分析法。
频域分析法
频率特性及其表示法 典型环节的频率特性
稳定裕度和判据
频率特性指标
2013-12 2
c(t ) ae
jt
A j ( ) jt A a e A( )e e A( )e e 2j 2j A( ) A sin(t ( ))
jt j ( ) jt
说明 线性系统的稳态输出是和输入具有相同频率的正弦信号,
其输出与输入的幅值比为 输出与输入的相位差
u(t ) 2 cos(20t 30)
Sinresponse2orderb.m
2013-12
0 -0.5 -1 -1.5 -2
y(t) u(t) 0 1 2 3 t/s 4 5
13
6
5.1
设系统的传递函数为
频率特性的概念
C ( s) U ( s) G( s) R( s ) V ( s)
11
5.1
频率特性的概念
2013-12
12
红 —输 入 , 蓝 —全 响 应 , 黑 —稳 态 响 应 6 yss(t)
4
2
u(t ) 2 cos(5t 30)
Sinresponse2order.m
u(t)
幅值
0
-2
-4
-6 y(t) -8 0 1 2 3 t/s 4 5
红 —输 入 , 蓝 —全 响 应 , 黑 —稳 态 响 应 2 1.5 6 1 0.5 幅值 yss(t)
U o ( j ) 1 1 (5-15) G( j ) U i ( j ) 1 RCj 1 Tj
G( j ) 1 1 T 2 2
G( j ) G( j ) e j ( )
( ) arctgT
2013-12
式中
T RC
17
5.1
2013-12 27
5.2典型环节频率特性及曲线的绘制
5.2.1 比例环节 G(s)=K
G ( j )
=K
L( ) 20log K
( ) 0
幅频特性和相频特性曲线 请看下页
2013-12
28
5.2典型环节频率特性及曲线的绘制
比例环节的Bode图
L(ω)/dB
0dB
20lgK
ω
频率特性的概念
G ( j ) 称为电路的频率特性。
它由该电路的结构和参数决定,与输入信号的幅值与相位无关。
G( j) 是 G ( j ) 的幅值
它表示在稳态时,电路的输出与输入的幅值之比。 ( ) 是 G ( j ) 的相角
它表示在稳态时,输出信号与输入信号的相位差。
由于 G( j) 和 ( ) 都是输入信号频率
6.数学基础是傅立叶变换。
2013-12
5.1频率特性的概念及其表示法 5.1.1 频率特性的基本概念
频率特性又称频率响应,指在正弦信号作用下输出的稳态响应; 它是系统(或元件)对不同频率正弦输入信号的响应特性。
2 1.5 1
2 5 4 3
0.5 0 -0.5 -1
线性系统
1 0 -1 -2 -3
p
j p
p
传递 函数
s
微分 方程
d dt
系统
频率 特性
s j
2013-12
三种模型间的关系,请同学们理解记忆
21
5.1.2 频率特性的表示方法 (1)对数坐标图 (Bode diagram or logarithmic plot) (Polar plot) (Log-magnitude versus phase plot)
(2)极坐标图 (3)对数幅相图
(1)Bode图或伯德图或对数频率特性图 (2)Nyquist图或奈奎斯特图 (3)Nichols图或尼柯尔斯图
2013-12 22
5.1.2 频率特性的表示方法
◆对数频 对数幅频特性 20log G( j) dB G( j ) () 率特性图 相频特性
L( )
结论
Ar=1 ω=0.5
2013-12
给稳定的系统输入一个正弦,其稳态输出是与输入 同频率的正弦,幅值随ω而变,相角也是ω的函数。
ω=1
ω=2
ω=2.5
ω=4
9
相角问题
AA ① 稳态输出 迟后于输入的 角度为: B φ= 360o A ②该角度与ω有 关系 , ∴为φ(ω) ③该角度与初始 角度无关 , ∴ …
第5章 线性系统的频域分析法 Frequency-response analysis
本章难点
• 开环频率特性的绘制;
• 乃奎斯特判据的原理及其应用;
• 剪切频率及相角、幅值裕度的求取;
• 二阶系统频率特性指标和时域指标的换算;
• 典型二型系统频、时域指标的定性关系。
2013-12 4
第5章 线性系统的频域分析法 Frequency-response analysis
待定系数
n
c(t ) ae
a G( s)
jt
ae
jt
bi e pit
i 1
n
t 趋向于零 (5-4)
A A A ( s j ) G ( j ) ( s j ) G ( j ) s j s j ( s j )(s j ) 2j s2 2
φ(ω)
ω
0°
2013-12
29
返回
20log(K) 20
10
0
(dB) Ö±´ ·
-10
-20
-30
-40 -2 10
