多点地质统计学_理论_应用与展望 (1)
PPT
汇报提纲
研究现状 目标与内容 过程论述 结论
研究现状
多点地质统计学是目前储层地质随机建模的研 究热点方向。相对于传统的两点地质统计学方 法，多点地质统计学在进行储层地质建模时能 够利用更多空间点数据（n>2）之间的相关性 进行统计计算，因此建立的模型更加满足实际 的情况。 多点地质统计学算法snesim是其中一种基于 概率统计的方法，由于snesim算法的参数设 置较为复杂，因此该算法的各种参数对模型的 控制需要进行研究和分析，从而指导如何使用 该算法建立高质量的储层模型。
硬数据条件化
向网格中加载硬数据：
硬数据条件化模拟结果：
非平稳模拟
旋转角控制河道局部的方向 仿射性控制河道宽度
手绘旋转与仿射性图像：
1.3
0.8 0.5 15°
75°
45°
格式转换：
参数文件复制：
参数设置：
运行得到实现：
涠洲11-2油田4井区岩相模拟
研究区属于辫状河三角洲前缘亚相,微相种类较多,面积较大，但 是钻井较少且分布集中,为了减少没有井控制的地方模拟的不确 定性,本次采用录井解释的砂泥岩相进行岩相模拟，相的种类减 少，有助于减少模拟的不确定性.
利用不同油组的平面沉积微相图作为训练图像：
序贯指示法模拟结果：
snesim算法模拟结果：
用多点法模拟的岩相展布图较为连续且具有一定的真实性
结论
设置不同参数对程序的影响： 目标比例能有效控制模拟结果相比例 目标相比例的设置应与训练图像边际 概率相近，否则要考虑更换训练图像 旋转角控制河道局部的方向，仿射性 控制河道宽度 用多点法模拟的岩相展布图较为连续 且具有一定的真实性
地质统计学简介及其应用
基本理论介绍：
变差函数分析实际是确定数据在方向和距离两方面的变化率
头
尾
滞后距(Lag)
散 点 图
半变差函数
半变差函数图的构成
变差函数图中各部分的名称
基台
变程
跃迁
变差函数图 的构图机理
关 系
变差函数图
半变差函数
H-散点图
二 维 变 差 函 数 模 型
主轴变差图
附轴变差图
三 维 变 差 函 数 模 型
权系数的确定
普通克里金
普遍采用于成图的算法；
远离数据点的值是寻找范围内的数据点的平均值。
3、非稳态克里金 (Nostationary Kriging)
非稳态克里金
比较灵活的克里金算法，因为可以设置网格点的值； 网格点的平均值来自于大范围的数据，而成图区只是一部分。
4、内在趋势克里金
(Universal Kriging)
且统计数据要达到一定的数量。
主要优点是：考虑了数据场的方向性。 其核心是：寻找到相邻数据点对所求点的权。
二、克里金算法介绍
常 用 的 几 种 克 里 金 算 法
1、简单克里金
2、普通克里金 3、非稳态克里金 4、内在趋势克里金
（泛克里金）
（Simple Kriging)
(Ordinary Kriging) (Nostationary Kriging) (Universal Kriging)
组成变差函数模型的结构类型
ห้องสมุดไป่ตู้
球型
高斯
跃 迁
指数
幂函数
变差模型结构
半 变 差 函 数
滞后距
四、一个应用实例
---应用三维属性数据建立砂体模型
多点地质统计学原理、方法及应用__概述及解释说明
多点地质统计学原理、方法及应用概述及解释说明1. 引言1.1 概述本文旨在探讨多点地质统计学的原理、方法及应用，为读者提供一个全面了解该领域的概述。
多点地质统计学是一门研究如何有效地利用多变量数值以及空间数据进行地质分析和预测的学科。
它通过综合多种数据，包括物理测量数据、遥感图像数据和野外调查数据等，来实现对不同地质现象和过程的建模与研究。
1.2 文章结构本文按照以下结构组织内容：首先介绍多点地质统计学的基本原理，包括其定义与概念、基本假设以及原理解释。
随后，针对多点地质统计学的方法进行详细阐述，探讨数据收集与预处理、变量选择和缺失值处理以及统计模型拟合与优化算法应用等关键步骤。
接下来，我们将通过具体案例研究来展示多点地质统计学在矿产资源评估与勘探、地下水资源管理与保护以及石油勘探与开发中的应用实践。
最后，在结论部分对全文进行概括总结，并展望未来多点地质统计学研究的发展方向。
1.3 目的本文旨在全面介绍多点地质统计学的原理、方法及应用，以帮助读者对该领域有一个清晰的认识。
通过阐述基本原理和方法，读者可以了解多点地质统计学在地质分析和预测中的重要性。
此外，通过具体案例的引入，读者将能够更好地理解多点地质统计学在实际问题中的应用价值和潜力。
最后，通过对未来研究方向的展望，读者可以获得一些启示，并为自己在该领域开展研究提供参考。
2. 多点地质统计学原理2.1 定义与概念多点地质统计学是一种广泛应用于地质科学领域的统计学方法。
它通过对多个地点上的地质数据进行收集、分析和解释，旨在揭示地下资源的分布规律和空间变异性。
多点地质统计学基于一系列假设和方法，能够提供可靠的预测结果和决策依据。
2.2 基本假设在多点地质统计学中，存在几个基本假设：- 空间自相关假设：相邻位置上的地质现象存在关联性，即一个位置的观测值可能受到相邻位置观测值的影响。
- 空间平稳假设：在整个研究区域内，不同位置上的地质变量具有类似的变异性。
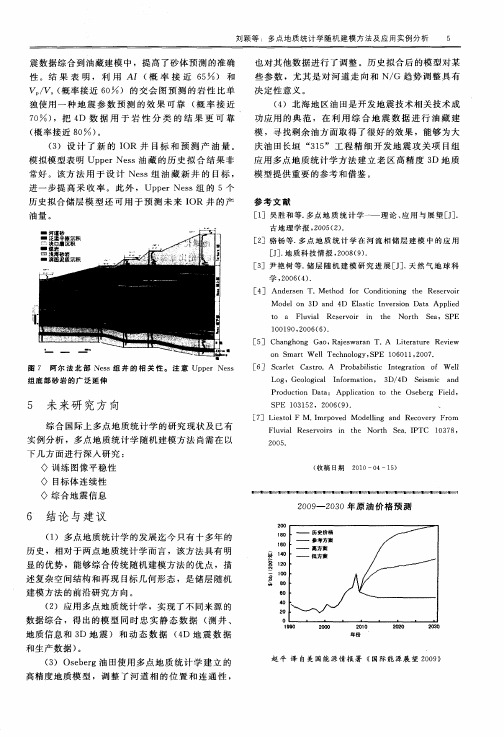
2009--2030年原油价格预测
［ ］ Ｃ ａ ｇ ｏ ｇ Ｇ ｏ Ｒ ｊｓ ｒｎ Ｔ Ａ Ｌ ｔｒ ｔｒ ｅ ｉ ５ ｈ ｎ ｈ ｎ ａ ， ａｅｗａａ ． ｉ ａｕ ｅ Ｒ ｖｅ ｅ ｗ
模 型提供 重要 的参考 和借 鉴 。
参 考 文 献
Ｉ ］ 吴 胜 和 等 ． 点 地 质 统 计 学— — 理 论 、 用 与 展 望 Ｉ］ － １ 多 应 － ． Ｊ 古地 理学 报 ，０ ５ ２ ． ２０ （） ［ ］骆 杨 等． 点 地 质 统 计 学 在 河 流 相 储 层 建 模 中 的 应 用 ２ 多 ［］ 地 质 科 技 情 报 ，０ ８ ９． Ｊ． ２ ０ （） ［］ 尹 艳 树 等 ． 层 随 机 建 模 研 究 进 展 ［ ］ 天 然 气 地 球 科 ３ 储 Ｊ．
油量 。
（ ）北 海地 区油 田是开 发地震 技术相关 技术 成 ４ 功应用 的典 范 ，在 利 用 综 合 地 震 数 据 进 行 油 藏 建 模 ，寻找剩余 油方 面取得 了很好 的效 果 ，能 够为 大 庆油 田长垣 “ １ ”工 程 精 细 开发 地 震攻 关 项 目组 ３５
应 用多点 地质 统计学 方法 建 立老 区高精 度 ３ Ｄ地 质
赵 平 译 自美 国能 源 情 报 署 《 国际 能 源展 望 ２ ０ 》 ０ ９
Ｌｏ ｇ，Ｇｅ ｌｇｃ ｌ Ｉ ｆｒ ａｉｎ， ３ ４ Ｓ ｉｍｉ ａ ｄ ｏｏ ｉａ ｎｏ ｍ ｔ Ｄ／ Ｄ ｏ ｅｓ ｃ ｎ
Ｐｒ ｄｕｃ ｉｎ ｏ ｔｏ Ｄａ ａ： Ａ ｐ ｉａ ｉ ｎ ｏ ｈｅ ｔ ｐｌｃ ｔｏ ｔ ｔ Ｏ ｓ ｂｅ ｇ ｅ ｒ Ｆｉｌ ｅｄ，
地质统计学在地质及矿业中的应用及发展
地质统计学在地质及矿业中的应用及发展【摘要】地质统计学是一门重要的地质学分支，通过对地质数据的分析和解释，可以帮助我们更好地认识地质现象和地质资源。
在地质学中，地质统计学可以用于地质勘探、矿产资源评价、矿床预测和地质灾害预测等方面。
在矿业领域，地质统计学的应用也非常广泛，可以帮助矿业公司提高勘探效率和资源利用率。
地质统计学在实践中也存在一些局限性，比如样本数量不足或数据质量不高等问题。
未来，随着技术的不断发展和完善，地质统计学在地质及矿业中的应用将会更加广泛，为地质矿产领域的发展提供更多可能性。
地质统计学在地质及矿业中的重要性不可忽视，需要不断加强研究和实践。
【关键词】地质统计学、地质勘探、矿产资源评价、矿床预测、地质灾害预测、资源勘查、发展方向、局限性、重要性。
1. 引言1.1 地质统计学的概念地质统计学，是统计学与地质学相结合的一门交叉学科，主要研究地质现象的空间变异性及其规律性。
地质统计学通过对地质数据进行统计分析，揭示地质现象之间的关联性和规律性，从而为地质学和矿业提供科学依据。
地质统计学的方法包括样本普查、空间插值、随机模拟等。
这些方法可以帮助地质学家和矿业工作者更好地分析和解释地质数据，发现地下资源的分布规律，预测地质灾害的发生可能性，优化资源勘查的方案等。
地质统计学是一门在地质学和矿业中具有重要意义的学科，在研究地质现象的空间变异性和规律性方面发挥着至关重要的作用。
随着技术的发展和方法的进步，地质统计学将在地质及矿业领域发挥越来越重要的作用。
1.2 地质统计学在地质学中的重要性地质统计学在地质学中的重要性体现在对地质数据的分析与解释上。
地质统计学通过数理统计的方法，可以对地质数据进行合理的处理和分析，从而帮助地质学家更好地理解地质现象和地质过程。
在地质调查和勘探中，地质统计学可以帮助地质学家发现地质异常、地质断裂和矿产资源的分布规律，为矿产资源的勘探和评价提供科学依据。
地质统计学还可以帮助地质学家进行地质灾害的预测和评估。
储层多点地质统计学随机建模方法
储层多点地质统计学随机建模方法摘要：多点地质统计学使用训练图像代替变差函数，将更多的地质资料整合到储层建模过程中，使得最终模型更加符合地质认识。
随着研究的不断深入，越来越多的地质工作人员开始熟悉这一方法，凭借自身的独特优势，多点地质统计学将在储层建模领域占得重要的一席。
关键词：多点地质统计学训练图像储层建模一、多点地质统计学与训练图像基于变差函数的传统地质统计学随机模拟是目前储层非均质性模拟的常用方法。
然而，变差函数只能建立空间两点之间的相关性，难于描述具有复杂空间结构和几何形态的地质体的连续性和变异性。
针对这一问题，多点地质统计学方法应运而生。
该方法着重表达空间中多点之间的相关性，能够有效克服传统地质统计学在描述空间形态较复杂的地质体方面的不足。
多点地质统计学的基本工具是训练图像，其地位相当于传统地质统计学中的变差函数。
对于沉积相建模而言，训练图像相当于定量的相模式，实质上就是一个包含有相接触关系的数字化先验地质模型，其中包含的相接触关系是建模者认为一定存在于实际储层中的。
二、地质概念模型转换成图像训练地质工作人员擅于根据自己的先验认识、专业知识或现有的类比数据库来建立储层的概念模型。
当地质工作人员认为某些特定的概念模型可以反映实际储层的沉积微相接触关系时，这些概念模型就可以转换或直接作为训练图像来使用。
利用训练图像整合先验地质认识，并在储层建模过程中引导井间相的预测，是多点地质统计学模拟的一个突破性贡献。
可以将训练图像看作是一个显示空间中相分布模式的定量且直观的先验模型。
地质解释成果图、遥感数据或手绘草图都可以作为训练图像或建立训练图像的要素来使用。
理想状态下，应当建立一个训练图像库，这样一来建模人员就可以直接选取和使用那些包含目标储层典型沉积模式的训练图像，而不需要每次都重新制作训练图像。
三、多点模拟原理进行多点模拟，需要使用地质统计学中的序贯模拟。
但是，多点模拟与传统的基于变差函数的两点模拟是不同的。
多点地质统计学随机建模方法原理详细教程
多点地质统计学随机建模方法原理详细教程多点地质统计学（Multiple-Point Geostatistics，简称MPGS）是一种用于地质建模的统计学方法，旨在综合考虑多个地质属性之间的空间关系，可以用于模拟地质体结构和属性的空间分布。
下面是一个详细的MPGS建模方法的教程。
1.数据收集和准备首先，需要收集和准备地质数据。
这些数据可以包括钻孔数据、采矿数据、地球物理数据等。
数据应该包括多个不同属性的测量结果。
2.数据预处理对收集的数据进行预处理是为了消除异常值、填充缺失值和准备数据用于建模。
这些步骤可以包括数据清洗、插值等。
3.定义模型网格创建一个用于建模的三维网格，通常由正交的网格单元组成。
网格的尺寸和边界应根据实际问题的要求进行选择。
4.模式提取在做MPGS建模之前，需要从数据中提取出具有空间一致性和相关性的模式。
这可以通过模式提取算法实现，如基于模拟退火算法的直方图匹配。
5.模式匹配在模型建模过程中，需要通过模式匹配找到与已知数据最相似的地质模式。
这可以通过计算模式之间的相似性指标，如多点统计函数（MPS）实现。
6.模式合成一旦找到与已知数据相似的地质模式，可以根据模式之间的空间关系来生成新的地质模式。
这可以通过使用概率或变异性模型来实现。
7.模型重建利用已生成的地质模式，可以在模型网格单元上对地质属性进行插值，以重建地质体的结构和属性分布。
这可以使用插值方法，如克里金插值、逼近法等。
8.模型评估和修正完成模型重建后，需要评估模型的性能并根据需求对模型进行修正。
可以利用模型与实际数据之间的比较以及其他准则来评估模型的准确性和合理性。
9.模型应用完成最终的地质建模后，可以将模型应用于相关的地质问题，如矿产资源评估、地质风险评估等。
以上是MPGS建模方法的详细教程。
这种方法在地质建模中广泛应用，可以提供更准确和全面的地质属性分布信息，对于地质资源开发和管理具有重要意义。
地统计学理论、发展及应用现状研究综述
地统计学理论、发展及应用现状研究综述本文是刘爱利老师14年出版《地统计学概论》一书内容摘选，分享下，顺便给刘老师的书打个广告！一、背景设想有这样一些情景：情景 1 精准农业中的测土配方施肥都需要从田间采集土壤样本，再监测每个样本的土壤养分含量，但精准施肥过程中还需要知道非采样点的土壤肥力状况。
情景 2 人们希望了解除气象台站的气温、降水量情况外，更关心气象台站之间地区的气温和降水量。
情景 3 环保工作者希望了解大气中二氧化硫浓度在城市中的连续变化情况，污染物扩散呈现出的空间分布规律。
情景 4 地貌学家需要知道地形在空间的连续变化情况，而不只是某几个采样点的高程。
也就是说，在上述情境中，人们不仅仅需要了解有限的空间采样点情况，更关心自然现象在空间的连续变化。
因此，此类问题可归结为“如何将离散的空间采样点转化为连续表面”的问题。
那么如何做到这一点呢？以土地施肥为例，一种解决方法是加密采样，然而由于人力、物力、财力等客观因素的限制，样本数量不可能无限增多，事实上也不可能做到在无限多的点上采样；另一种方法是通过已有的土壤样本值来估计其他未取样点上的值，从而得到土壤养分在整个土地上的连续分布情况，即空间插值。
空间插值的方法很多，主要分为确定性插值和地统计插值两种方法。
常用的确定性插值方法包括反距离加权插值法、全局多项式插值法、径向基函数插值法等，该类方法往往直接通过周围观测点的值内插或者通过特定的数学公式来内插，而较少考虑观测点的整体空间分布情况。
与此相比，地统计插值法是建立在对观测点的空间自相关分析基础之上，依据自然现象的空间变异规律进行插值的，从而可以得到无偏最优估计量，并且能给出插值的精度。
相比于经典概率论和数理统计学，地统计学在空间预测和不确定性分析方面具有明显的优势。
目前，地统计学应用领域从最初的地质、采矿领域，已逐步拓展到土壤、气象、农业、生态、环境、公关卫生、社会科学等多个领域，显示出越来越强大的生命力。
多点地质统计学
多点地质统计学Multiple-point geostatistic是相对于传统的两点地质统计学而言的,主要应用于储层表征与建模中.传统的地质统计学在储层建模中主要应用于两大方面:其一,应用各种克里金方法建立确定性的模型,这类方法主要有简单克里金、普通克里金、泛克里金、协同克里金、贝叶斯克里金、指示克里金等;其二,应用各种随机建模的方法建立可选的、等可能的地质模型,这类方法主要有高斯模拟(如序贯高斯模拟)、截断高斯模拟、指示模拟(如序贯指示模拟)等。
上述方法的共同特点是空间赋值单元为象元(即网格),故在储层建模领域将其归属为基于象元的方法。
这些方法均以变差函数为工具,亦可将其归属为基于变差函数的方法。
变差函数局限性（传统地质统计学）变差函数只能把握空间上两点之间的相关性,亦即在二阶平稳或本征假设的前提下空间上任意两点之间的相关性,因而难于表征复杂的空间结构和再现复杂目标的几何形态(如弯曲河道)。
弯曲河道的3种不同的空间结构(图1a,b,c)在横向上(东西方向,图1d)和纵向上(南北方向,图1e)的变差函数十分相似,这说明应用变差函数不能区分这3种不同的空间结构及几何形态,因此,基于变差函数的传统地质统计学插值和模拟方法难于精确表征具有复杂空间结构和几何形态的地质体。
现有的储层随机建模的另一途径是基于目标的方法,它是以目标物体为基本模拟单元,进行离散物体的随机模拟(Haldorsen and Damsleth,1990;Holdenet al.,1998)。
主要方法为示性点过程(亦称标点过程),其根据先验地质知识、点过程理论及优化方法(如模拟退火)表征目标地质体的空间分布,因此这种方法可以较好地再现目标体几何形态。
但这种方法亦有其不足:1)每类具有不同几何形状的目标均需要有特定的一套参数(如长度、宽度、厚度等),而对于复杂几何形态,参数化较为困难;2)由于该方法属于迭代算法,因此当单一目标体内井数据较多时,井数据的条件化较为困难,而且要求大量机时2多点地质统计学的基本概念多点统计学着重表达多点之间的相关性。
多点地质统计学python
多点地质统计学python摘要：1.多点地质统计学简介2.Python 在多点地质统计学中的应用3.多点地质统计学的优势与挑战4.未来发展趋势与展望正文：一、多点地质统计学简介多点地质统计学是一门研究如何利用多个空间位置的数据，来描述和推断地下地质结构的学科。
在资源勘探、地质灾害评估等领域具有重要的应用价值。
随着科技的发展，尤其是计算机技术的进步，多点地质统计学的研究方法和技术也在不断更新。
二、Python 在多点地质统计学中的应用Python 作为一门功能强大的编程语言，在地质统计学领域具有广泛的应用。
Python 提供了丰富的库和工具，如NumPy、SciPy、Matplotlib 等，可以方便地进行数据处理、分析和可视化。
在地质统计学中，Python 可以应用于数据预处理、地质体模拟、统计分析等方面，极大地提高了研究效率和准确度。
三、多点地质统计学的优势与挑战多点地质统计学具有以下优势：1.数据驱动：通过分析多个空间位置的数据，提高了对地下地质结构的认识和预测能力。
2.精确度高：利用统计学方法和现代计算技术，可以提高地质模型的精确度和可靠性。
3.适用范围广：可以应用于多种地质环境和资源勘探项目。
然而，多点地质统计学也面临一些挑战，如数据采集和处理难度大、计算复杂度高、模型参数选取不合适等。
这些问题需要研究人员不断探索和优化。
四、未来发展趋势与展望随着计算机技术的进一步发展，多点地质统计学在未来将取得更多突破。
以下几个方面是未来的发展趋势：1.大数据与人工智能的结合：利用大数据技术和人工智能算法，提高地质数据的分析和挖掘能力。
2.模型优化与集成：不断优化现有模型，探索多种模型的集成方法，提高地质统计学的预测能力和可靠性。
3.跨学科研究：与其他学科如地球物理学、数学、计算机科学等进行交叉研究，拓宽研究领域和方法。
多点地质统计学python -回复
多点地质统计学python -回复"多点地质统计学python"是一种基于Python编程语言的地质统计学方法，它通过使用多点统计技术来分析地质数据和建立地质模型。
多点地质统计学python可以用于地质建模、矿产资源评估、油气勘探等地质领域。
本文将逐步介绍多点地质统计学python的基本原理、数据处理步骤以及应用案例。
第一步：理解多点地质统计学的基本原理多点地质统计学是一种从多个样本点中提取信息进行推断的统计学方法，它考虑了地质数据在空间上的相关性和变异性。
这种方法的基本原理是通过对多个样本点进行统计分析，揭示地质变量的分布和空间结构。
多点地质统计学方法在地质学领域得到广泛应用，可以实现对地质数据的建模和预测。
第二步：了解多点统计技术在python中的实现Python是一种功能强大且易于使用的编程语言，具有丰富的数据处理和分析库，例如NumPy、Pandas和Matplotlib等。
这些库提供了处理大型地质数据集和执行统计分析的工具。
在python中，可以使用这些库来实现多点地质统计学方法，例如多点统计算法、样本点选择和空间变异性分析等。
第三步：处理地质数据集在使用多点地质统计学python之前，首先需要准备一个地质数据集。
这个数据集包含了地质变量的观测值，例如地层厚度、属性值或矿石品位等。
地质数据集通常以表格形式存储，可以使用Pandas库将数据导入到python环境中进行处理。
第四步：分析地质数据集在有了地质数据集之后，可以使用多点地质统计学python来分析数据。
首先，可以使用NumPy库计算地质数据的统计指标，例如均值、方差和协方差等。
这些统计指标可以用来揭示地质变量的中心趋势和空间关系。
接下来，可以使用多点统计算法来分析地质数据的变异性和空间结构。
其中，常见的多点地质统计学方法包括变差函数、半变异函数和变异权重等。
这些方法可以用来评估地质数据的变异性，并揭示地质变量之间的空间关联性。
基于矢量信息的多点地质统计学算法
基于矢量信息的多点地质统计学算法冯文杰;吴胜和;印森林;石书缘;刘俊玲【期刊名称】《中南大学学报（自然科学版）》【年(卷),期】2014(045)004【摘要】在Snesim算法的基础上,提出基于地质矢量信息的多点地质统计学算法(VMPS).以冲积扇为例,研究冲积扇地质矢量坐标系统,并在训练图像中融入地质矢量信息,形成基于矢量信息的训练图像.同时,对训练图像扫描机制进行改进,利用矢量信息统计数据事件和区域相比例,建立基于地质矢量信息的搜索树.在模拟过程中根据当前模拟区块的矢量信息,提取与之关系最密切的数据事件计算重复数,得到适应当前模拟区域的条件概率分布,从而满足局部平稳的条件,再现不同沉积相带不同地质特征.通过概念模型和实际储层模拟检验表明:VMPS的模拟效果明显优于Snesim,能适应“非平稳性”突出条件下的地质建模.【总页数】8页(P1261-1268)【作者】冯文杰;吴胜和;印森林;石书缘;刘俊玲【作者单位】中国石油大学(北京)地球科学学院,北京,102249;油气资源与探测国家重点实验室(中国石油大学),北京,102249;中国石油大学(北京)地球科学学院,北京,102249;油气资源与探测国家重点实验室(中国石油大学),北京,102249;中国石油大学(北京)地球科学学院,北京,102249;油气资源与探测国家重点实验室(中国石油大学),北京,102249;中国石油勘探开发研究院,北京,100083;中国石油大学(北京)地球科学学院,北京,102249;油气资源与探测国家重点实验室(中国石油大学),北京,102249【正文语种】中文【中图分类】TE122【相关文献】1.多点地质统计学算法Snesim参数敏感性分析 [J], 王红;李少华2.多点地质统计学DS-MPS算法在储层沉积相建模中的应用 [J], 耿丽慧;侯加根;李宇鹏;李兆刚;曲鹏3.多点地质统计学在数字岩心重构中的算法研究 [J], 严俊;田园诗4.基于局部各向异性的非平稳多点地质统计学算法 [J], 喻思羽;李少华;段太忠;王鸣川5.多点地质统计学算法的C#实现及应用 [J], 郭凤云;苗长运;因版权原因，仅展示原文概要，查看原文内容请购买。
Petrel中文操作手册2010-(6~9章)_1
第六章相建模（Facies Modeling）6.1 Petrel2010版本中相建模技术的大发展Petrel相建模（Facies Modeling）现有方法主要包括：多点地质统计学相模拟、基于目标的河流相模拟，基于像元的序贯指示模拟、截断高斯模拟，带趋势的截断高斯模拟，指示克里金模拟、神经网络方法，用于详细表征相带分布特征的确定性和随机性相建模技术，而且可以交互使用。
同时用户可以导入自己的算法和人工赋值的方法，建立沉积相模型。
Petrel2010在原有版本基础上对相建模方法做了较大的改进，主要体现在以下四个方面：1）全新的MPS多点统计相模拟算法在Petrel2010版本中，引进了多点地质统计学相模拟方法，该方法的引进改变了过去传统的两点统计地质学方法，而发展为多点地质学，解决了过去两点统计关系上变差函数的不足，特别是对储层非均质性描述上的不足，多点统计地质学能够充分描述复杂几何形状砂体的空间连续性和变异性。
多点统计地质学是建立在多个点的相关关系上，它在解决描述空间变量的连续性和变异性方面得到越来越广泛的应用。
斯坦福大学的Journel教授曾指出多点地质统计学是今后地质统计学发展的方向，它的优势已越来越显著。
2）基于快速傅立叶变换的高斯模拟算法一种新的新的高斯模拟算法在Petrel 2010.1.中被引用，这种算法与GSLIB的序贯随机模拟方式不同。
A 它比SGS运算速度提高了很多B 它不是序贯算法C 它可以并行运算D 它可以进行快速的协同模拟设定如同上面提到的，这种高斯算法不同于序贯模拟的序贯算法，允许并行计算，采用的算法是傅立叶变换算法，这种算法具有快速、并行、在大的范围变程内优选最合理的变程等优点，这种算法的界面与序贯高斯模拟算法有些类似。
3）进一步改进克里金算法在2010.1版本中引用了新的克里金算法，这是完全不同于标准GSLIB 克里金的一种设计，其搜索性能和并行运算都有很大改进。
克里金可以沿网格方向、也可以沿海平面进行插值。
地质统计学方法
地质统计学方法一、引言地质统计学是地质学中的一个重要分支，它运用统计学的理论和方法来分析和解释地质现象和地质数据。
地质统计学的发展与地质学研究的需要密切相关，它可以帮助地质学家更好地理解地质现象、预测地质事件以及优化地质资源的开发利用。
本文将介绍地质统计学方法的基本原理和常用技术，以及其在地质学中的应用。
二、地质统计学方法的基本原理地质统计学方法的基本原理是基于概率统计的理论，它认为地质现象和地质数据的分布具有一定的规律性。
地质统计学方法通过对地质数据进行采样、观测和分析，可以得到地质现象的统计特征和概率模型，进而进行地质事件的预测和模拟。
三、地质统计学方法的常用技术1. 变量分析变量分析是地质统计学中最基本的技术之一，它主要用于研究地质现象和地质数据的变量特征。
常用的变量分析方法包括：频数分析、概率分布函数拟合、变异系数计算等。
这些方法可以帮助地质学家了解地质现象的变量分布规律，从而为后续的地质建模和预测提供依据。
2. 空间分析空间分析是地质统计学中另一个重要的技术，它主要用于研究地质现象和地质数据的空间特征。
常用的空间分析方法包括：半方差函数分析、克里金插值、空间统计模型建立等。
这些方法可以帮助地质学家揭示地质现象的空间分布规律，从而为地质资源的勘探和开发提供指导。
3. 地质模拟地质模拟是地质统计学中的一项重要技术，它主要用于通过随机模拟方法生成符合实际地质条件的模拟数据。
常用的地质模拟方法包括：高斯模拟、马尔可夫链模拟、蒙特卡洛模拟等。
这些方法可以帮助地质学家预测地质事件的概率和可能性，提高地质资源的开发效率。
四、地质统计学方法在地质学中的应用1. 地质资源评价地质统计学方法可以帮助地质学家评价地质资源的分布和储量，从而为资源的合理开发提供依据。
通过对地质数据的变量分析和空间分析，可以揭示地质资源的分布规律和富集规律，进而进行资源量的估算和评价。
2. 地质灾害预测地质统计学方法可以帮助地质学家预测地质灾害的发生概率和可能性，提前做好防灾准备工作。
数字岩心技术在致密砂岩储层含油饱和度评价中的应用
［ ９ ］ 陈培元 ， 姜楠 ， 杨辉 廷 ， 等． 由 两 点 到 多 点 的 地 质 统 计 学 储 层 建 模
理 论模 拟 发现 ，胶 结指 数 和饱 和度 指数 在低 渗 透 储 层 中受 储层 孔 隙结构 特征 的影 响最 大 。通 过研 究 区 实际 岩 电资料 的分 析 ，建立 了储 层饱 和 度指 数 和胶 结 指 数 与储 层孔 隙结 构特 征参 数之 间 的关 系 ，确立 了二 者 计算 模 型 ， 为精 确求 取储 层含 油饱 和度 奠定 了基 础 。 胶 结 指数 计算 公式 为
图 ７ 地 层 水 电 阻 率 对 饱 和 度 指数 的 影 响
实验 得 到 地层 水 电阻 率 分别 为 Ｏ ． ２ ５ ． Ｏ ． ４ ４ Ｑ・ ｍ 时 的饱 和度指 数 ｎ ｏ ． ２ ５ ， ｎ ｏ ． ４ ４ 值关 系 （ 见图 ８ ） 。 可 以看 出 ， 地层 水 电阻率 ０ ． ２ ５ Ｑ・ １ ２ ＇ １ 时饱 和度指数 较大 。
［ ４］ 宋 子 齐 ， 杨红刚 ， 孙颖， 等． 利 用 岩 石 物 理 相 分 类 研 究 特 低 渗 透 储 层 参数建模［ Ｊ ］ ． 断 块油 气 田 ， ２ ０ １ ０ ， １ ７ （ ６ ） ： ６ ７ ２ — ６ ７ ７ ． ［ ５ ］ 刘伟 ， 林承焰 ， 刘键 ， 等． 柴西 北 地 区油 泉 子 油 田低 渗 透 储 层 特 征 与 成因分析［ Ｊ ］ ． 石油学报 ， ２ ０ ０ ９ ， ３ ０ （ ３ ） ： ９ ２ — ９ ６ ．
［ １ １ ］张 婷 ， 徐守余 ， 王子敏． 储 层 微 观孔 喉 网络 图形 识 别 方 法 ［ Ｊ ］ ． 吉林 大
学学报 ： 地球科学版 ， ２ ０ １ １ ， ４ １ （ ５ ） ： １ ６ ４ ６ — １ ６ ５ ０ ．
多点地质统计学在三维岩心孔隙分布建模中的应用
多点地质统计学在三维岩心孔隙分布建模中的应用张丽;孙建孟;孙志强;姜黎明;刘学锋【摘要】Multiple-point geostatistics and its principle and methods of building 3D distribution of core pore structure were presented. The 3D pore structure model was reconstructed using multiple-point geostatistical methods on the basis of 2D thin sections of Fontaineblean sandstone, and the accuracy of this method was evaluated by calculating local porosity distribution function and average percolation probability function in real 3D digital cores and the reconstructed digital cores. The results show that the characteristics of pore structures reconstructed by this method are similar to those of real 3D digital cores, and also have similar homogeneity and strong pore connectivity. The reconstruction of 3D pore structure model can be used to characterize the pore connectivity and homogeneity of the real core,but also can be used as the basis for simulation of other physical characteristics.%介绍多点地质统计学及其用于三维岩心孔隙结构建模的原理和方法.基于多点地质统计方法,以均质性较好的Fontaineblean砂岩的二维薄片为基础,重构三维孔隙结构模型,并且应用局部孔隙度理论和渗流概率函数进行准确性评价.结果表明:由此获取的孔隙结构模型与真实三维岩心孔隙分布十分相近,且具有相似的均质性和孔隙连通性；重构的三维孔隙结构模型不仅可以用来表征真实岩心的孔隙连通性和均质性,而且也可以作为其他物理特性模拟的基础.【期刊名称】《中国石油大学学报（自然科学版）》【年(卷),期】2012(036)002【总页数】5页(P105-109)【关键词】多点地质统计方法;二维薄片;三维数字岩心;孔隙分布;局部孔隙度理论【作者】张丽;孙建孟;孙志强;姜黎明;刘学锋【作者单位】中国石油大学地球科学与技术学院,山东青岛266580;中国石油大学地球科学与技术学院,山东青岛266580;山东科技大学研究生院,山东青岛266510;中国石油大学地球科学与技术学院,山东青岛266580;中国石油大学理学院,山东青岛266580【正文语种】中文【中图分类】TE19岩心是从地层获得的最直观、可靠的数据资料，其中包含的信息如粒径分布、沉积构造、孔隙结构［1］等特征，是进行数字岩石物理实验的基础。
《地质统计学》ppt课件
〔2〕在运用方面有了本质性的突破。采用地质统计学方法 提交地质勘探成果为消费部门所接受，开场成为地质勘探、 油田和矿山开发的运用方法，与消费实际结合得越来越严 密。。
〔3〕开发出了一系列软件系统。如西安石油学院的的KMS
2、统计概率
频率：设随机事件A，在次实验中发生m次，其比值m/n称为 随机事件A的频率
显然 当反复实验的次数充分大时，随机事件A的频率〔A〕 经常稳定在一个确定的数字附近，这就是概率。
概率：在一定的一样条件下，反复作n次实验中发生了m次， 当n充分大时，随机事件A的频率m/n稳定在某一数字P附近， 称数值P为该随机事件的概率。 记为 P(A)=P
2、构成阶段〔20世纪50年代末—60年代〕
50年代末，法国概率统计学家马特隆〔G Matheron〕在克里格 及西舍尔研讨的根底上，对十几个不同类型的矿床继续深化研 讨，于1962年首先提出了区域化变量〔regionalized variable〕的概念，为了更好地研讨具有随机性和构造性的自 然景象，他提出了地质统计学〔Geostatt;从而为地质统计学奠定了实际根底。
克里格算法的实值是利用临近的数值 Z(μa),a=1.2.3…n，估计一个未取样值Z(μ)。 主要研讨各种克里格的数学根底，不同克里格方法 的表达式及其运用条件，克里格在矿产估算中的运 用。
4、随机模拟
随机模拟是从一个随机函数(RF)模型中提取多个等 概率的一切随机变量〔RV〕的结合实现。 在随机模拟中，研讨的内容包括随机模拟的定义及 其与插值的区别，随机模拟的根本原理，随机模拟 的分类，典型的随机模拟方法及其计算机实现。
多点地质统计学建模的发展趋势
多点地质统计学建模的发展趋势石书缘;尹艳树;冯文杰【摘要】从算法研究、训练图像处理和实际应用三个方面详细解剖了国内外多点地质统计学的发展历程,在此基础上,分析了多点地质统计学主流的几种算法的核心原理、适用范围及优缺点,以此来对储层建模的发展趋势作出展望.目前,多点地质统计学虽是随机建模的一种前沿研究热点,但由于其尚未成熟,仍需对建模算法进行研究.为此,在前人研究的基础上,重点分析了多点地质统计学的发展趋势:合理处理训练图像；合理利用软信息；选择合适的相似性方法；选择合适的标准化方法；合理利用平稳性；算法间的耦合；选择合适的过滤器；拓展缝洞型碳酸盐岩模拟.最后,提出多点地质统计学在储层建模方面,应从增加储层的模拟区域、提高模拟精度、扩大储层相的模拟范围和提高计算机模拟效率等方面进行改进.%Starting with algorithm designing, training image,and practical application,the authors analyzed multiple-point statistics research trends both in China and abroad. On such a basis, the core principles of the main four MPS algorithms, their applicable ranges and advantages as well as disadvantages were analyzed,so as to forecast the trend of reservoir modeling. Multiple-point geostatistics is an international forefront research tool in stochastic modeling; nevertheless, as the algorithm is not yet mature, it should be further improved. On the basis of previous researches, the existing problems of the multiple-point geostatistics that need to be modified and the direction of the processing of training images are proposed, such as suitable processing of training image, choice of similarity methods, choice of standardized data,smoothing,couplingamong algorithms,and expansion of the simulation extent for fractured-vuggy carbonate reservoir. In order to improve the usage of multiple-point geostatistics for reservoir stochastic modeling,we should spare no efforts to increase the simulation area,improve simulation accuracy,expand the scope of simulation of reservoir types,save simulation time and improve simulation efficiency.【期刊名称】《物探与化探》【年(卷),期】2012(036)004【总页数】6页(P655-660)【关键词】储层建模;多点地质统计学;模拟精度;缝洞型碳酸盐岩模拟;发展趋势【作者】石书缘;尹艳树;冯文杰【作者单位】中国石油勘探开发研究院,北京 100083;长江大学地球科学学院,湖北荆州 434023;中国石油大学地球科学学院,北京 102249【正文语种】中文【中图分类】TE319目前，中国东部大部分油田进入高含水开发阶段，在新区勘探难度加大的情况下，对老油田进行挖潜寻找剩余油及拓展深层碳酸盐岩勘探开发已成为当前油气勘探开发的几个主要发展方向。
多点地质统计学随机建模方法原理详细教程
多点地质统计学随机建模方法原理详细教程多点地质统计学随机建模是一种应用于地质领域的统计学建模方法，它主要用于处理地质参数在空间上的变化规律。
该方法的原理基于地质参数的随机性和空间相关性，通过构建具有地质属性的随机模型，可以模拟地质现象的空间分布。
具体而言，多点地质统计学随机建模方法主要包括以下几个步骤：1.数据准备：收集与地质参数相关的数据，例如岩性、厚度、含矿物质等。
要求数据具有一定的地质意义和空间分布规律。
2.变量描述：对收集到的数据进行统计分析，包括计算均值、方差、协方差等统计指标，以描述地质参数的分布特征。
3.变量变换：根据地质参数的实际特征，对数据进行变换，使其符合正态分布、对数正态分布或其他分布类型。
4.空间相关性建模：通过计算地质参数之间的空间相关性，可利用协方差函数、变差函数或半方差函数等，建立地质参数之间的空间相关模型。
5.随机模拟：根据变量的统计特征和空间相关模型，结合随机数生成算法，生成符合实际情况的具有随机性和空间相关性的地质参数数据。
6.模型验证：对生成的地质模型进行验证，比较随机模拟结果与实际数据的吻合程度。
可以使用统计指标如均值、方差、协方差等进行对比分析。
7.地质模型应用：根据随机模拟结果，可以进一步进行岩层插值、矿产资源评估和地质灾害风险评估等相关研究及应用。
总的来说，多点地质统计学随机建模方法是将统计学原理应用于地质参数的空间分布建模，通过对地质参数的统计特征和空间相关性的建模，生成具有随机性和空间相关性的地质模型。
这种方法可以提供地质领域研究的基础数据和分析手段，为地质灾害风险评估、资源勘探和环境评价等问题提供科学依据。
统计学在地质学中的应用
统计学在地质学中的应用地质学作为一门研究地球历史和构造的学科，其数据量庞大且复杂，因此需要一种有效的方法来整理、分析和解释这些数据。
统计学的应用在地质学中扮演着关键的角色，它为地质学家提供了宝贵的工具和技术，以更好地理解和解释地球过程。
一、样本分析在地质学中，样本分析是一项重要的工作。
地质学家需要收集各种类型的样本，包括岩石、土壤、化石等，以了解地球的历史和构造。
统计学可以帮助地质学家确定样本的数量和取样位置，并提供验证结果的可靠性的方法。
通过采用统计学的方法，地质学家能够更好地确定样本的代表性，并有效地利用资源。
二、数据分析对于地质学的研究，数据分析是非常重要的工作。
统计学为地质学家提供了各种分析方法，以帮助他们从数据中发现模式、趋势和关联。
其中一个常用的方法是回归分析，它可以帮助地质学家确定变量之间的关系，并进行预测。
另外，统计学的聚类分析和主成分分析等方法也被广泛应用于地质学的数据分析中。
三、可视化展示统计学不仅可以帮助地质学家分析数据，还可以帮助他们将数据可视化展示出来。
可视化可以提供地质学研究的更直观的结果，并帮助地质学家更好地传递和解释自己的发现。
在地质学中，常用的可视化方法包括统计图表、地质图、地质剖面图等。
通过统计学的方法，地质学家可以更好地展示地球的构造和演化历史。
四、风险评估在地质学中，风险评估是一个重要的任务。
统计学可以帮助地质学家评估各种地质灾害的概率和可能性，并帮助制定相应的预防措施。
通过统计学的方法，地质学家可以分析历史数据和地质特征，以预测可能的地震、火山喷发等自然灾害，并提出相应的风险管理策略。
总结：统计学在地质学中的应用是多方面的，从样本分析、数据分析到风险评估，都能从中获得收益。
通过统计学的手段，地质学家能够更好地理解和解释地球过程，为地质学的研究提供有力支持。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第7卷
第1期
吴胜和等 : 多点地质统计学
理论、应用与展望
139
现有的储层随机建模的另一途径是基于目标的 方法 , 它是以目标物体为基本模拟单元 , 进行离散 物体 的 随 机 模 拟 ( Haldorsen and Damsleth, 1990; Holden et al , 1998) 。主要方法为示性点过程 ( 亦 称标点过程) , 其根据先验地质知识、点过程理论及 优化方法 ( 如模拟退火 ) 表征目标地质体的空间分 布, 因此这种 方法可以较好地再 现目标体几何形 态。但这种方法亦有其不足: 1) 每类具有不同几 何形状的目标均需要有特定的一套参数 ( 如长度、 宽 度、厚度等) , 而对于复杂几何形态 , 参数化较为困 难; 2) 由于该方法属于迭代算法, 因此当单一目 标体内井数据较多时 , 井数据的条件化较为困难 , 而且要求大量机时。 鉴于传统的基于变差函数的随机建模方法和基 于目标的随机建模方法存在的不足 , 多点地质统计 学方法应运而生。在多点地质统计学中 , 应用 训 练图像 代替变差函数表达地质 变量的空间结构 性, 因而可克服传统地质统计学不能再现目标几何 形态的不足, 同时, 由于该方法仍然以象元为模拟 单元, 而且采用序贯算法 ( 非迭代算法 ) , 因而很容 易忠实硬数据, 并具有快速的特点 , 故克服了基于 目标的随机模拟算法的不足。因此 , 多点地质统计 学方法综合了基于象元和基于目标的算法优点, 同 时可克服已有的缺陷。
多点地质统计学是相对于传统的两点地质统计 学而言的。地质统计学是法国巴黎国立高等矿业学 院马特隆教授 ( G Matheron) 于 1962 年创立的。最 初应用于采矿业中, 主要解决矿床普查勘探、矿山 设计到矿山开采整个过程中各种储量计算和误差估 计问题。后来在石油工业中得到了迅速的发展, 主 要 应 用 于 储 层 表 征 与 建 模 中 ( Haldorsen and Damslet h, 1990; Srivastava, 1994; 裘怿 楠和贾爱 林, 2000; 王 家 华 和 张 团 峰, 2001; 吴 胜 和 等 , 1999) 。 传统的地质统计学在储层建模中主要应用于两 大方面: 其一, 应用各种克里金方法建立确定性的 模型, 这类方法主要有简单克里金、普通克里金、 泛克里金、协同克里金、贝叶斯克里金、指示克里 金等 ; 其二, 应用各 种随机建 模的方法 建立可选
油学 院北京研究生部 , 获硕士学位 ; 1998 年毕业于石油大学 ( 北京 ) , 获博士学位 。 现为石油 大学( 北京 ) 教授 、 博 士生导师 , 主要从事储层地质学 、 油藏描述及三维地质建模的教学与科研工作 。
Multiple point geostatistics: theory, application and perspective
Wu Shenghe Li Wenke
Univer sity of Petr oleum, Beij ing 102249
Abstract
T his paper presents systematically the principle and met hods of mult iple point geo
分别处于 s k 1
s kn 状态时的概率, 也可表述为 n 个 = 1, n} ( 1)
数据指示值乘积的数学期望 , 即 : Prob { d n } = P rob { S ( u ) = sk ;
n
= E [
= 1
I ( u ; k )]
在实际建模过程中 , 上述多点统计或概率难于 通过稀疏 的井资料来获取 , 而需要借助于训 练图 像。训练图像为能够表述实际储层结构、几何形态 及其分布 模式的数字化图像。对于沉积相建 模而 言, 训练图像相当于定量的相模式, 它不必忠实于 实际储层内的井信息, 而只反映一种先验的地质概 念, 如图 2 ( b) 为一个反映河道( 黑色 ) 与河道间 ( 白 色) 分布的训练图像。一个给定的数据事件的概率 则可通过应用该数据事件对训练图像进行扫描来获 取。 对于任一给定的数据样板 T , 定义 侵 蚀的 训练 图像
st at ist ics, and a case study of stochast ic modeling is made, t aking t he f luv ial reservoir of the M inghuazhen Format ion of Neog ene in a certain block of Bohai Bay Basin in China as an example Mult iple point geost atistics is a promising discipline in stochastic reservoir modeling T his ap proach combines t he easy conditioning of pix el based algorit hms w ith the ability t o reproduce object ge ometry of object based techniques It overcomes t he draw backs that t radit ional variogram based tw o point geost at ist ics can not ex press joint variabilit y of more than tw o locat ions at a time and reproduce crisp geometries T hrough t he t heory and case analysis som e present problems and further study sug gestions are discussed such as t he st at ionarity of training images, object cont inuity, and int egration of sof t informat ion Key words multiple point geost at istics, reservoir, stochast ic modeling About the first author Wu Shenghe, born in 1963, was graduated w ith a B S degree f rom East China Petroleum Instit ute in 1983, obtained a M S degree f rom Beijing Graduate School of East China Pet roleum Inst it ute in 1986, and received his Ph D degree f rom Universit y of Petroleum in Beijing in 1998 Now he is a prof essor at Universit y of Pet roleum ( Beijing ) , and is mainly engaged in reservoir geolog y, reservoir descript ion and 3D geological modeling
摘 要 系统地介绍了多点地质统计学的基本原理 及方法 , 并 以我国 渤海湾 盆地某区 块新近 系明化 镇组河
流相储层为例 , 进行了多点统计学随机建模的实例分析 。 多点地质统计学为储层随机 建模的国 际前沿研究 方向 。 该方 法综合了基于象元的方法易忠实条件数据以及基于 目标的方 法易再 现目标 几何形 态的优 点 , 同时克 服了传 统的基于变差函数的二点统计学不能表达复杂空间结 构和再 现目标 几何形 态的不足 。 通过理 论与实 例研究 , 分 析了 目前多点统计学尚存在的问题 ( 包括训练图像平稳性 问题 、 目标连续性问题以及综 合软信息 的问题等 ) 及未来 发展的方向 。 关键词 多点地质统计学 储层 随机建模 第一作者简介 吴胜和 , 男 , 1963 年生 , 1983 年毕业于华东石油学院 , 获学士学位 ; 1986 年毕业 于华东石
第7卷 第1期 2005 年 2 月来自古地理
学
报
JOU RNAL OF PALA EOG EOG RAPHY
Vol 7 N o 1 Feb 2005
文章编号 : 1671- 1505 ( 2005) 01- 0137- 08
文献标识码 : A
多点地质统计学
吴胜和
理论、应用与展望
李文克
石油大学 , 北京 102249
Caers J and Zhang T 2002 M ultiple point Geost at ist ics: a quantit at ive vehicle f or int egrat ing geologic analogs int o multiple reservoir models
图 1 不能充分反映空间各向异性的变差函数 ( Caers and Zhang, 2002 ) F ig 1 T he variogram as a poor descr iptor of geolog ical hetero geneity
a、 b 和 c 为用黑色、白色图元代表的弯曲河道的 3 种不同空间结构 ; d 和 e 分别代表 3 种结构东西方向和南北方向的变差函数
国家
十五 重大科技攻关项目 ( 2001BA 605A09) 部分研究成果 改回日期 : 2004 年 8 月 19 日
收稿日期 : 2004 年 5 月 31 日
138
古
地
理
学
报
2005 年 2 月
的、等可能的地质模型 , 这类方法主要有高斯模拟
1
多点地质统计学的提出