人教版万有引力定律
合集下载
高中物理人教版必修第二册教学课件《万有引力定律》
R＋h2
m地 m
D．在赤道上空高出地面 h 处的高山上测量时，弹簧测力计读数为 F3＝G
R＋h2
)
AC
[针对训练]
1．(2021·山东等级考)从“玉兔”登月到“祝融”探火，我国星
际探测事业实现了由地月系到行星际的跨越。已知火星质量
约为月球的9倍，半径约为月球的2倍，“祝融”火星车的质
量约为“玉兔”月球车的2倍。在着陆前，“祝融”和“玉兔”都会经历一个由着陆平
＝0.6，cos 37°＝0.8，结果可用根式表示)
第七章 万有引力与宇宙航行
万有引力定律
一、行星与太阳的引力
第6章 圆周运动
（1）行星绕太阳运动的轨道十分接近圆，太阳处在圆心；
6.4
生活中的圆周运动
（2）行星做匀速圆周运动；
（3）所有行星轨道半径 r 的三次方与它公转周期 T 的二次方
的比值都相等，即：
r3
k
2
T
问题导入
各行星都围绕着太阳运行，说明太阳与行星之间的引力是使行星如
r
m
F 4 k 2
r
2
一、行星与太阳的引力
5. 太阳对行星的作用力只跟行星质量,半径有关吗？还能从什么角度帮助我们向前更进一步？
6.牛顿第三定律能否帮助我们得到
结论：
m
F 4 k 2
r
2
′∝
太
2
？
其中 4 2 k 均为常量，与行星、太阳均无关。
（1）太阳对行星的引力跟行星的质量成正比，
O
mg
将地球视为一个规则的球体
由于地球的自转，地面不同位置的人会
做半径不同的匀速圆周运动：
=
4. 人在赤道上的受力分析
m地 m
D．在赤道上空高出地面 h 处的高山上测量时，弹簧测力计读数为 F3＝G
R＋h2
)
AC
[针对训练]
1．(2021·山东等级考)从“玉兔”登月到“祝融”探火，我国星
际探测事业实现了由地月系到行星际的跨越。已知火星质量
约为月球的9倍，半径约为月球的2倍，“祝融”火星车的质
量约为“玉兔”月球车的2倍。在着陆前，“祝融”和“玉兔”都会经历一个由着陆平
＝0.6，cos 37°＝0.8，结果可用根式表示)
第七章 万有引力与宇宙航行
万有引力定律
一、行星与太阳的引力
第6章 圆周运动
（1）行星绕太阳运动的轨道十分接近圆，太阳处在圆心；
6.4
生活中的圆周运动
（2）行星做匀速圆周运动；
（3）所有行星轨道半径 r 的三次方与它公转周期 T 的二次方
的比值都相等，即：
r3
k
2
T
问题导入
各行星都围绕着太阳运行，说明太阳与行星之间的引力是使行星如
r
m
F 4 k 2
r
2
一、行星与太阳的引力
5. 太阳对行星的作用力只跟行星质量,半径有关吗？还能从什么角度帮助我们向前更进一步？
6.牛顿第三定律能否帮助我们得到
结论：
m
F 4 k 2
r
2
′∝
太
2
？
其中 4 2 k 均为常量，与行星、太阳均无关。
（1）太阳对行星的引力跟行星的质量成正比，
O
mg
将地球视为一个规则的球体
由于地球的自转，地面不同位置的人会
做半径不同的匀速圆周运动：
=
4. 人在赤道上的受力分析
新人教版高中物理必修二 课件6.3 ：万有引力定律(共14张PPT)
第三节 万有引力定律
一 万有引力定律
1内容:自然界中任何两个物体都是相互吸 引的，引力的大小跟这两个物体的质量 的乘积成正比，跟它们的距离的二次方 成反比.万有引力.swf
2公式：F G m1m2
G
6.67
1011
N
r •
2
m
2
/
kg2
3适用范围 1)质点之间的相互作用 2)两个物体是质量分布均匀的球体 3)常见的两个物体间引力不适用
思考:把一质量为m的物体放在 地心上,问它和地球之间的万有 引力是多少?
例2:质量为M的均匀实心球体半径为R,球心 为O点.在球的右测挖去一个半径为R/2的小 球,将该小球置于OO`连线上距O为L的P点， O`为挖去小球后空腔部分的中心，则大球 剩余部分对P点小球的引力F为多少?
· O O`
万有引力定律的证明
里地 卡定
比利 文律
较 准 确
用 扭 秤
迪 许 （
一 百 多
年 ， 即
地装 年 在
测 出 了
置 ， 第
－
以 后 ，
牛 顿 发
引一 英 现
力 常 量
次 在 实 验 室
） ， 巧 妙
国 物 理 学 家
万 有 引 力
引力常量的测定有着非常重要的意义. 它不仅用实验证明了万有引力的存在, 更使得万有引力有了真正的实用价值. 例如,可以用测定地球表面物体重力加 速度的方法,测定地球的质量.也是这 一应用,卡文迪许被人们称为”能称出 地球质量的人”
。2021年3月18日星期四2021/3/182021/3/182021/3/18
15、会当凌绝顶，一览众山小。2021年3月2021/3/182021/3/182021/3/183/18/2021
一 万有引力定律
1内容:自然界中任何两个物体都是相互吸 引的，引力的大小跟这两个物体的质量 的乘积成正比，跟它们的距离的二次方 成反比.万有引力.swf
2公式：F G m1m2
G
6.67
1011
N
r •
2
m
2
/
kg2
3适用范围 1)质点之间的相互作用 2)两个物体是质量分布均匀的球体 3)常见的两个物体间引力不适用
思考:把一质量为m的物体放在 地心上,问它和地球之间的万有 引力是多少?
例2:质量为M的均匀实心球体半径为R,球心 为O点.在球的右测挖去一个半径为R/2的小 球,将该小球置于OO`连线上距O为L的P点， O`为挖去小球后空腔部分的中心，则大球 剩余部分对P点小球的引力F为多少?
· O O`
万有引力定律的证明
里地 卡定
比利 文律
较 准 确
用 扭 秤
迪 许 （
一 百 多
年 ， 即
地装 年 在
测 出 了
置 ， 第
－
以 后 ，
牛 顿 发
引一 英 现
力 常 量
次 在 实 验 室
） ， 巧 妙
国 物 理 学 家
万 有 引 力
引力常量的测定有着非常重要的意义. 它不仅用实验证明了万有引力的存在, 更使得万有引力有了真正的实用价值. 例如,可以用测定地球表面物体重力加 速度的方法,测定地球的质量.也是这 一应用,卡文迪许被人们称为”能称出 地球质量的人”
。2021年3月18日星期四2021/3/182021/3/182021/3/18
15、会当凌绝顶，一览众山小。2021年3月2021/3/182021/3/182021/3/183/18/2021
【课件】万有引力定律+课件-高一下学期物理人教版(2019)必修第二册
力趋于无限大.( × )
(3)由于太阳质量大，太阳对行星的引力大于行星对太阳的
引力.( × ) (4)牛顿发现了万有引力定律，并测出了引力常量.( × )
例2.(2021·湖南省高二学业考试)关于万有引力及其计
算公式F＝ Gmr1m2 2 ，下列说法正确的是（ D ）
A. 万有引力只存在于质量很大的两个物体之间 B. 根据公式知，r趋近于0时，F趋近于无穷大 C. 计算地球对卫星的引力时，r是指卫星到地球表 面的距离
实际测量：
在牛顿的时代，重力加速度已经能够比较精确地测定，也能较精 确的测定月球与地球间的距离和月球公转周期。
月球运动周期： T 27.3天
月球轨道半径： r 60R地 60 6400km
则月球绕地球的向心加速度为：
an
4 2r
T2
4 3.142 60 6400103 [(27.3 24) 3600]2
F引 Fn
1.太阳对行星的引力
4 2r
F引 Fn m T 2
不同的行星公转周期是不同的，T与r之间是存 在联系的，应设法消去上式中的T
开普勒第三定律：r 3 T2
k,变形为T2 =
r3 k
, 代入上式得到
4 2k
F引=m r2
4 2k
m r2
也就是F引
m r2
结论：太阳对不同行星的引力，与行星的质量
个人接近时他们不会吸在一起？我们通常分析物 体的受力时是否需要考虑物体间的万有引力？请 你根据实际情况，应用合理的数据，通过计算说 明以上两个问题。
例1.试估算两个质量50kg的同学相距0.5m时之间 的万有引力约有多大？（假设人可看做质点）
例2.那么太阳与地球之间的万有引力又是多大呢？ 太阳的质量为 M=2.0×1030kg，地球质量为 m=6.0×1024kg，日地之间的距离为 r=1.5×1011m。
(3)由于太阳质量大，太阳对行星的引力大于行星对太阳的
引力.( × ) (4)牛顿发现了万有引力定律，并测出了引力常量.( × )
例2.(2021·湖南省高二学业考试)关于万有引力及其计
算公式F＝ Gmr1m2 2 ，下列说法正确的是（ D ）
A. 万有引力只存在于质量很大的两个物体之间 B. 根据公式知，r趋近于0时，F趋近于无穷大 C. 计算地球对卫星的引力时，r是指卫星到地球表 面的距离
实际测量：
在牛顿的时代，重力加速度已经能够比较精确地测定，也能较精 确的测定月球与地球间的距离和月球公转周期。
月球运动周期： T 27.3天
月球轨道半径： r 60R地 60 6400km
则月球绕地球的向心加速度为：
an
4 2r
T2
4 3.142 60 6400103 [(27.3 24) 3600]2
F引 Fn
1.太阳对行星的引力
4 2r
F引 Fn m T 2
不同的行星公转周期是不同的，T与r之间是存 在联系的，应设法消去上式中的T
开普勒第三定律：r 3 T2
k,变形为T2 =
r3 k
, 代入上式得到
4 2k
F引=m r2
4 2k
m r2
也就是F引
m r2
结论：太阳对不同行星的引力，与行星的质量
个人接近时他们不会吸在一起？我们通常分析物 体的受力时是否需要考虑物体间的万有引力？请 你根据实际情况，应用合理的数据，通过计算说 明以上两个问题。
例1.试估算两个质量50kg的同学相距0.5m时之间 的万有引力约有多大？（假设人可看做质点）
例2.那么太阳与地球之间的万有引力又是多大呢？ 太阳的质量为 M=2.0×1030kg，地球质量为 m=6.0×1024kg，日地之间的距离为 r=1.5×1011m。
6-3-1万有引力定律-高中物理课件(人教版必修二)
解：
=3.5×1022N
3.5×1022 N 非常大，能够拉断直径为 9000 m 的钢柱． 万有引力的宏观性： 引力在天体与天体间,天体与物体间才 比较显著,在通常物体间的引力可忽略不计.
课堂练习
1. 要使两物体间的万有引力减小到原来的1/4，下列办法可采用 的是（ ABC ）
A. 使两个物体质量各减小一半，距离不变 B. 使其中一个物体的质量减小到原来的1/4，距离不变 C. 使两物体的距离增为原来的2倍，质量不变 D. 距离和两物体质量都减小为原来的1/4
牛顿思考流程
行星绕太阳公转的向心 力是太阳对行星的引力
F
m日m行 r2
卫星绕行星公转的向
心力是行星对卫星的
引力
F
m行 m卫 r2
地面上物体所受重
力来自地球对物体
的引力
F
m地 m
r2
一切物体间都存在引力
F
m1m2 r2
1.内容：自然界中任何两个物体都相互吸引，引力的方向在它们的连线上，
引力的大小F与物体的质量m1和m2的乘积成正比，与它们的距离r的二次方
4. 操场两边放着半径为r1、r2，质量分别为m1、m2的篮球和足球，两
者的直线间距为r，这两球间的万有引力大小为（ C ）
A.
G
m1m2 r2
B.
大于G
m1m2 r2
C.
小于G
m1m2 r2
D.无法判断
r
5、如图所示，r 虽然大于两球的半径，但两球的半径不能忽略，而球的
质量分布均匀，大小分别为m1与m2，则两球间万有引力的大小为( D )
Mm F G r2 “天上”的力与“人间”的力是同一种力
月 ─ 地检验
=3.5×1022N
3.5×1022 N 非常大，能够拉断直径为 9000 m 的钢柱． 万有引力的宏观性： 引力在天体与天体间,天体与物体间才 比较显著,在通常物体间的引力可忽略不计.
课堂练习
1. 要使两物体间的万有引力减小到原来的1/4，下列办法可采用 的是（ ABC ）
A. 使两个物体质量各减小一半，距离不变 B. 使其中一个物体的质量减小到原来的1/4，距离不变 C. 使两物体的距离增为原来的2倍，质量不变 D. 距离和两物体质量都减小为原来的1/4
牛顿思考流程
行星绕太阳公转的向心 力是太阳对行星的引力
F
m日m行 r2
卫星绕行星公转的向
心力是行星对卫星的
引力
F
m行 m卫 r2
地面上物体所受重
力来自地球对物体
的引力
F
m地 m
r2
一切物体间都存在引力
F
m1m2 r2
1.内容：自然界中任何两个物体都相互吸引，引力的方向在它们的连线上，
引力的大小F与物体的质量m1和m2的乘积成正比，与它们的距离r的二次方
4. 操场两边放着半径为r1、r2，质量分别为m1、m2的篮球和足球，两
者的直线间距为r，这两球间的万有引力大小为（ C ）
A.
G
m1m2 r2
B.
大于G
m1m2 r2
C.
小于G
m1m2 r2
D.无法判断
r
5、如图所示，r 虽然大于两球的半径，但两球的半径不能忽略，而球的
质量分布均匀，大小分别为m1与m2，则两球间万有引力的大小为( D )
Mm F G r2 “天上”的力与“人间”的力是同一种力
月 ─ 地检验
物理人教版(2019)必修第二册7.2万有引力定律(共25张ppt)
观察与思考
利用已知行星与太阳间引力公式推导月球加速度
1.已知月心到地心的距离约为地球半径的60倍，则月球绕地球做圆周运
动的加速度与物体在地面附近下落时的加速度比值是多少？
月球受地球引力为： =
地月
2
地
月 =
= 2
月
苹果受地球引力为： =
地 苹
2
地
苹 =
= 2
观察与思考
思考1：生活中的匀速圆周运动遵从怎样的动力学规律？
合力提供向心力，即合 =
2
4π2
= 2 =2
思考2：行星绕太阳可看做匀速圆周运动，什么力提供
向心力？
太阳对行星的引力提供行星做圆周运动的向心力
观察与思考
思考3：太阳对行星的引力提供向心力，那么这
3
由开普勒三定律： 2
6.67×10－11 m2/kg2。
卡文迪什
4.对万有引力定律的理解
普遍性 宇宙间任何两个有质量的物体之间都存在着相互吸引的力
相互性 两个有质量的物体之间的万有引力是一对作用力和反作用力
宏观性
地面上的一般物体之间的万有引力比较小，与其他力比较可忽略不计，但在
质量巨大的天体之间或天体与其附近的物体之间，万有引力起着决定性作用
m太m
(2)太阳与行星间的引力公式 F＝G 2 中，G与太阳、行星都没有关
r
系。( √ )
(3)太阳对行星的引力大小等于行星对太阳的引力大小。(
√)
(4)太阳对行星的引力与行星的质量成正比，与太阳质量无关。
(
×)
月—地检验
观察与思考
如图甲所示秋天苹果成熟后会从树上落下来；如图乙所示为月球绕着地
物理人教版(2019)必修第二册7.2万有引力定律(共24张ppt)
)
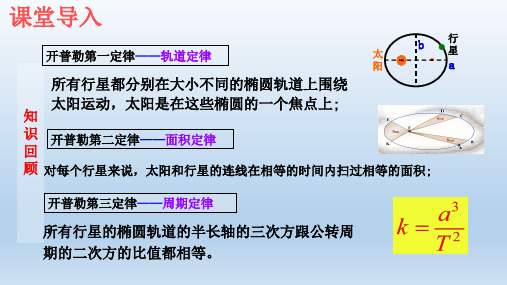
A、
G
m1m2 r2
C、
G
m1m2 (r1 r2 )2
B、
Байду номын сангаас
G
m 1 m2 r12
D 、G (r
m1m2 r1 r2 )2
r1
r2
r
3、如图所示，在距一个质量为M，半径为R，密度均匀的球体 表面R处，有一个质量为m的质点。此时M对m的万有引力为F1。 当从M中挖去如图所示半径为R/2的球体时，剩下部分对m的万 有引力为F2，则F1与F2的比为多少？
思考：两个物体距离越近，相互之间的引力就越大，对吗？
适用条件： 1、严格来讲，公式只适用于两个质点。 2、两个质量分布均匀的球体 3、质量分布均匀的球体与质点
m1
m2 r
四.引力常量G
卡文迪什也因此被称为“能称出地球质量的人”
亨利·卡文迪什
卡文迪什扭秤实验的测量方法 放大法
1.扭秤装置把微小力通过杠杆旋转 明显反映出来（一次放大）；
2.扭转角度（微小形变）通过光标 的移动来反映（二次放大），从而 确定物体间的万有引力。 实验数据：G=6.67×10-11 N·m2/kg2 实验意义：
①引力常量的普适性成了万有引力定 律正确性的有力证据；
②开创了微小量测量的先河，使科学 放大思想得到推广；
巩固练习
例1.计算两个质量都为50kg，相距0.5m的同学之间的万有引力 （两个同学可以看成质点）
地表处万有引力和重力的关系
赤道：F G m2r
两极：F=G
思考：为什么随着纬 度的增加，重力加速 度增大？
高空处万有引力和重力的关系
重力就是万有引力
mg GMm (R h)2
思考：为什么随着高 度的增加，重力加速 度减小？
【最新】人教版高一物理必修二教学课件 6.3 万有引力定律 (共36张PPT)
F
1m
F
1kg
G引力常量最早由卡文迪许测出G＝6.67×10－11N·m2／kg2
万有引力定律的意义
17世纪自然科学最伟大的成果之一，第一次揭示 了自然界中的一种基本相互作用的规律，在人类认 识自然的历史上树立了一座里程碑。
在文化发展史上的重大意义：统一了地面物体运 动规律和天体运动规律，使人们建立了有能力理解 天地间的各种事物的信心，解放了人们的思想，在 科学文化的发展史上起了积极的推动作用。
卡文迪许扭秤实验
光杠杆“放大”
卡文迪许(英国)
力矩“放大” Kθ =2 F L=2 L (Gmm’/r2)
原理:力矩平衡
“能称出地球质量的人” 知:g、R、G求M 重力近似等于万有引力 G M m/R2=m g M =gR2/G 地球密度ρ =M/V=（R2g/G)÷(4π R3/3 )=3g/(4π GR)
2、测中心天体的质量M和密度ρ
4 2 r 3 M GT 2 3 r GT 2 R3
3
中心天体 太阳 太阳 地球 地球 其他行星
环绕天体 地球 其他行星 月球 人造卫星 卫星
环绕m
中心M R
r
已知地球绕太阳公转的轨道半径是1.50×1011m，公转 周期是3.16×107s，求太阳质量M?
R2 g 2 g0 r
1 9.8 g g0 2.7 103 m / s 2 3600 3600
r
月球圆周运动向心加速度
4 2 r 4 2 60 6400 103 a 2 T (27.3 24 3600)2 =2.7 10-3m / s 2
两者相等说明了地球对苹果的引力和地球对月球的引力 是同一性质的力,都是万有引力。
人教版必修二73《万有引力定律》课件
索和宇宙研究提供了方向。
引力波探测
02
万有引力定律的深入研究将有助于引力波探测技术的发展，为
揭示宇宙奥秘提供更多线索。
暗物质和暗能量研究
03
万有引力定律可能为我们理解暗物质和暗能量等宇宙之谜提供
新的视角和思路。
THANKS。
详细描述
万有引力是一种在宏观低速领域适用的自然规律。在微 观高速领域，由于量子效应和相对论效应的影响，万有 引力的适用范围受到限制。在微观领域，需要使用量子 力学和相对论来描述物体之间的相互作用。然而，在宏 观低速领域，万有引力定律能够很好地描述物体之间的 相互作用，尤其是天体之间的相互作用。因此，在天文 学、地球物理学等领域中，万有引力定律具有重要的应 用价值。
他进一步思考，地球上的物体 受到的引力与它们的质量成正 比，而与它们之间的距离的平 方成反比。
牛顿认为，这种引力规律可能 适用于宇宙中的任何两个物体 。
牛顿的假设
牛顿假设宇宙中任何两个物体都 受到相互之间的引力作用，这个 力与它们的质量成正比，与它们
之间的距离的平方成反比。
他进一步假设，这个引力作用是 瞬时的，不受物体之间的距离影
万有引力定律为卫星轨道设计和航天器发射提供了理论基础，对 现代导航和航天技术发展至关重要。
地球科学
万有引力定律有助于研究地球的重力、地震和气候变化等现象。
日常生活
万有引力定律影响着我们日常生活中的许多事物，如物体的重量、 物体的落地等。
对未来科技发展的启示
探索宇宙
01
万有引力定律激发了人类对宇宙的探索热情，为未来的太空探
暗物质与暗能量
宇宙大爆炸理论认为，宇宙中存在暗物质和暗能量等未知的物质和能量形式。这 些物质和能量对宇宙的演化起着重要的作用，也对万有引力定律提出了新的挑战 和研究方向。
人教必修第二册第七章2.万有引力定律课件(34张)
[交流讨论] (1)你与同桌间的万有引力约为多少？(已知 G＝6.67×10－11 N·m2/kg2) (2)芝麻粒重力约为你和同桌之间引力的多少倍？为什么万有引力没把你和同桌吸到 一起？ (3)平时在对某物体受力分析时需要分析该物体受到的万有引力吗？ 提示：(1)F 万＝Gmr1m2 2 ＝6.67×10－11×605.×5525 N≈1.0×10－6 N (2)芝麻粒的重力约为 4.0×10－5 N，约为你和同桌之间引力的 40 倍。这时的引力很小， 远小于人和地面间的最大静摩擦力，所以两个人靠近时，不会吸引到一起。 (3)由(1)(2)知，平常两个物体间的万有引力非常小，故在进行受力分析时，一般不考 虑两物体的万有引力，除非是物体与天体、天体与天体间的相互作用。
2．适用条件： (1)严格地说，万有引力定律只适用于质点间的相互作用，其中 r 是两质点间的距离。 (2)万有引力定律也适用于计算两个质量分布均匀的球体间的相互作用，其中 r 是两 个球体球心间的距离。 (3)计算一个均匀球体与球外一个质点间的万有引力也适用，其中 r 为球心与质点间 的距离。 (4)两个物体间的距离远远大于物体本身的大小时，公式也近似适用，其中 r 为两物 体质心间的距离。
(2)引力常量测定的意义 ①卡文迪什利用扭秤装置通过改变小球的质量和距离，证实了万有引力的存在 及万有引力定律的正确性。 ②引力常量的确定使万有引力定律能够用于__定__量__计__算_，显示出真正的实用价 值。 ③卡文迪什扭秤实验是物理学上非常著名和重要的实验，_扭__秤__实验巧妙地将 _微__小__量进行_放__大__，开创了测量_弱__力__的新时代。
1．两个简化模型： (1)匀速圆周运动模型：由于太阳系中行星绕太阳做椭圆运动的轨迹的两个焦点靠得 很近，行星的运动轨迹非常接近圆，所以将行星的运动看成匀速圆周运动。 (2)质点模型：由于天体间的距离很远，研究天体间的引力时将天体看成质点，即天 体的质量集中在球心上。 提醒： (1)把行星的轨道简化为圆后，行星绕太阳的运动就简化成了匀速圆周运动，太阳对 行星的引力提供了行星做圆周运动的向心力。 (2)牛顿是在椭圆轨道下推导出太阳和行星间的引力大小的。
7.2万有引力定律-高一物理(人教版2019必修第二册)
7.2万有引力定律 一：知识精讲归纳一．万有引力定律(1)内容自然界中任何两个物体都相互吸引，引力的方向在它们的连线上，引力的大小与物体的质量m 1和m 2的乘积成正比，与它们之间距离r 的二次方成反比．(2)公式 F ＝G m 1m 2r 2. 3．符号意义(1)G 为引力常量，其数值由英国物理学家卡文迪许测量得出，常取G ＝6.67×10－11N·m 2/kg 2. (2)r 为两个质点间的距离或质量均匀的两个球体的球心间的距离． 二．万有引力的四个特性三．万有引力的效果万有引力F ＝G MmR 2的效果有两个，一个是重力mg ，另一个是物体随地球自转需要的向心力F n ＝mrω2，如图623所示，重力是万有引力的一个分力．图6231．重力与纬度的关系地面上物体的重力随纬度的升高而变大．(1)赤道上：重力和向心力在一条直线上F ＝F n ＋mg ，即G Mm R 2＝mrω2＋mg ，所以mg ＝G MmR 2－mrω2. (2)地球两极处：向心力为零，所以mg ＝F ＝G Mm R 2.(3)其他位置：重力是万有引力的一个分力，重力的大小mg ＜G MmR 2，重力的方向偏离地心． 2．重力与高度的关系由于地球的自转角速度很小，故地球自转带来的影响很小，一般情况下认为在地面附近：mg ＝G Mm R 2，若距离地面的高度为h ，则mg ＝G Mm (R ＋h )2(R 为地球半径，g 为离地面h 高度处的重力加速度)．所以距地面越高，物体的重力加速度越小，则物体所受的重力也越小．二：考点题型归纳题型一：万有引力定律的理解1．（2023春·安徽亳州·高一安徽省亳州市第一中学校考阶段练习）关于万有引力定律及公式122m m F G r ＝，下列说法正确的是（ ） A ．公式122m m F Gr ＝只适用于计算天体与天体之间的万有引力B ．当两物体的距离很近时，两物体间已不存在万有引力，故不能用公式122m m F G r ＝计算 C ．地球表面的物体受到地球的万有引力可用公式122m m F Gr ＝计算 D ．教室内，同学与课桌之间也有万有引力，并能直接运用公式122m m F Gr ＝计算 2．（2023·高一课时练习）下列关于万有引力定律说法正确的是（ ） A ．牛顿发现了万有引力定律，伽利略测得了引力常量 B ．根据表达式122m m F Gr =可知，当r 趋近于零时，万有引力趋近于无穷大 C ．万有引力恒量G 的单位是22N m kg -⋅⋅D ．两物体间的万有引力总是大小相等、方向相反，是一对平衡力 3．（2021·高一课时练习）关于万有引力定律，下列说法正确的是（ ） A ．万有引力定律只适用于天体，不适用于地面物体B ．若两位同学重心之间的距离远大于他们的尺寸，则这两位同学之间的万有引力的大小可用122m m F G r =近似计算 C ．万有引力大小的计算式122m m F Gr =中，对于不同星体G 的值不同 D ．地面上自由下落的苹果受到了地球的引力，而天空中运行的月亮没有受到地球的引力题型二：万有引力常量的G 的测定4．（2022春·湖南邵阳·高一期末）牛顿发现了万有引力定律一百多年后，英国物理学家卡文迪什在实验室里通过测量几个铅球之间的引力，从而测出了引力常量G 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.（一种方法）当研究物体不能看作质点时，可 以把物体假想分割成无数个质点，求出每个 质点受到的引力，然后求合力。
⑴如两形状不规则的物体：
m1 重心 L ①如果物体的大小相对于L大小不能忽略时，它 们的万有引力大小就不能用F引= Gm1m2/L2 求解。 ②如果物体的大小相对于L大小可以忽略时，它
面（附近）上的
物体，所受重力 等于万有引力
引力常量G的测定
1789年，英国物理学家卡文迪许 （H.Cavendish）利用扭秤，成功地测出 了引力常量G的数值，证明了万有引力定 律的正确。 卡文迪许解决问题的思路是，将 不易观察的微小变化量，转化为容易观 察的显著变化量，再根据显著变化量与 微小量的关系算出微小的变化量。
万有引力与重力的关系
物体在赤道上随地球做圆周运动， 合外力提供向心力
F引 F支 mw r
2
F支 F引 mw2r
以前知道静止在地面上 的物体
mg F支
mg F引 mw r
2
可见，重力 只是物体所受万
有引力的一个分
力，只是由于另 一个分力F向特 别小，所以一般 近似认为地球表
已知：太阳的质量为M=2.0×1030kg，地球质量为
m=5.8×1025kg，日地之间的距离为R=1.5×1011km
F=GMm/R2
=6.67×10-11×2.0×1030×6.0×1024/(1.5×1011)2
=3.5×1022(N) 3.5×1022N非常大，能够拉断直径为9000km的钢柱。 而太阳对质量为50kg的人，引力很小，不到0.3N。 当然我们感受不到太阳的引力。
▲行星轨道都是椭圆，但有圆近似，故计算时
可以认为是匀速圆周运动，太阳处在圆周轨道的圆 心处。
牛顿同时代的一些科学家， 如胡克、哈雷等对这一问题的 认识则更进一步，胡克认为， 行星围绕太阳运动是因为受到 太阳对它的引力，甚至证明了 如果行星的轨道是圆形的，它 所受的引力的大小跟行星到太 阳的距离二次方成反比。但是 他们无法证明在椭圆轨道下， 引力也遵循同样的规律，更没 能严格地证明这种引力的一般 规律。
3、引力常数的测定——卡文迪许扭秤
G=6.67×10－11 N· m2/kg2
G的物理意义——两质量各为1kg的物体相距1m时
万有引力的大小。
扭称原理流程图：
引力
放 大
金属丝 扭转
平面镜 放大 反射光 转动角度 转动
放 大
引力 力矩
扭转 力矩
金属丝 扭 转角度
光点 移动
引力常量得出的意义：
①证明了万有引力的存在，使万有引力定律 进入了真正实用的时代；
（2）根据F引= GMm/r2 因为： F引 ∝ Mm/r2 ， a∝1/r2
a=g/602=2.72×10-3m/s2
万有引力定律：
自然界中任何两个物体都是相互吸引的，引 力的大小跟这两个物体的质量的乘积成正比，跟 它们的距离的二次方成反比。
数学表达式：
Gm1m2 F= r2
单位：质量（kg）；距离（m）
F引 ∝ Mm/r2
写成等式：F引=
GMm/r2
地”检验)
已知月球绕地球的公转周期为27.3天，地 球半径为6.37×106m.轨道半径为地球半径的60 倍。月球绕地球的向心加速度 ？
（1
a=4π2r/T2 =2.71×10-3m/s2
G：是引力常数，其值为6.67259×10-11N· m2/kg2
适用条件： 1、可看成质点的两物体间 2、质量分布均匀球体的球体间 r 是两球心间的距离
适用条件
1. 严格讲，只适用于质点间的引力计算，而 当两物体间距离远远大于物体的尺寸时， 物体可看作质点。
2.特别地，当两物体是质量分布均匀的球体， 又不能看作质点时，它们间的引力计算时， r取球心间距离。
所以可以得出结论：太阳对行星的引力跟行星的
质量成正比，跟行星到太阳的距离的二次方成反比。 即：F∝m/r2
太阳对行星的引力 （F引）跟行星的质 量有关，F引与太阳质量有关吗？？
K与太阳质量有关
因为：F引=4π2km/r2
那么究竟F引与太阳质量有什么关系呢？？
牛顿根据牛顿第三定律大胆的猜想：既然太阳对行星 的引力与行星的质量成正比，也应该与太阳的质量成正比。
把行星绕太阳运动看作匀速圆周运动
r
R
近似化
如果认为行星绕太阳做匀速圆周运动，那么，太阳对 行星的引力F应为行星所受的向心力，即：
F引= F向=mw2r＝mv2/r 怎么办 因为： w＝2π/T ； v=2πr/T 呢？？ 得：F引=m(2πr/T)2/r= 4π2mr/T2 根据开普勒第三定律：r3/T2是常数k F引=4π2mr/T2= 4π2(r3/T2) m/r2 有：F引=4π2km/r2
我们感受不到呢？
假设质量均为60千克的两位同学，相距1米，他们
之间的相互作用的万有引力多大？ F=Gm1m2/R2 =6.67×10-11×60×60/12 =2.4×10-7(N) 2.4×10-7N是一粒芝麻重的几千分之一，这么小的 力人根本无法察觉到。
◆ 那么太阳与地球之间的万有引力又是多大呢？
②开创了微小量测量的先河，使科学放大思 想得到推广； ③卡文迪许被称为“第一个称量地球质量的 人”！
万有引力定律
__________________ _______________________
Law of Universal Gravitation
开普勒定律的得出为牛顿发现万有 引力定律打下了坚实的基础
在运用开普勒定律时注意：
▲定律不仅适用于行星，也适用于卫星。只不 过比值R3/T2=k’大小由行星决定。
重心
m2
们的万有引力大小就可以用F引= Gm1m2/L2 求解。
⑵如两质量分布均匀的球体：
m1 重心 L 无论球体的大小相对于L大小不能忽略也好， 重心
m2
可以忽略也罢，它们的万有引力大小都可以用
F引= Gm1m2/L2 求解。
为什么我们感觉不到旁边同学的引力呢？？
◆ 我们人与人之间也一样存在万有引力，可是为什么
⑴如两形状不规则的物体：
m1 重心 L ①如果物体的大小相对于L大小不能忽略时，它 们的万有引力大小就不能用F引= Gm1m2/L2 求解。 ②如果物体的大小相对于L大小可以忽略时，它
面（附近）上的
物体，所受重力 等于万有引力
引力常量G的测定
1789年，英国物理学家卡文迪许 （H.Cavendish）利用扭秤，成功地测出 了引力常量G的数值，证明了万有引力定 律的正确。 卡文迪许解决问题的思路是，将 不易观察的微小变化量，转化为容易观 察的显著变化量，再根据显著变化量与 微小量的关系算出微小的变化量。
万有引力与重力的关系
物体在赤道上随地球做圆周运动， 合外力提供向心力
F引 F支 mw r
2
F支 F引 mw2r
以前知道静止在地面上 的物体
mg F支
mg F引 mw r
2
可见，重力 只是物体所受万
有引力的一个分
力，只是由于另 一个分力F向特 别小，所以一般 近似认为地球表
已知：太阳的质量为M=2.0×1030kg，地球质量为
m=5.8×1025kg，日地之间的距离为R=1.5×1011km
F=GMm/R2
=6.67×10-11×2.0×1030×6.0×1024/(1.5×1011)2
=3.5×1022(N) 3.5×1022N非常大，能够拉断直径为9000km的钢柱。 而太阳对质量为50kg的人，引力很小，不到0.3N。 当然我们感受不到太阳的引力。
▲行星轨道都是椭圆，但有圆近似，故计算时
可以认为是匀速圆周运动，太阳处在圆周轨道的圆 心处。
牛顿同时代的一些科学家， 如胡克、哈雷等对这一问题的 认识则更进一步，胡克认为， 行星围绕太阳运动是因为受到 太阳对它的引力，甚至证明了 如果行星的轨道是圆形的，它 所受的引力的大小跟行星到太 阳的距离二次方成反比。但是 他们无法证明在椭圆轨道下， 引力也遵循同样的规律，更没 能严格地证明这种引力的一般 规律。
3、引力常数的测定——卡文迪许扭秤
G=6.67×10－11 N· m2/kg2
G的物理意义——两质量各为1kg的物体相距1m时
万有引力的大小。
扭称原理流程图：
引力
放 大
金属丝 扭转
平面镜 放大 反射光 转动角度 转动
放 大
引力 力矩
扭转 力矩
金属丝 扭 转角度
光点 移动
引力常量得出的意义：
①证明了万有引力的存在，使万有引力定律 进入了真正实用的时代；
（2）根据F引= GMm/r2 因为： F引 ∝ Mm/r2 ， a∝1/r2
a=g/602=2.72×10-3m/s2
万有引力定律：
自然界中任何两个物体都是相互吸引的，引 力的大小跟这两个物体的质量的乘积成正比，跟 它们的距离的二次方成反比。
数学表达式：
Gm1m2 F= r2
单位：质量（kg）；距离（m）
F引 ∝ Mm/r2
写成等式：F引=
GMm/r2
地”检验)
已知月球绕地球的公转周期为27.3天，地 球半径为6.37×106m.轨道半径为地球半径的60 倍。月球绕地球的向心加速度 ？
（1
a=4π2r/T2 =2.71×10-3m/s2
G：是引力常数，其值为6.67259×10-11N· m2/kg2
适用条件： 1、可看成质点的两物体间 2、质量分布均匀球体的球体间 r 是两球心间的距离
适用条件
1. 严格讲，只适用于质点间的引力计算，而 当两物体间距离远远大于物体的尺寸时， 物体可看作质点。
2.特别地，当两物体是质量分布均匀的球体， 又不能看作质点时，它们间的引力计算时， r取球心间距离。
所以可以得出结论：太阳对行星的引力跟行星的
质量成正比，跟行星到太阳的距离的二次方成反比。 即：F∝m/r2
太阳对行星的引力 （F引）跟行星的质 量有关，F引与太阳质量有关吗？？
K与太阳质量有关
因为：F引=4π2km/r2
那么究竟F引与太阳质量有什么关系呢？？
牛顿根据牛顿第三定律大胆的猜想：既然太阳对行星 的引力与行星的质量成正比，也应该与太阳的质量成正比。
把行星绕太阳运动看作匀速圆周运动
r
R
近似化
如果认为行星绕太阳做匀速圆周运动，那么，太阳对 行星的引力F应为行星所受的向心力，即：
F引= F向=mw2r＝mv2/r 怎么办 因为： w＝2π/T ； v=2πr/T 呢？？ 得：F引=m(2πr/T)2/r= 4π2mr/T2 根据开普勒第三定律：r3/T2是常数k F引=4π2mr/T2= 4π2(r3/T2) m/r2 有：F引=4π2km/r2
我们感受不到呢？
假设质量均为60千克的两位同学，相距1米，他们
之间的相互作用的万有引力多大？ F=Gm1m2/R2 =6.67×10-11×60×60/12 =2.4×10-7(N) 2.4×10-7N是一粒芝麻重的几千分之一，这么小的 力人根本无法察觉到。
◆ 那么太阳与地球之间的万有引力又是多大呢？
②开创了微小量测量的先河，使科学放大思 想得到推广； ③卡文迪许被称为“第一个称量地球质量的 人”！
万有引力定律
__________________ _______________________
Law of Universal Gravitation
开普勒定律的得出为牛顿发现万有 引力定律打下了坚实的基础
在运用开普勒定律时注意：
▲定律不仅适用于行星，也适用于卫星。只不 过比值R3/T2=k’大小由行星决定。
重心
m2
们的万有引力大小就可以用F引= Gm1m2/L2 求解。
⑵如两质量分布均匀的球体：
m1 重心 L 无论球体的大小相对于L大小不能忽略也好， 重心
m2
可以忽略也罢，它们的万有引力大小都可以用
F引= Gm1m2/L2 求解。
为什么我们感觉不到旁边同学的引力呢？？
◆ 我们人与人之间也一样存在万有引力，可是为什么