高中数学频率与概率检测试题(附答案)-学习文档
高中数学北师大版必修三学业分层测评第3章 1.1 频率与概率 1.2 生活中的概率 Word版含解析

学业分层测评(建议用时:分钟)[学业达标]一、选择题.下列事件中,是随机事件的为( ).水涨船高.冬天下雪.水中捞月.冬去春来【解析】水涨船高.冬去春来为必然事件.水中捞月是不可能事件.冬天下雪为随机事件.【答案】.某工厂生产的产品合格率是,这说明( ).该厂生产的件产品中不合格的产品一定有件.该厂生产的件产品中合格的产品一定有件.合格率很大,该厂生产的件产品中没有不合格产品.该厂生产的产品合格的可能性是【解析】合格率是说明该厂生产的产品合格的可能性是.【答案】.“今天北京的降雨概率是,上海的降雨概率是”,下列说法不正确的是( ).北京今天一定降雨,而上海一定不降雨.上海今天可能降雨,而北京可能没有降雨.北京和上海都可能没降雨.北京降雨的可能性比上海大【解析】概率反映了随机事件发生的可能性的大小,但对某一随机事件来说,在一次试验中可能发生也可能不发生,故项不正确.【答案】.根据山东省教育研究机构的统计资料,今在校中学生近视率约为,某配镜商要到一中学给学生配镜,若已知该校学生总数为人,则该眼镜商应带眼镜的数目为( ).副.副.不少于副.不多于副【解析】根据概率相关知识,该校近视生人数约为×=,结合实际情况,眼镜商应带眼镜数不少于副,故选.【答案】.从存放号码分别为,…,的卡片的盒子中,有放回地取次,每次取一张卡片并记下号码,统计结果如下:....【解析】==.【答案】二、填空题.下列事件:①贺天奉在一次比赛中,罚球一次,命中;②测得某天的最高气温是℃;③掷一次骰子,向上一面的数字是;④度量四边形的内角和,结果是°,其中必然事件有,不可能事件有,随机事件有.【解析】①命中与否不确定,是随机事件;②测得某天的最高气温是℃,是不可能事件;③掷骰子,向上的点数是,是随机事件;④度量四边形的内角和,结果是°,是必然事件.【答案】④②①③.某工厂为了节约用电,规定每天的用电量指标为度,按照上个月的用电记录,在天中有天的用电量超过指标,若第二个月仍没有具体的节电措施,则该月的第一天用电量超过指标的概率是.【解析】由频率的定义可知用电量超过指标的频率为=,频率约为概率.【答案】.某人捡到不规则形状的五面体石块,他在每个面上作了记号,投掷了次,并且记录了每个面落在桌面上的次数(如下表).如果再投掷一次,请估计石块的第面落在桌面上的概率约是.。
频率与概率(含答案)

频率与概率1.数据的收集方法:普查:为一特定目的而对所有考察对象的全面调查抽样调查:为一特定目的而对部分考察对象作调查2.事件的判断:确定事件,必然事件。
3概率的意义的说确性,简单的概率的计算,概率的计算的两种方法(列表法,画数状图法)4游戏的公平与不公平问题。
一、选择题1.【05江】以上说法合理的是()A、小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30%B、抛掷一枚普通的正六面体骰子,出现6的概率是1/6的意思是每6次就有1次掷得6C、某彩票的中奖机会是2%,那么如果买100彩票一定会有2中奖。
D、在一次课堂进行的试验中,甲、乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51。
2.【05江】一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来的情况下,为估计白球的个数,小刚向其中放入8个黑球,摇匀后从中随机摸出一个球记下颜色,再把它放回盒中,不断重复,共摸球400次,其中88次摸到黑球,估计盒约有白球()A、28个B、30个C、36个D、42个3.【05】有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”, “08”和“”的字块,如果婴儿能够排成“2008”或者“2008”,则他们就给婴儿奖励.假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是:A.16B.14C.13D.124.【05】如图,小明周末到外婆家,走到十字路口处,记不清前面哪条路通往外婆家,那么他能一次选对路的概率是(A)12(B)13(C)14(D)05.【05】在一个暗箱里放入除颜色外其它都相同的3个红球和11个黄球,搅拌均匀后随机任取一个球,取到是红球的概率是( )A、311B、811C、1114D、3146.【05课改】在100奖卷中,有4中奖,小红从中任抽1,他中奖的概率是A、14B、120C、125D、1100(第11题)7.【05】有6背面相同的扑克牌,正面上的数字分别是4,5,6,7,8,9.若将这六牌背面朝上洗匀后,从中任意抽取一,那么这牌正面上的数字是9的概率为A.23 B. 12 C. 13 D. 168.【05】随机掷一枚均匀的硬币两次,两次正面都朝上 的概率是( ) A 、41 B 、21 C 、43 D 、19.【05】下列说确的是A .抛一枚硬币正面朝上的机会与抛一枚图钉钉尖着地的机会一样大.B .为了了解火车站某一天过的列车车辆数,可采用普查的方式进行.C .彩票中奖的机会是1%,买100一定会中奖.D .市某中学学生小亮,对他所在的住宅小区的家庭进行调查,发现拥有空调的家庭占65%,于是他得出市拥有空调家庭的百分比为65%的结论.10.【05海门】 下列事件中,是确定事件的是A .明年元旦海门会下雨B .成人会骑摩托车C .地球总是绕着太阳转D .去要乘火车11.【05】如图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等,四位同学各 自发表了下述见解:甲:如果指针前三次都停在了3号扇 形,下次就一定不会停在3号扇形了乙:只要指针连续转 六次,一定会有一次停在6号扇形丙:指针停在奇数号扇形 的概率和停在偶数号扇形的概率相等丁:运气好的时候,只 要在转动前默默想好让指针停在6号扇形,指针停在6号扇 形的可能性就会加大。
频率与概率(含答案)

第二节频率与概率【回忆与思考】【例题经典】能够理解用试验得到的频率当作概率用例1〔2022年成都市〕含有4种花色的36张扑克牌的牌面都朝下,•每次抽出一张记下花色后再原样放回,洗匀牌后再抽.不断重复上述过程,•记录抽到红心的频率为25%,那么其中扑克牌花色是红心的大约有________张.【点评】频率为25%,就作为概率即36×25%=9〔即可〕能够根据实际情况制作模拟试验例2你几月份过生日?和同学交流,看看6个同学中是否有2个人同月过生日,开展调查,看看6个月中2个人同月过生日的概率大约是多少?【点评】以12月份为号编球或用计算器作模拟试验.能借助用频率估计理论概念的方法解决问题例3〔2022年临安市〕为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合鱼群中以后,再捕捞200条,假设其中有标记的鱼有10条,那么估计池塘里有鱼________条.【点评】这种方法本身就是一种估算,不能说它是一种准确值.【考点精练】一、根底练习1.某市对2400名年满15岁的男生的身高进行了测量,结果身高〔单位:m〕在1.68~1.70这一小组的频率为0.25,那么该组的人数为〔〕A.400人B.150人C.60人D.15人2.〔2022年河南省〕有一个不透明的布袋中,红色、黑色、白色的玻璃共有40个,除颜色外其它完全相同.小李通过屡次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%,那么口袋中白色球的个数很可能是〔〕A.6 B.16 C.18 D.243.〔2022年常德市〕右图是某中学七年级学生参加课外活动人数的扇形统计图,•假设参加舞蹈类的学生有42人,那么参加球迷活动的学生人数有〔〕A.145 B.147 C.149 D.1514.甲、乙、丙、丁四名运发动参加4×100米接力赛,•甲必须为第一接力棒或第四接棒的运发动,那么这四名运发动在比赛过程的接棒顺序有〔〕A.3种B.4种C.6种D.12种5.〔2022年青岛市〕一个口袋中有12个白球和假设干个黑球,•在不允许将球倒出来数的前提下,小亮为估计口袋中黑球的个数,采用了如下方法:•每次先从口袋中摸出10个球,求出其中白球数与10的比值,再把球放回口袋中摇匀.不断重复上述过程5次,得到的白球数与10的比值分别为:0.4,0.1,0.2,0.1,0.2,根据上述数据,•小亮可估计口袋中大约有_______个黑球.6.〔2022年温州市〕右图是由8•块相同的等腰直角三角形黑白瓷砖镶嵌而成的正方形示意图,一只蚂蚁在上面自由爬动,并随机停留在某块瓷砖上,•蚂蚁留在黑色瓷砖上的概率是_______.7.在一个有10万人的小镇,随机调查了2000人,其中有250•人看中央电视台的早间新闻,在该镇随便问一个人,他看早间新闻的概率大约是________.8.某口袋中有红色、黄色、蓝色玻璃球共72个.小明通过屡次摸球试验后,发现摸到红球、黄球、蓝球的概率依次是35%,25%和40%,•试估计口袋中三种玻璃球的数目依次是______.9.〔2022年泉州市〕在一个不透明的箱子里放有除颜色外,其余都相同的4个小球,其中红球有3个、白球1个.搅匀后,从中同时摸出2个小球,•请你写出这个实验中的一个可能事件:_________.二、水平提升10.〔2022年河南省〕一枚均匀的正方体骰子,六个面分别标有数字1,2,3,4,5,6,连续抛掷两次,朝上的数字分别是m,n.假设把m,n作为点A的横、纵坐标,那么点A〔•m,n〕在函数y=2x的图象上的概率是多少?11.〔2022年大连市〕在围棋盒中有x颗黑色棋子和y颗白色棋子,从盒中随机地取出一个棋子,如果它是黑色棋子的概率是38.〔1〕试写出y与x的函数关系式.〔2〕假设往盒中再放进10颗黑色棋子,那么取得黑色棋子的概率变为12,求x和y的值.12.有2个信封,每个信封内各装有四张卡片,其中一个信封内的四张卡片上分别写有1,2,3,4四个数,另一个信封内的四张卡片上分别写出5,6,7,8四个数,甲、乙两人商定了一个游戏,规那么是:从这两个信封中各随机抽取一张卡片,•然后把卡片上的两个数相乘,如果得到的积大于20,那么甲获胜,否那么乙获胜.〔1〕请你通过列表〔或画树状图〕计算甲获胜的概率;〔2〕你认为这个游戏公平吗?为什么?13.〔2022年泉州市〕在两个布袋中分别装有三个小球,这三个小球的颜色分别为红色、白色、绿色,其他没有区别,把两袋小球都搅匀后,再分别从两袋中各取出一个小球,试求取出两个相同颜色小球的频率〔要求用树状图或列表方法求解〕.14.〔2022年遂宁市〕将分别标有数字2,3,5的三张质地,•大小完全一样的卡片反面朝上放在桌面上.〔1〕随机抽取一张,求抽到奇数的概率;〔2〕随机抽取一张作为个位上的数字〔不放回〕,再抽取一张作为十位上的数字,•能组成哪些两位数?并求出抽取到的两位数恰好是35的概率.三、应用与探究15.〔2022年扬州市〕在一个不透明的口袋里装有只有颜色不同的黑、•白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,•再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:〔1〕请估计:当n很大时,摸到白球的频率将会接近_______;• 〔2〕假设你去摸一次,•你摸到白球的概率是________,•摸到黑球的概率是_______;〔3〕试估算口袋中黑、白两种颜色的球各有多少只?〔4〕解决了上面的问题,小明同学猛然顿悟,过去一个悬而未决的问题有方法了.这个问题是:在一个不透明的口袋里装有假设干个白球,•在不允许将球倒出来数的情况下,如何估计白球的个数〔可以借助其他工具及用品〕?请你应用统计和概率的思想和方法解决这个问题,写出解决这个问题的主要步骤及估算方法.答案:例题经典例1:9张例2:略例3:20000条考点精练1.A 2.B 3.B 4.D 5.48 6.1 27.12500人8.25个18个•29个9.摸到两个红球10.解:根据题意,以〔m,n〕为坐标的点A共有36个, 而只有〔•1,2〕,〔2,4〕,〔3,6〕三个点在函数y=2x图象上,所以,所求概率是336=112,即:点A在函数y=2x图象上的概率是11211.〔1〕y=53x 〔2〕x=15,y=2512.〔1〕•利用列表法得出所有可能的结果,如右表:由表格可知,该游戏所有可能的结果共16种,其中两张卡片上的数字之积大于20的有5种,所以甲获胜的概率为P甲=5 16〔2〕这个游戏对双方不公平,由于甲获胜的概率P甲=5 16,乙获胜的概率P乙=1116,1116≠516,所以,游戏对双方是不公平的.13.1 314.〔1〕23〔2〕1615.〔1〕0.6 〔2〕0.6,0.4〔3〕黑球有8个,白球12个〔4〕略。
高中数学频率检测试卷(有解析)

高中数学频率检测试卷(有解析)3.1.3频率与概率一、细心填一填(每题3分,共30分)1、任意掷一枚平均硬币两次,两次差不多上同一面朝上的概率是_1/2 ____2、小明、小刚、小亮三人正在做游戏,现在要从他们三人中选出一人去帮王奶奶干活,则小明被选中的概率为=1/3______, 小明未被选中的概率为=_2/3_____3、张强得身高今后会长到4米,那个事件得概率为___0______。
4、从一副扑克牌(除去大小王)中任抽一张。
则抽到红心的概率为= 1/4;抽到黑桃的概率为= 1/4;抽到红心3的概率为= 1/525、任意翻一下2021年日历,翻出1月6日的概率为1/366翻出4月3 1日的概率为0 。
6、单项选择题是数学试题的重要组成部分,当你遇到不明白做的情形时,假如你随便选一个答案(假设每个题目有4个备选答案),那么你答对的概率为1/4。
7、某班的联欢会上,设有一个摇奖节目,奖品为钢笔、图书和糖果,标于一个转盘的相应区域上(转盘被平均等分为四个区域,如图)。
转盘能够自由转动。
参与者转动转盘,当转盘停止时,指针落在哪一区域,就获得哪种奖品,则获得钢笔的概率为1/4。
8、一位汽车司机预备去商场购物,然后他随意把汽车停在某个停车场内,停车场分A、B两区,停车场内一个停车位置正好占一个方格且一个方格除颜色外完全一样,则汽车停在A区蓝色区域的概率是1/2 ,B区蓝色区域的概率是4/99、如图表示某班21位同学衣服上口袋的数目。
若任选一位同学,则其衣服上口袋数目为5的概率是4/2110、一个小妹妹将10盒蔬菜的标签全部撕掉了。
现在每个盒子看上去都一样。
然而她明白有三盒玉米,两盒菠菜,四盒豆角,一盒土豆。
她随机地拿出一盒并打开它。
则盒子里面是玉米的概率是3/10,盒子里面不是菠菜的概率是8/10= 4/5。
二、耐心选一选(每题3分,共30分)1、实验中学初三年级进行了一次数学测验,参考人数共540人,为了了解这次数学测验成绩,下列所抽取的样本中较为合理的是(D )A、抽取前100名同学的数学成绩B、抽取后100名同学的数学成绩C、抽取(1)、(2)两班同学的数学成绩D、抽取各班学号为3号的倍数的同学的数学成绩2、从A地到C地,可供选择的方案是走水路、走陆路、走空中.从A 地到B地有2条水路、2条陆路,从B地到C地有3条陆路可供选择,走空中从A地不经B地直截了当到C地.则从A地到C地可供选择的方案有( D )A、20种B、8种C、5种D、13种3、一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( B )A、B、C、D、4、下列事件发生的概率为0的是(C )A、随意掷一枚平均的硬币两次,至少有一次反面朝上;B、今年冬天黑龙江会下雪;C、随意掷两个平均的骰子,朝上面的点数之和为1;D、一个转盘被分成6个扇形,按红、白、白、红、红、白排列,转动转盘,指针停在红色区域。
人教B版(2019)高中数学必修第二册 第五章统计与概率5.3.4频率与概率同步习题(含答案)
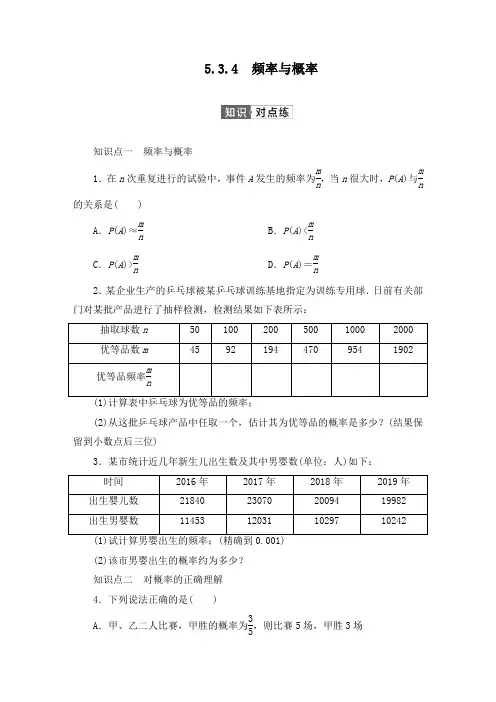
5.3.4 频率与概率知识点一频率与概率1.在n次重复进行的试验中,事件A发生的频率为mn,当n很大时,P(A)与mn的关系是( )A.P(A)≈mnB.P(A)<mnC.P(A)>mnD.P(A)=mn2.某企业生产的乒乓球被某乒乓球训练基地指定为训练专用球.日前有关部门对某批产品进行了抽样检测,检测结果如下表所示:抽取球数n 5010020050010002000 优等品数m 45921944709541902优等品频率m n(2)从这批乒乓球产品中任取一个,估计其为优等品的概率是多少?(结果保留到小数点后三位)3.某市统计近几年新生儿出生数及其中男婴数(单位:人)如下:时间2016年2017年2018年2019年出生婴儿数21840230702009419982 出生男婴数11453120311029710242(2)该市男婴出生的概率约为多少?知识点二对概率的正确理解4.下列说法正确的是( )A.甲、乙二人比赛,甲胜的概率为35,则比赛5场,甲胜3场B.某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈C.随机试验的频率与概率相等D.天气预报中,预报明天降水概率为90%,是指降水的可能性是90%5.围棋盒里放有同样大小的9枚白棋子和1枚黑棋子,每次从中随机摸出1枚棋子后再放回,一共摸10次,你认为一定有一次会摸到黑棋子吗?说明你的理由.知识点三用频率估计概率6.从某校高二年级的所有学生中,随机抽取20人,测得他们的身高(单位:cm)分别为:162,153,148,154,165,168,172,171,173,150,151,152,160,165,164,179,149,158,159,175.根据样本频率分布估计总体分布的原理,在该校高二年级的所有学生中任抽一人,估计该生的身高在155.5~170.5 cm之间的概率约为( )A.25B.12C.23D.137.在检测一批相同规格共500 kg航空用耐热垫片的品质时,随机抽取了280片,检测到有5片非优质品,则这批垫片中非优质品约为( ) A.8.834 kg B.8.929 kgC.10 kg D.9.835 kg8.随着互联网的普及,网上购物已逐渐成为消费时尚,为了解消费者对网上购物的满意情况,某公司随机对4500名网上购物消费者进行了调查(每名消费者限选一种情况回答),统计结果如下表:“满意”的概率是( )A.715B.25C.1115D.13159.某人捡到不规则形状的五面体石块,他在每个面上用数字1~5进行了标记,投掷100次,记录下落在桌面上的数字,得到如下频数表:10.某工厂为了节约用电,规定每天的用电量指标为1000度,按照上个月的用电记录,在30天中有12天的用电量超过指标,若这个月(按30天计)仍没有具体的节电措施,则该月的第一天用电量超过指标的概率约是________.11.对某批产品进行抽样检查,数据如下:抽查________件产品.12.某教授为了测试贫困地区和发达地区的同龄儿童的智力出了10个智力题,每个题10分,然后做了统计,统计结果如表:贫困地区到0.001);(2)求两个地区参加测试的儿童得60分以上的概率.13.某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如表:赔付金额(元)01000200030004000 车辆数500130100150120(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.14.假设甲、乙两种品牌的同类产品在某地区市场上销售量相等,为了解它们的使用寿命,现从这两种品牌的产品中分别随机抽取100个进行测试,结果统计如图所示:(1)估计甲品牌产品寿命小于200 h的概率;(2)这两种品牌产品中,某个产品已使用了200 h,试估计该产品是甲品牌的概率.15.近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计1000吨生活垃圾,数据统计如下(单位:吨):“厨余垃圾”箱“可回收物”箱“其他垃圾”箱厨余垃圾400100100可回收物3024030其他垃圾202060(1)试估计厨余垃圾投放正确的概率;(2)试估计生活垃圾投放错误的概率;(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,写出a,b,c的值(结论不要求证明),并求此时s2的值.:易错点一混淆概率与频率的概念把一枚质地均匀的硬币连续掷了1000次,其中有496次正面朝上,504次反面朝上,则可认为掷一次硬币正面朝上的概率为________.易错点二对用频率估计概率的方法理解不透致误已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989据此估计,该运动员三次投篮恰有两次命中的概率为________.一、单项选择题1.从一批电视机中随机抽出10台进行质检,其中有一台次品,下列说法正确的是( )A.次品率小于10% B.次品率大于10%C.次品率等于10% D.次品率接近10%2.某人将一枚硬币连抛10次,正面朝上的情形出现了6次,若用A表示正面朝上这一事件,则A的( )A.概率为35B.频率为35C.频率为6 D.概率接近0.63.从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码,统计结果如表:卡片号码12345678910 取到的次数101188610189119A.0.53 B.0.5C.0.47 D.0.374.若在同等条件下进行n次重复试验得到某个事件A发生的频率f(n),则随着n的逐渐增大,有( )A.f(n)与某个常数相等B.f(n)与某个常数的差逐渐减小C.f(n)与某个常数的差的绝对值逐渐减小D.f(n)在某个常数的附近摆动并趋于稳定5.对一批产品的长度(单位:毫米)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上为一等品,在区间[15,20)和[25,30)上为二等品,在区间[10,15)和[30,35]上为三等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是( )A.0.09 B.0.20C.0.25 D.0.456.某厂生产的电器是家电下乡政府补贴的指定品牌,其产品是优等品的概率为90%,现从该厂生产的产品中任意地抽取10件进行检验,结果前9件产品中有8件是优等品,1件是非优等品,那么第10件产品是优等品的概率为( ) A.90% B.小于90%C.大于90% D.无法确定7.有下列说法:①抛掷硬币出现正面向上的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上;②如果某种彩票的中奖概率为110,那么买10张这种彩票一定能中奖;③在乒乓球、排球等比赛中,裁判通过上抛均匀塑料圆板并让运动员猜着地时是正面还是反面来决定哪一方先发球,这样做不公平;④一个骰子掷一次得到点数2的概率是16,这说明一个骰子掷6次会出现一次点数2.其中不正确的说法是( )A.①②③④ B.①②④C.③④ D.③8.某市交警部门在调查一起车祸过程中,所有的目击证人都指证肇事车是一辆普通桑塔纳出租车,但由于天黑,均未看清该车的车牌号码及颜色,而该市有两家出租车公司,其中甲公司有100辆桑塔纳出租车,3000辆帕萨特出租车,乙公司有3000辆桑塔纳出租车,100辆帕萨特出租车.交警部门应先调查哪家公司的车辆较合理?( )A.甲公司B.乙公司C.甲与乙公司D.以上都对二、多项选择题9.下列说法中,正确的有( )A.频率是反映事件发生的频繁程度,概率是反映事件发生的可能性大小B.百分率是频率,但不是概率C.频率是不能脱离试验次数n的实验值,而概率是具有确定性的不依赖于试验次数的理论值D.频率是概率的近似值,概率是频率的稳定值10.下列说法正确的是( )A.事件A的概率为P(A),必有0≤P(A)≤1B.事件A的概率P(A)=0.999,则事件A是必然事件C.用某种药物对患有胃溃疡的500名病人进行治疗,结果有380人有明显的疗效.现有胃溃疡的病人服用此药,则估计有明显疗效的概率约为76% D.某奖券的中奖率为50%,则某人购买此奖券10张,一定有5张中奖11.李老师在某大学连续3年主讲经济学院的高等数学,下表是李老师这门课3年来学生的考试成绩(取整数)分布:法正确的是( )A.估计她得90分以上(含90分)的概率约为0.067B.估计她得60~69分的概率约为0.150C.估计她得60分以上(含60分)的概率约为0.982D.估计她得59分以下(含59分)的概率约为0.10812.某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买,则下列说法正确的是( )B.估计顾客同时购买乙和丙的概率为0.2C.估计顾客在甲、乙、丙、丁中同时购买3种商品的概率为0.4D.如果顾客购买了甲,则该顾客同时购买乙、丙、丁中的丙的可能性最大三、填空题13.一家保险公司想了解汽车的挡风玻璃破碎的概率,公司收集了20000辆汽车的数据,时间是从某年的5月1日到下一年的4月30日,共发现有600辆汽车的挡风玻璃破碎,则一辆汽车在一年内挡风玻璃破碎的概率的近似值是________.14.一个容量为20的样本,数据的分组及各组的频数如下:[10,20)2个;[20,30)3个;[30,40)x个;[40,50)5个;[50,60)4个;[60,70]2个.则x等于________;根据样本的频率估计概率,数据落在[10,50)的概率约为________.15.玲玲和倩倩是一对好朋友,她俩都想去观看某明星的演唱会,可手里只有一张票,怎么办呢?玲玲对倩倩说:“我向空中抛2枚同样的一元硬币,如果落地后一正一反,就我去;如果落地后两面一样,就你去!”你认为这个游戏公平吗?答:________.16.某公司有5万元资金用于投资开发项目,如果成功,一年后可获收益12%;一旦失败,一年后将丧失全部资金的50%.下表是去年200例类似项目开发的实施结果.四、解答题17.电影公司随机收集了电影的有关数据,经分类整理得到下表:(1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;(2)随机选取1部电影,估计这部电影没有获得好评的概率;(3)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化,假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加0.1,哪类电影的好评率减少0.1,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)18.某中学从参加高一年级上学期期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示的频率分布直方图.观察图形的信息,回答下列问题:(1)估计这次考试的及格率(60分及以上为及格);(2)从该校高一年级随机选取一名学生,估计这名学生该次期末考试成绩在70分以上(包括70分)的概率.19.某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40) 天数21636257 4(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.20.甲、乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台机床生产的零件各100件进行检测,检测结果统计如下:测试指标[85,90)[90,95)[95,100)[100,105)[105,110)甲机床81240328 乙机床7184029 6(2)甲机床生产1件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20,假设甲机床某天生产50零件,请估计甲机床该天的日利润(单位:元);(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层随机抽样的方法抽取5件,从这5件中任意抽取2件进行质量分析,求这2件都是乙机床生产的概率.5.3.4 频率与概率知识点一频率与概率1.在n次重复进行的试验中,事件A发生的频率为mn,当n很大时,P(A)与mn的关系是( )A.P(A)≈mnB.P(A)<mnC.P(A)>mnD.P(A)=mn答案 A解析根据概率的定义,当n很大时,频率是概率的近似值.2.某企业生产的乒乓球被某乒乓球训练基地指定为训练专用球.日前有关部门对某批产品进行了抽样检测,检测结果如下表所示:抽取球数n 5010020050010002000 优等品数m 45921944709541902优等品频率m n(2)从这批乒乓球产品中任取一个,估计其为优等品的概率是多少?(结果保留到小数点后三位)解(1)表中乒乓球为优等品的频率依次是0.900,0.920,0.970,0.940,0.954,0.951.(2)由(1)知,随着抽取的球数n的增加,计算得到的频率值虽然不同,但都在常数0.950的附近摆动,所以任意抽取一个乒乓球检测时,其为优等品的概率约为0.950.3.某市统计近几年新生儿出生数及其中男婴数(单位:人)如下:(2)该市男婴出生的概率约为多少?解(1)2016年男婴出生的频率为1145321840≈0.524.同理可求得2017年、2018年和2019年男婴出生的频率分别为0.521,0.512,0.513.(2)该市男婴出生的概率约为0.52.知识点二对概率的正确理解4.下列说法正确的是( )A.甲、乙二人比赛,甲胜的概率为35,则比赛5场,甲胜3场B.某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈C.随机试验的频率与概率相等D.天气预报中,预报明天降水概率为90%,是指降水的可能性是90%答案 D解析A中,此概率只说明发生的可能性大小,具有随机性,并非一定是比赛5场甲胜3场;B中,此治愈率只说明发生的可能性大小,具有随机性,并非10个病人一定有1人治愈;C中,随机试验的频率可以估计概率,并不等于概率;D中,概率为90%,即可能性是90%.故选D.5.围棋盒里放有同样大小的9枚白棋子和1枚黑棋子,每次从中随机摸出1枚棋子后再放回,一共摸10次,你认为一定有一次会摸到黑棋子吗?说明你的理由.解不一定.有放回地摸10次棋子相当于做10次重复试验,因为每次试验的结果都是随机的,所以摸10次棋子的结果也是随机的.可能有两次或两次以上摸到黑棋子,也可能没有一次摸到黑棋子.知识点三用频率估计概率6.从某校高二年级的所有学生中,随机抽取20人,测得他们的身高(单位:cm)分别为:162,153,148,154,165,168,172,171,173,150,151,152,160,165,164,179,149,158,159,175.根据样本频率分布估计总体分布的原理,在该校高二年级的所有学生中任抽一人,估计该生的身高在155.5~170.5 cm之间的概率约为( )A.25B.12C.23D.13答案 A解析从已知数据可以看出,在随机抽取的这20名学生中,身高在155.5~170.5 cm之间的学生有8人,频率为25,故可估计在该校高二年级的所有学生中任抽一人,其身高在155.5~170.5 cm之间的概率约为2 5 .7.在检测一批相同规格共500 kg航空用耐热垫片的品质时,随机抽取了280片,检测到有5片非优质品,则这批垫片中非优质品约为( ) A.8.834 kg B.8.929 kgC.10 kg D.9.835 kg答案 B解析由题意可得,该批垫片中非优质品约为5280×500≈8.929 kg.8.随着互联网的普及,网上购物已逐渐成为消费时尚,为了解消费者对网上购物的满意情况,某公司随机对4500名网上购物消费者进行了调查(每名消费者限选一种情况回答),统计结果如下表:满意情况不满意比较满意满意非常满意人数200n 21001000 “满意”的概率是( )A.715B.25C.1115D.1315答案 C解析由题意,得n=4500-200-2100-1000=1200,所以随机调查的网上购物消费者中对网上购物“比较满意”或“满意”的总人数为1200+2100=3300,所以随机调查的网上购物消费者中对网上购物“比较满意”或“满意”的频率为33004500=1115.由此估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率为1115.故选C.9.某人捡到不规则形状的五面体石块,他在每个面上用数字1~5进行了标记,投掷100次,记录下落在桌面上的数字,得到如下频数表:落在桌面的数字1234 5 频数3218151322答案0.35解析落在桌面的数字不小于4,即4,5的频数共13+22=35,所以频率为35100=0.35,所以估计落在桌面的数字不小于4的概率约为0.35.10.某工厂为了节约用电,规定每天的用电量指标为1000度,按照上个月的用电记录,在30天中有12天的用电量超过指标,若这个月(按30天计)仍没有具体的节电措施,则该月的第一天用电量超过指标的概率约是________.答案0.4解析由频率的定义可知用电量超过指标的频率为1230=0.4,由频率估计概率,知第一天用电量超过指标的概率约是0.4.11.对某批产品进行抽样检查,数据如下:抽查________件产品.答案1000解析根据题表中数据可知合格品出现的频率依次为0.94,0.92,0.96,0.95,0.95,故合格品出现的概率约为0.95,因此要从该批产品中抽到950件合格品大约需要抽查1000件产品.12.某教授为了测试贫困地区和发达地区的同龄儿童的智力出了10个智力题,每个题10分,然后做了统计,统计结果如表:贫困地区到0.001);(2)求两个地区参加测试的儿童得60分以上的概率.解(1)贫困地区的频率分别逐渐趋近于0.5和0.55.故所求概率分别为0.5和0.55.13.某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如表:(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.解(1)设A表示事件“赔付金额为3000元”,B表示事件“赔付金额为4000元”,样本车辆总数n=500+130+100+150+120=1000,以频率估计概率得P(A)=1501000=0.15,P(B)=1201000=0.12.由于投保金额为2800元,赔付金额大于投保金额对应的情形是赔付金额为3000元或4000元,所以其概率为P(A)+P(B)=0.15+0.12=0.27.(2)设C表示事件“投保车辆中新司机获赔4000元”,由已知,样本车辆中车主为新司机的有0.1×1000=100辆,而赔付金额为4000元的车辆中,车主为新司机的有0.2×120=24辆.所以样本车辆中新司机车主获赔金额为4000元的频率为24100=0.24,由频率估计概率,得P(C)=0.24.14.假设甲、乙两种品牌的同类产品在某地区市场上销售量相等,为了解它们的使用寿命,现从这两种品牌的产品中分别随机抽取100个进行测试,结果统计如图所示:(1)估计甲品牌产品寿命小于200 h的概率;(2)这两种品牌产品中,某个产品已使用了200 h,试估计该产品是甲品牌的概率.解(1)甲品牌产品寿命小于200 h的频率为5+20100=14,用频率估计概率,所以甲品牌产品寿命小于200 h的概率为1 4 .(2)根据抽样结果,寿命大于200 h的产品共有75+70=145个,其中甲品牌产品有75个,所以在样本中,寿命大于200 h的产品是甲品牌的频率是75145=1529,用频率估计概率,所以已使用了200 h的该产品是甲品牌的概率为15 29.15.近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计1000吨生活垃圾,数据统计如下(单位:吨):“厨余垃圾”箱“可回收物”箱“其他垃圾”箱厨余垃圾400100100可回收物3024030其他垃圾202060(2)试估计生活垃圾投放错误的概率;(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,写出a,b,c的值(结论不要求证明),并求此时s2的值.求:错误!解(1)由题意可知,厨余垃圾600吨,投放到“厨余垃圾”箱400吨,故厨余垃圾投放正确的概率为400600=23.(2)由题意可知,生活垃圾投放错误有200+60+20+20=300,故生活垃圾投放错误的概率为3001000=3 10.(3)由题意可知,∵a+b+c=600,∴a,b,c的平均数为200,∴s2=13[(a-200)2+(b-200)2+(c-200)2]=13(a2+b2+c2-120000),∵(a+b+c)2=a2+b2+c2+2ab+2bc+2ac≥a2+b2+c2,因此有当a=600,b=0,c =0时,有s2=80000.易错点一混淆概率与频率的概念把一枚质地均匀的硬币连续掷了1000次,其中有496次正面朝上,504次反面朝上,则可认为掷一次硬币正面朝上的概率为________.易错分析由于混淆了概率与频率的概念而致误,事实上频率是随机的,而概率是一个确定的常数,与每次试验无关.答案0.5正解通过做大量的试验可以发现,正面朝上的频率都在0.5附近摆动,故掷一次硬币,正面朝上的概率是0.5,故填0.5.易错点二对用频率估计概率的方法理解不透致误已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989据此估计,该运动员三次投篮恰有两次命中的概率为________.易错分析(1)对随机数表认识不到位,不能准确找出恰有两次命中的组数;(2)对用频率估计概率的方法理解不到位,不能求出“运动员三次投篮恰有两次命中”的概率.答案1 4正解20组随机数中,恰有两次命中的有5组,用频率估计概率,因此,该运动员三次投篮恰有两次命中的概率为P=520=14.一、单项选择题1.从一批电视机中随机抽出10台进行质检,其中有一台次品,下列说法正确的是( )A.次品率小于10% B.次品率大于10%C.次品率等于10% D.次品率接近10%答案 D解析抽出的样本中次品率为110,即10%,所以总体中次品率大约为10%.2.某人将一枚硬币连抛10次,正面朝上的情形出现了6次,若用A表示正面朝上这一事件,则A的( )A.概率为35B.频率为35C.频率为6 D.概率接近0.6 答案 B解析因为抛了10次硬币,正面朝上的情形出现了6次,我们说频率为3 5,而不能说概率为35.3.从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码,统计结果如表:卡片号码 1 2 3 4 5 6 7 8 9 10 取到的次数101188610189119A .0.53B .0.5C .0.47D .0.37答案 A解析 取到号码为奇数的次数为10+8+6+18+11=53,所以f =53100=0.53,所以估计取到号码为奇数的概率约为0.53.4.若在同等条件下进行n 次重复试验得到某个事件A 发生的频率f (n ),则随着n 的逐渐增大,有( )A .f (n )与某个常数相等B .f (n )与某个常数的差逐渐减小C .f (n )与某个常数的差的绝对值逐渐减小D .f (n )在某个常数的附近摆动并趋于稳定 答案 D解析 由频率和概率的关系知,在同等条件下进行n 次重复试验得到某个事件A 发生的频率f (n ),随着n 的逐渐增加,频率f (n )逐渐趋近于概率.5.对一批产品的长度(单位:毫米)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上为一等品,在区间[15,20)和[25,30)上为二等品,在区间[10,15)和[30,35]上为三等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是( )A.0.09 B.0.20C.0.25 D.0.45答案 D解析由频率分布直方图的性质可知,样本数据在区间[25,30)上的频率为1-5×(0.02+0.04+0.06+0.03)=0.25,则二等品的频率为0.25+0.04×5=0.45,故任取1件产品为二等品的概率为0.45.6.某厂生产的电器是家电下乡政府补贴的指定品牌,其产品是优等品的概率为90%,现从该厂生产的产品中任意地抽取10件进行检验,结果前9件产品中有8件是优等品,1件是非优等品,那么第10件产品是优等品的概率为( ) A.90% B.小于90%C.大于90% D.无法确定答案 A解析概率是一个确定的常数,在试验前已经确定,与试验次数无关.故选A.7.有下列说法:①抛掷硬币出现正面向上的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上;②如果某种彩票的中奖概率为110,那么买10张这种彩票一定能中奖;③在乒乓球、排球等比赛中,裁判通过上抛均匀塑料圆板并让运动员猜着地时是正面还是反面来决定哪一方先发球,这样做不公平;④一个骰子掷一次得到点数2的概率是16,这说明一个骰子掷6次会出现一次点数2.其中不正确的说法是( )A.①②③④ B.①②④C.③④ D.③答案 A解析概率反映的是随机性的规律,但每次试验出现的结果具有不确定性,因此①②④错误;③中抛掷均匀塑料圆板出现正面与反面的概率相等,是公平的,因此③错误.8.某市交警部门在调查一起车祸过程中,所有的目击证人都指证肇事车是一辆普通桑塔纳出租车,但由于天黑,均未看清该车的车牌号码及颜色,而该市有。
10.3频率与概率-同步练习(含解析)高中数学人教A版(2019)必修第二册

10.3频率与概率 同步练习学校:___________姓名:___________班级:___________考号:___________一、单选题1.抛一枚硬币的试验中,下列对“伯努利大数定律”的理解正确的是( )A .大量的试验中,出现正面的频率为0.5.B .不管试验多少次,出现正面的概率始终为0.5C .试验次数增大,出现正面的经验概率为0.5D .试验次数每增加一次,下一次出现正面的频率一定比它前一次更接近于0.52.敏感性问题多属个人隐私.对敏感性问题的调查方案,关键是要使被调查者愿意作出真实回答又能保守个人秘密.例如为了调查中学生中的早恋现象,现有如下调查方案:在某校某年级,被调查者在没有旁人的情况下,独自一人回答问题.被调查者从一个罐子中随机抽一只球,看过颜色后即放回,若抽到白球,则回答问题A ;若抽到红球,则回答问题B .且罐中只有白球和红球.问题A :你的生日是否在7月1日之前?(本次调查中假设生日在7月1日之前的概率为12)问题B :你是否有早恋现象?已知一次实际调查中,罐中放有白球2个,红球3个,调查结束后共收到1585张有效答卷,其中有393张回答“是”,如果以频率替代概率,则该校该年级学生有早恋现象的概率是( )(精确到0.01)A .0.08B .0.07C .0.06D .0.053.甲同学在数学探究活动中做抛硬币实验,共抛掷了2000次,其中正面朝上的有1034次,则下列说法正确的是( )A .抛掷一枚硬币,正面朝上的概率为0.517B .甲同学的实验中,反面朝上的频率为0.483C .抛掷一枚硬币,反面朝上的概率小于0.5D .甲同学的实验中,正面朝上的频率接近0.5174.下列结论:①如果()0.9999P A =,那么A 为必然事件:②若事件A 与B 是互斥事件,则()()1P A P B +=;③概率是随机的,试验前不能确定;④若事件A 与B 是对立事件,则A 与B 一定是互斥事件.其中是正确的个数是( )A .1B .2C .3D .45.下列说法中,正确的是( )A .某种彩票中奖的概率是1%,因此买100张该种彩票一定会中奖B .做7次拋硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的概率是37C .若事件,,A B C 两两互斥,则()()()1P A P B P C ++=D .任意投掷两枚质地均匀的骰子,则点数和是3的倍数的概率是136.某学校在高三年级中抽取200名学生,调查他们课后完成作业的时间,并根据调查结果绘制了如下频率分布直方图.根据此直方图得出了下列结论,其中不正确的是( )A .所抽取的学生中有40人在2.5小时至3小时之间完成作业B .该校高三年级全体学生中,估计完成作业的时间超过4小时的学生概率为0.1C .估计该校高三年级学生的平均做作业的时间超过3小时D .估计该校高三年级有一半的学生做作业的时间在2.5小时至4.5小时之间7.进入8月份后,我市持续高温,气象局一般会提前发布高温橙色预警信号(高温橙色预警标准为24小时内最高气温将升至37摄氏度以上),在今后的3天中,每一天最高气温在37摄氏度以上的概率是35.用计算机生成了20组随机数,结果如下:116 785 812 730 134 452 125 689 024 169 334 217 109 361 908 284 044 147 318 027若用0,1,2,3,4,5表示高温橙色预警,用6,7,8,9表示非高温橙色预警,则今后的3天中恰有2天发布高温橙色预警信号的概率估计是( )A.35B.12C.1320D.258.从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码,统计结果如下:卡片号码12345678910取到的次数1110585121910119则取到号码为奇数的频率是()A.0.53B.0.51C.0.49D.0.47二、多选题9.某校高三年级有(1),(2),(3)三个班,一次期末考试,统计得到每班学生的数学成绩的优秀率(数学成绩在120分以上的学生人数与该班学生总人数之比)如表所示:班级(1)(2)(3)优秀率80%85%75%则下列说法一定正确的是()A.(2)班学生的数学成绩的优秀率最高B.(3)班的学生人数不一定最少C.该年级全体学生数学成绩的优秀率为80%D.若把(1)班和(2)班的数学成绩放在一起统计,得到优秀率为83%,则(1)班人数多于(2)班人数10.下述关于频率与概率的说法中,错误的是()A.设有一大批产品,已知其次品率为0.1,则从中任取100件,必有10件是次品B.做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的概率是3 7C.随机事件发生的频率就是这个随机事件发生的概率D.利用随机事件发生的频率估计随机事件的概率,即使随机试验的次数超过10000,所估计出的概率也不一定很准确.11.一座对外封闭的小岛上共有,,A B C 三座城市,三座城市第k 年居住人口分别为,,k k k x y z (单位万人,因为统计方法的影响,,,k k k x y z 可能不为整数或有理数),假设出生率与死亡率相当(即总人口不变),每年人口都会在三座城市间流动,如A 城每年有16留在A 城,有12去往B 城,有13去往C 城,总体流动情况如下表所示:城市每年去往A每年去往B每年去往C A161213B131612C121316则以下说法中,正确的有( )A .若11136,48,24x y z ===,则()()333,,36,36,36x y z =B .若三座城市人口均保持每年稳定不变,则111x y z ==C .无论初始人口如何分布,经过足够久的年份后,三座城市的人口数会趋向相同D .每两年的人口流动情况为下表所示:城市每两年去往A 每两年去往B 每两年去往C A133613361036B103613361336C13361036133612.高中某学校对一次高三联考物理成绩进行统计分析,随机抽取100名学生成绩得到如图所示的频率分布直方图,其中分组的区间为[)[)[)[)[)[]40,50,50,60,60,70,70,80,80,90,90,100,同时计划从样本中随机抽取个体进行随访,若从样本随机抽取个体互不影响,把频率视为概率,则下列结论正确的是( )A .学生成绩众数估计为75分B .考生成绩的第75百分位成绩估计为80分C .在[90,100]内随机抽取一名学生访谈,则甲被抽取的概率为0.01D .从[)40,50和[90,100]内各抽1名学生,[)70,80抽2名学生调研,又从他们中任取2人进行评估测试,则这2人来自不同组的概率为0.13三、填空题13.为研究吸烟是否与患肺癌有关,某肿瘤研究所采取有放回简单随机抽样的方法调查了10000人,已知非吸烟者占比75%,吸烟者中患肺癌的有63人,根据统计结果表明,吸烟者患肺癌的概率是未吸烟者患肺癌的概率的4.2倍,则估计本次研究调查中非吸烟者患肺癌的人数是 .14.在一个不透明的纸盒中装有4个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.8附近,则袋子中红球约有 个.15.在某地区进行流行病学调查,随机调查了100位某种疾病患者的年龄,得到如下的样本数据的频率分布直方图,由此可估计该地区一位这种疾病患者的年龄位于区间[20,70)的概率为.16.某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:利用该指标制定一个检测标准,需要确定临界值c ,将该指标大于c 的人判定为阳性,小于或等于c 的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为()p c ;误诊率是将未患病者判定为阳性的概率,记为()q c .假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.则当漏诊率()0.5p c =%时,误诊率()q c =.四、解答题17.某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:利用该指标制定一个检测标准,需要确定临界值c ,将该指标大于c 的人判定为阳性,小于或等于c 的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为()p c ;误诊率是将未患病者判定为阳性的概率,记为()q c .假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.(1)当临界值97.5c =时,求漏诊率()p c 和误诊率()q c ;(2)设函数()()()f c p c q c =+,当]95,[105c ∈时,求()f c 的解析式,并求()f c 在区间[95,105]上的最大值.18.为了解一个鱼塘中养殖的鱼的生长情况,从这个鱼塘中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:kg ),并将所得数据分组(每组包含左端值,不包含右端值),画出频率分布直方图,如图所示.(1)根据直方图作频率分布表;1.15,1.30中的概率为多少;(2)估计数据落在[)(3)将上面捕捞的100条鱼分别做一记号后再放回鱼塘,几天后再从鱼塘的多处不同位置捕捞出120条鱼,其中带有记号的鱼有6条,请根据这一情况来估计该鱼塘中鱼的总条数.19.某射击运动员进行双向飞碟射击训练,七次训练的成绩记录如下:射击次数n100120150100150160150n819512081119127121击中飞碟次数A(1)求各次击中飞碟的频率;(保留三位小数)(2)该射击运动员击中飞碟的概率约为多少?20.目前,随着人们的生活节奏的加快,人们出行时乘坐的交通工具也逐渐多样化.某公司为了了解员工上个月上、下班时,A B两种交通工具乘坐情况,从全公司所有的1000名员工中随机抽取了100人,发现样本中,A B两种交通工具都不乘坐的有5人,样本中仅乘坐A和仅乘坐B的员工月交通费用分布情况如下:交通费用交通工具不大于600元大于600元仅乘坐A27人3人仅乘坐B24人1人(1)估计该公司员工中上个月,A B两种交通工具都乘坐的人数;(2)从样本中仅乘坐B的员工中随机抽取1人,求该员工上个月交通费用大于600元的概率;(3)已知上个月样本中的员工乘坐交通工具方式在本月没有变化.现从样本中仅乘坐B的员工中随机抽查1人,发现他本月交通费用大于600元.结合(2)的结果,能否认为样本中仅乘坐B的员工中本月交通费用大于600元的人数有变化?请说明理由.21.甲、乙两人准备参加某电视台举办的地理知识抢答赛.比赛规则为:每轮比赛每人随机在题库中抽取一道题作答,答对得1分,答错或不答得0分,最后得分多的获胜.为了在比赛中取得比较好的成绩,甲、乙两人在比赛前进行了针对性训练,训练后的答题情况如下表:甲乙练习题目个数120120答错个数2420若比赛中每个人回答正确与否相互之间没有影响,且用频率代替概率.(1)估计甲、乙两人在比赛时答对题的概率;P A.(2)设事件A=“某轮比赛中甲得1分或乙得1分”,求()参考答案:1.B【分析】根据频率、概率、经验概率的概念分析可得答案.【详解】对于A,大量的试验中,出现正面的频率越来越接近于0.5,故A不正确;对于B,事件发生的概率是一个常数,与试验次数无关,所以不管试验多少次,出现正面的概率始终为0.5,故B正确;对于C,经验概率是指特定的事件发生的次数占总体试验样本的比率,随着试验次数增大,出现正面的经验概率约为0.5,故C不正确;对于D,试验次数每增加一次,不能判断下一次出现正面的频率比它前一次更接近于0.5,D不正确.故选:B2.A【分析】根据古典概型分别求出抽到红球的概率和抽到白球的概率,并且计算出回答问题A、B的人数,从而可分别计算出回答问题A、B的人中答“是” 的人数以及比例.【详解】从罐子中随机抽一个球, 抽到红球的概率为33 235=+,抽到白球的概率为22 235=+,所以回答问题A的人数是215856345⨯=人回答问题B的人数是315859515⨯=人,回答问题A的人中答“是” 的人数是1 6343172⨯=,所以回答问题B的人中答“是” 的人数是39331776-=,则估计该校该年级学生有早恋现象的概率为760.08 951=,故选:A3.B【分析】根据概率与频率的关系判断.【详解】甲同学的实验中,正面朝上的频率为0.517,反面朝上的频率为0.483,故B正确;抛掷一枚硬币,正面朝上与反面朝上的概率均为0.5,为定值,故AC错误;甲同学的实验中,正面朝上的频率就是0.517,而不是接近0.517,故D错误.故选:B4.A【分析】根据必然事件、互斥事件、对立事件、概率等知识确定正确答案.【详解】必然事件的概率是1,所以①错误.若事件A 与B 是互斥事件,则()()1P A P B +≤,所以②错误.概率是理论值,是固定值,与实验前后无关,所以③错误.若事件A 与B 是对立事件,则A 与B 一定是互斥事件,所以④正确.所以正确的有1个.故选:A 5.D【分析】根据随机事件的概念即可说明A 、B ;举例即可说明C 项;列举出事件包含的样本点的个数,根据古典概型的概率公式,计算即可得出D 项.【详解】对于A 项,由于事件结果的随机性,购买100张彩票不一定会中奖,故A 错误;对于B 项,做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的频率是37,不是概率为37,故B 错误;对于C 项,事件,,A B C 两两互斥,比如投掷质地均匀的骰子试验中,三个事件:投掷出1点,2点,3点,这三个事件两两互斥,但这三个事件的和事件发生的概率为12,故C 错误;对于D 项,任意投掷两枚质地均匀的骰子共包含36个等可能的样本点,其中点数和是3的倍数的情况有()()()()()()()()()()()()1,2,1,5,2,1,2,4,3,3,3,6,4,2,4,5,5,1,5,4,6,3,6,6,共12个样本点,根据古典概型的概率公式,可得概率是121363=,故D 正确.故选:D.6.C【分析】根据频率分布直方图结合统计、概率相关知识逐项分析判断.【详解】对于A ,在2.5小时至3小时之间的人数为0.40.520040⨯⨯=人,故A 正确;对于B ,该校高三年级全体学生中,估计完成作业的时间超过4小时的学生概率为()0.10.10.50.1+⨯=,故B 正确;对于C ,该校高三年级学生的平均做作业的时间为()0.1 1.250.3 1.750.5 2.250.4 2.750.3 3.250.2 3.750.1 4.250.1 4.750.5 2.75⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯⨯=,故C 不正确;对于D ,由图可估计该校高三年级学生做作业的时间在2.5小时至4.5小时之间的频率为()0.40.30.20.10.50.5+++⨯=,估计该校高三年级有一半的学生做作业的时间在2.5小时至4.5小时之间,故D 正确.故选:C .7.B【分析】查出20个随机数中表示今后3天中恰有2天发布高温橙色预警信号的随机数的个数,根据古典概型的概率公式,即可求得答案.【详解】由题意可知表示今后的3天中恰有2天发布高温橙色预警信号的随机数有:116 812 730 217 109 361 284 147 318 027共10个,故今后的3天中恰有2天发布高温橙色预警信号的概率估计是101202=,故选:B8.B【分析】运用频率定义计算即可.【详解】由题意知,取到号码为奇数的频率为115519110.51100++++=.故选:B.9.AB【分析】由题目表格中的数据,逐一判断选项,可得答案.【详解】选项A :显然(2)班学生的数学成绩的优秀率最高,故A 正确;选项B :只根据优秀率的大小,无法比较每个班人数的多少,故B 正确;选项C :该年级全体学生数学成绩的优秀率为全年级数学成绩优秀的学生人数与全年级学生总人数之比,由于各班的学生人数不知道,所以不能计算该年级全体学生数学成绩的优秀率,故C 错误;选项D :设(1)班、(2)班数学成绩优秀的人数分别为x ,y ,(1)班、(2)班人数分别为a ,b ,则80%x a =,85%y b=,得80%x a =,85%y b =,又(1)班和(2)班放在一起统计的优秀率为83%,即83%x y a b +=+,即80%85%83%a b a b+=+,即80858383a b a b +=+,得23b a =,则a b <,故D 错误.故选:AB.10.ABC【分析】根据频率与概率的关系,结合各选项的描述判断正误.【详解】对于A: 从中任取100件,可能有10件,A 错误;对于B: 做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的频率是37,不是概率为37,B 错误;对于C:多次重复试验中事件发生的频率在某一常数附近,此常数为概率,与描述不符,C 错误;对于D:10000次的界定没有科学依据,“不一定很准确"的表达正确,试验次数越多,频率越稳定在概率值附近,但并非试验次数越多,频率就等于概率,D 正确.故选: ABC.11.BCD【分析】由题意知,(),,k k k x y z 与()111,,k k k x y z +++满足的关系式,逐项计算即可得出答案.【详解】由题意知(),,k k k x y z 与()111,,k k k x y z +++满足关系式:111111632111263111326k k k k k k k k k k k k x x y z y x y z z x y z +++⎧=++⎪⎪⎪=++⎨⎪⎪=++⎪⎩,其中*k ∈N ,对于A ,当11136,48,24x y z ===,则211121112111111=34632111=34263111=40326x x y z y x y z z x y z ⎧=++⎪⎪⎪=++⎨⎪⎪=++⎪⎩,则322232223222111=37632111=36263111=35326x x y z y x y z z x y z ⎧=++⎪⎪⎪=++⎨⎪⎪=++⎪⎩,故A 错误;对于B ,在上述关系式中令111,,k k k k k k x x y y z z +++===,反解线性方程组,即可知k k k x y z ==恒成立,从而111x y z ==,故B 正确;对于C ,由流动比例的轮换对称性及总人口不变,知三座城市人口趋于相同,故C 正确;对于D ,将111111632111263111326k k k kk k k k k k k k x x y z y x y z z x y z +++⎧=++⎪⎪⎪=++⎨⎪⎪=++⎪⎩代入211121112111111632111263111326k k k k k k k k k k k k x x y z y x y z z x y z ++++++++++++⎧=++⎪⎪⎪=++⎨⎪⎪=++⎪⎩,则211121112111131310363636101313363636131013363636k k k k k k k k k k k k x x y z y x y z z x y z ++++++++++++⎧=++⎪⎪⎪=++⎨⎪⎪=++⎪⎩,故D 正确.故选:BCD.12.AB【分析】根据频率分布直方图估计出众数,第75百分位数可判断AB ;利用频率估计概率,古典概型等知识可判断CD.【详解】由频率分布直方图得,成绩在[)70,80的频率最高,所以估计成绩的众数为75分,故A 正确;因为0.010100.015100.020100.030100.75⨯+⨯+⨯+⨯=,所以估计第75百分位成绩为80分,故B 正确;因为成绩在[90,100]内的人数为1000.0101010⨯⨯=,所以随机抽取一名学生访谈,甲被抽取的概率为0.1,故C 错误;记从[)40,50抽取的1名学生为a ,从[90,100]抽取的1名学生为b ,从[)70,80抽取的2名学生为c ,d ,则从这4人中抽取2人,所有的可能结果为ab ,ac ,ad ,bc ,bd ,cd ,共6种,其中不同组的有ab ,ac ,ad ,bc ,bd ,共5种,所以这2人来自不同组的概率为56,故D 错误;故选:AB.13.45【分析】设非吸烟者患肺癌的概率为x ,根据题意列出方程,求出x ,即可得到答案【详解】本次研究调查中,非吸烟者有7500人,吸烟者样本量有2500人,设非吸烟者患肺癌的人数是x 人,则63 4.225007500x =⨯,45x =,因此,本次研究调查中非吸烟者患肺癌的人数为45人.故答案为:45.14.16【分析】设袋中红球有x 个,根据概率的概念列式求解即可.【详解】设袋中红球有x 个,根据题意,得0.84x x=+,解得:16x =,经检验:16x =是分式方程的解,所以袋中红球有16个.故答案为:1615.0.89【分析】根据频率分布直方图计算出这种疾病患者的年龄位于不在区间[20,70)频率,结合对立事件的概率公式得到概率.【详解】设A ={一人患这种疾病的年龄在区间[20,70)},所以()1()1(0.0010.0020.0060.002)1010.110.89P A P A =-=-+++⨯=-=.故答案为:0.8916.3.5%【分析】先根据左边的频率分布直方图得到97.5c =,再根据右边的频率分布直方图可得()q c .【详解】依题可知,左边图形第一个小矩形的面积为50.0020.5%⨯>,所以95100c <<,所以()950.0020.5%c -⨯=,解得:97.5c =,由右边的频率分布直方图可得()()0.0110097.550.0020.035 3.5%q c =⨯-+⨯==.故答案为:3.5%17.(1)0.5%,3.5%;(2)0.0080.82,95100()0.010.98,100105c c f c c c -+≤≤⎧=⎨-<≤⎩,0.07.【分析】(1)根据题意,由第一个图求出97.5c ≤的矩形面积,再根据第二个图求出97.5c ≥的矩形面积即可解出.(2)根据题意,确定分段点100,即可得出()f c 的解析式,再根据分段函数的最值求法即可解出.【详解】(1)依题意,()(95)0.002(97.595)0.0020.0050.5%p c c =-⨯=-⨯==,()0.01(97.595)50.0020.035 3.5%q c =⨯-+⨯==.(2)当[]95,100c ∈时,()()()(95)0.002(100)0.0150.0020.0080.82f c p c q c c c c =+=-⨯+-⨯+⨯=-+,当95c =时,max ()0.06f c =;当(100,105]c ∈时,()()()50.002(100)0.012(105)0.0020.010.98f c p c q c c c c =+=⨯+-⨯+-⨯=-,当105c =时,max ()0.07f c =,所以0.0080.82,95100()0.010.98,100105c c f c c c -+≤≤⎧=⎨-<≤⎩,()f c 在区间[95,105]上的最大值为0.07.18.(1)答案见解析(2)0.47(3)2000【分析】(1)根据小矩形面积为各组频率求出频率列表即可;(2)数据落在[)1.15,1.30中的概率即为[)1.15,1.30之间矩形面积之和;(3)根据分层抽样的比例关系即可得到答案.【详解】(1)根据频率分布直方图可知,频率=组距⨯(频率/组距),故可得下表分组频率[)1.00,1.050.05[)1.05,1.100.20[)1.10,1.150.28[)1.15,1.200.30[)1.20,1.250.15[)1.25,1.300.02(2)0.300.150.020.47++=,所以数据落在[)1.15,1.30中的概率约为0.47.(3)设水库中鱼的总条数约为x 条,则1206100x =,即12010020006x ⨯==,所以水库中鱼的总条数约为2000条.19.(1)0.810,0.792,0.800,0.810,0.793,0.794,0.807(2)0.800【分析】(1)根据射击次数及击中飞碟次数计算频率即可;(2)根据频率与概率的关系可得解.【详解】(1)根据表格中数据,击中飞碟的频率依次为8195120810.810,0.792,0.800,0.810100120150100====,1191271210.793,0.794,0.807150160150===.(2)由(1)可知该射击运动员在同一条件下击中飞碟的频率都在0.800附近摆动,所以该运动员击中飞碟的概率约为0.800.20.(1)400人(2)125(3)答案见解析【分析】(1)根据样本数据可计算得到样本中,A B 两种交通工具都乘坐的员工数,用样本估计总体可得结果;(2)根据古典概型概率公式直接求解即可;(3)根据随机事件概率比较小的特点来进行分析作答即可.【详解】(1)由题意知:样本中上个月仅乘坐A 的员工有27330+=人,仅乘坐B 的员工有24125+=人,,A B 两种交通工具都不乘坐的有5人,∴样本中,A B 两种交通工具都乘坐的员工有1003025540---=人,用样本估计总体,该公司员工中上个月,A B 两种交通工具都乘坐的人数为401000400100⨯=人.(2)记事件C :从样本中仅乘坐B 的员工中随机抽取1人,该员工上个月的交通费用大于600元,则()1124125P C ==+.(3)由(2)知:()125P C =;答案一:可以认为有变化.理由如下:()P C 比较小,概率比较小的事件一般不容易发生,一旦发生,就有理由认为本月交通费用大于600元的人数发生了变化,可以认为有变化.答案二:无法确定有没有变化.理由如下:事件C 是随机事件,()P C 比较小,一般不容易发生,但还是有可能发生的,无法确定有没有变化.21.(1)甲、乙两人在比赛时答对题的概率分别为4556,(2)2930【分析】(1)根据题中条件计算出频率,用频率代替概率即可;(2)根据互斥事件的概率加法公式进行计算即可.【详解】(1)由题意,可以估计甲在比赛时答对题的概率为:11202441205p -==,乙在比赛时答对题的概率为:21202051206p -==.(2)设事件B =“某轮比赛中甲得1分”,事件C =“某轮比赛中乙得1分”,则事件A BC BC BC =⋃⋃,所以41154529()()()()56565630P A P BC P BC P BC =++=⨯+⨯+⨯=.(或1129()1()15630P A P BC =-=-⨯=).。
人教版高中数学必修第二册10.3 频率与概率 同步练习(含答案)
人教版高中数学必修第二册10.3频率与概率同步练习基础过关练题组一频率与概率的意义1.下列说法中正确的是()A.任何事件发生的概率总是在区间(0,1)内B.频率是客观存在的,与试验次数无关C.随着试验次数的增加,频率一般会越来越接近概率D.概率是随机的,在试验前不能确定2.某人将一枚均匀的正方体骰子连续抛掷了100次,出现6点的次数为19,则()A.出现6点的概率为0.19B.出现6点的频率为0.19C.出现6点的频率为19D.出现6点的概率接近0.193.抛掷一枚质地均匀的硬币,如果连续抛掷1000次,那么第999次出现正面朝上的概率是()A.1999B.11000C.9991000D.124.(2019江苏无锡高一期末)某种彩票中奖的概率为110000,则下列说法正确的是()A.买10000张彩票一定能中奖B.买10000张彩票只能中奖1次C.若买9999张彩票未中奖,则第10000张必中奖D.买一张彩票中奖的可能性是110000题组二用频率估计概率5.从存放号码分别为1,2,…,10的卡片的盒子中有放回地取100次,每次取一张卡片并记下号码,统计结果如下:卡片号码12345678910取到的次数101188610189119则取到的号码为奇数的概率估计值是()A.0.53B.0.5C.0.47D.0.376.从某自动包装机包装的白糖中随机抽取20袋,测得各袋的质量如下(单位:g): 492496494495498497501502504496497503 506508507492496500501499用频率估计概率,该自动包装机包装的白糖质量在497.5~501.5g之间的概率约为()A.0.16B.0.25C.0.26D.0.247.假设甲、乙两种品牌的同类产品在某地区市场上的销售量相等,为了解它们的使用寿命,现从这两种品牌的产品中分别随机抽取100个进行测试,统计结果如图所示:(1)估计甲品牌产品寿命小于200小时的概率;(2)这两种品牌产品中,某个产品已使用了200小时,试估计该产品是甲品牌的概率.题组三用随机模拟方法估计概率8.用随机模拟方法估计概率时,其准确程度取决于()A.产生的随机数的大小B.产生的随机数的个数C.随机数对应的结果D.产生随机数的方法9.掷两枚均匀的骰子,用随机模拟方法估计出现点数之和为9的概率时,产生的整数随机数中,每个数字为一组()A.1B.2C.9D.1210.在利用整数随机数进行随机模拟试验中,整数a到整数b之间(包括a,b,且a<b)的每个整数出现的可能性是.11.一个盒中装有10支圆珠笔,其中7支一级品,3支二级品,任取一支,用随机模拟的方法求取到一级品的概率.12.一个袋中有7个大小、形状相同的小球,其中6个白球,1个红球,现任取1个,若为红球就停止,若为白球就放回,搅拌均匀后再接着取,试设计一个模拟试验计算恰好第三次摸到红球的概率.能力提升练题组一用频率估计概率1.(2019广东深圳中学高二下期中,)港珠澳大桥于2018年10月24日正式通车,它是中国境内一座连接香港、珠海和澳门的桥隧工程,桥隧全长55千米,桥面为双向六车道高速公路,大桥通行限速100km/h.现对大桥某路段上汽车行驶速度进行抽样调查,画出频率分布直方图(如图).根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过90km/h的概率分别为()A.85,0.25B.90,0.35C.87.5,0.25D.87.5,0.352.()在调查运动员是否服用过兴奋剂的时候,给出两个问题作答,无关紧要的问题是:“你的电话号码的尾数是奇数吗?”敏感的问题是:“你是否服用过兴奋剂?”然后要求被调查的运动员掷一枚均匀的硬币,如果出现正面,就回答第一个问题,否则回答第二个问题.被调查者不必告诉调查人员自己回答的是哪一个问题,只需回答“是”或“否”,由于回答哪一个问题只有被测试者自己知道,所以应答者一般乐意如实地回答问题.用这种方法调查了300名运动员,得到80个“是”的回答,则这群人中服用过兴奋剂的百分率大约为()A.4.33%B.3.33%C.3.44%D.4.44%3.()某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:上年度出险次数01234≥5保费0.85a a 1.25a 1.5a 1.75a2a随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:出险次数01234≥5频数605030302010(1)记A为事件“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;(2)记B为事件“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;(3)求续保人本年度平均保费的估计值.题组二随机模拟方法的应用4.(2020山东济南历城二中高一下月考,)为了配合新冠疫情防控,某市组织了以“停课不停学,成长不停歇”为主题的“空中课堂”教学活动,为了了解一周内学生的线上学习情况,从该市抽取了1000名学生进行调查,根据所得信息制作了如图所示的频率分布直方图.(1)为了估计从该市任意抽取的3名同学中恰有2人线上学习时间在[200,300)的概率P,特设计如下随机模拟试验:先由计算器产生0到9之间取整数值的随机数,依次用0,1,2,3,…,9的前若干个数字表示线上学习时间在[200,300)内,剩余的数字表示线上学习时间不在[200,300)内;再以每三个随机数为一组,代表线上学习的情况.假设用上述随机模拟方法产生了如下30组随机数,请根据这批随机数估计概率P; 907966191925271569812458932683431257 393027556438873730113669206232433474 537679138598602231(2)为了进一步进行调查,用比例分配的分层随机抽样方法从这1000名学生中抽取20名学生,在抽取的20人中,再从线上学习时间在[350,450)的同学中任意选择2名,求这2名同学来自同一组的概率.答案全解全析基础过关练1.C必然事件发生的概率为1,不可能事件发生的概率为0,所以任何事件发生的概率总在区间[0,1]内,故A中说法错误;B,D混淆了频率与概率的概念.故选C.2.B根据已知条件只能得到这100次随机试验中出现6点的频率为19100=0.19.3.D抛掷一枚质地均匀的硬币,每次都只出现两种结果:正面朝上,反面朝上,每种结果出现的可能性相等,故所求概率为12.4.D彩票中奖的概率为110000是指买一张彩票中奖的可能性为110000,D正确;买10000张这种彩票中奖为随机事件,即买10000张彩票,可能有一张中奖,可能有多张中奖,也可能不中奖,故A,B错误;若买9999张彩票未中奖,则第10000张彩票中奖的概率依然是110000,不是买10 000张彩票一定能中奖,C错误.故选D.5.A由题表得,取到的号码为奇数的频率是10+8+6+18+11100=0.53,所以取到的号码为奇数的概率的估计值为0.53.6.B样本中白糖质量在497.5~501.5g之间的有5袋,所以该自动包装机包装的白糖质量在497.5~501.5g之间的频率为520=0.25,则概率约为0.25.7.解析(1)由题图得,甲品牌产品寿命小于200小时的频率为5+20100=14,用频率估计概率,所以甲品牌产品寿命小于200小时的概率为14.(2)由题图得,甲、乙两品牌产品寿命大于200小时的共有75+70=145(个),其中甲品牌产品有75个,所以在样本中,寿命大于200小时的产品是甲品牌的频率是75145=1529,用频率估计概率,所以已使用了200小时的该产品是甲品牌的概率为1529.8.B随机数数量越多,概率越接近实际数.9.B由于掷两枚均匀的骰子,所以产生的整数随机数中,每2个数字为一组.10.答案1 - +1解析[a,b]中共有b-a+1个整数,每个整数出现的可能性相等,所以每个整数出现1 - +1.11.解析设事件A=“取到一级品”,①用计算机的随机函数RANDBETWEEN(1,10)或计算器产生1到10之间的整数随机数,用1,2,3,4,5,6,7表示取到一级品,8,9,10表示取到二级品;②每一个数作为一组,产生N组随机数;③统计其中出现1至7之间数的次数N1;④计算频率f n(A)= 1 ,即为事件A发生的概率的近似值.12.解析本题答案不唯一.用1,2,3,4,5,6表示白球,7表示红球,利用计算器或计算机产生1到7之间(包括1和7)取整数值的随机数.因为要求恰好第三次摸到红球的概率,所以每三个随机数作为一组.例如,产生20组随机数:666743671464571561156567732375716116614445117573552274114662相当于做了20次试验,在这些数组中,前两个数字不是7,第三个数字恰好是7就表示第一次、第二次摸到的是白球,第三次摸到的是红球,它们分别是567和117,共两组,因此恰好第三次摸到红球的概率约为220=0.1.能力提升练1.D由题中直方图知,众数为85+902=87.5,用频率估计概率得,行驶速度超过90 km/h的概率为0.05×5+0.02×5=0.35,故选D.2.B因为掷一枚硬币出现正面向上的概率为12,所以大约有150人回答第一个问题,又电话号码的尾数是奇数的概率为12,所以在回答第一个问题的150人中大约有75人回答了“是”,所以另外5个回答“是”的人服用过兴奋剂.因此我们估计5150×100%≈3.33%的人服用过兴奋剂.3.解析(1)事件A发生当且仅当一年内出险次数小于2.由所给数据知,一年内出险次数小于2的频率为60+50200=0.55,故P(A)的估计值为0.55.(2)事件B发生当且仅当一年内出险次数大于1且小于4.由所给数据知,一年内出险次数大于1且小于4的频率为30+30200=0.3,故P(B)的估计值为0.3.(3)由所给数据得下表:保费0.85a a 1.25a 1.5a 1.75a2a频率0.300.250.150.150.100.05调查的200名续保人的平均保费为0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a×0.05=1.1925a(元).因此,续保人本年度平均保费的估计值为1.1925a元.4.解析(1)由频率分布直方图可知,线上学习时间在[200,300)的频率为(0.002+0.006)×50=0.4,所以可以用数字0,1,2,3表示线上学习时间在[200,300)内,数字4,5,6,7,8,9表示线上学习时间不在[200,300)内.观察题中随机数组可得,3名同学中恰有2人线上学习时间在[200,300)的有191,271,812,932,431,393,027,730,206,433,138,602,共12个.用频率估计概率可得,该市3名同学中恰有2人线上学习时间在[200,300)的概率P=1230=0.4.(2)抽取的20人中,线上学习时间在[350,450)的同学有20×(0.003+0.002)×50=5人,其中线上学习时间在[350,400)的同学有3名,设为A,B,C,线上学习时间在[400,450)的同学有2名,设为a,b,用(x,y)表示样本空间中的样本点,则从5名同学中任取2名的样本空间Ω={(A,B),(A,C),(A,a),(A,b),(B,C),(B,a),(B,b),(C,a),(C,b),(a,b)},共10个样本点,用M表示“2名同学来自同一组”这一事件,则M={(A,B),(A,C),(B,C),(a,b)},共4个样本点,所以P(M)=410=0.4.。
人教B版高中数学必修三同步测试:313频率与概率(有答案)
人教B版高中数学必修三同步测试:3.1.3频率与概率一、单选题1. 设某厂产品的次品率为2%,估算该厂8000件产品中合格品的件数大约为()A.160B.7840C.7998D.78002. 下列结论正确的是()A.对事件A的概率P(A)必有0<P(A)<1B.若事件A的概率P(A)=0.999,则事件A是必然事件C.用某种药物对患有胃溃疡的500名病人治疗,结果有380人有明显的疗效,现有胃溃疡的病人服用此药,则估计其会有明显疗效可能性为76%D.某奖券中奖率为50%,则某人购买此奖券10张,一定有5张中奖3. 某市的天气预报中,有“降水概率预报”,例如预报“明天降水概率为90%”,这是指()A.明天该地区约有90%的地方会降水,其余地方不降水B.明天该地区约90%的时间会降水,其余时间不降水C.气象台的专家中,有90%认为明天会降水,其余的专家认为不降水D.明天该地区降水的可能性为90%4. 抛掷一枚质地均匀的正方体骰子(六个面上分别写有1, 2, 3, 4, 5, 6),若前3次连续抛到“6点朝上”,则对于第4次抛掷结果的预测,下列说法中正确的是()A.一定出现“6点朝上”B.出现“6点朝上”的概率大于C.出现“6点朝上”的概率等于D.无法预测“6点朝上”的概率二、双空题某人抛掷一枚硬币100次,结果正面朝上53次,设正面朝上为事件A,则事件A出现的频数为________,事件A出现的频率为________.三、填空题一家保险公司想了解汽车的挡风玻璃破碎的概率,公司收集了20000辆汽车,时间是从某年的5月1日到下一年的5月1日,共发现有600辆汽车的挡风玻璃破碎,则一辆汽车在一年时间里挡风玻璃破碎的概率近似为________.四、解答题有人说:“掷一枚骰子一次得到的点数是2的概率是,这说明掷一枚骰子6次会出现一次点数是2.”对此说法,同学中出现了两种不同的看法:一些同学认为这种说法是正确的.他们的理由是:因为掷一枚骰子一次得到点数是2的概率是,所以掷一枚骰子6次得到一次点数是2的概率P=×6=1,即“掷一枚骰子6次会出现一次点数是2”是必然事件,一定发生.还有一些同学觉得这种说法是错误的,但是他们却讲不出是什么理由来.你认为这种说法对吗?请说出你的理由.某教授为了测试贫困地区和发达地区的同龄儿童的智力,出了10个智力题,每个题10分.然后作了统计,下表是统计结果:贫困地区:发达地区:(1)利用计算器计算两地区参加测试的儿童中得60分以上的频率(精确到千分位);(2)分析贫富差距为什么会带来人的智力的差别.随机抽取往年的一个年份,对西安市该年4月份的天气情况进行统计,结果如下:(1)在今年4月份任取一天,估计西安市在该天不下雨的概率;(2)西安市某学校拟从今年4月份的一个晴天开始举行连续两天的运动会,估计运动会期间不下雨的概率.参考答案与试题解析人教B版高中数学必修三同步测试:3.1.3频率与概率一、单选题1.【答案】B【考点】离散型随机变量的期望与方差概率的应用列举法计算基本事件数及事件发生的概率【解析】8000×(1−2%=7840(件),故选B.【解答】此题暂无解答2.【答案】C【考点】命题的真假判断与应用二次函数的应用函数的最值及其几何意义【解析】由概率的基本性质事件A的概率P(A)的值满足:01(())1,故A错误;必然事件概率为1,故B错误;某奖券中奖率为50%,则某人购买此券105,不一定有5张中奖,故D错误.故选C.【解答】此题暂无解答3.【答案】D【考点】概率的应用离散型随机变量的期望与方差回归分析【解析】概率是对随机事件发生可能性大小的度量,选D.【解答】此题暂无解答4.【答案】C【考点】互斥事件与对立事件离散型随机变量的期望与方差 进行简单的合情推理 【解析】因为骰子质地均匀,所以掷一次6点朝上的概率为16,所以第4次抛掷6点朝上的概率为16故选C 【解答】 此题暂无解答 二、双空题 【答案】 53,0.53【考点】用频率估计概率 【解析】正面朝上53次,则正面朝上的频数为53:正面朝上的频率为0.53;故填53.53 【解答】 此题暂无解答 三、填空题【答案】 0.03【考点】用频率估计概率 【解析】记“一部汽车在一年时间里挡风玻璃破碎”为事件A 由概率的统计定义知,事件A 发生的概率大约为 60020000=3100=0.03【解答】 此题暂无解答 四、解答题【答案】 见解析 【考点】古典概型及其概率计算公式 相互独立事件的概率乘法公式列举法计算基本事件数及事件发生的概率【解析】试题分析:这种说法是错误的.上述认为说法正确的同学,其计算概率的方法自然也是错误的.按照摸球是否有放回分两类讨论,用类比的方法举例说明理由.试题解析:这种说法是错误的.上述认为说法正确的同学,其计算概率的方法自然也是错误的.为了弄清这个问题,我们不妨用类比法,即把问题变换一下说法原题中所说的问题类似于“在一个不透明的盒子里放有6个标有数字1,2,3.4,5.6的同样大小的球,从盒中摸一个球恰好摸到2号球的概率是16那么摸6次球是否一定会摸到一次2号球呢?”在这个摸球问题中,显然还缺少一个摸球的规则,即每次摸到的球是否需要放回盒子里?显然如果摸到后不放回,那么摸6次球一定会摸到一次2号球如果摸到球后需要放回,那么摸6次球就不一定会摸到一次2号球了.由此看来,我们先要弄清这个摸球问题与上面的掷骰子问题是否完全类同,是否应当有每次摸到的球还要放回盒子里的要求我们先看看上面掷骰子问题中的规则,在掷骰子问题中,表面上好像没写着什么规则,但实际上却藏有一个自然的规则,即第一次如果掷得某个数(如3),那么后面还允许继续掷得这个相同的数.于是摸球问题要想与掷骰子问题中的规则相同,显然每次摸到的球必须要放回盒子里才妥当.那么摸6次球就不一定会摸到一次2号球了.【解答】此题暂无解答【答案】(1)见解析;(2)见解析.【考点】独立性检验离散型随机变量及其分布列频率分布直方图【解析】(1)得60分以上的人数除以相应的参加测试的人数为得60分以上的频率,分别计算填入表格;(2)由该地区生活水平落后,导致儿童的健康和发育以及育事业发展落后.【解答】(1)贫困地区:】参加测试的人数】30】50】100】200】500】800】得60分以上的人数】16】27】52】104】265】402】得60分以上的频率】0.533】0.540】0.520】0.520】0.530】0.503发达地区:】参加测试的人数】30】50】100】200】500】800】得60分以上的人数】17】29】56】111】276】440】得60分以上的频率】0.567】0.580】0.560】0.555】0.552】0.550(2)经济上的贫困导致该地区生活水平落后,儿童的健康和发育会受到一定的影响:另外经济落后也会使教育事业发展落后,这都是贫富不同带来的智力差别的原因【答案】(1)13.15(2)运动会期间不下雨的概率为78【考点】几何概型计算(与长度、角度、面积、体积有关的几何概型)列举法计算基本事件数及事件发生的概率古典概型及其概率计算公式【解析】此题暂无解析【解答】(1)在容量为30的样本中,从表格中得,不下雨的天数是26,以频率估计概率,4月份任选一天,西安市不下雨的概率是2630=1315(2)称相邻两个日期为“互邻日期对”(如1日与2日,2日与3日等)这样在4月份中,前一天为晴天的互邻日期对有16对,其中后一天不下雨的有14个,所以晴天的次日不下雨的频率为1416=78,以频率估计概率,运动会期间不下雨的概率为78试题解析:(1)在容量为30的样本中,不下雨的天数是26,以频率估计概率,4月份任选一天,西安市不下雨的概率是1315(2)称相邻两个日期为“互邻日期对”(如1日与2日,2日与3日等)这样在4月份中,前一天为晴天的互邻日期对有16对,其中后一天不下雨的有14个,所以晴天的次日不下雨的频率为78,以频率估计概率,运动会期间不下雨的概率为78。
新教材高中数学第十章概率_事件的相互独立性频率与概率练习含解析新人教A版必修第二册
事件的相互独立性 频率与概率(25分钟 50分)一、选择题(每小题5分,共20分)1.“某彩票的中奖概率为1100 ”意味着( )A .买100张彩票就一定能中奖B .买100张彩票能中一次奖C .买100张彩票一次奖也不中D .购买彩票中奖的可能性为1100【解析】选D.概率是描述事件发生的可能性大小.2.已知A ,B 是两个相互独立事件,P(A),P(B)分别表示它们发生的概率,则1-P(A)P(B)是下列哪个事件的概率( ) A .事件A ,B 同时发生 B .事件A ,B 至少有一个发生 C .事件A ,B 至多有一个发生 D .事件A ,B 都不发生【解析】选C.P(A)P(B)是指A ,B 同时发生的概率,1-P(A)·P(B)是A ,B 不同时发生的概率,即至多有一个发生的概率.3.某年级有12个班,现要从2班到12班中选1个班的学生参加一项活动,有人提议:掷两个骰子,得到的点数之和是几就选几班,这种选法( ) A .公平,每个班被选到的概率都为112B .公平,每个班被选到的概率都为16C .不公平,6班被选到的概率最大D .不公平,7班被选到的概率最大【解析】选D.P(1)=0,P(2)=P(12)=136 ,P(3)=P(11)=118 ,P(4)=P(10)=112 ,P(5)=P(9)=19 ,P(6)=P(8)=536 ,P(7)=16.4.(2021·新高考Ⅰ卷)有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( ) A .甲与丙相互独立 B .甲与丁相互独立 C .乙与丙相互独立 D .丙与丁相互独立【解析】选B.设甲、乙、丙、丁事件的发生概率分别为P(A),P(B),P(C),P(D). 则P(A)=P(B)=16 ,P(C)=56×6 =536, P(D)=16.对于A 选项,P(AC)=0;对于B 选项, P(AD)= 16×6 =136 ;对于C 选项, P(BC)= 16×6 =136 ;对于D 选项,P(CD)=0.若两事件X ,Y 相互独立,则P(XY)=P(X)P(Y),因此B 选项正确. 二、填空题(每小题5分,共10分)5.某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至多命中一次的概率为1625 ,则该队员每次罚球的命中率为________. 【解析】设此队员每次罚球的命中率为p , 则1-p 2=1625 ,所以p =35 .答案:356.A ,B 两人进行一局围棋比赛,A 获得的概率为0.8,若采用三局两胜制举行一次比赛,现采用随机模拟的方法估计B 获胜的概率.先利用计算器或计算机生成0到9之间取整数值的随机数,用0,1,2,3,4,5,6,7表示A 获胜;8,9表示B 获胜,这样能体现A 获胜的概率为0.8.因为采用三局两胜制,所以每3个随机数作为一组.例如,产生30组随机数:034 743 738 636 964 736 614 698 637 162 332 616 804 560 111 410 959 774 246 762 428 114 572 042 533 237 322 707 360 751,据此估计B 获胜的概率为________.【解析】由30组随机数,采用三局两胜制得到B 获胜满足的基本事件有: 698,959,共2个,所以B获胜的概率为p=230=115.答案:115三、解答题(每小题10分,共20分)7.元旦就要到了,某校将举行庆祝活动,每班派1人主持节目.高一(2)班的小明、小华和小利实力相当,又都争着要去,班主任决定用抽签的方式决定.机灵的小强给小华出主意,要小华先抽,说先抽的机会大.你是怎样认为的?说说看.【解析】其实抽签不必分先后,先抽后抽,中签的机会是一样的.我们取三张卡片,上面标上1,2,3,抽到1就表示中签,设抽签的次序为甲、乙、丙,则可以把情况填入下表:从上表可以看出:甲、乙、丙依次抽签,一共有六种情况,第一、二两种情况,甲中签;第三、五两种情况,乙中签;第四、六两种情况,丙中签.甲、乙、丙中签的可能性都是相同的,即甲、乙、丙的机会是一样的,先抽后抽,机会是均等的,不必争先恐后.8.天气预报说,在接下来的一个星期里,每天涨潮的概率为20%,请设计一个模拟试验计算下个星期恰有2天涨潮的概率.【解析】利用计算机产生0~9之间取整数值的随机数,用1,2表示涨潮,用其他数字表示不涨潮,这样体现了涨潮的概率是20%,因为时间是一周,所以每7个随机数作为一组,假设产生20组随机数:7032563 2564586 3142486 56778517782684 6122569 5241478 89715683215687 6424458 6325874 68943315789614 5689432 1547863 35698412589634 1258697 6547823 2274168相当于做了20次试验,在这组数中,如果恰有两个是1或2,就表示恰有两天涨潮,它们分别是3142486,5241478,3215687,1258697,共有4组数,于是一周内恰有两天涨潮的4 20=15.概率近似值为。
7.3频率与概率-2023-2024学年高一数学北师版必修第一册同步练习(含解析)
7.3频率与概率-2023-2024学年高一数学北师版必修第一册同步练习(含解析)7.3频率与概率一、选择题1.高考数学试题中,有12道选择题,每道选择题有4个选项,其中只有1个选项是正确的,即随机选择其中一个选项正确的概率是.某家长说:“要是都不会做,每题都随机选择其中一个选项,则一定有3道题答对”.这句话()A.正确B.错误C.不一定D.无法确定2.某篮球运动员投篮的命中率为98%,估算该运动员投篮1 000次命中的次数为()A.98B.980C.20D.9983.从12件同类产品中(其中10件正品,2件次品),任意抽取6件产品,下列说法中正确的是()A.抽出的6件产品必有5件正品,1件次品B.抽出的6件产品中可能有5件正品,1件次品C.抽取6件产品时,逐个不放回地抽取,前5件是正品,第6件必是次品D.抽取6件产品时,不可能抽得5件正品,1件次品4.给出下列三个命题,其中正确命题的个数是()①设有一大批产品,已知其次品率为0.1,则从中任取100件,必有10件是次品;②做7次抛硬币的试验,结果3次出现正面,因此,出现正面的概率是;③随机事件发生的频率就是这个随机事件发生的概率.A.0 B.1 C.2 D.35.经过市场抽检,质检部门得知市场上食用油合格率为80%,经调查,某地市场上的食用油大约有80个品牌,则不合格的食用油品牌大约有()A.64个B.640个C.16个D.160个二、填空题6.在一次考试中,某班学生的及格率是80%,这里所说的80%是________(填“概率”或“频率”).7.一个总体分为A,B两层,用分层抽样方法从总体中抽取一个容量为10的样本.已知B层中每个个体被抽到的概率都为,则总体中的个体数为________.8.对某批产品进行抽样检查,数据如下,根据表中的数据,如果要从该批产品中抽到950件合格品,则大约需要抽查________件产品.抽查件数50 100 200 300 500合格件数47 92 192 285 475三、解答题9.某种疾病治愈的概率是30%,有10个人来就诊,如果前7个人没有治愈,那么后3个人一定能治愈吗?如何理解治愈的概率是30% 10.如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下表:所用时间/分10~20 20~30 30~40 40~50 50~60选择L1的人数6 12 18 12 12选择L2的人数0 4 16 16 4(1)试估计40分钟内不能赶到火车站的概率;(2)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率.11.下列命题中的真命题有()①做9次抛掷一枚均匀硬币的试验,结果有5次出现正面,因此,出现正面的概率是;②盒子中装有大小均匀的3个红球,3个黑球,2个白球,那么每种颜色的球被摸到的可能性相同;③从-4,-3,-2,-1,0,1,2中任取一个数,取得的数小于0和不小于0的可能性相同;④分别从2名男生,3名女生中各选一名作为代表,那么每名学生被选中的可能性相同.A.0个B.1个C.2个D.3个12.为了了解我国机动车的所有人缴纳车船使用税情况,调查部门在某大型停车场对机动车的所有人进行了如下的随机调查:向被调查者提出三个问题:(1)你的车牌号码的最后一位是奇数吗?(2)你缴纳了本年度的车船使用税吗?(3)你的家庭电话号码的倒数第二位是偶数吗?调查人员给被调查者准备了一枚骰子,让被调查者背对调查人员掷一次骰子.如果出现一点或二点则回答第一个问题;如果出现三点或四点则回答第二个问题;如果出现五点或六点则回答第三个问题(被调查者不必告诉调查人员自己回答的是哪一个问题,只需回答“是”或“否”,所以都如实做了回答).结果被调查的3 000人中1 200人回答了“否”,由此估计在这3 000人中没有缴纳车船使用税的人数大约是()A.600 B.200 C.400 D.30013.山东某家具厂为游泳比赛场馆生产观众座椅,质检人员对该厂所产2 500套座椅进行抽检,共抽检了100套,发现有5套次品,则该厂所产2 500套座椅中大约有________套次品.14.某个地区从某年起几年内的新生婴儿数及其中男婴数如表(结果保留两位有效数字):时间范围1年内2年内3年内4年内新生婴儿数5 544 9 013 13 520 17 191男婴数2 716 4 899 6 812 8 590男婴出生频率(1)表中的男婴出生频率分别是________;(2)这一地区男婴出生的概率约是________.15.某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:上年度出险次数0 1 2 3 4 ≥5保费0.85a a 1.25a 1.5a 1.75a 2a随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:出险次数0 1 2 3 4 ≥5频数60 50 30 30 20 10(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;(3)求续保人本年度平均保费的估计值.参考答案1.B[概率的本质含义是事件发生的可能性大小,要是都不会做,每题都随机选择其中一个选项,只能说可能有3道题答对.]2.B[由概率的意义可知该运动员投篮1 000次命中的次数估计为1 000×98%=980.]3.B[由概率的意义可知抽出的6件产品中可能有5件正品,1件次品.]4.A[①概率指的是可能性,错误;②频率为,而不是概率,故错误;③频率不是概率,错误.]5.C[80×(1-80%)=16.]6.频率[80%是及格人数与全体人数的比,是频率,而不是概率.]7.120[设总体中的个体数为x,则=,所以x=120.]8.1000[∵ 根据题表中数据可知合格品出现的频率为0.94,0.92,0.96,0.95,0.95,∵ 合格品出现的概率约为0.95,故要从该批产品中抽到950件合格品大约需要抽查1000件产品.故答案为1000.]9.[解]不一定.如果把治疗一个病人当作一次试验,治愈的概率是30%,是指随着试验次数的增加,大约有30%的病人能治愈,对于一次试验来说,其结果是随机的.因此,前7个病人没有治愈是有可能的,而对后3个病人而言,其结果仍是随机的,既有可能治愈,也有可能不能治愈.10.[解](1)由已知共调查了100人,其中40分钟内不能赶到火车站的有12+12+16+4=44(人),所以用频率估计相应的概率为0.44.(2)选择L1的有60人,选择L2的有40人,故由调查结果得频率为所用时间/分10~20 20~30 30~40 40~50 50~60选择L1的人数0.1 0.2 0.3 0.2 0.2选择L2的人数0 0.1 0.4 0.4 0.111.A[命题①中,抛掷一枚硬币出现正面的概率是;命题②中摸到白球的概率要小于摸到红球与黑球的概率;命题③中取得小于0的数的概率大于取得不小于0的数的概率;命题④中每名男生被抽到的概率为,而每名女生被抽到的概率为.]12.A[因为骰子出现一点或二点、三点或四点、五点或六点的概率相等,都等于,所以应有1 000人回答了第一个问题.因为车牌号码的最后一位数是奇数还是偶数的概率也是相等的,所以在这1 000人中应有500人的车牌号码是偶数,这500人都回答了“否”;同理也有1 000人回答了第三个问题,在这1 000人中有500人回答了“否”.因此在回答“否”的1 200人中约有200人是对第二个问题回答了“否”,由概率的统计定义可知在这3 000人中约有600人没有缴纳车船使用税.]13.125[设有n套次品,由概率的统计定义可知=,解得n=125.所以该厂所产2 500套座椅中大约有125套次品.]14.(1)0.49,0.54,0.50,0.50(2)0.50[频率=,可以利用频率来求近似概率.(1)中各频率为0.49,0.54,0.50,0.50.(2)由(1)得概率约为0.50.]15.[解](1)事件A发生当且仅当一年内出险次数小于2.由所给数据知,一年内出险次数小于2的频率为=0.55,故P(A)的估计值为0.55.(2)事件B发生当且仅当一年内出险次数大于1且小于4.由所给数据知,一年内出险次数大于1且小于4的频率为=0.3,故P(B)的估计值为0.3.(3)由所给数据得保费0.85a a 1.25a 1.5a 1.75a 2a频率0.30 0.25 0.15 0.15 0.10 0.05调查的200名续保人的平均保费为0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a×0.05=1.192 5a.因此,续保人本年度平均保费的估计值为1.192 5a.1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学频率与概率检测试题(附答案)
随机事件的概率频率与概率同步练习(一)
1.下面的事件:○1在标准的气压下,水加热到90℃时沸腾;○2在常温下,铁熔化;○3掷一枚硬币,出现正面;○4实数的绝对值不小于0.其中不可能事件有()A.1个 B.2个 C.3个 D.4个
2.下列事件是随机时间的个数是()
○1在常温下,焊锡熔化;○2明天下雨;○3函数在定义域内为增函数;○4自由下落物体是匀加速直线运动A.0 B.1 C.2 D.3
3.下面说法中正确的是()
A.任一事件的概率总在(0,1)之间
B.必然事件的概率一定是1
C.不可能事件的概率不一定是0
D.概率就是频率
4.有下面事件:○1如果a,b R,那ab=ba;○2某人买彩票中奖;○33 + 510.其中必然事件有
A.○2 B.○3 C.○1 D.○2○3
5.掷两个均匀的子,它落地时向上的点数和为7的概率是_____________.
6.某人抛掷一枚硬币100次,结果正成朝上53次,设正面朝上为事件A,则事件A出现的频数为,事件A出现的频率
为。
7.某射手在同一条件下进行射击,结果如下表所示:
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心频率
(1)计算表中击中靶心的各个频率;
(2)这个射手射击一次,击中靶心的概率约是多少?8.下面的表中列出10次实验抛掷硬币的试验结果,n为每次实验抛掷硬币的次数,m为硬币正面向上的次数。
计算每次实验中“正面向上”这一事件的频率,并考查它的概率。
实验序号抛掷的次数n 正面向上的次数m “正面向上”出现的频率
1 500 251
2 500 249
3 500 256
4 500 253
5 500 251
6 500 246
7 500 244
8 500 258
9 500 262
10 500 247
对于给定的随机事件A,如果随着试验次数的增加,事件A 发生的频率稳定在某个常数P(A)上,称P(A)为事件A 的概率。
请用以上知识解决以下9-13题。
9.抛掷一个均匀的正方体玩具(每个面上分别标着数字1,2,3,4,5,6),落地时向上的点数为5的概率是()A、 B、 C、 D、
10.不做大量的重复试验,就下列事件直接分析它的概率大小。
(1)掷一枚均匀硬币,出现“正面向上”的概率是多少?(2)掷一枚骰子,出现“正面是3”的概率是多少?出现“正面是3的倍数”的概率是多少?出现“正面是奇数”的概率是多少?
(3)本班有60名学生,其中女生24人,现任选1人,则被选中的男生的概率是多少?被选中的是女生的概率是多少?
11.有50张卡片(从1号到50号),从中任取一张,问所取卡片的号数是偶数的情况有多少种?所取卡片的号数是
偶数的概率为多少?
12.某人进行打靶练习,共射击10次,其中有2次击中10环,有3次击中9环,有4次击中8环,有1次未中靶,试计算此人中靶的频率,假设此人射击一次,试问中靶的概率大约是多少?
13.一箱内有十张标有0到9的卡片,从中任取一张,则取到卡片的数字不小于6的概率是多少?
14.试判断下列事件是随机事件、必然事件还是不可能事件:(1)我国东南沿海某地明年将3次受到热带气旋的侵袭;(2)若a为实数,则;
(3)某人开车通过10个路口都将遇到绿灯;
(4)抛一石块,下落;
(5)一个正六面体的六个面分别写有数字1、2、3、4、5、6,将它抛掷两次,数字之和大于12。
15.用一台自动机床加工一批螺母,从中任意抽出100个逐个进行直径检验,结果如下:
直径个数直径个数
1
26
2
15
10
8
17
2
17
2
从这100个螺母中,任意抽取一个,求事件A()、事件B ()、事件C(d6.96)的频率。
事件的分类是概率一章中的基础内容,贯穿本章始终、频率、概率是今后高考的重要内容之一,会进行多角度地考查。
16.下列事件是随机事件的有()
A、若a、b、c都是实数,则a(bc)=(ab)c
B、没有空气和水,人也可以生存下去
C、掷一枚硬币,出现反面
D、在标准大气压下,水的温度达到90??时沸腾
17.在1、2、3、4共四个数中,可重复选取两个数,其中一个数是另一个数的2倍的概率是()
A、 B、 C、 D、
答案:
1、B
2、C
3、B
4、C
5、
6、53;0.53。
