机械原理课后答案第三章作业
机械原理第2、3、4、6章课后答案西北工业大学(第七版)

第二章 机构的结构分析题2-11 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
解:1)取比例尺,绘制机构运动简图。
(图2-11a)2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件,但齿轮1和凸轮2是固装在轴A 上,只能作为一个活动件,故 3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数,此简易冲床不能运动,即不能实现设计意图。
分析:因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案:可以在机构的适当位置增加一个活动构件和一个低副,或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-11b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-11c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-11d)。
11(c)题2-11(d)5364(a)5325215436426(b)321讨论:增加机构自由度的方法一般是在适当位置上添加一个构件(相当于增加3个自由度)和1个低副(相当于引入2个约束),如图2-1(b )(c )所示,这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度,如图2-1(d )所示。
题2-12 图a 所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
西北工业大学机械原理课后答案第3章-1
解法一:
速度分析:先确定构件3得绝对瞬心P36,利用瞬心多边形,如图(b)
由构件3、5、6组成得三角形中,瞬心P36、P35、P56必在一条直线上,由构件3、4、6组成得三角形中,瞬心P36、P34、P46也必在一条直线上,二直线得交点即为绝对瞬心P36。
第三章平面机构得运动分析
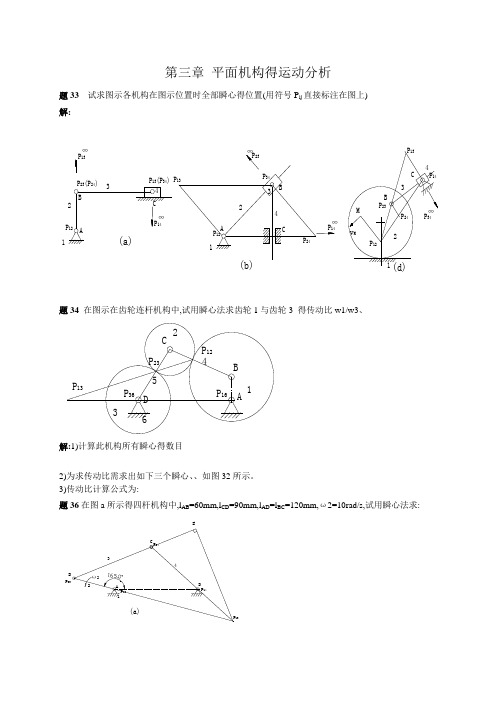
题33试求图示各机构在图示位置时全部瞬心得位置(用符号Pij直接标注在图上)
解:
题34在图示在齿轮连杆机构中,试用瞬心法求齿轮1与齿轮3得传动比w1/w3、
解:1)计算此机构所有瞬心得数目
2)为求传动比需求出如下三个瞬心、、如图32所示。
3)传动比计算公式为:
题36在图a所示得四杆机构中,lAB=60mm,lCD=90mm,lAD=lBC=120mm,ω2=10rad/s,试用瞬心法求:
解:1)速度分析:
以F为重合点(F1、F5、、F4)有速度方程:
以比例尺速度多边形如图37 (b),由速度影像法求出VB、VD
2)加速度分析:以比例尺
有加速度方程:由加速度影像法求出aB、aD
题316在图示得凸轮机构中,已知凸抡1以等角速度转动,凸轮为一偏心圆,其半径,试用图解法求构件2得角速度与角加速度。
4)当时,P13与C点重合,即AB与BC共线有两个位置。作出得两个位置。
量得
题312在图示得各机构中,设已知各构件得尺寸、原动件1以等角速度ω1顺时针方向转动。试用图解法求机构在图示位置时构件3上C点得速度及加速度。
解:a)速度方程:
加速度方程:
b)速度方程:
加速度方程:
c)速度方程:
加速度方程:
题314在图示得摇块机构中,已知lAB=30mm,lAC=100mm,lBD=50mm,lDE=40mm。曲柄以等角速度ω1=10rad/s回转,试用图解法求机构在φ1=45°位置时,点D与点E得速度与加速度,以及构件2得角速度与角加速度。
机械原理课后习题答案(朱理)
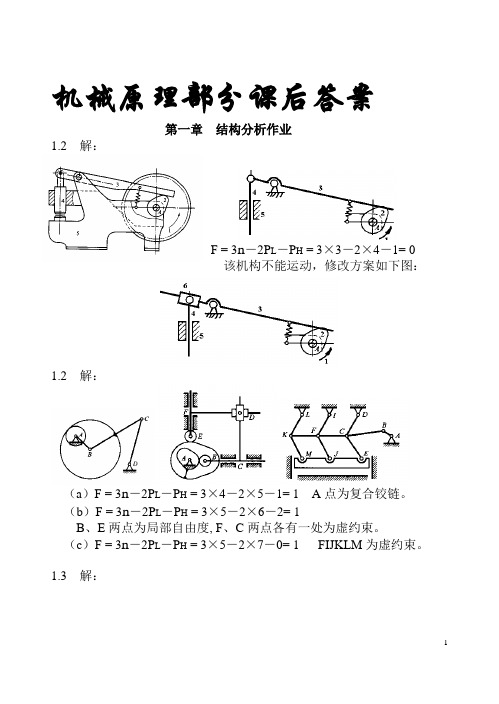
机械原理部分课后答案第一章结构分析作业1.2 解:F = 3n-2P L-P H = 3×3-2×4-1= 0该机构不能运动,修改方案如下图:1.2 解:(a)F = 3n-2P L-P H = 3×4-2×5-1= 1 A点为复合铰链。
(b)F = 3n-2P L-P H = 3×5-2×6-2= 1B、E两点为局部自由度, F、C两点各有一处为虚约束。
(c)F = 3n-2P L-P H = 3×5-2×7-0= 1 FIJKLM为虚约束。
1.3 解:F = 3n-2P L-P H = 3×7-2×10-0= 11)以构件2为原动件,则结构由8-7、6-5、4-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图a)。
2)以构件4为原动件,则结构由8-7、6-5、2-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图b)。
3)以构件8为原动件,则结构由2-3-4-5一个Ⅲ级杆组和6-7一个Ⅱ级杆组组成,故机构为Ⅲ级机构(图c)。
(a) (b) (c)第二章 运动分析作业2.1 解:机构的瞬心如图所示。
2.2 解:取mmmm l /5=μ作机构位置图如下图所示。
1.求D 点的速度V D13P D V V =而 25241314==P P AE V V E D ,所以 s mm V V E D /14425241502524=⨯==2. 求ω1s rad l V AE E /25.11201501===ω3. 求ω2因 98382412141212==P P P P ωω ,所以s rad /46.0983825.1983812=⨯==ωω 4. 求C 点的速度V Csmm C P V l C /2.10154446.0242=⨯⨯=⨯⨯=μω2.3 解:取mmmm l /1=μ作机构位置图如下图a 所示。
1. 求B 2点的速度V B2V B2 =ω1×L AB =10×30= 300 mm/s 2.求B 3点的速度V B3V B3 = V B2 + V B3B2大小 ? ω1×L AB ? 方向 ⊥BC ⊥AB ∥BC 取mm s mm v /10=μ作速度多边形如下图b 所示,由图量得:mmpb 223= ,所以smm pb V v B /270102733=⨯=⨯=μ由图a 量得:BC=123 mm , 则mmBC l l BC 1231123=⨯=⨯=μ3. 求D 点和E 点的速度V D 、V E利用速度影像在速度多边形,过p 点作⊥CE ,过b 3点作⊥BE ,得到e 点;过e 点作⊥pb 3,得到d 点 , 由图量得:mmpd 15=,mmpe 17=,所以smm pd V v D /1501015=⨯=⨯=μ , smm pe V v E /1701017=⨯=⨯=μ;smm b b V v B B /17010173223=⨯=⨯=μ4. 求ω3s rad l V BC B /2.212327033===ω5. 求n B a 222212/30003010smm l a AB n B =⨯=⨯=ω6. 求3B aa B3 = a B3n + a B3t = a B2 + a B3B2k + a B3B2τ 大小 ω32L BC ω12L AB 2ω3V B3B2 ?方向 B →C ⊥BC B →A ⊥BC ∥BC 22233/5951232.2s mm l a BC n B =⨯=⨯=ω223323/11882702.222s mm V a B B k B B =⨯⨯=⨯=ω取mm s mm a 2/50=μ作速度多边形如上图c 所示,由图量得:mmb 23'3=π ,mmb n 20'33=,所以233/11505023's mm b a a B =⨯=⨯=μπ2333/10005020's mm b n a at B =⨯=⨯=μ7. 求3α233/13.81231000s rad l a BC tB ===α8. 求D 点和E 点的加速度a D 、a E利用加速度影像在加速度多边形,作e b 3'π∆∽CBE ∆, 即 BE eb CE e CB b 33''==ππ,得到e 点;过e 点作⊥3'b π,得到d 点 , 由图量得:mme 16=π,mmd 13=π,所以2/6505013s mm d a a D =⨯=⨯=μπ ,2/8005016s mm e a a E =⨯=⨯=μπ 。
机械原理 谢进版 第二版 课后参考答案

BC、CD、AD 四杆中有一杆为虚约束,如果将构件 AD 视为虚约束,去掉虚约束,则点B、 C均为复合铰链,没有局部自由度; (d) 、 F 3n 2Pl Ph 3 4 2 6 0 0 ,系统不能运动,所以也就不是一个机 构。 从图中可以看出, 铰链点 C 是构件 BC 上的点, 其轨迹应当是以铰链点 B 为圆心的圆, 同时,铰链点 C 又是构件 CD 上的点,轨迹应当是移动副 F 约束所允许的直线,两者是矛 盾的,所以,系统不能运动。系统中没有局部自由度、复合铰链、虚约束。 (e) 、F 3n 2Pl Ph 3 5 2 6 3 ,机构没有确定的运动。没有局部自由度、 复合铰链、虚约束。 3-7 计算题 3-7 图所示齿轮-连杆机构的自由度。
邻接矩阵为:
e1 e2 v1 LM v2 v3 v4 1 0 0 1 1 1 0 0
e3 0 1 1 0
e4 0 0; 1 1 v1 AM v2 v3 v4
v1 v2 0 1 0 1 1 0 1 0
v3 0 1 0 1
v4 1 0 1 0
3-3 题 3-3 图为外科手术用剪刀。其中弹簧的作用是保持剪刀口张开,并且便于医生单手操
共 92 页
第3页
题 3-2 图 解:该机构由机架 4、原动件 1 和从动件 2、3 组成,共 4 个构件,属于平面四杆机构。 机构中构件 1、4,构件 1、2,构件 3、4 之间的相对运动为转动,即两构件间形成转动副, 转动副中心分别位于 A、B、C 点处;构件 2、3 之间的相对运动为移动,即两构件间形成移 动副,移动副导路方向与构件 2 的中心线平行。 原动件 1 相对机架 4 转动, 带动从动件 2 转动的同时, 从动件 2 相对从动件 3 发生移动。 从动件 2 转动的同时也带动了从动件 3 相对机架的转动。 因此, 偏心轮 1 的转动进而使液压 油完成从右边进口处进入并流向左边出口处的整个过程。 选择比例尺 l =0.002m/mm,分别量出各构件的运动尺寸,绘出机构运动简图,并标明 原动件及其转动方向,如题图 3-2 所示。 其机构示意图和机构拓扑图如上图所示。 其关联矩阵为:
机械原理(第二版)课后答案(朱理主编)

机械原理作业(部分答案)第一章结构分析作业1.2 解:(a)F = 3n-2P L-P H = 3×4-2×5-1= 1 A点为复合铰链。
(b)F = 3n-2P L-P H = 3×5-2×6-2= 1B、E两点为局部自由度, F、C两点各有一处为虚约束。
(c)F = 3n-2P L-P H = 3×5-2×7-0= 1 FIJKLM为虚约束。
1.3 解:第二章运动分析作业2.1 解:机构的瞬心如图所示。
2.2 解:取mmmm l /5=μ作机构位置图如下图所示。
1.求D 点的速度V D13P D V V =而 25241314==P P AE V V E D ,所以 s mm V V E D /14425241502524=⨯==2. 求ω1s rad l V AE E /25.11201501===ω3. 求ω2因 98382412141212==P P P P ωω ,所以s rad /46.0983825.1983812=⨯==ωω 4. 求C 点的速度V Csmm C P V l C /2.10154446.0242=⨯⨯=⨯⨯=μω2.3 解:取mmmm l /1=μ作机构位置图如下图a 所示。
1. 求B 2点的速度V B2V B2 =ω1×L AB =10×30= 300 mm/s 2.求B 3点的速度V B3V B3 = V B2 + V B3B2大小 ? ω1×L AB ? 方向 ⊥BC ⊥AB ∥BC 取mm s mm v /10=μ作速度多边形如下图b 所示,由图量得:mmpb 223= ,所以smm pb V v B /270102733=⨯=⨯=μ由图a 量得:BC=123 mm , 则mmBC l l BC 1231123=⨯=⨯=μ3. 求D 点和E 点的速度V D 、V E利用速度影像在速度多边形,过p 点作⊥CE ,过b 3点作⊥BE ,得到e 点;过e 点作⊥pb 3,得到d 点 , 由图量得:mmpd 15=,mmpe 17=,所以smm pd V v D /1501015=⨯=⨯=μ , smm pe V v E /1701017=⨯=⨯=μ;smm b b V v B B /17010173223=⨯=⨯=μ4. 求ω3s rad l V BC B /2.212327033===ω5. 求n B a 222212/30003010smm l a AB n B =⨯=⨯=ω6. 求3B aa B3 = a B3n + a B3t = a B2 + a B3B2k + a B3B2τ 大小 ω32L BC ? ω12L AB 2ω3V B3B2 ?方向 B →C ⊥BC B →A ⊥BC ∥BC 22233/5951232.2s mm l a BCn B =⨯=⨯=ω223323/11882702.222s mm V a B B k B B =⨯⨯=⨯=ω取mms mm a 2/50=μ作速度多边形如上图c 所示,由图量得:mmb 23'3=π ,mmb n 20'33=,所以233/11505023's mm b a a B =⨯=⨯=μπ2333/10005020's mm b n a at B =⨯=⨯=μ7. 求3α233/13.81231000s rad l a BC tB ===α8. 求D 点和E 点的加速度a D 、a E利用加速度影像在加速度多边形,作e b 3'π∆∽CBE ∆, 即 BE eb CE e CB b 33''==ππ,得到e 点;过e 点作⊥3'b π,得到d 点 , 由图量得:mm e 16=π,mmd 13=π,所以2/6505013s mm d a a D =⨯=⨯=μπ ,2/8005016s mm e a a E =⨯=⨯=μπ 。
机械原理_课后习题答案免费(全面)高教版 西北工大

2) 求vC2
v C 2 = v B + v C 2 B = v C 3 + vC 2 C 3
方向: 大小: ⊥AB
√
⊥BC ?
0 0
∥BC ?
取
μv = 0.005
m/s mm
作速度图
b
题3-10 解(续2)
[解] (2)速度分析
v B → vC 2 → v D , v E → ω 2
1) 求vB 2) 求vC2 3) 求vD 和求vE 用速度影像法
C
E
vC = v B + vCB v D = v B + v DB
(2) 求vE
D p(a, f )
v E = vC + v EC = v D + v ED
b d e c
题3-5 解
b) 解: 顺序 (1) 求vC
v B → vC → v E → v F
D B vB A E G F C
vC = v B + vCB
√
0 0
∥CD ?
b2 (b1) (b3)
其中 a B3B2 = 2ω2 v B3B2 = 0(∵ v B3B2 = 0)
a B1 ⎛ m / s 2 ⎞ 取 μa = ⎜ ⎟ 作加速度图 p ' b '1 ⎝ mm ⎠
题3-8 c) 解(续2)
[解] (3)加速度分析 a B 2 ( = a B1 ) → a B 3 → a C 3 1) 求aB2 A 1 ω1 2) 求aB3
取
√ v ⎛m/s⎞ μ v = B1 ⎜ ⎟ 作速度图 pb1 ⎝ mm ⎠
3) 求vC3 : 用速度影像法
v C 3 = 0 同时可求得 ω3 =
机械原理第三章作业答案
P13
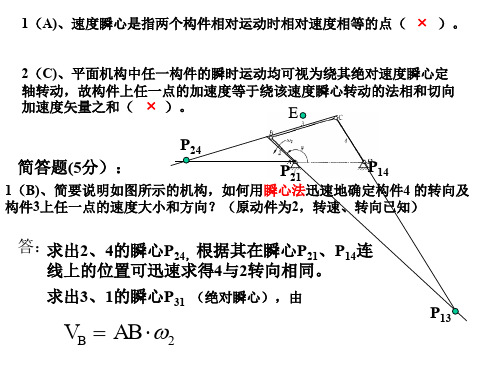
2(C)、既然机构中各构件与其速度图和加速度图之间均存在影像关系, 因此整个机构与其速度和加速度图之间也存在影像关系,对吗?
答:不对
速度、加速度影像原理只适用于同一构件上的点求速度 和加速度,不适用于整个机构。
3(C)、当用速度瞬心法和用速度影像法求同一构件(如图所示机构连杆3 上)上任意一点P的速度时它们的求解条件有何不同?各有何特点?
B
3(C)、图示机构中,已知 lAC lBC lCD lCE lDF lEF 20mm ,
滑块1及2分别以匀速且 v1 v2 0.002 m / s 做反向移动,试求机构在
位置时的速度大小之比 vF v1
解:对C点进行速度分析 建立方程为
。
1 v1 A
7
3 30°
C
D
6
F
4
① VC VA VCA VB VCB
B
2
v2
5
E
b
p
60
a°
d c
e
vF f v1
pf
3 pc
3
pa pa
3
pc 3 pa
pf 3pc 3 3 pa
3-9、试判断在图示的两机构所在位置中,B点是否都存在 哥氏加速度?。并思考下列问题:
1)、在什么条件下才存在哥氏加速度?
答:用速度瞬心法求构件(如3)上任意
P
点(如P)速度时需找出相关的瞬心;
而用速度影像法求点速度时,需先在
速度多边形中求出同一构件(如3)
上任意两点(如B、C两点)的速度。
瞬心法较简便,但有时瞬心不怎好求;影像法只对同一 构件上的点适用,不适用于整个机构。
机械原理第3章作业题及答案
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
l 0.001m/mm
2 3
v 0.005m/s/mm
D
1
B p(a, c3 ) A
4
c2
1
p' (a' , c3 ' )
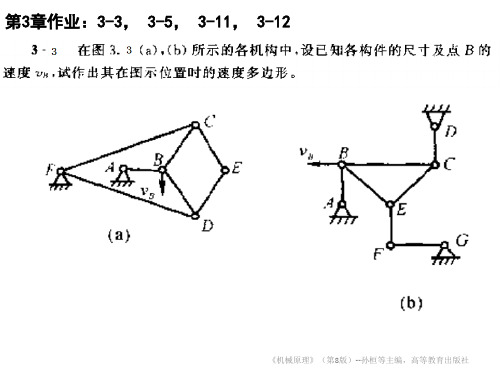
第3章作业:3-3, 3-5, 3-11, 3-12
《机械原理》(第8版)--孙桓等主编,高等教育出版社
解: (b)依次列出以下机构速度 分析的 作出速度多边形如图所 示。 vC vB vCB
大小 ? 方向 ⊥FC √ √ ? ⊥BC
矢量分析方程,并选取 合适的比例尺
vD
vB
vC
大小 ? 方向 ⊥CD
vB vCB
√ √ ? ⊥CB
可得vC vB ,于是,可知: 构件3在该瞬间角速度为零, 也知:vE vC vB vF vE vFE
大小 ? 方向 ⊥FG √ √ ? ⊥FG
《机械原理》(第8版)--孙桓等主编,高等教育出版社
4
c2
1
p' (a' , c3 ' )
k'
2 a 0.05m/s /mm
C(C2 , C3 )
E
e
d
c2 '
e' d' b'
b
3)运用速度影像原理,可求的D点和E的速度
n2 '
BD 50 BD bd bc 2 49.1 19.94 mm , bd BC 123 .1 BC bc2 vD v pd 0.005 45.2 0.226m / s, 方向是由p d DE 40 DE de de bd 19.94 16 mm , BD 50 BD bd vE v pe 0.005 34.5 0.173m / s, 方向是由p e
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-3 在图a所示的四杆机构中,lAB=60mm,lCD=90mm, lAD= lBC =120mm,ω2=10rad/s,试用瞬心法求:
1)当ψ=165°时,点C的速度VC;
解:1)取μL=3mm/mm,作 机构运动简图,定出瞬心 P13 的位置,如图b。
P13 为构件3的绝对瞬心, 则:
ω3 = VB / lBP13 = ω2 lAB /(μL BP13) =10×60/(3×78)=2.56(rad/s)
•
θ =2
•
s3
100cos60 °θ•1
+ 300 cosθ2
•
θ=2 0
•
解得:s3 = -0.962(m/s)= V3 • θ 2 = -1.697(rad/s)= ω2
θ1
解:以L1 ,L2 ,s3 ,e 分别表示各杆的向量,则向量方程式为:
L1 + L2 = s3 + e
e 用复数表示为:L1 eiθ 1 + L2 eiθ 2 = s3 ei•0 + ei•2
(*)
按欧拉公式展开:100(cosθ1+isinθ1)+ 300 (cosθ2+isinθ2) = s3 + 30i
e L1 eiθ 1 + L2 eiθ 2 = s3 ei•0 + ei•2
(*)
按欧拉公式展开:100(cosθ1+isinθ1)+ 300 (cosθ2+isinθ2) = s3 + 30i
分离虚、实部:100 cos60 ° + 300cosθ2= s3 (1)
100 sin60 ° + 300sinθ2=30 (2)
3-1 试求图示各机构在图示位置时的全部瞬心(用符号Pij 直接标注在图上)。
3-2 在图示齿轮—连杆组合机构中,试用瞬心法求齿轮1 与齿轮的传动比ω1 / ω3。
解: 1)K=N(N-1)/2=6(6 -1 )/ 2 =15 2)为了求传动比ω1 / ω3需求出:P16、P36、P13。 3) ω1 / ω3 = P36 P13 / P16 P13= DK / AK( ω3与ω1同向)
VC = ω3 lCP13 = ω3 μL CP13 = 2.56×3 ×52 /1000=0.4(m/s)
2)当ψ=165°时,构件3的BC线上速度最小的一点E的位置 及速度的大小;
解:因BC线上速度最小 之点必与P13点的距离最 近,故从P13引BC线的垂 线交于点E,如图b。则: VE = ω3 lP13E
= ω3 μL P13E = 2.56×3 ×46.5/1000 =0.357(m/s)
3)当VC =0时, ψ角之值(有两解)。
解:作出VC =0时机 构的两个位置,即 AB与BC共线的两 个位置,如图c。量 出:
ψ1=26.4 ° ψ2=226.6 °
3-14 在图示的机构中,已知原动件1以等速度ω1=10rad/s逆时针方 向转动,lAB=100mm,lBC=300mm,e=30mm。当θ1=60°时,试 用复数法求构件2的角位移θ2、角速度ω2及构件3的速度V3。
由(2)式解得:sinθ2= -0.1887
θ2=349.12 °
对(*)式求导: (
•
L1θ 1
)
i eiθ 1
+(
•
L2 θ 2
)
i
eiθ
2
=
•
s3 +0
欧拉公式展开:L1θ•1i (cosθ1+isinθ1)+
•
L2 θi(2cosθ2+isinθ2) =
•
s3
分离虚、实部: - 100sin60 °θ•1 - 300 sinθ2
