公务员考试行测年龄问题秒解技巧
公务员行测《年龄问题解题技巧》

年龄问题解题技巧年龄问题是公务员考试行测中的一种常见题型,国家公务员考试网认为,解决这类问题首先要了解年龄的三大特点:(1)两个人年龄差不变(2)两个年龄的倍数关系是变化的量(随着年龄的增长,两个人的倍数关系会越来越小,无限接近于1倍)(3)每个人的年龄的增长量相同(过一年长一岁)。
年龄问题的常见解题方法:画时间轴,代入排除,方程,整除等等,下面我们通过几道真题给大家进行讲解例1.一位长寿老人出生于19世纪90年代,有一年他发现自己年龄的平方刚好等于当年的年份。
问这位老人出生于哪一年? ( )。
A.1894年B.1892年C.1898年D.1896年【答案】由题意可知,当他 44岁那年为1936年,所以1936-44=1892,因此答案为B。
【点评】在年龄问题中,大家需要记住两个平方数,,原因在于考试中会出现比如某一个人出生的年份是一个平方数这一类的条件,但出现这一类条件的时候我们基本就可以把数字锁定为1936,因为只有此数符合题意,比如43的平方为1849,不可能成立,而记住目的在于考试可能会出现家里的孩子过了多少年后,此时的年份是平方数,我们就可以锁定为2025,所以,大家一定要牢牢记住。
例2.有一位百岁老人出生于二十世纪,2015年他的年龄各数字之和正好是他在2012年的年龄的各数字之和的三分之一,问该老人出生的年份各数字之和是多少(出生当年算作0岁)。
A.14B.15C.16D.17【答案】生于二十世纪,所以2015年老人的年龄最大也不会超过2015-1900=115,因为2012年和2015年相差3年,而2012年他的年龄是3的倍数,那么,2015年他的年龄也一定是3的倍数,且年龄的个位数字小于3,所以2015年的年龄=111、出生年份=2015-111=1904,各位数字之和=1+9+0+4=14,选A。
【点评】此题涉及到了整除的思想,而且还需要根据实际情况进行数字之间关系的分析,所以,有的时候数量关系题,尤其是与我们生活实际的数量题目,除了要有一些数学思维之外,还需要我们能联系实际考虑问题,做题与猜题相结合,迅速做出答案。
2015年河北公务员考试行测答题技巧:年龄问题巧回答

2015年河北公务员考试行测答题技巧:年龄问题巧回答行测答题技巧:在公务员行测的数量关系部分,有一类问题叫年龄问题。
年龄问题的题型特征是题目中会出现一个或者多个人的年龄变化,求某个人的年龄。
这类年龄问题的解题核心是年龄差不变。
解题方法有三种:代入排除法,列表法和方程法。
下面通过几道题看看年龄问题的解法。
例1.小鲸鱼说:“妈妈,我到您现在这么大时,您就31岁啦!”大鲸鱼说:“我像你这么大年龄时,你只有1岁。
”请问小鲸鱼现在几岁?A.13B.12C.11D.10【答案】C。
解析:方法一:代入排除法。
代入A选项,如果小鲸鱼现在13岁,则大鲸鱼13岁,小鲸鱼只有1岁,年龄差是12岁,则大鲸鱼现在13+12=25岁,当小鲸鱼长到25岁时,大鲸鱼应该是25+12=37岁,不对;同理,代入C选项,如果小鲸鱼现在11岁,则大鲸鱼11岁,小鲸鱼只有1岁,年龄差是10岁,则大鲸鱼现在11+10=21岁,当小鲸鱼长到21岁时,大鲸鱼应该是21+10=31岁,正确。
选C。
方法二:列表法。
题目中有大小两只鲸鱼,有三个时间点,过去,现在,将来,故可以列下表:设大鲸鱼现在y岁,小鲸鱼现在x岁。
过去现在将来大鲸鱼xy31小鲸鱼1xy根据年龄差不变列方程:x-1=y-xy-x=31-y解得:x=11。
选C。
例2. 甲、乙、丙、丁四人,其中每三个人的岁数之和分别是55、58、62、65。
这四个人中年龄最小的是( )。
A.7岁B.10岁C.15岁D.18岁【答案】C。
解析:由题意可知,65岁肯定是年龄较大的三个人的年龄和,55肯定是年龄较小的三个人年龄和,而且把四个数加起来,正好相当于把每个人算了3次,因此四个人的岁数和为(55+58+62+65)÷3=80,那么年龄最小的为80-65=15岁。
选C。
例3. 在一个家庭里,现在所有成员的年龄加在一起是73岁。
家庭成员中有父亲、母亲、一个女儿和一个儿子,父亲比母亲大3岁,女儿比儿子大2岁。
行测技巧:学会举一反三,搞定年龄问题
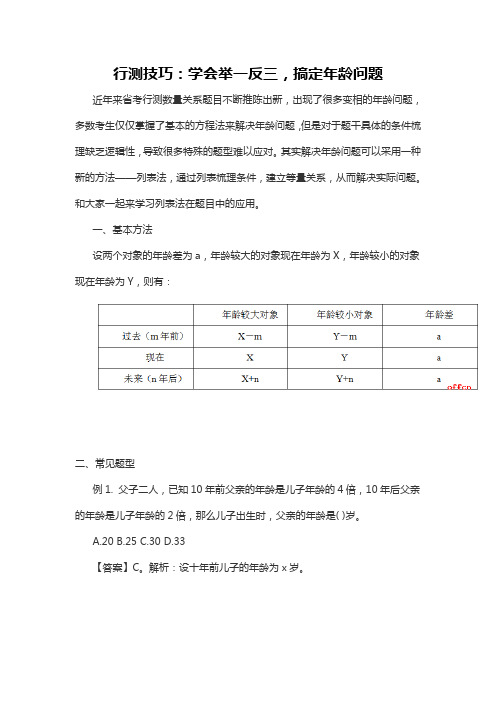
行测技巧:学会举一反三,搞定年龄问题近年来省考行测数量关系题目不断推陈出新,出现了很多变相的年龄问题,多数考生仅仅掌握了基本的方程法来解决年龄问题,但是对于题干具体的条件梳理缺乏逻辑性,导致很多特殊的题型难以应对。
其实解决年龄问题可以采用一种新的方法——列表法,通过列表梳理条件,建立等量关系,从而解决实际问题。
和大家一起来学习列表法在题目中的应用。
一、基本方法设两个对象的年龄差为a,年龄较大的对象现在年龄为X,年龄较小的对象现在年龄为Y,则有:二、常见题型例1. 父子二人,已知10年前父亲的年龄是儿子年龄的4倍,10年后父亲的年龄是儿子年龄的2倍,那么儿子出生时,父亲的年龄是( )岁。
A.20B.25C.30D.33【答案】C。
解析:设十年前儿子的年龄为x岁。
根据题意,有4x+20=2(x+20),x=10,所以十年前儿子年龄为10岁,父亲年龄为40,所以儿子出生时,父亲年龄为30岁。
故答案为C。
例2. 今年甲乙丙三人年龄之和为83,甲今年25岁,当乙像甲现在这么大时,甲乙两人年龄之和比丙当时的年龄还大2岁。
问乙今年的年龄为多少岁?A.10B.12C.14D.15【答案】A。
解析:设今年乙的年龄为x岁,丙的年龄为y岁。
根据题干信息有:x+y+25=83,25+(25-x)+25=y+(25-x)+2,解得x=10,y=48,故答案为A。
例3. 现在父母年龄和是他们几个子女年龄和的6倍,两年前父母年龄和是他们几个子女年龄和的10倍,六年后父母年龄和是他们几个子女年龄和的3倍,那么他们有几个子女?A.2B.3C.4D.5【答案】B。
解析:设现在n个子女的年龄和为x,则现在父母的年龄和为6x。
根据题意有:6x-4=10(x-2n),6x+12=3(x+6n),解得x=14,n=3,故答案为B。
例4. 有80颗珠子,5年前,姐妹两人按年龄的比例分配,恰好分完;今年,她们再次按年龄的比例重新分配,又恰好分完。
行测数量关系技巧:年龄问题的巧解方法

行测数量关系技巧:年龄问题的巧解方法公务员行测考试主要是考量大家的数学推理能力和逻辑分析能力,下面由小编为你精心准备了“行测数量关系技巧:年龄问题的巧解方法”,持续关注本站将可以持续获取更多的考试资讯!行测数量关系技巧:年龄问题的巧解方法在行测考试中,年龄问题都我们考查的一个重点考题型,但此类题型难度并不大,总共涉及三个知识点和两种解题方法,理应是每位考生必须“拿下”的考题。
小编专家在此进行全面讲解:一、年龄问题的主要的题型特点①任何两人年龄差不变;②任何两人年龄之间的倍数关系是变化的;③每过一年,所有的人都长了一岁。
具体分类如下:1.随时间推移,年龄差不变;2.随时间推理,年龄倍数在减少;3.过N年,长N岁。
二、如何巧解年龄问题解决年龄问题的关键在于“年龄差不变”。
一般说来,解决年龄问题需要从表示年龄间关系的条件入手理解数量关系例1:今年小宁8岁,妈妈32岁,那么再过多少年妈妈的岁数是小宁的2倍?下面就为考生讲解如何巧妙解答年龄问题。
由差倍问题公式可得,小宁年龄为24÷(2-1)=24岁,即小宁24岁时,妈妈的年龄等于小宁的2倍,因此再过24-8=16年。
三、多人之间的年龄问题多人之间的年龄问题在行测考试中出现的频率略有增加,它主要考查多个人之间的年龄关系变化。
解决此类题目的重点为规律③:每过一年,所有的人都长了一岁。
例题2:父亲与两个儿子的年龄和为84岁,12年后父亲的年龄等于两个儿子的年龄之和,请问父亲现在多少岁?A.24B.36C.48D.60解析:此题答案为C。
12年后,父亲与两个儿子的年龄和应该是84+12×3=120岁,将父亲12年后的年龄看做1倍,那么12年后父亲的年龄为120÷2=60岁,现在的年龄为60-12=48岁。
四、年龄推理题年龄推理题在行测考试中出现较少,它需要考生通过寻求年龄间的特殊情况来得到突破口,从而最终得出答案。
常见的特殊情况为:经过了N年,所有人增长的岁数和不是N的倍数,这说明N年前有人没有出生,从而可直接求出该人的年龄。
行测年龄问题解题技巧

行测年龄问题解题技巧年龄问题相较其他题型而言隐含条件较多,即与生活常识结合较多,从而以较短的题目长度充分考查应试者的思维能力。
在年龄问题中,简单常识有:每人每年长1岁;两个人的年龄差不变;两个人的年龄倍数关系随着时间的推移而不断变小等。
本文通过例题来详细讲解年龄问题。
【例1】有一个上世纪80年代出生的人,如果他能活到80岁,那么有一年他的年龄的平方数正好等于那一年的年份。
问此人生于那一年?A.1980年B.1983年C.1986年D.【解析】此人出生的年龄介于1980~1989,如果活到80岁,则活过的年份介于1980~2069之间,年龄的平方介于1980~2069年之间,只有45×45=2025满足,所以出生年份为2025-45=1980。
故选答案A。
【例2】甲乙丙三人在2021年的年龄周岁之和为60,2021年甲是丙年龄的两倍,2021年乙是丙年龄的两倍,问甲是哪一年出生的?A.1988B.1986C.1984D.1982【解析】设甲、乙、丙在2021年的岁数为x、y、z。
由题意有:x+y+z=60,x+2=2z+2,y+3=2z+3,解得x=24,则甲是在1984年出生的。
故选答案C。
【例3】孙儿孙女的平均年龄是10岁,孙儿年龄的平方减去孙女年龄的平方所得的数值,正好是爷爷出生年份的后两位,爷爷生于上个世纪40年代。
问孙儿孙女的年龄差是多少岁?A.2B.4C.6D.8【解析】设孙儿为x岁,孙女为y岁,则x+y=20。
依题意可得40≦x2 -y2<50,化简得40≦x+yx-y <50,将x+y=20代入,可得2≦x-y<2.5,因为年龄差必定为整数,所以x-y=2。
故选答案A。
【例4】李工程师家里有4口人,母、妻、儿、本人。
2021年,4人的年龄和为152岁,平均年龄正好比李工程师年龄小2岁,比妻子大2岁,若2021年时,妻子年龄正好是儿子的6倍,问哪一年时,母亲年龄正好是妻子年龄的2倍?A.2021年B.2021年C.2021年D.2021年【解析】由题意,2021年四人的年龄和为152岁,则平均年龄为152÷4=38岁,故2021年李工程师年龄为40岁,妻子年龄为36岁。
2022年公务员行测数量关系中年龄问题

2022年公务员行测数量关系中年龄问题行测全部是选择题,如果你找到了适合自己的答题速度和准确率的黄金结合点,你就离上岸不远了!想拿高分要学会放弃,更要掌握技巧,全力争取。
下面小编给大家带来关于公务员行测数量关系中年龄问题,希望会对大家的工作与学习有所帮助。
公务员行测数量关系中年龄问题一、年龄问题解题原则:1)年龄差不变;2)每个人都是自然增长;3)任何两人年龄之间的倍数关系是变化的。
我们通过例题来讲解一下:例1、在一个家庭中有爸爸、妈妈、女儿和儿子。
现在把所有成员的年龄加在一起是77岁,爸爸比妈妈大3岁,女儿比儿子大2岁。
5年前,全家所有人的年龄总和是58岁。
现在爸爸的年龄是多少岁?A.67B.32C.35D.78答案:C【解析】:根据题意“爸爸、妈妈、女儿和儿子。
现在把所有成员的年龄加在一起是77岁”,可得到5年前全家所有人的年龄和是58岁,由每个人都是增长,可知现在全家人的年龄总和应该是58+4×5=78岁。
但实际上的年龄总和却是77岁,差了1岁。
就说明有一个人只长了4岁,这个人只能是儿子因为5年前尚未出生。
女儿就应该是4+2=6岁,现在父母的年龄和是77-4-6=67岁,根据题意又已知知他们的年龄差是3岁,可求出爸爸的年龄是(67+3)÷2=35岁。
因此选择C选项。
例2、1998年,小张的年龄是小王的年龄的4倍。
2002年,小张的年龄是小王的年龄的3倍。
问小张、小王二人2000年的年龄分别是多少岁?A.34岁,12岁B.32岁,8岁C.36岁,12岁D.34岁,10岁答案:D【解析】:设1998年小王的年龄是x岁,则小张的年龄是4x岁。
从98年到02这四年4年,两个年龄都增长4岁,那么这个时候,小张的年龄是4x+4岁,小王的年龄为x+4岁。
由小张的年龄是小王年龄的3倍,因此有4x+4=3(x+4)可求得x=8。
也就是说1998年,小王的年龄是8岁,则2000年的年龄是10岁,因此选择D 选项。
年龄问题解决方案

公务员考试解决方案系列年龄问题求解方案华图公务员考试研究中心 沈 栋年龄问题是公务员行测数学运算部分常考的一个考点。
年龄问题是从现实生活中抽出来 的一类题目,有很强的生活背景,因此年龄问题的求解上技巧性比较强。
我们在本文中简单 谈以下年龄问题的求解方案。
首先,求解年龄问题,需要熟悉下面三条内容。
1、每人每年长一岁。
2、两个人的年龄差始终保持不变。
3、两个人的年龄倍数随着时间的推移不断减少。
这三条是我们求解年龄问题中所谓的隐含条件。
简单阐述为:由第一条,我们知道每个人的年龄都必然是整数,那么在很多问题中就有 可能通过整除迅速得出答案, 此外每个人年龄的增长速度是一样的, 那么有些年龄问题就可 以转化为行程问题解决。
由第二条, 年龄差不变, 那么基于此年龄问题列方程的依据就有了, 就是根据不同时刻的年龄差是一样的来列方程。
由第三条, 年龄倍数随着时间推移不断减小, 如果知道倍数,那么可以通过考察是否整除来解决,如果知道两个年份的年龄倍数,那么其 他年份的年龄倍数的范围就知道了,可以帮助排除选项。
其次,对年龄问题,列方程和代入法是最常用的解题方法。
列方程:依据之一是题目中给出的等式关系,这种情况下特别需要注意题目中出现“一 样” “相等” “相同”等字词的地方,这些地方往往就是列方程的依据。
依据之二是年龄差保 持不变,如果题目涉及不同年份,且无特别明显的其他列方程依据提示,则往往据年龄差不 变来列方程。
代入法:因为年龄都是小于 100 的正整数,将选项的数字代回到题目条件中去验证,运 算速度往往是很快的。
很多题目中给的条件含有倍数关系, 这在我们代入验证的时候可以首 先考虑用整除性质进行验证,可以更节省时间。
所以特别要注意,求解年龄问题特别优先考虑列方程和代入法。
最后,重点说明年龄差保持不变。
这一条是多数年龄问题中难题的突破口和切入点。
对 于复杂的年龄问题, 在读完题目后没有发现直接的方法或列方程的依据, 那么此时年龄差保 持不变往往是突破口。
数量题做不对?你不懂这3个技巧

数量题做不对?你不懂这3个技巧在历年国考的行测中,年龄问题屡有出现。
其中有三类题,是数量关系题中最常见的题型。
今天图图老湿就用三道典型例题,教你年龄问题的快速解题方法。
一、带入排除在数量关系有一种尤为重要的方法-带入排除,而在遇到条件关系复杂的年龄问题时,可优先考虑带入排除。
【例1】小李的弟弟比小李小2岁,小王的哥哥比小王大2岁、比小李大5岁。
1994年,小李的弟弟和小王的年龄之和为15。
问2014年小李与小王的年龄分别为多少岁( )A.25、32B.27、30C.30、27D.32、25解:题目中所给关系较多,正面求解会相对繁琐,而问题所问的小李和小王的年龄关系在题目中体现为:小王的哥哥比小王大2岁、比小李大5岁。
可得小王比小李大3岁,观察选项,只有B选项符合。
二、特定规律由于年龄特定的规律,因而其解题的固定知识点要牢记:(1)过N年,每人都长N岁;(2)两个人的年龄差在任何时间节点都不发生改变。
【例2】张先生今年70岁,他有三个孙子。
长孙20岁,次孙13岁,幼孙7岁。
问多少年后,三个孙子年龄之和与祖父的年龄相同( )A.10B.15C.18D.20解:可设x年后,三个孙子的年龄之和与祖父相同。
由过N年,每人都长N岁,可得70+x=20+13+7+3x,得x=15。
三、“三观要正”、常识要懂在一些年龄问题中,出题人常会给出年龄范围或者年龄关系,而这些范围或者关系一定要满足我们正常认知范畴。
比如“百岁老人”即一百出头,不能考虑太过离谱。
【例3】小王与父亲属相相同,小王的母亲比他父亲小4岁,某个蛇年小王的母亲年龄正好是小王的3倍(年龄按阴历年份计算,出生当年算0岁),则小王的属相可能是( )A.蛇B.马C.羊D.猴解:设小王年龄为x,则母亲为3x,父亲为3x+4;父亲年龄应当比儿子大12,24,36,……。
按照正常三观,两代人年龄差应为24岁,因此3x+4-x=24,x=10。
现为蛇年,根据常识可得小王属相应为羊。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
公务员考试行测年龄问题秒解技巧
公务员考试行测年龄问题秒解技巧
年龄问题一直是公务员行测考试数量关系题中常考的一种题型,也是很多考生容易做错的题型,其实只要掌握了基本的核心,年龄问题便可迎刃而解。
公考老师指出,年龄问题一般能够经过整除、代入排除、列方程等方法便很快得到答案,而年龄差不变是很多年龄问题的切入点和突破口。
一、年龄问题的两个核心
1.每个人过N年,都长N岁(年龄均为整数);
2.两人年龄差不变。
二、基本题型
1.父子二人,已知前父亲的年龄是儿子的4倍,后父亲的年龄是儿子的2倍。
那么儿子出生时,父子的年龄是( )
A.20
B.25
C.30
D.33
【答案】C
【解析】对于年龄问题,我们首先考虑整除加代入排除法。
根据题目“ 前父亲的年龄是儿子的4倍”,可知当时父亲的年龄比儿子多三倍,即两者的年龄差为3的倍数,排除A、B。
代入C, 前父亲的年龄为40岁,儿子的年龄为10岁。
那么现在父亲的年龄为50岁,儿子的年龄为20岁,后父亲的年龄为60岁,儿子的年龄为30岁。
满足题意,故选C。
