集成光学2
合集下载
集成光学器件的材料
7.3.2 ZnO晶体
7.4 聚合物材料和玻璃材料（无定形材料）
7.4.1 聚合物材料
主要材料包括： 聚异丁烯酸甲酯（PMMA)、环氧树脂（expoxy)、苯丙环丁烯（benzocy-clobutene，BCB)、氟化聚酰亚胺（polyimide）、聚碳酸酯（polycarborates，PC） 物理特性：电光和热光 特点： 价格低，制作简单 可以淀积在半导体衬底上，易于实现混合集成 光波导损耗低、与光纤的耦合损耗也低 可以有效利用折射率的变化获得强度和相位的调制 通过调节有机材料组份以强化电光或声光特性
02
亚铁磁性晶体，通过掺杂提高法拉第旋转角
03
1100~1500nm的光吸收系数很低
04
主要制作光隔离器，也可制作调制器、开关等
05
衬底---钆镓石榴石GGG（Nd3Ga5O12)等
06
薄膜制备---化学汽相淀积、溶胶-凝胶、射频溅射
07
7.5 磁性材料
表7.3 闪锌矿型GaN、AlN材料体系主要特性
特性
GaN
AlN
禁带宽度（eV）（T=300K）
3.2~3.3
5.11（理论值）
晶格常数（Å）
4.52
4.33（理论值）
折射率
n=2.5
7.3 介质材料（dielectric material ）
介质材料---介电常数比较高的材料，可分为微波介质材料、光学介质材料；按材料的状态和性质分为光学晶体、光学玻璃 等
3.54
1550 nm LD
In0.47Ga0.53As
0.75
1.67
3.56
长波长PD/APD
表7.2 纤锌矿型GaN、AlN材料体系主要特性
7.4 聚合物材料和玻璃材料（无定形材料）
7.4.1 聚合物材料
主要材料包括： 聚异丁烯酸甲酯（PMMA)、环氧树脂（expoxy)、苯丙环丁烯（benzocy-clobutene，BCB)、氟化聚酰亚胺（polyimide）、聚碳酸酯（polycarborates，PC） 物理特性：电光和热光 特点： 价格低，制作简单 可以淀积在半导体衬底上，易于实现混合集成 光波导损耗低、与光纤的耦合损耗也低 可以有效利用折射率的变化获得强度和相位的调制 通过调节有机材料组份以强化电光或声光特性
02
亚铁磁性晶体，通过掺杂提高法拉第旋转角
03
1100~1500nm的光吸收系数很低
04
主要制作光隔离器，也可制作调制器、开关等
05
衬底---钆镓石榴石GGG（Nd3Ga5O12)等
06
薄膜制备---化学汽相淀积、溶胶-凝胶、射频溅射
07
7.5 磁性材料
表7.3 闪锌矿型GaN、AlN材料体系主要特性
特性
GaN
AlN
禁带宽度（eV）（T=300K）
3.2~3.3
5.11（理论值）
晶格常数（Å）
4.52
4.33（理论值）
折射率
n=2.5
7.3 介质材料（dielectric material ）
介质材料---介电常数比较高的材料，可分为微波介质材料、光学介质材料；按材料的状态和性质分为光学晶体、光学玻璃 等
3.54
1550 nm LD
In0.47Ga0.53As
0.75
1.67
3.56
长波长PD/APD
表7.2 纤锌矿型GaN、AlN材料体系主要特性
集成光学第二章第4节 23页PPT文档
k1x k2x k3x kx
k1y
k4y
k5y
ky
kjz, j1,2, 5
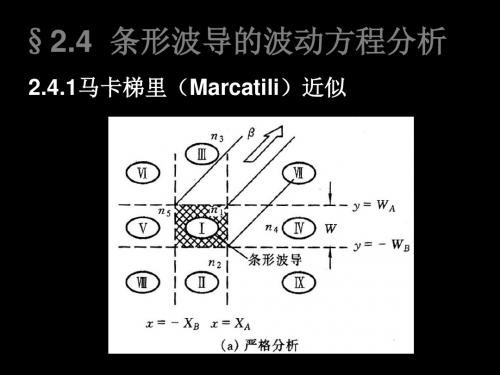
2.4.2
E
x mn
模式分析
1 由.E 麦m 克x n 斯模 韦中 方程各 ，场 有 量 的 关 系 Ey z ＋ i E y 0
E i 0 H , H i E
H
x
1 0n
2
2H x y2
Ez
i
1 0
n
2
H x y
Hz
i 1
H x x
2xH 2x2yH 2xk02n2 2 Hx0
E
y mn
的本征方程为
k x X A X B m a r c ta n k x a r c ta n k x m 1 ,2 ,3
i
E
x
E z x
i
0H
y
分量方程为
E y x
E x y
i
0H
z
H z y
i
H
y
i
0n 2E
x
H z x
i
0n 2E
y
H y x
i
0n 2E
z
各电磁场分量可以用 H y 写成
Hx0
E
x
0
H
y
1 0n
《集成光学课程简介》课件
提升光子集成电路的信息处理能力，实现更快速 、更准确的光子计算和光子通信。
THANKS
感谢观看
新型光子材料的探索与应用
新型光子材料的探索和应用为集成光学的发展提供了更多可能性， 如拓扑光子学、非线性光子学等领域的发展。
集成光学面临的挑战与机遇
技术瓶颈
目前的光子集成芯片还存在一些 技术瓶颈，如高损耗、低稳定性 等问题，需要进一步研究和突破
。
市场需求
随着5G、物联网等技术的普及， 市场对光子集成芯片的需求越来越 大，为集成光学的发展提供了广阔 的市场前景。
光波导具有低损耗、低成本、 高集成度等优点，是集成光学 中的核心元件。
光波导的传输模式分为单模和 多模，单模光波导具有更高的 传输质量和更远的传输距离。
光波导器件
光波导器件是利用光波导原理制 成的各种光子器件，如光调制器
、光开关、光滤波器等。
光波导器件具有小型化、集成化 、高性能等优点，广泛应用于光 通信、光传感、光计算等领域。
04
集成光学的前沿研究
光子晶体
总结词
光子晶体是一种具有周期性折射率变 化的介质，能够控制光的传播行为。
详细描述
光子晶体具有类似于电子能带结构的 特性，能够实现对特定频率光子的禁 带特性，从而实现光子局域、光子带 隙和光子操控等功能。
光子集成电路
总结词
光子集成电路是一种集成了多个光子器件的集成光路，可以实现光信号的产生、调制、传输和检测等功能。
详细描述
光子集成电路具有低损耗、高集成度、高速传输等优点，是实现光通信、光计算和光传感等应用的关键技术之一 。
光量子计算与量子通信
总结词
光量子计算和量子通信是基于量子力学原理的信息处理和通信方式，具有高度安全性和 并行性。
THANKS
感谢观看
新型光子材料的探索与应用
新型光子材料的探索和应用为集成光学的发展提供了更多可能性， 如拓扑光子学、非线性光子学等领域的发展。
集成光学面临的挑战与机遇
技术瓶颈
目前的光子集成芯片还存在一些 技术瓶颈，如高损耗、低稳定性 等问题，需要进一步研究和突破
。
市场需求
随着5G、物联网等技术的普及， 市场对光子集成芯片的需求越来越 大，为集成光学的发展提供了广阔 的市场前景。
光波导具有低损耗、低成本、 高集成度等优点，是集成光学 中的核心元件。
光波导的传输模式分为单模和 多模，单模光波导具有更高的 传输质量和更远的传输距离。
光波导器件
光波导器件是利用光波导原理制 成的各种光子器件，如光调制器
、光开关、光滤波器等。
光波导器件具有小型化、集成化 、高性能等优点，广泛应用于光 通信、光传感、光计算等领域。
04
集成光学的前沿研究
光子晶体
总结词
光子晶体是一种具有周期性折射率变 化的介质，能够控制光的传播行为。
详细描述
光子晶体具有类似于电子能带结构的 特性，能够实现对特定频率光子的禁 带特性，从而实现光子局域、光子带 隙和光子操控等功能。
光子集成电路
总结词
光子集成电路是一种集成了多个光子器件的集成光路，可以实现光信号的产生、调制、传输和检测等功能。
详细描述
光子集成电路具有低损耗、高集成度、高速传输等优点，是实现光通信、光计算和光传感等应用的关键技术之一 。
光量子计算与量子通信
总结词
光量子计算和量子通信是基于量子力学原理的信息处理和通信方式，具有高度安全性和 并行性。
集成光学传感器的研究及应用
集成光学传感器的研究及应用随着科技的不断进步和发展，光学传感器作为一种重要的测量技术也越来越受到人们的关注和重视。
在众多的光学传感器中，集成光学传感器因其体积小、重量轻、安装方便等优点，在很多领域都有着广泛的应用。
那么什么是集成光学传感器？它有哪些研究内容和应用领域呢？本文将从这几个方面进行介绍。
一、集成光学传感器的定义集成光学传感器又称为微波导技术传感器，是将光学波导与传感元件进行整合，利用微波导技术形成的一种新型传感器。
与传统的光学传感器相比，集成光学传感器具有体积小、重量轻、功耗低、制作工艺简单等特点。
二、集成光学传感器的研究内容1. 光学波导的设计与制作光学波导是集成光学传感器的核心部件，是将光信号从发光元件传输到接收元件的介质。
光学波导的设计与制作是集成光学传感器的重要研究内容之一。
现有的光学波导形式有很多种，如折射型波导、反射型波导、光纤波导等。
2. 光学传感机理的研究集成光学传感器是通过光学波导中发生的物理现象实现信号检测的，因此了解光学传感的机理对于研究和应用集成光学传感器具有重要意义。
光学传感的机理主要包括折射、反射、散射、吸收等。
3. 信号处理集成光学传感器的信号处理主要包括信号采集、信号运算、信号判别等。
目前普遍采用的信号处理技术有时域分析、频域分析和小波分析等。
三、集成光学传感器的应用领域集成光学传感器可以应用于生物医学、环境监测、工业生产等多个领域。
以下是它的主要应用领域：1. 医疗诊断：集成光学传感器可以用于癌症检测、糖尿病监测等医疗诊断领域。
2. 环境监测：集成光学传感器可以用于土壤水分监测、大气污染检测等环境监测领域。
3. 工业生产：集成光学传感器可以用于气体检测、流量控制等工业生产领域。
四、结论集成光学传感器是一种新型的光学传感技术，具有广泛的应用前景。
随着科技的不断进步和发展，相信这种传感技术在未来会得到更加广泛的应用和发展。
《集成光学第一章》课件
利用集成光学器件实现高灵敏度、高 分辨率的光学传感，用于环境监测、 生物医疗等领域。
2023
PART 02
集成光学的基本原理
REPORTING
光的波动理论
01
02
03
光的波动理论
描述光在介质中的传播行 为，包括光速、波长、频 率等物理量。
光的干涉
当两束或多束相干光波相 遇时，它们会相互叠加产 生明暗相间的干涉现象。
光的衍射
光波在传播过程中遇到障 碍物时，会绕过障碍物边 缘产生衍射现象。
光的干涉和衍射
光的干涉
01
当两束或多束相干光波相遇时，它们会相互叠加产生明暗相间
的干涉现象。
光的衍射
02
光波在传播过程中遇到障碍物时，会绕过障碍物边缘产生衍射
现象。
干涉和衍射的应用
03
在光学仪器、通信等领域有广泛的应用，如干涉仪、衍射光栅
2023
PART 05
集成光学的发展前景
REPORTING
新材料的应用
硅基材料
硅基材料在集成光学领域具有广泛的应用，其具有高折射 率、低损耗、易于加工等特点，可用于制造高性能的光波 导器件。
聚合物材料
聚合物材料具有柔韧性好、成本低等优点，适合大规模集 成和柔性光子器件的制造。
氮化硅材料
氮化硅材料具有高热导率、化学稳定性好等特点，可用于 制造高温、高稳定性的光波导器件。
息技术的重要发展方向。
光通信技术
光通信技术是以光波为信息载体，利用集成光学技术实现高速、 大容量的信息传输和处理，是未来通信领域的重要发展方向。
2023
REPORTING
THANKS
感谢观看
总结词
集成光学电路设计
集成光学电路设计随着信息技术的不断进步，光学电路在通信和计算领域中扮演着越来越重要的角色。
光学电路的高频带宽、低传输损耗以及抗干扰能力强的特点，使其成为当今高速数据传输和处理的理想选择。
本文将重点介绍集成光学电路的设计原理和方法。
一、集成光学电路的概述集成光学电路是指将光学和电路技术相结合，将光学元件、光学传输线、光检测器等组合在一起的器件。
它通过将多个光学组件集成在一张芯片上，实现了传统光学器件的集约化和高度集成。
集成光学电路具有占用空间小、性能可靠、工作频率高等优点，被广泛应用于光通信、生物传感、光子计算等领域。
二、集成光学电路设计的基本原理在进行集成光学电路设计之前，需要了解光学器件和光学波导的原理。
光学器件包括激光器、光检测器、光调制器等，它们分别用于产生、接收和调制光信号。
光学波导是将光信号在芯片表面进行传输的管道，可以分为直波导和曲折波导两种形式。
集成光学电路设计的基本原理是通过将光学器件和光学波导集成在一起，形成特定的光学电路结构。
设计时需要考虑波长选择、传输损耗、耦合效率等因素，并采用合适的设计方法和工艺流程。
常用的设计方法有布拉格光栅、光环等方法，工艺流程包括光子掩膜、刻蚀、镀膜等步骤。
三、集成光学电路设计的步骤1. 确定设计需求：首先需要明确设计的功能和性能要求，包括工作频率、波长范围、传输距离等。
2. 器件选择与设计：根据设计需求，选择合适的光学器件，并将其进行布局和优化设计。
3. 光学电路布局设计：根据器件的相互连接关系，进行光学电路的布局设计。
需要考虑光路长度、耦合效率和互连方式等因素。
4. 电路仿真和优化：使用光学电路仿真软件对电路进行模拟和优化，以获得最佳的工作性能。
5. 工艺制作和调试：根据设计结果，制作相应的光学芯片，并进行调试和测试，以确保其性能与设计要求一致。
四、集成光学电路设计的挑战与前景集成光学电路设计面临着许多挑战，例如器件尺寸缩小、损耗降低、制作工艺复杂等。
第6章集成光学
2 23
2 arctan(p )
212
2 arctan(nn1222
q
)
2 23
2
arc tan(nn2322
p
)
其中p、q为消逝系数
p ( 2 k02n32 )1/ 2 q ( 2 k02n12 )1/ 2
反射波发生相位突变的物理意义
全反射时，光穿入约束层内一定厚度，导 致反射波与入射波相位的不连续
m是导波的模阶数，不同的m，对应一 系列的β。该方程称为模式方程（特征方 程、本征值方程）
4.对称波导，非对称波导，强非对称波导
5. 波导中光波的传播，对于TE波，解波动
方程
2Ey (t)
ni2 c2
2Ey t 2
解的形式 Ey (x, z,t) y (x) exp[ i(t z)]
Y方向，波不受约束，场与 y无关
b.波导定向耦合器 平行放置，间隙小，消 逝场耦和
2.外耦合类型及其机制 a.直接耦合：利用一透镜 将激光束聚焦，直接照 射到波导的端部。 效率低：薄膜薄，端面 不平
b.棱镜耦合器
提高了耦合效率：耦合 方式连续耦合
结构：n3>n1>n4>n2 原理：当θ3>θ3c时，入 射 底 场→棱部扩镜反散激射到光光空束B3合气A3与成隙棱驻，镜波按 exp[-(k0n3sinθ3)x]衰减→ 继续扩散到薄膜中形成 导膜(消逝场)
m
d
n
得到 0 2n / m
光栅周期一定时，只有该式确
定的特定波长的光才能受到强
烈的反射
m=1，一级光栅
m=3，三级光栅
* 解理面反馈激光器中，发射光 谱多个峰值
分布反馈激光器中，一个峰， 可选纵模
集成光学ppt课件 第二章第2节 平板波导的射线光学理论
而12 0
TE波的色散方程变为
1
w k0 n 1 2n2 2marctan n n 1 2 2 2 n n3 2 2 2 2,m 0,1 ,2
故某一模式的截止波长为
w
cTE2
1 n12n22
marctann n122 2 n n3 22 21 2
T E 模
n 1 2 n e 2 ff 1 2k 0 w m a rc ta n n n 1 2 2 2 n n 1 e 2 2 ff n n e 2 f2 f 2 1 2 a rc ta n n n 1 3 2 2 n n 1 e 2 2 ff n n e 2 f3 2 f 1 2
§2.2平板波导的射线光学理论
• 2.2.1光波导的分类 • (a)平板波导(slab waveguide) • (b)条形波导(strip waveguide) • (c)圆柱波导(cylindrical waveguide)
平板波导
n3cladding
n1 core n2substract
c 1 3 i c 1 2 时 ， 形 成 衬 底 辐 射 波 ；
i c 1 2 且 c 1 3 时 ， 形 成 传 导 波 或 导 行 波 。
2.2.2 用射线方法研究平板光波导的导模
h n1 k0
1. 波矢的横向分量
把波矢分解为平行于波导的分量（相位常数为β）和垂直 于波导的分量（相位常数为h），三者关系为：
T M 模
如何理解模的概念？
(1)模式是光波导中一个常用的概念。 (2)从数学方面理解，模式是满足亥姆霍兹方程其在波导中心
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
华南师范大学 集成光学
kx n1k1 cos
横向波矢
12 主讲人：刘柳
特征方程
2k x a m tan (
1
2
kx
) tan (
1
3
kx
)
在这里，我们求解对称波导的情况，n1=n2 m (1) 2 a k x a tan k x a
2
与射线法结果一致
2 k n
2 2
华南师范大学 集成光学
2 2 0 2
7
主讲人：刘柳
边界条件
边界条件为：边界处切向Ey分量连续，切向分 E y E 量Hz也连续，由 x i H 知 x 连续
y 0 z
x
n3
入射波阵面
A θ
t=2a
n1
z
C
n2
一次反射波阵面
二次反射波阵面
时谐电磁场的麦克斯韦方程组
H i E
华南师范大学 集成光学 3 主讲人：刘柳
E i0H
波动方程
• 将矢量各分量展开，得：
E z E y i0 H x y z E x E z i0 H y z x E y E x i0 H z x y
一次反射波阵面
二次反射波阵面
E y i0 H z TE模(横电模) x H z i H i E y x x
华南师范大学 集成光学
设波沿着z方向传播，则沿z方向场的变化可用一个传输因子exp(iβz)来表示 0 E Hx H y y Ex TM模(横磁模)
14 主讲人：刘柳
图解法求解特征方程
12 10
m=0 m=1 m=2
模式数量
2 k 2 a 2 (n 2 n 2 ) 0 1 2 M
向下取整
6 8 10 12
8
a (π )
pt
6
4
2
0
0
2
4
kxa (π )
m 2 a k x a tan k x a 2
华南师范大学 集成光学 8
tan(k x a )
2
kx
主讲人：刘柳
边界条件
x
n3
入射波阵面
A θ
t=2a
n1
z
C
E3 exp[ 3 ( x a )] x a E y ( x) E1 cos(k x x ) a x a E exp[ ( x a )] x a 2 2
x
8
a (π )
pt
6
4
d
2 0
n3
0
2
4
6
8
10
12
kxa (π )
O
i
n2
k1 i ’i
n1 z
m 2 a k x a tan k x a 2
华南师范大学 集成光学
2 2 2 ( a)2 (kx a)2 k0 a (n12 n2 )
cTM
n 2 m arctan 1 n3
2 2 n2 n3 2 2 n1 n2
• 对于对称平板波导，TE0和TM0的截止波长 均为无限长
华南师范大学 集成光学 18 主讲人：刘柳
特征方程与色散曲线
m 2 a k x a tan k x a 2
华南师范大学 集成光学
2 2 2 ( a)2 (kx a)2 k0 a (n12 n2 )
15
主讲人：刘柳
图解法求解特征方程
12 10
m=0 m=1 m=2
0阶模总是存在 1阶模存在条件:
k a (n n )
2 0 2 2 1 2 2
8
a (π )
6
pt
2
4
2阶模存在条件:
E3 exp[ 3 ( x a )] x a E y ( x) E1 cos(k x x ) a x a E exp[ ( x a )] x a 2 2
(1) x= -a处，
E1 cos(kx a ) E2
kx E1 sin(kx x ) |xa 2 E2 exp[2 ( x a)]|xa (kx E1 sin(kx a ) 2 E2 )
• 特征方程中有4个参数（n1,n2,a,），改变任何一个结 构参数都要对方程重新求解，不利于应用。为此作归一 化处理。 • 传播常数范围： k0n2 k0n1 • 归一化传播常数：
b
• 波导参数V：
华南师范大学 集成光学
2 / k n 0 2 2
n n
H z H y i E x y z H x H z i E y z x H y H x i E z x y
x
n3
入射波阵面
A θ
t=2a
n1
z
C
并且考虑到y方向是均匀的，即
0 y
n2
特征方程（本征值方程）
x
n3
入射波阵面
A θ
n1
t=2a
k1
z
C
n2
一次反射波阵面
二次反射波阵面
2k x a m tan (
1
2
kx
) tan (
1
3
kx
)
2n1k0t cos 12 13 2m
2 2 2 1 n1 sin n2 12 2 tan 2 2 n1 cos 1/ 2
tan(k x a )
2
kx
tan(k x a )
3
kx
TE模
2k x a m tan (
1
集成光学
2
kx
10
) tan (
1
3
kx
)
关于的函数
华南师范大学
主讲人：刘柳
特征方程（本征值方程）
TE模的特征方程： 1 2 1 3 2k x a m tan ( ) tan ( )
n2
y
华南师范大学 集成光学
2 Ey x 2
5
2 2 2 k n 0 2 Ey 0
主讲人：刘柳
波动方程的解
2 Ey x 2
2 2 2 k n 0 1 Ey 0
上式为波动方程，也叫做Helmholtz方程，他的通解可表示为：
E y a1 cos kT x a2 sin kT x a1 cos kT x a1 exp jkT x a2 exp jkT x a1 exp j kT x
图解法求解特征方程
12 10
m=0 m=1 m=2
单模条件
( a) (k x a )
2 2
8
a (π )
2
6
pt
4
2
k a (n n )
2 0 2 2 1 2 2
0 2 4 6 8 10 12
2
0
kxa (π )
m 2 a k x a tan k x a 2
其中
kT k02n12 2 ，通常个成为横向波矢。a1, a2, 为待定系数。
集成光学 6 主讲人：刘柳
华南师范大学
波动方程的解（场分布）
cladding E3 exp[ 3 ( x a)] x a E y ( x) E1 cos(k x x ) a x a core E exp[ ( x a)] x a substrate 2 2
2 2 kx 2 k0 n1 2
2 2 22 2 k0 n2 2 2 32 2 k0 n3
2 2 2 1 n1 sin n3 13 2 tan 2 2 n cos 1
1/ 2
n1k1 sin kz
传播常数
i H y E z x Ez i E i0 H y x x
4
主讲人：刘柳
波动方程（TE模）
0 E Hx y E y i0 H z x H z i H i E y x x
上节课内容
x
d O i
n2
n3
波导的模方程：
k1 i ’i
n1 z
2n1k0t cosi 12 13 2m
12 13 为上下两个波导界面的全反射相移
传播常数：=n1k0sini 有效折射率neff: neff= /k0= n1sini
导波存在条件：
华南师范大学 集成光学
3
kx
华南师范大学
集成光学
9
主讲人：刘柳
特征方程（本征值方程）
x
n3
入射波阵面
A θ
t=2a
n1
z
C
n2
一次反射波阵面
二次反射波阵面
E3 exp[ 3 ( x a )] x a E y ( x) E1 cos(k x x ) a x a E exp[ ( x a )] x a 2 2
0 2 4 6 8 10 12
2
0
2 k02 a 2 (n12 n2 )
kxa (π )
m 2 a k x a tan k x a 2
华南师范大学 集成光学
kx n1k1 cos
横向波矢
12 主讲人：刘柳
特征方程
2k x a m tan (
1
2
kx
) tan (
1
3
kx
)
在这里，我们求解对称波导的情况，n1=n2 m (1) 2 a k x a tan k x a
2
与射线法结果一致
2 k n
2 2
华南师范大学 集成光学
2 2 0 2
7
主讲人：刘柳
边界条件
边界条件为：边界处切向Ey分量连续，切向分 E y E 量Hz也连续，由 x i H 知 x 连续
y 0 z
x
n3
入射波阵面
A θ
t=2a
n1
z
C
n2
一次反射波阵面
二次反射波阵面
时谐电磁场的麦克斯韦方程组
H i E
华南师范大学 集成光学 3 主讲人：刘柳
E i0H
波动方程
• 将矢量各分量展开，得：
E z E y i0 H x y z E x E z i0 H y z x E y E x i0 H z x y
一次反射波阵面
二次反射波阵面
E y i0 H z TE模(横电模) x H z i H i E y x x
华南师范大学 集成光学
设波沿着z方向传播，则沿z方向场的变化可用一个传输因子exp(iβz)来表示 0 E Hx H y y Ex TM模(横磁模)
14 主讲人：刘柳
图解法求解特征方程
12 10
m=0 m=1 m=2
模式数量
2 k 2 a 2 (n 2 n 2 ) 0 1 2 M
向下取整
6 8 10 12
8
a (π )
pt
6
4
2
0
0
2
4
kxa (π )
m 2 a k x a tan k x a 2
华南师范大学 集成光学 8
tan(k x a )
2
kx
主讲人：刘柳
边界条件
x
n3
入射波阵面
A θ
t=2a
n1
z
C
E3 exp[ 3 ( x a )] x a E y ( x) E1 cos(k x x ) a x a E exp[ ( x a )] x a 2 2
x
8
a (π )
pt
6
4
d
2 0
n3
0
2
4
6
8
10
12
kxa (π )
O
i
n2
k1 i ’i
n1 z
m 2 a k x a tan k x a 2
华南师范大学 集成光学
2 2 2 ( a)2 (kx a)2 k0 a (n12 n2 )
cTM
n 2 m arctan 1 n3
2 2 n2 n3 2 2 n1 n2
• 对于对称平板波导，TE0和TM0的截止波长 均为无限长
华南师范大学 集成光学 18 主讲人：刘柳
特征方程与色散曲线
m 2 a k x a tan k x a 2
华南师范大学 集成光学
2 2 2 ( a)2 (kx a)2 k0 a (n12 n2 )
15
主讲人：刘柳
图解法求解特征方程
12 10
m=0 m=1 m=2
0阶模总是存在 1阶模存在条件:
k a (n n )
2 0 2 2 1 2 2
8
a (π )
6
pt
2
4
2阶模存在条件:
E3 exp[ 3 ( x a )] x a E y ( x) E1 cos(k x x ) a x a E exp[ ( x a )] x a 2 2
(1) x= -a处，
E1 cos(kx a ) E2
kx E1 sin(kx x ) |xa 2 E2 exp[2 ( x a)]|xa (kx E1 sin(kx a ) 2 E2 )
• 特征方程中有4个参数（n1,n2,a,），改变任何一个结 构参数都要对方程重新求解，不利于应用。为此作归一 化处理。 • 传播常数范围： k0n2 k0n1 • 归一化传播常数：
b
• 波导参数V：
华南师范大学 集成光学
2 / k n 0 2 2
n n
H z H y i E x y z H x H z i E y z x H y H x i E z x y
x
n3
入射波阵面
A θ
t=2a
n1
z
C
并且考虑到y方向是均匀的，即
0 y
n2
特征方程（本征值方程）
x
n3
入射波阵面
A θ
n1
t=2a
k1
z
C
n2
一次反射波阵面
二次反射波阵面
2k x a m tan (
1
2
kx
) tan (
1
3
kx
)
2n1k0t cos 12 13 2m
2 2 2 1 n1 sin n2 12 2 tan 2 2 n1 cos 1/ 2
tan(k x a )
2
kx
tan(k x a )
3
kx
TE模
2k x a m tan (
1
集成光学
2
kx
10
) tan (
1
3
kx
)
关于的函数
华南师范大学
主讲人：刘柳
特征方程（本征值方程）
TE模的特征方程： 1 2 1 3 2k x a m tan ( ) tan ( )
n2
y
华南师范大学 集成光学
2 Ey x 2
5
2 2 2 k n 0 2 Ey 0
主讲人：刘柳
波动方程的解
2 Ey x 2
2 2 2 k n 0 1 Ey 0
上式为波动方程，也叫做Helmholtz方程，他的通解可表示为：
E y a1 cos kT x a2 sin kT x a1 cos kT x a1 exp jkT x a2 exp jkT x a1 exp j kT x
图解法求解特征方程
12 10
m=0 m=1 m=2
单模条件
( a) (k x a )
2 2
8
a (π )
2
6
pt
4
2
k a (n n )
2 0 2 2 1 2 2
0 2 4 6 8 10 12
2
0
kxa (π )
m 2 a k x a tan k x a 2
其中
kT k02n12 2 ，通常个成为横向波矢。a1, a2, 为待定系数。
集成光学 6 主讲人：刘柳
华南师范大学
波动方程的解（场分布）
cladding E3 exp[ 3 ( x a)] x a E y ( x) E1 cos(k x x ) a x a core E exp[ ( x a)] x a substrate 2 2
2 2 kx 2 k0 n1 2
2 2 22 2 k0 n2 2 2 32 2 k0 n3
2 2 2 1 n1 sin n3 13 2 tan 2 2 n cos 1
1/ 2
n1k1 sin kz
传播常数
i H y E z x Ez i E i0 H y x x
4
主讲人：刘柳
波动方程（TE模）
0 E Hx y E y i0 H z x H z i H i E y x x
上节课内容
x
d O i
n2
n3
波导的模方程：
k1 i ’i
n1 z
2n1k0t cosi 12 13 2m
12 13 为上下两个波导界面的全反射相移
传播常数：=n1k0sini 有效折射率neff: neff= /k0= n1sini
导波存在条件：
华南师范大学 集成光学
3
kx
华南师范大学
集成光学
9
主讲人：刘柳
特征方程（本征值方程）
x
n3
入射波阵面
A θ
t=2a
n1
z
C
n2
一次反射波阵面
二次反射波阵面
E3 exp[ 3 ( x a )] x a E y ( x) E1 cos(k x x ) a x a E exp[ ( x a )] x a 2 2
0 2 4 6 8 10 12
2
0
2 k02 a 2 (n12 n2 )
kxa (π )
m 2 a k x a tan k x a 2
华南师范大学 集成光学