《工程力学》复习指导含答案
工程力学复习题及参考答案

课程考试复习题及参考答案工程力学一、填空题:1.受力后几何形状和尺寸均保持不变的物体称为。
2.构件抵抗的能力称为强度。
3.圆轴扭转时,横截面上各点的切应力与其到圆心的距离成比。
4.梁上作用着均布载荷,该段梁上的弯矩图为。
5.偏心压缩为的组合变形。
6.柔索的约束反力沿离开物体。
7.构件保持的能力称为稳定性。
8.力对轴之矩在情况下为零。
9.梁的中性层与横截面的交线称为。
10.图所示点的应力状态,其最大切应力是。
11.物体在外力作用下产生两种效应分别是。
12.外力解除后可消失的变形,称为。
13.力偶对任意点之矩都。
14.阶梯杆受力如图所示,设AB和BC段的横截面面积分别为2A和A,弹性模量为E,则杆中最大正应力为。
15.梁上作用集中力处,其剪力图在该位置有。
16.光滑接触面约束的约束力沿指向物体。
17.外力解除后不能消失的变形,称为。
18.平面任意力系平衡方程的三矩式,只有满足三个矩心的条件时,才能成为力系平衡的充要条件。
19.图所示,梁最大拉应力的位置在点处。
20.图所示点的应力状态,已知材料的许用正应力[σ],其第三强度理论的强度条件是。
21.物体相对于地球处于静止或匀速直线运动状态,称为。
22.在截面突变的位置存在集中现象。
23.梁上作用集中力偶位置处,其弯矩图在该位置有。
24.图所示点的应力状态,已知材料的许用正应力[σ],其第三强度理论的强度条件是。
25.临界应力的欧拉公式只适用于杆。
26.只受两个力作用而处于平衡状态的构件,称为。
27.作用力与反作用力的关系是。
28.平面任意力系向一点简化的结果的三种情形是。
29.阶梯杆受力如图所示,设AB和BC段的横截面面积分别为2A和A,弹性模量为E,则截面C的位移为。
30.若一段梁上作用着均布载荷,则这段梁上的剪力图为。
二、计算题:1.梁结构尺寸、受力如图所示,不计梁重,已知q=10kN/m,M=10kN·m,求A、B、C处的约束力。
2.铸铁T梁的载荷及横截面尺寸如图所示,C为截面形心。
工程力学复习题答案

工程力学复习题答案一、单项选择题1. 刚体在平面内运动时,其运动学描述不包括以下哪一项?A. 平移B. 旋转C. 振动D. 变形答案:D2. 材料力学中,下列哪一项不是应力的类型?A. 正应力B. 剪应力C. 拉应力D. 扭应力答案:C3. 在梁的弯曲问题中,以下哪一项不是梁的内力?A. 剪力B. 弯矩C. 扭矩D. 轴力答案:C二、多项选择题1. 以下哪些因素会影响材料的弹性模量?A. 材料类型B. 温度C. 材料的微观结构D. 材料的密度答案:A, B, C2. 根据胡克定律,以下哪些描述是正确的?A. 应力与应变成正比B. 比例系数称为弹性模量C. 应力与应变成反比D. 弹性模量是材料的固有属性答案:A, B, D三、填空题1. 在材料力学中,材料在外力作用下发生形变,当外力移除后,材料能够恢复原状的性质称为_______。
答案:弹性2. 当梁受到均布载荷时,其最大弯矩通常出现在梁的_______。
答案:中点3. 材料的屈服强度是指材料在受到外力作用时,从弹性变形过渡到塑性变形的临界应力值,通常用_______表示。
答案:σy四、简答题1. 简述材料力学中应力集中的概念及其对结构设计的影响。
答案:应力集中是指在构件的局部区域,由于几何形状、材料不连续性或其他原因,导致应力值远高于周围区域的现象。
这种现象可能导致结构的局部应力超过材料的强度极限,从而引发裂纹或断裂,对结构的安全性和可靠性造成影响。
因此,在结构设计中,应尽量避免应力集中的产生,或采取适当的措施来降低其影响。
2. 描述梁在弯曲时的正应力分布规律。
答案:梁在弯曲时,其横截面上的正应力分布规律是:在中性轴上,正应力为零;在中性轴上方,正应力为拉应力,且随着距离中性轴的增加而增大;在中性轴下方,正应力为压应力,且随着距离中性轴的增加而增大。
这种分布规律可以用弯曲应力公式σ=My/I来描述,其中M是弯矩,y是距离中性轴的距离,I是横截面的惯性矩。
工程力学复习题及答案

工程力学复习题及答案一、选择题1. 工程力学中,牛顿第二定律表达的是()。
A. 力是物体运动的原因B. 力是物体运动状态改变的原因C. 力是物体形状改变的原因D. 力是物体质量改变的原因2. 以下哪项不是材料力学研究的范畴?()A. 材料的弹性B. 材料的塑性C. 材料的热传导D. 材料的疲劳3. 在静力学中,力的合成遵循()。
A. 几何法则B. 代数法则C. 物理法则D. 化学法则二、填空题4. 根据胡克定律,弹簧的弹力与弹簧的形变量成正比,比例系数称为______。
5. 材料在受到外力作用时,若其内部应力超过材料的______,则会发生断裂。
6. 工程力学中的虚功原理是指,在平衡状态下,任何微小的位移变化都不会引起外力对系统做______。
三、简答题7. 简述材料力学中的应力-应变关系。
8. 描述静力学中三力平衡的条件。
9. 解释什么是弹性模量,并说明其在工程中的应用。
四、计算题10. 一根长为L的均匀杆,其一端固定,另一端受到垂直于杆的力F 作用。
求杆的弯曲角度。
11. 一块矩形钢板,长为a,宽为b,厚度为t,受到均匀分布的压力p。
计算钢板的最大弯曲应力。
12. 一个质量为m的物体,从静止开始自由下落,忽略空气阻力,求物体下落h高度时的速度。
五、论述题13. 论述在工程结构设计中,如何考虑材料的疲劳寿命。
14. 讨论在桥梁设计中,如何应用静力学原理来确保结构的稳定性。
六、案例分析题15. 某建筑工地上,一台起重机在吊装重物时发生倒塌。
分析可能的原因,并提出预防措施。
16. 某高速公路的路面出现裂缝,分析裂缝产生的原因,并提出修复方案。
七、实验题17. 设计一个实验来测量材料的弹性模量。
18. 描述如何通过实验验证胡克定律。
八、综合应用题19. 一个悬臂梁,其一端固定,另一端承受一个集中载荷。
分析梁的受力情况,并计算最大弯矩。
20. 一个圆柱形储气罐,其壁厚为d,内径为D,承受内部压力p。
计算储气罐的最大主应力。
《工程力学》考试复习题库(含答案)

《工程力学》考试复习题库(含答案)一、选择题1. 工程力学是研究()A. 材料力学性能B. 力的作用和物体运动规律C. 结构的计算和分析D. 机器的设计与制造答案:B2. 在静力学中,力的作用效果取决于()A. 力的大小B. 力的方向C. 力的作用点D. A、B、C均正确答案:D3. 平面汇交力系的平衡条件是()A. 力的代数和为零B. 力矩的代数和为零C. 力的投影和为零D. 力的投影和为零且力矩的代数和为零答案:D4. 拉伸或压缩时,杆件横截面上的正应力等于()A. 拉力或压力B. 拉力或压力除以横截面面积C. 拉力或压力乘以横截面面积D. 拉力或压力除以杆件长度答案:B5. 材料在屈服阶段之前,正应力和应变的关系符合()A. 胡克定律B. 比例极限C. 屈服强度D. 断裂强度答案:A二、填空题1. 工程力学中的基本单位有()、()、()。
答案:米、千克、秒2. 二力平衡条件是:作用在同一个物体上的两个力,必须()、()、()。
答案:大小相等、方向相反、作用在同一直线上3. 材料的弹性模量表示材料在弹性范围内抵抗()的能力。
答案:变形4. 在剪切力作用下,杆件横截面沿剪切面发生的变形称为()。
答案:剪切变形5. 梁的挠度是指梁在受力后产生的()方向的位移。
答案:垂直三、判断题1. 力偶的作用效果只与力偶矩大小有关,与力偶作用点位置无关。
()答案:正确2. 在拉伸或压缩过程中,杆件的横截面面积始终保持不变。
()答案:正确3. 材料的屈服强度越高,其抗断裂能力越强。
()答案:错误4. 在受弯构件中,中性轴是弯矩等于零的轴线。
()答案:错误5. 梁的挠度曲线是梁的轴线在受力后的实际位置。
()答案:正确四、计算题1. 一根直径为10mm的圆形杆,受到轴向拉力1000N的作用。
求杆件的伸长量。
答案:杆件的伸长量约为0.005mm。
2. 一根简支梁,受到均布载荷q=2kN/m的作用,跨度l=4m。
求梁的最大挠度。
工程力学课后习题答案解析
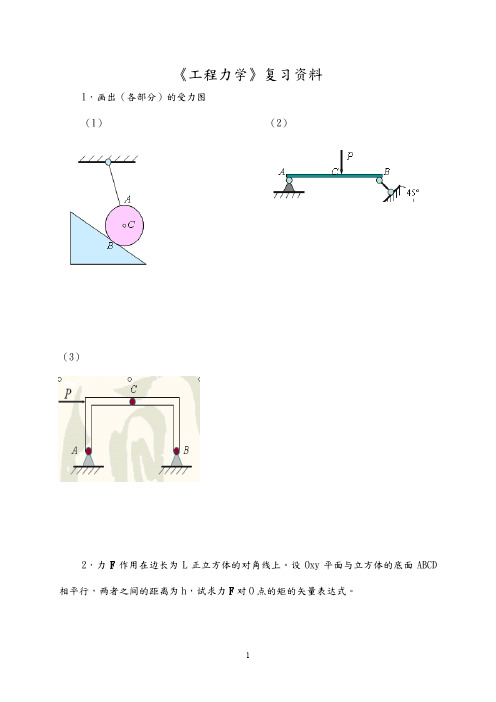
《工程力学》复习资料1.画出(各部分)的受力图(1)(2)(3)2.力F作用在边长为L正立方体的对角线上。
设Oxy平面与立方体的底面ABCD 相平行,两者之间的距离为h,试求力F对O点的矩的矢量表达式。
解:依题意可得:ϕθcos cos ⋅⋅=F F xϕθsin cos ⋅⋅=F F y θsin ⋅=F F z 其中33sin =θ 36cos =θ 45=ϕ 点坐标为:()h l l ,, 则()3)()(3333333j i h l F k F j F i F F M +⋅+=-+-= 3.如图所示力系由F 1,F 2,F 3,F 4和F 5组成,其作用线分别沿六面体棱边。
已知:的F 1=F 3=F 4=F 5=5kN, F 2=10 kN ,OA=OC/2=1.2m 。
试求力系的简化结果。
解:各力向O 点简化 0.0.0.523143=-==-==+-=C O F A O F M C B F A O F M C O F C O F M Z Y X 即主矩的三个分量 kN F F Rx 55==kN F F Ry 102==kN F F F F RZ 5431=+-=即主矢量为: k j i 5105++合力的作用线方程 Z y X ==24.多跨梁如图所示。
已知:q=5kN ,L=2m 。
试求A 、B 、D 处的约束力。
取CD 段0=∑ci M 0212=-⋅ql l F D 解得 kN F D 5=取整体来研究,0=∑iy F02=+⋅-+D B Ay F l q F F 0=∑ix F 0=Ax F0=∑iAM 032=⋅+⋅-⋅l F l ql l F D B 联合以上各式,解得 kN F F Ay A 10-== kN F B 25=5.多跨梁如图所示。
已知:q=5kN ,L=2m ,ψ=30°。
试求A 、C 处的约束力。
(5+5=10分)取BC 段0=∑iy F0cos 2=⋅+⋅-ϕC B F l q F 0=∑ix F 0sin =⋅-ϕC Bx F F0=∑icM 022=⋅⋅+⋅-l l q l F By联合以上各式,解得 kN F Bx 77.5= kN F By 10= kN F C 574.11=取整体研究0=∑ix F0sin =⋅-ϕC Ax F F 0=∑iy F 0cos 2=⋅+⋅-ϕC Ay F l q F0=∑iAM 04cos 32=⋅⋅+⋅⋅-l F l l q M C A ϕ 联合以上各式,解得 kN F Ax 774.5= kN F Ay 10= m kN M A ⋅=406.如图无底的圆柱形容器空筒放在光滑的固定地面上,内放两个重球。
工程力学二复习题及答案

工程力学二复习题及答案1. 简述牛顿第三定律的内容及其在工程力学中的应用。
答案:牛顿第三定律指出,对于任何两个相互作用的物体,它们之间的作用力和反作用力大小相等、方向相反。
在工程力学中,这一定律用于分析和计算结构中力的平衡,例如在桥梁设计中考虑支撑力和载荷力的平衡。
2. 描述胡克定律,并解释其在材料力学中的重要性。
答案:胡克定律表明,在弹性限度内,材料的应力与应变成正比。
这一定律在材料力学中至关重要,因为它允许工程师预测材料在受力时的行为,从而设计出能够承受预定载荷的结构。
3. 列出三种常见的应力类型,并解释每种应力的特点。
答案:常见的应力类型包括拉伸应力、压缩应力和剪切应力。
拉伸应力发生在材料被拉伸时,导致材料长度增加;压缩应力发生在材料被压缩时,导致材料长度减小;剪切应力发生在材料受到平行于其表面的力时,导致材料形状发生倾斜。
4. 简述材料的弹性模量和屈服强度,并说明它们在工程设计中的作用。
答案:弹性模量是材料在弹性阶段应力与应变比值的度量,反映了材料抵抗形变的能力。
屈服强度是材料开始发生塑性变形的应力值,标志着材料从弹性状态转变为塑性状态的临界点。
在工程设计中,这两个参数帮助工程师确定材料在不同载荷下的行为,以确保结构的安全性和可靠性。
5. 描述梁的弯曲应力公式,并解释其在梁设计中的应用。
答案:梁的弯曲应力公式为σ=My/I,其中σ是弯曲应力,M是弯矩,y是距离中性轴的距离,I是截面的惯性矩。
这个公式在梁设计中用于计算不同截面位置的应力,以确保梁在预期载荷下不会发生破坏。
6. 解释什么是临界载荷,并给出一个计算临界载荷的公式。
答案:临界载荷是指结构开始失稳的最小载荷。
对于一个两端铰接的柱子,其临界载荷公式为Pcr=π²EI/(KL)²,其中Pcr是临界载荷,E是材料的弹性模量,I是截面惯性矩,K是柱子的有效长度系数,L 是柱子的实际长度。
7. 简述达朗贝尔原理,并说明其在动力学分析中的应用。
工程力学期末复习题参考答案
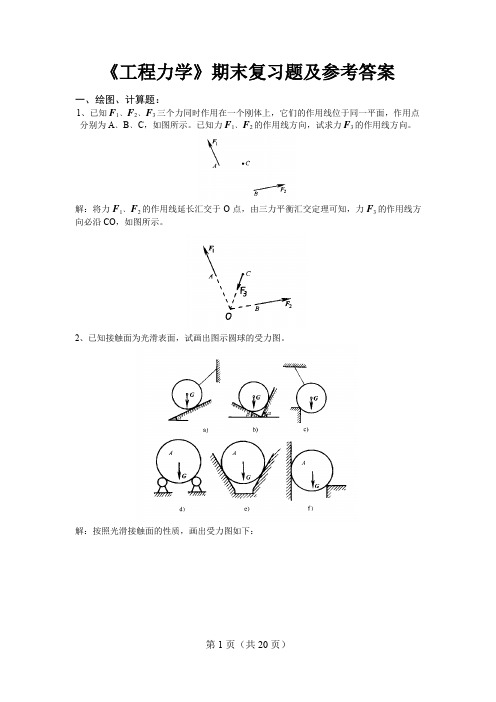
《工程力学》期末复习题及参考答案一、绘图、计算题:1、已知F1﹑F2﹑F3三个力同时作用在一个刚体上,它们的作用线位于同一平面,作用点分别为A﹑B﹑C,如图所示。
已知力F1﹑F2的作用线方向,试求力F3的作用线方向。
解:将力F1﹑F2的作用线延长汇交于O点,由三力平衡汇交定理可知,力F3的作用线方向必沿CO,如图所示。
2、已知接触面为光滑表面,试画出图示圆球的受力图。
解:按照光滑接触面的性质,画出受力图如下:3、试画出各分图中物体AB的受力图。
解:物体AB的受力图如图所示。
4、如图所示,简易起重机用钢丝绳吊起重量G=10kN的重物。
各杆自重不计,A、B、C三处为光滑铰链联接。
铰链A处装有不计半径的光滑滑轮。
求杆AB和AC受到的力。
解:画A处光滑铰链销钉受力图(见图),其中重物重力G垂直向下;AD绳索拉力F T沿AD方向,大小为G;AB 杆拉力F BA 沿AB 方向;AC 杆受压,推力F CA 沿CA 方向。
以A 为原点建立Axy 坐标系,由平衡条件得到如下方程:030sin 45sin ,0001=--=∑=T BA CA niix F F F F (a)030cos 45cos ,0001=--=∑=G F F F T CA ni iy (b)由(b)式得kN G F CA 4.2645cos )130(cos 00=+=,代入(a )式得kN F F F T CA BA 66.135.010707.04.2630sin 45sin 00=⨯-⨯=-=所以杆AB 受到的力kN F BA 66.13=,为拉力;杆AC 受到的力kN F CA 4.26=,为压力。
5、拖车的重量G =250kN ,牵引车对它的作用力F =50kN ,如图所示。
求当车辆匀速直线行驶时,车轮A 、B 对地面的正压力。
解:画拖车受力图,如图所示,拖车受6个力的作用:牵引力F ,重力G ,地面法向支撑力F NA 、F NB ,摩擦力F A 、F B 。
《工程力学》详细版习题参考答案

∑ Fx
=FAx
+
FBx
+
FCx
=− 1 2
F
+
F
−
1 2
F
=0
∑ Fy
= FAy
+
FBy
+
FCy
= − 3 2
F
+
3 F = 0 2
∑ M B= FBy ⋅ l=
3 Fl 2
因此,该力系的简化结果为一个力偶矩 M = 3Fl / 2 ,逆时针方向。
题 2-2 如图 2-19(a)所示,在钢架的 B 点作用有水平力 F,钢架重力忽 略不计。试求支座 A,D 的约束反力。
(a)
(b)
图 2-18
解:(1)如图 2-18(b)所示,建立直角坐标系 xBy。 (2)分别求出 A,B,C 各点处受力在 x,y 轴上的分力
思考题与练习题答案
FAx
= − 12 F ,FAy
= − 3 F 2
= FBx F= ,FBy 0
FCx
= − 12 F ,FCy
= 3 F 2
(3)求出各分力在 B 点处的合力和合力偶
(3)根据力偶系平衡条件列出方程,并求解未知量
∑ M =0 − aF + 2aFD =0
《工程力学》
可解得 F=Ay F=D F /2 。求得结果为正,说明 FAy 和 FD 的方向与假设方向相同。 题 2-3 如 图 2-20 ( a ) 所 示 , 水 平 梁 上 作 用 有 两 个 力 偶 , 分 别 为
3-4 什么是超静定问题?如何判断问题是静定还是超静定?请说明图 3-12 中哪些是静定问题,哪些是超静定问题?
(a)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学 重点及其公式材料力学的任务 (1)强度要求; (2)刚度要求; (3)稳定性要求。
变形固体的基本假设 (1)连续性假设;(2)均匀性假设;(3)各向同性假设;(4)小变形假设。
外力分类:表面力、体积力;内力:构件在外力的作用下,内部相互作用力的变化量,即构件内部各部分之间的因外力作用而引起的附加相互作用力 截面法:(1)欲求构件某一截面上的内力时,可沿该截面把构件切开成两部分,弃去任一部分,保留另一部分研究(2)在保留部分的截面上加上内力,以代替弃去部分对保留部分的作用。
(3)根据平衡条件,列平衡方程,求解截面上和内力。
应力: dA dPA P p A =∆∆=→∆lim 0 正应力、切应力。
变形与应变:线应变、切应变。
杆件变形的基本形式 (1)拉伸或压缩;(2)剪切;(3)扭转;(4)弯曲;静载荷:载荷从零开始平缓地增加到最终值,然后不在变化的载荷动载荷:载荷和速度随时间急剧变化的载荷为动载荷。
失效原因:脆性材料在其强度极限b σ破坏,塑性材料在其屈服极限s σ时失效。
二者统称为极限应力理想情形。
塑性材料、脆性材料的许用应力分别为:[]3n s σσ=,[]bbn σσ=,强度条件:[]σσ≤⎪⎭⎫⎝⎛=maxmax A N ,等截面杆 []σ≤A N max轴向拉伸或压缩时的变形:杆件在轴向方向的伸长为:l l l -=∆1,沿轴线方向的应变和横截面上的应力分别为:l l ∆=ε,AP A N ==σ。
横向应变为:b b b b b -=∆=1'ε,横向应变与轴向应变的关系为:μεε-='。
胡克定律:当应力低于材料的比例极限时,应力与应变成正比,即 εσE =,这就是胡克定律。
E 为弹性模量。
将应力与应变的表达式带入得:EANl l =∆ 静不定:对于杆件的轴力,当未知力数目多于平衡方程的数目,仅利用静力平衡方程无法解出全部未知力。
圆轴扭转时的应力 变形几何关系—圆轴扭转的平面假设dx d φργρ=。
物理关系——胡克定律dxd G G φργτρρ==。
力学关系dA dx d G dx d GdA T AA A⎰⎰⎰===22ρφφρρτρ 圆轴扭转时的应力:tp W T R I T ==max τ; 圆轴扭转的强度条件: ][max ττ≤=tW T,可以进行强度校核、截面设计和确定许可载荷。
圆轴扭转时的变形:⎰⎰==l pl p dx GI T dx GI T ϕ; 等直杆:pGI Tl=ϕ 圆轴扭转时的刚度条件: pGI Tdx d =='ϕϕ,][180max max ϕπϕ'≤⨯='p GI T 弯曲内力与分布载荷q 之间的微分关系)()(x q dx x dQ =;()()x Q dx x dM =;()()()x q dx x dQ dxx M d ==22 Q 、M 图与外力间的关系a )梁在某一段内无载荷作用,剪力图为一水平直线,弯矩图为一斜直线。
b )梁在某一段内作用均匀载荷,剪力图为一斜直线,弯矩图为一抛物线。
c )在梁的某一截面。
()()0==x Q dxx dM ,剪力等于零,弯矩有一最大值或最小值。
d )由集中力作用截面的左侧和右侧,剪力Q 有一突然变化,弯矩图的斜率也发生突然变化形成一个转折点。
梁的正应力和剪应力强度条件[]σσ≤=WM maxmax ,[]ττ≤max 提高弯曲强度的措施:梁的合理受力(降低最大弯矩m ax M ,合理放置支座,合理布置载荷,合理设计截面形状 塑性材料:[][]c t σσ=,上、下对称,抗弯更好,抗扭差。
脆性材料:[][]c t σσ<, 采用T 字型或上下不对称的工字型截面。
等强度梁:截面沿杆长变化,恰使每个截面上的正应力都等于许用应力,这样的变截面梁称为等强度梁。
二向应力状态分析—解析法 (1)任意斜截面上的应力ατασσσσσα2sin 2cos 22xy yx yx --++=;ατασστα2cos 2sin 2xy yx +-=(2)极值应力 正应力:yx xytg σστα--=220,22min max )2(2xy y x yx τσσσσσσ+-±+=⎭⎬⎫ 切应力:xyy x tg τσσα221-=, 22min max )2(xy y x τσσττ+-±=⎭⎬⎫ (3)主应力所在的平面与剪应力极值所在的平面之间的关系α与1α之间的关系为:4,2220101πααπαα+=+=,即:最大和最小剪应力所在的平面与主平面的夹角为45°扭转与弯曲的组合(1)外力向杆件截面形心简化(2)画内力图确定危险截面(3)确定危险点并建立强度条件 按第三强度理论,强度条件为:[]σσσ≤-31 或[]στσ≤+224, 对于圆轴,W W t 2=,其强度条件为:][22σ≤+WT M 。
按第四强度理论,强度条件为:()()()[][]σσσσσσσ≤-+-+-21323222121 ,经化简得出:[]στσ≤+223,对于圆轴,其强度条件为:][75.022σ≤+WT M 。
第一部分 静力学 判断题1、力的三要素是大小、方向、作用线。
( F )2、两个力只能合成唯一的一个力,故一个力也只能分解为唯一的两个力。
( F )3、力偶对其作用面内任意一点之矩恒等于力偶矩,与矩心位置无关。
( T )4、作用于刚体上的力F ,可以平移到刚体上的任一点,但必须同时附加一个力偶。
( T )5、作用力和反作用力必须大小相等、方向相反,且作用在同一直线上和同一物体上。
( F ) 1、物体的形心不一定在物体上。
( T ) 2、作用力与反作用力是一组平衡力系。
( F )mF 3、两个力在同一轴上的投影相等,此两力必相等。
( F ) 4、力系的合力一定比各分力大。
( F ) 5、两个力在同一轴上的投影相等,此两力必相等。
( F ) 1、作用力与反作用力是一组平衡力系。
( F ) 2、作用在任何物体上的力都可以沿其作用线等效滑移 ( F )3、图示平面平衡系统中,若不计定滑轮和细绳的重力,且忽略摩擦,则可以说作用在轮上的矩为m 的力偶与重物的重力F 相平衡。
( F F )4、作用在同一刚体上的两个力,使刚体处于平衡的必要和充分的条件是: 这两个力大小相等、方向相反、作用线沿同一条直线。
( T )5、物体的重心和形心虽然是两个不同的概念,但它们的位置却总是重合 的。
( F )1、如果力F R 是F 1、F 2两力的合力,用矢量方程表示为 F R = F 1 + F 2,则三力大小之间的关系为 D 。
A .必有F R = F 1 + F 2 B .不可能有F R = F 1 + F 2 C .必有F R >F 1,F R >F 2 D .可能有F R <F 1,F R <F 2 第二部分 材料力学部分 判断题1、杆件的基本变形有四种:轴向拉伸或压缩、剪切、挤压和弯曲。
( F )2、当作用于杆件两端的一对外力等值、反向、共线时,则杆件产生轴向拉伸或压缩变形。
( F )3、轴力的大小与杆件的横截面面积有关。
( F )4、拉(压)杆中,横截面上的内力只与杆件所受外力有关。
( T )5、轴力的大小与杆件的材料无关。
( T )1、轴力越大,杆件越容易被拉断,因此轴力的大小可以用来判断杆件的强度。
( F )2、从某材料制成的轴向拉伸试样,测得应力和相应的应变,即可求得其E = σ / ε 。
( F )3、构件抵抗变形的能力称为刚度。
( T )4、轴向拉压杆任意斜截面上只有均匀分布的正应力,而无剪应力。
( F )5、材料的弹性模量E 是一个常量,任何情况下都等于应力和应变的比值( F ) 1、正应变的定义为Eσε= ( F )2、对于拉伸曲线上没有屈服平台的合金塑性材料,工程上规定2.0σ作为名义屈服极限,此时相对应的应变为%2.0=ε ( F )3、在有集中力作用处,梁的剪力图要发生突变,弯矩图的斜率要发生突变。
T4、圆环形截面的W=()34116απ-D ( F )5、在研究一点的应力状态时,正应力为零的平面称为主平面。
( F ) 选择题1、 两根受相同轴向拉力作用的杆件,它们的材料和横截面面积相同,杆 1的长度为杆2的2倍,试比较它们的轴力和轴向变形。
正确结论为:( C )A .两杆的轴力和轴向变形相同B .两杆的轴力相同,杆1的轴向变形比杆2的小C .两杆的轴力相同,杆1的轴向变形比杆2的大D .两杆的变形相同,杆1的轴力比杆2大2、低碳钢的拉伸过程中,( B )阶段的特点是应力几乎不变,而应变却显著增加。
A .弹性 B .屈服 C .强化 D ..颈缩3、二根圆截面拉杆,材料及受力均相同,两杆直径d 1 / d 2 =2 ,若要使二杆轴向伸长量相同,那么它们的长度比 l 1 / l 2 应为( D )。
A . 1B . 2C . 3D . 44、图示圆截面悬臂梁,若其它条件不变,而直径增加一倍,则其最大正应力是原来的( A )倍。
A :81B :8C :2D :215、图示结构,其中AD 杆发生的变形为( C )。
A .弯曲变形B .压缩变形C .弯曲与压缩的组合变形D .弯曲与拉伸的组合变形6、三根试件的尺寸相同,材料不同,其应力应变关系如图所示,( A ) 试件弹性模量最大。
A .(1)B .(2)C .(3)1、平面汇交四个力作出如下图所示力多边形,表示力系平衡的是( A )。
2、截面C 处扭矩的突变值为( B )。
A .A mB .C mC .c A m m +D .)(21c A m m +3、 某点为平面应力状态(如图所示),该点的主应力分别为:( B ) A .MPa 501=σ MPa 02=σ MPa 303=σ B .MPa 501=σ MPa 02=σ MPa 303-=σ C .MPa 501=σ MPa 302=σ MPa 03=σ4、在研究一点的应力状态时,引用主平面的概念,所谓主平面是指( C )。
A .正应力为零的平面 B .剪应力最大的平面C .剪应力为零的平面D .正应力应力均为零的平面5、一直径为d 的实心圆轴,按强度条件计算其受扭转时的容许转力矩为T ,当此轴的横截面面积增加一倍时,其容许扭转力矩将为( B )。
A .2T;B .22TC .4T.D .42T 1、作为脆性材料的极限应力是( D )A. 比例极限 B 弹性极限 C .屈服极限 D .强度极限2、为了保证结构的安全和正常工作,对构件承载能力要求是( D )A .强度要求;B .强度要求和刚度要求;C .刚度要求和稳定性要求;D .强度要求、刚度要求和稳定性要求。
