实验二 控制系统的动态响应及其稳定性分析(优.选)
系统响应及系统稳定性实验报告

系统响应及系统稳定性实验报告系统响应及系统稳定性实验报告引言:系统响应和系统稳定性是控制论中重要的概念。
在工程和科学领域中,我们经常需要对系统的响应和稳定性进行评估和分析,以便设计和优化控制系统。
本实验旨在通过实际测量和数据分析,探讨系统响应和系统稳定性的相关概念。
一、实验背景控制系统是由输入、输出和系统本身组成的。
系统响应是指系统对输入信号的反应。
而系统稳定性则是指系统在长时间运行中是否趋于稳定状态。
了解系统的响应和稳定性对于设计和优化控制系统至关重要。
二、实验目的1. 了解系统响应和系统稳定性的概念和定义。
2. 掌握测量系统响应和稳定性的方法和技巧。
3. 分析实验数据,评估系统的响应和稳定性。
三、实验装置和方法本实验使用了一个简单的电路系统作为示例。
实验装置包括一个信号发生器、一个电路板和一个示波器。
实验步骤如下:1. 将信号发生器连接到电路板的输入端,设置合适的频率和振幅。
2. 将示波器连接到电路板的输出端,用于测量输出信号。
3. 通过改变信号发生器的输入信号,观察并记录系统的响应。
四、实验结果与数据分析在实验中,我们通过改变信号发生器的输入信号频率和振幅,记录了系统的输出信号。
根据实验数据,我们可以绘制出系统的频率响应曲线和幅频特性曲线。
1. 频率响应曲线频率响应曲线是描述系统对不同频率输入信号的响应的曲线。
通过绘制频率响应曲线,我们可以观察到系统对于不同频率信号的增益和相位变化。
从实验数据中绘制的频率响应曲线中,我们可以观察到系统在低频时具有较高的增益,而在高频时增益逐渐降低。
2. 幅频特性曲线幅频特性曲线是描述系统对不同幅度输入信号的响应的曲线。
通过绘制幅频特性曲线,我们可以观察到系统对于不同幅度信号的增益变化。
从实验数据中绘制的幅频特性曲线中,我们可以观察到系统在低幅度信号时具有较高的增益,而在高幅度信号时增益逐渐饱和。
五、系统稳定性分析系统稳定性是指系统在长时间运行中是否趋于稳定状态。
实验2二阶系统的阶跃响应及稳定性分析实验
实验室二二阶系统的阶跃响应及稳定性分析实验一.实验目的1.熟悉二阶模拟系统的组成。
2.研究二阶系统分别工作在等几种状态下的阶跃响应。
3.学习掌握动态性能指标的测试方法,研究典型系统参数对系统动态性能和稳定性的影响。
二,实验内容1.ZY17AutoC12BB自动控制原理实验箱。
2.双踪低频慢扫示波器。
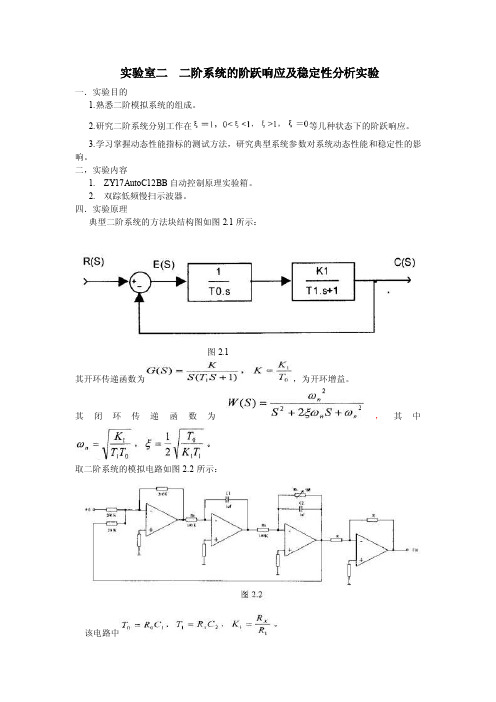
四.实验原理典型二阶系统的方法块结构图如图2.1所示:图2.1其开环传递函数为,为开环增益。
其闭环传递函数为,其中取二阶系统的模拟电路如图2.2所示:该电路中该二阶系统的阶跃响应如图所示:图2.3.1,2.3.2,2.3.3,2.3.4和2.3.5分别对应二阶系统在过阻尼,临界阻尼,欠阻尼,不等幅阻尼振荡(接近于0)和零阻尼(=0)几种状态下的阶跃响应曲线。
改变元件参数Rx大小,可研究不同参数特征下的时域响应。
当Rx为50k时,二阶系统工作在临界阻尼状态;当Rx<50K时,二阶系统工作在过阻尼状态;当Rx>50K时,二阶系统工作在欠阻尼状态;当Rx继续增大时,趋近于零,二阶系统输出表现为不等幅阻尼振荡;当=0时,二阶系统的阻尼为零,输出表现为等幅振荡(因导线均有电阻值,各种损耗总是存在的,实际系统的阻尼比不可能为零)。
五. 实验步骤1.利用实验仪器,按照实验原理设计并连接由一个积分环节和一个惯性环节组成的二阶闭环系统的模拟电路。
此实验可使用运放单元(一),(二),(三),(五)及元器件单元中的可调电阻。
(1)同时按下电源单元中的按键开关S001,S002,再按下S003,调节可调电位器W001,使T006(-12V—+12V)输出电压为+1V,形成单位阶跃信号电路,然后将S001,S002再次按下关闭电源。
(2)按照图2.2连接好电路,按下电路中所用到运放单元的按键开关。
(3)用导线将连接好的模拟电路的输入端于T006相连接,电路的输出端与示波器相连接。
(4)同时按下按键开关S001,S002时,利用示波器观测该二阶系统模拟电路的阶跃特性曲线,并由实验测出响应的超调量和调节时间,将结果记录下来。
控制实验报告二典型系统动态性能和稳定性分析

实验报告2报告名称:典型系统动态性能和稳定性分析一.实验目的K学习和掌出动态性能指标的测试方法.2藥研究典型系统参数对系统功态性能和稳疋H的影响实验内容1>观测二阶系统的阶跃响应.测出其超调试和调节时间,并研究其参数变化对动态性能和稳定性的影响.2.观测三阶系统的阶跃响应•测出其超调量和调节时间.并研究其参数变化对动态性能和稳定性的腦响三善实验过程及分析1.典型二阶系统结构图以及电路连接图如F所示’200*对电路连接图分析可以得到相关参数的农达式:7*o = /?oG: = 0 =矢K = ¥ =岛根据所连接的电路图的九件參数可以得到J (闭坏传递函故为 因此•调整比的用值•能够调节闭环传递函数中的阻尼系数•调节系统性能. 当为过阻尼系统*系统对阶跃响应不超调.响应速度慢•因此仃如卜的实验曲线当时,为临界阻尼系统,系统对阶跃响应恰好不超调.在不发生超调的 情况卜有说快的响应速度,因此有如下的实验曲线。
对比上下两张图片,町以发 现系统故厉的稳态误差都比较明显.应该与实骗仪器的粘密腹有关。
同时我们还 观察了这个系统对斜坡输入的响戒,其特点是输出曲线转折处之后有轻微的上凸 的部分,最后输出十分接近输入。
当0 vfv 1时.为欠IM 尼系统,系统对阶跃超调,响应速復很快.因此有如 下的实验曲线。
w(sr+2z 吠:其中从=5说;? = ^1000001.典型三阶系统结构图以及电路连接图如下所示:20C*"所连接的电路图可以知道其开环传递函数为:其屮.&的单•位为kQ,系统特征方程为S3+12S2+2O S+2O/C=O,根据劳斯判据诃以知道:系统稳定的条件为0<K<12・系统临界稳泄的条件为KJ2. 系统不稳定的条件为K>12,调节也可以调肯K,从而调节系统的性能。
具体实验图像如下:川软件仿真K典熨2阶系统取5-5.程序为:G=tf(5(Mh5Orqrt(2),5O]);step(G)调节时间为5s左右。
【自控原理实验】实验二 典型系统动态性能和稳定性分析

实验二典型系统动态性能和稳定性分析一.实验目的1.学习和掌握动态性能指标的测试方法。
2.研究典型系统参数对系统动态性能和稳定性的影响。
二.实验内容1.观测二阶系统的阶跃响应,测出其超调量和调节时间,并研究其参数变化对动态性能和稳定性的影响。
2.观测三阶系统的阶跃响应,测出其超调量和调节时间,并研究其参数变化对动态性能和稳定性的影响。
三.实验步骤1.熟悉实验箱,利用实验箱上的模拟电路单元,参考本实验附录中的图2.1.1和图2.1.2,设计并连接由一个积分环节和一个惯性环节组成的二阶闭环系统的模拟电路(如用U9、U15、U11和U8连成)。
注意实验接线前必须对运放仔细调零(出厂已调好,无需调节)。
信号输出采用U3单元的O1、信号检测采用U3单元的I1、锁零接U3单元的G1。
2.利用实验设备观测该二阶系统模拟电路的阶跃特性,并测出其超调量和调节时间。
3.改变该二阶系统模拟电路的参数,观测参数对系统动态性能的影响。
4.利用实验箱上的模拟电路单元,参考本实验附录中的图2.2.1和图2.2.2,设计并连接由一个积分环节和两个惯性环节组成的三阶闭环系统的模拟电路(如用U9、U15、U11、U10和U8连成)。
5.利用实验设备观测该三阶系统模拟电路的阶跃特性,并测出其超调量和调节时间。
6.改变该三阶系统模拟电路的参数,观测参数对系统稳定性与动态指标的影响。
7.分析实验结果,完成实验报告。
软件界面上的操作步骤如下:①按通道接线情况:通过上位机界面中“通道选择”选择I1、I2路A/D通道作为被测环节的检测端口,选择D/A通道的O1(“测试信号1”)作为被测对象的信号发生端口.不同的通道,图形显示控件中波形的颜色将不同。
②硬件接线完毕后,检查USB口通讯连线和实验箱电源后,运行上位机软件程序,如果有问题请求指导教师帮助。
③进入实验模式后,先对显示模式进行设置:选择“X-t 模式”;选择“T/DIV ”为1s/1HZ 。
自动控制原理实验二系统的动态性能与稳态研究

自动控制原理实验二系统的动态性能与稳态研究系统的动态性能与稳态是自动控制原理中的重要概念,对于系统的分析和设计具有重要意义。
本实验将通过实际的控制系统,研究动态性能与稳态的相关特性。
实验目的:1.理解系统的动态性能和稳态的概念。
2.通过实验研究不同参数对系统动态性能和稳态的影响。
3.掌握如何调节参数以改善系统的动态性能和稳态。
实验器材:1.控制系统实验装置。
2.控制器。
3.传感器。
4.计算机及相关软件。
实验步骤:1.将控制系统实验装置连接好,包括传感器和执行器。
2.设置基本的控制系统参数,如比例增益、积分时间和微分时间。
3.对系统进行稳态分析,记录输出信号的稳定值。
4.通过改变控制器的参数,观察系统的动态响应特性。
例如,改变比例增益,观察系统的超调量和调节时间的变化。
5.改变积分时间和微分时间,观察系统的超调量和调节时间的变化。
6.对不同参数组合进行实验,总结参数与系统性能之间的关系。
实验结果:通过实验可以得到一些重要的结论:1.比例增益的增大可以减小超调量,但同时也可能引起系统的震荡。
2.积分时间的增大可以减小偏差,但也可能导致系统的不稳定。
3.微分时间的增大可以提高系统的稳定性,但也可能引起系统的震荡。
实验结论:本实验通过实际的控制系统,研究了动态性能和稳态的相关特性。
通过改变控制器的参数,可以调节系统的动态性能和稳态。
在实际应用中,需要根据具体的控制要求,选择合适的参数组合,以达到系统的稳定性和性能要求。
实验结果对于掌握自动控制原理中的动态性能和稳态概念,以及参数调节方法具有重要意义。
实验二 二阶系统的动态特性与稳定性分析

实验二二阶系统的动态特性与稳定性分析自动控制原理实验报告实验名称:班级:姓名:学号:二阶系统的动态特性与稳定性分析一、实验目的1、掌握二阶系统的电路模拟方法及其动态性能指标的测试技术过阻尼、临界阻尼、欠阻尼状态2、分析二阶系统特征参量(ωn,ξ)对系统动态性能的影响;3、分析系统参数变化对系统稳定性的影响,加深理解“线性系统稳定性至于其结构和参数有关,与外作用无关”的性质;4、了解掌握典型三阶系统的稳定状态、临界稳定、不稳定状态;5、学习二阶控制系统及其阶跃响应的Matlab仿真和simulink实现方法。
二、实验内容1、构成各二阶控制系统模拟电路,计算传递函数,明确各参数物理意义。
2、用Matlab和simulink仿真,分析其阶跃响应动态性能,得出性能指标。
3、搭建典型二阶系统,观测各个参数下的阶跃响应曲线,并记录阶跃响应曲线的超调量σ%、峰值时间tp以及调节时间ts,研究其参数变化对典型二阶系统动态性能和稳定性的影响;4、搭建典型三阶系统,观测各个参数下的阶跃响应曲线,并记录阶跃响应曲线的超调量σ%、峰值时间tp以及调节时间ts,研究其参数变化对典型三阶系统动态性能和稳定性的影响;5、将软件仿真结果与模拟电路观测的结果做比较。
三、实验步骤1、二阶系统的模拟电路实现原理将二阶系统:G(s)=可分解为一个比例环节,一个惯性环节和一个积分环节+2ξsωns+ωn2nG(s)=0236(+s+R1R3R6R2R4R5C1R2R4R5C1C2s)3 2n24512==3+s+s2s+2ξωns+ωnR2R4R5C1C2R6C2(s)=Ui(s)2、研究特征参量ξ对二阶系统性能的影响将二阶系统固有频率ωn=12.5保持不变,测试阻尼系数ξ不同时系统的特性,搭建模拟电路,改变电阻R6可改变ξ的值当R6=50K时,二阶系统阻尼系数ξ=0.8当R6=100K时,二阶系统阻尼系数ξ=0.4当R6=200K时,二阶系统阻尼系数ξ=0.2(1)用Matlab软件仿真实现二阶系统的阶跃响应,计算超调量σ%、峰值时间tp以及调节时间ts。
控制系统的稳定性分析实验报告范文

控制系统的稳定性分析实验报告范文下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!控制系统的稳定性分析实验报告1. 引言控制系统的稳定性分析是控制工程领域的重要研究方向之一。
自控实验报告二典型系统的时域响应和稳定性分析

自控实验报告二典型系统的时域响应和稳定性分析实验二典型系统的时域响应和稳定性分析一、实验目的1.研究二阶系统的特征参量(ξ、ωn) 对过渡过程的影响。
2.研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3.熟悉 Routh 判据,用 Routh 判据对三阶系统进行稳定性分析。
二、实验设备PC 机一台,TD-ACC+(或 TD-ACS)教学实验系统一套。
三、实验原理及内容1.典型的二阶系统稳定性分析(1) 结构框图:如图 1.2-1 所示。
(2) 对应的模拟电路图:如图 1.2-2 所示。
(3) 理论分析系统开环传递函数为:G(s)=k1T0S(T1S+1)=K1T0S(T1S+1); 开环增益K=K1T0(4) 实验内容先算出临界阻尼、欠阻尼、过阻尼时电阻 R 的理论值,再将理论值应用于模拟电路中,观察二阶系统的动态性能及稳定性,应与理论分析基本吻合。
在此实验中(图 1.2-2)2.典型的三阶系统稳定性分析(1) 结构框图:如图 1.2-3 所示。
(2) 模拟电路图:如图 1.2-4 所示。
(3) 理论分析系统的开环传函为:G(s)H(s)=500RS(0.1S+1)(0.5S+1)(其中K=500R)系统的特征方程为: 1 +G(s)H(s)=0 S3+12S2+20S+20K=0。
(4) 实验内容实验前由 Routh 判断得 Routh 行列式为:四、实验步骤1.将信号源单元的“ST”端插针与“S”端插针用“短路块”短接。
由于每个运放单元均设臵了锁零场效应管,所以运放具有锁零功能。
将开关设在“方波”档,分别调节调幅和调频电位器,使得“OUT”端输出的方波幅值为 1V,周期为 10s 左右。
2. 典型二阶系统瞬态性能指标的测试(1) 按模拟电路图 1.2-2 接线,将 1 中的方波信号接至输入端,取 R = 10K。
(2) 用示波器观察系统响应曲线 C(t),测量并记录超调 MP、峰值时间 tp 和调节时tS。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 控制系统的动态响应及其稳定性分析
一、实验目的
1. 学习瞬态性能指标的测试技术; 2. 记录不同开环增益时二阶系统的阶跃响应曲线,并测出系统的超调量σ%、峰
值时间t p 和调节时间t s ;
3. 熟悉闭环控制系统的稳定和不稳定现象,并加深理解线性系统的稳定性只与其
结构和参量有关,而与外作用无关的性质。
二、实验仪器
1. MATLAB 软件 三、实验原理
对一个二阶系统加入一个阶跃信号时,系统就有一个输出响应,其响应将随着系统参数变化而变化。
二阶系统的特性由两个参数来描述:一个为系统的阻尼比ξ,一个为系统的无阻尼自然频率ω。
当两个参数变化时,都会引起系统的调节时间、超调量、振荡次数的变化。
在系统其它参数不变时,可通过改变系统增益系数K 来实现ξ、ωn 的变化,二阶系统结构图如图3-1。
图3-1 二阶系统的结构原理图
其闭环传递函数的标准形式为
22
22
112211221)1()()(n
n n s s T T K s T s T T K
K s T s T K s R s C ωξωω++=+
+=++=, 无阻尼自然频率21T T K
n =
ω, 阻尼比1
2
4KT T =ξ, 当ξ=1时,系统为临界阻尼,此时可求出K 为0.625,ω为2.5。
若改变K 值,就可以改变ξ值:当K >0.625时,ξ<1为过阻尼;当K <0.625时,ξ>1为过阻尼。
三阶系统的结构图如图3-2所示。
图3-2 三阶系统的结构原理图
其开环传递函数为
)
1)(1()(213++=
s T s T T K
s G ,
改变惯性时间常数T 2和开环增益K ,可以得到不同的阶跃响应。
若调节K 值大小,可改变系统的稳定性,且用劳斯(Routh )判据验证。
用劳斯判据可以求出:系统临界稳定的开环增益为7.5。
即K <7.5时,系统稳定;K >7.5时,系统不稳定。
四、实验内容
1、观察二阶系统在单位阶跃信号作用下的响应曲线,按)
12.0(5.0)(+=
s s K
s G 的单位
负反馈系统,设计好实验线路,加入单位跃阶(1V )信号,从示波器上观察不同开环增益时系统的响应曲线。
并记录K 分别为10,5,2,1时的四条响应曲线,从响应曲线上求得超调量σ%、调整时间t s 和峰值时间t p 。
2. 选择某个稳定时刻,分别使用速度反馈控制和比例微分控制改善系统性能(比例系数为1,自己选择微分系数及速度反馈系数),记录改善前的单位阶跃输出机改善后的单位阶跃输出波形。
分析改善的原因。
3、观察三阶系统(单位负反馈)在单位阶跃信号作用下的系统响应曲线。
)
1)(1()(213++=
s T s T T K
s G
(1)按K=10,T 1=0.2s ,T 2=0.05s ,T 3=0.5s 设计实验线路,观察并记录单位阶跃响应
曲线,用劳斯判据求出系统临界稳定的开环增益。
(2)按T 1=0.2s ,T 2=0.1s ,T 3=0.5s 设计实验线路,观察并记录K 分别为5、7.5、10
三条响应曲线。
六、实验思考
1. 开环增益K 和惯性环节时间常数对系统的性能有什么影响? 如何观察三阶系统的发散振荡响应曲线?为什么最后出现等幅振荡现象?
答:由于ωn 、ζ由T 和K 值决定,因此它们将影响系统的响应曲线,从而将影响系统的稳定性能。
当K>7.5的时候,三阶系统的响应曲线已经不再是理论发散的振荡响应曲线,而是恒为等幅振荡,这可能是由于放大器本身电源幅值的限制。
实验数据记录如下:
K=10,T 1=0.2s ,T 2=0.05s ,T 3=0.5
K=5,T 1=0.2s ,T 2=0.1s ,T 3=0.5s
K=7.5,T1=0.2s,T2=0.1s,T3=0.5s K=10,T1=0.2s,T2=0.1s,T3=0.5s
K=0.625 ξ=1时,系统为临界阻尼K=1
K=2 K=5
K=10
K=5 微分系数0.05 K=10 微分系数0.05
速度反馈系统
K=5 微分系数0.005 PD反馈
最新文件---------------- 仅供参考--------------------已改成word文本--------------------- 方便更改。
