广东省廉江市实验学校2016-2017学年高二下学期限时检测7数学理试题 精品

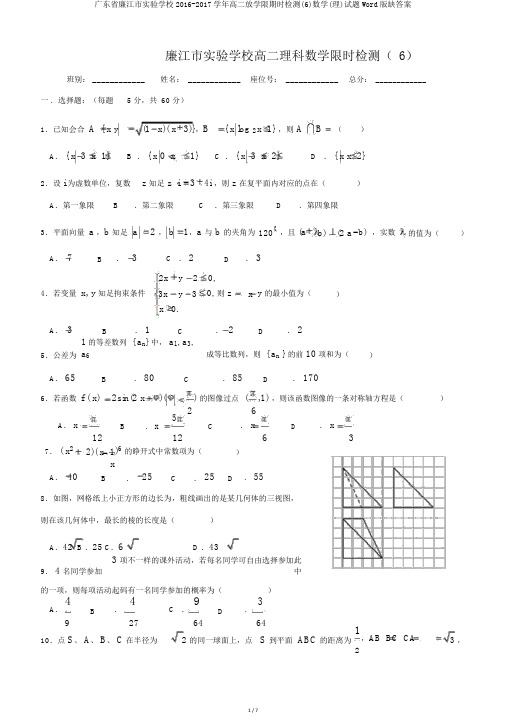
廉江市实验学校高二理科数学限时检测（7）
一、选择题（每小题5分，共40分） 1．若不等式的解集是R ，则m 的范围是( )
A.
B.
C.
D.
2．已知点(,)P a b 与点(1,0)Q 在直线2310x y +-=的两侧，且0, 0a b >>， 则1
a b
-的取值范围是（ ）
A ．(,3)-∞-
B ．1(,0)3-
C ．(3,)+∞
D ．1(0,)3
3．已知
，则
的最小值是( )
A. 4
B. 3
C. 2
D. 1 4．给出如下四个命题：
①若“p 且q ”为假命题，则p 、q 均为假命题；
②命题“若a b >，则221a b >-”的否命题为“若a b ≤，则221a b ≤-”； ③“2,11x x ∀∈+≥R ”的否定是“2,11x x ∃∈+≤R ”； ④在△ABC 中，“A B >”是“sin sin A B >”的充要条件. 其中不正确．．．
的命题的个数是（ ） A ．4 B ．3 C ．2 D ．1
5．已知a ，b ，c ∈R ，命题“若a+b+c=3，则a 2
+b 2
+c 2
≥3”的否命题是（ ） A ．若a+b+c ≠3，则a 2
+b 2
+c 2
＜3 B ．若a+b+c=3，则a 2
+b 2
+c 2
＜3 C ．若a+b+c ≠3，则a 2
+b 2
+c 2
≥3 D ．若a 2
+b 2
+c 2
≥3，则a+b+c=3 6．命题“2
,10x R x ∀∈+>”的否定是( )
(A)2
,10x R x ∀∈+≤ (B)2
,10x R x ∃∈+> (C)2
,10x R x ∀∈+< (D)2
,10x R x ∃∈+≤ 7．已知命题P ：存在(,),cos 122
x x ππ
∈-
≥；命题q ：任意(,0),23x x x ∈-∞<，则下
列命题为真命题的是（ ）
A ．p q ∧
B ．p q ⌝∧
C ．p q ⌝∨
D ．p q ∧⌝
8．已知:α“2=a ”；:β“直线0=-y x 与圆2)(22=-+a y x 相切”．则α是β的（ ）
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既非充分也非必要条件
二、填空题（每小题5分，共20分）
9．把命题“012,02
00<+-∈∃x x R x ”的否定写在横线上__________．
10．已知p:-4＜x-a ＜4，q:(x-2)(3-x)＞0,若⌝p 是⌝q 的充分条件，则实数a 的取值范围是 .
11．已知命题p ：“x R ∃∈，使2
3
208
ax ax +->”，若命题p 是假命题，则实数a 的取值范围为 . 12
．
已
知
命题:p “
[]20,20，x x a ∀∈-≥”，命题
:
q “2
220x R x ax a ∃∈++-=，”，若命题“p 且q ”是真命题，则实数a 的取值范围是 .
三、解答题（本小题满分12分）
13．已知命题]2,1[:∈∀x p ，02≥-a x ，命题R :0∈∃x q ，使得01)1(020<+-+x a x .
若“p 或q 为真”，“p 且q 为假”，求实数a 的取值范围.
参考答案
1．A
【解析】要想应用上面的结论，就得保证是二次的，才有判别式，但二次项系数含有参数m ，所以要讨论m-1是否是0。

（1）当m-1=0时，元不等式化为2>0恒成立，满足题意； （2）
时，只需
，所以，
，选A.
2．A 【解析】
试题分析：由已知，(231)(21301)0,2310a b a b +-⨯+⨯-<+-<，画出可行域，如图所示
.
1
a b
-表示可行域内的点(,)b a 与定点01M(，）连线的斜率，
观察图形可知MA 的斜率最大为10
3103
-=--，故选A .
考点：简单线性规划的应用，直线的斜率计算公式. 3．A 【解析】由，得
，即
，所以
，
由
，
当且仅当，即，取等号，所以最小值为4，选A.
4．C 【解析】
试题分析：①：若p 且q 是假命题，则p ，q 中至少有一个假命题，∴①错误；②：否命题需对原命题的条件和结论都进行否定，∴②正确；③对原命题结论的否定应为12<+x x ，∴③错误；④：显然正确，故不正确的命题个数为2个. 考点：1.命题及其关系；2.充分条件与必要条件. 5．A
【解析】根据四种命题的定义，
命题“若a+b+c=3，则a 2
+b 2
+c 2
≥3”的否命题是 “若a+b+c ≠3，则a 2
+b 2
+c 2＜3” 故选A 6．D 【解析】
试题分析：解：命题“2,10x R x ∀∈+>”的否定是“2,10x R x ∃∈+≤” 故选D.
考点：全称命题与特称命题. 7．D 【解析】
试题分析：cos 01=，故命题P 为真命题，在(,0)x ∈-∞上，2x y =的图象恒在3x
y =的
上方，所以23x x
>成立，命题q 为假命题，所以p q ∧⌝为真命题.
考点：命题的真假判断. 8．A 【解析】
试题分析：若直线0=-y x 与圆2)(2
2
=-+a y x 2.
a ==±因此“2=a ”
是“2a =±”的充分非必要条件，选A. 考点：直线与圆相切 9．012,2
≥+-∈∀x x R x 【解析】
试题分析：命题“012,02
00<+-∈∃x x R x ”的否定为“012,2
≥+-∈∀x x R x ”． 考点：命题的否定． 10．［-1,6］ 【解析】
试题分析：∵⌝p 是⌝q 的充分条件，∴p 是q 的必要条件，又p:a-4＜x ＜a+4，q:2<x<3, ∴
42
43
a a -≤⎧⎨
+≥⎩,∴-1≤a ≤6,即实数a 的取值范围是［-1,6］ 考点：本题考查了简易逻辑的运用
点评：等价变换是判断充分、必要条件的重要手段之一，特别是对于否定的命题，常通过它的等价命题，即逆否命题来考查条件与结论间的充分、必要关系． 11．30a -≤≤
【解析】解：因为命题p ：“x R ∃∈，使2
3
208
ax ax +-
>”，若命题p 是假命题，则说明命题的否定式真命题，那么则2
23
,20308
x R ax ax a a ∀∈+-≤∴∆=+≤，因此实数a 的取值范围为30a -≤≤ 12．{2}a a ≤-
【解析】解：命题:p “[]20,20，x x a ∀∈-≥”，命题:q “2
220x R x ax a ∃∈++-=，”，
若命题“p 且q ”是真命题，则p,q 都是真命题，则由[]，20,200x x a a ∀∈-≥∴≤ 且由
，或222
22044(2)02021
x R x ax a a a a a a a ∃∈++-=⇔--≥⇔+-≥⇔≤-≥
综上可得{2}a a ≤- 13．3>a 或11≤≤-a . 【解析】
试题分析：有条件求出命题p 、q 为真的a 的取值范围，再由p 或q 为真，p 且q 为假， 则p 与q 一真一假，分两种情况求出结论.
试题解析：由条件知，2
x a ≤对]2,1[∈∀x 成立，∴1≤a ；
∵R 0∈∃x ，使得01)1(02
0<+-+x a x 成立.
∴不等式01)1(020<+-+x a x 有解，∴04)1(2>--=∆a ，解得3>a 或1-<a ；
（6分） ∵p 或q 为真，p 且q 为假， ∴p 与q 一真一假． ①p 真q 假时，11≤≤-a ； ②p 假q 真时，3>a .
∴实数a 的取值范围是3>a 或11≤≤-a . （12分） 考点：复合命题的真假，函数的值域、函数的零点和函数的性质及应用.。