北邮信息论201209级期末考题
《信息论》期末考试试题(A卷)标准答案

(1) 每幅画面所含信息量: H log 2 10 信息传输速率:
9.97 105 bit
(2 分)
R 30 H 30 log 2 10300000 29.90 Mbps
(2) AWGN 信道容量:
(1 分)
C W log 2 (1 SNR) 6 106 log 2 (1 1000) 59.80 Mbps
(2+1 分) (3 分)
(3)求为实现电视信号可靠传输信道所需的最小带宽和对应的信号平均功率; (3+2 分) (4)求信息传输速率达到容量时的频谱利用率和对应的 Eb / N 0 (dB ) 。 解 信噪比换算: SNR 10
SNR[ dB ]/10
(3+2 分)
1030/10 1000
的符号熵为 (2/5)H(1/2,1/4,1/4)+ (3/5)H(1/3)=1.151 比特/符号。 4.设试验信道输入与输出符号集均为 {1, 2,3, 4} ,输入概率分别为 1/2,1/4,1/8,1/8,失 真测度为 d(i, j)= (i - j)2 ,1 i, j 4 ; 则 Dmin 0 , Dmax 9/8=1.125 。
3 次扩展信源符号 000 001 010 100 011 101 110 111 平均码长 概 率 0.729 0.081 0.081 0.081 0.009 0.009 0.009 0.001 编 0 100 101 110 11100 11101 11110 11111 0.5327 码
(5 分)
个二元一一对应信道传输,且每秒只传送两个符号; (1) 若要求信息无失真传输,信源能否不进行编码而直接与信道相接? (3 分) (2) 能否采用适当的编码方式然后通过信道进行无失真传输?为什么? (2+3 分) (3) 确定一种编码方式并进行编码,使得传输满足不失真要求;同时请说明信源采用这 种编码后, 编码器输出与信道输入之间应设置何种装置? (10+2 分) 解
北邮信息论期末考试试题标准答案

l 如果对数的底不定,可以不写单位。
9
8
C = C1 = log2 (5 / 3) 比特/自由度 (共 4 分,步骤酌情给分)
信道输入概率分布为
p(x) =
1
− x2
e 18
3 2π
(2 分)
信道输入的熵为
h( X ) =
1 log(2π e ×9) = 2
1 2
log
2
(18π
e)
比特/自由度
(2 分)
注:
l 对数可以化到最简,不必算出结果;
北京邮电大学 2008——2009 学年第 一 学期
《信息论》期末考试试题(B 卷)标准答案
姓名
班级
学号
分数
注:所有答案均写在答题纸上,试卷和答题纸一起上交。
一、判断题(正确打√,错误打×)(共 10 分,每小题 1 分)
(1) 差熵为零的连续信源的输出平均不确定性为零; (2) 在通过一一对应的变换后,连续信源的差熵一定会变化;
=
∫
p( x)[ 1 2
log(2π
e
×
9)]dx
=
1 2
log2 (18π
e)
比特/自由度
(4 分)
(3)
I ( X ;Y ) = h(Y ) − h(Y | X )
C = max h(Y ) − h(Y | X )
Y 为高斯分布时达到容量
C = 1 log(2π e× 25) − 1 log(2π e ×9)
ML 准则确定译码函数,并求信息传输速率和平均译码错误率;
(2+2+2 分)
(4) 如果利用 n 长重复码传送 0、1 符号,求信息传输速率和平均译码错
信息论与编码期末考试题----学生复习

《信息论基础》参考答案一、填空题1、信源编码的主要目的是提高有效性,信道编码的主要目的是提高可靠性。
2、信源的剩余度主要来自两个方面,一是信源符号间的相关性,二是信源符号的统计不均匀性。
3、三进制信源的最小熵为0,最大熵为bit/符号。
4、无失真信源编码的平均码长最小理论极限制为信源熵(或H(S)/logr= H r (S))。
5、当R=C或(信道剩余度为0)时,信源与信道达到匹配.6、根据信道特性是否随时间变化,信道可以分为恒参信道和随参信道。
7、根据是否允许失真,信源编码可分为无失真信源编码和限失真信源编码。
8、若连续信源输出信号的平均功率为,则输出信号幅度的概率密度是高斯分布或正态分布或时,信源具有最大熵,其值为值。
9、在下面空格中选择填入数学符号“”或“"(1)当X和Y相互独立时,H(XY)=H(X)+H(X/Y)=H(Y)+H(X)。
(2)(3)假设信道输入用X表示,信道输出用Y表示.在无噪有损信道中,H(X/Y)〉 0, H(Y/X)=0,I(X;Y)<H(X)。
二、若连续信源输出的幅度被限定在【2,6】区域内,当输出信号的概率密度是均匀分布时,计算该信源的相对熵,并说明该信源的绝对熵为多少.=2bit/自由度该信源的绝对熵为无穷大.三、已知信源(1)用霍夫曼编码法编成二进制变长码;(6分)(2)计算平均码长;(4分)(3)计算编码信息率;(2分)(4)计算编码后信息传输率;(2分)(5)计算编码效率。
(2分)(1)编码结果为:(2)(3)(4)其中,(5)四、某信源输出A、B、C、D、E五种符号,每一个符号独立出现,出现概率分别为1/8、1/8、1/8、1/2、1/8。
如果符号的码元宽度为0。
5。
计算:(1)信息传输速率。
(2)将这些数据通过一个带宽为B=2000kHz的加性白高斯噪声信道传输,噪声的单边功率谱密度为。
试计算正确传输这些数据最少需要的发送功率P。
解:(1)(2)五、一个一阶马尔可夫信源,转移概率为.(1) 画出状态转移图。
《信息论》期末考试试题( 卷)标准答案

。
4) R(D)是满足 D 准则下平均传送每信源符号的所需的最少比特数,它是定义域 上的严格递减函数。
5) AWGN 信道下实现可靠通信的信噪比下界为-1.59dB,此时对应的频谱利用率 为 0。
6)若某离散无记忆信源有 N 个符号,并且每个符号等概出现,对这个信源进行 二元 Huffman 编码,当 N = 2i (i 是正整数)时,每个码字的长度是 i ,平 均码长是 i 。
2 1) 求此马氏源的平稳分布;(4 分) 2) 求此马氏源的熵;(3 分) 3)求平稳马氏源的二次扩展源的所有符号概率;(3 分) 4)对此二次扩展源进行二元 Huffman 编码并求编码后平均码长和编码效率。 (3+2 分)
解:
1) 此马氏源的平稳分布: (π1
π2
π3
) =(1 3
1 3
1 3
)
3 × 1 × (− 1 log 1 − 1 log 1 − 1 log 1) = 1.5比特/信源符号 2) 此马氏源的熵: 3 2 2 4 4 4 4
3)平稳马氏源的二次扩展源的所有符号及概率为: p(x1x2 ) = p(x1 ) p(x2 x1)
1 00: 6
1 11: 6
1 22: 6
编码效率为: l 19
2.(共 10 分)有两枚硬币,第一枚是正常的硬币,它的一面是国徽,另一面是 面值;第二枚是不正常的硬币,它的两面都是面值。现随机地抽取一枚硬币,进 行 2 次抛掷试验,观察硬币朝上的一面,其结果为:面值、面值。
1)求该试验结果与事件“取出的是第一枚硬币”之间的互信息;(4 分)
1) 求该信道的信道容量;(2 分)
2) 当传输速率达到容量时,确定 M 与 n 的关系。(2 分)
信息论与编码期末考试题

信息论与编码期末考试题信息论与编码期末考试题(一)一、判断题.1.当随机变量和相互独立时,条件熵等于信熵.()2.由于构成同一空间的基底不是唯一的,所以不同的基底或生成矩阵有可能生成同一码集.()3.一般情况下,用变长编码得到的平均码长比定长编码大得多.()4.只要信息传输率大于信道容量,总存在一种信道编译码,可以以所要求的任意小的误差概率实现可靠的通信.()5.各码字的长度符合克拉夫特不等式,是唯一可译码存在的充分和必要条件.()6.连续信和离散信的熵都具有非负性.()7.信的消息通过信道传输后的误差或失真越大,信宿收到消息后对信存在的不确定性就越小,获得的信息量就越小.8.汉明码是一种线性分组码.()9.率失真函数的最小值是.()10.必然事件和不可能事件的自信息量都是.()二、填空题 1、码的检、纠错能力取决于 .2、信编码的目的是;信道编码的目的是 .3、把信息组原封不动地搬到码字前位的码就叫做.4、香农信息论中的三大极限定理是、、 .5、设信道的输入与输出随机序列分别为和,则成立的条件..6、对于香农-费诺编码、原始香农-费诺编码和哈夫曼编码,编码方法惟一的是 .7、某二元信,其失真矩阵,则该信的= .三、计算题.1、某信发送端有2种符号,;接收端有3种符号,转移概率矩阵为.(1)计算接收端的平均不确定度;(2)计算由于噪声产生的不确定度;(3)计算信道容量以及最佳入口分布.2、一阶马尔可夫信的状态转移图如右图所示,信的符号集为.(1)求信平稳后的概率分布;(2)求此信的熵;(3)近似地认为此信为无记忆时,符号的概率分布为平稳分布.求近似信的熵并与进行比较.3、设码符号为,信空间为试构造一种三元紧致码.4、设二元线性分组码的生成矩阵为.(1)给出该码的一致校验矩阵,写出所有的陪集首和与之相对应的伴随式;(2)若接收矢量,试计算出其对应的伴随式并按照最小距离译码准则试着对其译码.(二)一、填空题 1、信编码的主要目的是,信道编码的主要目的是。
(整理)信息论期末考试试题1.doc

安徽大学2011—2012学年第1学期 《信息论》考试试卷(AB 合卷)院/系 年级 专业 姓名 学号一、填空题1、接收端收到y 后,获得关于发送的符号是x 的信息量是 。
2、香农信息的定义 。
3、在已知事件z Z ∈的条件下,接收到y 后获得关于事件x 的条件互信息(;|)I x y z 的表达式为 。
4、通信系统模型主要分成五个部分分别为: 。
5、研究信息传输系统的目的就是要找到信息传输过程的共同规律,以提高信息传输的可靠性、有效性、 和 ,使信息传输系统达到最优化。
6、某信源S 共有32个信源符号,其实际熵H ∞=1.4比特/符号,则该信源剩余度为 。
7、信道固定的情况下,平均互信息(;)I X Y 是输入信源概率分布()Px 的 型凸函数。
信源固定的情况下,平均互信息(;)I X Y 是信道传递概率(|)P y x 的 型凸函数。
8、当信源与信道连接时,若信息传输率达到了信道容量,则称此信源与信道达到匹配。
信道剩余度定义为 。
9、已知信源X 的熵H (X )=0.92比特/符号,则该信源的五次无记忆扩展信源X 5的信息熵5()H X = 。
10、将∞H ,6H ,0H ,4H ,1H 从大到小排列为 。
11、根据香农第一定理,对于离散无记忆信源S ,用含r 个字母的码符号集对N 长信源符号序列进行变长编码,总能找到一种无失真的唯一可译码,使每个信源符号所需平均码长满足: 。
12、多项式剩余类环[]())q F x f x 是域的充要条件为 。
13、多项式剩余类环[](1)n q F x x -的任一理想的生成元()g x 与1n x -关系为 。
14、有限域122F 的全部子域为 。
15、国际标准书号(ISBN )由十位数字12345678910a a a a a a a a a a 组成(诸i a ∈11F ,满足:1010(mod11)ii ia=≡∑),其中前九位均为0-9,末位0-10,当末位为10时用X 表示。
信息论与编码期末考试题----学生复习

《信息论基础》参考答案一、填空题1、信源编码的主要目的是提高有效性,信道编码的主要目的是提高可靠性。
2、信源的剩余度主要来自两个方面,一是信源符号间的相关性,二是信源符号的统计不均匀性。
3、三进制信源的最小熵为0,最大熵为bit/符号。
4、无失真信源编码的平均码长最小理论极限制为信源熵(或H(S)/logr= H r (S))。
5、当R=C或(信道剩余度为0)时,信源与信道达到匹配.6、根据信道特性是否随时间变化,信道可以分为恒参信道和随参信道。
7、根据是否允许失真,信源编码可分为无失真信源编码和限失真信源编码。
8、若连续信源输出信号的平均功率为,则输出信号幅度的概率密度是高斯分布或正态分布或时,信源具有最大熵,其值为值。
9、在下面空格中选择填入数学符号“”或“"(1)当X和Y相互独立时,H(XY)=H(X)+H(X/Y)=H(Y)+H(X)。
(2)(3)假设信道输入用X表示,信道输出用Y表示.在无噪有损信道中,H(X/Y)〉 0, H(Y/X)=0,I(X;Y)<H(X)。
二、若连续信源输出的幅度被限定在【2,6】区域内,当输出信号的概率密度是均匀分布时,计算该信源的相对熵,并说明该信源的绝对熵为多少.=2bit/自由度该信源的绝对熵为无穷大.三、已知信源(1)用霍夫曼编码法编成二进制变长码;(6分)(2)计算平均码长;(4分)(3)计算编码信息率;(2分)(4)计算编码后信息传输率;(2分)(5)计算编码效率。
(2分)(1)编码结果为:(2)(3)(4)其中,(5)四、某信源输出A、B、C、D、E五种符号,每一个符号独立出现,出现概率分别为1/8、1/8、1/8、1/2、1/8。
如果符号的码元宽度为0。
5。
计算:(1)信息传输速率。
(2)将这些数据通过一个带宽为B=2000kHz的加性白高斯噪声信道传输,噪声的单边功率谱密度为。
试计算正确传输这些数据最少需要的发送功率P。
解:(1)(2)五、一个一阶马尔可夫信源,转移概率为.(1) 画出状态转移图。
北邮(信息工程)数据库系统概论期末习题及答案
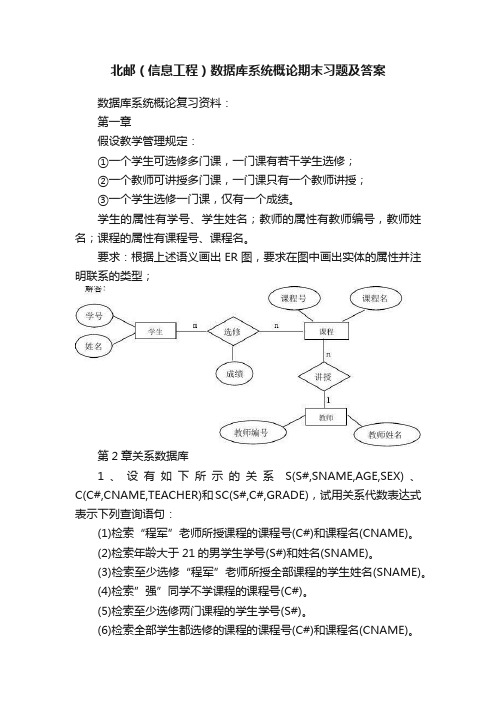
北邮(信息工程)数据库系统概论期末习题及答案数据库系统概论复习资料:第一章假设教学管理规定:①一个学生可选修多门课,一门课有若干学生选修;②一个教师可讲授多门课,一门课只有一个教师讲授;③一个学生选修一门课,仅有一个成绩。
学生的属性有学号、学生姓名;教师的属性有教师编号,教师姓名;课程的属性有课程号、课程名。
要求:根据上述语义画出ER图,要求在图中画出实体的属性并注明联系的类型;第2章关系数据库1、设有如下所示的关系S(S#,SNAME,AGE,SEX)、C(C#,CNAME,TEACHER)和SC(S#,C#,GRADE),试用关系代数表达式表示下列查询语句:(1)检索“程军”老师所授课程的课程号(C#)和课程名(CNAME)。
(2)检索年龄大于21的男学生学号(S#)和姓名(SNAME)。
(3)检索至少选修“程军”老师所授全部课程的学生姓名(SNAME)。
(4)检索”强”同学不学课程的课程号(C#)。
(5)检索至少选修两门课程的学生学号(S#)。
(6)检索全部学生都选修的课程的课程号(C#)和课程名(CNAME)。
(7)检索选修课程包含“程军”老师所授课程之一的学生学号(S#)。
(8)检索选修课程号为k1和k5的学生学号(S#)。
(9)检索选修全部课程的学生姓名(SNAME)。
(10)检索选修课程包含学号为2的学生所修课程的学生学号(S#)。
(11)检索选修课程名为“C语言”的学生学号(S#)和姓名(SNAME)。
解:本题各个查询语句对应的关系代数表达式表示如下:(1). ∏C#,CNAME(σTEACHER=‘程军’(C))(2). ∏S#,SNAME(σAGE>21∧SEX=”男”(C)) (3). ∏SNAME{s[∏S#,C#(sc )÷∏C#(σTEACHER=‘程军’(C))]}(4). ∏C#(C)- ∏C#(σSNAME=‘强’(S) SC) (5). ∏S#(σ[1]=[4]∧[2]≠[5] (SC × SC))(6). ∏C#,CNAME(C (∏S#,C#(sc)÷∏S#(S)))(7). ∏S#(SC∏C#(σTEACHER=‘程军’(C)))(8). ∏S#,C#(sc )÷∏C#(σC#=’k1’∨ C#=’k5’(C)) (9). ∏SNAME{s[∏S#,C#(sc )÷∏C#(C)]}(10). ∏S#,C#(sc )÷∏C#(σS#=’2’(SC))(11). ∏S#,SNAME{s[∏S#(SCσCNAME=‘C 语言’(C))]}2、关系R 和S 如下图所示,试计算R ÷S 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1/10 1/10
0
0 0 1 0 1 1 0.2 0.2 0 0.4 1 0.6 1.0
1
1/10
2
1/10 1/10
3 5
0 0 1 0.2 1 0 1 1 0.15 0.35
1/10 1/10
7 9
1/20
4
(6 分)
采用最佳策略的判平均每次提问的次数为 Huffman 编码的平均码长为 0.25+0.2+0.2+0.2+0.15+0.4+0.35+0.6+1=3.35,所以平均最少需要问 3.35 个问题才能知道车 主的车尾号。(4 分)
C2 {1, 010, 011, 000}, C3 {0, 01, 001, 000}, C4 {1, 00, 010, 010} ,其中 属于唯一可译码, 属于最优码。
属于非奇异码,
1
答案: ( C1 , C2 , C3 , C1 , C2 , C1 ) (3)某信源输出符号集为{A、B、C、D、E},每一个符号独立出现,出现概率分别为 1/8、 1/8、 1/8、 1/2、 1/8, 该信源熵为 此时,信息传输速率为 比特/符号。 如果编码以后符号的码元宽度为 0.5μs, bps。将这些数据通过一个带宽为 B=2MHz 的加性高斯白
pa1
pa2
pa3
1 pa pa3 pa4 1 / 2 1 2 pa2 1 / 2
(4分)
六、计算题(15 分)
有三个箱子,第一个箱子中有 3 个黑球 1 个白球,第二个箱子中有 2 个黑球 3 个白球, 第三个箱子中有 3 个黑球 2 个白球。现随机取出一个箱子,再从这个箱子中任取一球。 1)如果取出的是白球,求这一结果与事件“取出的球是第一个箱子”之间的互信息。 (4 分) 2)利用最佳判决准则确定取出白球和黑球的箱子分别会是哪一只? 3)如果重复做取球实验并对所取箱子的序号进行最佳判决,求平均错误率。 4)如果球总是从第一个箱子中取出,求利用最佳判决准则的错误率。 解:设 x=1,2,3 分别表示事件“取出的球是第 x 个箱子”, y=0 表示“取出的球为白球”,y=1 表示“取出的球为黑球”,则 p(xy) X 1 2 3 0 1/12 1/5 2/15 P(y=0)=5/12 Y 1 1/4 2/15 1/5 P(y=1)=7/12 (4 分) (3 分) (4 分)
姓名
班级
学号
分数
注:所有答案均写在答题纸上,试卷和答题纸一起上交。
一、判断题(正确打√,错误打×) (共 10 分,每小题 1 分)
(1)离散信源 X 的 N 次扩展源的熵是信源 X 熵的 N 倍。 (2)熵、联合熵、条件熵及平均互信息的取值均不小于零。 (3)对于有限状态马氏链,平稳分布恒存在且唯一。 (4)连续信源输出的消息经过一一对应变换后,信源熵一定会发生变化。 ( ( ( ( ) ) ) )
H (X ) ; I (U ;V ) 。
H (X |Y)
H ( X | YV ) ;I ( X ;V | Y )
=, , )
H (Y ) ;I ( X ; Y )
(从符号集{ , ,>,<,,= }中选择) 答案:(= ,
( 2 ) 设 信 源 符 号 集 为 {a, b, c, d } , 分 别 进 行 了 4 种 分 组 编 码 , C1 {1,01,001, 000},
2
问题,并只能用是、否来回答。求此人平均至少需要问几个问题才能知道车主的尾号是多 少?(注:写出计算过程。 ) 解: 尾号分布概率 尾号 概率 p 0 1/10 1 1/10 2 1/10 3 1/10 4 1/20 5 1/10 6 1/8 7 1/10 8 1/8 9 1/10
对其进行二元 Huffman 编码,如下图所示:
(5)并联信道每次传输能够使用所有子信道,而和信道每次传输只能使用一个子信道。 ( )
(6) 由有噪信道编码定理可知, 码率接近信道容量且译码差错任意小的信道编码是存在 的。 (7)对于二元无记忆对称信道,最小汉明距离译码准则是最佳译码准则。 (8)唯一可译码一定满足 Kraft 不等式。 ( ( ( ) ) ) )
(9) 一个 AWGN 信道, 1MHz 带宽的信道容量是 2MHz 带宽的信道容量的 2 倍。 (
(10)对于给定的输入分布,必存在一种最差的信道,此信道的干扰最大,而输出端获 得的信息量最小。 答案(×√ ××√,√×√×√) ( )
二、填空题(共 20 分,每空 2 分)
( 1 ) 设 离 散 符 号 集 U , X , Y , V 构 成 马 氏 链 , 则 H (2 X )
2
(2 分) (3 分)
由 0 D 1, 可知, 1 D 0.9 因此,
0.1 D 1
所以最小失真为 0.1 。
四、计算题 (10 分)
汽车尾号为 0~9 之间的整数,先对汽车尾号进行调查,假设调查结果是:尾号为 4 的 概率为 1/20,尾号为 6 和 8 的各占 1/8,其他情况所占概率相同。现在要求某人向一车主提
3)
(4 分)
E 3 进行等能量分配,每个子信道分配到的能量为 E1 E2 E3 1 ,此时:
1 15 1 1 1 1 1 1 C log 1 log 1 log 1 log 2 4 1 2 2 2 4 2 =0.9534比特 /3个自由度=0.3178比特 /自由度 同样条件下,最佳能量分配得到的容量:
C X Y log 2C1 2C2 log 20 20.1887 1.0974 比特/符号。
达到容量时,两个子信道的使用概率分别为:
(2分)
1 2C C
1
X Y
20.1887 1.0974 0.5327, 2 2C2 C X Y 20 1.0974 0.4673
五、计算题(20 分)
两信道 CH1 和 CH2 级联构成级联信道,其中 CH1 的输入 X 与输出 Y 的符号集分别为
3
A {a1 , a2 , a3 , a4 } 和 B {b1 , b2 , b3 } ,转移概率矩阵如图(左)所示;CH2 的输出 Z 与输入 Y
的转移概率如图(右)所示: 1) 2) 求 CH1 的信道容量和达到容量时的输入概率分布; 求级联信道的容量和达到容量时的输入概率分布。 (6 分+4 分) (6 分+4 分)
a , b 两个子信道分配到的能量大于 0,但是 c 子信道分配到的能量等于 0,依据注水原
理知道 2 B 4 ,所以 1 E 5 。
(4 分)
7
E 1 E 1 C log 1 1 log 1 2 2 1 2 2 B 1 1 log B log 2 2 2 1 log B log 2 2 3 [log( E 3) log 2]比特/3个自由度 2 1 1 [ log( E 3) log 2]比特/自由度 3 2
5
(2分)
q1 =q2 =1 / 2, C X Z 1 H (5 / 12) 0.0201 比特/符号。
(2分)
达到容量时的输入概率分布满足:
7 / 12 5 / 12 pa4 7 / 12 7 / 12 5 / 12 7 / 12 1 2 5 / 12 5 / 12
a1
3 4 1 4
b1
a2
1 43 4b2来自a31b3
1
a4
CH1的容量可以利用和信道公式计算。
4
子信道1为二元对称信道,容量为 C1 1 H (1 / 4) 0.1887 比特/符号; (2分) 子信道2为离散无噪信道,容量为 C2 log 2 1 0 。 根据和信道容量的公式: (2分)
(4 分)
1 125 4 1 3 1 1 1 C log 1 log 1 log 1 log 1.9829比特/3个自由度 2 1 2 2 2 4 2 8 (4 分) 0.6610比特 /自由度 2)
E1 1 B E 3 E2 2 B B 2 E E E. 2 1
3)在发送端不了解信道信息的情况下,只能进行等能量分配。求 E 3 时等能量分配得到 的信道容量,并与 2)中的容量进行比较。 解: 1)
E1 1 B E2 2 B E3 4 B E1 E2 E3 8.
(2 分+2 分)
解得: E1 4, E2 3, E3 1, B 5
噪声信道传输,噪声的单边带功率谱密度为 N 0 10 6 W / Hz ,若要保证信息正确传输,发送 功率 P 至少为 答案: (2, 4 106 , 6) W。
三、简答题(5 分)
已知一等概离散二元信源,每秒发出 1 个符号,经过信道容量为 0.81 bit/s 的信道传输, 其信息率失真函数为: R ( D ) 1 D (0 D 1)
pa1 0.5327/2=0.26635,
输入概率分布为: pa2 0.5327/2=0.26635,
pa3 pa4 0.4673
(4分)
2) CH2 的转移概率矩阵为:
c1 c2 b1 2 / 3 1 / 3 b2 1/ 3 2 / 3 7 / 12 5 / 12 b3
级联信道的概率转移矩阵为二者的乘积,为:
c1 a1 7 / 12 a2 5 / 12 a3 7 / 12 a4 7 / 12
c2
5 / 12 7 / 12 5 / 12 5 / 12 (2分)
