第九章多元线性回归异方差问题
多元线性回归(共线性 异方差 自相关)

多元线性回归
南开大学商学院 周宝源
w1xi1 + w2 xi 2 + ... + wk xik = 0
a Collinearity Diagnostics
Model 1
Dimension Eigenvalue 1 2.930 2 6.971E-02 3 1.060E-04
Condition Index 1.000 6.483 166.245
Variance Proportions (Constant) X1 X2 .01 .00 .00 .98 .00 .00 .00 1.00 1.00
(二)原因
1、经济变量的惯性 、 2、模型设定偏琦:省略解释变量的影响 、模型设定偏琦: 3、模型设定偏琦:错误的函数形式的影响 、模型设定偏琦: 4、滞后效应 、 5、其他原因 、
二、自相关主要后果
很可能高估R 很可能高估 2。 t-检验与 检验结果都变得无效。 检验与F-检验结果都变得无效 检验与 检验结果都变得无效。 其他
a. Predictors: (Constant), X b. Dependent Variable: Y
结
束
例:变量X、Y的部分 变量 、 的部分 数据如右表所示。 数据如右表所示。 下面运用图示法进行 分析模型是否存在严 重的异方差现象。 重的异方差现象。
从Analyze → Regression → Linear 打开 Linear 线性回归主对话框 将自变量与因变量分别选入相应框中。 点击“Plot”按钮,在新打开的对话框中将 将“DEPENDNT”选入“X”框中,将“*ZRESID” “*ZRESID”选入“Y”框中. 点击“Continue” 点击“OK”
第九章 REG-多元线性回归

多重共线性的处理方法
• • • • 剔除不重要的自变量; 增大样本容量; 把横截面数据与时间序列数据结合起来使用; 当样本资料来自时间序列时,可以对回归模型进 行差分,然后拟合差分后的模型; • 岭回归方法; • 主成分回归。
岭回归 自变量间存在多重共线性时
X 0,因此给 X 加上一个 k I(k 0), 那么 X X X k I接近奇异的程度会降低 X
K=0.02对应的岭回归方程为: import=-8.9277+0.057gdp+0.59542save+0.127consume 且三个变量的VIF都小于10,多重共线性不明显。
• • • • •
proc reg data=imports outest=result1 outvif; model import=gdp save consume/pcomit=1; run; proc print data=result1; 主成分回归 run;
2 ˆ ˆ 从而使 的方差阵 D ( ) (X )1对角线上的元素很大, X ˆ 也 var( ) 很大 i
多重共线性的判断
(1)方差膨胀因子VIF:
1 VIFj 1 R2 j
其中R 2为第j个自变量对模型中其余自变量进行线性回 j 归所得到的拟合优度。
一般来说,VIFj 10,表明自变量间存在高度共线性。
outest=result:要求把岭回归估计值输出到数据集result中 Outvif: 要求把岭回归估计的VIF输出到数据集result中 ridge=0.0 to 0.1 by 0.01 0.2 0.3 0.4 0.5;指定一组岭迹参数 Plot/ridgeplot; 要求绘制岭迹图
多元线性回归模型的异方差问题的浅析

多元线性回归模型的异方差问题的浅析作者:尚云艳祝师强孙浩来源:《科技风》2022年第15期摘要:“应用回归分析”课程是高校应用统计学专业均开设的专业核心课程,多元线性回归模型是非常重要的知识内容,但是由于其理论内容复杂,学生学习难度大,针对此问题,本文从权的概念出发,利用权倒数的性质论证了加权线性回归的合理性。
并以北京市15个经济开发区的销售收入数据为例,运用加权最小二乘估计方法改进模型,最后从残差图和拟合值绝对误差(率)两个方面进行比较,结果均表明加权线性回归效果好。
该方法应用于教学,为教学内容的设计提供了新的思路,便于学生掌握并深入学习。
关键词:异方差;加权最小二乘估计;残差分析;权文献标识码:A回归分析的发展经历了很长的一段历史,早在18世纪,F.Galton提出利用最小二乘原理进行回归分析[1],从那时开始,回归分析就越来越备受关注,但是随着回归分析的普及,在实际应用中往往出现违背线性回归假设的情况,比如,随机误差异方差、随机误差存在序列相关性、数据观测值异常等问题[2]。
特别是对随机误差异方差的情况,加权线性回归是对普通线性回归的一种改进,但是文献[3-4]中并未证明加权线性回归的合理性。
回归诊断是回归分析中必不可少的内容,由于回归假设都是针对随机误差项提出的,所以要从分析随机误差项ε的估计量(残差)入手,通过从残差和残差图分析来考察模型的合理性[5]。
本文主要讨论在随机误差异方差的情况下,怎样建立合理、合适的模型。
根据以往的经验,处理随机误差异方差问题的方法有加权最小二乘法(WLS)、BOX-COX变换法和方差稳定性变换法,这些方法应用于实际,可以消除或者减弱异方差对拟合模型造成的不良影响。
教科书上仅对加权线性回归的原理有所介绍,但是并没有涉及其本质内容。
本文通过权、权函数、权倒数的性质揭示了加权线性回归的本质,论证了其合理性。
以北京市经济开发区的销售收入数据为例,利用加权最小二乘法建立数学模型,并且进行比较分析,模拟结果表明加权线性回归比普通线性回归有一定的改进之处。
计量经济学多元线性回归多重共线性异方差实验报告

计量经济学实验报告多元线性回归、多重共线性、异方差实验报告一、研究目的和要求:随着经济的发展,人们生活水平的提高,旅游业已经成为中国社会新的经济增长点。
旅游产业是一个关联性很强的综合产业,一次完整的旅游活动包括吃、住、行、游、购、娱六大要素,旅游产业的发展可以直接或者间接推动第三产业、第二产业和第一产业的发展。
尤其是假日旅游,有力刺激了居民消费而拉动内需。
2012年,我国全年国内旅游人数达到亿人次,同比增长%,国内旅游收入万亿元,同比增长%。
旅游业的发展不仅对增加就业和扩大内需起到重要的推动作用,优化产业结构,而且可以增加国家外汇收入,促进国际收支平衡,加强国家、地区间的文化交流。
为了研究影响旅游景区收入增长的主要原因,分析旅游收入增长规律,需要建立计量经济模型。
影响旅游业发展的因素很多,但据分析主要因素可能有国内和国际两个方面,因此在进行旅游景区收入分析模型设定时,引入城镇居民可支配收入和旅游外汇收入为解释变量。
旅游业很大程度上受其产业本身的发展水平和从业人数影响,固定资产和从业人数体现了旅游产业发展规模的内在影响因素,因此引入旅游景区固定资产和旅游业从业人数作为解释变量。
因此选取我国31个省市地区的旅游业相关数据进行定量分析我国旅游业发展的影响因素。
二、模型设定根据以上的分析,建立以下模型Y=β0+β1X1+β2X2+β3X3+β4X4+Ut参数说明:Y ——旅游景区营业收入/万元X1——旅游业从业人员/人X2——旅游景区固定资产/万元X3——旅游外汇收入/万美元X4——城镇居民可支配收入/元收集到的数据如下(见表):表 2011年全国旅游景区营业收入及相关数据(按地区分)数据来源:1.中国统计年鉴2012,2.中国旅游年鉴2012。
三、参数估计利用做多元线性回归分析步骤如下:1、创建工作文件双击图标,进入其主页。
在主菜单中依次点击“File\New\Workfile”,出现对话框“Workfile Range”。
多元线性回归模型检验

多元线性回归模型检验引言多元线性回归是一种常用的统计分析方法,用于研究两个或多个自变量对目标变量的影响。
在应用多元线性回归前,我们需要确保所建立的模型符合一定的假设,并进行模型检验,以保证结果的可靠性和准确性。
本文将介绍多元线性回归模型的几个常见检验方法,并通过实例进行说明。
一、多元线性回归模型多元线性回归模型的一般形式可以表示为:$$Y = \\beta_0 + \\beta_1X_1 + \\beta_2X_2 + \\ldots + \\beta_pX_p +\\varepsilon$$其中,Y为目标变量,$X_1,X_2,\\ldots,X_p$为自变量,$\\beta_0,\\beta_1,\\beta_2,\\ldots,\\beta_p$为模型的回归系数,$\\varepsilon$为误差项。
多元线性回归模型的目标是通过调整回归系数,使得模型预测值和实际观测值之间的误差最小化。
二、多元线性回归模型检验在进行多元线性回归分析时,我们需要对所建立的模型进行检验,以验证假设是否成立。
常用的多元线性回归模型检验方法包括:1. 假设检验多元线性回归模型的假设包括:线性关系假设、误差项独立同分布假设、误差项方差齐性假设和误差项正态分布假设。
我们可以通过假设检验来验证这些假设的成立情况。
•线性关系假设检验:通过F检验或t检验对回归系数的显著性进行检验,以确定自变量与目标变量之间是否存在线性关系。
•误差项独立同分布假设检验:通过Durbin-Watson检验、Ljung-Box 检验等统计检验,判断误差项是否具有自相关性。
•误差项方差齐性假设检验:通过Cochrane-Orcutt检验、White检验等统计检验,判断误差项的方差是否齐性。
•误差项正态分布假设检验:通过残差的正态概率图和Shapiro-Wilk 检验等方法,检验误差项是否满足正态分布假设。
2. 多重共线性检验多重共线性是指在多元线性回归模型中,自变量之间存在高度相关性的情况。
计量经济学讲义——线性回归模型的异方差问题1

Gleiser检验与Park检验存在同样的弱点。
(9.3) (9.4) (9.5)
9.4 异方差的诊断-方法4:怀特(White)检验法
Yi = B1 + B 2 X 2 i + B3 X 3 i + u i
2、做如下辅助回归: (9.6) (9.7)
1、首先用普通最小二乘法估计方程(9.6),获得残差ei
E(Y|X)=α+β*X Y
+u +u -u -u -u +u
0
同方差(homoscedasticity)
X 0
E(Y|X)=α+β*X
异方差(heteroscedasticity)
X
一元线性回归分析-回归的假定条件
假定5 无自相关假定,即两个误差项之间不相关。 Cov(ui,uj) = 0。
ui
9.2 异方差的性质
例9.1 美国创新研究:销售对研究与开发的影响 ^ R&D = 266.2575 + 0.030878*Sales se=(1002.963) (0.008347) t =(0.265471) (3.699508) p =(0.7940) R2 = 0.461032 从回归结果可以看出: (1)随着销售额的增加,R&D也逐渐增加,即销售 额每增加一百万美元,研发相应的增加3.1 万美元。 (2)随着销售额的增加,R&D支出围绕样本回归线 的波动也逐渐变大,表现出异方差性。 (0.0019)
《多元线性回归》PPT课件

ˆ 0.7226 0.0003 15674 103 .172 1 ˆ β ˆ 0 . 0003 1 . 35 E 07 39648400 0 . 7770 2
x11 x x 1n x k1 x kn
假设6:回归模型是正确设定的
§3.2
多元线性回归模型的参数估计
一、普通最小二乘估计 二、参数估计量的性质 三、样本容量问题
参数估计的任务和方法
1、估计目标:回归系数βj、随机误差项方差б2 2、估计方法:OLS、ML或者MM * OLS:普通最小二乘估计 * ML:最大似然估计
E(X(Y Xβ )0
矩条件
*矩条件和矩估计量*
1、 E(X(Y Xβ ) 0 称为原总体回归方程的一组矩条件,表明了
原总体回归方程所具有的内在特征。
2、如果随机抽出原总体的一个样本,估计出的样本回归方程:
ˆ 能够近似代表总体回归方程的话,则应成立: ˆ X Y
1 ˆ)0 X (Y Xβ n
第三章
多元线性回归模型
§ 3.1 多元线性回归模型
§ 3.2 多元线性回归模型的参数估计 § 3.3 多元线性回归模型的统计检验 § 3.4 多元线性回归模型的预测 § 3.5 可线性化的多元非线性回归模型 § 3.6 受约束回归
§3.1
多元线性回归模型
一、模型形式 二、基本假定
一、模型形式
Yi 0 1 X 1i 2 X 2 i ... k X ki i 0 j X ji i
#参数估计的实例
例3.2.1:在例2.1.1的家庭收入-消费支出例中,
第9章多元线性回归习题答案
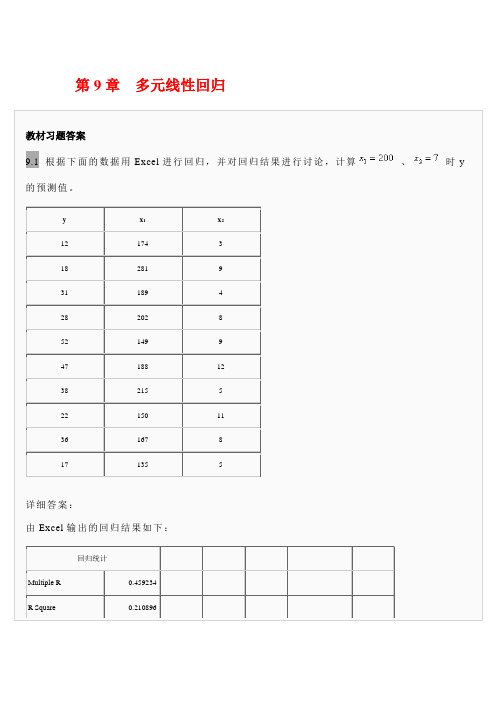
第9章多元线性回归教材习题答案9.1 根据下面的数据用Excel进行回归,并对回归结果进行讨论,计算、时y 的预测值。
y x1x212 174 318 281 931 189 428 202 852 149 947 188 1238 215 522 150 1136 167 817 135 5详细答案:由Excel输出的回归结果如下:回归统计Multiple R 0.459234R Square 0.210896Adjusted R Square -0.01456标准误差13.34122观测值10方差分析df SS MS F Significance F回归分析 2 332.9837 166.4919 0.93541 0.436485残差7 1245.916 177.988总计9 1578.9Coefficients 标准误差t Stat P-value Lower 95% Upper 95%Intercept 25.0287 22.27863 1.12344 0.298298 -27.6519 77.70928X Variable 1 -0.04971 0.105992 -0.46904 0.653301 -0.30035 0.200918X Variable 2 1.928169 1.47216 1.309755 0.231624 -1.55294 5.409276得到的回证方程为:。
表示,在不变的条件下,每变化一个单位,y平均下降0.04971个单位;表示,在不变的条件下,每变化一个单位,y平均增加1.928169个单位。
判定系数,表示在因变量y的变差中能够被y与和之间的线性关系所解释的比例为21.09%。
由于这一比例很低,表明回归方程的拟合程度很差。
估计标准误差,预测误差也较大。
方差分析表显示,Significance F=0.436485>a=0.05,表明y与和之间的线性关系不显著。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22
(一)加权最小二乘法
OLS是加权最小二乘法的特例 显然,当满足同方差假定时, w1 = w2 = = wn = 1/ = 常数 即权数相等且等于常数,加权最小二乘法,就是OLS法。
23
纠正异方差性的一个可行程序
(1)将y对x1, x2,…xk做回归并得到残差u; (2)将残差进行平方,然后再取自然对数而得到log(u2); (3)做log(u2)对x1, x2,…xk的回归并得到拟合值g; (4)求拟合值的指数:h=exp(g) (5)以1/h为权数用WLS来估计方程。 在(3)中做log(u2)对 y, y2 的回归本质上是完全一样的
2000
0
-2000
-4000
-6000
-8000
5
10
15
20
25
30
RESID
38
2 1
2 2
Ω Varε Eεε
2 n
2
两变量线性回归模型的异方差
Y
0
Xi
X
Xj
3
1、异方差的定义
异方差主要出现在截面数据分析中,例如大公司的利 润变化幅度要比小公司的利润变化幅度大,即大公司利润 的方差比小公司利润的方差大。这取决于公司的规模、产 业特点和研究开发支出多少等因素。又如高收入家庭通常 比低收入家庭对某些商品的支出有更大的方差。 例6-1:人均家庭支出(cum)和可支配收入(in)的关系模型
Var(ui)=σ2 * xi 其中σ2为常数,这时可以令权序列
wi 1/ xi
(2)误差方差与xi2成比例 Var(ui)=σ2 * xi2
其中σ2为常数,这时可以令权序列 wi 1/ xi
19
(一)加权最小二乘法
方差已知的情形 实例:住房支出模型
给出由四组家庭住房支出和年收入组成的截面数据, 建立住房支出模型,并检验和修正异方差。
根据图形中的分布选择
l 1,1或 1 2
2、再检验零假设 =0(不存在异方差)。如果零假设
被拒绝,则表明可能存在异方差。
10
(四)怀特检验
假设有如下模型:
yi B0 B1x1i B2 x2i ui (3)
基本步骤: 1、首先用OLS方法估计回归方程(3)式。 2、然后作辅助回归:
16
(一)加权最小二乘法
方差已知的情形
假设已知随机误差项的方差为var(ui)= i2 , 设权数wi与异 方差的变异趋势相反, wi =1/i,, 将原模型两端同乘以wi。
wi使异方差经受了“压缩”和“扩张”变为同方差。
17
(一)加权最小二乘法
方差已知的情形
对于一元线性回归模型y=b0+b1x+u,加权最小化残差平方
price 0 1lotsize 2sqrft 3bdrms
发现:采用水平模型存在异方差性,但采用对数模型不 存在异方差性。
14
三、异方差的解决方法
加权最小二乘法 模型的重新设定
15
(一)加权最小二乘法
基本思路:赋予残差的每个观测值不同权数,从而 使模型的随机误差项具有同方差性。
X
32
异方差:残差随收入增大而增大
2000
1000
0
-1000
-2000
5
10
15
20
25
30
RESID
33
4、异方差模型的估计
加权最小二乘法 在分析收入对储蓄的影响的时候,权数变量可以
选取 hi=inci
于是基本模型savi=a0+a1 inci+ei变为
savi / inci a0 (1/ inci ) a1 inci
i
1 Var
r 0 r x1 i r 0 r1xi
i
2r0
r0
r1xi
r1xi
2
21
(一)加权最小二乘法
(4)用随机误差项的近似估计量求权重序列 首先利用OLS估计原模型得到残差序列 ui ,然后利
用残差序列的绝对值的倒数序列作为加权序列, 即令
wi 1/ ui
给出中国1998年各地区城镇居民平均每人全年家庭交 通及通讯支出(cum)和可支配收入(in)的数据,估计两者 之间的关系模型
4
2、异方差的影响
1、OLS估计量不再是BLUE,其是无偏和一致的,但并 非有效的,即不再具有方差最小性。
2、检验假设的统计量不再成立,建立在t分布和F分布之 上的置信区间和假设检验不可靠。
3、利用原始模型中的解释变量作形如上式(2)的回归,记
下这个回归的R平方Ru22 。
4、检验零假设是
H0 :1 2 k 0
对方程(2)进行F检验,或计算LM统计量进行检验。
LM
Hale Waihona Puke nR2 u2
~
2 k
9
(三)戈里瑟检验
1、通常拟合
e
和
X
之间的回归模型:
j
e
X
l j
24
实例: 采用Wooldridge中的数据Smoke.Raw中的数据来估计一 个对日香烟消费量的需求函数。 基本回归模型如下: cigs=a0+a1log(income)+a2log(cigpric)+a3educ +a4age+a5age2+a6restaurn 其中cigs为每天吸烟的数量; income为年收入; cigpric 为每包香烟的价格(以美分为单位);educ为受教育年 数;age为年龄;restaurn为一个二值变量(若此人居住 的州禁止在餐馆吸烟,则取值1,否则取值0)。
12
等价的White检验
(1)用OLS估计模型(3),得到残差和拟合值,计算它 们的平方;
(2)做回归
u2 0 1 y 2 y2 v
记下这个回归的R平方
(3)构造F或LM统计量并计算p值(前者为 F2,n-3分布,
后者用
2 2
分布。
13
(五) 实例
使用Wooldridge中的数据HPRICE.RAW中的数据 来检验一个简单的住房价格方程中的异方差性。水平 变量模型为(分别采用水平变量和其对数项分别进行 回归分析)
5
二、异方差的发现和判断
(一)残差的图形检验 (二)帕克检验(Park test) (三)戈里瑟检验(Glejser test) (四)怀特检验(White test)
6
(一)残差的图形检验
这是一种最直观的方法,它以某一变量(通常取因变 量)作为横坐标,以随机项的估计量e或e2为纵坐标, 根据作出的散点图直观地判断是否存在相关性。如果 存在相关性,则存在异方差。通常的方法是先产生残 差序列,再把它和因变量一起绘制散点图。 例6-2:利用该方法绘制上一章关于美国机动车消费量 的模型中QMG与残差的散点图。
600 400 200
0 -200 -400 -600
0
10000 20000 30000 40000 X
30
3、异方差检验 图示法检验: 残差平方与自变量呈比较典型的喇叭型
31
250000
200000
150000
RESID2
100000
50000
0
0
10000 20000 30000 40000
34
同质性
权数序列名 Proce=>Equation=>Option=>选定异方差、给出权数名==>OK
35
加权最小二乘法估计结果
36
加权最小二乘法残差与X的散点图
RESID
600 400 200
0 -200 -400 -600
0
10000 20000 30000 40000 X
37
WLS处理后的残差图
第九章 多元线性回归的异方差问题
一、异方差及其影响 二、异方差的发现和判断 三、异方差的解决方法
1
一、异方差及其影响
1、异方差的定义:
对于多元线性回归模型,如果随机扰动项的方差并非是
不变的常数,则称为存在异方差(heteroscedasticity)。
异方差可以表示为
Var
i
2 i
。或
和为
2
wi2
2
i
wi2
yi b0b1xi
获得的估计量就是加权最小二乘估计量。对于多元线性回
归模型y=Xβ+u,令权数序列wi =1/i ,W为N×N对角矩 阵,对角线上为wi ,其他元素为0。则变换后的模型为
Wy WX Wu
18
(一)加权最小二乘法
方差已知的情形 (1)误差方差与xi成比例
(3)其他的与自变量xi的加权形式f(xi)
f xi r0 r1xi
20
(一)加权最小二乘法
方差已知的情形
Var(
)
i
2 i
2
r
0
r
x1 i
y i
b0
b1xi
r0 r1xi r0 r1xi r0 r1xi
i
r0 r1xi
Var
7
(二)Breusch-Pagan检验
假设回归模型如下:
Y 0 1x1 2 x2 k xk u
